2. 南京理工大学 能源与动力工程学院,江苏 南京 210094;
3. 泰州市金海运船用设备有限责任公司,江苏 泰州 225324
2. College of Energy and Power, Nanjing University of Science and Technology, Nanjing 210094, China;
3. Taizhou City Jinhaiyun Vessel Facility Co., Ltd., Taizhou 225324, China
涵道螺旋桨[1]广泛应用于航空领域,同时在空气动力型船舶领域也有应用,如地效翼船、空气动力艇和气垫船等类型船舶上均可搭载涵道螺旋桨。涵道螺旋桨整体结构中,螺旋桨旋转产生推力,同时涵道产生附加推力,这是由于在涵道唇口处存在低压区,这种低压区的产生源于螺旋桨产生的吸流在唇口处形成绕流。由于涵道结构的存在,改变了涵道内的滑流场,间接导致桨尖损失降低,从而整个涵道螺旋桨结构的气动效率也得以提高。涵道螺旋桨的优势在于气动效率更高的同时兼顾安全。
国内大量学者使用各种网格方法对涵道螺旋桨气动特性进行了大量数值计算方法研究,许和勇等[2]在涵道螺旋桨和孤立螺旋桨的非定常数值方面分别进行了模拟,采用非结构动态网格嵌套方法,仿真结果和实验结果基本一致,进一步进行数值计算证实涵道壁面的存在能够有效抑制桨尖涡流的产生,从而减少螺旋桨桨尖的损失,使得桨尖区域的绕流特性得到改善。徐嘉等[3]对不同结构参数的涵道模型进行了数值模拟研究,研究涵道结构参数对涵道升力特性的影响,其仿真模型采用自适应笛卡尔网格以及Jameson有限体积法。程钰锋等[4]基于滑移网格方法数值研究涵道螺旋桨与孤立螺旋桨的非定常旋转流场特性,通过对比分析,得出以下涵道螺旋桨气动效率提高的相关机理:1)滑流区域内的环向诱导速度由于涵道的存在而减小,因此滑流区域的静压损失也减小;2)滑流速度的减小导致滑流损失相应减小,虽然推力同步减小,但由于涵道产生的附加推力要远大于这部分损失的推力;3)涵道的存在使得桨尖绕流特性发生改变,桨尖分离涡和叶素表明分离涡的消除增大了桨尖部位的叶素升阻比。
邓阳平等[5]使用滑移网格技术进行数值模拟并结合地面试验,对比分析不同近地高度下的涵道螺旋桨拉力和功率特性,揭示了地面效应对涵道螺旋桨气动特性的影响机理,地面的存在引起气流阻滞产生高压区以及向上的反弹气流,导致涵道螺旋桨整体拉力减小,系统所需功率增加。闫文辉等[6]对共轴对转螺旋桨的非定常气动干扰方面进行数值模拟,采用基于非定常雷诺平均Navier-Stokes(URANS)方程的数值模拟方法,同时结合了滑移网格技术,其研究成果包括共轴对转螺旋桨的气动特性及变化规律以及优化气动特性的相关建议。王红波等[7]基于结构/非结构混合网格并结合滑移网格技术对NASA涵道螺旋桨进行非定常数值模拟与分析,该CFD方法的时均计算结果与实验值的误差控制在5.3%以内,证明了该计算方法的可行性。芦志明[8]通过对悬停状态的孤立螺旋桨与涵道螺旋桨以及嵌入式涵道螺旋桨的气动特性今昔分析,得出嵌入式涵道螺旋桨相比于涵道螺旋桨所具有的优势。Qin等[9]研究了桨叶与导管间隙对泵喷推进器的影响,基于常用的导管螺旋桨模型(Ka4-70螺旋桨在19A导管中),采用SST k-ω湍流模型,验证了计算模型的可靠性。
相比于涵道螺旋桨广泛应用于航空领域,涵道螺旋桨在船舶领域的应用研究较少。因此,本文以某型在研应急救援气垫船的船用涵道螺旋桨为背景,该型气垫船对涵道螺旋桨推力要求为在额定转速n=5500 r/min时,怠速时静推力不低于500 N,航速为20 kn时推力不低于300 N,对去掉涵道后的孤立螺旋桨和涵道螺旋桨的气动特性进行数值模拟对比研究和分析,判断涵道螺旋桨和孤立螺旋桨推力性能是否满足该型气垫船的设计要求,分析了涵道螺旋桨的气动机理,对该型气垫船的研制与开发提供数据支撑和理论指导。
1 数值计算模型 1.1 控制方程控制方程包括连续性方程和动量守恒方程,由于不考虑流体的压缩性,将流体视为不可压缩流体,因此其控制方程为:
| $ \frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_y}}}{{\partial y}} + \frac{{\partial {v_z}}}{{\partial z}} = 0 ,$ | (1) |
| $ \begin{split} & \frac{{\partial (\rho u)}}{{\partial t}} + {\rm{div}}(\rho uu) = {\rm{div}}(\mu {\rm{grad}}u) - \frac{{\partial p}}{{\partial x}} + {F_x},\\ & \frac{{\partial (\rho v)}}{{\partial t}} + {\rm{div}}(\rho vu) = {\rm{div}}(\mu {\rm{grad}}v) - \frac{{\partial p}}{{\partial y}} + {F_y},\\ & \frac{{\partial (\rho w)}}{{\partial t}} + {\rm{div}}(\rho wu) = {\rm{div}}(\mu {\rm{grad}}w) - \frac{{\partial p}}{{\partial z}} + {F_z} 。\end{split} $ | (2) |
式中:
本文采用的湍流模型为SST模型(Shear Stress Transport Model)。SST模型的优点有:1)在近壁面的边界层区域使用k-ω模型,充分发挥k-ω模型在近壁面湍流耗散小、收敛性好的优势;2)在远场区域使用
湍动能方程
| $ \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{{{\Gamma }}_k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k} ,$ | (3) |
耗散率方程
| $ \begin{gathered} \frac{\partial }{{\partial t}}(\rho \omega ) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \\ \frac{\partial }{{\partial {x_j}}}\left( {{{{\Gamma }}_\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega } 。\\ \end{gathered} $ | (4) |
式中:
滑移网格(Sliding Mesh)是基于动参考系坐标模型(Multiple Reference Frames Method)和混合平面法(Mixing Plane Method)发展起来的。滑移网格方法区别于常规网格方法的内容在于,前者方法中的体单元形状和网格点的距离一直不变的同时,网格节点只有刚体运动。滑移网格方法在计算域的划分上,是通过部件的旋转和静止来划分相关定义区域的,即旋转的部件被旋转域包围,静止的部件被静止域包围,两者之间的连接通过不重叠的2个面即交界面(Interface)实现。因此,计算域之间需通过构造插值点,以插值的方式进行流场信息传递,从而实现区域之间的耦合计算。滑移网格方法中采取了非定常计算方法,这与多参考坐标系方法的准定常计算方法也存在一定差异。后者所设置的旋转域在计算时是在非惯性旋转坐标系下求解,也就是其设置的旋转域实际上静止,而前者设置的旋转域和交界面两侧的信息实际上是实时随着时间而改变。
2 数值方法验证及结果分析 2.1 数值验证模型美国兰利研究中心的Kalman J. Grunwald和Kenneth W. Goodson于1962年对垂直起降飞行器动力系统进行了风洞试验研究,试验工况为进速v=30 m/s,桨叶固定转速n=8000 r/min。
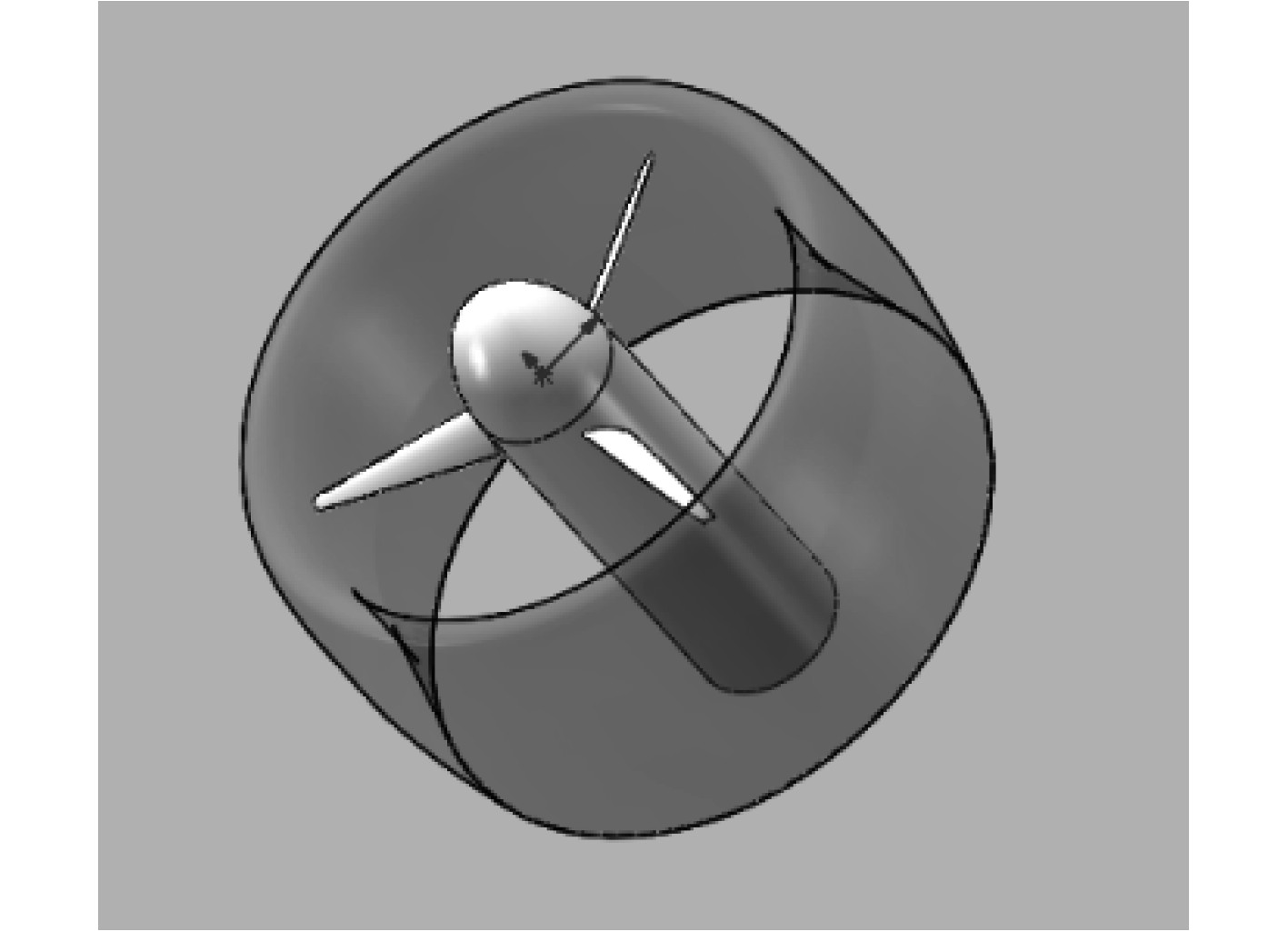
本文中使用的验证模型为该风洞试验所用模型,以此来验证CFD计算方法的结果可信度,涵道螺旋桨的几何参数见表1,几何模型如图1所示,涵道翼型见文献 [10 − 11]。
|
|
表 1 NASA涵道螺旋桨主要参数 Tab.1 Main parameters of NASA ducted propeller |
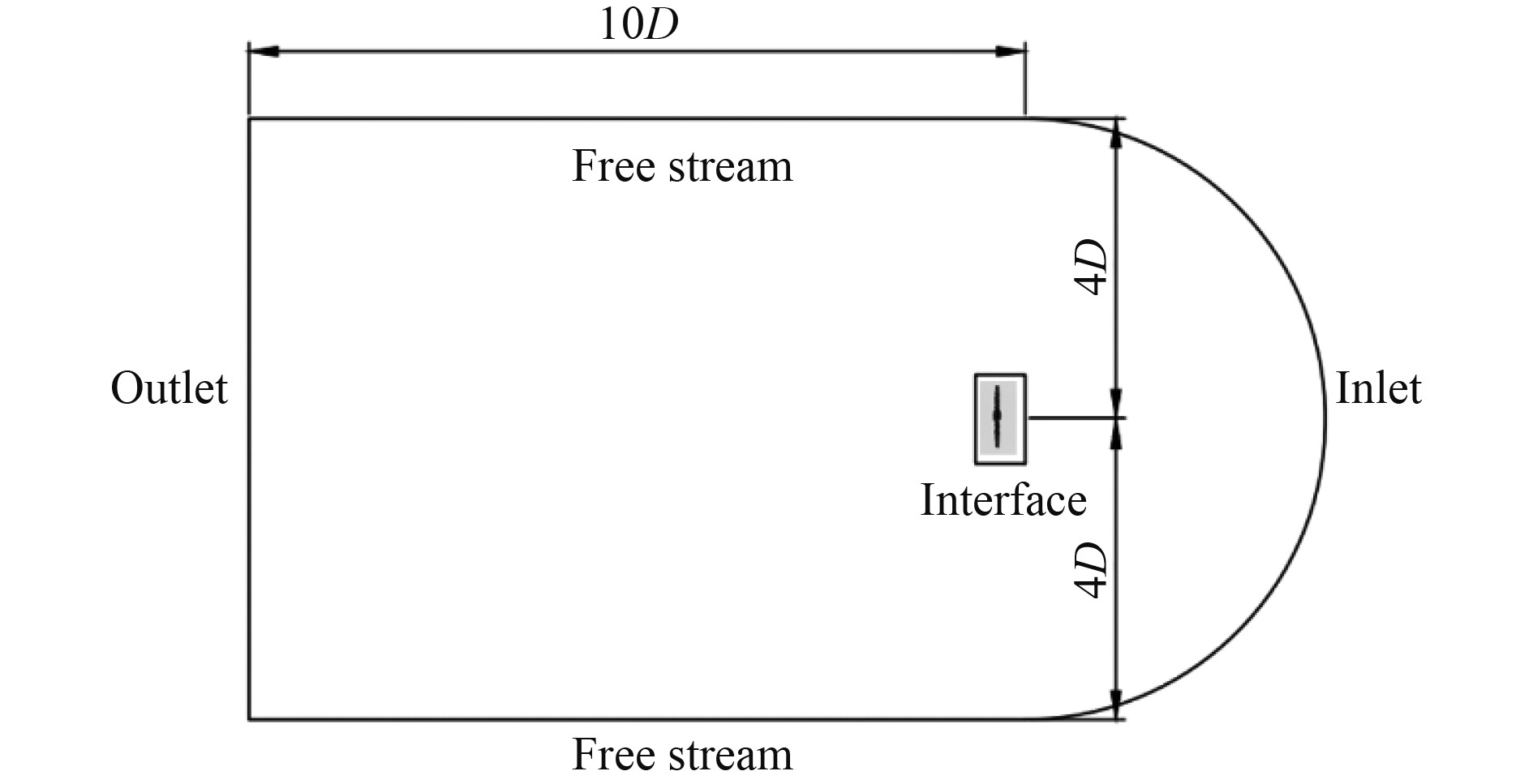
本文数值模拟主要是对涵道螺旋桨在0°迎角下的气动特性计算,因此采用半球体与圆柱体构成的组合体计算域,计算域大小及边界条件设置如图2所示。
|
图 1 NASA 涵道螺旋桨几何模型 Fig. 1 Geometric model of NASA ducted propeller |
|
图 2 计算域和边界条件 Fig. 2 Compute domains and boundary conditions |
本文采用滑移网格模拟螺旋桨的真实旋转,将三维空间计算域划分为旋转区域和静止区域,其中旋转区域通过包围螺旋桨桨叶,并以相同的角速度绕旋转轴进行旋转实现螺旋桨转动,旋转域和静止域之间通过构建交界面来实现各流场信息的交换。
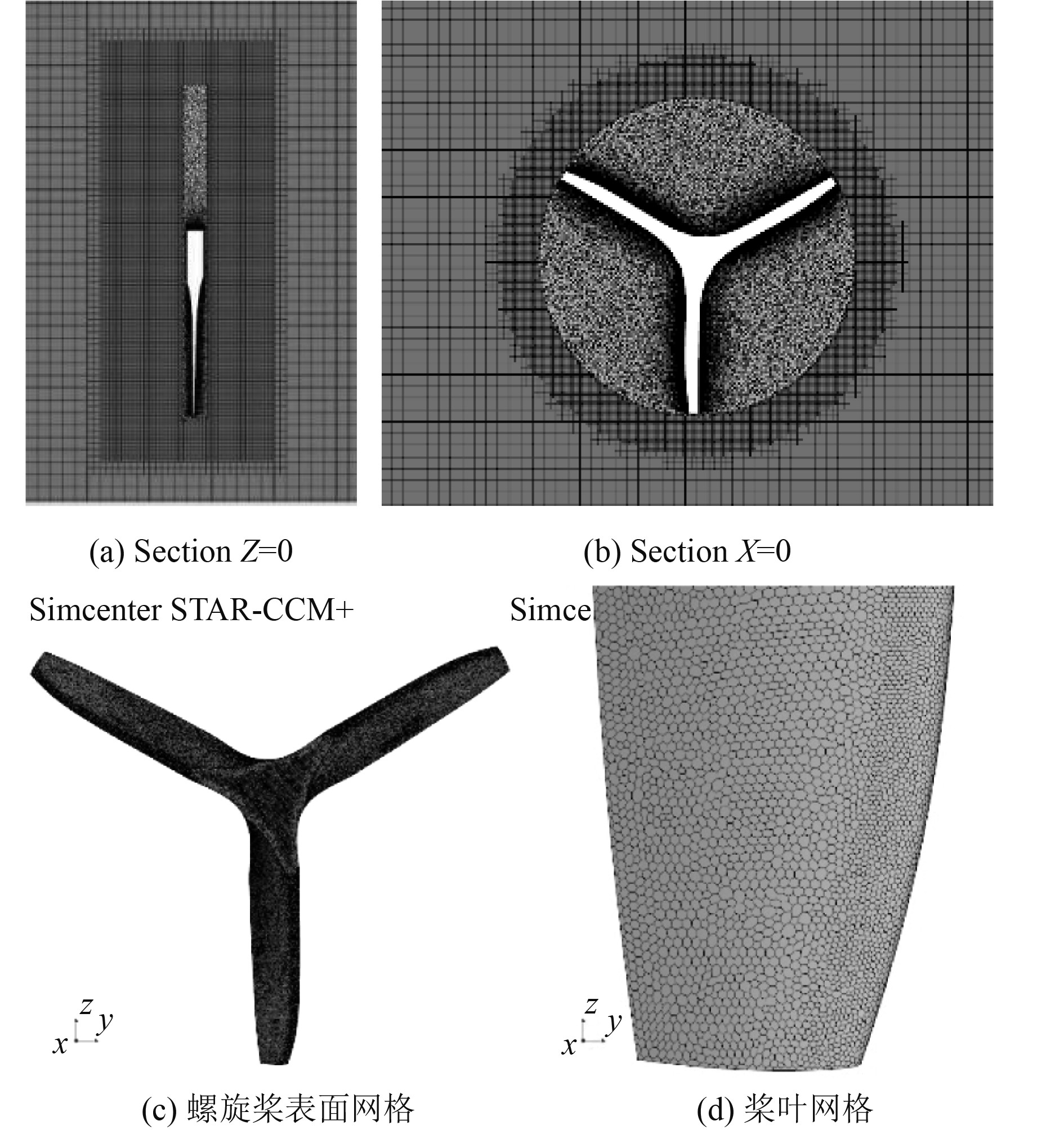
为了能够精准地捕捉涵道螺旋桨周围的流场形态,同时有效节省计算资源,本文主要采用非结构化网格与结构化网格构成的混合网格,对旋转区域采用较密的多面体网格(Polyhedral Mesh)以此来精确描述高速旋转下的桨叶外形,静止区域采用较疏的结构化网格(Trimmed Mesh)以此来减少网格计算量。涵道螺旋桨表面网格和剖面网格划分情况如图3所示。

|
图 3 NASA涵道螺旋桨网格划分 Fig. 3 Grid partitioning of NASA ducted propeller |
由于桨叶表面以及桨叶附近区域的网格数量对螺旋桨的计算结果产生影响,因此需进行网格不确定度分析研究网格数量对螺旋桨气动性能计算的影响。本文设计3套不同疏密程度的网格方案,即MA(2.39 × 107),MB(4.97 × 107)和MC(1.156 × 108)。本文所采用网格划分均以螺旋桨直径D为基本参数,边界层数为5,3套网格划分的具体参数如表2所示。
|
|
表 2 网格设置参数 Tab.2 Grid parameter Setting |
数值计算设置条件与上述风洞试验工况相同,即进速v=30 m/s,桨叶固定转速n=8 000 r/min。表3给出了涵道螺旋桨在轴流下桨叶和涵道推力的计算值与实验值的对比,可看出,3种不同网格方案的数值计算结果与实验值误差均在8%以内,证明了基于多面体与切割体混合网格的滑移网格求解方法能够准确解算涵道螺旋桨的复杂流动问题。
|
|
表 3 NASA涵道螺旋桨模型计算值和实验值对比 Tab.3 The comparison between the calculated results and the measured values of NASA ducted propeller model |
从计算结果可知,随着网格数量的增加,推力系数、扭矩系数和涵道拉力系数与试验结果的差别逐渐缩小,网格收敛性得到验证。综合考虑计算资源和精度需求,将MB方案视为最优计算方案,因此后续计算中均采用MB方案进行网格划分。
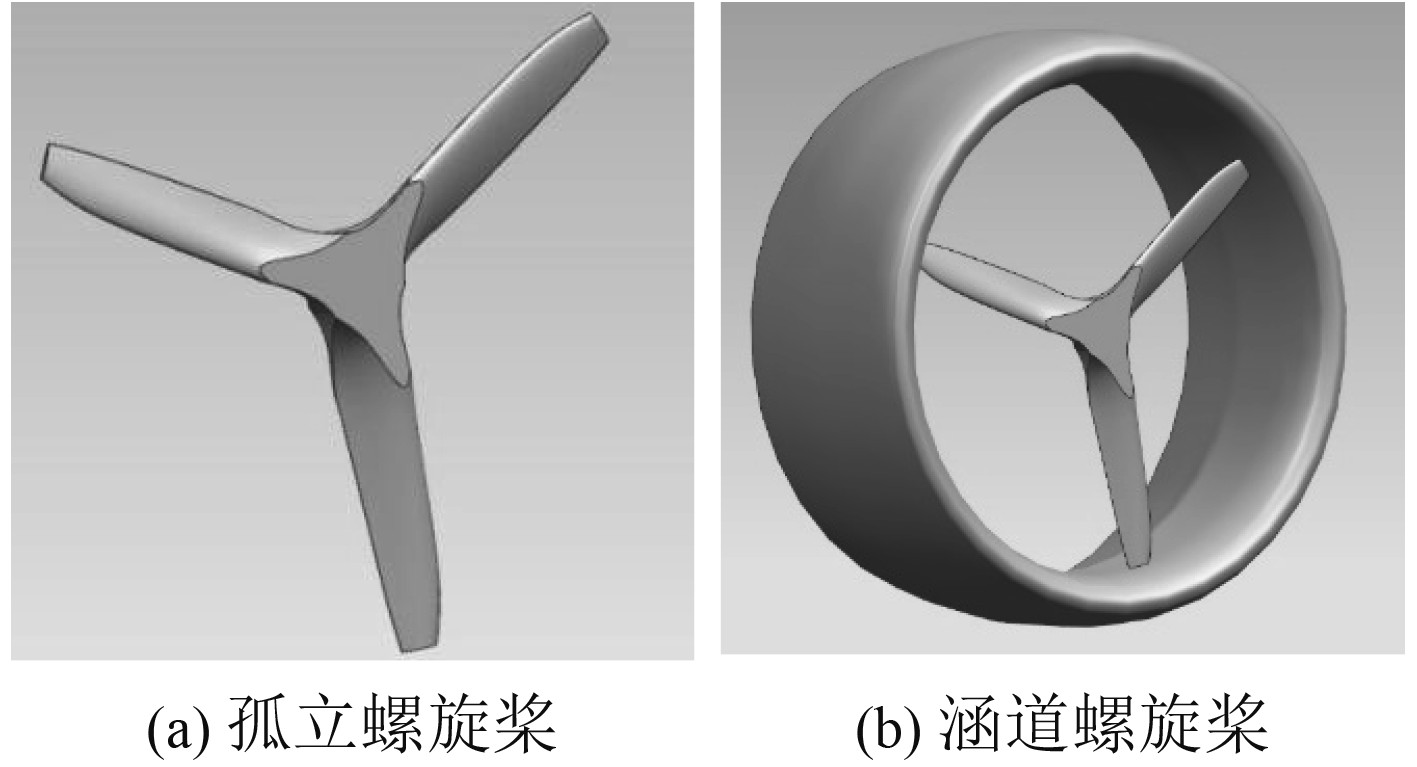
3 船用涵道螺旋桨计算模型 3.1 涵道螺旋桨和孤立螺旋桨模型为对比孤立螺旋桨与涵道螺旋桨的气动特性,孤立螺旋桨即为涵道螺旋桨去掉涵道之后的螺旋桨。本文数值计算所用的去掉涵道后的孤立螺旋桨和三叶涵道螺旋桨的三维模型如图4所示,主要参数见表4和表5。
|
图 4 孤立螺旋桨和涵道螺旋桨几何模型 Fig. 4 Geometric model of ducted propeller |
|
|
表 4 涵道螺旋桨主要尺寸参数 Tab.4 Main dimension parameters of ducted propeller |
|
|
表 5 涵道结构参数 Tab.5 Ducted culvert structure parameters |
孤立螺旋桨和涵道螺旋桨的网格划分情况与上述验证模型中方法一致,相关网格划分参数参考上述MB方案,其表面网格和剖面网格划分情况分别如图5和图6所示。
|
图 5 孤立螺旋桨网格划分 Fig. 5 Grid partitioning of open propeller |

|
图 6 涵道螺旋桨网格划分 Fig. 6 Grid partitioning of ducted propeller |
使用本文的计算方法对怠速时孤立螺旋桨和涵道螺旋桨在不同转速下的气动特性进行了计算,得出各参数随转速的变化曲线。通过比较孤立螺旋桨与涵道螺旋桨流场之间的差别,分析了涵道螺旋桨的气动机理。对不同航速状态下的涵道螺旋桨也进行了气动特性数值模拟,分析了该型涵道螺旋桨在不同航行速度状态下的推力性能。
4.1 气动特性分析为了确认该型孤立螺旋桨推力性能是否能够满足该型气垫船设计要求,对该三叶螺旋桨的静推力进行实验,如将三叶螺旋桨固定在实验台架上,并测试孤立螺旋桨的静推力随转速变化情况。实验测得该型孤立螺旋桨在额定转速n=5500 r/min时的静推力为470 N,不能满足该型气垫船设计要求。
孤立螺旋桨的数值模拟采用上述网格划分及仿真模型,计算条件与实验工况保持一致,桨叶固定转速n=3000~5500 r/min,将孤立螺旋桨的数值模拟结果与实验数据进行对比,具体结果见表6。可见模拟结果与实验数据吻合良好,说明该计算方法对该型螺旋桨的气动特性模拟效果较好。
|
|
表 6 孤立螺旋桨推力系数计算值与实验值对比 Tab.6 Thrust coefficient comparison of open propeller between simulation and experiment |
图7~图9为在不同转速下,孤立螺旋桨和涵道螺旋桨的推力系数、功率系数及工作效率的变化情况。
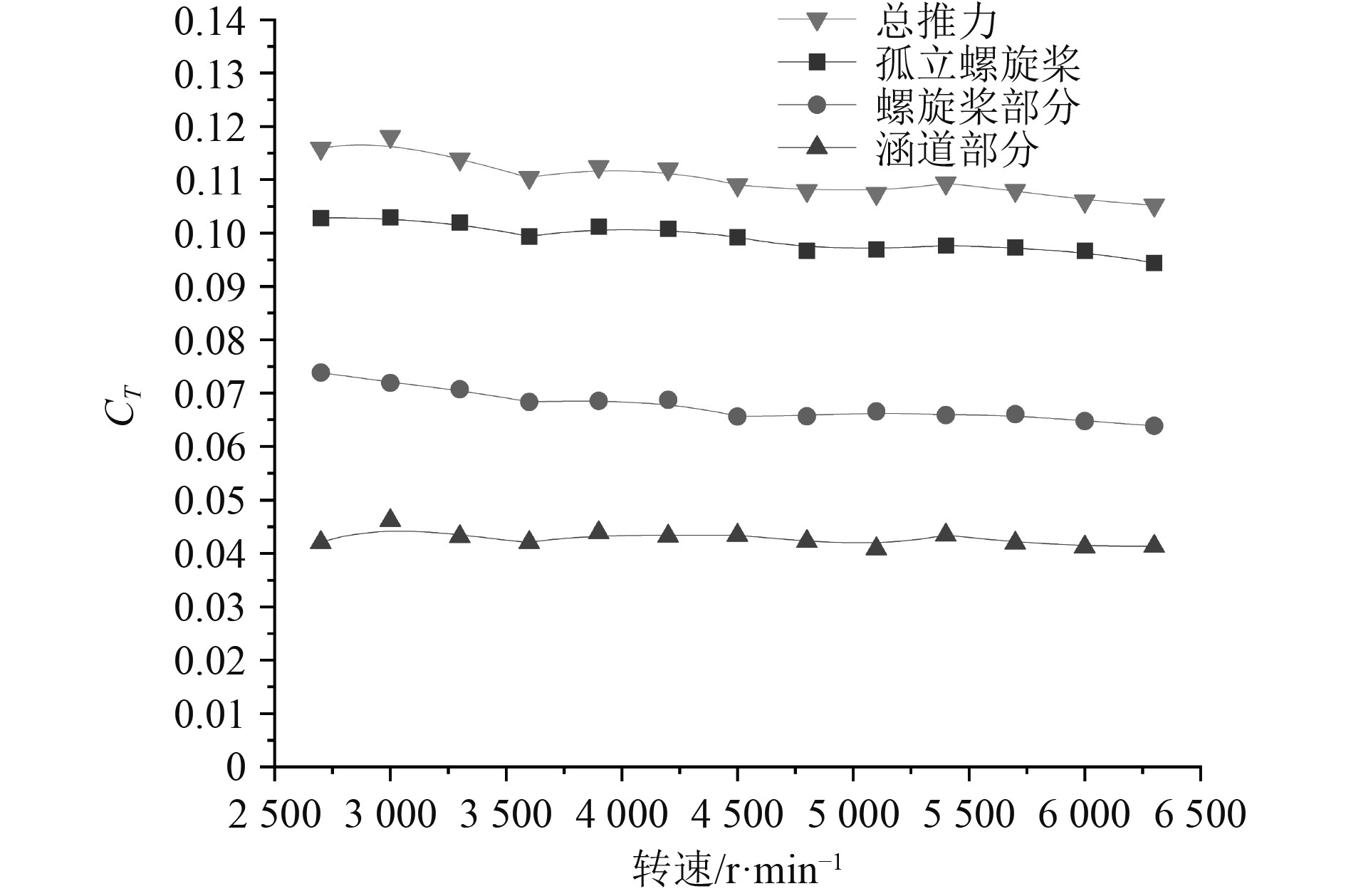
|
图 7 孤立螺旋桨和涵道螺旋桨推力系数 Fig. 7 The thrust coefficient of open and ducted propeller |
|
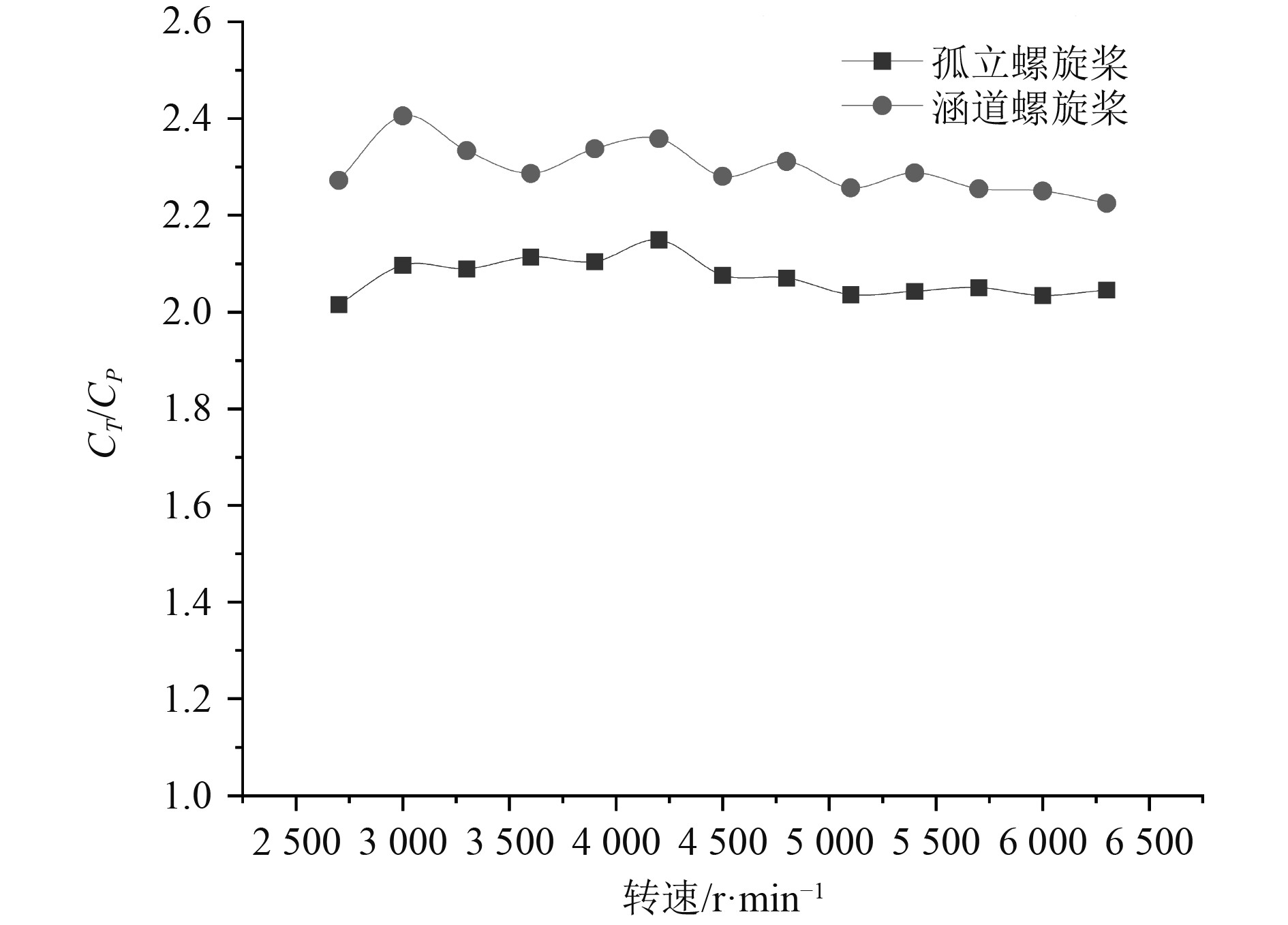
图 9
孤立螺旋桨和涵道螺旋桨 |
由图7可知:相同转速下,1)涵道螺旋桨整体结构中螺旋桨部分产生推力小于孤立螺旋桨所产生推力;2)涵道部分产生附加推力;3)涵道螺旋桨整体产生的总推力高出孤立螺旋桨推力11%。这是由于螺旋桨产生的推力来源于桨叶前后存在的压差,涵道的存在使得前后压差变小,直接导致桨叶部分产生的推力小于孤立螺旋桨;涵道也处于该压差区域内,对于涵道部分而言,也可通过压差产生额外推力。
图8为涵道螺旋桨的功率系数比孤立螺旋桨要低13%左右,这是由于相同转速下,涵道螺旋桨整体结构中螺旋桨部分产生推力比孤立螺旋桨更小,桨叶扭矩相对应地减小,因此其所需功率同步减小。

|
图 8 孤立螺旋桨和涵道螺旋桨功率系数 Fig. 8 The power coefficient of open and ducted propeller |
由图9可知,涵道螺旋桨的工作效率即
图10和图11分别为孤立螺旋桨和涵道螺旋桨在中垂面轴向上的速度分布场图,可看出桨叶旋转产生的气流,经涵道整流后速度较孤立螺旋桨低,但气流更均匀平整,且随转速的增加,涵道的整流作用更加明显。
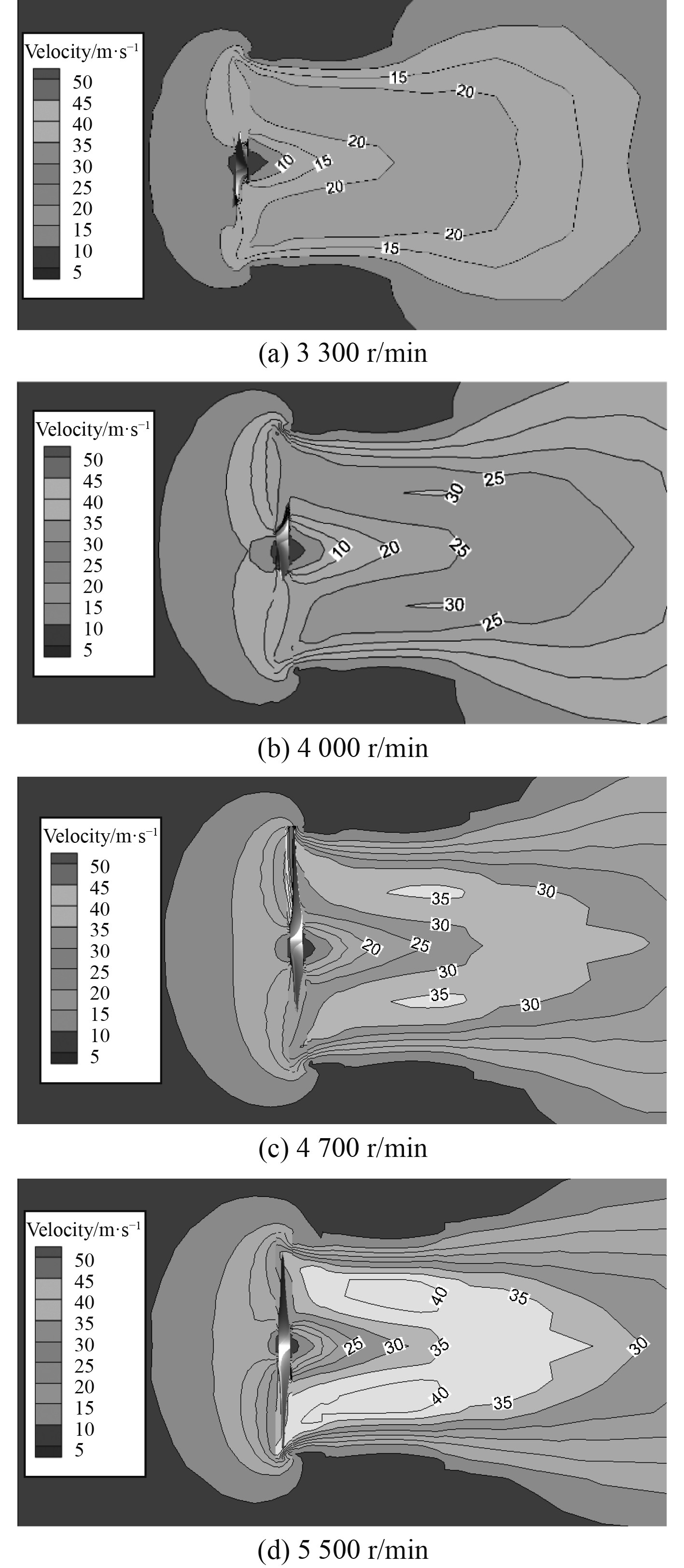
|
图 10 孤立螺旋桨速度场图 Fig. 10 Velocity field of open propeller |

|
图 11 涵道螺旋桨速度场图 Fig. 11 Velocity field of ducted propeller |
从图12可知,螺旋桨迎风面前部产生低压区,同时背风面后部由于气流压缩产生高压区。涵道的存在扩大了前部低压区的范围,因此涵道产生了附加推力。
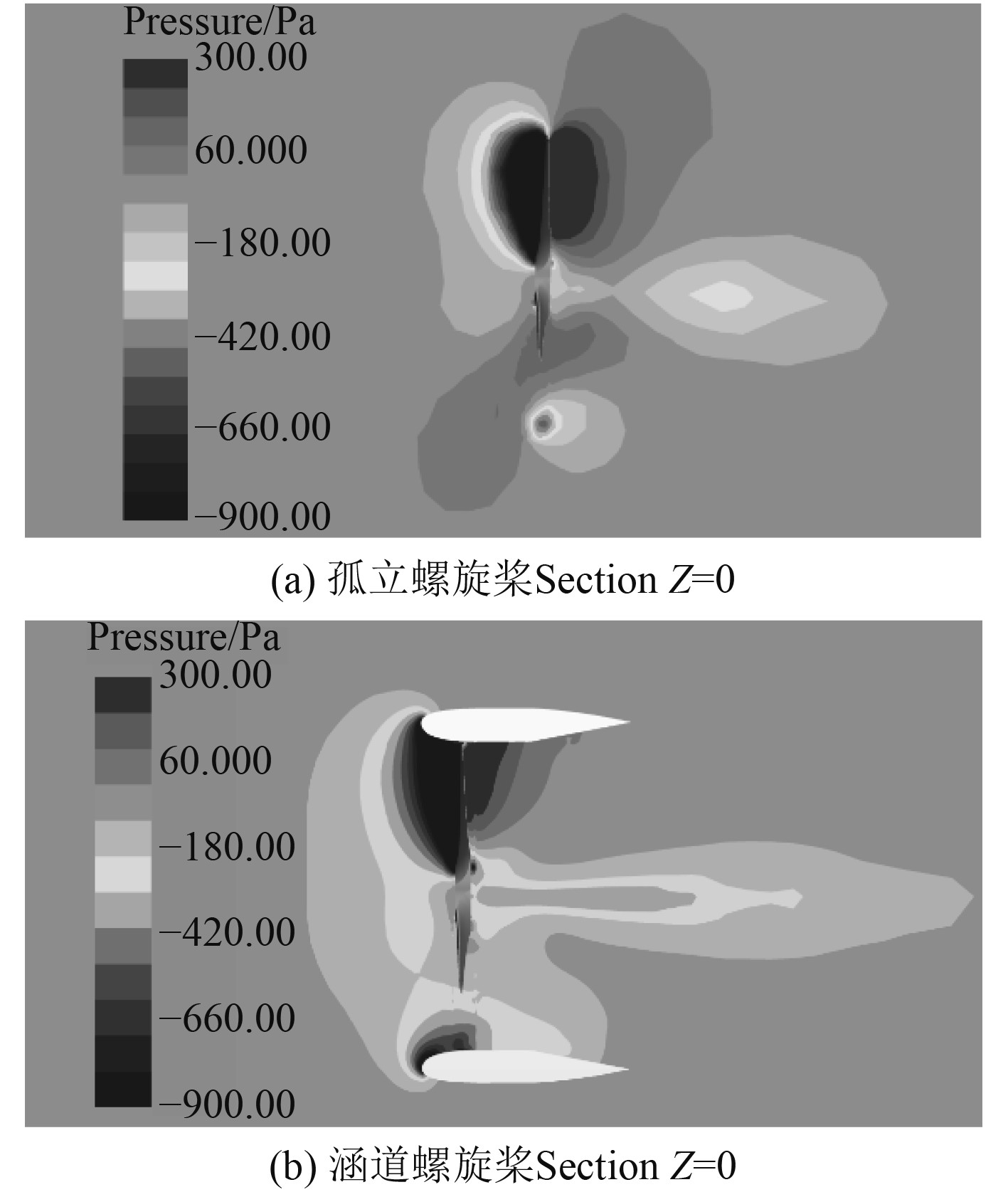
|
图 12 孤立螺旋桨和涵道螺旋桨压力云图 Fig. 12 Pressure cloud picture of open and ducted propeller |
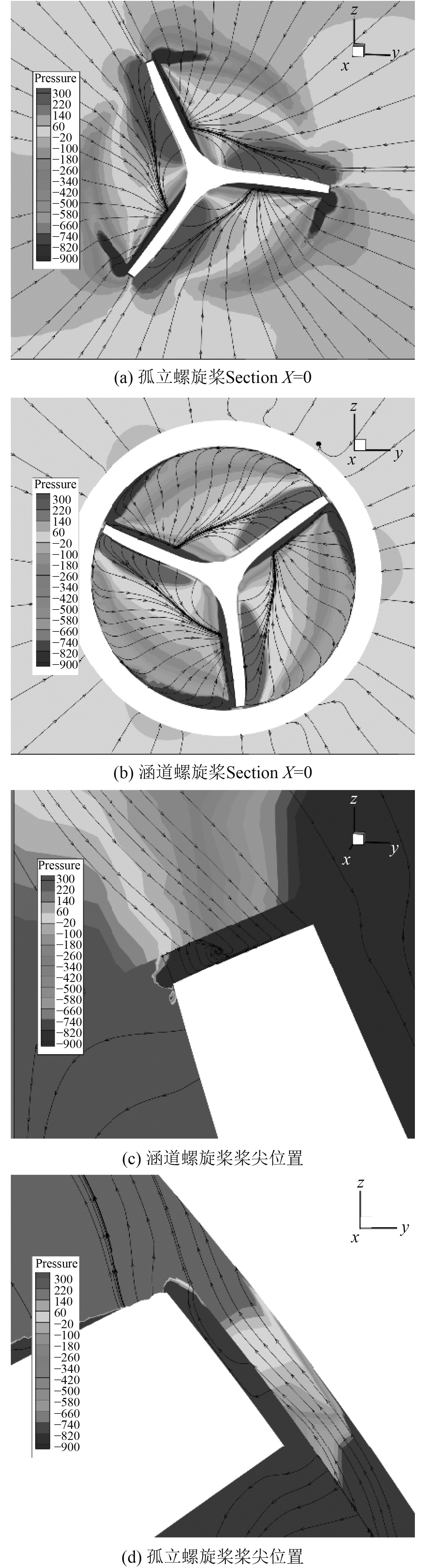
图13为涵道螺旋桨和孤立螺旋桨的流线比较,可看出,孤立螺旋桨桨尖位置存在绕流现象,即部分气流从桨叶背风面绕过桨尖回流至迎风面,导致产生桨尖涡,损失了部分孤立螺旋桨的动能。
|
图 13 孤立螺旋桨和涵道螺旋桨流线和压力云图 Fig. 13 Streamline and pressure cloud picture of open propeller and ducted propeller |
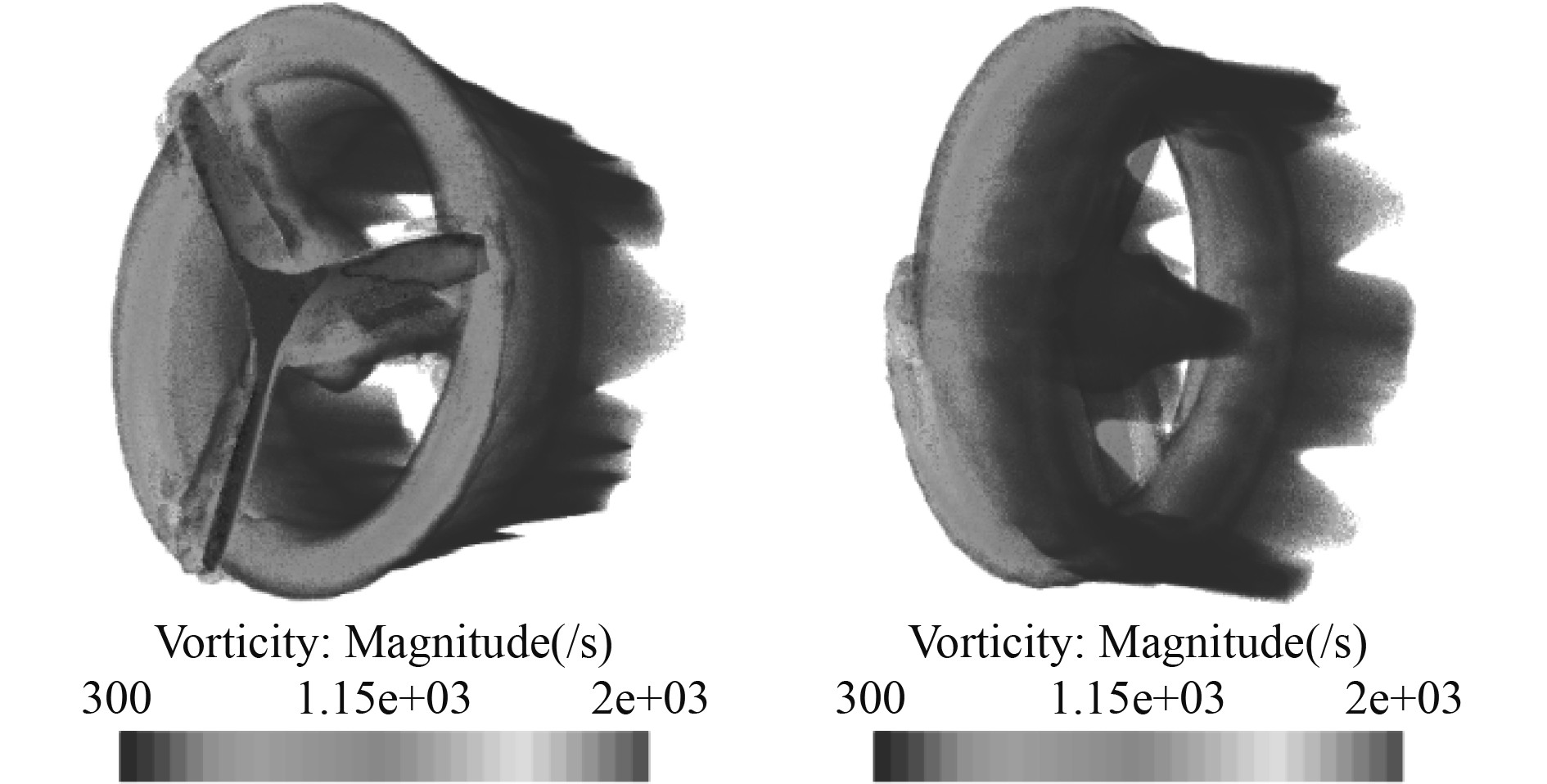
螺旋桨在涵道中旋转时,涵道壁改变了螺旋桨桨尖位置的绕流特性,减少了桨尖涡的形成。这一点从图14和图15的涵道螺旋桨和孤立螺旋桨的涡量对比中可直观看到涡量产生半径明显较小。
|
图 14 孤立螺旋桨涡量场(5500 r/min) Fig. 14 Vorticity field of open propeller (5500 r/min) |

|
图 15 涵道螺旋桨涡量场(5500 r/min) Fig. 15 Vorticity field of ducted propeller (5500 r/min) |
基于上述计算模型和方法,对涵道螺旋桨保持额定转速n=5500 r/min,在不同航速工况下的推力性能表现做出了仿真模拟。
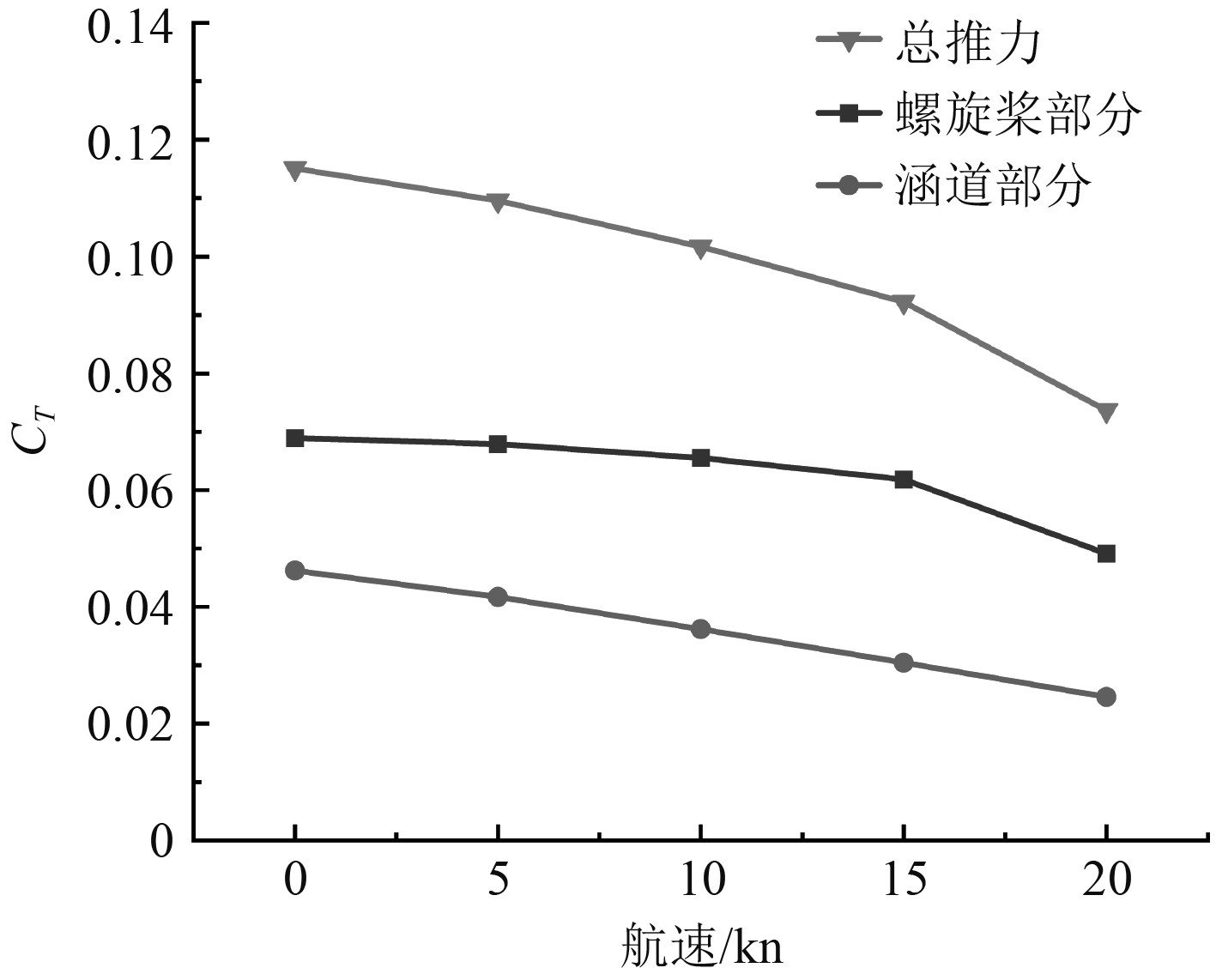
图16为涵道螺旋桨不同航速下推力系数情况,在怠速状态下,涵道螺旋桨总推力系数为0.1096,对应推力为516 N,满足不低于500 N的设计要求;在航速增加到20 kn过程中,涵道螺旋桨的推力系数最低为0.0737,对应推力为327 N,满足在航速20 kn时,推力不低于300 N的设计要求。
|
图 16 涵道螺旋桨不同航速下的推力系数 Fig. 16 Thrust coefficient of ducted propeller under different advance ratio |
因此,该型涵道螺旋桨的性能表现满足该气垫船的设计要求。
5 结 语本文采用滑移网格方法对船用三叶涵道螺旋桨和对应的孤立螺旋桨的气动特性及流场进行分析,通过对涵道螺旋桨和孤立螺旋桨的数值模拟对比研究以及实验数据对比,得到的主要结论有:
1)基于滑移网格技术的CFD计算方法能准确地计算螺旋桨和涵道之间的相对旋转运动问题,计算得到NASA涵道螺旋桨气动特性,拉力系数、扭矩系数以及涵道升力系数与实验值吻合较好;计算得到的三叶孤立螺旋桨推力系数与实验值误差在6%以内,表明计算模型处理此类问题的有效性。
2)涵道的存在扩大了螺旋桨前后的低压区,使涵道在压差作用下产生附加推力,涵道螺旋桨整体总推力较孤立螺旋桨提高了10%。
3)涵道壁改变了桨尖流线特性,抑制了桨尖涡的形成,减小螺旋桨动能损失,螺旋桨工作效率提高了25%。
4)额定转速下,该型涵道螺旋桨在怠速状态下的推力和航速20 kn时的最小推力均满足该型气垫船的设计要求。
当前数值计算没有涉及到涵道结构参数对涵道螺旋桨产生推力的影响以及相应的涵道结构设计优化过程,后续将针对涵道结构变化对推力的影响进行研究,并同步进行涵道实体制造与实验验证。
| [1] |
刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006.
|
| [2] |
许和勇, 叶正寅. 涵道螺旋桨与孤立螺旋桨气动特性的数值模拟对比[J]. 航空动力学报, 2011, 26(12): 2820-2825. |
| [3] |
徐嘉, 范宁军, 赵澍. 涵道飞行器涵道本体气动特性研究[J]. 弹箭与制导学报, 2009, 29(4): 174-178. DOI:10.3969/j.issn.1673-9728.2009.04.050 |
| [4] |
程钰锋, 郑小梅, 脱伟, 等. 涵道螺旋桨气动机理数值分析[J]. 直升机技术, 2021(2): 8-15. |
| [5] |
邓阳平, 米百刚, 詹浩, 等. 涵道螺旋桨地面效应试验与数值计算研究[J]. 西北工业大学学报, 2020, 38(5): 1038-1046. DOI:10.3969/j.issn.1000-2758.2020.05.017 |
| [6] |
闫文辉, 汤斯佳, 王奉明, 等. 共轴对转螺旋桨的非定常气动干扰[J]. 航空动力学报, 2021, 36(7): 1398-1405. |
| [7] |
王红波, 祝小平, 周洲, 等. 垂直/短矩起降飞机机翼内埋式风扇布局气动特性分析[J]. 航空动力学2016, 31(1): 161−167.
|
| [8] |
芦志明. 涵道螺旋桨飞行器总体设计[D]. 南京: 南京航空航天大学, 2016.
|
| [9] |
QIN D H, PAN G, HUANG Q G, et al. Numerical investigation of different tip clearances effect on the hydrodynamic performance of pump jet propulsor[J]. International Journal of Computational Methods, 2018, 15(5): 2−24.
|
| [10] |
GRUNWALD K J, GOODSON K W. Aerodynamic loads on an isolated shround-propeller configuration for angle of attack from-10° to 110°[R]. NASA TN D-995, 1962.
|
| [11] |
YAGGY P F , MORT K W. A wind-tunnel investigation of a 4-foot-diameter ducted fan mounted on the tip of a semispan wing[R]. NASA TN D-776, 1961.
|
 2024, Vol. 46
2024, Vol. 46
