0 引　言

舰载武器是国内外军用舰船实现对海打击、防空反导和反潜作战任务的主要实现手段，射界作为舰载武器火力覆盖范围的重要表征量，将直接影响全舰的作战效能。在军用舰船有限的空间资源条件下和确保武器发射安全性的前提下，应统筹安排全舰舰载武器的布局，设计武器的安全射界范围，并通过对布局的不断调整，优化全舰武器的安全射界，发挥全舰武器的作战效能。

在全贯通甲板船型的武器射界设计中，进行跨大甲板导弹武器安全射界设计，是在确保武器发射安全性的前提下，全面发挥导弹武器效能的有效手段。

1 全贯通飞行甲板船型武器布置情况

在航母、两栖攻击舰等全贯通甲板船型的设计中，舰载导弹武器一般布置在主甲板层以下的两舷舷台，受船体影响，不可避免的均存在首尾部盲区，尾部射界盲区可通过设置尾部舷台进行补盲，而船首部是舰船破浪的主要受力部位，船体抨击很大，不适宜设置首部舷台，纵观国内外航母、两栖攻击舰等船型，针对首部盲区主要有3种处理方案：1）将导弹武器设置在飞行甲板最前部，如日本的“日向”级、“出云”级直升机护卫舰；2）通过首部斜角设计，扩大首部武器的射界，如美国的“福特”级航空母舰，英国的“伊丽莎白女王”号航空母舰等；3）将导弹武器设置在上层建筑前部，利用武器与飞行甲板的高度差覆盖首部区域，如美国的“黄蜂”级两栖攻击舰、“美国”级两栖攻击舰等^[1]。

图1所示为日本的“出云”级直升机护卫舰飞行甲板布置图，采用飞行甲板最前方的“密集阵”舰炮布置方案的优点在于有效补充了首部和右舷射界，缺点在于导弹武器设置于飞行甲板上，舰载机在飞行甲板的布列调运与武器使用存在较大干涉。

图2所示为美国的“福特”级航空母舰飞行甲板布置图，采用两舷舷台的导弹武器布置方案，主要优点在于导弹武器布置于船体突出舷台，周围障碍物分布比较简单，首部斜角设计也消除了首部射界盲区，缺点在于一是左右舷武器射界虽在方位角上完成了全面覆盖，但由于首部障碍物的存在，在首部交汇区或多或少存在近界盲区，近界盲区主要由武器布置位置和首部斜角决定；二是首部斜角设计对飞行甲板利用率有一定影响。

如图3所示为美国的“黄蜂”级两栖攻击舰飞行甲板布置图，采用上层建筑的导弹武器布置方案主要优点在于对飞行甲板没有限制，甲板使用率较高，缺点在于火箭助飞导弹是从零开始加速，初始速度很小，在飞越飞行甲板的过程中经历时间较长，在此过程中舰船纵摇、横摇、升沉运动带来的甲板上翘幅度较大，在低射角条件下存在导弹尾喷火焰对飞行甲板上的飞机等设施造成损坏，甚至导弹飞行轨迹与甲板运动轨迹产生干涉，造成导弹爆炸等重大事故发生的可能，需开展导弹武器跨大甲板发射的射界设计，保证导弹武器安全发射。

2 舰载导弹武器跨大甲板安全射界设计方法 2.1 舰载武器传统射界设计方法

目前，驱逐舰、护卫舰、登陆舰等传统船型的舰载武器安全射界设计主要采用光学射线法，主要考虑武器火线高、武器与障碍物相对位置、安全裕量等因素确定武器安全射界，较少考虑导弹/炮弹飞行过程中船体运动带来的影响^[2]。主要基于2个原因：1）机枪、舰炮等武器的弹药出膛速度较快（一般可达800 m/s）；2）驱逐舰、护卫舰等船型舰载武器一般布置于船体首尾部或左右两舷舷边，周围障碍物分布比较简单，武器与障碍物距离普遍较小。因此，弹药从武器口射出到飞过障碍物的时间极短，在此过程中的船体摇摆、机动等带来的影响可忽略不计。

而在跨大甲板导弹武器安全射界的设计中，由于飞越甲板航程远，飞行时间长，飞行过程中船体摇摆、升沉等运动带来影响不可忽略，传统的光学射线法在跨大甲板导弹武器的安全射界设计中并不完全适用，需在此基础上，引入飞行时间的概念，考虑弹体飞行和船体运动的空间轨迹交互，提出一种改进的安全射界设计方法^[3]。

2.2 跨大甲板导弹武器射界设计要素

以“黄蜂”级两栖攻击舰上建艏部配置的“海拉姆”舰空导弹为例，基于飞行时间的跨大甲板武器安全射界设计的关键设计要点包括甲板障碍物运动轨迹仿真、导弹弹体飞行轨迹轨迹仿真和干涉判断^[4]。

值得注意的是，船体障碍物由于结构固联，在舰艇坐标系下相对位置均能保持不变，而导弹在飞行过程中已脱离了与船体的机械连接，难以在舰艇坐标系下进行解算^[5]。因此，需建立以船体摇摆中心为坐标原点的船体平动坐标系（船体航行速度与导弹飞行的速度相比是高阶小量，在计算中可忽略不计），分别开展甲板障碍物运动轨迹和导弹弹体飞行轨迹的仿真^[6-8]。

1）“海拉姆”舰载导弹弹体模拟飞行航迹

舰载导弹武器发射主要经历全约束期运动、半约束期运动、空气动力学飞行3个阶段，在全约束期，导弹与发射装置完全约束，发射装置在伺服系统作用下，相对船体摇心保持相对稳定状态，该阶段对导弹飞行轨迹影响较小^[9]；在半约束期，导弹弹体部分已离开发射管进行自由运动，而另一部分尚在发射管中被部分约束，在此过程中导弹弹体自由运动与发射管约束运动相互作用，形成了半约束期的导弹发射初始速度V_x、V_y、V_z和初始扰动加速度δ₀（持续时间为Δt）^[10]；在空气动力学飞行阶段，主要是考虑火箭发动机推力、空气阻力和重力联合作用下，产生的相对加速度δ_x、δ_y和δ_z。因此，舰载导弹武器飞行航迹可简化表述为：

$ {L}_{\mathrm{x}}={\int }_{0}^{\mathrm{t}}({V}_{{x}}+{\int }_{0}^{\Delta t}{\delta }_{0{x}})+{\delta }_{x}\cdot t，$

$ {L}_{\mathrm{y}}={\int }_{0}^{\mathrm{t}}({V}_{y}+{\int }_{0}^{\Delta \mathrm{t}}{\delta }_{0{y}})+{\delta }_{y}\cdot t，$

$ {L}_{\mathrm{z}}={\int }_{0}^{\mathrm{t}}({V}_{{z}}+{\int }_{0}^{\Delta \mathrm{t}}{\delta }_{0{z}})+{\delta }_{z}\cdot t。$

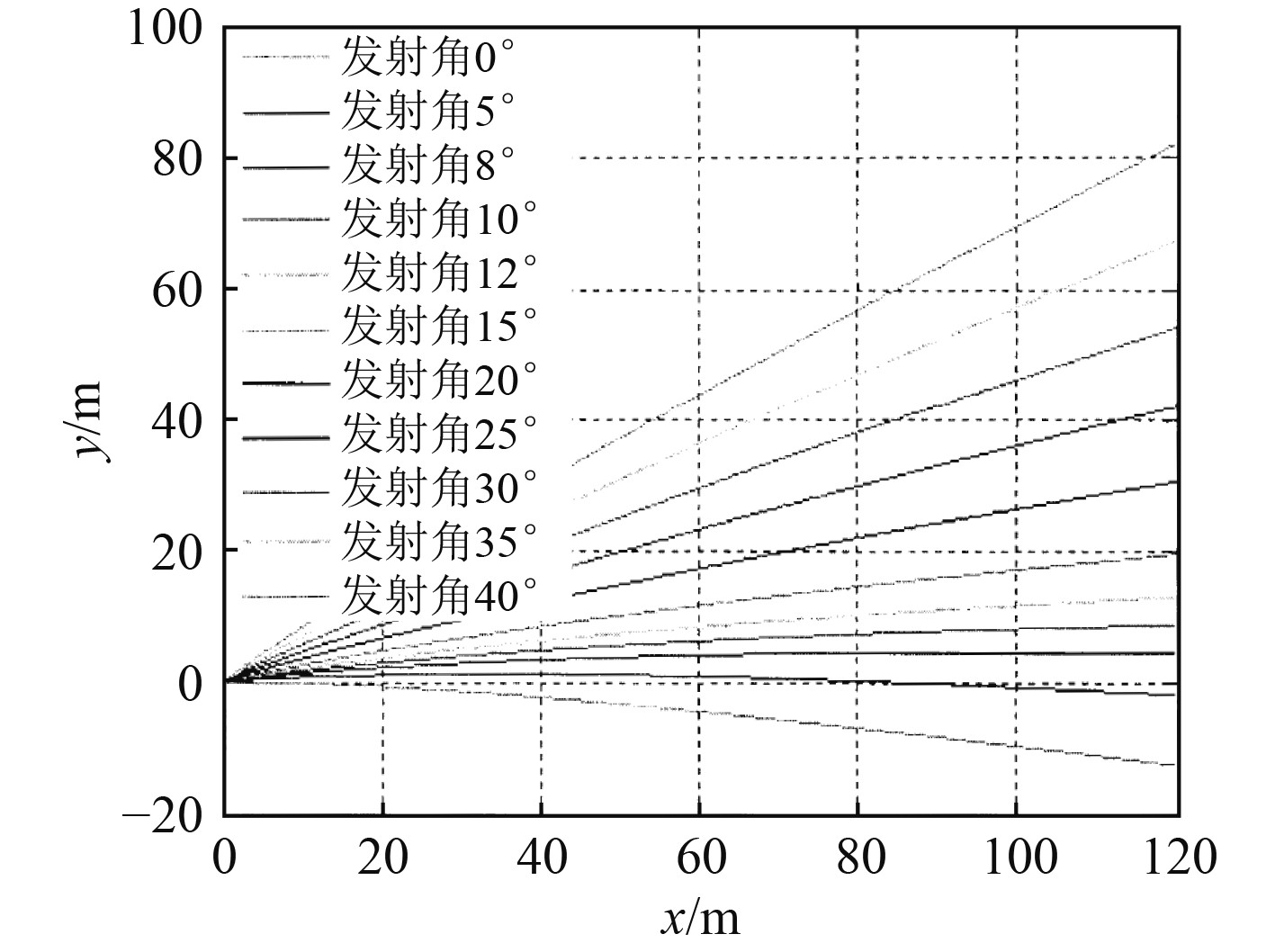
根据互联网查阅的“海拉姆”舰空导弹发射参数进行仿真模拟，可得不同发射角下，舰载导弹在不同发射角（大地坐标系下）飞行轨迹如图4所示。

2）“黄蜂”级两栖攻击舰舰面典型点运动轨迹

在船体平动坐标系下，由于船体的摇摆运动，甲板上典型点在大地坐标系下均会产生不同程度的偏移，导弹发射点位置在动态变化、飞行甲板上的障碍点也在动态变化。

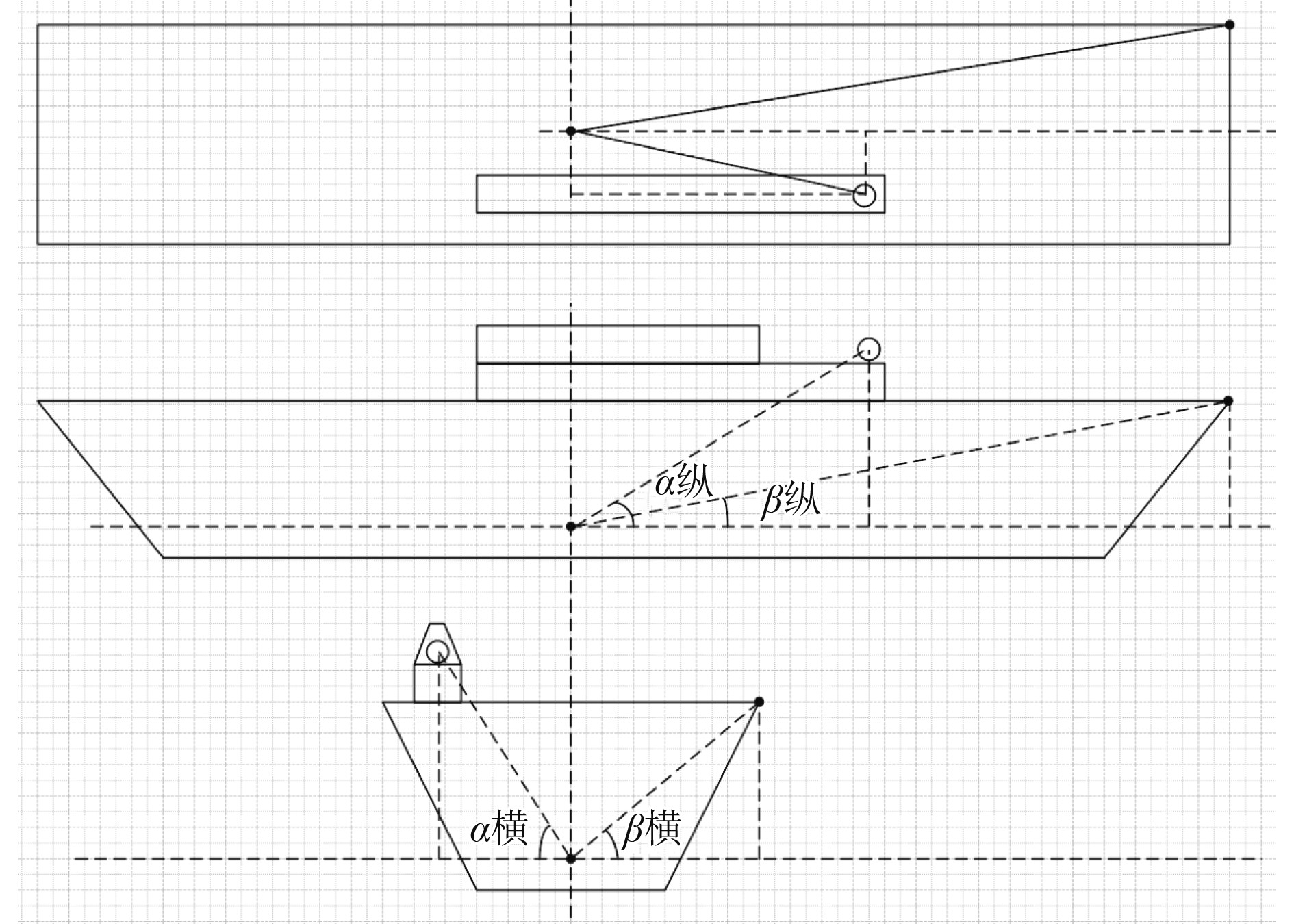
“黄蜂”级两栖攻击舰飞行甲板武器布置示意如图5所示，当船体平衡状态下计船体摇心的坐标为（0,0,0），典型点坐标为（x,y,z），此时目标点与摇心连线在船体中纵平面上的投影角度为α_纵，${\mathrm{\alpha }}_{\mathrm{纵}}= {\mathrm{tan}}^{-1}\dfrac{{z}}{{x}}$，典型点与摇心连线在船体中横平面上的投影角度为α_横，${\mathrm{\alpha }}_{\mathrm{横}}={\mathrm{tan}}^{-1}\dfrac{{z}}{{y}}$。

船体运动是船体响应海浪波谱的不规则运动，一般舰船设计中需模拟实测波谱进行舰船耐波性计算，为简化计算模型，这里将船体纵摇、横摇、垂荡运动均简化为正弦运动，计纵摇的最大角度为θ纵，周期为T纵；横摇的最大角度为θ横，周期为T横；垂荡的最大幅度为Z垂，周期为T垂；以平衡状态为初始，经过时间t，船体与平衡状态的夹角分别为：

$ {\Delta \mathrm{\alpha }}_{\mathrm{纵}}\left({t}\right)={\mathrm{\theta }}_{\mathrm{纵}}\mathrm{sin}\left(\frac{2{\text{π}} }{{{T}}_{\mathrm{纵}}}{t}\right)，$

$ {\Delta \mathrm{\alpha }}_{\mathrm{横}}\left({t}\right)={\mathrm{\theta }}_{\mathrm{横}}\mathrm{sin}\left(\frac{2{\text{π}} }{{{T}}_{\mathrm{横}}}{t}\right)。$

考虑纵摇半径${{L}}_{\mathrm{纵}}=\sqrt{{x}^{2}+{{z}}^{2}}$，横摇半径${{L}}_{\mathrm{横}}=\sqrt{{y}^{2}+{{z}}^{2}}$，因此，t时刻的典型点高度轨迹为：

$\begin{aligned} & {{H}}_{\mathrm{典}\mathrm{型}\mathrm{点}}\left({t}\right)={{L}}_{\mathrm{纵}}\mathrm{sin}\left({\mathrm{\alpha }}_{\mathrm{纵}}+{\Delta \mathrm{\alpha }}_{\mathrm{纵}}\left({t}\right)\right)+\\ & {{L}}_{\mathrm{横}}\mathrm{sin} \left({\mathrm{\alpha }}_{\mathrm{横}}+{\Delta \mathrm{\alpha }}_{\mathrm{横}}\left({t}\right)\right)-{z}+{Z}_{\mathrm{垂}}\mathrm{sin}\left(\frac{2 {\text{π}}}{{{T}}_{\mathrm{垂}}}{t}\right)。\end{aligned}$

2.3 跨大甲板导弹武器安全射界设计方法

基于以上两点分析，发射点在船体平衡状态下坐标为（x₁,y₁,z₁），假定t时刻导弹发射离开发射装置，此时的发射点高度为：

$ \begin{split} & {H}_{\mathrm{发}\mathrm{射}\mathrm{点}}\left({t}\right)=\sqrt{x_1^2+z_1^2}\cdot \mathrm{sin} \\ & \left(\mathrm{tan}^{-1}\frac{z_1}{x_1}+\mathrm{\theta}_{\mathrm{纵}}\mathrm{sin}\left(\frac{2 {\text{π}}}{{T}_{\mathrm{纵}}}{t}\right)\right)+ \\ & \sqrt{y_1^2+z_1^2}\cdot \mathrm{sin}\left(\mathrm{tan}^{-1}\frac{z_1}{y_1}+\mathrm{\theta}_{\mathrm{横}}\mathrm{sin}\left(\frac{2 {\text{π}}}{{T}_{\mathrm{横}}}{t}\right)\right)- \\ & {{z}}_1+{Z}_{\mathrm{垂}}\mathrm{sin}\left(\frac{2 {\text{π}}}{{T}_{\mathrm{垂}}}{t}\right)。\end{split} $

计障碍点在船体平衡状态下坐标为（x₂,y₂,z₂），当导弹飞行Δt时间至甲板障碍点上空，带入某发射角条件下的飞行轨迹可知该时刻导弹飞行高度为H₁，即此时导弹实际飞高为${{H}}_{\mathrm{发}\mathrm{射}\mathrm{点}}\left({t}\right)+H_1$，而此时障碍点高度为：

$ \begin{split} &{H}_{\mathrm{障}\mathrm{碍}\mathrm{点}}\left({t}+\Delta{t}\right)=\sqrt{x_2^2+z_2^2}\cdot\mathrm{sin} \\ & \left(\mathrm{tan}^{-1}\frac{z_2}{x_2}+\mathrm{\theta}_{\mathrm{纵}}\mathrm{sin}\left(\frac{2\text{π}}{{T}_{\mathrm{纵}}}\left({t}+\Delta{t}\right)\right)\right)+ \\ & \sqrt{y_2^2+z_2^2}\cdot\mathrm{sin}\left(\mathrm{tan}^{-1}\frac{z_2}{y_2}+\mathrm{\theta}_{\mathrm{横}}\mathrm{sin}\left(\frac{2\text{π}}{{T}_{\mathrm{横}}}\left({t}+\Delta{t}\right)\right)\right)- \\ & {z}_2+{Z}_{\mathrm{垂}}\mathrm{sin}\left(\frac{2\text{π}}{\mathrm{T}_{\mathrm{垂}}}\left({t}+\Delta{t}\right)\right)。\end{split} $

当${{H}}_{\mathrm{发}\mathrm{射}\mathrm{点}}\left({t}\right)+H_1-{{H}}_{\mathrm{障}\mathrm{碍}\mathrm{点}}\left({t}+\Delta {t}\right)$大于设计裕量时，可判定该目标点（x₁,y₁,z₁）满足t时刻导弹安全发射条件，考虑到纵摇周期、横摇周期、垂荡周期不存在相关性，通过对发射时间t进行足够长时间的采样（一般采样周期不小于1000 s，采样间隔不大于0.1 s），可完成所有横摇、纵摇、垂荡运动初始点的组合遍历，即完成武器在某俯仰发射角条件下，针对某障碍物所有发射时机的安全性验证。

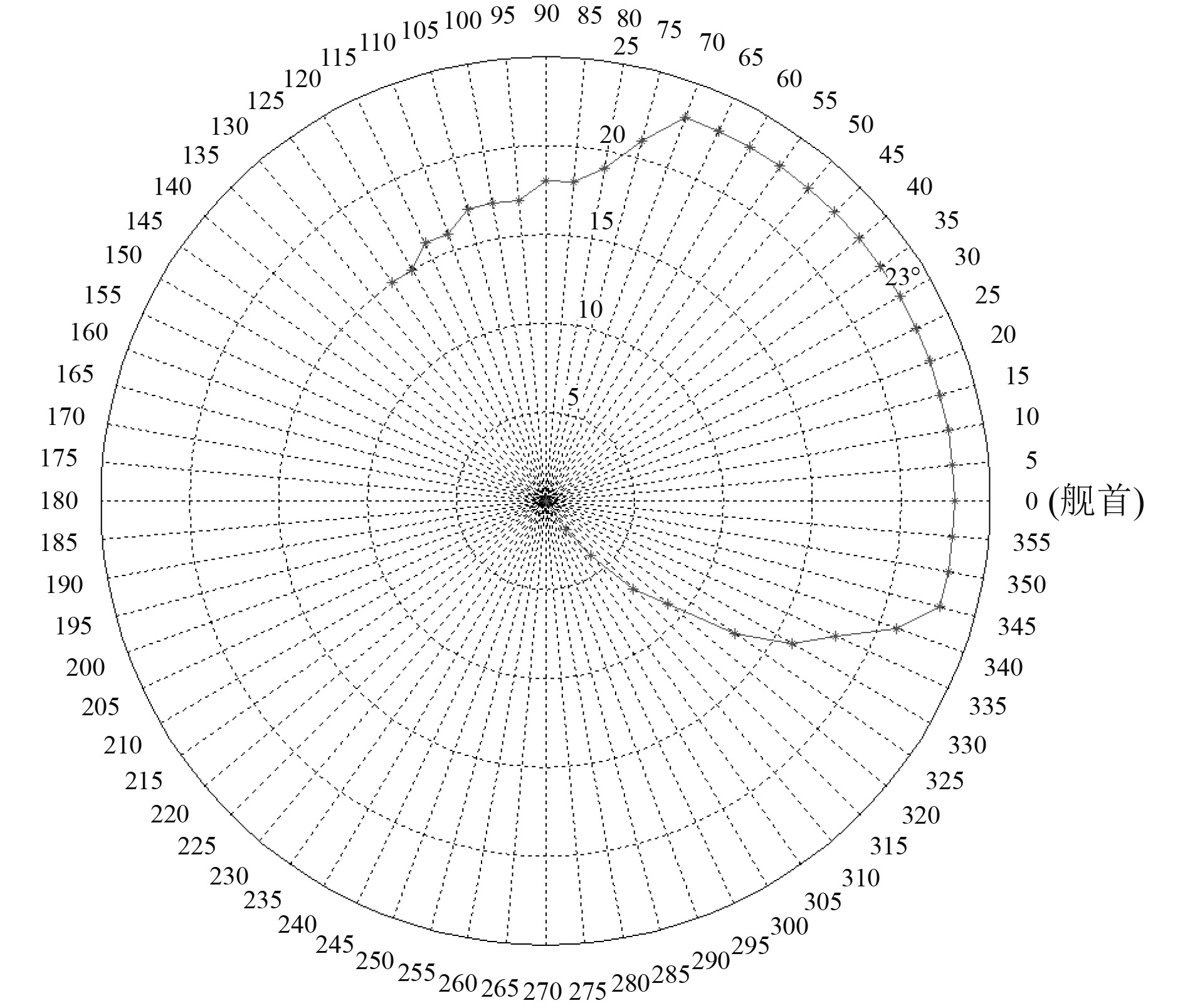
利用计算机程序对导弹发射俯仰角范围和导弹发射水平范围内甲板重点障碍物进行遍历，形成了“海拉姆”舰空导弹安全射界，如图6所示。

根据互联网查阅到的资料可判断，“黄蜂”级两栖攻击舰飞行甲板上的主要障碍物均低于首部“海拉姆”舰空导弹发射装置，根据传统的射界设计方法，考虑设计裕量后导弹大部分方位角的安全发射低角应不大于0°，但根据图6所示，改进后的射界设计方法得出导弹在首部方位的安全射界低角达到23°，可见，若按照传统射界设计方法进行安全射界估算，存在较大安全风险。

3 结　语

传统船型的舰载武器主要采用光学射线法进行安全射界设计，但在跨大甲板导弹武器的安全射界设计中并不能完全适用。本文以“黄蜂”级两栖攻击舰配置的“海拉姆”舰空导弹为例，在射界设计中引入了飞行时间的概念，考虑弹体飞行和船体运动的空间轨迹交互，提出了一种改进的安全射界设计方法。相比传统射界设计方法，改进后的安全射界设计方法在统一的船体平动坐标系下考虑了导弹弹体的飞行轨迹和船体障碍物的运动轨迹，更好体现了导弹弹体运动和船体运动的相对关系，提高了导弹武器安全射界的安全裕度。