船舶通信网络在保障海上安全、提高运营效率等方面发挥着越来越重要的作用[1]。然而,由于船舶通信网络的特殊性,如覆盖范围广、节点移动性强、网络拓扑动态变化等,使其网络流量的准确估计面临诸多挑战[2]。网络流量估计对于船舶通信网络的性能优化、资源调度和安全监测具有重要意义。因此,设计一个有效的船舶通信网络流量估计数学模型成为了一项重要的任务[3]。目前,针对船舶通信网络流量估计数学模型设计问题,学者们进行了相关研究和实践。例如,徐海兵等[4]利用双向GRU结构,捕捉网络流量的时序依赖关系,并预测未来的流量变化。通过实验验证,该模型在多个数据集上均取得了较好的预测效果。但该模型输入的历史数据完整性较差,影响网络流量估计的可靠性。薛自杰等[5]旨在结合时间序列特征和空间特征,以更全面地描述网络流量的动态变化。通过融合不同维度的特征,提高流量估计的准确性和稳定性。实验结果表明,该模型可有效估计船舶通信网络流量。但该模型的特征选择主要依赖于领域知识和经验,具有一定的主观性,缺乏客观、自动的特征选择方法,限制了模型的泛化能力和应用范围。大数据统计方法能够利用大量的历史和实时数据,确保数据的完整性和可靠性,为流量估计提供更准确的基础。为此,设计基于大数据统计的船舶通信网络流量估计数学模型,为实际应用提供理论支持和实践指导。
1 船舶通信网络流量估计数学模型 1.1 船舶通信网络流量的嵌入维数与延迟时间计算利用C-C算法计算船舶通信网络流量的延迟时间
| $ Q\left( {m,N,r,\tau } \right) = \frac{{2\displaystyle\sum\limits_{1 \leqslant i < j \leqslant K} {\theta \left( {r - {d_{ij}}} \right)} }}{{K\left( {K - 1} \right)}}。$ | (1) |
式中:dij相空间内相点
令船舶通信网络流量时间序列的互信息函数为:
| $ {A_1}\left( {o,N,r,\tau } \right) = Q\left( {o,N,r,\tau } \right) - oQ\left( {1,N,r,\tau } \right)。$ | (2) |
通过分块平均思想,求解式(2)得到:
| $ {A_2}\left( {o,N,r,\tau } \right) = \frac{{\displaystyle\sum {\left[ {Q\left( {o,\frac{N}{\tau },r,\tau } \right) - oQ\left( {1,\frac{N}{\tau },r,\tau } \right)} \right]} }}{\tau } ,$ | (3) |
令
| $ {A_2}\left( {o,r,\tau } \right) = \frac{{\displaystyle\sum {\left[ {Q\left( {o,r,\tau } \right) - oQ\left( {1,r,\tau } \right)} \right]} }}{\tau }。$ | (4) |
利用
| $ \Delta {A_2}\left( {o,\tau } \right) = \max \left\{ {{A_2}\left( {o,{r_j},\tau } \right)} \right\} - \min \left\{ {{A_2}\left( {o,{r_{ji}},\tau } \right)} \right\}。$ | (5) |
利用
因此互信息函数
令船舶通信网络流量时间序列的较小嵌入维数是
| $ {Q_N}\left( r \right) = \frac{{\displaystyle\sum\limits_{i = 1,j = 1}^K {\theta \left( {r - {d_{ij}}} \right)} }}{{{K^2}}}。$ | (6) |
以
极限学习机属于大数据统计技术的一部分,可以用于处理大规模数据集,提升船舶通信网络流量估计精度。
利用C-C算法计算
| $ \begin{gathered} \min \left( {\frac{{\beta _i^{\rm{T}}{\beta _i} + \gamma \delta _i^{\rm{T}}{\delta _i}}}{2}} \right) \\ s.t.\mathop {}\nolimits_{} {y_i} = \sum\limits_i^L {{\beta _i}f\left( {{w_i}{{\hat x}_i} + {b_i}} \right) - {\delta _i}}。\end{gathered} $ | (7) |
式中:
通过拉格朗乘子获取式(7)的目标优化函数,公式如下:
| $ \begin{gathered} J\left( {w,\delta ,{\beta _i}} \right) = \frac{{\beta _i^{\mathrm{T}}{\beta _i} + \gamma \delta _i^{\mathrm{T}}{\delta _i}}}{2} - w\left( {{H_i}{\beta _i} - {G_i} - \delta } \right) ,\\ s.t.\mathop {}\nolimits_{} {y_i} = \sum\limits_i^L {{\beta _i}f\left( {{w_i}{{\hat x}_i} + {b_i}} \right) - {\delta _i}}。\\ \end{gathered} $ | (8) |
式中:
计算式(8)的偏导获取:
| $ \left\{ \begin{gathered} \frac{{\partial J}}{{\partial {\beta _i}}} \to \beta _i^{\mathrm{T}} = w{H_i},\\ \frac{{\partial J}}{{\partial \delta }} \to \gamma {\delta ^{\mathrm{T}}} + w = 0 ,\\ \frac{{\partial J}}{{\partial w}} \to {H_i}{\beta _i} - G - \delta = 0 。\\ \end{gathered} \right. $ | (9) |
依据式(9)得到船舶通信网络流量估计数学模型为:
| $ y = \sum\limits_{i = 1}^L {{\beta _i}f\left( {{w_i}\hat x + {b_i}} \right)}。$ | (10) |
通过Map/Reduce机制,对多个极限学习机并行展开建模,完成大规模船舶通信网络流量估计。基于大数据统计的船舶通信网络流量估计模型框架如图1所示。
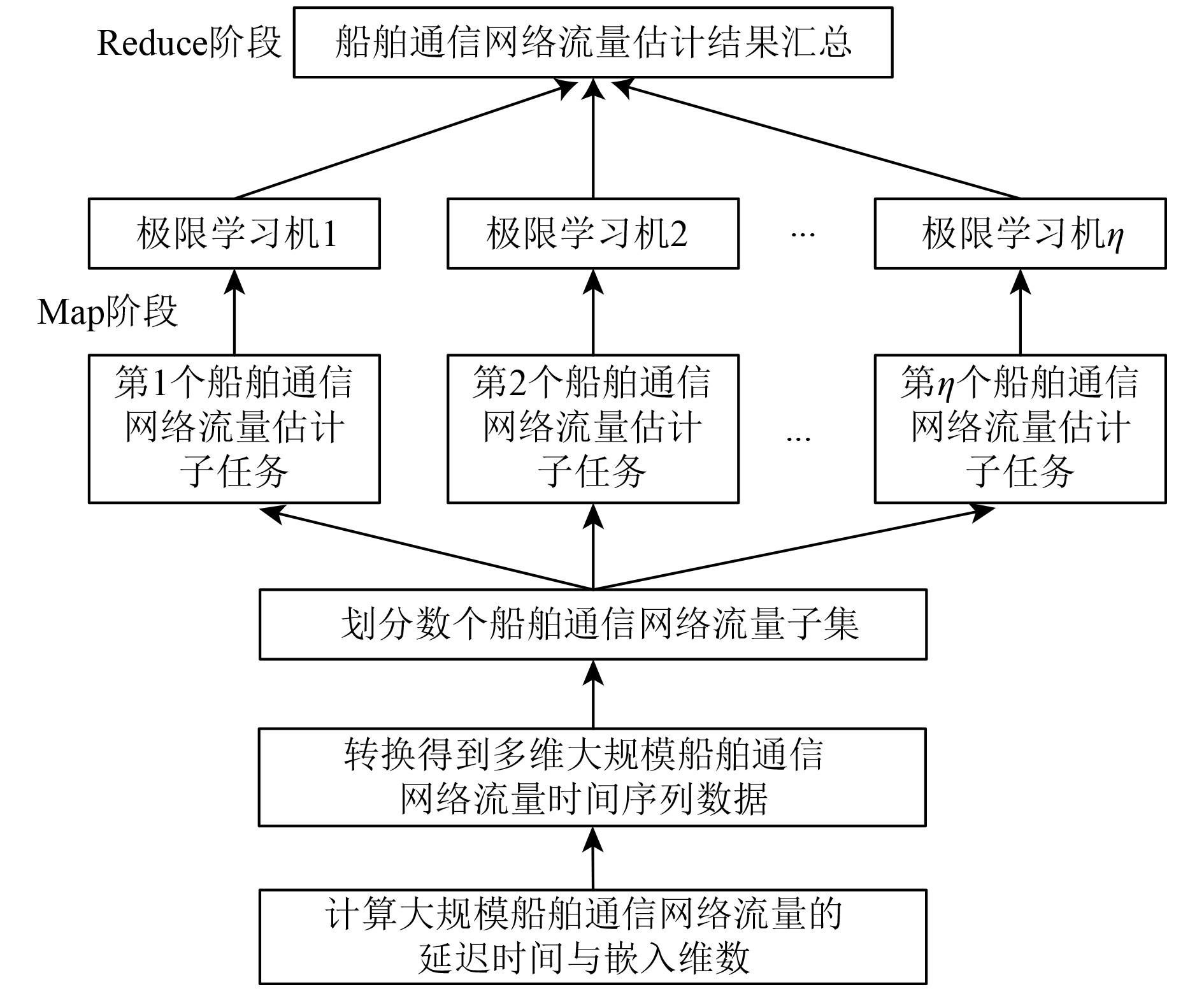
|
图 1 基于大数据统计的网络流量估计模型框架 Fig. 1 Network traffic estimation model framework based on big data statistics |
以某船舶通信网络流量数据集为实验对象,该网络流量内共包含820个数据点,以800个数据点为训练集,20个数据点为测试集,该船舶通信网络流量训练集的变化情况如图2所示。可以看出,该船舶通信网络流量的变化幅度主要在0 ~1.2 Mbit/s。
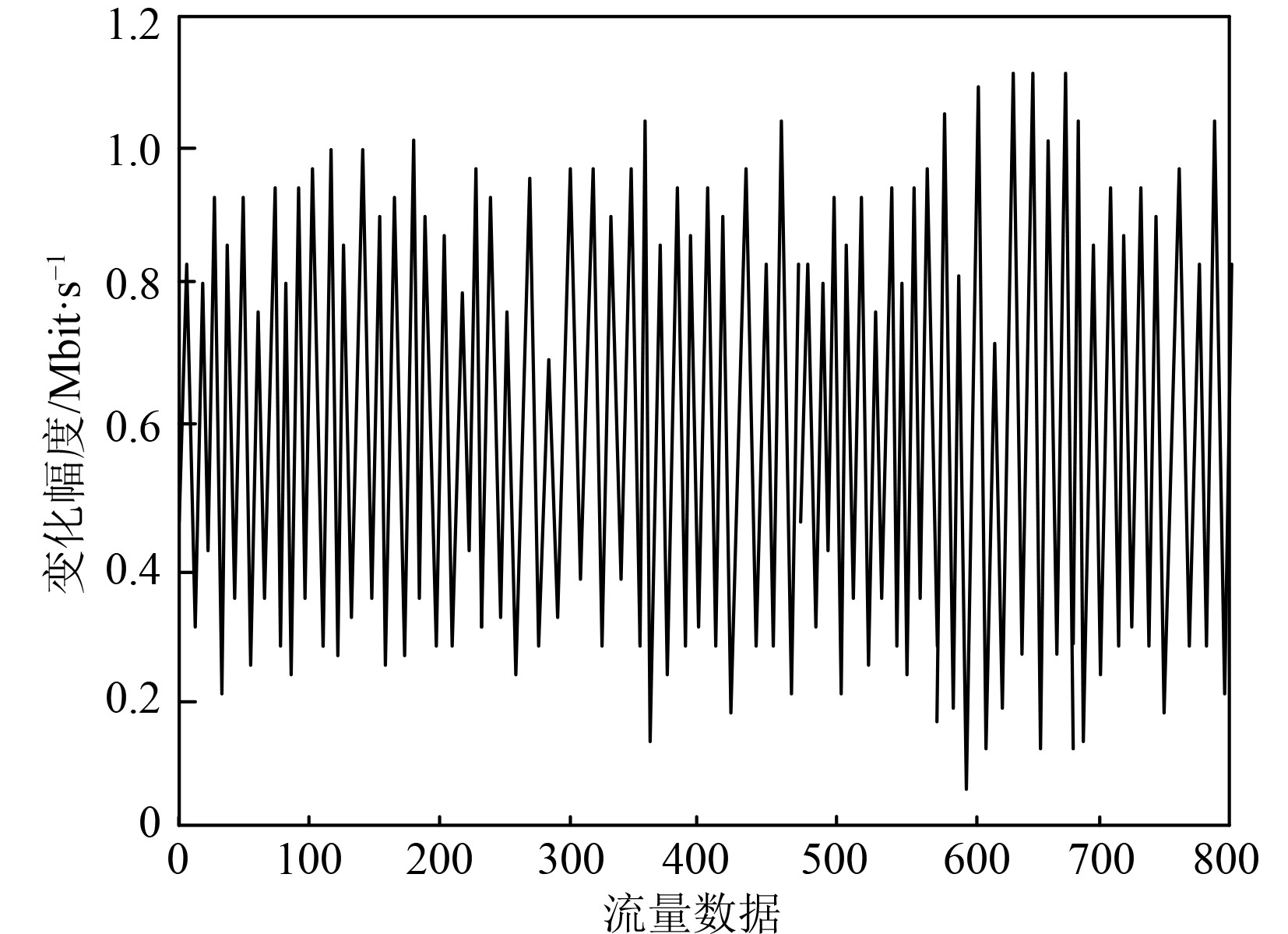
|
图 2 船舶通信网络流量变化情况 Fig. 2 Changes of ship communication network traffic |
利用本文模型确定船舶通信网络流量的延迟时间与嵌入维数,确定结果如图3所示。分析图3(a)可知,随着延迟时间的延长,船舶通信网络流量的互信息函数不断下降,当延迟时间达到5 min时,互信息函数降至最低,并趋于稳定,说明5 min便是船舶通信网络流量的最佳延时时间。分析图3(b)可知,随着嵌入维数的增长,船舶通信网络流量的关联函数逐渐上升,并接近饱和,当嵌入维数达到6维时,关联函数升至最高,并趋于稳定,说明6维是船舶通信网络流量的最佳嵌入维数。
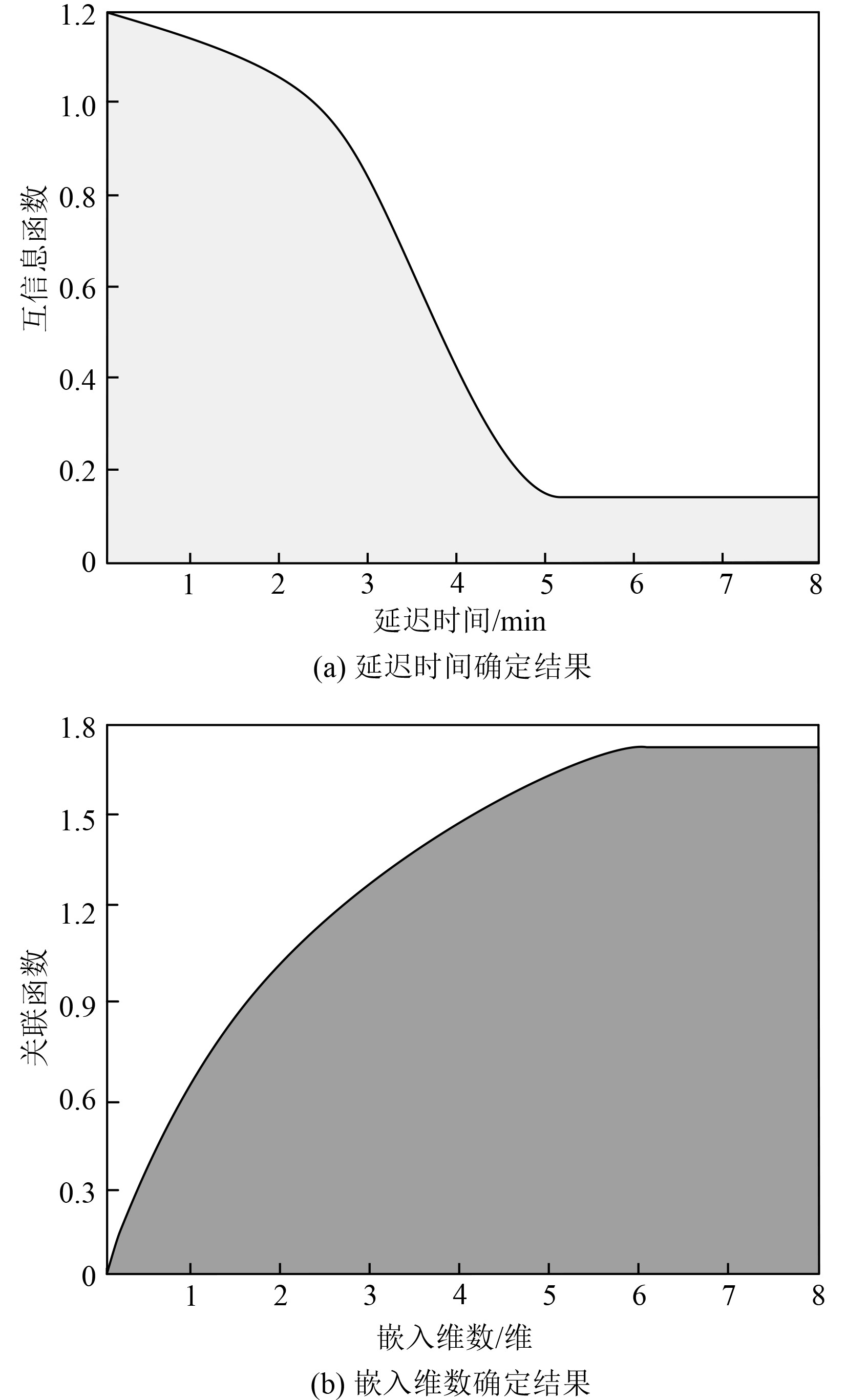
|
图 3 网络流量延迟时间与嵌入维数确定结果 Fig. 3 Results of determining network traffic delay time and embedding dimension |
利用本文模型估计测试集内船舶通信网络流量,估计结果如图4所示。可以看出,使用本文模型估计的船舶通信网络流量与实际流量之间存在非常接近的关系,这表明本文模型具有较高的网络流量估计精度。具体而言,本文模型通过利用嵌入维数和延迟参数将原始网络流量时间序列转换为多维网络流量时间序列,从而能够更好地捕捉网络流量的动态特性和模式。这种方法考虑了网络流量的非线性和复杂性,能够更准确地反映实际网络流量的变化情况,为船舶航行安全和通信服务质量提供有力保障。
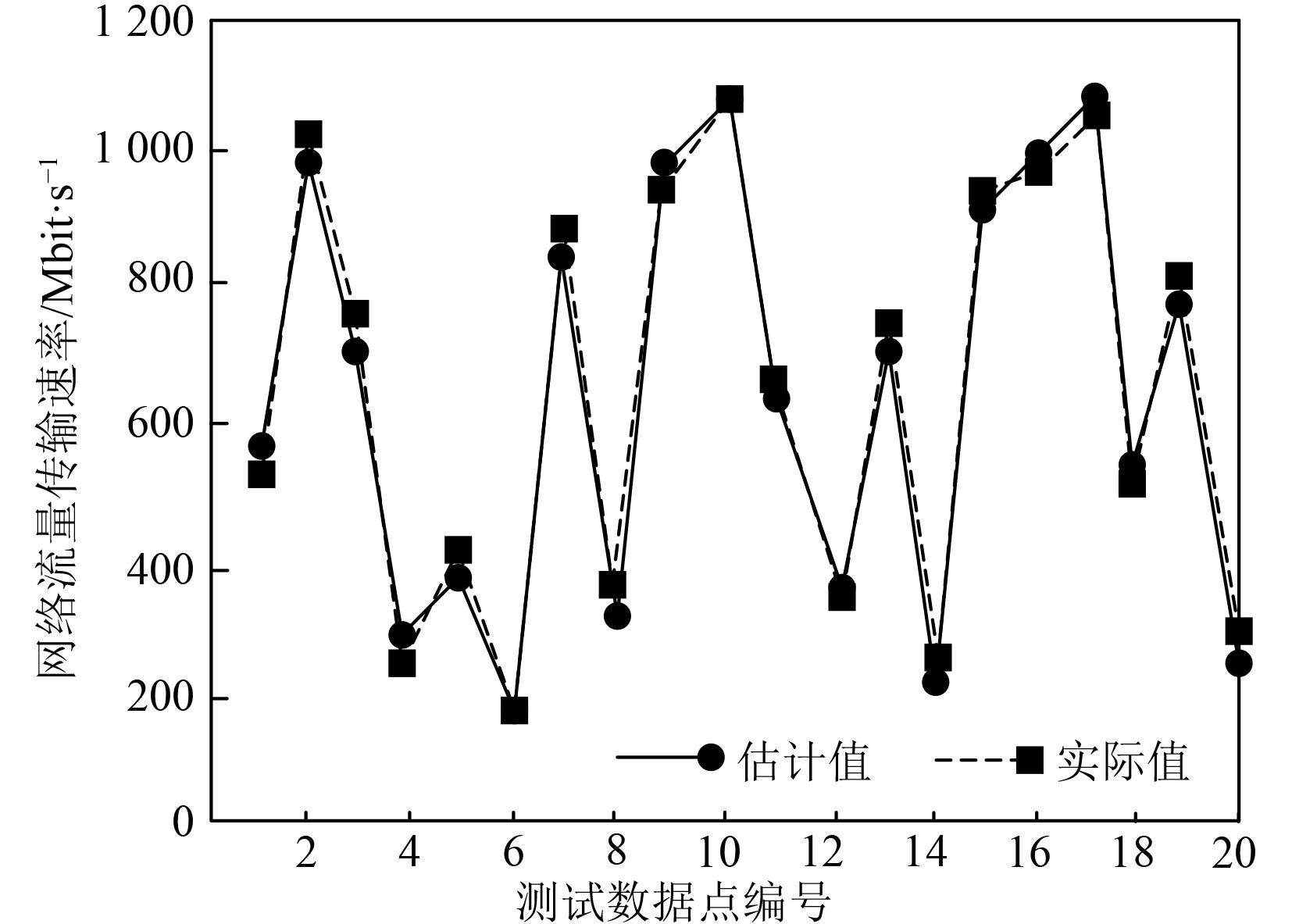
|
图 4 船舶通信网络流量估计结果 Fig. 4 Traffic estimation results of ship communication network |
通过充分利用大数据的规模和多样性优势,建立一个更为精确和可靠的数学模型来估计船舶通信网络的流量。本文模型不仅能够帮助更好地理解网络流量的动态变化,还可以为各种实际应用提供关键的决策支持。例如,通过预测未来的流量模式,可以提前进行资源调度和流量控制,以避免潜在的网络拥塞问题。此外,准确的流量估计还有助于提高船舶通信的安全性和效率。
| [1] |
刘敬贤, 高广旭, 刘奕, 等. 基于卷积神经网络及长短时记忆网络的短时船舶交通流量预测[J]. 中国航海, 2022, 45(2): 56-61+68. LIU Jing-xian, GAO Guang-xu, LIU Yi, et al. Short-term water traffic flow prediction with convolutional neural network and long short-term memory network[J]. Navigation of China, 2022, 45(2): 56-61+68. |
| [2] |
杨家轩, 许洲锦, 来源, 等. 基于概率攻击图的船舶网络安全评估模型[J]. 大连海事大学学报, 2023, 49(1): 26-33. YANG Jia-xuan, XU Zhou-jin, LAI Yuan, et al. Ship cyber security assessment model based on probability attack graph[J]. Journal of Dalian Maritime University, 2023, 49(1): 26-33. |
| [3] |
高勇, 陆钱春, 李锋. 面向IP网络扩容应用的复杂网络流量预测方法[J]. 电信科学, 2023, 39(9): 21-31. GAO Yong, LU Qian-chun, LI Feng. A complex network traffic prediction method for IP network expansion applications[J]. Telecommunications Science, 2023, 39(9): 21-31. |
| [4] |
徐海兵, 郭久明. 基于双向GRU模型的网络流量预测的研究[J]. 电子技术应用, 2022, 48(2): 19-22+27. XU Hai-bing, GUO Jiu-ming. Research on network traffic prediction based on Bi-GRU model[J]. Application of Electronic Technique, 2022, 48(2): 19-22+27. |
| [5] |
薛自杰, 卢昱妃, 宁芊, 等. 基于时空特征融合的网络流量预测模型[J]. 哈尔滨工业大学学报, 2023, 55(5): 30-38. XUE Zi-jie, LU Yu-fei, NING Qian, et al. Network flow prediction based on spatial-temporal features fusion[J]. Journal of Harbin Institute of Technology, 2023, 55(5): 30-38. |
 2024, Vol. 46
2024, Vol. 46
