临近空间是距地面20 ~ 100 km的高空区域[1],临近空间平台凭借高度特性,不仅可获得更准确的信息,也可最大程度躲避地面攻击,故临近空间战略价值受到很多人的关注。临近空间飞行器是该领域的重点研究内容,因传统预警系统无法实现该目标的精准探测,故临近空间飞行器具有较高的安全保障,这使其在军事侦察、电子对抗等作业领域有更广阔的发展空间[2]。利用导航雷达对临近空间低动态目标进行有效跟踪,对保障海域安全、国防安全等具有重大意义。
周琳等[3]为提高空间目标跟踪效果,采用无迹卡尔曼滤波器估计空间目标运行轨迹,但该方法计算难度大,且容易受到量测数据误差等影响,降低目标跟踪精度;傅虹景等[4]在对雷达量测点迹进行融合等处理的基础上,采用扩展卡尔曼滤波算法跟踪目标,确定其移动轨迹,但该方法对初始值要求较高,一旦其值选取不合适,将大大降低目标跟踪效果。
鉴于以上方法存在的问题,本文提出船舶导航雷达临近空间低动态目标跟踪方法,设计的基于衰减记忆的最小二乘滤波器,无需利用目标运动模型等先验知识即可实现低动态目标的精准跟踪,具有强大的适应性和鲁棒性,可适用于复杂环境下目标的稳定跟踪。
1 船舶导航雷达临近空间低动态目标跟踪 1.1 低动态飞行器运动对雷达量测的影响分析船舶导航雷达是一种用于探测和跟踪目标的雷达系统[5],利用电磁波的发射与反射原理,当电磁波遇到目标后会反射回来形成回波信号。在船舶领域,船舶导航雷达为船员提供航行和避障的精确指引。通过实时显示周围海域的详细信息,船舶导航雷达为船员提供重要的决策依据,保障航行的安全和效率。
通过下式描述船舶导航雷达发射的LFM脉冲信号:
| $ s\left( t \right) = rect\left( {t/\tau } \right)\cos \left[ {\pi t\left( {2{f_0} + \mu t} \right)} \right] 。$ | (1) |
式中:
当低动态飞行器按照速度
| $ {s_r}\left( t \right) = rect\left( {\gamma \left( {t - {t_0}} \right)/\tau } \right)\cos \left[ {\pi \gamma \left( {t - {t_0}} \right)\left( {2{f_0} + \mu \gamma \left( {t - {t_0}} \right)} \right)} \right]。$ | (2) |
式中:
对
| $ {s_0}\left( t \right) = \left( {\tau - \left| {t - {t_0}} \right|} \right) \times \left( {\left| {t - {t_0}} \right| + {f_d}} \right) 。$ | (3) |
式中:
| $ \Delta r = \frac{{{f_d} \times c}}{\lambda }。$ | (4) |
式中,
利用船舶导航雷达对
|
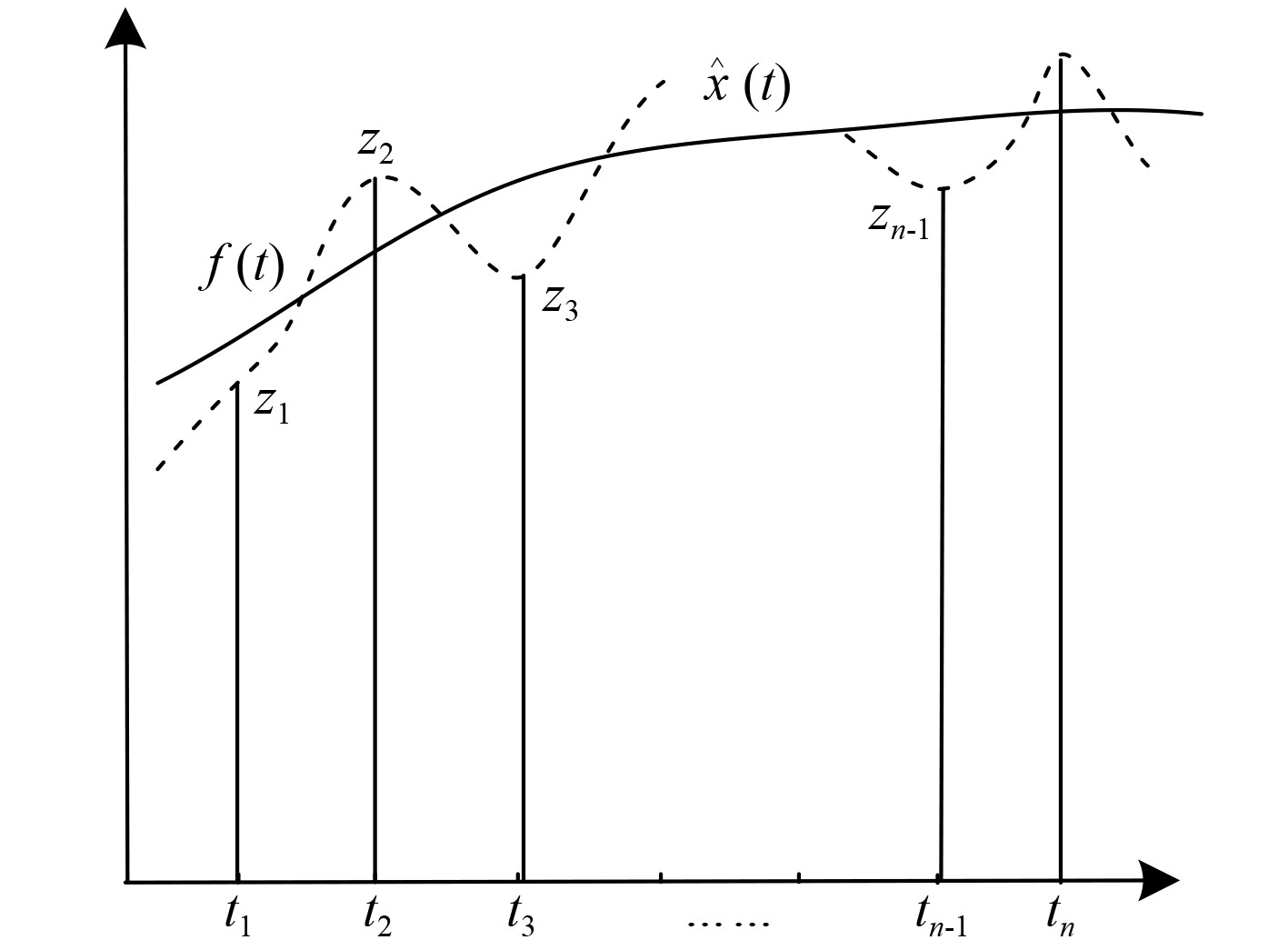
图 1 最小二乘滤波的基本原理 Fig. 1 Basic principle of least squares filtering |
| $ \hat x\left( t \right) = {a_0} + {a_1}t + {a_2}{t^2} + \cdots + {a_m}{t^m} = \sum\limits_{j = 0}^m {{a_j}{t^j}}。$ | (5) |
式中:
| $\left\{ \begin{gathered} {\varepsilon _1} = \left( {{a_0} + {a_1}{t_1} + {a_2}t_1^2 + \cdots + {a_m}t_1^m} \right) - {z_1} ,\\ {\varepsilon _2} = \left( {{a_0} + {a_1}{t_2} + {a_2}t_2^2 + \cdots + {a_m}t_2^m} \right) - {z_2} ,\\ \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \vdots \\ {\varepsilon _n} = \left( {{a_0} + {a_1}{t_n} + {a_2}t_n^2 + \cdots + {a_m}t_n^m} \right) - {z_n}。\\ \end{gathered} \right. $ | (6) |
可简化为:
| $ {\varepsilon _i} = \sum\limits_{j = 0}^m {{a_j}{t^j}} - {z_n}。$ | (7) |
应用最小二乘滤波方法对移动目标进行跟踪,是通过最小化观测数据与预测数据之间的误差平方和实现目标状态的估计,无需获取目标运动模型和机动特性等先验知识[6-7],因此,该方法在难以通过精确数学模型进行描述的动态目标追踪中,展现了更高的实用性。通过最小二乘滤波方法对临近空间低动态目标进行跟踪,存在目标机动响应延迟高的问题,这无疑会提高船舶导航雷达对低动态飞行器跟踪误差。针对以上问题,本文提出基于衰减记忆的最小二乘滤波方法,即在处理接近
基于衰减记忆最小二乘滤波的临近空间低动态目标跟踪步骤具体为:
步骤1 首先通过船舶导航雷达对临近空间低动态目标进行探测,确定其量测点迹
步骤2 依照衰减记忆原则,从原始点迹集合中筛选部分历史量测点迹
步骤3 将步骤二确定的坐标值转换到极坐标系下。
利用基于衰减记忆最小二乘滤波方法对临近空间低动态目标进行跟踪,确定的
以飞行在临近空间的高空长航时无人机为实验对象,利用船舶导航雷达对其进行探测跟踪,获取其位置、速度、方向等量测数据,船舶导航雷达目标探测距离最大值为1 100 km,距离、位置以及方向探测精度分别为10 m、0.15°、0.10°。将研究方法应用到临近空间低动态目标跟踪中,在Maltab工具上对目标跟踪轨迹进行模拟,分析研究方法的目标跟踪性能。
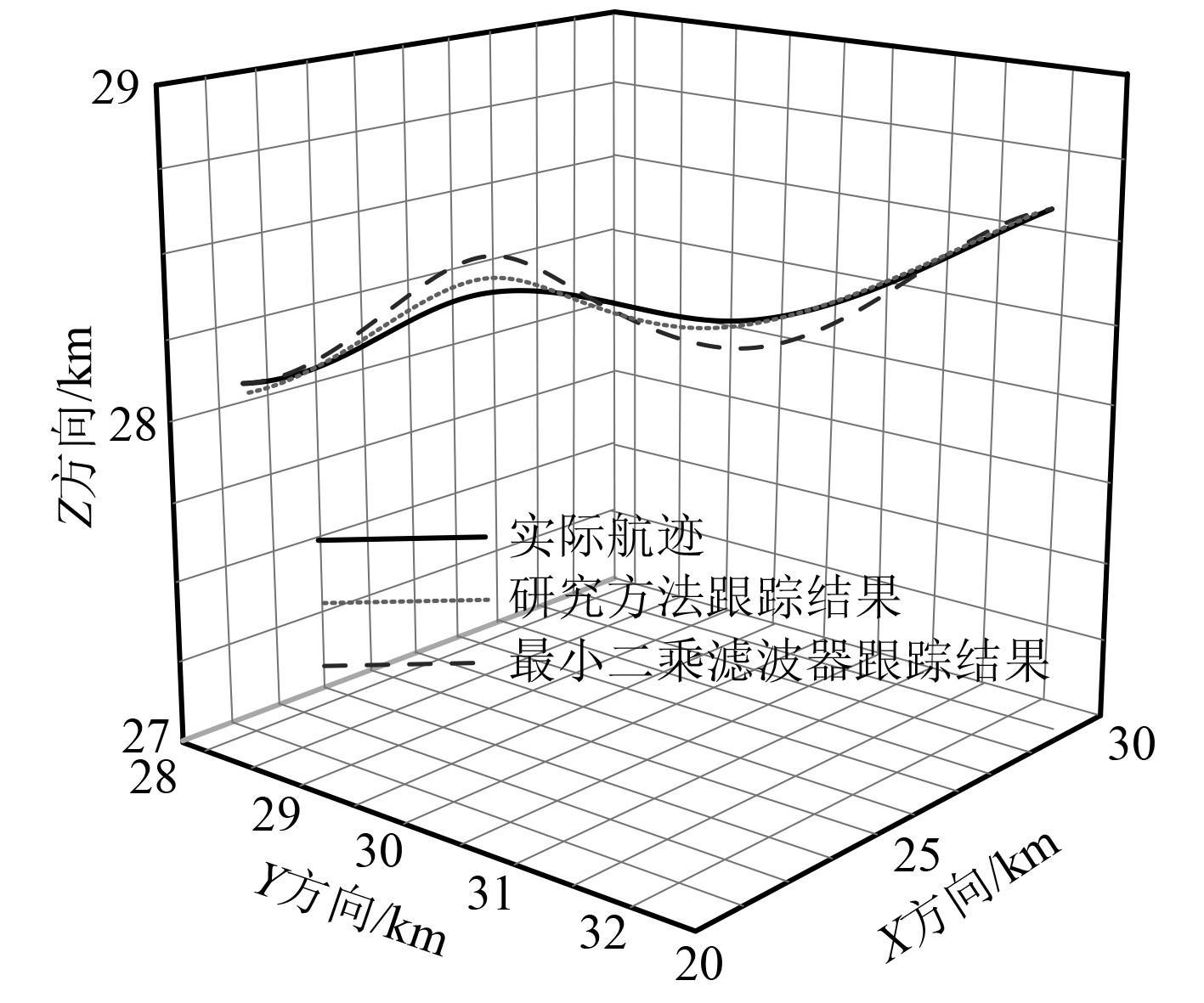
为验证研究方法的目标跟踪性能,将改进前的最小二乘滤波器作为对比,在匀速飞行条件下,改进前后高空长航时无人机轨迹跟踪结果如图2所示。
|
图 2 匀速飞行下的目标跟踪结果 Fig. 2 Target tracking results under constant speed flight |
可知,利用研究方法对高空长航时无人机进行追踪,得到的飞行轨迹曲线与实际航迹曲线大体保持一致的走势规律,且二者基本重合;改进前的跟踪轨迹曲线虽与实际航迹曲线呈现相似的规律,但仍存在一定偏差,且偏差高于研究方法。这说明通过对最小二乘滤波器进行改进,可有效提升临近空间低动态目标跟踪精度,防止目标跟踪丢失。
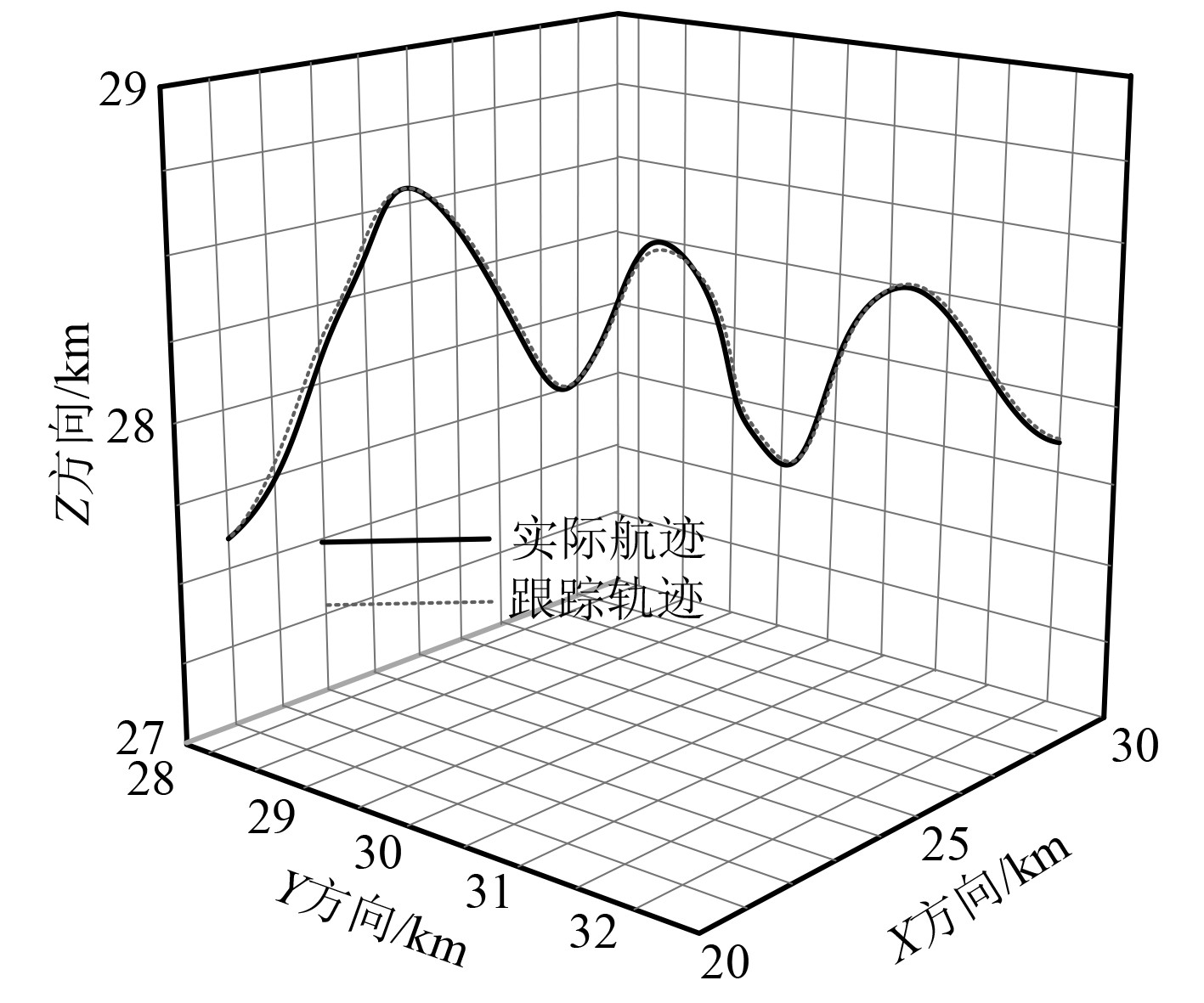
设定高空长航时无人机以200 m/s的初始速度作匀加速运动,当速度上升到最大速度340 m/s后,保持匀速飞行。在此条件下,应用研究方法对高空长航时无人机进行跟踪,将目标跟踪结果与该无人机实际航迹进行对比,通过比较2条轨迹差异,分析研究方法的目标跟踪效果。目标跟踪结果与实际航迹对比分析如图3所示。
|
图 3 目标跟踪结果与实际航迹对比分析 Fig. 3 Comparative analysis of target tracking results and actual flight path |
可知,利用船舶导航雷达对正在临近空间匀加速飞行的高空长航时无人机进行探测跟踪,目标航迹跟踪结果为一条不规律曲线,该曲线中存在数个波峰、波谷。目标跟踪轨迹与该无人机实际航迹大体保持相同的走势规律,且二者具有较高的贴合度。实验结果表明,研究方法可实现临近空间低动态目标跟踪,且能取得较好的跟踪效果。
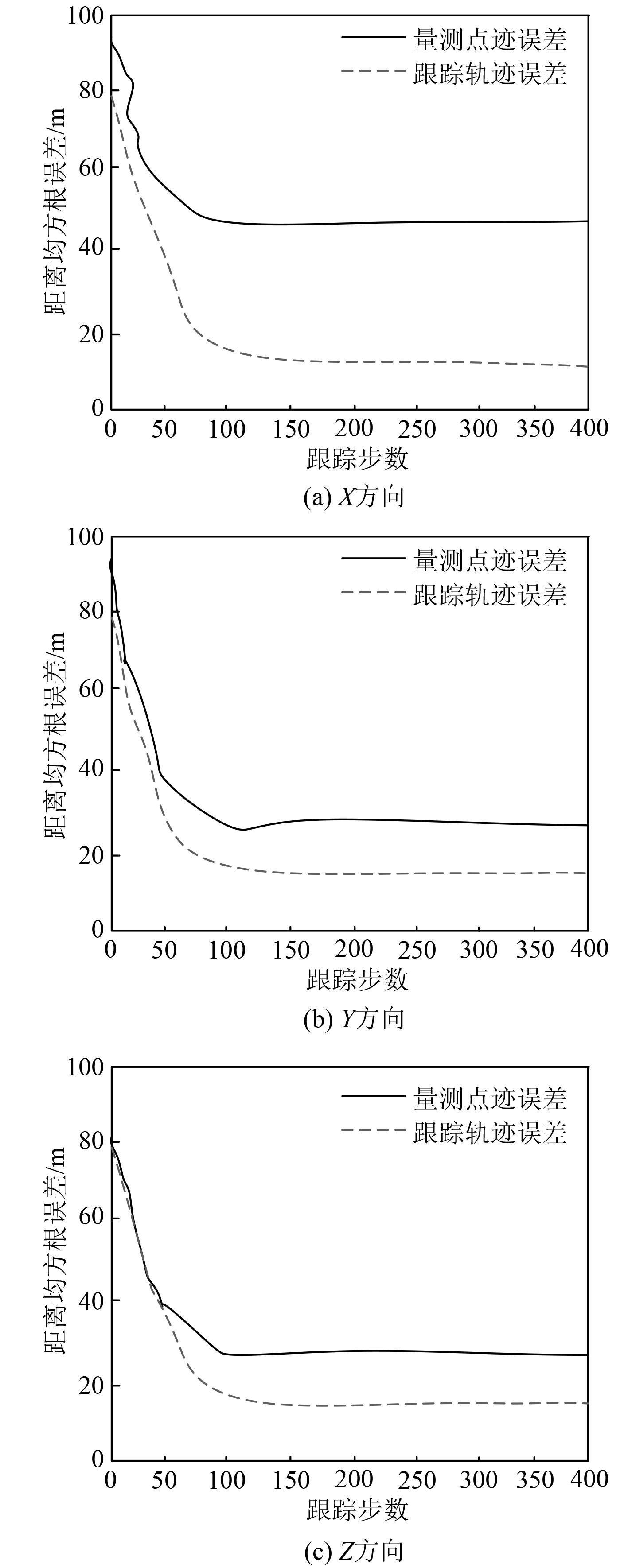
为实现目标轨迹跟踪效果的量化分析,本文对目标跟踪轨迹在X、Y、Z方向上的距离均方根误差进行计算,将其与量测数据的距离均方根误差计算结果进行对比,验证研究方法的实用性能,实验结果如图4所示。
|
图 4 目标跟踪轨迹与实际航迹位置均方根误差对比 Fig. 4 Comparison of root mean square error between target tracking trajectory and actual track position |
可知,采用研究方法对低动态目标进行跟踪,随着跟踪步数的不断增加,目标跟踪轨迹在X、Y、Z方向上的距离均方根误差曲线呈不断降低趋势变化,跟踪步数达到100步后,3个方向上的距离均方根误差曲线均开始慢慢趋于平稳,最终误差均不超过15 m。滤波前量测点迹在X、Y、Z方向上的均方根误差最终稳定在50 m之内,远远高于目标跟踪轨迹在3方向上的误差。实验结果表明,研究方法通过对量测点迹进行滤波,使临近空间动态目标跟踪效果获得显著提升,达到为后续任务提供目标信息的目的。
3 结 语临近空间低动态目标运动产生的距离时延误差会给导航雷达探测带来一定困难,为此本文研究船舶导航雷达临近空间低动态目标跟踪方法,设计的基于衰减记忆的最小二乘滤波器无需事先获取低动态目标运动模型等先验知识,依据衰减记忆原则对历史量测点迹进行选取,从而实现低动态目标跟踪。本文通过对匀速、匀加速飞行条件下的高空长航时无人机轨迹跟踪结果等进行对比分析,验证研究方法的有效性。通过实验得到如下结论:
1)考虑临近空间低动态飞行器运动产生的误差,更有利于目标跟踪效果的提升。本文方法可有效提升临近空间低动态目标跟踪精度,防止目标跟踪丢失。
2)研究方法可实现临近空间低动态目标跟踪,跟踪轨迹曲线与实际航迹曲线具有较高重合度。
3)跟踪轨迹在X、Y、Z方向上的距离均方根误差均低于15 m,明显小于量测点迹在3方向上的均方根误差。
| [1] |
罗健. 雷达探测临近空间高超声速目标关键技术研究[J]. 雷达科学与技术, 2021, 19(6): 640-650. LUO Jian. Research on key technologies of radar detection of near space hypersonic weapon[J]. Radar Science and Technology, 2021, 19(6): 640-650. |
| [2] |
李君龙, 周荻, 王冠, 等. 临近空间目标跟踪与预报技术研究[J]. 现代防御技术, 2021, 49(3): 1-12+29. LI Jun-long, ZHOU Di, WANG Guan, et al. Research on tracking and prediction technology of near space target[J]. Modern Defense Technology, 2021, 49(3): 1-12+29. |
| [3] |
周琳, 刁伟峰, 王祎. 基于可观性分析的高精度空间目标跟踪方法[J]. 雷达科学与技术, 2021, 19(5): 485-490. ZHOU Lin, DIAO Wei-feng, WANG Wei. A high-precision spatial target tracking method based on observability analysis[J]. Radar Science and Technology, 2021, 19(5): 485-490. |
| [4] |
傅虹景, 贾春宁, 于守江, 等. 一种适用于双波段旋转相控阵雷达的目标跟踪方法[J]. 无线电工程, 2022, 52(9): 1533-1538. FU Hong-jing, JIA Chun-ning, YU Shou-jiang, et al. A target tracking method suitable for dual band rotating phased array radar[J]. Radio Engineering, 2022, 52(9): 1533-1538. |
| [5] |
王明洋, 任鸿翔, 郑民民. 基于Android的航海雷达仿真训练系统[J]. 计算机仿真, 2020, 37(9): 11-15. WANG Ming-yang, REN Hong-xiang, ZHENG Min-min. An android based navigation radar simulation training system[J]. Computer Simulation, 2020, 37(9): 11-15. |
| [6] |
乔钢柱, 朱良泽, 丁智慧. 基于多项式最小二乘滤波的时间序列相似性度量[J]. 测试技术学报, 2020, 34(4): 28-33. QIAO Gang-zhu, ZHU Liang-ze, DING Zhi-hui. Time series similarity measurement based on polynomial least squares filtering[J]. Journal of Testing Technology, 2020, 34(4): 28-33. |
| [7] |
畅言, 鲁金, 罗利强. 一种基于最小二乘的航迹滤波方法[J]. 火控雷达技术, 2021, 50(3): 64-66. CHANG Yan, LU Jin, LUO Li-qiang. A Track Filtering Method Based On Least Squares[J]. Fire Control Radar Technology, 2021, 50(3): 64-66. |
 2024, Vol. 46
2024, Vol. 46
