0 引　言

船舶在海洋环境中的行驶受到许多因素的影响，其中雾霾天气下能见度不足是一个较为严重的问题^[1-2]。雾霾天气下，船舶驾驶员难以准确判断周围环境和航道情况，从而增加了碰撞、搁浅等事故的风险^[3]。因此，提高雾天船舶的安全性和运营效率已成为亟待解决的问题。

冯珂等^[4]探索了在复杂气象海况条件下船舶航行的安全辨识和优化方法，考虑到复杂气象海况，并构建了航行优化模型，将决策变量在空间分布和时间序列上的耦合特性作为先验知识，解决航线不平滑的问题。王壮等^[5]在已知海况信息和航线信息的前提下，对船舶航线进行识别，并对航速进行动态优化。构建航线分段模型，将总航程、航行时间、主机转速等设定为模型的约束条件，利用遗传算法进行求解。杨家轩等^[6]利用密度的空间聚类算法，对船舶轨迹进行聚类，并对航线进行识别。利用Hausdorff距离作为船舶轨迹之间的相似度度量，完成对船舶轨迹的聚类，人工确定DBTCAN算法的输入参数，完成参数的自适应确定，以此实现对航线的智能识别。以上方法没有考虑雾天激光雷达回波信号强度下幅度减弱的情况，船舶航线辨识准确率不理想。

为了解决上述方法存在的问题，提出基于激光雷达回波信号的雾天船舶航线快速辨识方法。

1 雾天激光雷达回波信号预处理 1.1 激光雷达回波信号增强处理

信号累积增强的本质是通过累积激光雷达系统作用区域内若干回波信号生成高强度回波信号，采用增强后回波信号实现目标辨识^[7]。

假设用f表示激光雷达脉冲重复频率，则脉冲周期为T=1f，L表示激光信号覆盖范围直径距离，依据脉冲激光雷达距离测量理论分割T^[8]，分割后每个时间单元Δt均与一个距离单元ΔL相对应。在全周期内采用相同间隔划分T，则分割单元数量M=T/Δt，距离单元ΔL=cΔt/2，其中c表示光速，取值为c=3×10⁸ m/s。

选取加法作为激光雷达回波信号累积方法。以上回波信号累积方法建立在全部回波信号相互独立基础上，即接收系统响应时长$ {t_r} $远小于相邻脉冲时间间隔$ {t_p} $，采用累积连续多个重复周期内激光雷达回波信号的方式增强信号。

用$ {Z_i} = \left[ {{z_0},{z_1}, \cdots ,{z_w}} \right] $表示单个脉冲激光雷达回波信号序列，$ {S_i} = \left[ {{s_0},{s_1}, \cdots ,{s_w}} \right] $表示噪声序列，其中$ w $表示采样总数，则可得到回波信号和噪声信号能量$ {P_Z} $和$ {P_S} $，如下所示：

$ \left\{ \begin{gathered} {P_Z} = \sum\limits_{j = 0}^w {x_j^2} ,j \in w ，\\ {P_S} = \sum\limits_{j = 0}^w {s_j^2} ,j \in w 。\\ \end{gathered} \right. $

(1)

根据式（1）可得当前功率信噪比$ SN{R_i} $，具体计算公式为：

$ SN{R_i}=\frac{{{P_Z}}}{{{P_S}}}=\frac{{\displaystyle\sum\limits_{j = 0}^w {x_j^2} }}{{\displaystyle\sum\limits_{j = 0}^w {s_j^2} }} 。$

(2)

在完成k次累积后，信号功率为k²P_Z，噪声功率为kP_S，由此可得k次累积后信噪比，如下所示：

$ SN{R_k}{\text{ = }}\frac{{{k^2}{P_Z}}}{{k{P_S}}} = kSN{R_i} 。$

(3)

通过分析式（1）和式（3）可以看出，多脉冲激光雷达回波信号累积增强方法在提升微弱回波信号信噪比过程中的效果优异，能够增强微弱信号^[9]。

1.2 激光雷达回波信号去噪

为了提升后续船舶航线快速辨识效果，需要采用改进的经验模态分解（EMD）算法对累积增强后的回波信号进行去噪处理^[10]，EMD通过自适应分解含噪信号获取有限个固有模态函数（IMFs），其中每个IMF分量均为原信号频率分量子集构成的振荡信号，通过将IMFs和残差相加可实现信号去噪。

假设$ x\left( n \right) $表示真实信号，$ s\left( n \right) $表示噪声信号，则激光雷达回波信号$ y\left( n \right) = x\left( n \right) + s\left( n \right) $，通过传统EMD算法重构后信号$ y'\left( n \right) =\displaystyle \sum\limits_{i = {k_{th}}}^Q {{g^{\left( i \right)}}\left( n \right)} + r\left( n \right) $，其中$ {g^{\left( i \right)}}\left( n \right) $表示第$ i $个IMF分量，$ Q $表示IMFs分量总数，$ r\left( n \right) $表示残差，$ {k_{th}} $表示$ y\left( n \right) $与IMF分量间相关性参数^[11]。则存在$ {\dot y_m}\left( n \right) = y\left( n \right) -\displaystyle \sum\limits_{i = 1}^m {{g^{\left( i \right)}}\left( n \right)} $，由此可得$ y\left( n \right) $与$ {\dot y_m}\left( n \right) $之间相关系数$ \eta \left( m \right) $，用$ D $表示IMF分量长度，$ d \in D $，$ m $表示$ \eta \left( m \right) $开始低于常数$ B $时数值，则

$ \eta \left( m \right){\text{ = }}\frac{{\displaystyle\sum\limits_{d = 1}^D {y\left( n \right){{\dot y}_m}\left( n \right)} }}{{\sqrt {\displaystyle\sum\limits_{d = 1}^D {{y^2}\left( n \right)} \sum\limits_{d = 1}^D {{{\left( {{{\dot y}_m}} \right)}^2}\left( n \right)} } }}。$

(4)

一般情况下，$ \eta \left( m \right) $会逐渐减小并降至最小值，依据设定的$ B $值，可以确定$ {k_{th}} $位置，即首个相关分量位置，如下所示：

$ {k_{th}}{\text{ = }}\arg \mathop {last}\limits_{1 \leqslant m \leqslant Q} \left\{ {\eta \left( m \right) \geqslant B} \right\} + 1。$

(5)

式中，$ last $表示$ \eta \left( m \right) $中最后一个大于等于$ B $的值。在确定$ {k_{th}} $位置后，前$ {k_{th}} - 1 $项IMFs为不相关分量，其余为相关分量。

2 基于激光雷达回波信号的船舶航线快速辨识 2.1 船舶航线特征提取

增强去噪后激光雷达回波信号中包含信息主要为扫描点到激光雷达之间距离、回波脉冲宽度、水平角度和回波返回层等，滤除角度过大、距离过远的回波信号。采用剩余信号构造栅格图，计算全部栅格点平均回波脉冲宽度，为缓解不同层的不同性质影响检测精度，先实施分层映射后再对结果加以整合，实现栅格化处理。

有效区分船舶航线和水面是船舶航线特征提取的重点，分别以回波脉冲宽度和点数为横、纵坐标构建直方图^[13]，结合实际情况采用合适尺度划分直方图。一般情况下，船舶航线特征和水面特征在直方图中大多分布在不同区间，即依据回波脉冲宽度能够实现船舶航线特征与水面特征的划分。用$ P = \left( {1,2, \cdots ,{P_w}} \right) $表示划分后回波脉冲宽度级别，$ {m_i} $表示级别$ i $中总点数，$ {M_w} $表示全部级别总点数，则存在$ {M_w}=\displaystyle\sum\limits_{i = 1}^{{P_w}} {{m_i}} $，则脉冲宽度属于级别$ i $的概率$ {\phi _w}\left( i \right) = {{{m_i}}/ {{M_w}}} $。设置船舶航线与水面的区分阈值$ {V_w} $，则将船舶航线记作$ {O_1} \in \{ 1,2, \cdots , {V_w} \} $，水面记作$ {O_r} \in \left\{ {{V_w} + 1,{V_w} + 2, \cdots ,{P_w}} \right\} $，$ \phi \left( {i\left| {{O_1}} \right.} \right) $和$ \phi \left( {i\left| {{O_r}} \right.} \right) $分别表示级别$ i $脉冲宽度存在于$ {O_1} $和$ {O_r} $中的概率，则船舶航线和水面特征值$ {\mu _1} $、$ {\mu _r} $，两者脉冲宽度划分级均值$ {\tau _1} $、$ {\tau _r} $和方差$ \sigma _1^2 $、$ \sigma _r^2 $如下所示：

$ \begin{gathered} \left\{ \begin{gathered} {\mu _1} = \frac{{\displaystyle \sum\limits_{i = 1}^{{V_w}} {{m_i}} }}{{{M_w}}} = \displaystyle \sum\limits_{i = 1}^{{V_w}} {{\phi _w}\left( i \right)}，\\ {\mu _r} = \frac{{\displaystyle \sum\limits_{i = {V_w} + 1}^{{V_w}} {{m_i}} }}{{{M_w}}} = \displaystyle \sum\limits_{i = {V_w} + 1}^{{V_w}} {{\phi _w}\left( i \right) = 1 - {\mu _1}} 。\\ \end{gathered} \right. \\ \left\{ \begin{gathered} {\tau _1} = \frac{{\displaystyle \sum\limits_{i = 1}^{{V_w}} {i \times {m_i}} }}{{\displaystyle \sum\limits_{i = 1}^{{V_w}} {{m_i}} }} = \frac{{\displaystyle \sum\limits_{i = 1}^{{V_w}} {{\phi _w}\left( i \right) \times i} }}{{{\mu _1}}}，\\ {\tau _r} = \frac{{\displaystyle \sum\limits_{i = {V_w} + 1}^{{V_w}} {i \times {m_i}} }}{{\displaystyle \sum\limits_{i = {V_w} + 1}^{{V_w}} {{m_i}} }} = \frac{{\displaystyle \sum\limits_{i = {V_w} + 1}^{{V_w}} {{\phi _w}\left( i \right) \times i} }}{{{\mu _r}}} 。\\ \end{gathered} \right. \\ \left\{ \begin{gathered} \sigma _1^2 = \displaystyle \sum\limits_{i = 1}^{{V_w}} {{{\left( {i - {\tau _1}} \right)}^2} \times \phi \left( {i\left| {{O_1}} \right.} \right)} ，\\ \sigma _r^2 = \displaystyle \sum\limits_{i = {V_w} + 1}^{{V_w}} {{{\left( {i - {\tau _r}} \right)}^2} \times \phi \left( {i\left| {{O_r}} \right.} \right)} 。\\ \end{gathered} \right. \end{gathered} $

(6)

依据式（6）计算船舶航线和水面之间类内方差$ G\left( {{V_w}} \right) = {\mu _1} \times \sigma _1^2 + {\mu _r} \times \sigma _r^2 $，通过不断迭代获取最小$ G\left( {{V_w}} \right) $值，当满足$ \max \left[ {G\left( {{V_w}} \right)} \right],1 \leqslant {V_w} \leqslant {P_w} $时，$ {V_w} $为区分宽度级的最佳阈值。

采用最小类内方差得到船舶航线和水面最佳分割阈值后，引入$ 3\sigma $原理过滤粗大误差，获取船舶航线脉宽度动态阈值。用$ \left( {{V_1},{V_2}, \cdots ,{V_m}} \right) $表示脉冲宽度区间$ \left( {0,5{V_w}} \right) $内全部样本值，依据式（6）计算对应均值和标准差$ \sigma $，$ \sigma = \sqrt {{\sigma ^2}} $，由$ 3\sigma $原理可知，根据船舶航线的脉冲宽度，可靠阈值区间为$ \left( {\tau - 3\sigma ,\tau + 3\sigma } \right) $，在排除粗大误差后，点的特征种子点被定义为满足区间$ \left( {\tau - 3\sigma ,\tau + 3\sigma } \right) $的点。

完成特征种子点提取后，引入基于高斯核函数的高斯加权搜索法对种子点附近回波信号点加以搜索，确定种子点附近回波信号是否为特征点^{[14 − 15]}。

假设$ A = \left\{ {{A_1},{A_2}, \cdots {A_n}} \right\} $为满足船舶航线脉冲宽度可靠阈值区间$ \left( {\tau - 3\sigma ,\tau + 3\sigma } \right) $点的集合，满足该条件的点均为船舶航线特征点，以$ A $中每个点$ {A_i} $为圆心，$ R $为半径建立圆$ C $，$ i = 1,2, \cdots ,m $，$ R $依据实际需求确定，将圆内属于和不属于$ A $的点分别记作$ a = \left\{ {{a_1},{a_2}, \cdots ,{a_p}} \right\} $和$ b = \left\{ {{b_1},{b_2}, \cdots ,{b_q}} \right\} $。在实际应用中，点与圆纵向直径之间距离越小，则属于船舶航线特征点概率越大，反之则属于船舶航线特征点概率越小，因此构建$ {b_i} $相对于$ {a_j} $属于船舶航线特征点的目标函数$ P\left( {{b_i}\left| {{a_j}} \right.} \right) $，$ {b_i} \in b $，$ {a_j} \in a $，用$ {b_{xi}} $、$ {b_{yi}} $和$ {a_{xj}} $和$ {a_{yj}} $分别表示$ {b_i} $和$ {a_j} $的横、纵坐标，则$ P\left( {{b_i}\left| {{a_j}} \right.} \right) $如下所示：

$ \left\{ \begin{aligned} & P\left( {{b_i}\left| {{a_j}} \right.} \right) = \frac{1}{{\sqrt {2\text{π} } {\sigma _s}}} \cdot \exp \left( {\frac{{ - {{\left| {{{\left( {{b_{xi}} - {a_{xj}}} \right)} \mathord{\left/ {\vphantom {{\left( {{b_{xi}} - {a_{xj}}} \right)} {\left( {{b_{yi}} - {a_{yj}}} \right)}}} \right. } {\left( {{b_{yi}} - {a_{yj}}} \right)}}} \right|}^2}}}{{2\sigma _s^2}}} \right)，\\ & {\sigma _s}{\text{ = }}\sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^t {{{\left| {\dfrac{{{e_{xi}} - {a_{xj}}}}{{{e_{yi}} - {a_{yj}}}}} \right|}^2}} }}{{t - 1}}}。\end{aligned} \right. $

(7)

假设$ E = \left\{ {{e_1},{e_2}, \cdots ,{e_t}} \right\} $为全部可能出现于圆中的像素点，$ {e_i} \in E $，式中，$ {e_{xi}} $和$ {e_{yi}} $表示$ {e_i} $的横、纵坐标，$ {\sigma _s} $表示$ {e_i} $与$ {a_j} $之间标准差，$ | {{{( {{b_{xi}} - {a_{xj}}} )} /{( {{b_{yi}} - {a_{yj}}} )}}} | $表示$ {b_i} $相对于$ {a_j} $的偏离程度，其值分布在$ \left( {0, + \infty } \right) $范围内。由于分散程度过大，将其直接作为种子点并不合适，因此引入高斯核变换映射$ {b_i} $为满足高斯分布随机变量的概率密度函数，由此得到种子点与$ {b_i} $影响因素融合公式：

$ {P_{{b_i}}} = \sum\limits_{j = 1}^p {\frac{1}{{\sqrt {2{\text{π}} } {\sigma _s}}} \cdot } \exp \left( {\frac{{ - {{| {{{( {{b_{xi}} - {a_{xj}}} )}/ {( {{b_{yi}} - {a_{yj}}} )}}} |}^2}}}{{2\sigma _s^2 \cdot \dfrac{1}{p}}}} \right)。$

(8)

统计每帧激光雷达回波图像中属于和不属于船舶航线的像素点，并依据式（8）计算每个像素点的$ {P_{{b_i}}} $，可得到船舶航线与非船舶航线的$ {P_{{b_i}}} $分布情况。分析计算结果可知，当$ {P_{{b_i}}} > 0.65 \times \dfrac{1}{{\sqrt {2{\text{π}} } {\sigma _s}}} $时，可判定$ {b_i} $为船舶航线特征点，将其加入集合$ A $，同时将$ {A_i} $由$ A $转出加入集合$ W $，若$ A = \emptyset $，则搜索结束，完成船舶航线特征点提取，集合$ W $为全部船舶航线特征点集合计算式为：

$ \begin{aligned} W = &\left\{ {{w_1},{w_2}, \cdots ,{w_m}} \right\} = \\ &\left\{ {\left( {{w_{x1}},{w_{y1}}} \right),\left( {{w_{x2}},{w_{y2}}} \right), \cdots ,\left( {{w_{xm}},{w_{ym}}} \right)} \right\}。\end{aligned} $

(9)

其中，$ \left( {{w_{xi}},{w_{yi}}} \right) $表示特征点横、纵坐标。

2.2 船舶航线识别

引入最小二乘法对聚类后特征点拟合处理，生成船舶航线轮廓。最小二乘法拟合是通过持续优化给定数据点获取最优曲线函数，使给定数据点与曲线之间距离平方和数值最小的优化方法。将提取出的船舶航线特征点集$ W $作为给定数据点集，$ {\alpha _0} $、$ {\alpha _1} $、$ {\alpha _2} $表示最小二乘法待求取未知参数，则拟合后二次曲线方程为：

$ {w_{yi}} = {\alpha _0} + {\alpha _1}{w_{xi}} + {\alpha _2}w_{xi}^2。$

(10)

分析可知，拟合过程即为获取$ {\alpha _0} $、$ {\alpha _1} $、$ {\alpha _2} $的最佳估计值的过程，使满足条件“特征点与曲线之间距离平方和数值最小”的过程，构建误差函数$ \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right) $：

$ \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right) = \sum\limits_{i = 1}^m {{{\left( {{\alpha _0} + {\alpha _1}{w_{xi}} + {\alpha _2}w_{xi}^2 - {w_{yi}}} \right)}^2}}。$

(11)

当$ \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right) $最小时，对$ \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right) $求取$ {\alpha _0} $、$ {\alpha _1} $、$ {\alpha _2} $的偏导，使偏导值为0，得到下式：

$ \left\{ \begin{gathered} \frac{{\partial \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right)}}{{\partial {\alpha _0}}} = 2\sum\limits_{i = 1}^m {{{\left( {{\alpha _0} + {\alpha _1}{w_{xi}} + {\alpha _2}w_{xi}^2 - {w_{yi}}} \right)}^2} = 0}，\\ \frac{{\partial \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right)}}{{\partial {\alpha _1}}} = 2\sum\limits_{i = 1}^m {{{\left( {{\alpha _0} + {\alpha _1}{w_{xi}} + {\alpha _2}w_{xi}^2 - {w_{yi}}} \right)}^2}{w_{xi}} = 0} ，\\ \frac{{\partial \psi \left( {{\alpha _0},{\alpha _1},{\alpha _2}} \right)}}{{\partial {\alpha _2}}} = 2\sum\limits_{i = 1}^m {{{\left( {{\alpha _0} + {\alpha _1}{w_{xi}} + {\alpha _2}w_{xi}^2 - {w_{yi}}} \right)}^2}w_{xi}^2 = 0}。\end{gathered} \right. $

(12)

整理式（12）可得二次多项式函数拟合方程组：

$ \left( {\begin{array}{*{20}{c}} m&{\displaystyle \sum\limits_{i = 1}^m {{w_{xi}}} }&{\displaystyle \sum\limits_{i = 1}^m {w_{xi}^2} } \\ {\displaystyle \sum\limits_{i = 1}^m {{w_{xi}}} }&{\displaystyle \sum\limits_{i = 1}^m {w_{xi}^2} }&{\displaystyle \sum\limits_{i = 1}^m {w_{xi}^3} } \\ {\displaystyle \sum\limits_{i = 1}^m {w_{xi}^2} }&{\displaystyle \sum\limits_{i = 1}^m {w_{xi}^3} }&{\displaystyle \sum\limits_{i = 1}^m {w_{xi}^4} } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\alpha _0}} \\ {{\alpha _1}} \\ {{\alpha _2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\displaystyle \sum\limits_{i = 1}^m {{w_{yi}}} } \\ {\displaystyle \sum\limits_{i = 1}^m {{w_{xi}}} {w_{yi}}} \\ {\displaystyle \sum\limits_{i = 1}^m {w_{xi}^2} {w_{yi}}} \end{array}} \right) 。$

(13)

求解式（13）即可得到$ {\alpha _0} $、$ {\alpha _1} $、$ {\alpha _2} $取值，从而得到船舶航线特征点拟合二次曲线方程，实现雾天船舶航线的快速辨识

3 实验与结果

为了验证基于激光雷达回波信号的雾天船舶航线快速辨识方法的整体有效性，需要测试基于激光雷达回波信号的雾天船舶航线快速辨识研究。

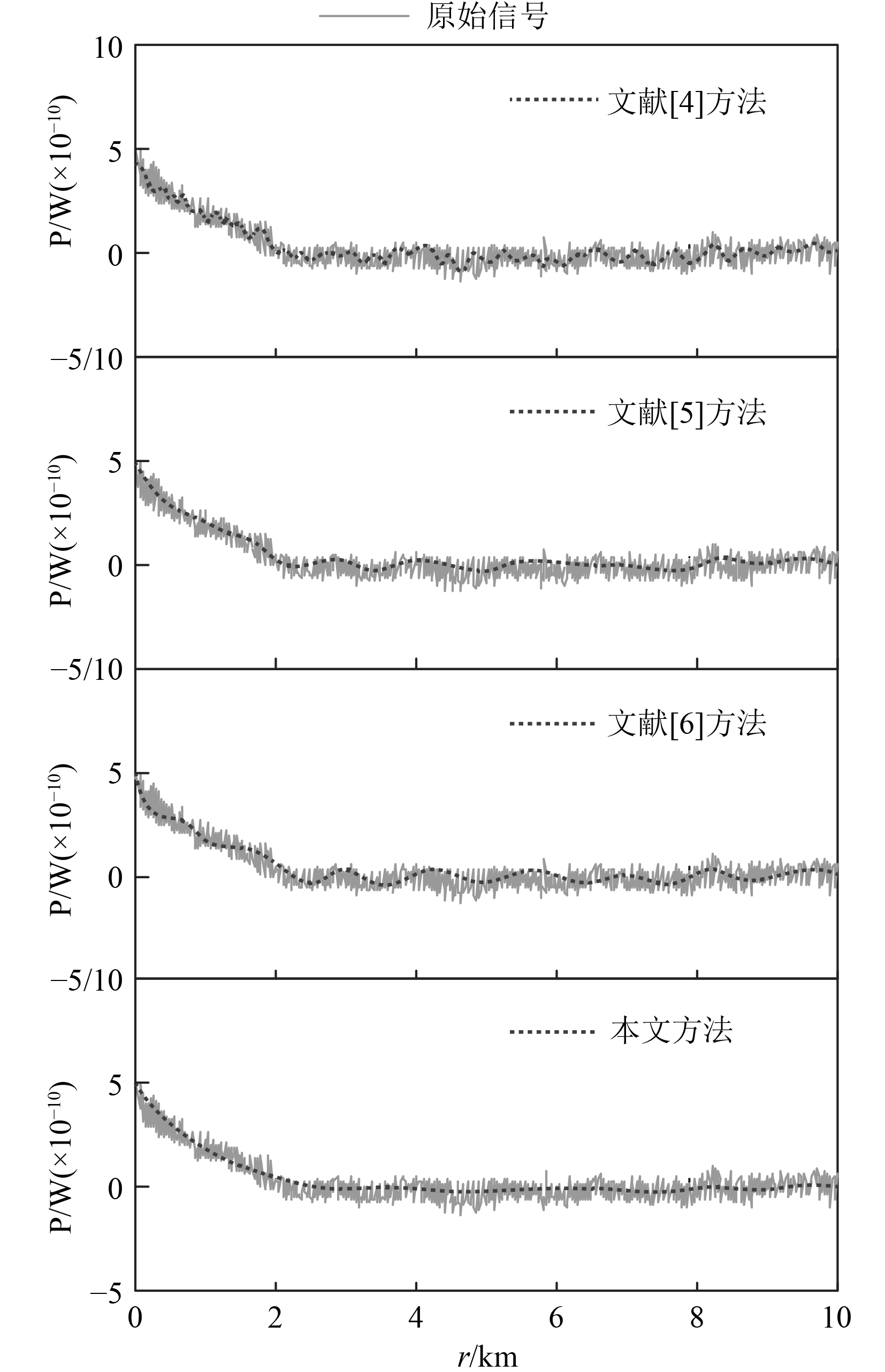
实验以文献[4]方法、文献[5]方法和文献[6]方法为对照检测本文方法雾天船舶航线辨识性能，首先分别采用4种方法处理雾天激光雷达回波信号，得到处理后回波信号如图1所示。

可以看出，本文方法、文献[4]方法、文献[5]方法和文献[6]方法均具有一定程度的信号去噪效果，但本文方法处理后激光雷达回波信号更为平滑，波动更小，即所提方法去噪效果更好。

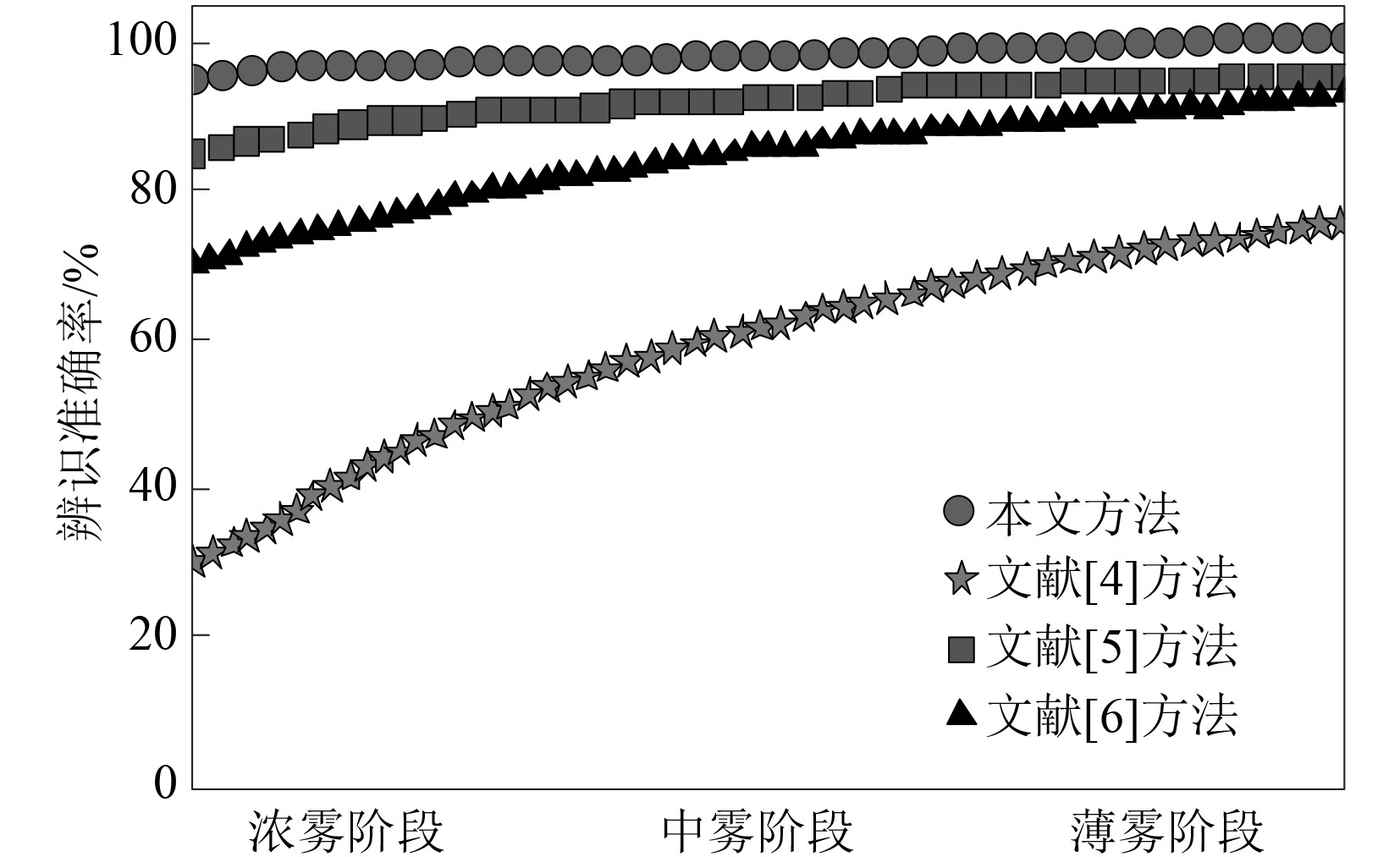
为了进一步验证本文方法、文献[4]方法、文献[5]方法和文献[6]方法处理后激光雷达回波信号在雾天船舶航线辨识中的效果，模拟雾天环境并采用4种算法分别辨识船舶航线，在实验过程中，随着温度等多种因素的影响下，雾浓度逐渐下降，将雾浓度划分为浓雾、中雾和薄雾3个阶段，4种方法在3个阶段下的船舶航线辨识准确率变化趋势如图2所示。

可以看出，在实验初期，雾浓度较高，本文方法、文献[4]方法、文献[5]方法和文献[6]方法均处在准确率最低阶段，但本文方法准确率最高，最低点在95%左右，其次为文献[5]方法，最低点在85%左右，再次为文献[6]方法，最低点在70%左右，最次为文献[4]方法，最低点在30%左右，随着实际时间变化，雾浓度逐渐降低，4种方法的辨识准确率逐渐升高。在雾浓度下降到最低点时，本文方法辨识准确率达到100%，文献[4]方法在75%左右，文献[5]方法在95%左右，文献[6]方法在93%左右，实验全过程中，本文方法辨识准确率始终高于文献[4]方法、文献[5]方法和文献[6]方法，说明本文方法在不同雾浓度中均具有更为优异的船舶航线辨识效果，因为本文方法对雾天激光雷达含噪回波信号去噪处理，得到更为平滑的回波信号，从而保证了船舶航线辨识效果。

4 结　语

与其他成像技术相比，激光雷达回波信号在雾天环境下受影响较小，识别效果更为稳定，但在雾浓度逐渐上升的过程中，激光雷达回波信号逐渐被噪声淹没，信噪比直线下降。为获取更为优质的回波信号，实现雾天船舶航线快速辨识，需要对信号加以处理。为了解决目前存在去噪后回波信号波动较大、输出信噪比较低、均方根误差较高、船舶航线辨识准确率不理想的问题，提出基于激光雷达回波信号的雾天船舶航线快速辨识研究，通过回波信号累积增强信号并采用改进的经验模态分解算法去噪信号，获取到船舶航线和水面分割阈值后引入3σ原理过滤粗大误差，实现船舶航线特征种子点提取，利用最小二乘法拟合特征点，完成雾天船舶航线辨识。实验结果表明，本文所提方法能够有效地平滑回波信号，提高输出信噪比，降低均方根误差，具有更高的船舶航线辨识准确率，为保证雾天交通安全提供有效指导。