0 引　言

自适应波束形成技术^[1]是根据一定标准和权值，在基阵接收信号加权叠加之后，使得处理得到的信号在所应用的准则下质量最优，进而减少主瓣宽度、抑制旁瓣以及降低背景噪声产生的影响。自适应波束形成技术是目前波束形成技术发展的重要方向，同时也是高分辨技术研究的热点。

典型常规波束形成方法^[2-3]（Conventional Beamforming，CBF）拥有模型简单、运算快速、不易受坏道影响等优点，因此该算法可以做到实时探测、实时处理，但常规波束形成所提供的阵增益有限，难以抑制海洋噪声中的强干扰噪声^[4]，而且其空间分辨率受到限制，因此常规波束形成算法对波束宽度范围内的多目标无能为力。

自适应波束形成方法可以有效提高波束形成干扰抑制能力，而自适应波束形成算法中较为典型的算法是Capton提出的最小方差无畸变响应（Minimum Variance Distortionless Response Beamforming，MVDR）波束形成技术^{[5 − 7]}。MVDR波束形成方法具有较好的方位分辨能力和较强的干扰抑制能力，尤其在低信噪比条件下，具有良好的强相关噪声抑制能力。

随着自适应波束形成方法和空间谱估计理论的发展，出现了多重信号分类方法（Multiple Signal Classification，MUSIC）^{[8 − 10]}。MUSIC算法通过阵列接收数据的协方差矩阵进行特征分解，从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间，然后利用2个子空间的正交性来估计目标参数。

目前，国内外对于自适应波束形成的研究虽然已趋近于成熟，但大部分研究都是理论分析，缺乏海试数据验证。本文将基于海试数据通过不同波束形成方法进行处理，总结分析各波束形成方法的性能及适用条件，为实际装备的使用提供一定参考。

1 自适应波束形成 1.1 MVDR算法原理

MVDR算法的基本准则是在保证主波束方向上无畸变通过的前提之下，使得总阵列的输出信号功率最小化，如下式：

$ \left\{ \begin{aligned} & {{W^H}a({\theta _d}) = 1} ，\\ & {P = \mathop {\min }\limits_W {W^H}{{\boldsymbol{R}}_{\boldsymbol{x}}}W} 。\end{aligned} \right. $

(1)

式中，$ {{\boldsymbol{R}}_{\boldsymbol{x}}} = {\boldsymbol{E}}\left\{ {X(t){X^H}(t)} \right\} $为基阵输入协方差矩阵。

利用拉格朗日乘数法求解上式，解得目标方位谱函数为：

$ {P_{MVDR}} = \frac{1}{{{\alpha ^H}(\theta ){\boldsymbol{R}}_{\boldsymbol{x}}^{{\boldsymbol{ - 1}}}\alpha (\theta )}}。$

(2)

1.2 MUSIC算法原理

MUSIC算法是一种利用子空间进行波束形成的自适应波束形成方法，将阵列接收信号的协方差矩阵直接进行特征分解，并将协方差矩阵的特征值从大到小进行排序，进而利用目标的个数得到协方差矩阵中的信号子空间以及噪声子空间，利用2个子空间的正交性得到目标信号的空间谱参数，具体流程如下：

步骤1　将阵列输入信号作相关处理，得到协方差矩阵$ {{\boldsymbol{R}}_{\boldsymbol{x}}} $：

$ {{\boldsymbol{R}}_{\boldsymbol{x}}} = {\boldsymbol{E}}[X{X^H}] = A{{\boldsymbol{R}}_{\boldsymbol{s}}}{A^H} + {{\boldsymbol{R}}_{\boldsymbol{n}}} 。$

(3)

式中：$ H $为矩阵共轭转置；${{\boldsymbol{R}}_{\boldsymbol{s}}} = {\boldsymbol{E}}[S{S^H}]$为信号的相关矩阵；${{\boldsymbol{R}}_{\boldsymbol{n}}} = {\sigma ^2}{\boldsymbol{I}}$为噪声的相关矩阵；${\sigma ^2}$为噪声功率；$ {\boldsymbol{I}} $为$ M \times M $阶的单位矩阵。

步骤2　通过对阵列协方差矩阵的特征分解，将矩阵${{\boldsymbol{R}}_{\boldsymbol{x}}}$的特征值进行从大到小的排序。

步骤3　根据协方差矩阵的特征值得到信号子矩阵和噪声子矩阵，其中，前N个较大的特征值为信号子矩阵，剩余的特征值为噪声子矩阵，用各噪声特征向量为列，构造一个噪声矩阵${{\boldsymbol{E}}_{\boldsymbol{n}}}$：

$ \boldsymbol{E}_{\boldsymbol{n}}=[v_{N+1},v_{N+2},...,v_M]，$

(4)

其中，N为目标个数。

步骤4　得到目标信号的空间谱${P_{mu}}(\theta )$：

$ {P_{mu}}(\theta ) = \frac{1}{{{a^H}(\theta ){{\boldsymbol{E}}_{\boldsymbol{n}}}{{\boldsymbol{E}}_{\boldsymbol{n}}}^{\boldsymbol{H}}a(\theta )}} = \frac{1}{{{{\left\| {{{\boldsymbol{E}}_{\boldsymbol{n}}}^{\boldsymbol{H}}a(\theta )} \right\|}^2}}} 。$

(5)

其中，$\alpha \left( \theta \right)$为目标信号方向矢量。

2 算法研究

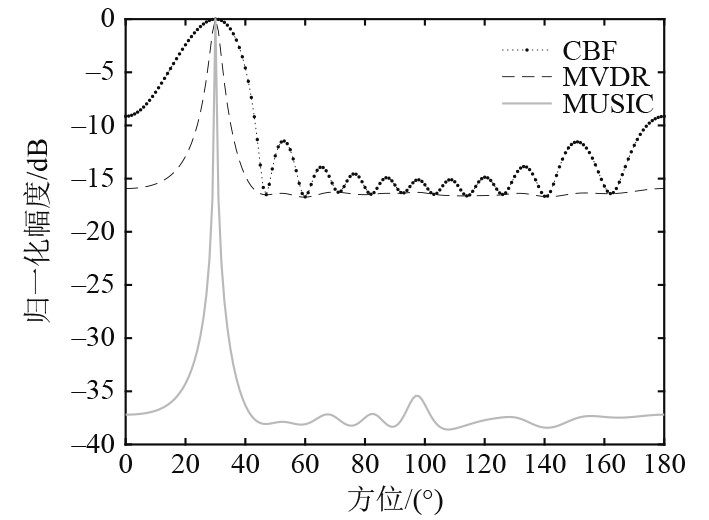
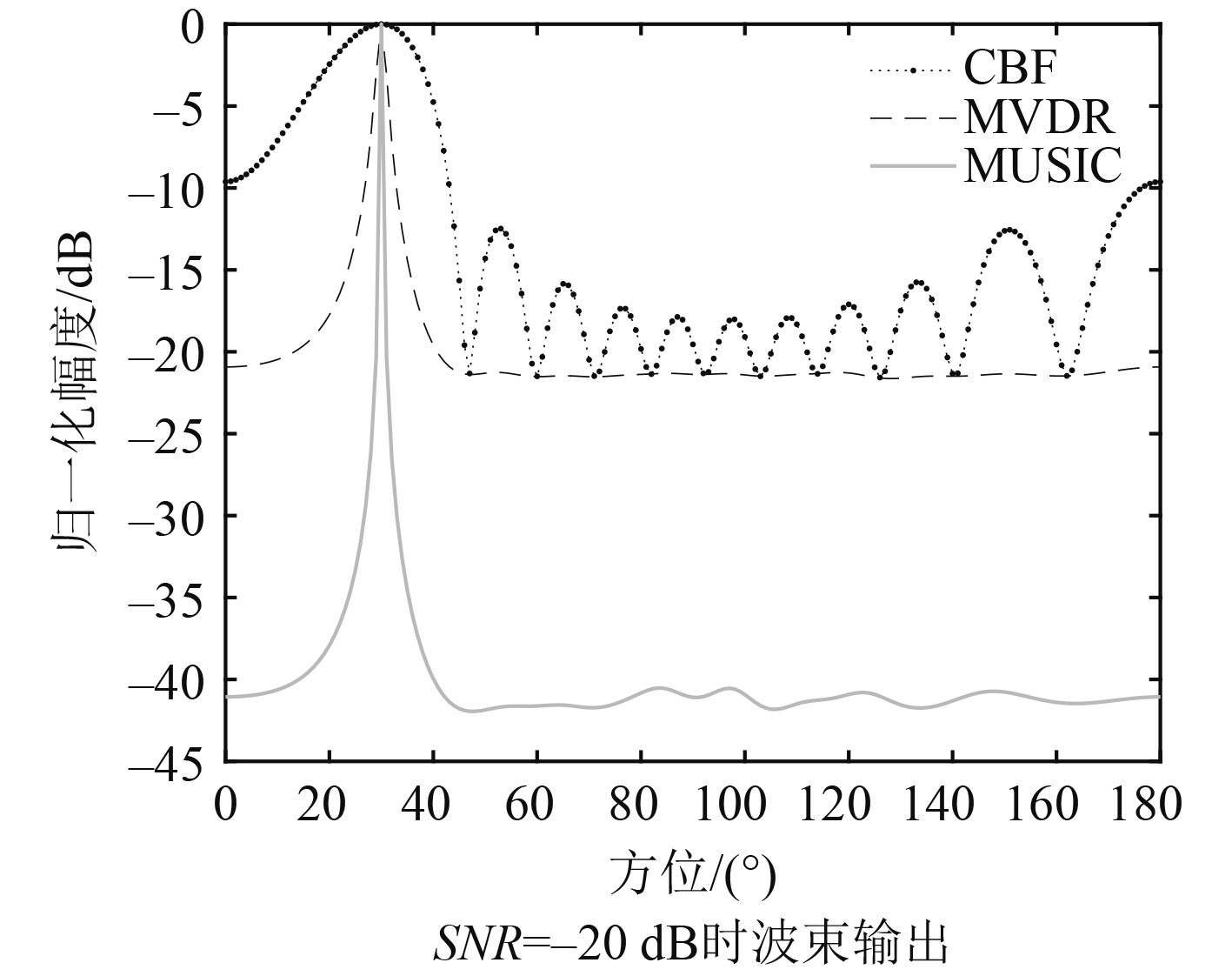
采用等间隔直线阵，阵元数目为11，阵列间距为半波长，单目标信号的方位为30°，信噪比SNR分别取0 dB和−20 dB，仿真CBF、MVDR和MUSIC等3种算法在不同信噪比情况下得到的波束形成输出。结果如图1和图2所示。

由图1可知，MVDR和MUSIC算法具有较窄的主瓣宽度，CBF算法的主瓣宽度相对较宽。图1和图2比较可知信噪比降至20 dB后，MVDR算法得到的主瓣宽度明显变大，而MUSIC算法得到的主瓣宽度变化较小，其主瓣仍然尖锐。

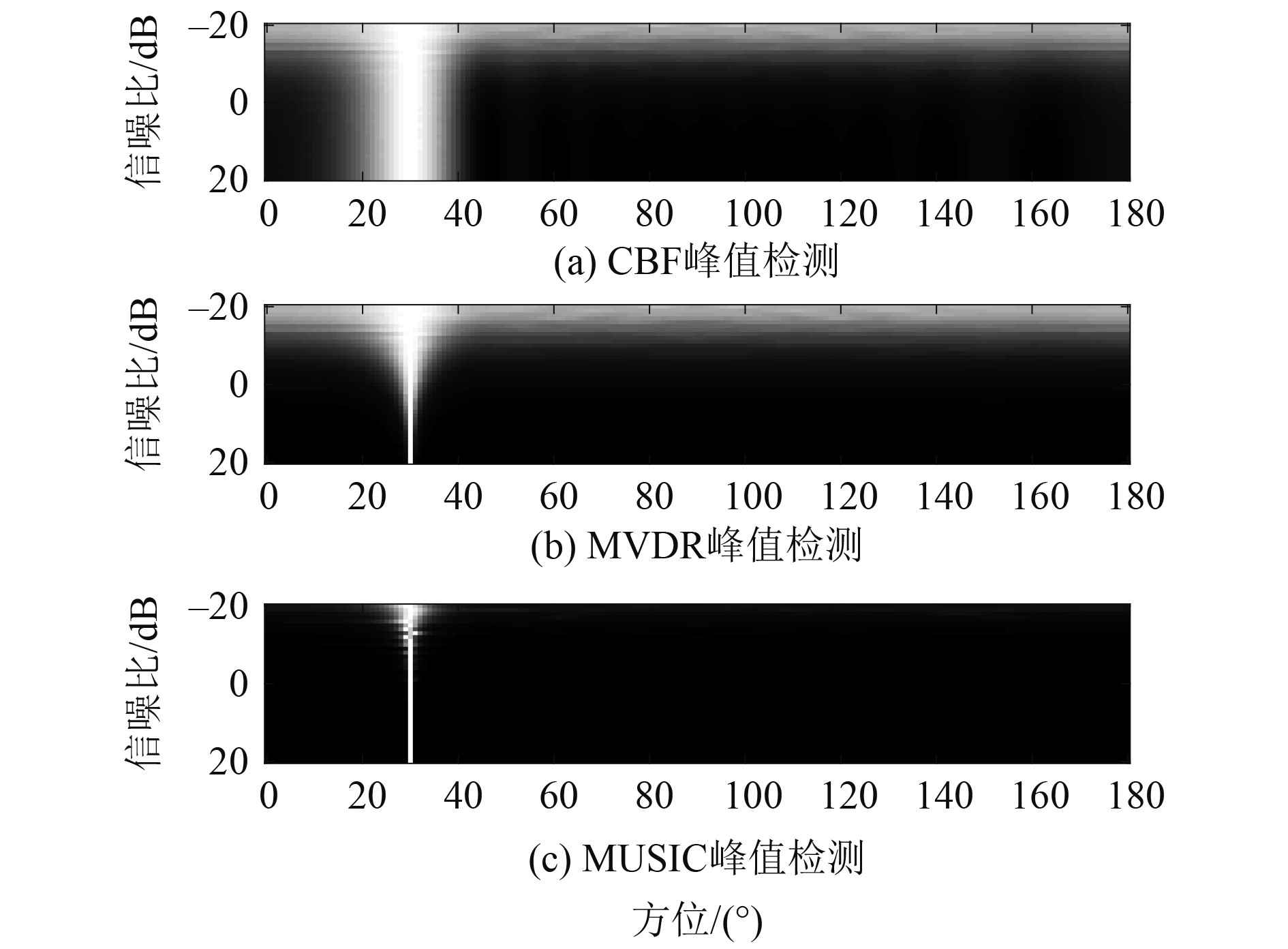
为了更加直观地看出MUSIC、MVDR以及CBF等3种算法受信噪比变化的影响，仿真各算法在不同信噪比情况下得到的波束形成输出。单目标信号的方位为30°。图3为信噪比在[–20,20]区间变化的时候，3种算法检测能力的变化。

可知，3种算法的波束宽度对于信噪比的适应性有着明显的区别，MUSIC算法的波束宽度最小，且随着信噪比变化较小，大约在信噪比变化至–15 dB左右误差变大，对目标信号的处理出现较大模糊，而MVDR算法在信噪比为–5 dB时处理目标信号出现模糊。

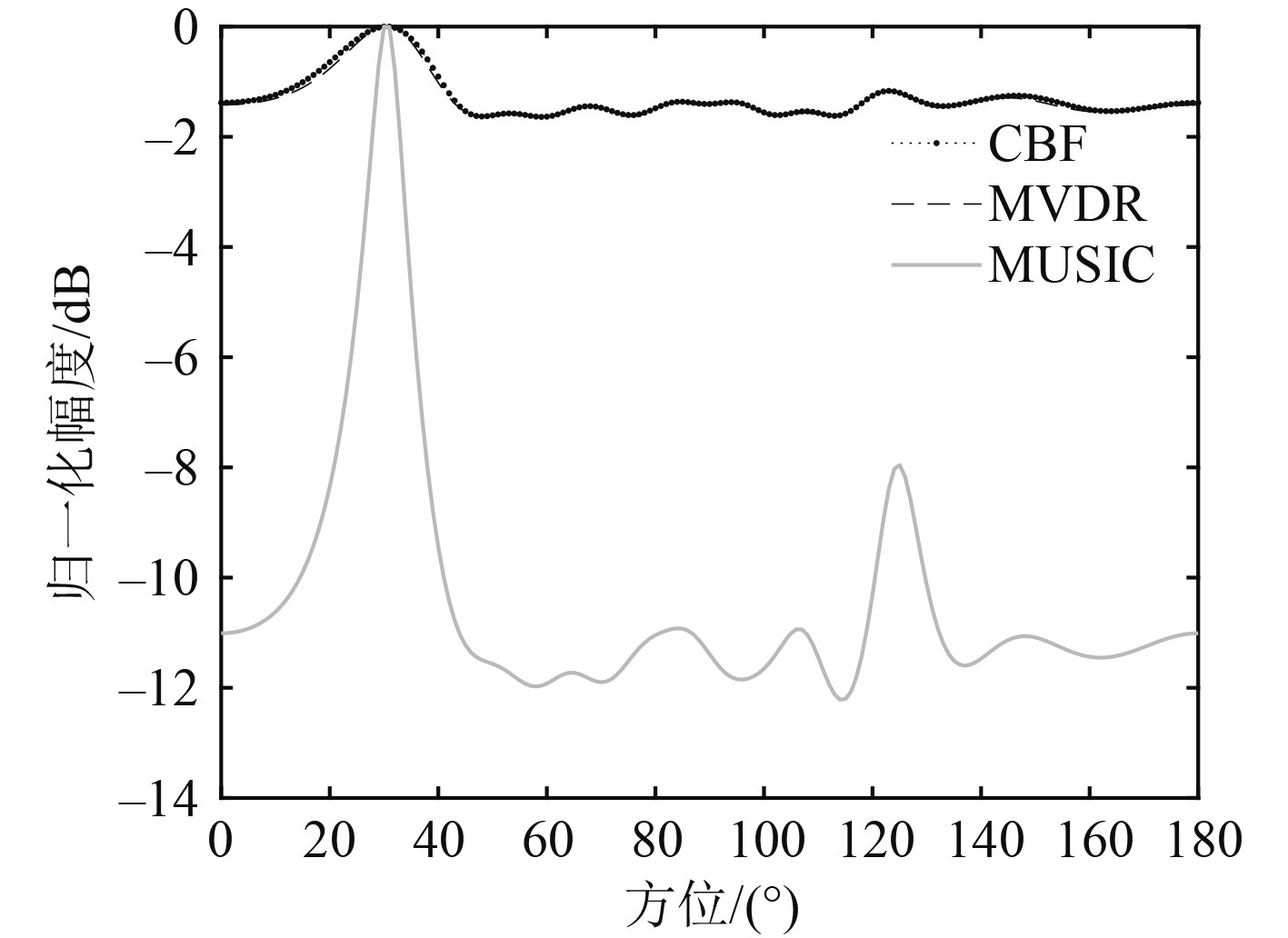
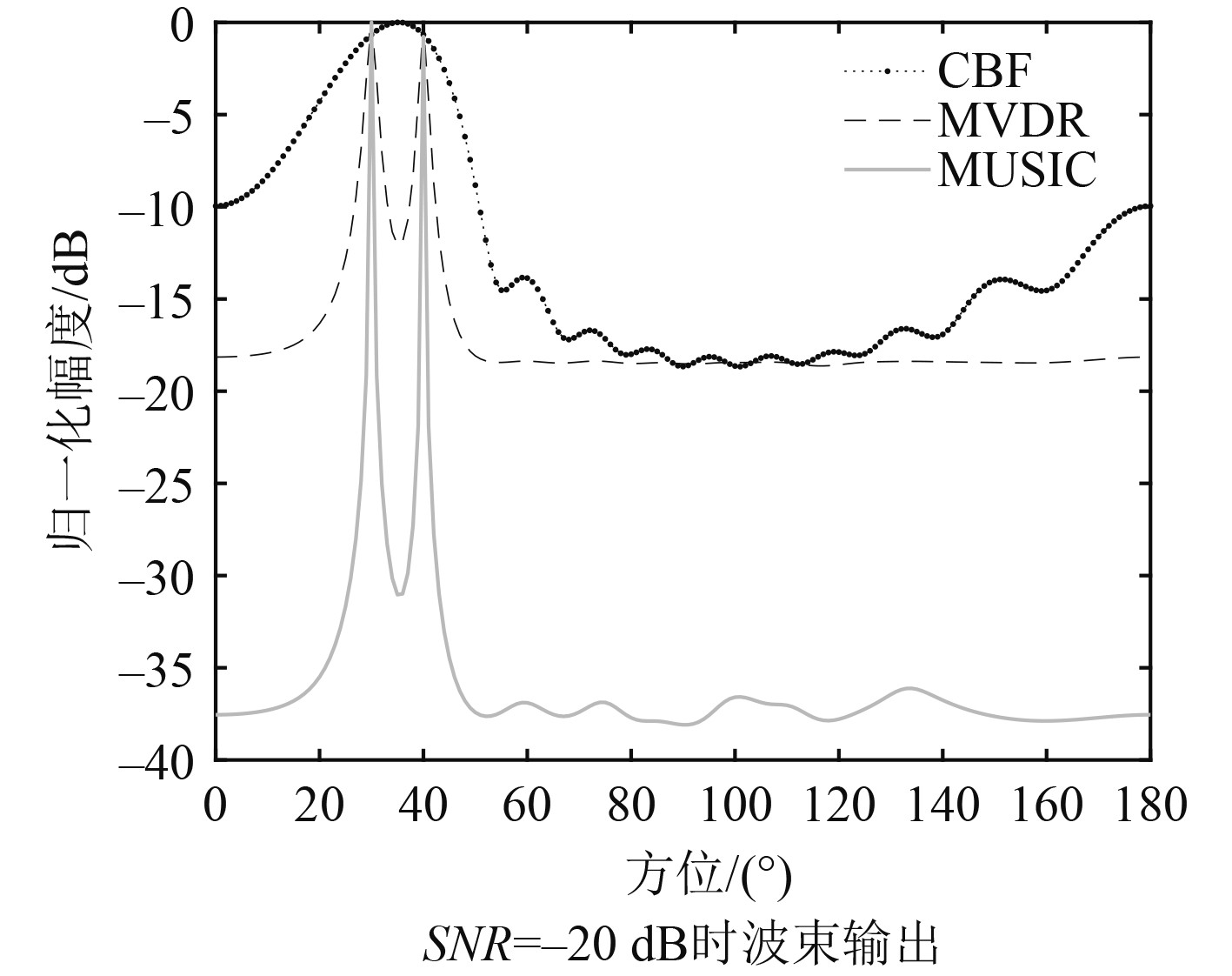
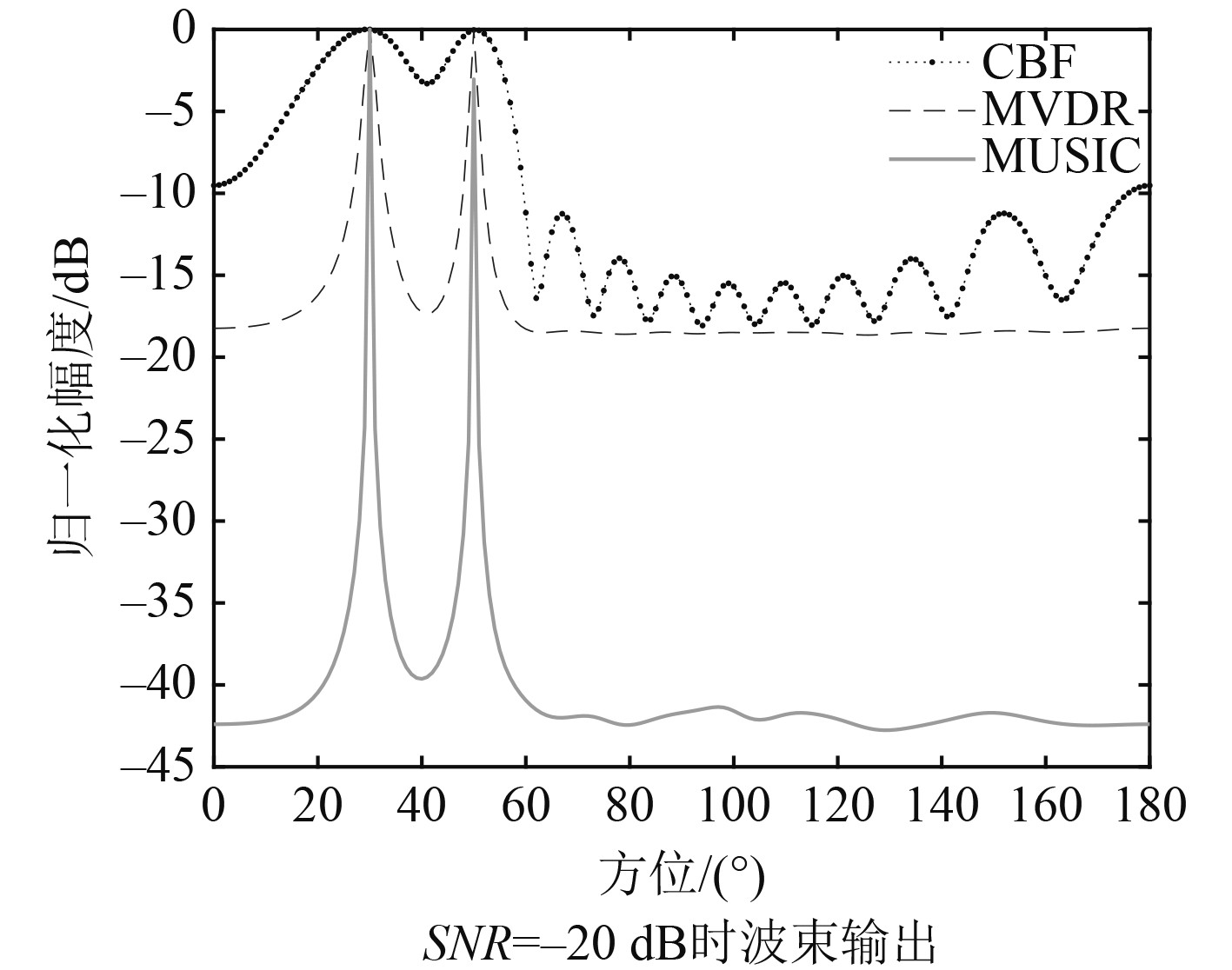
分析MVDR、MUSIC以及CBF算法对多个目标的分辨能力。等间隔直线阵的阵元数为11，阵元间距为半波长，两目标方位差分别取0°、10°和20°，信噪比取5 dB，分别仿真各算法在不同入射角情况下得到的波束形成输出。

由图4可知，若目标方位一致，各算法都无法分辨出2个目标。由图5可知，2个目标方位差在10°时，CBF算法仍然难以分辨2个目标，而自适应波束形成可以清晰分辨。由图6可知，2个目标信号方位差20°时，CBF算法才可以将目标分辨出来。综合对比，MUSIC算法对于多目标的分辨能力要略优于MVDR算法。

3 海试数据处理

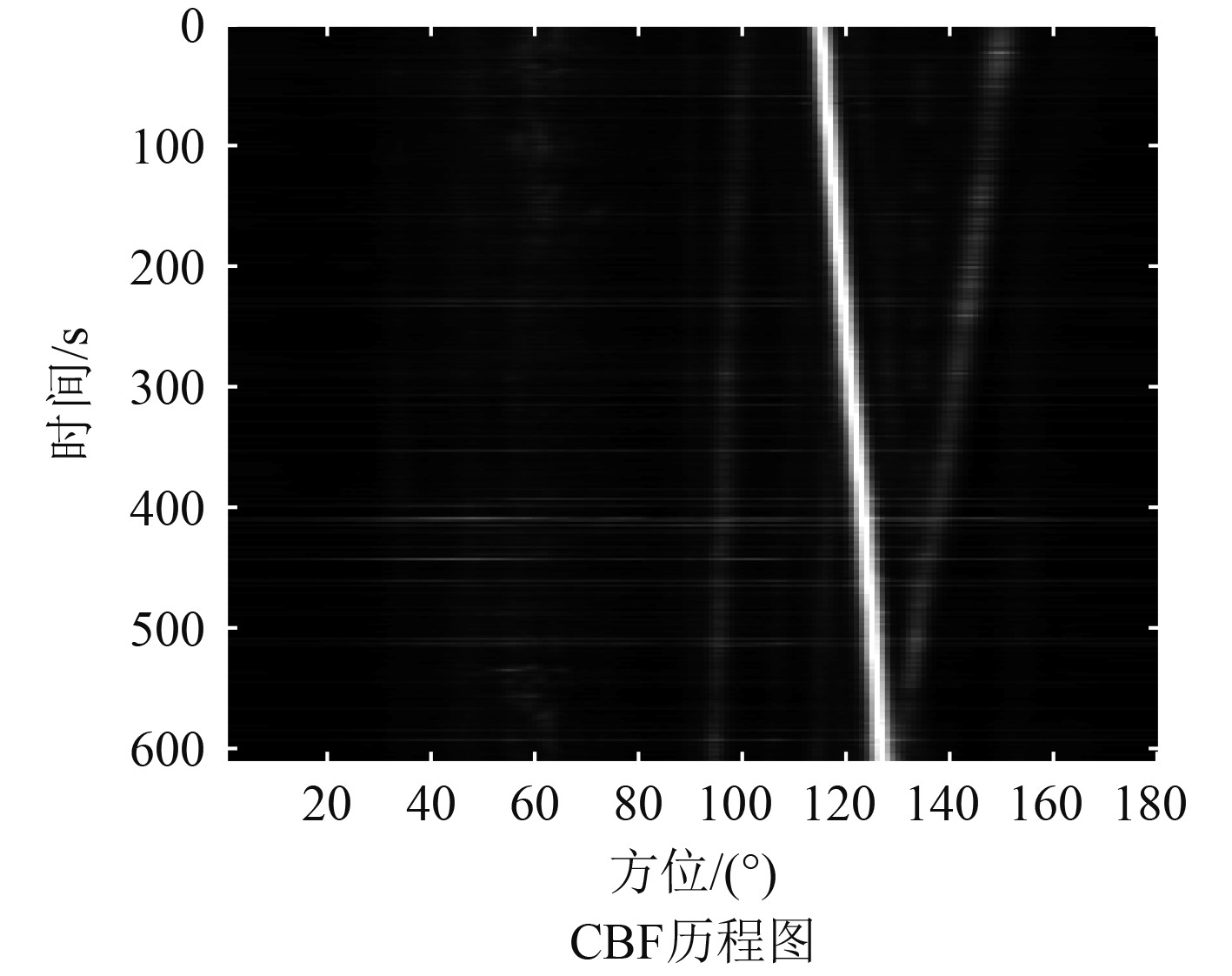
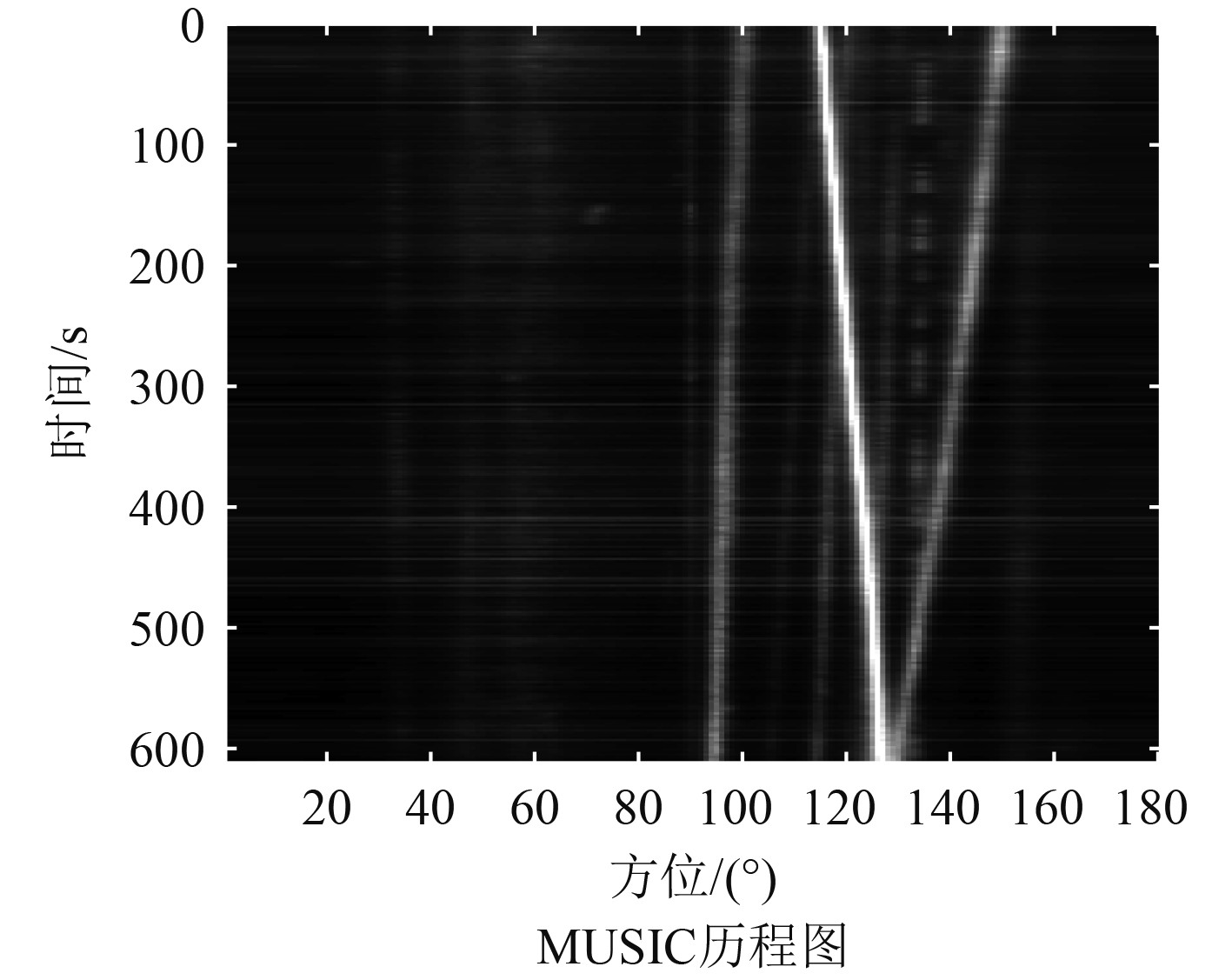
本文海试数据为线列阵在海洋环境下接收3个目标信号得到的试验数据。频域范围为800～1200 Hz，基阵阵元数为64，阵元间距为0.5 m，目标附近海域声速为1 466 m/s。利用CBF、MUSIC和MVDR算法对海试数据处理得到目标历程图。

通过图7～图9可以比较得出，CBF算法目标分辨能力较弱，难以分辨出方位差距较小的目标信号，也难以识别能量较小的目标信号；而2种自适应算法对于目标信号的分辨能力要远远大于常规波束形成算法，对于相邻的目标信号仍然可以有效的将其识别分辨；对比图8和图9，MUSIC算法抑制杂波能力要强于MVDR算法，而且MUSIC算法处理目标信号得到的波束宽度要比MVDR算法要更加尖锐，这2点使得MUSIC算法得到的历程图更加清晰。

通过表1可以得到3种处理方法对于海试数据的处理速度的快慢，其中，CBF算法处理海上试验数据的速度最快，需要354.5 s左右，而MVDR算法处理速度最慢，需要3284 s。MUSIC算法运算时间介于两者之间，需要499 s。根据MVDR波束形成的原理可以知道，MVDR算法需要计算协方差的逆矩阵，处理的数据越多计算时间越久。

4 结　语

1）CBF算法模型简单，运算时间短，目标分辨率极差，受信噪比变化影响较大，在实际应用时，实时性强，可以较快地识别信号能量强的目标，不需要目标数量，但是对于信号能量弱的目标以及方位相邻的目标性能较差。

2）MUSIC算法时间较长，目标分辨率强，抑制杂波的能力强，可以较为准确、清晰地识别出多目标信号。在实际应用时，处理复杂的目标信号需要较长运算时间，且需知目标的数量。

3）MVDR算法运算时间长，目标分辨率较强，抑制杂波的能力较强，不需要目标数量，在实际应用时，处理目标信号十分复杂，该算法运算处理目标信号需要很长的时间。

综合分析，在声呐的实际使用中，CBF算法更适用于实时性要求较高、目标数量较少的方位探测；MUSIC算法更适用于实时性要求不高、目标数量较多、目标数量已知的方位探测；MVDR算法更适用于实时性要求不高、目标数量较多、目标数量未知的方位探测。