大型新能源电动船舶是指以电能部分或完全替代传统燃油产生动力的船舶。相比传统柴油机推进船,这种船舶具有更节能、低排放以及能源使用多样化等特点[1]。该类船舶所使用的电池主要是磷酸铁锂电池,具有较高的能量密度和安全性[2]。在正常情况下,该电池具有较长的循环寿命,能够满足多次充放电循环需求。但是在对该电池进行充电时,如果充电电流、充电电压以及荷电状态等发生较大变化,会导致电池发生明显的能量损耗,甚至会降低电池的使用寿命[3]。因此,为保证电池在使用过程中,长期处于稳定、健康状态,并保证大型新能源电动船舶电池的使用寿命,需进行电池快速充电控制。
孙金磊等[4]为实现电池充电控制,结合电池自身的电量不均衡特性,依据电池荷电状态为依据,实现对电池状态数据的聚处理类,依据聚类结果进行均衡充电控制。然而,该方法在应用过程中,仍旧会存在较为明显的能量损失。李忠瑞等[5]为实现电池充电控制,参考电池的工作特性,利用外环和能量同时控制方式,设定控制参数,并且对充电过程中的负载变化进行补偿,以此实现充电控制。但是,该方法在瞬态响应工况下难以对充电电流进行控制。
为实现对大型新能源电动船舶电池的快速充电控制,通过构建大型新能源电动船舶电池等效电路,分析其运行特性,在此基础上构建电池充电控制目标函数,并通过模糊控制规则确定最优控制策略,以此获取目标函数的适应度结果后,通过改进布谷鸟算法对目标函数适应度函数搜索,获取最优的快速充电控制结果。
1 船舶电池快速充电控制 1.1 船舶电池等效电路分析为实现大型新能源电动船舶电池快速充电控制,需分析该电池的运行状态,构建大型新能源电动船舶电池等效电路,其是结合实际充放电数据以及循环工况拟合完成,其是依据电容和电阻等原件进行电池运行过程中的电压响应情况的描述[6 − 7],依据极化损耗和欧姆损耗描述电池的运行特性。
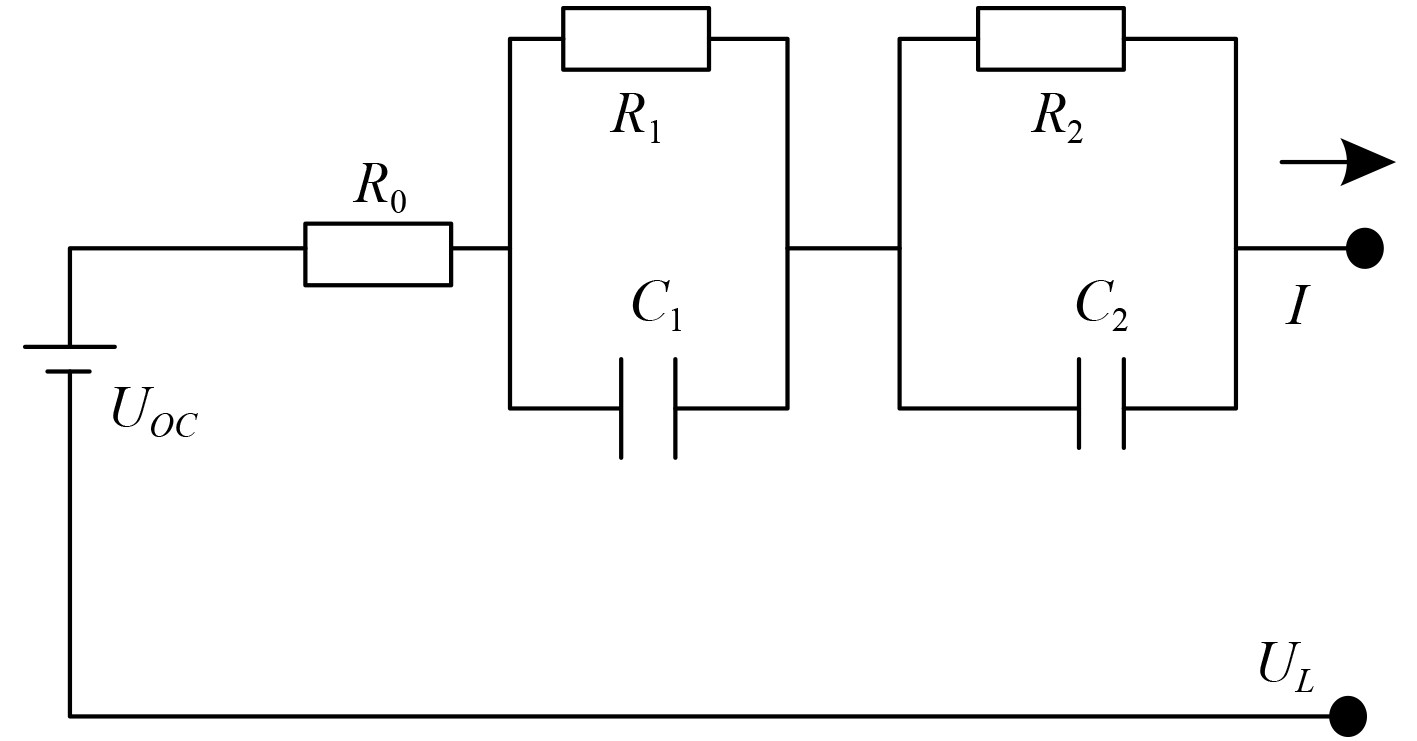
大型新能源电动船舶电池二阶等效电路结构如图1所示。
|
图 1 大型新能源电动船舶电池二阶等效电路 Fig. 1 Second Order equivalent circuit of large new energy electric ship battery |
以基尔霍夫定律为参考依据,在负载电流为
| $ \left\{ \begin{gathered} {{\tilde U}_1} = - \frac{{{U_1}}}{{{R_1}{C_1}}} + \frac{I}{{{C_1}}} ,\\ {{\tilde U}_2} = - \frac{{{U_2}}}{{{R_2}{C_2}}} + \frac{I}{{{C_2}}}。\\ \end{gathered} \right. $ | (1) |
| $ {U_L} = {U_{OC}} - {U_1} - {U_2} - I{R_0} $ | (2) |
式中:
依据安时积分法,在电池额定容量
| $ SOC\left( k \right) = SOC\left( {k - 1} \right) - \left( {\frac{{\eta \Delta t}}{{{Q_n}}}} \right){i_{k - 1}} 。$ | (3) |
式中:
结合图1模型,将
| $ {U_L}\left( k \right) = {U_{OC}}\left( {SOC} \right) - {U_1}\left( k \right) - {U_2}\left( k \right) - I\left( k \right){R_0} 。$ | (4) |
式中,
在电池快速充电过程中,如果电流较大,可减少充电时间,但是会导致极化电压明显增加,从而导致能量损耗增加[8]。因此,为保证电池能够在长时间内保持稳定、健康的状态,确定电池快速充电控制目标函数。以最大充电电流
| $ \max I\left( {SOC} \right) = \frac{{{U_z} - {U_{OC}}\left( {SOC} \right)}}{{R\left( {SOC,I} \right)}},$ | (5) |
| $ f = \sum\limits_{k = 1}^{N - 1} {\left[ {{w_1}{L_{time}}\left( k \right) + {w_2}{L_{loss}}\left( k \right)} \right]}。$ | (6) |
式中:
为保证控制效果,采用模糊控制器的控制规则确定控制策略。
控制过程中,控制器在结合最大充电电流、充电时间以及能量损耗对于电池电压的影响,将电压理想最大电压和实际最大电压之间差值
1)模糊化:大型新能源电动船舶电池在快速充电过程中,即使电池个体存在一定差异,但是其电压上升斜率趋势几乎一致,并且当电池电压接近饱和状态时,电压变化率显著。基于此,选择将
2)模糊推理:模糊推理主要是对各个变量的模糊关系集进行模糊运算,以此获取模糊控制规则。结合模糊输入和规则库中输入和输出之间的关联,计算控制器的模糊输出结果,其计算公式为:
| $ {C^ * } = \left( {{A^ * } \otimes {B^ * }} \right) \odot G $ | (7) |
式中:
3)清晰化:为获取精准控制量,将获取的
| $ \Delta \tilde U = \frac{{\displaystyle\sum\limits_i {\mu \left( {{U_L}} \right){U_L}} }}{{\displaystyle\sum\limits_i {\mu \left( {{U_L}} \right)} }}。$ | (8) |
式中,
将
| $ F\left( x \right) = w \times {f^o} + b。$ | (9) |
式中:
为验证应用效果,以某大型新能源电动船舶作为测试对象,设计实验。
该船舶使用的电池为锂电池,电池的相关参数如表1所示;电池充电平台参数如表2所示。
|
|
表 1 船用锂电池的相关参数 Tab.1 Relevant parameters of marine lithium batteries |
|
|
表 2 电池充电平台参数 Tab.2 Battery Charging Platform Parameters |
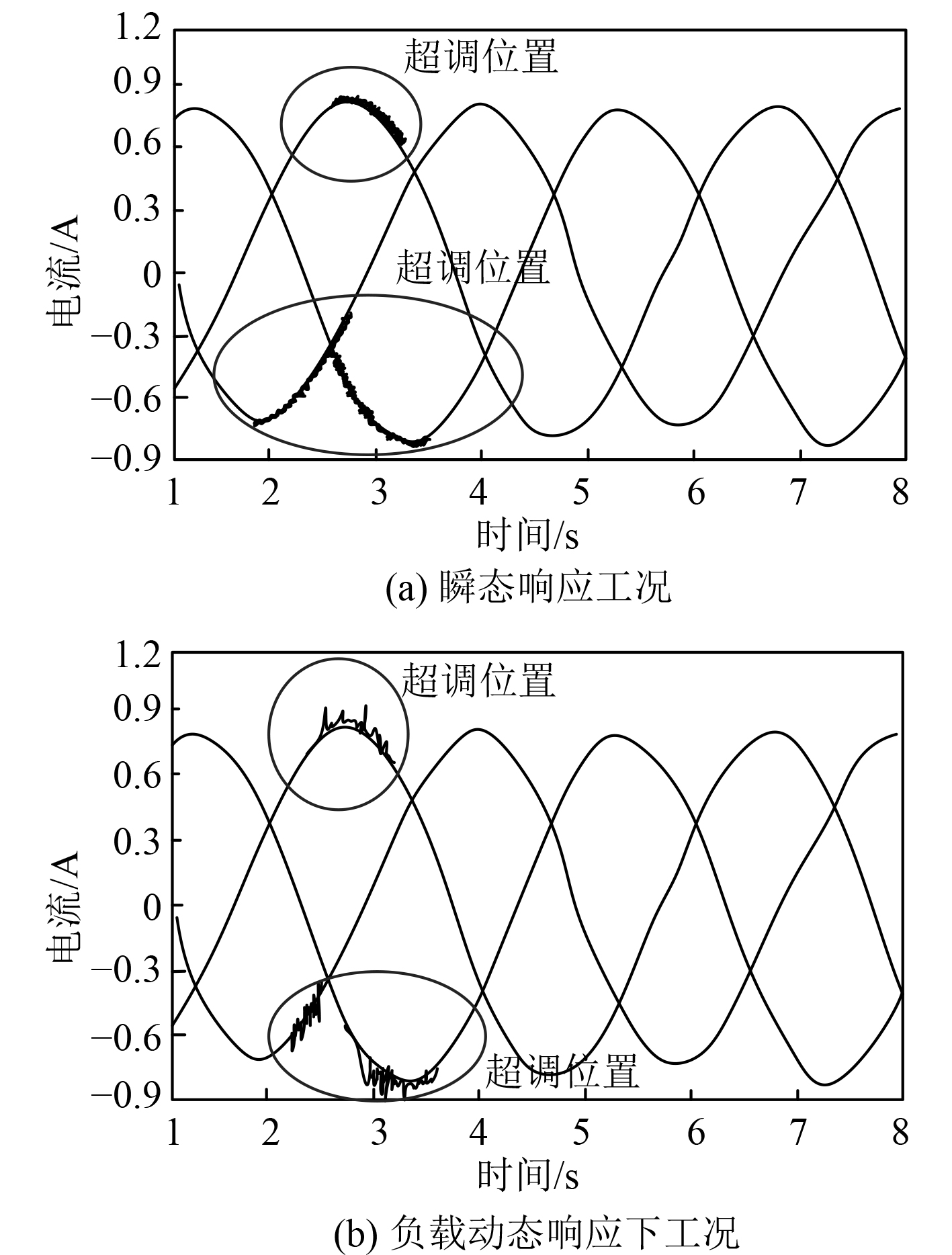
为验证控制效果,在电池电压分别处于瞬态响应和负载动态响应2种运行工况下,采用本文方法对其进行快速充电控制,获取2种工况下,本文方法控制后电池最大充电电流的控制结果以及电压结果,如图2和图3所示。
|
图 2 电池最大充电电流的控制结果 Fig. 2 Control results of the maximum charging current of the battery |
|
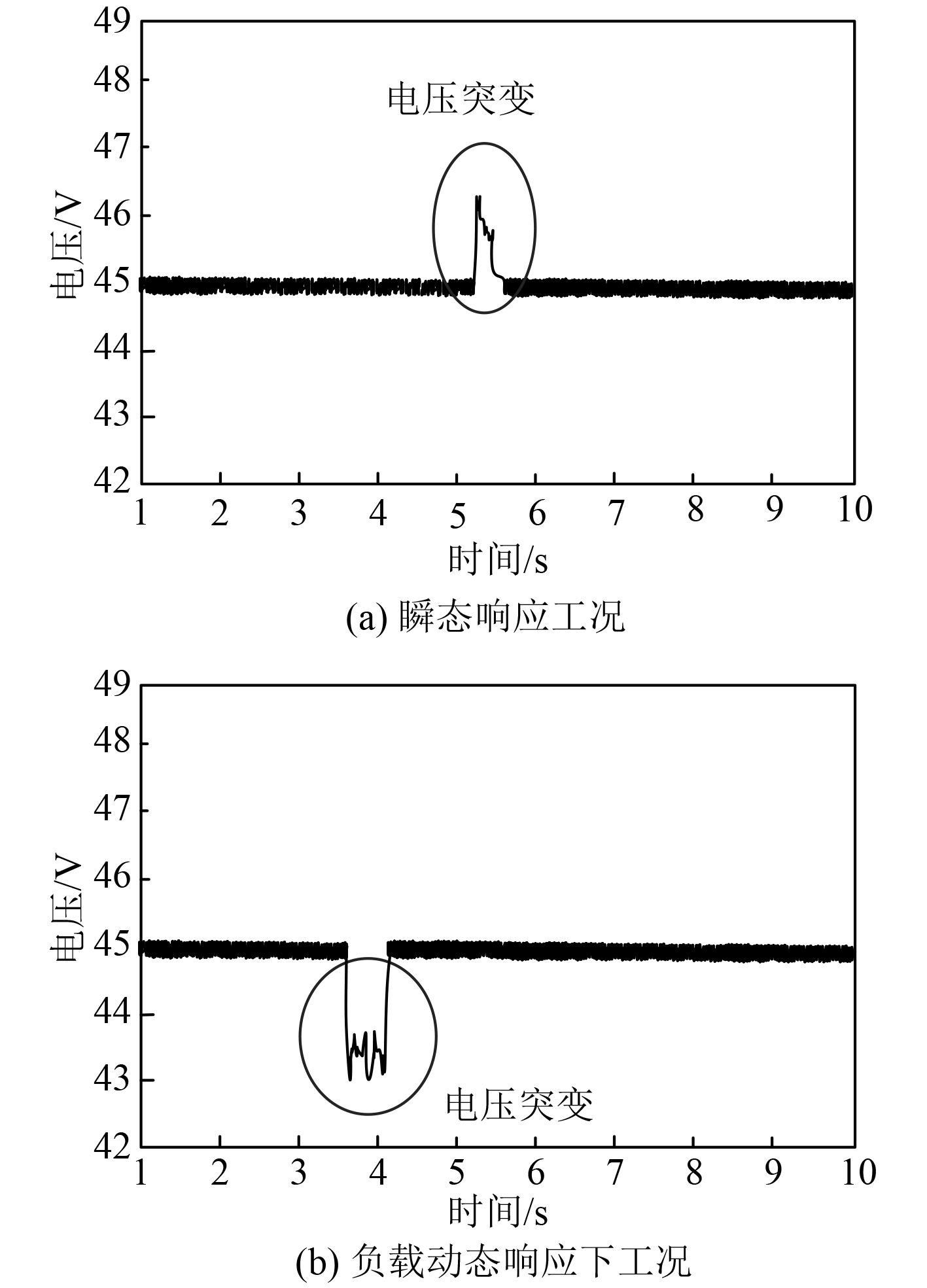
图 3 电池充电电压控制结果 Fig. 3 Battery charging voltage control results |
可知,在2种运行工况下,电池在充电过程中,直流电环输出电压发生不同程度的突变后,可在极短时间内完成充电控制,使电池充电电压下降至45 V,最大程度接近标准输出电压;并且在2种运行工况下,持续充电电流发生超调后,本文方法依旧可在极短时间内完成电流充满电流控制,保证电流位于允许的持续充电最大电流范围内,位于−0.9~+0.9C之间。因此,本文方法的控制效果良好,满足电池快速充电控制。
为进一步验证本文方法电池快速充电控制效果,获取该方法在恒流充电以及五阶充电2种充电模式下,本文方法应用前、后,电池快速充电的能量损耗结果,如表3所示。
|
|
表 3 电池快速充电的能量损耗结果 Tab.3 Energy loss results of fast charging of batteries |
可知,大型新能源电动船舶电池在恒流充电以及五阶充电2种充电模式下,采用本文方法对其进行控制前,充电能量损耗均在1500 J以上;采用本文方法进行控制后,电池快速充电的能量损耗结果均在1305 J以下。这是因为本文方法在进行大型新能源电动船舶电池快速充电控制过程中,以能量损耗作为目标函数,因此,能够结合损耗程度完成充电控制。
3 结 语大型新能源电动船舶电池稳定而持久的动力输出,对于船舶安全、稳定航向具有重要意义。在电池持续使用的过程中,其快速充电水平决定电池的使用寿命以及充电效果。因此,为保证电池的循环充电使用寿命,实现电池最佳充电控制,本文提出了一种快速充电控制方法。该方法结合模糊控制器以及改进布谷鸟寻优算法,获取最佳的电池快速充电控制结果。对该方法的应用效果展开相关测试后得出,该方法具有较好的应用效果,能够有效完成对大型新能源电动船舶电池快速充电过程中电流和电压的控制,保证充电时电池荷电状态的稳定,避免发生显著波动。
| [1] |
王绍远, 胡斌, 王良秀, 等. 基于卡尔曼滤波法的船用磷酸铁锂电池SOC仿真估算[J]. 船舶工程, 2022, 44(2): 89-93. |
| [2] |
王鹿军, 单恩泽. 基于动态式双阈值的锂电池组主被动均衡策略[J]. 电机与控制学报, 2022, 26(1): 126-136. |
| [3] |
邓吉利, 曹太强, 陈汝兵, 等. 蓄电池充电电流控制的LLC谐振变换器研究[J]. 电测与仪表, 2021, 58(4): 73-77+176. |
| [4] |
孙金磊, 邹鑫, 崔凯, 等. 基于电池模组重构的均衡充电控制方法[J]. 电源技术, 2022, 46(9): 1005-1008. |
| [5] |
李忠瑞, 聂子玲, 艾胜, 等. 一种基于非线性扰动观测器的飞轮储能系统优化充电控制策略[J]. 电工技术学报, 2023, 38(6): 1506-1518. |
| [6] |
吴丽君, 张朱浩伯, 曹鹏举, 等. 基于电压增益动态切换的无线充电控制方法[J]. 电力电子技术, 2021, 55(4): 87-91. DOI:10.3969/j.issn.1000-100X.2021.04.021 |
| [7] |
易磊, 黄启元, 李嘉泽, 等. 基于MPPT的光伏蓄电池脉冲充电技术研究[J]. 电源技术, 2022, 46(4): 437-440. DOI:10.3969/j.issn.1002-087X.2022.04.023 |
| [8] |
姚凤翔, 王检耀, 王鸿东, 等. 基于Icepak的船舶储能电池散热特性仿真分析[J]. 计算机仿真, 2023, 40(1): 517-522+538. |
 2024, Vol. 46
2024, Vol. 46
