作为中压直流综合电力系统的重要组成部分,十二相整流发电机担负着全船电能供给的重要任务,其在各种工况下运行的稳定性及良好的动态性能是全船安全可靠运行的重要前提[1-2]。随着电力电子技术的快速发展及舰船作战需求的不断提高,以电磁弹射、激光武器为代表的脉冲负载开始广泛应用于综合电力系统中[3-4],此类负载能在数秒内释放几百千瓦甚至几十兆瓦的功率,表现出典型的功率瞬变特性。传统基于燃气轮机的发电系统加载速率为35~50 MW/min,远低于100 MW/s的脉冲负载运行特性[5],因而舰船发电机组支持脉冲负载上舰的能力有限,当高能武器等具有瞬时大功率特性的负载投入时,会对发电机组的暂态电压质量造成剧烈冲击,甚至影响整个综合电力系统的安全稳定运行。因此,有必要深入研究脉冲负载作用下,十二相整流发电机直流侧最大电压调整率的解析计算方法,为突破脉冲负载瞬时功率需求与舰船电网容量的匹配性问题提供理论依据。
目前,针对十二相同步发电机整流系统的研究大多集中于数学及仿真建模[6-7]、稳定性分析[8-9]和故障特性分析[10-12]等方面,而对脉冲负载作用下发电机直流侧电压暂态性能的研究较少。Yi等[13]在Matlab/Simulink中建立了十二相整流同步发电机及其励磁系统的仿真模型,并对发电机突加负载后的调压性能进行了仿真分析,但没有从理论上给出直流侧电压的变化依据。Zhang等[14]推导了三相同步电机突加负载后的机端电压表达式,但是由于忽略了阻尼绕组的影响,其端电压的变化规律与现有的有阻尼电机略有不同。肖晗等[15]提出了一种基于负载等效的三相同步发电机整流系统直流侧瞬时电压的计算方法。综上所述,现有文献均未解决脉冲负载作用下,十二相整流发电机直流侧最大瞬态电压调整率的解析计算问题。无法从理论上定量揭示负载功率瞬变对直流侧电压幅值的影响规律,在一定程度上限制了发电机带载能力的充分利用和后续电压补偿方法的设计研究。
而相比于传统的三相同步发电机整流系统,十二相同步发电机整流系统具有更高的系统阶次及更为复杂的运行模式,这使得突加负载后机组暂态电压解析计算困难。为此,本文首先基于十二相同步发电机整流系统的拓扑结构和运行原理对其进行等效降阶处理,同时利用功率等效原则将直流负载折算到交流侧,建立起十二相同步发电机整流系统的等效三相同步电机模型,推导出十二相同步发电机整流系统在负载功率阶跃变化时,直流侧最大瞬态电压调整率的解析计算方法,阐明了负载功率突变对机端电压影响的主要因素,并通过时域仿真和物理试验验证了理论分析的正确性。
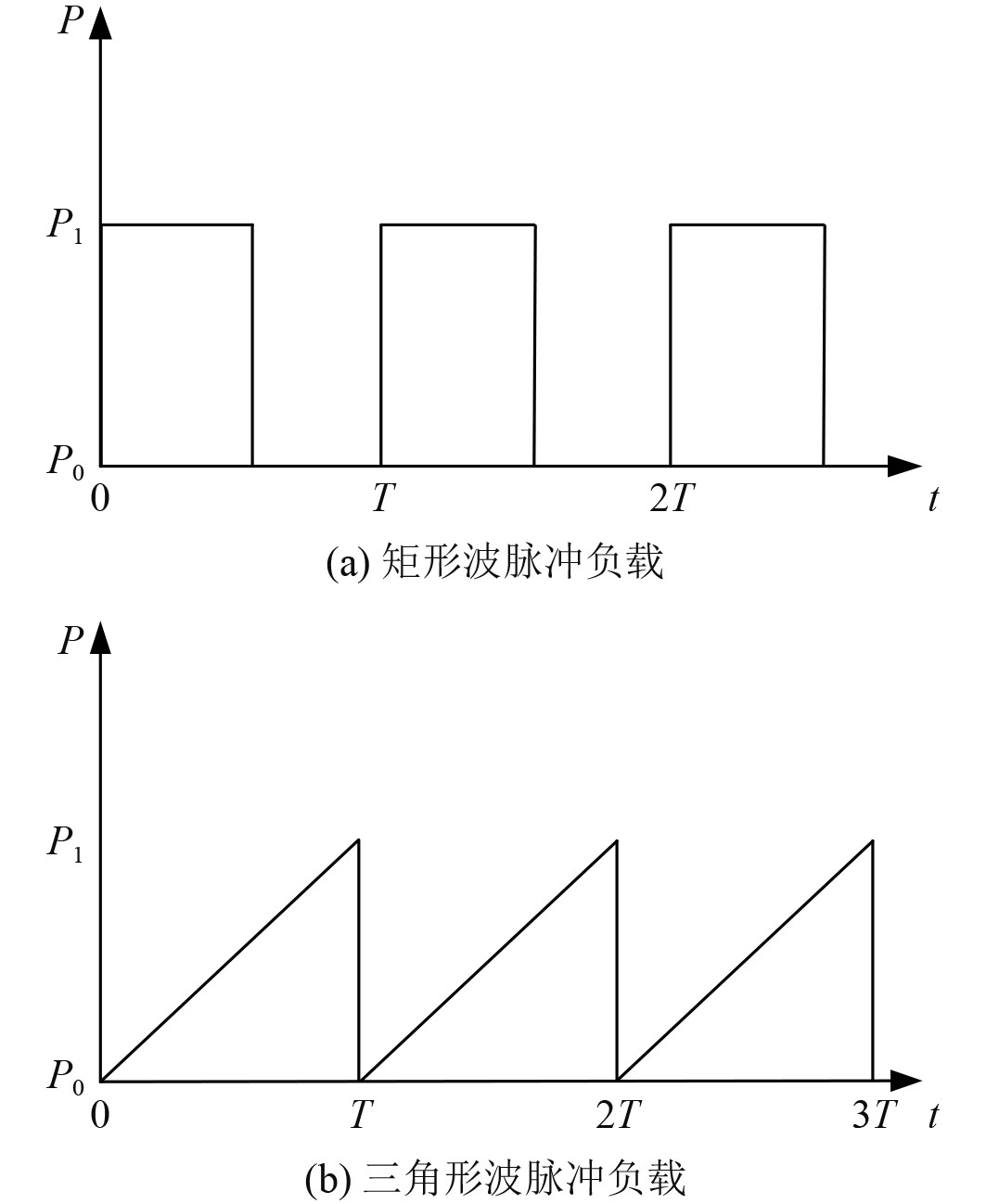
1 十二相整流发电机-脉冲负载系统的数学模型 1.1 脉冲负载模型脉冲负载会对供电系统产生周期连续性的高功率冲击,因而对舰船电力系统提出了较为严格的要求。根据储能形式的不同,脉冲负载的功率特性曲线可分为矩形波和三角形波,如图1所示。其中
|
图 1 典型脉冲负载的功率特性 Fig. 1 Power characteristic of typical pulse load |
由于整流发电机系统各状态变量在脉冲负载作用下的动态响应主要取决于负载功率阶跃变化的行为[16],因此在研究时考虑最严酷的工况。以常见的矩形波脉冲负载为例,基于十二相整流发电机的数学模型,定量分析脉冲负载作用下,十二相整流发电机的最大瞬态电压调整率。
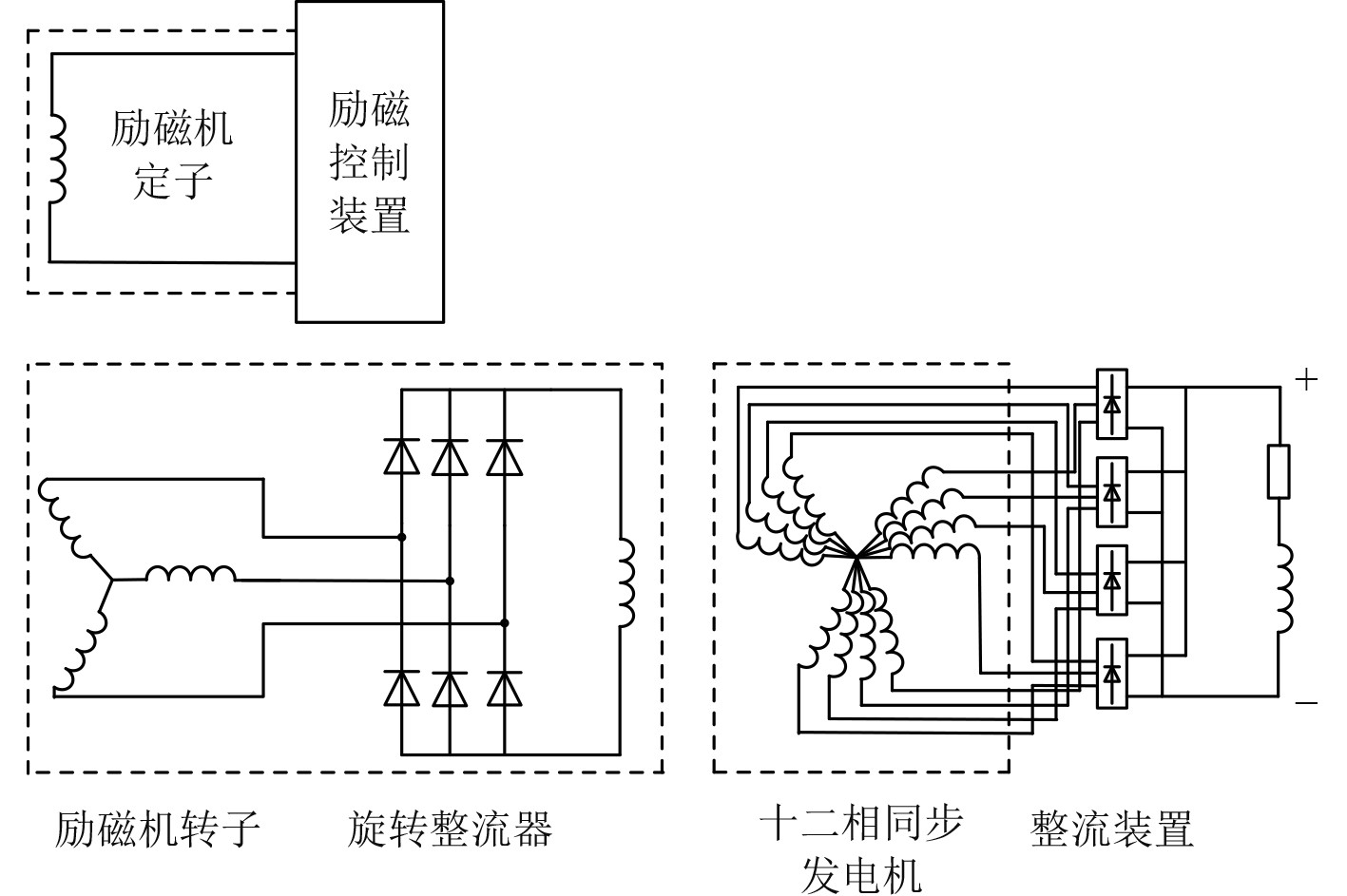
1.2 十二相整流发电机模型十二相整流同步发电机的基本结构如图2所示,主要由十二相同步发电机、十二相整流装置和励磁系统(包括主励磁机、旋转整流器、励磁控制装置等)组成。电机转子侧布置有励磁绕组
|
图 2 十二相整流同步发电机原理图 Fig. 2 Schematic diagram of twelve-phase rectifier generator |
基于理想化假设条件,建立电机在
| $ {\psi _{dq}} = {{\boldsymbol{X}}_{dq}}{i_{dq}} ,$ | (1) |
| $ {u_{dq}} = p{\psi _{dq}} + {\boldsymbol{A}}p\theta {\psi _{dq}} - {{\boldsymbol{R}}_{dq}}{i_{dq}} 。$ | (2) |
式中:
| $ \begin{split} {\psi _{dq}}{\text{ = }}& \left( {{\psi _{d1}}}\quad{{\psi _{q1}}}\quad{{\psi _{d2}}}\quad{{\psi _{q2}}}\quad{{\psi _{d3}}}\quad{{\psi _{q3}}}\quad{{\psi _{d4}}}\right.\\ & \left.{{\psi _{q4}}}\quad{{\psi _{fd}}}\quad{{\psi _{kd}}}\quad{{\psi _{kq}}} \right)^{\rm T},\end{split} $ |
| $ {i_{dq}} = {\left( {\begin{array}{*{20}{c}} {{i_{d1}}} & {{i_{q1}}} & {{i_{d2}}} & {{i_{q2}}} & {{i_{d3}}} & {{i_{q3}}} & {{i_{d4}}} & {{i_{q4}}} & {{i_{fd}}} & {{i_{kd}}} & {{i_{kq}}} \end{array}} \right)^{\rm T}} ,$ |
| $ {u_{dq}} = {\left( {\begin{array}{*{20}{c}} {{u_{d1}}} & {{u_{q1}}} & {{u_{d2}}} & {{u_{q2}}} & {{u_{d3}}} & {{u_{q3}}} & {{u_{d4}}} & {{u_{q4}}} & {{u_{fd}}} & {{u_{kd}}} & {{u_{kq}}} \end{array}} \right)^{\rm T}} ,$ |
| $ {{\boldsymbol{R}}_{dq}} = {\rm{diag}}{\left( {\begin{array}{*{20}{c}} {{r_s}} & {{r_s}} & {{r_s}} & {{r_s}} & {{r_s}} & {{r_s}} & {{r_s}} & {{r_s}} & {{r_{fd}}} & {{r_{kd}}} & {{r_{kq}}} \end{array}} \right)^{\rm T}} $ |
| $ \begin{split} & {\boldsymbol{A}} = {\rm{diag}}(\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{22}}}&{{A_{33}}}&{{A_{44}}}&0 \end{array}) , \\ & {A_{jj}} = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0 \\ 1&0&0 \\ 0&0&0 \end{array}} \right], j = 1,2,3,4 ,\end{split} $ |
| $ \begin{split} {X_{dq}} = \left[ {\begin{array}{*{20}{c}} { - {x_{dy}}}&0&{ - {x_{dm1}}}&{ - {x_{dqm1}}}&{ - {x_{dm2}}} \\ 0&{ - {x_{qy}}}&{{x_{dqm1}}}&{ - {x_{qm1}}}&{ - {x_{dqm2}}}\\ { - {x_{dm1}}}&{{x_{dqm1}}}&{ - {x_{dy}}}&0&{ - {x_{dm1}}}\\ { - {x_{dqm1}}}&{ - {x_{qm1}}}&0&{ - {x_{qy}}}&{{x_{dqm1}}}\\ { - {x_{dm2}}}&{ - {x_{dqm2}}}&{ - {x_{dm1}}}&{{x_{dqm1}}}&{ - {x_{dy}}}\\ {{x_{dqm2}}}&{ - {x_{qm2}}}&{ - {x_{dqm1}}}&{ - {x_{qm1}}}&0\\ { - {x_{dm3}}}&{ - {x_{dqm3}}}&{ - {x_{dm2}}}&{ - {x_{dqm2}}}&{ - {x_{dm1}}}\\ {{x_{dqm3}}}&{ - {x_{qm3}}}&{{x_{dqm2}}}&{ - {x_{qm2}}}&{ - {x_{dqm1}}} \\ { - {x_{fdy}}}&0&{ - {x_{fdy}}}&0&{ - {x_{fdy}}}\\ { - {x_{kdy}}}&0&{ - {x_{kdy}}}&0&{ - {x_{kdy}}}\\ 0&{ - {x_{kqy}}}&0&{ - {x_{kqy}}}&0 \end{array}} \right.\\ \left. {\begin{array}{*{20}{c}} {{x_{dqm2}}}&{ - {x_{dm3}}}&{{x_{dqm3}}}&{{x_{fdy}}}&{{x_{kdy}}}&0 \\ { - {x_{qm2}}}&{ - {x_{dqm3}}}&{ - {x_{qm1}}}&0&0&{{x_{kqy}}} \\ { - {x_{dqm1}}}&{ - {x_{dm2}}}&{{x_{dqm2}}}&{{x_{fdy}}}&{{x_{kdy}}}&0 \\ { - {x_{qm1}}}&{ - {x_{dqm2}}}&{ - {x_{qm2}}}&0&0&{{x_{kqy}}} \\ 0&{ - {x_{dm1}}}&{ - {x_{dqm1}}}&{{x_{fdy}}}&{{x_{kdy}}}&0 \\ { - {x_{qy}}}&{{x_{dqm1}}}&{ - {x_{qm1}}}&0&0&{{x_{kqy}}} \\ {{x_{dqm1}}}&{ - {x_{dy}}}&0&{{x_{fdy}}}&{{x_{kdy}}}&0 \\ { - {x_{qm1}}}&0&{ - {x_{qy}}}&0&0&{{x_{kqy}}} \\ 0&{ - {x_{fdy}}}&0&{{x_{fd}}}&{{x_{fdkd}}}&0 \\ 0&{ - {x_{kdy}}}&0&{{x_{fdkd}}}&{{x_{kd}}}&0 \\ { - {x_{kqy}}}&0&{ - {x_{kqy}}}&0&0&{{x_{kq}}} \end{array}} \right] 。\end{split} $ |
其中:下标
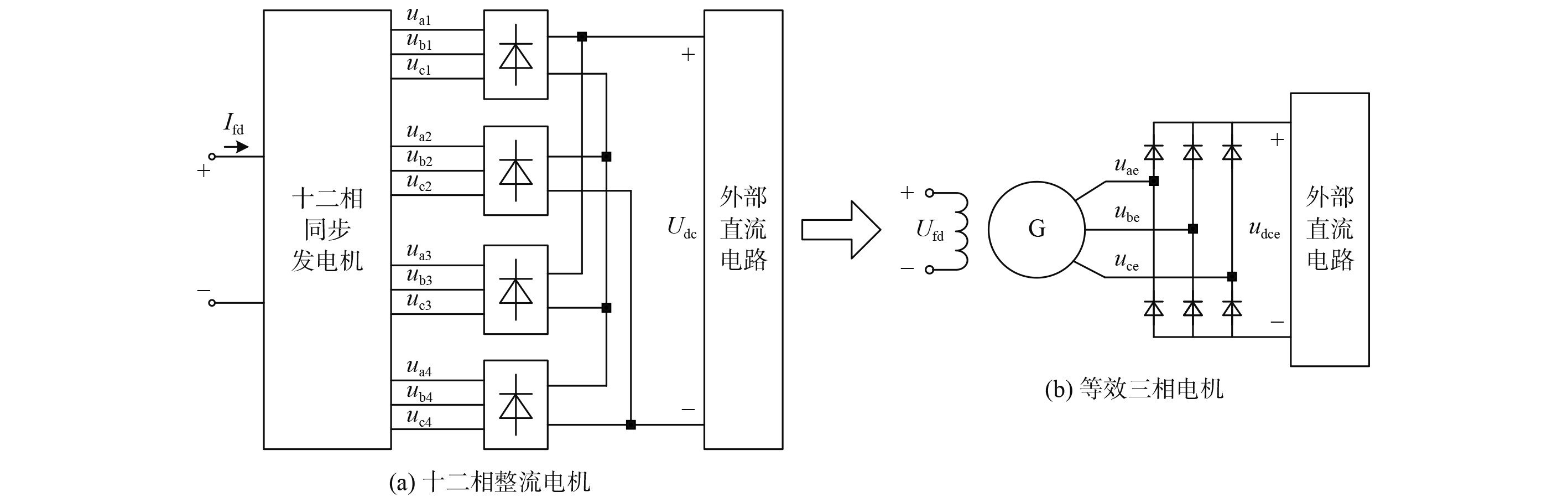
由于十二相同步发电机阶次高、运行模式复杂,为了对突加负载时直流侧电压跌落进行解析计算,需简化十二相电机模型的复杂程度,对其进行等效降阶处理[18-19],等效原理如图3所示。
|
图 3 十二相整流发电机等效原理图 Fig. 3 Schematic diagram of the equivalent principle of twelve-phase rectifier generator |
当十二相同步发电机各套单Y绕组输出平衡时,四者的电压、电流、磁链均近似相等,其中电流关系如下:
| $ \left\{ \begin{gathered} {i_{d1}} = {i_{d2}} = {i_{d3}} = {i_{d4}} = {i_d} ,\\ {i_{q1}} = {i_{q2}} = {i_{q3}} = {i_{q4}} = {i_q} 。\\ \end{gathered} \right. $ | (3) |
将式(3)代入式(1)给出的磁链方程,并根据变换前后功率不变的基本等效原则进行推导,可得等效三相同步电机的磁链方程:
| $ \left[ \begin{gathered} {\psi _{de}} \\ {\psi _{qe}} \\ {\psi _{fd}} \\ {\psi _{kd}} \\ {\psi _{kq}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{x_{de}}}&0&{{x_{afde}}}&{{x_{akde}}}&0 \\ 0&{{x_{qe}}}&0&0&{{x_{akqe}}} \\ {{x_{afde}}}&0&{{x_{fde}}}&{{x_{fdkde}}}&0 \\ {{x_{akde}}}&0&{{x_{fdkde}}}&{{x_{kde}}}&0 \\ 0&{{x_{akqe}}}&0&0&{{x_{kqe}}} \end{array}} \right]。$ | (4) |
式中,下标
|
|
表 1 十二相电机与其等效三相同步电机各参数之间的数学关系 Tab.1 Mathematical relationship between the parameters of twelve-phase rectifier generator and equivalent three-phase generator |
故等效三相同步电机的电压方程为:
| $ {u_{dqe}} = p{\psi _{dqe}} + Ap\theta {\psi _{dqe}} - {R_{dqe}}{i_{dqe}}。$ | (5) |
经过上述等效,图3(a)所示十二相整流同步发电机在脉冲负载作用下的动态响应过程可等效为其简化三相同步电机带脉冲负载运行,并以突加阻性负载来模拟脉冲负载的功率突变过程。为进一步计算电机直流侧电压最小值,需将直流电阻

|
图 4 直流侧线路电阻折算示意图 Fig. 4 Schematic diagram of the equivalent principle of DC residence |
可以看出,三相同步发电机整流侧突加纯阻性负载
| $ \frac{3}{2}{I^2}{r_{ac}} = \left[ {\frac{6}{{\text{π}} }\int_0^{\frac{{\text{π}} }{6}} {{{\left( {I\cos \omega t} \right)}^2}{\rm{d}}\omega t} } \right]{r_{dc}}。$ | (6) |
对式(6)进行求解,可得:
| $ {r_{ac}} \approx 0.609{r_{dc}}。$ | (7) |
假设脉冲负载功率突变前十二相整流发电机运行在空载额定转速工况下,发电机采用永磁副励磁机无刷励磁方式,通过调节主励磁机的励磁电压,将整流发电机直流侧输出电压建立到额定值。当负载功率突然增大时,突变的负载电流引起整流发电机直流侧输出电压迅速跌落,随即励磁系统开始作用,使直流侧输出电压重新恢复到额定运行状态。考虑到励磁系统作用的时间延迟,最大电压跌落与励磁系统的调节区间通常处于不同时间尺度,因此在对该变量进行解析计算时,认为可忽略励磁系统的调节作用。为进一步简化分析过程,在对脉冲负载的功率阶跃过程进行描述时,采用整流发电机直流侧突加阻性负载的方式。
根据文献[23],当电机在空载稳态时突加大小恒定的对称三相负载时,可将负载投入视作电机的突然三相短路,忽略变压器电势
| $ \left\{ \begin{gathered} {u_d} = - {\psi _q} - r{i_d} = {x_q}\left( p \right){i_q} - r{i_d} = 0 ,\\ {u_q} = {\psi _d} - r{i_q} = - {x_d}\left( p \right){i_d} - r{i_q} = {E_0}。\\ \end{gathered} \right. $ | (8) |
式中:
故定子电流满足:
| $ \left\{ \begin{gathered} {i_d} = \frac{{{x_q}\left( p \right){E_0}}}{{{r^2} + {x_d}\left( p \right){x_q}\left( p \right)}},\\ {i_q} = \frac{{r{i_d}}}{{{x_q}\left( p \right)}}。\\ \end{gathered} \right. $ | (9) |
其中:
| $ {x_d}\left( p \right) = \frac{{\left( {1 + T'_d p} \right)\left( {1 + T_d^{''}p} \right)}}{{\left( {1 + T'_{d0} p} \right)\left( {1 + T_{d0}^{''}p} \right)}}{x_d} ,$ | (10) |
| $ {x_q}\left( p \right) = \frac{{1 + T_q^{''}p}}{{1 + T_{q0}^{''}p}}{x_q} 。$ | (11) |
式中:
联立式(9)~式(10),并进行拉氏反变换,可得定子电流的时域解析式:
| $ \left\{ \begin{aligned} {i_d} = &\frac{{{x_q}{E_0}}}{{{r^2} + {x_d}{x_q}}} + \left[ \left( {\frac{1}{{{r^2} + x_d^{'}{x_q}}} - \frac{1}{{{r^2} + {x_d}{x_q}}}} \right){e^{ - \frac{t}{{T_{dz}^{'}}}}} +\right.\\ & \left. \left( {\frac{1}{{{r^2} + x_d^{''}{x_q}}} - \frac{1}{{{r^2} + x_d^{'}{x_q}}}} \right){e^{ - \frac{t}{{T_{dz}^{''}}}}} \right] {x_q}{E_0}+ \\ & \left( {\frac{{x_q^{''}}}{{{r^2} + x_d^{''}x_q^{''}}} - \frac{{{x_q}}}{{{r^2} + x_d^{''}{x_q}}}} \right){E_0}{e^{ - \frac{t}{{T_{qz}^{''}}}}},\\ \\ {i_q} = & \left[ \frac{1}{{{r^2} + {x_d}{x_q}}} + \left( {\frac{1}{{{r^2} + x_d^{'}{x_q}}} - \frac{1}{{{r^2} + {x_d}{x_q}}}} \right){e^{ - \frac{t}{{T_{dz}^{'}}}}}+ \right.\\ & \left( {\frac{1}{{{r^2} + x_d^{''}{x_q}}} - \frac{1}{{{r^2} + x_d^{'}{x_q}}}} \right){e^{ - \frac{t}{{T_{dz}^{''}}}}} + \\ &\left. \left( {\frac{1}{{{r^2} + x_d^{''}x_q^{''}}} - \frac{1}{{{r^2} + x_d^{''}{x_q}}}} \right){e^{ - \frac{t}{{T_{qz}^{''}}}}}\right]r{E_0}。\end{aligned} \right. $ | (12) |
式中,
| $ T_{dz}^{'} = \frac{{{r^2} + x_d^{'}{x_q}}}{{{r^2} + {x_d}{x_q}}}T_{d0}^{'} = \frac{{{r^2} + x_d^{'}{x_q}}}{{{r^2} + {x_d}{x_q}}}\frac{{{x_{fd}}}}{{{r_{fd}}}},$ | (13) |
| $ T_{dz}^{''} = \frac{{{r^2} + x_d^{''}{x_q}}}{{{r^2} + x_d^{'}{x_q}}}T_{d0}^{''} = \frac{{{r^2} + x_d^{''}{x_q}}}{{{r^2} + x_d^{'}{x_q}}}\left( {1 - \frac{{x_{afd}^2}}{{{x_{kd}}{x_{fd}}}}} \right)\frac{{{x_{kd}}}}{{{r_{kd}}}} ,$ | (14) |
| $ T_{qz}^{''} = \frac{{{r^2} + x_d^{''}x_q^{''}}}{{{r^2} + x_d^{''}{x_q}}}T_{q0}^{''} = \frac{{{r^2} + x_d^{''}x_q^{''}}}{{{r^2} + x_d^{''}{x_q}}}\frac{{{x_{kq}}}}{{{r_{kq}}}}。$ | (15) |
不考虑励磁系统的调节作用时,等效三相电机交流侧相电压幅值为:
| $ {u_{ac}} = \sqrt {\left( {r_L^2 + x_L^2} \right)\left( {i_d^2 + i_q^2} \right)} 。$ | (16) |
从式(12)可看出,相比于无阻尼绕组的情况[13],电机在考虑阻尼绕组后端电压在突加负载瞬间会产生更大的跌落,但随着阻尼绕组时间常数的衰减,电压开始回升,并在励磁绕组时间常数衰减结束后达到稳态值,故最大电压跌落将出现在波谷处,对式(16)进行求导可得驻点(
| $ {\left. {\frac{{{\rm{d}}u\left( t \right)}}{{{\rm{d}}t}}} \right|_{{t_d}}} = 0,$ | (17) |
| $ {u_{ac}}_{\min } = u\left( {{t_d}} \right)。$ | (18) |
考虑到十二相同步发电机整流系统的运行过程与交直流变换关系十分复杂[24],为了便于进行公式推导,假设突加负载瞬间整流电压输出的直流电压平均值不受换相重叠角的影响,则当十二相电机整流桥输出端采用四并的连接方式时,直流侧电压可表示为:
| $ {u_{dc}}_{\min } = \frac{{3\sqrt 3 }}{{\text{π}} }{u_{ac\min }}。$ | (19) |
则发电机直流侧最大电压调整率为:
| $ \Delta U{\text{ = }}\frac{{{U_{dcN}} - {U_{dc\min }}}}{{{U_{dcN}}}} \times 100\%。$ | (20) |
式中,
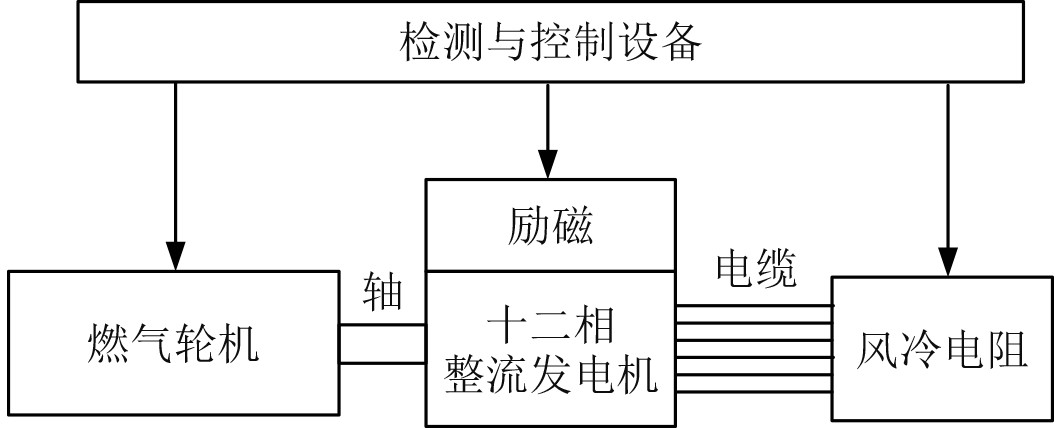
为验证数学模型及脉冲负载作用时,十二相整流同步发电机直流侧最大瞬态电压调整率解析计算方法的正确性,在Matlab/Simulink中建立十二相整流同步发电机及其控制系统的电磁暂态仿真模型,并基于某十二相整流同步发电机的原理样机进行突加负载试验,试验系统结构如图5所示,主要由1台燃气轮机、1台十二相整流发电机、风冷电阻及相关检测、控制设备组成。
|
图 5 试验系统结构图 Fig. 5 Structure diagram of experimental system |
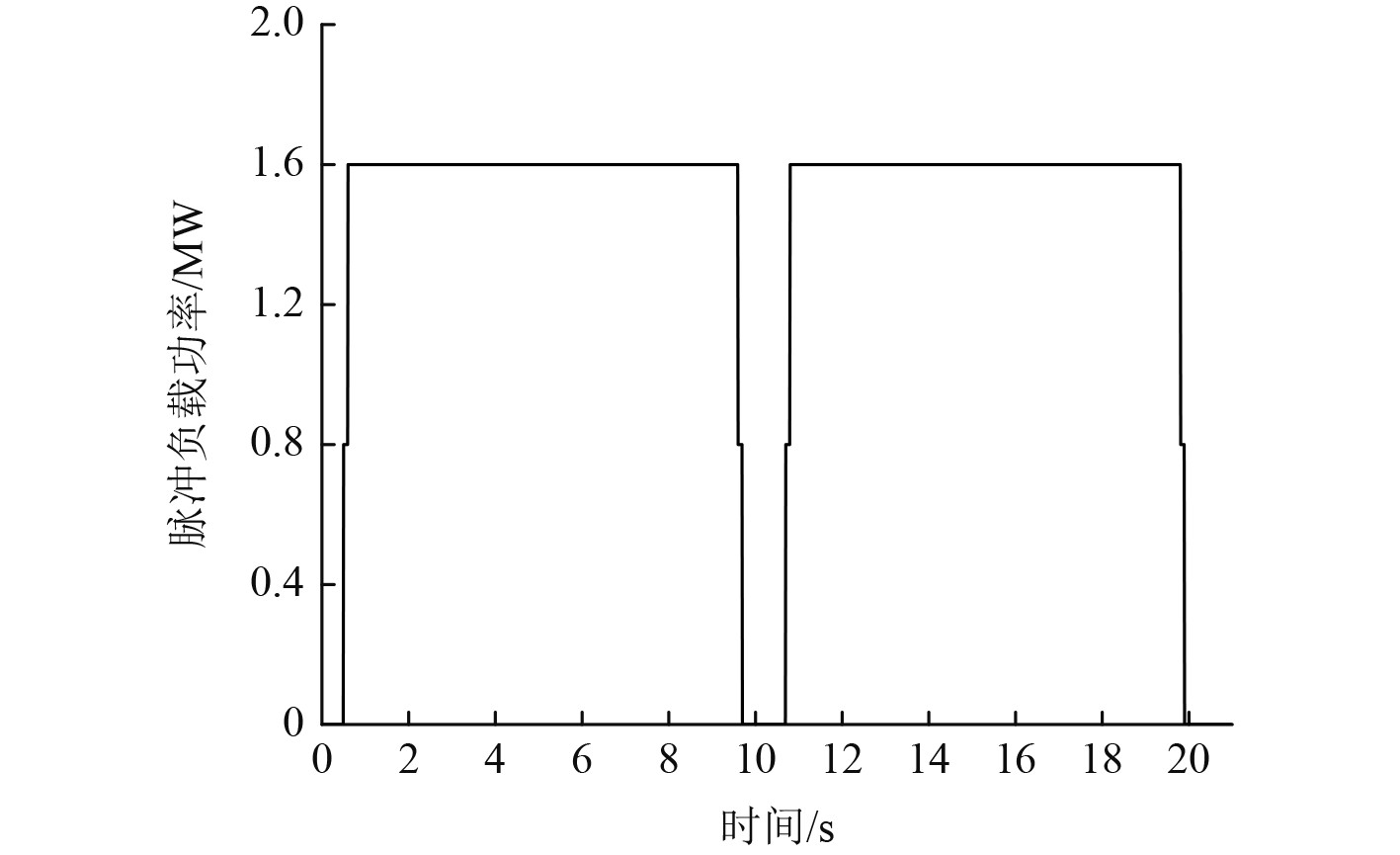
在试验过程中,整流桥直流侧为电阻负载,其阻值
|
图 6 脉冲负载的功率特性 Fig. 6 Power characteristic of pulse load |
利用式(12)~式(20)可解析计算出该脉冲负载作用下十二相整流发电机的最大电压调整率
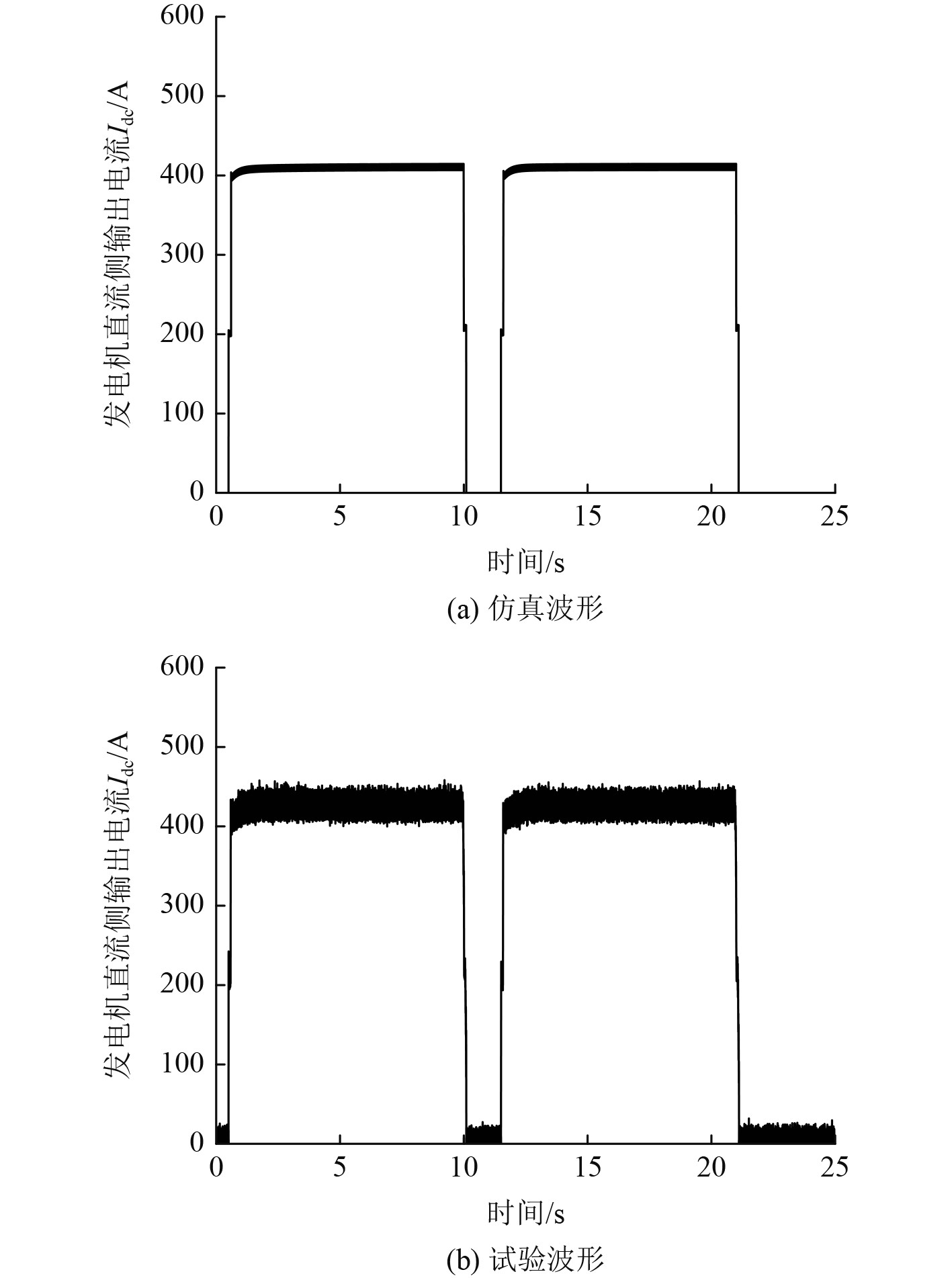
|
图 7 脉冲负载作用下十二相整流发电机直流侧电流 Fig. 7 The output current of twelve-phase rectifier generator with pulse load |
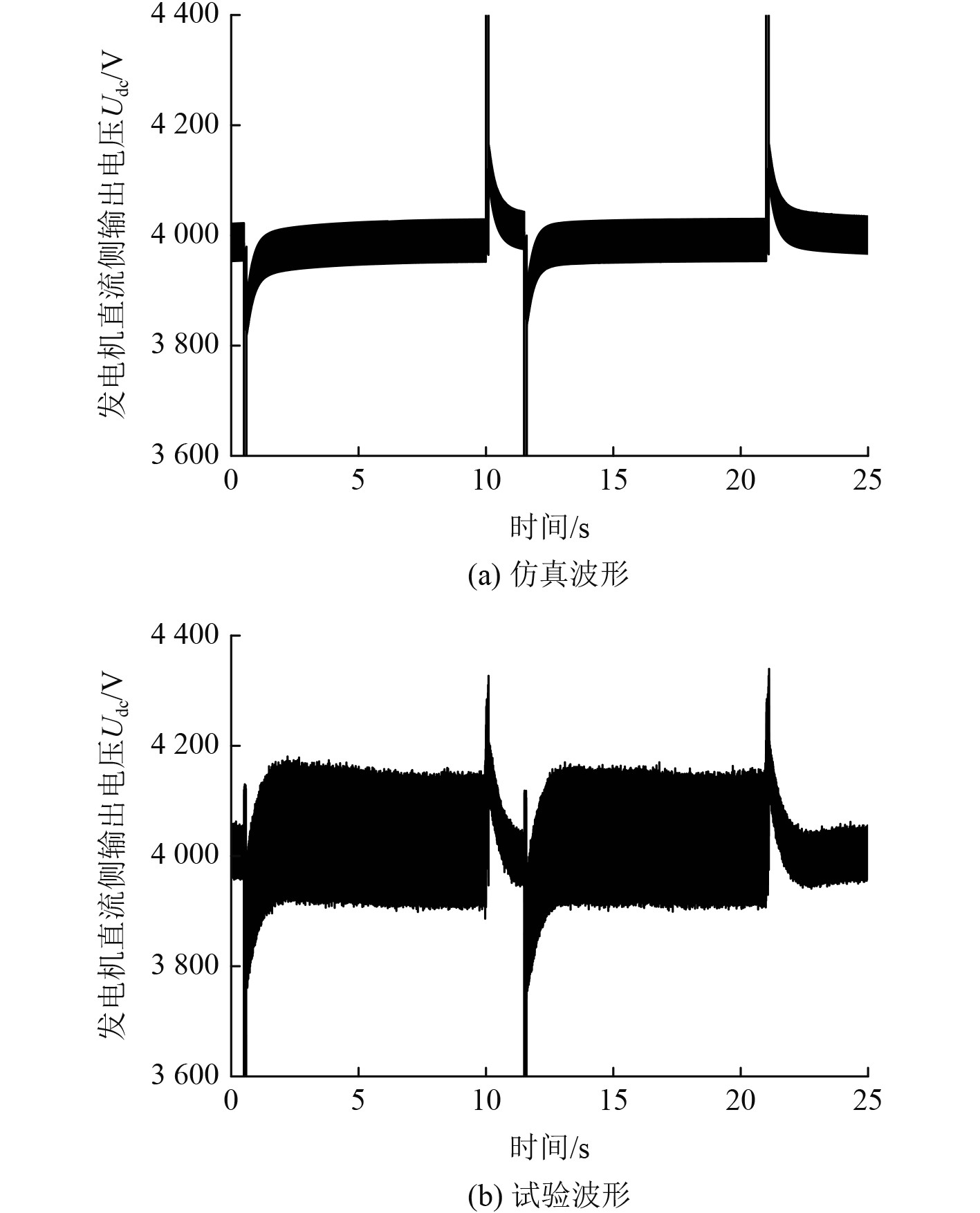
|
图 8 脉冲负载作用下十二相整流发电机直流侧电压 Fig. 8 The output voltage of twelve-phase rectifier generator with pulse load |
针对脉冲负载作用下,十二相整流发电机直流侧最大瞬态电压调整率缺乏理论计算依据的问题,本文对十二相同步发电机进行等效降阶处理,同时利用功率等效原则将直流侧负载折算到交流侧,建立了十二相整流同步发电机的等效三相同步电机模型。基于此,推导了十二相整流同步发电机在矩形波脉冲负载下,直流侧最大瞬态电压调整率的解析计算方法,将理论计算结果与时域仿真及物理试验结果对比,得到以下结论:
1)十二相整流同步发电机在空载稳态时,突加矩形波脉冲负载后,直流侧最大电压调整率的理论计算结果与时域仿真及物理试验结果能够较好吻合,说明由降阶等效带来的误差处于工程计算允许的范围内,验证了该解析计算方法的有效性,并为机组动态加载过程中,负载功率瞬变边界的划定提供了理论依据。
2)解析计算结果表明,脉冲负载作用下十二相整流发电机直流侧最大瞬态电压调整率与电机自身的参数及负载功率阶跃的大小有关。当负载给定时,可通过优化电机参数或加快励磁系统的响应速度来改善电压跌落,这为未来十二相整流同步发电机组动态性能的优化指明了方向。
| [1] |
马伟明. 舰船动力发展的方向——综合电力系统[J]. 海军工程大学学报, 2002, 14(6): 1–5+9. MA Weiming. Integrated power systems--trend of ship power development[J]. Journal of Naval Engineering University, 2002, 14(6):1–5+9 |
| [2] |
付立军, 刘鲁锋, 王刚, 等. 我国舰船中压直流综合电力系统研究进展[J]. 中国舰船研究, 2016, 11(1): 72–79. FU Lijun, Liu Lufeng, WANG Gang, et al. The research progress of the medium voltage DC integrated power system in China[J]. Chinese Journal of Ship Research, 2016, 11(1): 72–79. |
| [3] |
FANG S, WANG Y, GOU B, et al. Toward future green maritime transportation: An overview of seaport microgrids and all-electric ships[J]. Transactions on Vehicular Technology, 2020, 69(1): 207–219.
|
| [4] |
GAO X. P, FU L J, HU J, et al. Voltage stability analysis of DC ship power system with pulse load[J]. The Journal of Engineering, 2019, 16, 2027–2031.
|
| [5] |
CUPELLI M, Lin Zhu and A. Monti, "Why ideal constant power loads are not the worst case condition from a control standpoint[J], " 2015 IEEE Power & Energy Society General Meeting, 2015, 1–1.
|
| [6] |
谢卫, 朱军. 十二相四Y移15°绕组同步电动机的数学模型及动态仿真[J]. 电工技术学报, 2004, 19(1): 2–6.
|
| [7] |
JATSKEVICH J, PEKAREK S D. Numerical validation of parametric average-value modeling of synchronous machine-rectifier systems for variable frequency operation[J]. IEEE Transactions on Energy Conversion, 2008, 23(1): 342-344. DOI:10.1109/TEC.2007.908365 |
| [8] |
MA W, AN H. Stability of a synchronous generator with diode-bridge rectifier and back-EMF load[J]. IEEE Transactions on Energy Conversion, 2000, 15(4): 458-463. DOI:10.1109/60.900508 |
| [9] |
张晓锋. 同步发电机整流系统的运行稳定性研究[D]. 北京: 清华大学, 1995.
|
| [10] |
吴新振, 张伟玲, 董海涛, 等. 十二相整流发电机二极管开路的故障运行分析[J]. 电工技术学报, 2017, 32(3): 157–163.
|
| [11] |
张艳辉, 郑晓钦, 吴新振, 等. 基于有限元场路耦合的十二相整流发电机系统定子匝间短路分析[J]. 电工技术学报, 2019, 34(9): 1842–1849.
|
| [12] |
张伟玲, 吴新振, 魏锟, 等. 十二相整流发电机缺桥故障运行分析[J]. 中国电机工程学报, 2016, 36(6): 1724–1730.
|
| [13] |
YI X, WANG D, GUO Y, et al. Transient voltage regulation performance simulation of a twelve-phase synchronous generator-rectifier system[C]// 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), 2014: 1−5.
|
| [14] |
ZHANG G F, M W M. Transient analysis of synchronous machines[M]. Wuhan: Hubei Science and Technology Press, 1999.
|
| [15] |
肖晗, 叶志浩, 纪锋, 等 突加负载对同步发电机整流系统直流侧电压的影响[J]. 海军工程大学学报, 2019, 31(1): 25−30.
|
| [16] |
邵英, 袁立军. 十二相同步发电机整流系统运行模式分析[J]. 中国电机工程学报, 2003, (7): 129−133.
|
| [17] |
WANG G, XIAO R and WU X. Analysis of integrated power system with pulse load by periodic orbit[J]. in IEEE Transactions on Plasma Science, 2019, 47(2): 1345–1351.
|
| [18] |
马伟明. 多相整流发电机及其系统的分析[M]. 杭州: 浙江大学出版社, 2020.
|
| [19] |
郝晓亮, 付立军, 马凡, 等. 中压直流综合电力系统建模与实时仿真实现方法[J]. 电网技术, 2021, 45(3): 1100–1109.
|
| [20] |
马凡, 付立军, 郭云珺, 等. 十二相同步发电机整流系统直流极间短路电流的解析计算方法[J]. 中国电机工程学报, 2021, 41(20): 7117−7126.
|
| [21] |
陈新刚, 冀路明, 孙俊忠. 考虑直流侧线路电阻时十二相发电机整流系统突然短路研究[J]. 中小型电机, 2003(6): 30−33.
|
| [22] |
肖晗, 叶志浩, 纪锋, 等. 储能装置投入对整流发电机突加负载时瞬时电压的影响[J]. 船舶工程, 2018, 40(12): 35−40. XIAO Han, YE Zhihao, JI Feng, et al. Influence of energy storage device on instantaneous voltage of rectifier generator with suddenly-applied load[J]. Ship Engineering, 2018, 40(12): 35−40. (in Chinese) |
| [23] |
李基成. 现代同步发电机励磁系统设计及应用[M]. 北京: 中国电力出版社, 2002.
|
| [24] |
高景德, 张磷征. 电机过渡过程的基本理论及分析方法[M]. 北京: 科学出版社, 1982.
|
| [25] |
雷津, 刘德志, 刘芬. 解析计算并联与串联结构的十二相同步发电机整流系统[J]. 中小型电机, 2005(6): 3−6.
|
 2024, Vol. 46
2024, Vol. 46
