2. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着各国对深海资源逐步探测与开发,深海装备迅速发展。AUV(自主水下航行器)作为一种深海装备,不受缆线限制,可灵活执行任务,在深海开发中具有重要作用[1]。考虑到AUV动力源有限[2],为提高作业时长,缩短下潜时间,可采用无动力垂直下潜方式。但是该方式未进行闭环控制,受海洋环境扰动,其下潜着陆位置难以控制[3]。因此研究其下潜运动特性,预报其下潜轨迹及参数非常重要。
研究深海AUV下潜运动规律,需要建立其深海下潜运动模型,并进行仿真预报。张天健等[4]针对深海环境下水下运载器的浮潜运动过程,提出一种数值仿真快速预报方法。宋保维等[5]对潜伏式武器水下释放后的下潜运动过程进行仿真,得到了不同运动阶段水下武器纵平面下潜的运动规律,但是并未考虑在较大攻角下阻力系数变化及水下涌浪的影响。高伟等[6]针对AUV深海下潜运动,建立其仿真模型,分析了小纵倾和螺旋两种下潜方式,得到了AUV下潜参数与本体控制量及环境力变化关系,但是并未对垂直或者大纵倾角下潜运动进行分析。以上研究并未涉及到空间六自由度下,使用欧拉角数学方程导致的姿态角解算奇异性问题,针对此种情况,徐正武等[7]将四元数运用在水下航行器数学模型中,避免了欧拉角求解奇异问题。赵志超等[8]采用四元数法建立了某AUV的运动方程及仿真模型,对其大纵倾上浮运动进行了研究,解决了欧拉角在表示纵倾过大时的运动参数求解奇异问题。
目前结合四元数法分析无动力垂直下潜运动特性,考虑控制参数及环境扰动影响的研究较少。本文以某深海AUV为研究对象,使用四元数代替欧拉角,通过工程软件Matlab中的Simulink仿真模块建立了环境扰动下的动力学仿真模型,避免了垂直下潜运动中欧拉角无法解算的问题。研究了负浮力、重浮心距离与舵角、初始纵倾角及环境扰动力对AUV下潜运动的作用规律,为深海装备无动力垂直下潜运动提供了一种可靠的预报方法。
1 数学模型及仿真建模 1.1 坐标系定义如图1所示,AUV需要2个坐标系表述其运动情况。通过惯性坐标系E-ξηζ描述AUV浮心的运动情况,通过体坐标系b-xyz描述AUV相对自身的运动情况。其中,惯性坐标系相对大地不动也称“定系”,体坐标系随AUV运动也称“动系”。
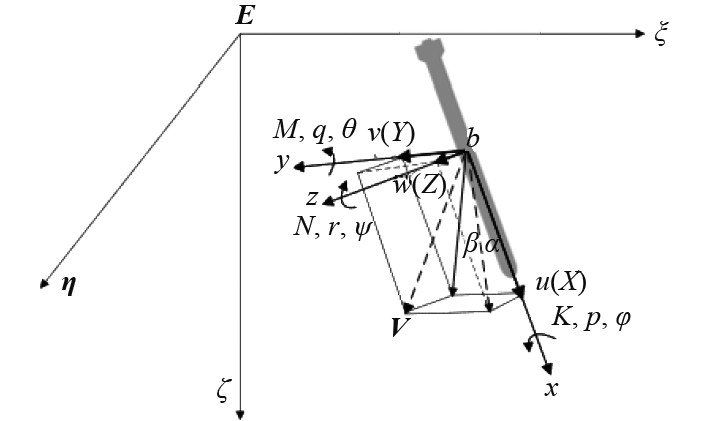
|
图 1 AUV坐标系示意图 Fig. 1 Coordinate system of AUV |
使用式(1)中7个向量描述AUV运动情况。
| $ \begin{split} & {{\boldsymbol{\eta }}_{\text{1}}}{\text{ = }}{[\xi {\text{ }}\eta {\text{ }}\zeta ]^{\text{T}}},{\text{ }}{{\boldsymbol{\eta }}_{\text{2}}} = {[\varphi {\text{ }}\theta {\text{ }}\psi ]^{\text{T}}},{\text{ }}{\boldsymbol{V}} = {[{V_\xi }{\text{ }}{V_\eta }{\text{ }}{V_\zeta }]^{\text{T}}} = {\left[ {u{\text{ }}v{\text{ }}w} \right]^{\text{T}}} \\ & {\boldsymbol{\Omega }} = {[p{\text{ }}q{\text{ }}r]^{\text{T}}},{\text{ }}{\boldsymbol{F}} = {[X{\text{ }}Y{\text{ }}Z]^{\text{T}}},{\text{ }}{\boldsymbol{M}} = {[K{\text{ }}M{\text{ }}N]^{\text{T}}},\\[-1pt] \end{split} $ | (1) |
式中:η1为AUV浮心在定系中的空间坐标;η2为AUV相对定系的姿态角;V为AUV定系航行速度,其中Vξ、Vη、Vζ分别为V在定系三轴上的分量,u、v、w分别为V在动系三轴上的分量;Ω为AUV相对定系角速度,其中p、q、r分别为Ω在动系三轴上的分量;F、M分别为作用在AUV上的合外力及力矩,其中X、Y、Z和K、M、N分别为F、M在动系下三轴上的分量。
AUV在2个坐标系下速度与角速度表示不同,可通过下式进行转换。
| $ {{\boldsymbol{\dot \eta }}_{\text{1}}}{\text{ = }}{{\boldsymbol{J}}_{\boldsymbol{1}}}({{\boldsymbol{\eta }}_2}){\boldsymbol{V}}{\text{ }},{\text{ }}{{\boldsymbol{\dot \eta }}_2}{\text{ = }}{{\boldsymbol{J}}_2}({{\boldsymbol{\eta }}_2}){\boldsymbol{\Omega }},$ | (2) |
式中,J1(η2)和J2(η2)为旋转变换矩阵,展开式如下:
| $ \begin{split} & {{{\boldsymbol{J}}_{\boldsymbol{1}}}({{\boldsymbol{\eta }}_2}) =}\\ & {{\left[ \begin{gathered} \cos \psi \cos \theta \quad {\text{ - sin}}\psi {\text{cos}}\varphi {\text{ + cos}}\psi \sin \theta \sin \varphi \quad {\text{ sin}} \psi {\text{sin}}\varphi + \cos \psi \sin \theta \cos \varphi \\ \sin \psi \cos \theta \quad{\text{ cos}}\psi {\text{cos}}\varphi + {\text{sin}}\psi \sin \theta \sin \varphi \quad{\text{ - cos}}\psi \sin \varphi + \sin \psi \sin \theta \cos \varphi \\ - \sin \theta {\text{ }}\quad\quad\quad\quad\quad\quad\quad \cos \theta \sin \varphi {\text{ }}\quad\quad\quad\quad\quad\quad \cos \theta \cos \varphi\quad {\text{ }} \\ \end{gathered} \right]}},\end{split} $ | (3) |
| $ {{\boldsymbol{J}}_2}({{\boldsymbol{\eta }}_2}) = \left[ \begin{array}{ccccccccc} 1& \sin \varphi \tan \theta & {\text{cos}}\varphi \tan \theta \\ 0& {\text{cos}}\varphi & {{ - }}\sin \varphi {\text{ }} \\ {\text{0}}& \sin \varphi /\cos \theta& \cos \varphi /\cos \theta \end{array} \right]。$ | (4) |
AUV在下潜过程中,受到重力、浮力、水动力、操纵舵力及环境扰动力作用,其中水动力可分为黏性水动力和惯性水动力。假设AUV对称于纵轴所在的水平面与垂直面,动系原点为浮心,并且整个下潜过程中重心与浮心位置不变,根据《潜艇操纵性》,AUV的空间运动方程可表示为[9]:
| $ \left[ \begin{gathered} {{\boldsymbol{\dot V}}} \\ {{\boldsymbol{\dot \Omega }}} \\ \end{gathered} \right] = {{\boldsymbol{M}}^{ - 1}}\left[ \begin{gathered} {{\boldsymbol{F}}_{hd}}{\boldsymbol{ + }}{{\boldsymbol{F}}_{hs}}{\boldsymbol{ + }}{{\boldsymbol{F}}_{op}}{\boldsymbol{ + }}{{\boldsymbol{F}}_\tau } \\ {{\boldsymbol{M}}_{hd}}{\boldsymbol{ + }}{{\boldsymbol{M}}_{hs}}{\boldsymbol{ + }}{{\boldsymbol{M}}_{op}}{\boldsymbol{ + }}{{\boldsymbol{M}}_\tau } \\ \end{gathered} \right]。$ | (5) |
式中:M为系数矩阵,与AUV自身物理量有关;Fhd、Mhd为AUV受到的黏性力项;Fhs、Mhs为静力项;Fop、Mop为舵力项;Fτ、Mτ为外部环境扰动力项。
1.3 四元数由于研究目标是AUV垂直下潜运动特性,纵倾角在90°附近,使用欧拉角解算会产生奇异性问题,无法获取AUV姿态,为避免这一问题,采用四元数代替欧拉角对AUV姿态角进行结算。四元数由两部分组成:表示物体旋转轴的空间矢量与表示旋转角的标量,可以将其表示为[10]:
| $\begin{aligned} & {\boldsymbol{q}} = {[\begin{array}{*{20}{c}} {\boldsymbol{\sigma }}&\eta \end{array}]^{\rm T}} = {[\begin{array}{*{20}{c}} {{\sigma _1}}&{{\sigma _2}}&{{\sigma _3}}&\eta \end{array}]^{\rm T}} = \\ & {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{\lambda }}\sin \tfrac{\beta }{2}}&{\cos \tfrac{\beta }{2}} \end{array}} \right]^{\rm T}}。\end{aligned}$ | (6) |
式中:λ为旋转轴的单位矢量;β为旋转角。
利用四元数进行坐标变换,式(2)可变为:
| $ {{\boldsymbol{\dot \eta }}_{\text{1}}}{\text{ = }}{{\boldsymbol{E}}_{\boldsymbol{1}}}({\boldsymbol{q}}){\boldsymbol{V}}{\text{ }},{\text{ }}{{\boldsymbol{\dot q}}_2}{\text{ = }}{{\boldsymbol{E}}_2}({\boldsymbol{q}}){\boldsymbol{\Omega }}。$ | (7) |
式中:E1(q)为四元数表示的速度变换矩阵;E2(q)为角速度变换矩阵,其展开式如下:
| $\begin{aligned} & {{\boldsymbol{E}}_1}({\boldsymbol{q}}) = \\ & \left[ {\begin{array}{*{20}{c}} {1 - 2(\sigma _2^2 + \sigma _3^2)}&{2({\sigma _1}{\sigma _2} - {\sigma _3}\eta )}&{2({\sigma _1}{\sigma _3} + {\sigma _2}\eta )} \\ {2({\sigma _1}{\sigma _2} + {\sigma _3}\eta )}&{1 - 2(\sigma _1^2 + \sigma _3^2)}&{2({\sigma _2}{\sigma _3} - {\sigma _1}\eta )} \\ {2({\sigma _1}{\sigma _3} - {\sigma _2}\eta )}&{2({\sigma _2}{\sigma _3} + {\sigma _1}\eta )}&{1 - 2(\sigma _1^2 + \sigma _2^2)} \end{array}} \right],\end{aligned}$ | (8) |
| $ {{\boldsymbol{E}}_2}({\boldsymbol{q}}) = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} \eta &{ - {\sigma _3}}&{{\sigma _2}} \\ {{\sigma _3}}&\eta &{{\sigma _1}} \\ { - {\sigma _2}}&{{\sigma _1}}&\eta \\ { - {\sigma _1}}&{ - {\sigma _2}}&{ - {\sigma _3}} \end{array}} \right]。$ | (9) |
式(5)中与姿态角有关的主要为静力Fhs和静力矩Mhs,因此式(5)变为:
| $\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_{hs}}({\boldsymbol{q}})}\\ {{{\boldsymbol{M}}_{hs}}({\boldsymbol{q}})} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {2(P - B)({\sigma _1}{\sigma _3} - {\sigma _2}\eta )}\\ {2(P - B)({\sigma _2}{\sigma _3} + {\sigma _1}\eta )}\\ {(P - B)[1 - 2(\sigma _1^2 + \sigma _2^2)]}\\ {P{y_g}[1 - 2(\sigma _1^2 + \sigma _2^2)] - 2P{z_g}({\sigma _2}{\sigma _3} + {\sigma _1}\eta )}\\ {2P{z_g}({\sigma _1}{\sigma _3} - {\sigma _2}\eta ) - P{x_g}[1 - 2(\sigma _1^2 + \sigma _2^2)]}\\ {2P{x_g}({\sigma _2}{\sigma _3} + {\sigma _1}\eta ) + 2P{y_g}({\sigma _1}{\sigma _3} - {\sigma _2}\eta )} \end{array}} \right],$ | (10) |
最终,AUV的动力学方程为:
| $ \left[ \begin{gathered} {{\boldsymbol{\dot V}}} \\ {{\boldsymbol{\dot \Omega }}} \\ \end{gathered} \right] = {{\boldsymbol{M}}^{ - 1}}\left[ \begin{gathered} {{\boldsymbol{F}}_{hd}}{{ + }}{{\boldsymbol{F}}_{hs}}({\boldsymbol{q}}){{ + }}{{\boldsymbol{F}}_{op}}{{ + }}{{\boldsymbol{F}}_\tau } \\ {{\boldsymbol{M}}_{hd}}{{ + }}{{\boldsymbol{M}}_{hs}}({\boldsymbol{q}}){{ + }}{{\boldsymbol{M}}_{op}}{{ + }}{{\boldsymbol{M}}_\tau } \\ \end{gathered} \right]。$ | (11) |
四元数与欧拉角是对AUV同一姿态的不同表示,两者之间可以相互转换,对比式(3)和式(6),可以得到:
| $ \left\{ {\begin{array}{*{20}{c}} { - \sin \theta = 2({\sigma _1}{\sigma _3} - {\sigma _2}\eta )},\\ {\cos \psi \cos \theta = 1 - 2(\sigma _2^2 + \sigma _3^2)} ,\\ {\sin \psi \cos \theta = 2({\sigma _1}{\sigma _2} + {\sigma _3}\eta )},\\ {\sin \varphi \cos \theta = 2({\sigma _2}{\sigma _3} + {\sigma _1}\eta )} ,\\ {\cos \varphi \cos \theta = 1 - 2(\sigma _1^2 + \sigma _2^2)} 。\end{array}} \right. $ | (12) |
将其化简可得欧拉角与四元数的转换关系为[11]:
| $ \left\{ \begin{gathered} \varphi = \arctan \frac{{2({\sigma _2}{\sigma _3}{\text{ + }}{\sigma _1}\eta )}}{{1 - 2(\sigma _1^2 + \sigma _2^2)}} ,\\ \theta = \arcsin [ - 2({\sigma _1}{\sigma _3} - {\sigma _2}\eta )] ,\\ \psi = \arctan \frac{{2({\sigma _1}{\sigma _2} + {\sigma _3}\eta )}}{{1 - 2(\sigma _2^2 + \sigma _3^2)}}。\end{gathered} \right. $ | (13) |
| $ \left\{ \begin{gathered} {\sigma _1} = \sin \frac{\varphi }{2}\sin \frac{\theta }{2}\cos \frac{\psi }{2} + \cos \frac{\varphi }{2}\cos \frac{\theta }{2}\sin \frac{\psi }{2},\\ {\sigma _2} = \cos \frac{\varphi }{2}\sin \frac{\theta }{2}\cos \frac{\psi }{2} + \sin \frac{\varphi }{2}\cos \frac{\theta }{2}\sin \frac{\psi }{2} ,\\ {\sigma _3} = \sin \frac{\varphi }{2}\cos \frac{\theta }{2}\cos \frac{\psi }{2} - \cos \frac{\varphi }{2}\sin \frac{\theta }{2}\sin \frac{\psi }{2},\\ \eta = \cos \frac{\varphi }{2}\cos \frac{\theta }{2}\cos \frac{\psi }{2} - \sin \frac{\varphi }{2}\sin \frac{\theta }{2}\sin \frac{\psi }{2} 。\end{gathered} \right. $ | (14) |
洋流是海水沿着一定方向按照一定规律并以相对稳定的速度进行的流动。洋流具备季度性,可认为在几个月内,其大小和方向在水平面内不变,速度只随深度变化而变化。不考虑涡流及垂直流影响,洋流速度变化情况如图2所示[12]。
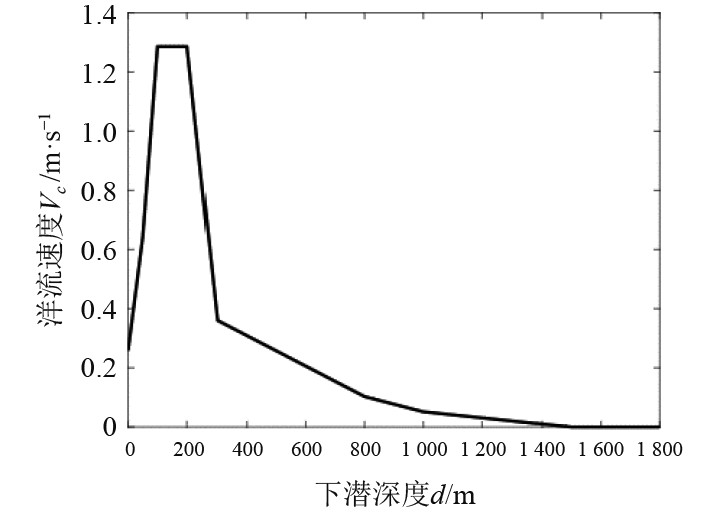
|
图 2 洋流速度随深度变化情况 Fig. 2 Ocean current velocity at different depths |
假设AUV受到洋流作用,在惯性系中,洋流速度Vc=[uc vc wc]T,体坐标系中,AUV相对洋流的速度Vr为:
| $ {{\boldsymbol{V}}_r} = {\boldsymbol{V}} - {({{\boldsymbol{E}}_1}({\boldsymbol{q}}))^{ - 1}}{{\boldsymbol{V}}_c} 。$ | (15) |
随着AUV不断下潜,深度不断增加,海水物理参数时刻变化着,AUV自身材料受到影响产生形变,导致AUV的排水体积、平均密度等发生变化,所受浮力也不断变化。其中压力和温度变化产生的效果明显[13]。温度和盐度随深度变化情况[14]如图3所示。深度小于1 km时,盐度和温度随深度增加迅速减小,之后温度趋于平缓,盐度先增加而后变得平缓。
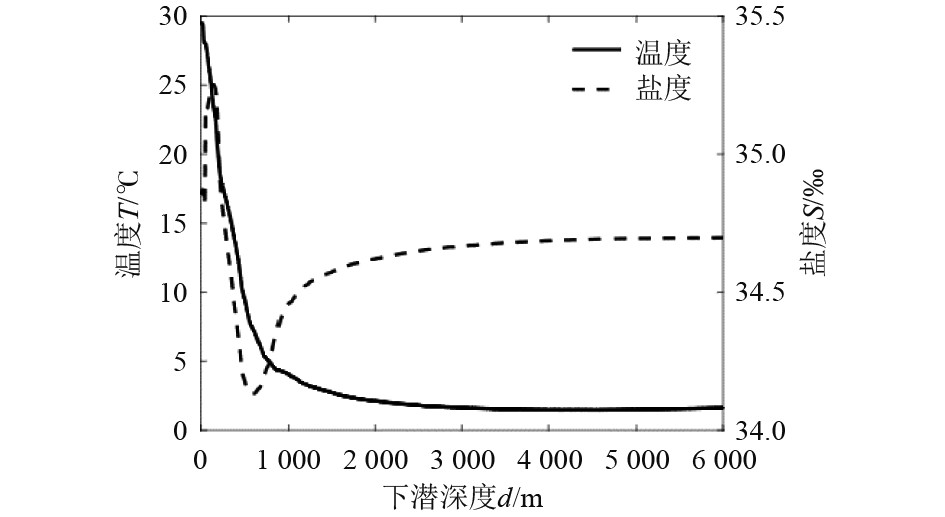
|
图 3 温度和盐度随深度变化情况 Fig. 3 Temperature and salinity values at different depths |
假设温度和盐度不变,海平面相对压力为0,压力变化量∆P为:
| $ \Delta P = {\rho _d}gd。$ | (16) |
式中:ρd为所处深度海水的平均密度,用海水的平均密度ρa代替计算;d为下潜深度。由文献[13]知下潜过程中温度、盐度和压力对AUV浮力的综合影响为:
| $ \begin{gathered} \Delta B = (\Delta {\rho _T}{V_0} - {\rho _0}\Delta {V_T} - \Delta {\rho _T}\Delta {V_T})g + 709\Delta Sg{V_0}+ \\ (\Delta {\rho _P}{V_0} - {\rho _0}\Delta {V_P} - \Delta {\rho _P}\Delta {V_P})g。\end{gathered} $ | (17) |
式中:∆ρT,∆VT分别为温度变化引起的海水密度和AUV排水体积的变化量;∆ρP,∆VP分别为压力变化引起的海水密度和AUV排水体积的变化量;∆S为盐度变化量。假设AUV为一整体,浮力变化的各项参数如表1所示。
|
|
表 1 AUV浮力变化计算参数值 Tab.1 Parameter values in AUV buoyancy change calculation |
将表1中各值代入式(16),得到AUV浮力变化量随深度变化情况,如图4所示。AUV下潜至6 000 m时,浮力相比海面增大了149.89 N。
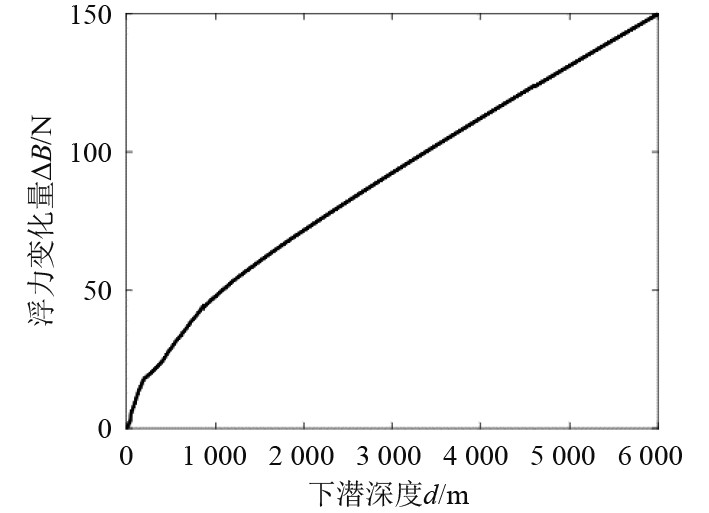
|
图 4 浮力变化量随深度变化情况 Fig. 4 Buoyancy change at different depths |
通过工程软件Matlab中的Simulink仿真模块,将前述基于四元数建立的AUV动力学模型与海洋扰动力模型合并,建立了AUV的空间无动力下潜仿真模型,如图5所示,该模型主要由力学模块和运算模块组成,其中力学模块包括水动力模块、静力模块、操纵力模块、洋流模块和浮力变化模块,运算模块包括动力学模块、运动学模块及四元数欧拉角转换模块。

|
图 5 AUV动力学仿真模型 Fig. 5 Dynamics simulation model of AUV |
为保证后续分析正确,应将仿真与试验结果比较,证明模型准确有效。根据AUV某航次试验情况,设置仿真条件为负浮力2 kg,下潜深度100 m,无舵角。仿真结果与试验情况对比如图6所示,可以看出,两者变化趋势相同,基本吻合。在下潜时间上,实航用时551 s,仿真用时543.1 s,误差低于2%,可以认为该动力学仿真模型准确,可以用于之后的垂直下潜运动规律分析。
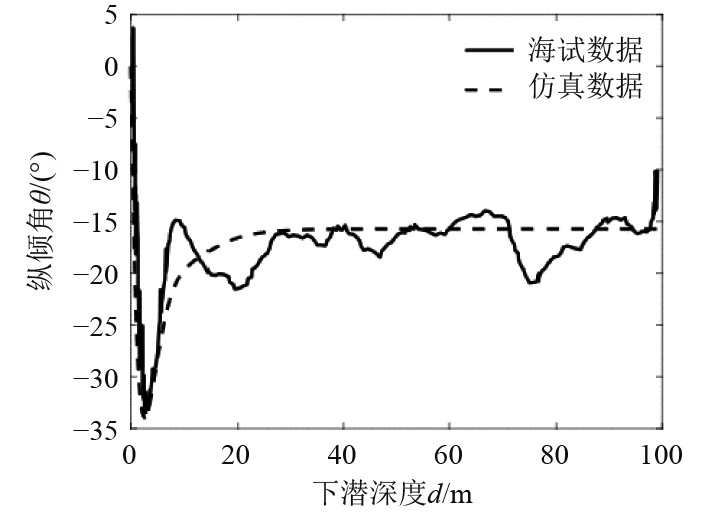
|
图 6 仿真模型准确性验证 Fig. 6 Accuracy verification of the simulation model |
与AUV垂直下潜相关的参数主要为重浮心纵向距离xg、垂向距离zg、负浮力W、水平舵角δs以及初始纵倾角θ0,共5个控制参数。设置AUV下潜条件为无洋流扰动并且无浮力变化,采用控制变量法对5个参数进行探究,分析它们对AUV垂直下潜运动的作用规律。
2.1.1 重浮心纵向距离与负浮力AUV重浮力纵向距离和负浮力是控制其垂直下潜的主要控制量。忽略环境扰动力,在整个下潜过程中,保持δs=10°和zg=0不变,初始纵倾角θ0=−90°,负浮力取5~30 kg内固定值,纵向距离取0.05L~0.25L内固定值,L为AUV长度。
在AUV下潜运动过程中,纵倾角和攻角在水静力矩、水动力矩和舵力矩共同作用下达到稳态。改变重浮心纵向距离和负浮力,会导致3种力矩产生不同程度的变化,最终AUV稳定在不同状态。从图7可以看出,保持重浮心纵向距离不变,负浮力增大会导致稳态纵倾角、攻角绝对值增大,但是由于纵倾角与攻角正方向定义不同,纵倾角是朝着远离η轴的方向变化,攻角则是朝着靠近η轴的方向变化。这是因为负浮力增大引起下潜速度增大,由于纵倾角接近–90°,轴向速度同比例增大,进而导致舵力矩增大,水动力矩增大。虽然增大负浮力是通过增大重力实现,导致了水静力矩的增大,但是其增大程度小于其他2种力矩,最终AUV通过减小纵倾角来增大水静力矩力臂,使得水静力矩能够与水动力矩和舵力矩平衡。由于负浮力增大使得AUV在惯性系中有向η轴靠近的趋势,因此攻角变化与负浮力呈负相关关系,同时相比于对纵倾角的影响,负浮力增大带给攻角的影响要小的多。保持负浮力不变,增大重浮心纵向距离,稳态纵倾角与攻角都呈增大趋势。负浮力较大时,由于纵倾角随纵向距离变化范围较大,因此调整重浮心纵向距离,对AUV纵倾角调节作用更大。负浮力较小时,由于纵倾角随纵向距离变化范围较小,调整纵向距离对AUV纵倾角的调节作用也有限。
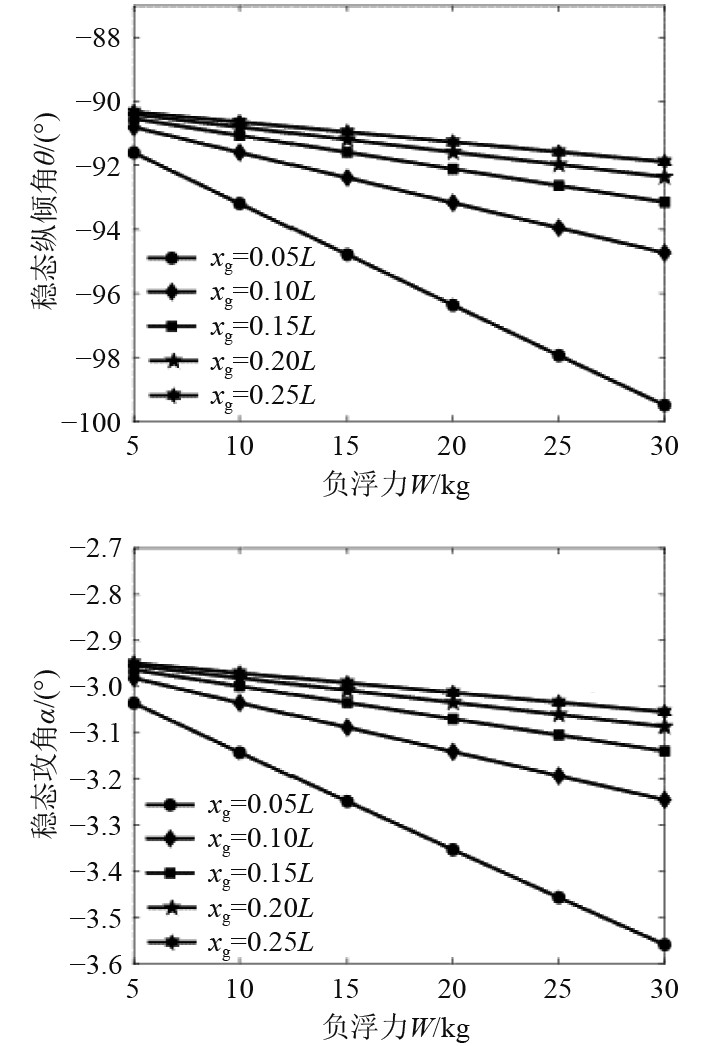
|
图 7 稳态纵倾角和攻角与重浮心纵向距离、负浮力的关系 Fig. 7 Relationship among steady pitch angle and attack angle, longitudinal distance between center of gravity and buoyancy, negative buoyancy |
忽略环境扰动力,在整个下潜过程中,保持参数W=30 kg和xg=0.25L不变,初始纵倾角为−90°,水平舵角取值范围为−20°~20°,间隔5°,重浮心垂向距离取值范围为0.05D~0.25D,间隔0.05D,D为AUV直径。输入上述参数,循环运行仿真模型,得到AUV稳态下潜参数受重浮心垂向距离和水平舵角作用的规律。
由图8可知,垂向距离不变时,稳态纵倾角及攻角与舵角呈负相关关系;水平舵角不变时,稳态纵倾角与垂向距离为正相关关系,攻角随垂向距离增大而小幅增大。设定下潜参数W=30 kg、xg=0.25L、zg=0,控制舵角在–20°~20°范围内,可保证AUV稳态纵倾角在−87°~−93°之间。
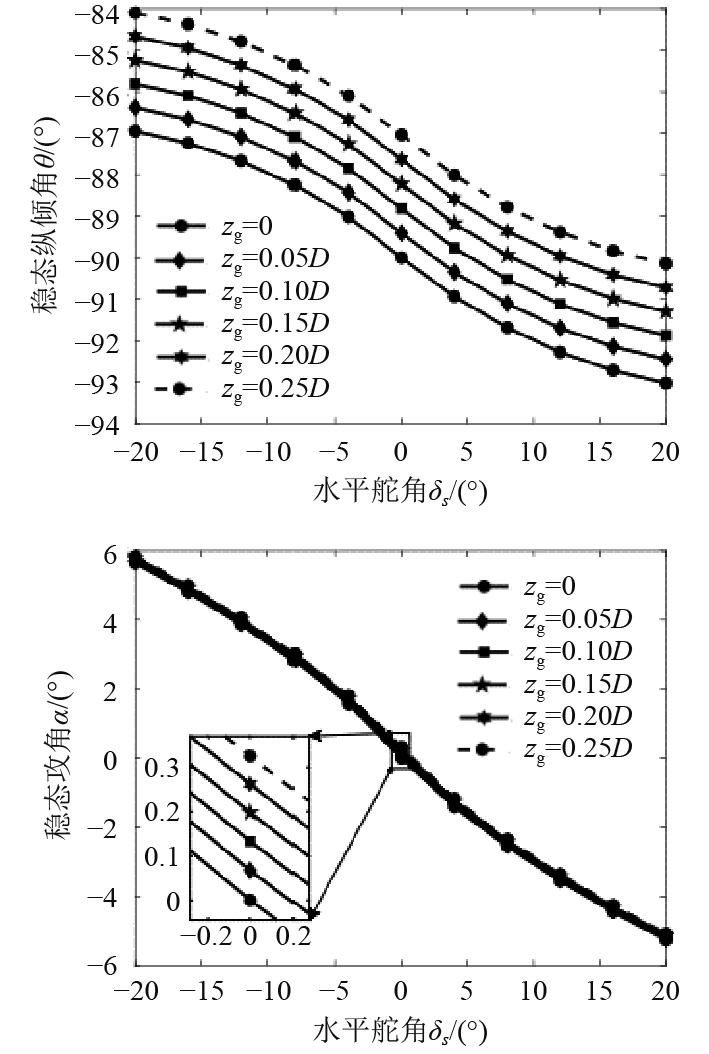
|
图 8 稳态纵倾角和攻角与重浮心垂向距离、水平舵角的关系 Fig. 8 Relationship among steady pitch angle and attack angle, vertical distance between center of gravity and buoyancy, horizontal rudder angle |
由图9可知,垂向距离一定时,舵角增大会引起水平速度增大,而垂向速度会先增大后减小,水平舵角呈二次关系,在舵角为0时达到最大值。水平舵角一定时,垂向距离增大引起水平速度增大,并导致垂向速度小幅减小。
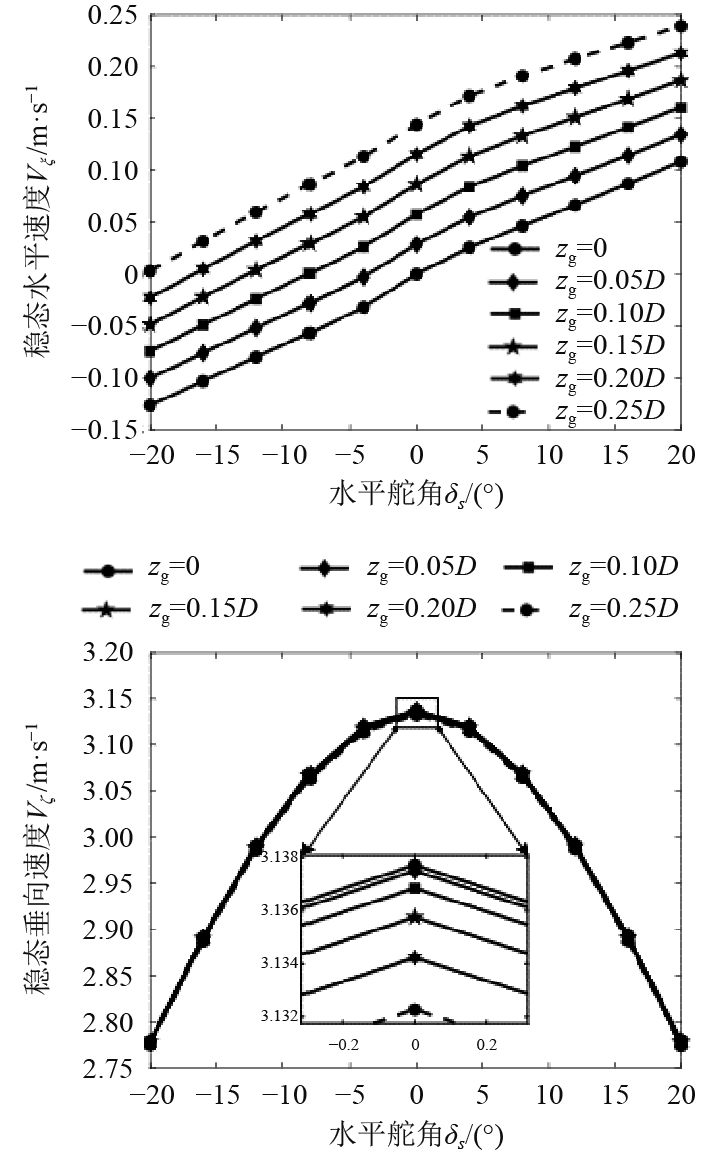
|
图 9 稳态水平速度和垂向速度与重浮心垂向距离、水平舵角的关系 Fig. 9 Relationship among steady horizontal velocity and vertical velocity, vertical distance between center of gravity and buoyancy, horizontal rudder angle |
综合以上,当将AUV的参数配置为W=30 kg、xg=0.25L、zg=0、δs=0,AUV稳定下潜后,纵倾角为−90°,下潜速度为3.1377 m/s。
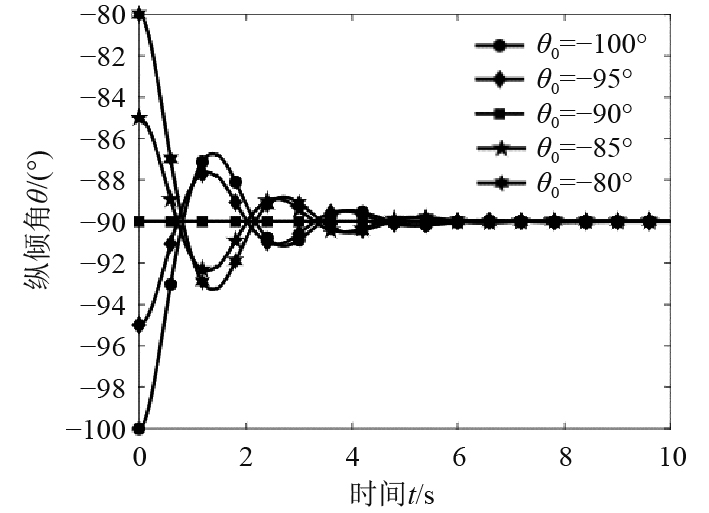
2.1.3 初始纵倾角AUV下潜时的初始纵倾角主要影响AUV到达稳态的时间。设置下潜参数W=30 kg、xg=0.25L、δs=0、zg=0不变,初始纵倾角为−100°~−80°内一系列固定值,忽略洋流和浮力变化影响,对AUV下潜模型进行仿真,得到下潜过程纵倾角随初始纵倾角的变化情况。
由图10可知,初始纵倾角对于AUV稳定后的运动参数没有影响,其作用范围主要在AUV稳定下潜前的这段时间。随着初始纵倾角绝对值的增大,纵倾角振荡周期变长,从而导致AUV到达稳定下潜状态的用时增加。同时可知,在−90°±10°范围内,振荡1.5个周期后,纵倾角变化幅度小于±1°,可认为初始纵倾角对纵倾角没有影响。
|
图 10 初始纵倾角对下潜过程纵倾角的影响 Fig. 10 Effect of initial pitch angle on pitch angle during diving |
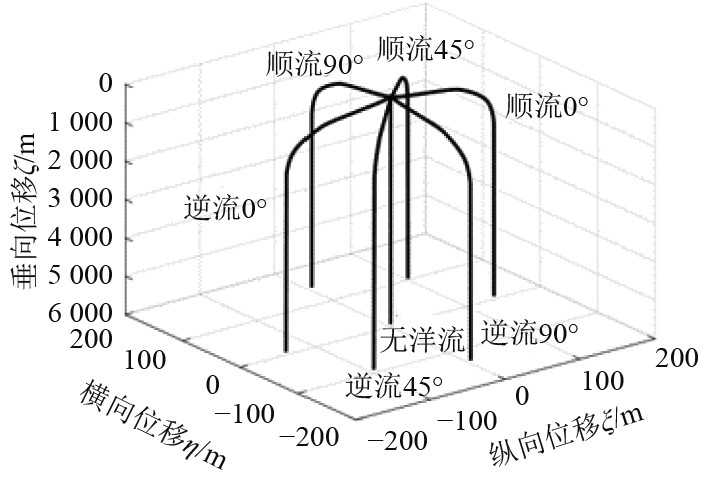
不考虑洋流的垂向扰动,将洋流简化为水平面均匀流,研究洋流变化对AUV垂直下潜运动状态和轨迹的影响。AUV的物理参数选择为,W=30 kg、xg=0.25 L、δs=0、zg=0,以垂直姿态下潜,通过改变洋流方向,得到不同洋流流向下AUV浮心的运动轨迹,如图11所示。
|
图 11 不同洋流下的AUV浮心运动轨迹 Fig. 11 Trajectories of the AUV buoyancy center under the different ocean currents |
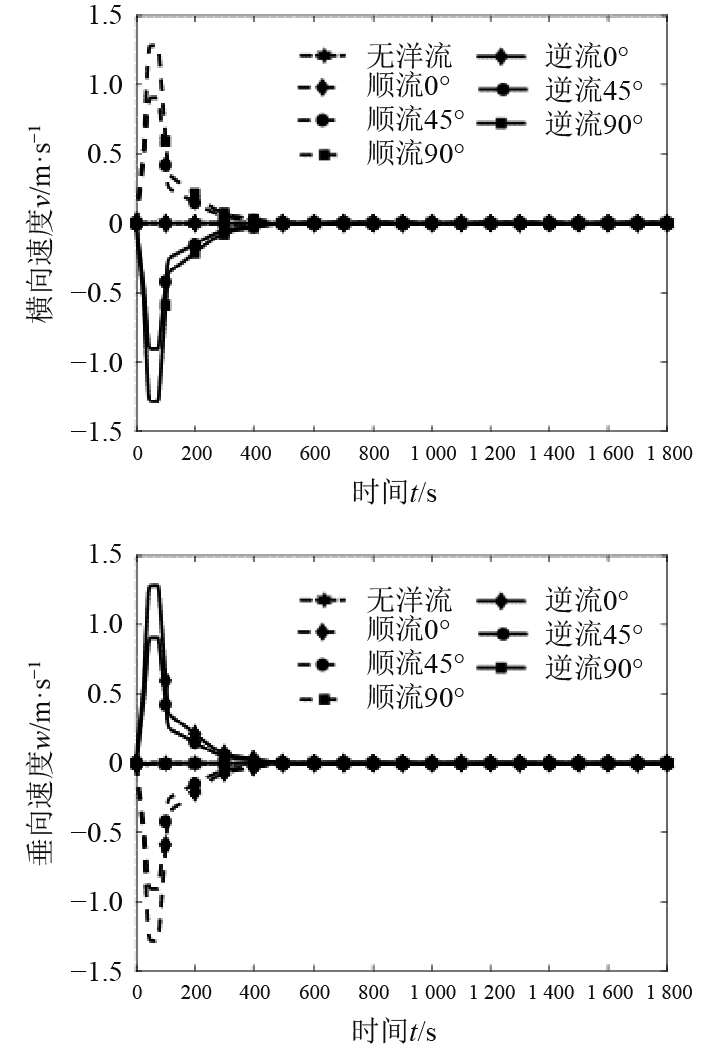
不同方向来流干扰下,AUV在下潜过程的水平偏移距离,如表2所示。可以看出,在初始下潜纵倾角为−90°并且无舵角的情况下,在对应海流的方向上,AUV水平偏移距离相等。由图12可知,在顺流情况下,AUV横向速度与洋流呈正相关关系,垂向速度与洋流呈负相关关系,逆流时相反。
|
|
表 2 洋流扰动下AUV水平面偏移距离 Tab.2 Horizontal drift distance of AUV under the disturbance of ocean current |
|
图 12 洋流变化对垂直下潜运动的影响 Fig. 12 The effects of ocean current changes on the vertical diving motion |
表3所示为各深海装备采用不同下潜方式,其偏移距离及下潜速度的情况。可以看出螺旋下潜偏移距离比较小[15],但是其下潜速度较慢。小纵倾角下潜[6,16]偏移距离过大且速度较慢。相比之下,采用纵倾角90°的垂直下潜方式,下潜速度大,能最大程度地节约下潜时间,进而有效减小了偏移距离。
|
|
表 3 深海装备无动力下潜水平面偏移距离及下潜速度 Tab.3 Horizontal drift distance and diving velocity of deep-sea equipment under unpowered diving |
在AUV下潜过程中,浮力随深度一直变化,从而影响AUV运动状态,因此需要研究浮力变化对下潜运动的影响。忽略洋流的影响,设定W=30 kg、xg=0.25L、δs=0、zg=0、θ0=−90°,自海平面下潜。通过仿真,得到了是否考虑浮力变化对垂向速度的影响。
由图13可知,有无浮力变化明显影响了AUV下潜速度。在不考虑浮力变化时,下潜开始约82 s后,速度达到最大值,考虑浮力变化时,下潜45 s后速度达到最大值。在速度达到最大值后,浮力变化效果能明显地体现出来,并且随着下潜深度增加,浮力不断增大,导致平衡状态朝速度减小方向移动。相比无浮力变化时,下潜至6000 m深时,速度减小至2.2011 m/s,减小了30%,同时下潜时间也增加至2328 s,增加了21%。从结果来看,有无浮力变化对下潜速度和下潜时间均有较大影响。

|
图 13 浮力变化对下潜速度的影响 Fig. 13 The effect of buoyancy change on the diving velocity |
基于四元数法并结合了海洋环境扰动力,通过工程软件Matlab中的Simulink仿真模块建立了深海AUV无动力垂直下潜运动仿真模型,探究了AUV下潜过程中,控制参数和海洋环境扰动力对其下潜过程的各物理参数及运动轨迹的影响,得到以下结论:采用四元数法能够解决在AUV纵倾角达到−90°或者接近−90°时,使用欧拉角解算产生的姿态运动学求解奇异问题,可以平滑预报其下潜运动;AUV采用无动力垂直下潜方式,下潜速度可达3.14 m/s,明显高于其他下潜方式,且水平偏移距离较小;深度变化会导致AUV浮力变化,该情况考虑与否对AUV下潜预报结果有较大影响,其中下潜时间会产生21%偏移,末端速度产生30%偏移。
| [1] |
李硕, 刘健, 徐会希, 等. 我国深海自主水下机器人的研究现状[J]. 中国科学: 信息科学, 2018, 48(9): 1152−1164. LI S, LIU J, XU H X, et al. Research status of autonomous underwater vehicles in China[J].Science China: Information Science, 2018, 48(9): 1152−1164. |
| [2] |
张翔. 无动力水下潜航器自由下潜的运动学及致力机理研究[D]. 武汉: 华中科技大学, 2021.
|
| [3] |
陈俊. 深渊着陆器技术及生物学应用研究[D]. 北京: 中国科学院大学, 2018.
|
| [4] |
张天健, 魏成柱, 张裕芳, 等. 大深度浮力驱动式水下运载器的浮潜运动研究[J]. 船舶工程, 2017, 39(12): 87-94. ZHANGT J, WEI C Z, ZHANG Y F, et al. Study on Floating and diving for deep-water buoyancy-driven vehicle[J]. Ship Engineering, 2017, 39(12): 87-94. |
| [5] |
练永庆, 宋保维, 李宗吉. 潜伏式武器水下施放后纵平面运动仿真[J]. 水下无人系统学报, 2019, 27(4): 413-419. LIAN Y Q, SONG B W, LI Z J. Simulation on motion in vertical plane of a latent weapon released underwater [J]. journal of unmanned undersea systems, 2017, 39(12): 87-94. |
| [6] |
高伟, 李天辰, 谷海涛, 等. 深海AUV无动力下潜运动特性研究[J]. 机器人, 2021, 43(6): 674-683. GAO W, LI T C, GU H T, et al. Unpowered diving motion characteristics of deep-sea autonomous underwater vehicle[J]. Robot, 2021, 43(6): 674-683. |
| [7] |
徐正武, 唐国元, 邓智勇, 等. 四元数在水下航行体运动建模中的应用[J]. 中国舰船研究, 2014, 9(2): 12-16. XU Z W, TANG G Y, DENG Z Y, et al. Applying the Four-parameter approach to establish the motion model of an AUV[J]. Chinese Journal of Ship Research, 2014, 9(2): 12-16. |
| [8] |
赵志超, 李天辰, 谷海涛, 等. 深海运载器无动力纵倾上浮运动特性研究[J]. 水下无人系统学报, 2022, 30(5): 586-596. ZHAO Z C, LI T C, GU H T, et al. Research on unpowered trim ascent motion characteristics of deep-sea vehicles[J]. Journal of Unmanned Undersea Systems, 2022, 30(5): 586-596. |
| [9] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 2021: 75−78.
|
| [10] |
马艳红, 胡军. 姿态四元数相关问题[J]. 空间控制技术与应用, 2008(3): 55-60. MA Y H, HU J. On attitude quaternion[J]. Aerospace Control and Application, 2008(3): 55-60. |
| [11] |
姚红, 程文华, 张雅声. 飞行器动力学与控制Simulink仿真[M]. 北京: 国防工业出版社, 2018: 3−20.
|
| [12] |
刘金夫. 洋流影响下的水下滑翔机垂直面内滑翔运动数值仿真[D]. 武汉: 华中科技大学, 2016.
|
| [13] |
武建国, 徐会希, 刘健, 等. 深海AUV下潜过程浮力变化研究[J]. 机器人, 2014, 36(4): 455 (in Chinese)460. WU J G, XU H X, LIU J, et al. Research on the buoyancy change of deep-sea autonomous underwater vehicle in diving process[J]. Robot, 2014, 36(4): 455 (in Chinese)460. |
| [14] |
Office of Ocean Exploration and Research. CAPSTONE CNMI & Mariana Trench MNM (ROV & Mapping)-EX1605L3[EB/OL]. (2014-02-25)[2023-04-01].https://www.ncei.noaa.gov/waf/okeanos-rov-cruises/ex1605l3/.
|
| [15] |
赵桥生, 何春荣, 李德军, 等. 载人潜水器空间运动仿真计算研究[C]//第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议论文集(下册). 合肥: 《水动力学研究与进展》杂志社, 2019: 372−378. ZHAO Q S, HE C R, LI D J, et al. Research on space motion simulation of manned submersible[C]// Proceedings of the 30th National Symposium on Hydrodynamics and the 15th National Symposium on Hydrodynamics (Vol. 2). Hefei: Journal of Hydrodynamics, 2019, 372−378. |
| [16] |
严升, 张润锋, 杨绍琼, 等. 水下滑翔机纵垂面变浮力过程建模与控制优化[J]. 中国机械工程, 2021, 33(1): 109-117. YAN S, ZHANG R F, YANG S Q, et al. Modelling and control optimization for underwater gliders of variable buoyancy process in the vertical plane[J]. China Mechanical Engineering, 2021, 33(1): 109-117. |
 2024, Vol. 46
2024, Vol. 46
