2. 自然资源部 第一海洋研究所,山东 青岛 266061
2. First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266061, China
随着人口的增长,陆地资源急剧消耗,探索海洋资源已成为解决这一问题的重要途径。然而,目前人类对于海洋的探索和了解仅限于5%左右[1]。无人船艇技术的发展有助于提升人类海洋的探索能力。无人船艇是一种依靠推进器提供动力远程操控的海上观测和勘探平台,具有可控、可扩展、自动、无人工作等优点,在水上和水下的勘察、水质监测和一些军事活动中具有广阔的应用前景[2]。
目前,对无人船的理论研究、技术创新和试验工作等研究已经投入了大量的人力和物力。在军用领域,美国、以色列和欧洲等国家处于领先地位,开发出具有攻击和侦察功能的无人船。例如,美国研制的“Spartan Scout”、“Seadoo Challenger2000”和“MUSCL”等无人船可执行反潜作战、监视侦察和情报收集等任务[3];以色列海军的“Protector”、“Stingary”、“Silver Marlin”等无人船能执行各类军事任务,如收集情报、侦察、特种作战等[4];英国研制的“Pacific 950”无人船主要任务是情报收集、边境控制和维护海上安全。国内对无人船的技术研究起步较晚,但随着研发力度的加大,也取得许多成果。例如,中国船舶第七一六研究所和第七〇二研究所共同研制的“JARI-USV”多用途无人作战,其配备舰载相控阵雷达和先进电子系统等设备,可用于执行反潜、防空和水面作战等任务;珠海云洲智能科技有限公司联合西安现代控制技术研究所和华中光电技术研究所研制的“瞭望者Ⅱ”无人船可承担敌情侦察和精确打击任务[5]。在军用领域中主要注重其功能技术问题,其次再考虑成本问题,所以军用设备一般都普适性差。
在民用领域,无人船技术也得到了广泛的研究和应用。例如,英国Plymouth大学研发的“Springer”无人船被用于执行内河、水库和沿海等浅水域污染物追踪和环境测量等任务[6];意大利热那亚CNR-ISSIA研究机构研制的“Charlie”无人船主要用于海洋取样、收集海洋大气数据和探测浅水区域鱼雷等[7];葡萄牙DSOR(动力系统和海洋机器人实验室)研发的“Delfim”无人船主要用于海洋数据的实时采集和传输[8]。国内在民用方面也已从最初的概念设计逐步过渡到实际运用阶段,并且取得一系列成果。上海大学研制的“精海”系列无人船可用于地貌探测、采集数据、海洋环境监测和海上应急救援处置等任务[9];珠海云洲智能科技有限公司打造和生产的“M80”海底探测无人船主要用于在特殊水域进行水文、气象和水下地形等信息的收集任务[10]。在民用领域中成本起到决定性作用。而现有的无人船减振效果差或无减振功能,大多是通过提高测量设备的性能来改善这一问题,这也增加了无人船的成本。
本文提出一种波浪自适应无人船,该船采用独特的隔振系统,能够显著提高了航行能力,并为数据采集提供了稳定的平台。其主要通过机械结构来降低无人船的振动,可以很大程度地减少设备成本。
1 波浪自适应无人船隔振系统设计 1.1 波浪自适应无人船总体结构波浪自适应无人船是一种全新的船舶类型,其设计能够顺应水面波动,从而保持平台的稳定和水平。它主要由左右橡胶浮筒、滑板、隔振系统、前后杆、推进系统和工作平台组成。其设计区别于传统的单体船和双体船,在船舶结构中增添了隔振系统,可以对海浪产生的不规则激励起到缓冲和吸收的作用,从而使得无人船搭载的工作平台处于平稳状态。
根据无人船的工作环境和应用场合,本文设计的波浪自适应无人船的具体参数如表1所示。
|
|
表 1 无人船的结构尺寸 Tab.1 The structural dimensions of the unmanned ship |
本文设计的隔振系统位于浮筒与工作平台之间,与前杆和滑板连接。通过气弹簧和弹簧组成的减振结构来平衡波浪产生的升沉运动,并通过鱼眼轴承来平衡波浪产生的横荡运动,进而确保无人船在波浪中行驶过程中工作平台能处于稳定状态。
隔振系统中的气弹簧和弹簧能够缓冲和吸收无人船在风浪中工作时产生的振动,使得振动幅值减小、频率增大,从而提高工作平台的稳定性、航行能力和数据采集质量。所以气弹簧的阻尼系数和弹簧的弹性系数是影响隔振系统性能的2个关键参数。为了选取合适的参数,本文将隔振系统简化为弹性系数
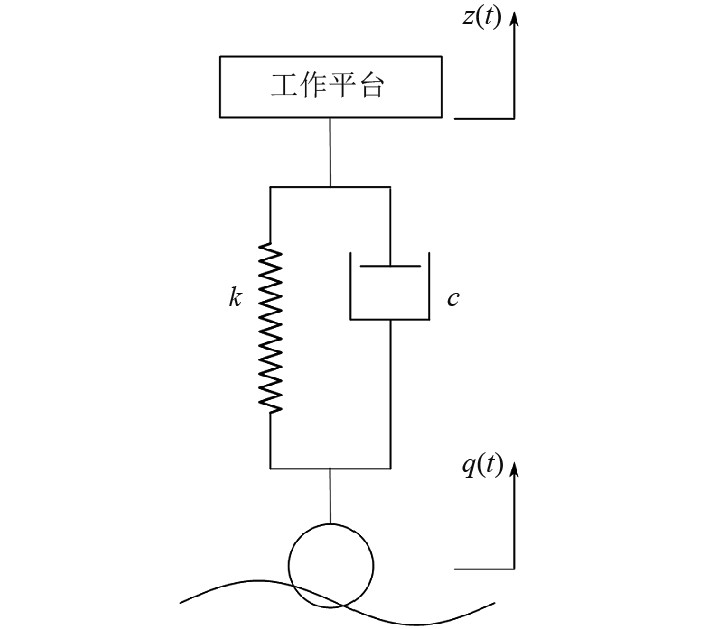
|
图 1 隔振系统模型图 Fig. 1 Vibration isolation system model diagram |
根据机械振动理论对系统进行受力分析,可以得到工作平台的运动学方程为:
| $ m\frac{{{{\mathrm{d}}^2}z\left( t \right)}}{{{\mathrm{d}}{t^2}}} + c\frac{{{\mathrm{d}}z\left( t \right)}}{{{\mathrm{d}}t}} + kz\left( t \right) = c\frac{{{\mathrm{d}}q\left( t \right)}}{{{\mathrm{d}}t}} + kq\left( t \right)。$ | (1) |
式中:m为无人船质量;c为气弹簧阻尼系数;k为弹簧弹性系数。
对式(1)进行拉普拉斯变换,可得到该模型的传递函数:
| $ H\left( s \right) = \frac{{Z\left( s \right)}}{{Q\left( s \right)}} = \frac{{2\xi {\omega _{{n}}}s + \omega _{{n}}^2}}{{{s^2} + 2\xi {\omega _{{n}}}s + \omega _{{n}}^{\text{2}}}}。$ | (2) |
式中:
根据式(2)传递函数建立Simulink求解模型,如图2所示。其中,采用阶跃信号为输入信号,模拟海浪的垂向运动,输出则为工作平台的垂向位移。
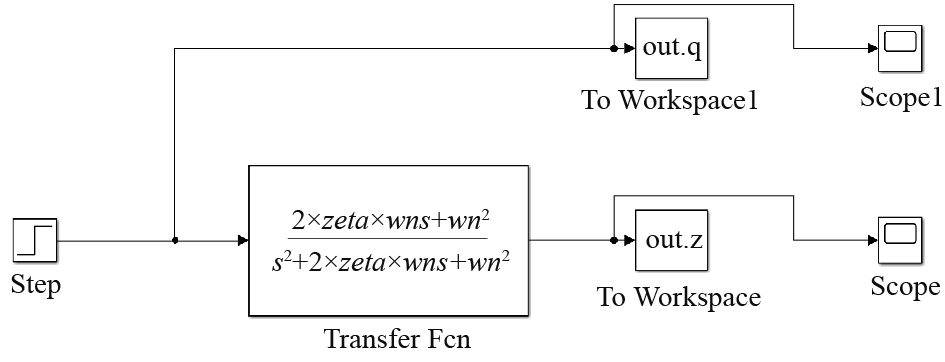
|
图 2 求解模型 Fig. 2 Solution model |
无人船工作时,受海浪的影响,浮筒会在垂向产生不规则振动,这些振动被气弹簧和弹簧组成的隔振系统缓冲和吸收。其中弹簧往复运动可以缓冲浮筒的垂向振动,而气弹簧能够有效地缓冲和吸收海浪波动和弹簧运动引起的振动。无人船工作平台的垂直稳定性受气弹簧的阻尼系数大小的影响。阻尼系数过小,工作平台的垂向波动就会变大;阻尼系数过大,会妨碍弹簧的运动。因此,在隔振系统的设计中,需要合理选择气弹簧的阻尼系数和弹簧的弹性系数。
通过Simulink建立的求解模型分析不同的相对阻尼系数对工作平台垂向位移的影响,并绘制了工作平台垂向位移曲线和Bode图,如图3和图4所示。可知,阻尼系数越小,工作平台垂向位移越大,缓冲时间也越长,截止频率响应也越陡峭。这说明系统频率与阻尼系数有关。综合考虑各方面因素,相对阻尼系数
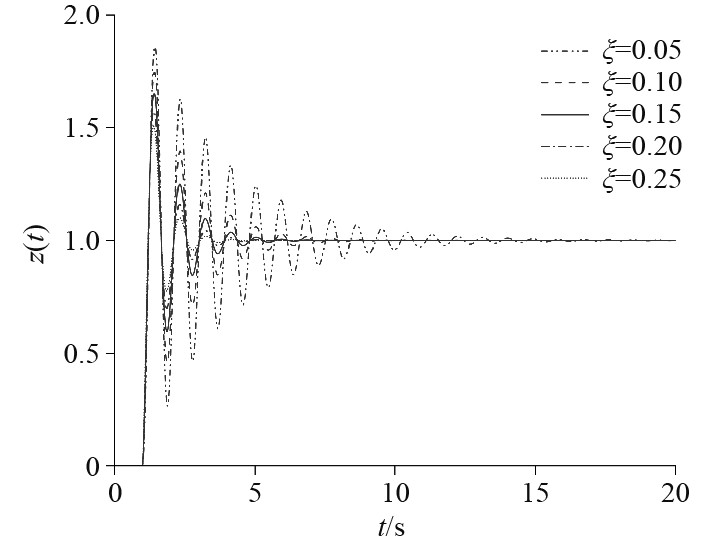
|
图 3 不同相对阻尼系数下隔振系统的阶跃响应曲线 Fig. 3 Step response curve of vibration isolation system with different relative damping coefficients |
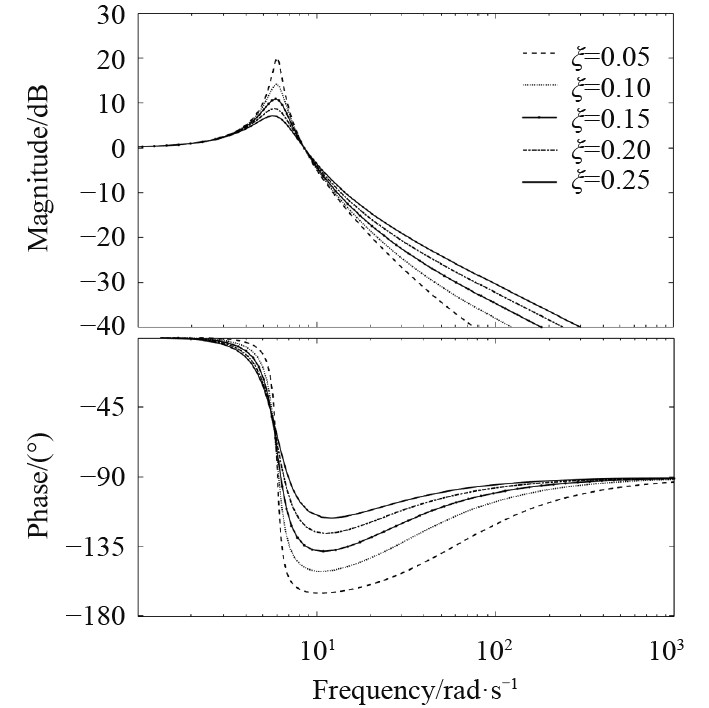
|
图 4 不同相对阻尼系数下隔振系统的 Bode 图 Fig. 4 Bode diagram of vibration isolation system with different relative damping coefficients |
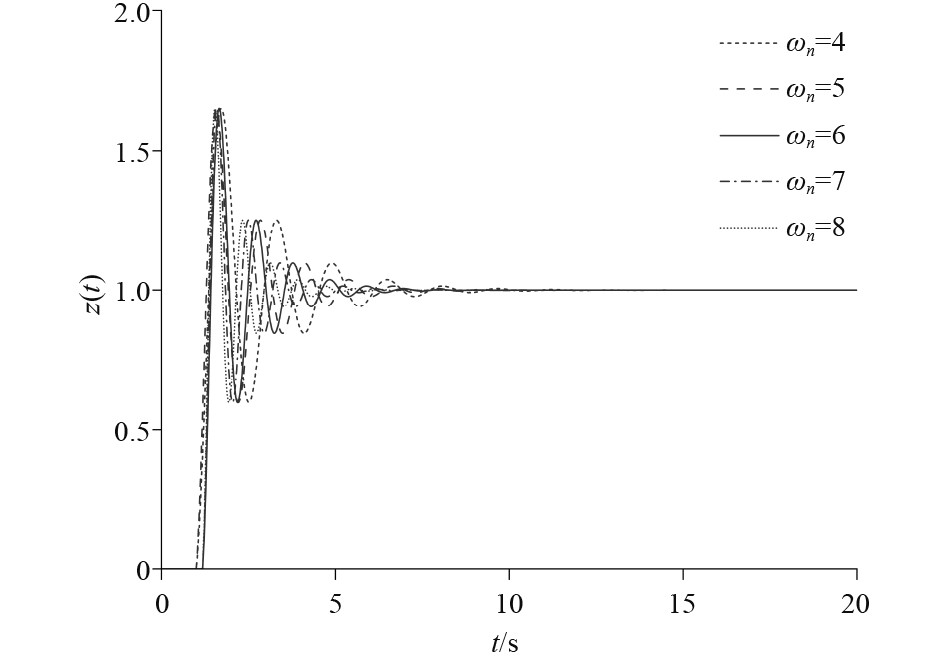
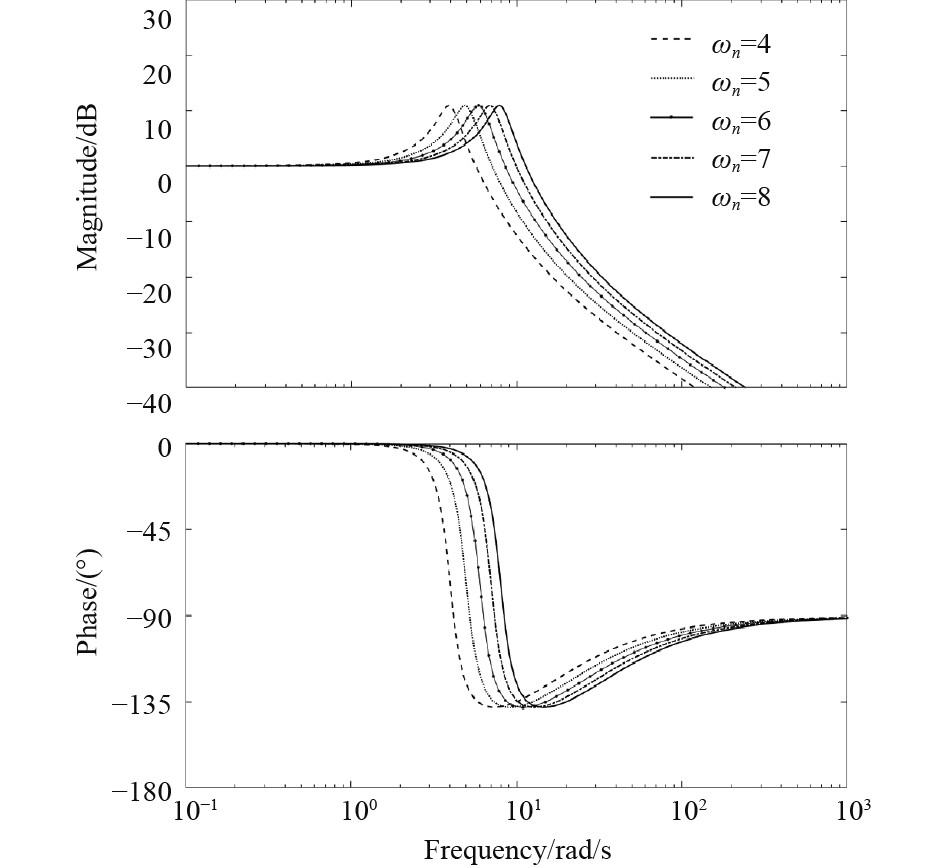
如图5和图6所示,通过分析隔振系统在不同固有频率下的阶跃响应曲线和Bode图。可知固有频率越小,隔振系统响应越缓慢;反之固有频率越大,隔振系统可以快速吸收振动,但也会导致无人船航行不稳定。因此综合考虑取固有频率
|
图 5 不同固有频率下隔振系统的阶跃响应曲线 Fig. 5 Step response curves of vibration isolation system atdifferent natural frequencies |
|
图 6 不同固有频率下隔振系统的Bode图 Fig. 6 Bode diagram of vibration isolation system at different natural frequencies |
为了简化问题,通常假设海浪是二因次的,即波浪只在一个固定的方向上运动,而且波峰线平行且无限长[11]。二因次不规则波浪可以看作是由无数个不同波幅和波长的单元规则波线性叠加而成[12],则其波高可表示为:
| $ \zeta \left( t \right) = \sum\limits_{i = 1}^\infty {{\xi _{{a_i}}}\cos \left( {{k_i}\zeta - {\omega _i}t + {\varepsilon _i}} \right)}。$ | (3) |
式中:
| $ \zeta \left( t \right) = \sum\limits_{i = 1}^\infty {{\zeta _{{a_i}}}\cos \left( {{\omega _i}t + {\varepsilon _i}} \right)}。$ | (4) |
本文选取皮尔逊-莫斯柯维奇谱,简称P-M谱,适用于开阔海面充分发展的海浪[13],其表达式为:
| $ {S_\zeta }\left( \omega \right) = \frac{{8.1 \times {{10}^{ - 3}}{g^2}}}{{{\omega ^5}}}\exp \left( { - \frac{{0.74{g^4}}}{{U{\omega ^4}}}} \right)。$ | (5) |
式中:
由海浪理论可知,单元规则波的单位面积具有的波能为:
| $ E = \frac{1}{2}\rho g\zeta _a^2。$ | (6) |
不规则波是由无数个单元规则波线性叠加而成,故任意频率间隔
| $ {E_{\Delta \omega }} = \frac{1}{2}\rho g\sum\limits_\omega ^{\omega + \Delta \omega } {\zeta _{{a_i}}^2}。$ | (7) |
因此可以看出波能与频率间隔
| $ {S_\zeta }\left( \omega \right)\Delta \omega = \frac{1}{2}\sum\limits_\omega ^{\omega + \Delta \omega } {\zeta _{{a_i}}^2}。$ | (8) |
当
| $ {\zeta _{{a_n}}} = \sqrt {2{S_\zeta }\left( {{\omega _i}} \right)\Delta \omega }。$ | (9) |
将式(9)波幅
| $ \zeta \left( t \right) = \sum\limits_{i = 1}^\infty {\sqrt {2{S_\zeta }\left( {{\omega _i}} \right)\Delta \omega } \cos \left( {{\omega _i}t + {\varepsilon _i}} \right)} 。$ | (10) |
由海浪理论可知,海浪频谱的频率分布为0 ~ ∞,但其能量主要集中在某段频率范围内。因此,在仿真海浪时,只需选取能量集中的频率区间,就可得到精度较高的仿真结果[14]。本文采用频率等分法对海浪模拟仿真,即根据海浪的波能谱密度函数,将能量集中的频段划分为若干等份,根据划分后的频谱计算海浪的各阶谐波振幅,然后建立海浪的模拟模型。不同海况下仿真频段和频率增量[15]如表2所示。
|
|
表 2 不同海况下仿真频段和频率增量 Tab.2 Simulation frequency band and frequency increment under different sea states |
本文以3级海况下的波浪自适应无人船为研究对象,对其隔振性能进行仿真研究。根据资料,3级海况下的风速小于8.5 m/s,故仿真频段选择0.3 ~ 3.0 rad/s,仿真增量为0.1 rad/s,有义波高取1.4 m。根据P-M谱,可以确定每个谐波频率
| $ \zeta \left( t \right) = \sum\limits_{i = 1}^{28} {\sqrt {2{S_\zeta }\left( {{\omega _i}} \right)\Delta \omega } \cos \left( {{\omega _i}t + {\varepsilon _i}} \right)} 。$ | (11) |
根据式(11),通过Matlab软件进行计算仿真,得到波高的仿真图,如图7所示。

|
图 7 3级海况下波高仿真随机曲线 Fig. 7 Stochastic curve of wave height simulation under level 3 sea state |
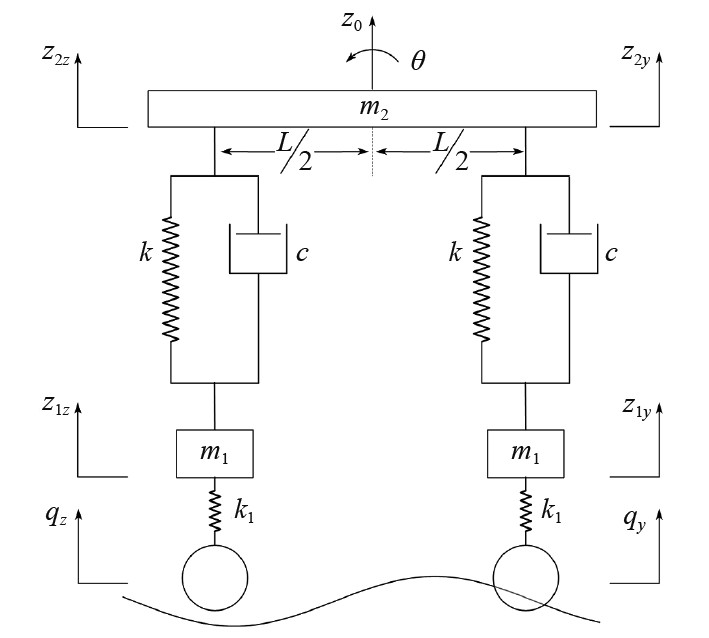
为了验证隔振系统的减振性能,本文根据无人船的三维模型建立了一种四自由度的无人船模型[16]。该模型以左右浮筒的垂向位移、工作平台的垂向位移和工作平台的横摇角度为自由度,如图8所示。
|
图 8 四自由度的无人船模型 Fig. 8 Four degrees of freedom unmanned ship model |
由于浮筒与海水间的水动力学过于复杂,所以此模型忽略浮筒与海水之间的水动力学的影响,只考虑海浪对浮筒的垂向位移影响。对质量块m1和m2进行受力分析,可得到运动学方程:
| $ \left\{ \begin{aligned} & {{m_1}{{z''}_{1z}} = k\left( {{z_{2z}} - {z_{1z}}} \right) + c\left( {{{z'}_{2z}} - {{z'}_{1z}}} \right) - {k_1}\left( {{z_{1z}} - {q_z}} \right)},\\ & {{m_1}{{z''}_{1y}} = k( {{z_{2y}} - {z_{1y}}} ) + c( {{{z'}_{2y}} - {{z'}_{1y}}} ) - {k_1}( {{z_{1y}} - {q_y}} )} ,\\ & {m_2}{{z''}_0} = - k( {{z_{2z}} - {z_{1z}}} ) - c( {{{z'}_{2z}} - {{z'}_{1z}}}) - k( {{z_{2y}} - {z_{1y}}} ) - \\ &\qquad\qquad c( {{{z'}_{2y}} - {{z'}_{1y}}} ),\\ & J\theta '' = \frac{L}{2}\left[ {k\left( {{z_{2z}} - {z_{1z}}} \right) + c\left( {{{z'}_{2z}} - {{z'}_{1z}}} \right)} \right] \\ &\qquad \quad - \frac{L}{2}[ k( {{z_{2y}} - {z_{1y}}} ) + c( {{{z'}_{2y}} - {{z'}_{1y}}} ) ] 。\end{aligned} \right. $ | (12) |
式中:m1、m2分别为浮筒和工作平台的质量;k、k1分别为隔振系统和浮筒的弹性系数;z0为工作平台的垂向位移;z1z、z1y为左右浮筒的垂向位移;z2z、z2y为隔振系统左右两侧的位移;q(t)为波浪位移;J为工作平台绕其质心的转动惯量。
由于模型考虑海浪运动对无人船产生横摇
| $ \left\{ {\begin{split} & {{z_{2z}} = {z_0} - \frac{L}{2}\tan \theta \approx {z_0} - \frac{L}{2}\theta },\\ & {{z_{2y}} = {z_0} + \frac{L}{2}\tan \theta \approx {z_0} + \frac{L}{2}\theta },\\ & {{{z'}_{2z}} = {{z'}_0} - \frac{L}{2}\theta '},\\ & {{{z'}_{2y}} = {{z'}_0} + \frac{L}{2}\theta '} 。\end{split}} \right. $ | (13) |
将式(13)代入式(11)可得
| $ \left\{ \begin{aligned} & {m_1}{{z''}_{1z}} = k\left( {{z_0} - \frac{L}{2}\theta - {z_{1z}}} \right) + c\left( {{{z'}_0} - \frac{L}{2}\theta ' - {{z'}_{1z}}} \right) -\\& \qquad\qquad {k_1}\left( {{z_{1z}} - {q_z}} \right),\\ & {m_1}{{z''}_{1y}} = k\left( {{z_0} + \frac{L}{2}\theta - {z_{1y}}} \right) + c\left( {{{z'}_0} + \frac{L}{2}\theta ' - {{z'}_{1y}}} \right) - \\& \qquad\qquad {k_1}\left( {{z_{1y}} - {q_y}} \right) ,\\ & {{m_2}{{z''}_0} = - k\left( {2{z_0} - {z_{1y}} - {z_{1z}}} \right) - c\left( {2{{z'}_0} - {{z'}_{1y}} - {{z'}_{1z}}} \right)},\\ & {J\theta '' = \frac{L}{2}k\left( {{z_{1y}} - L\theta - {z_{1z}}} \right) + \frac{L}{2}c\left( {{{z'}_{1y}} - L\theta ' - {{z'}_{1z}}} \right)} 。\end{aligned} \right. $ | (14) |
式中:m1=68 kg,m2=80 kg,k=2880 N/m,k1=12 N/m,c=144 N·s/m,J=29.47 kg·m2。
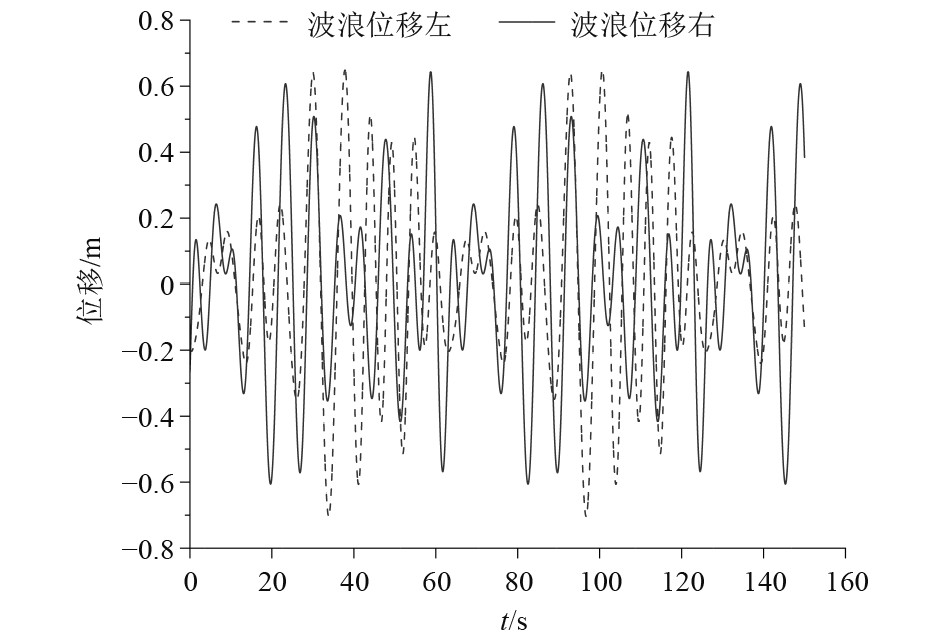
根据式(14)运动学方程,搭建Simulink求解模型,其中输入则为通过随机波浪求解的波高曲线,如图9所示。
|
图 9 作用在浮筒上的波浪位移曲线 Fig. 9 Wave displacement curve acting on a buoy |
海浪的不规则运动对船艇的航行和生产活动造成较大的影响。浮筒在海浪作用下运动,其位移与工作平台位移成正比关系。为了抑制工作平台的位移,需要减小浮筒位移。由图10浮筒和波浪位移对比可知,充气式橡胶浮筒的减振效果显著,能够吸收海浪产生的高频振动,提高船艇航行的平稳性。
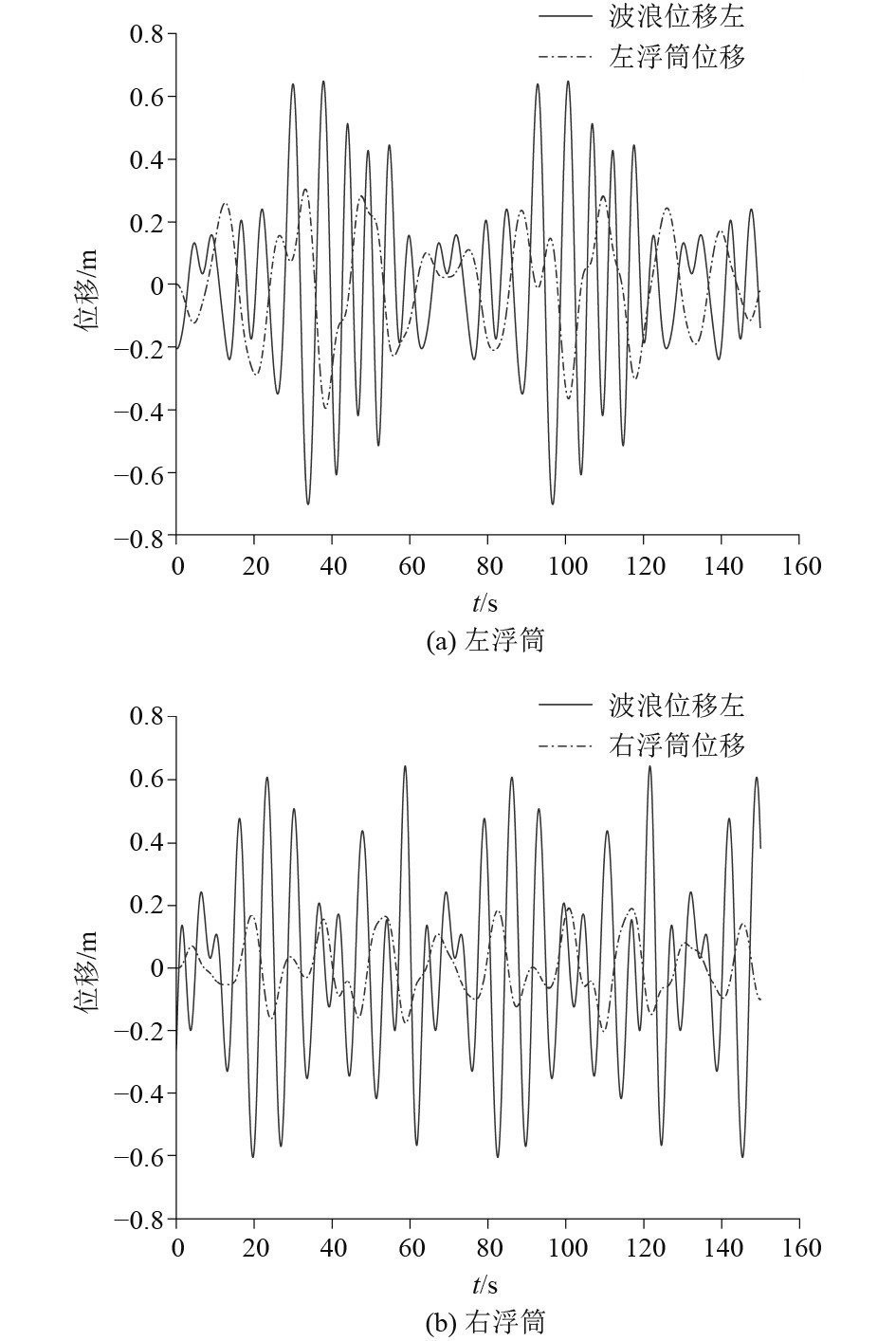
|
图 10 浮筒位移与波浪位移图 Fig. 10 Chart of buoy displacement and wave displacement |
工作平台主要作用是搭载设备仪器,因此需要具备较高的稳定性。由图11可知,工作平台位移与浮筒位移相比,隔振系统能够有效地吸收低频振动。经过浮筒和隔振系统的减振作用,工作平台的位移能够控制在较小的范围内。
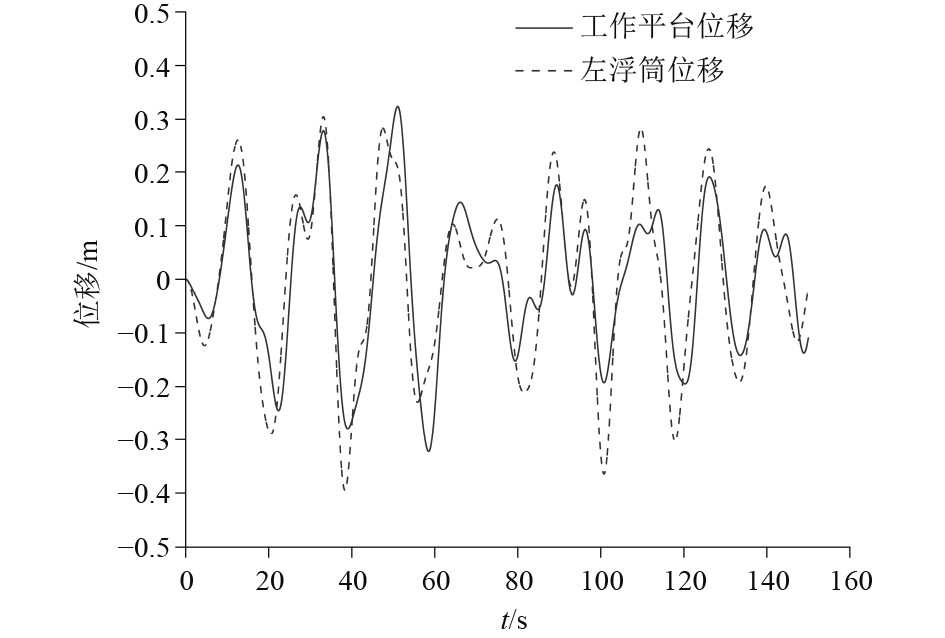
|
图 11 工作平台位移与浮筒位移图 Fig. 11 Working platform displacement and buoydisplacement diagram |
无人船在海上作业时,过大的横摇角度可能导致设备移位,影响设备的功能。本文设计的波浪自适应无人船的横摇运动幅度控制在11°以内,如图12所示,能够保证工作平台的稳定性。
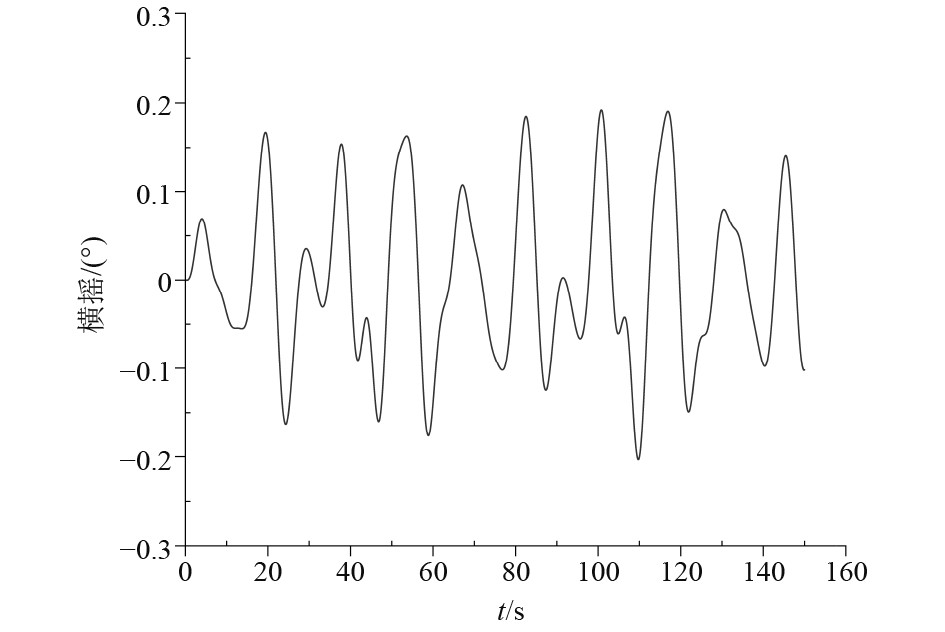
|
图 12 工作平台横摇运动示意图 Fig. 12 Schematic diagram of rolling motion of working platform |
本文研究分析了波浪自适应无人船的减振性能。无人船隔振系统参考汽车悬挂系统设计,通过计算确定其主要参数:相对阻尼系数
| [1] |
孙松, 孙晓霞. 对我国海洋科学研究战略的认识与思考[J]. 中国科学院院刊, 2016, 31(12): 1285-1292. |
| [2] |
聂玲, 张玲玲. 无人船艇关键技术及未来发展趋势[J]. 船舶物资与市场, 2022, 30(7): 12-14. |
| [3] |
赵亮, 王芳, 白勇. 水面无人艇路径规划的现状与挑战[J]. 船舶工程, 2022, 44(4): 1-7+48. |
| [4] |
朱宝星, 于复生, 梁为, 等. 无人式水面航行器的国内外发展趋势[J]. 船舶工程, 2020, 42(2): 20-23. |
| [5] |
方中华, 褚宏宪, 冯京, 等. 无人船艇在海洋地质调查中的应用及展望[J]. 海洋地质前沿, 2020, 36(3): 72-77. |
| [6] |
BAI X G, LI B H, XU X F, et al. A Review of current research and advances in unmanned surface vehicles[J]. Journal of Marine Science and Application, 2022, 21(2): 47-58. DOI:10.1007/s11804-022-00276-9 |
| [7] |
陈映彬. 无人船发展现状及其关键技术综述[J]. 科学技术创新, 2019(2): 60-61. |
| [8] |
曹娟, 王雪松. 国内外无人船发展现状及未来前景[J]. 中国船检, 2018(5): 94-97. DOI:10.3969/j.issn.1009-2005.2018.05.025 |
| [9] |
常继强, 蒲进菁, 庄振业, 等. 无人船在海洋调查领域的应用分析[J]. 船舶工程, 2019, 41(1): 6-10+78. |
| [10] |
蒲进菁, 刘涵, 江云华, 等. 无人船现状及发展趋势综述[J]. 海洋信息, 2020, 35(1): 6-11. |
| [11] |
李积德. 船舶耐波性[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007.
|
| [12] |
王小东, 周宇英, 刘丽. 随机海浪下的波浪发电装置浮体横摇运动仿真[J]. 系统仿真学报, 2014, 26(10): 2326-2329+2334. |
| [13] |
赵珂, 李茂华, 郑建丽, 等. 基于波浪谱的三维随机波浪数值模拟及仿真[J]. 舰船科学技术, 2014, 36(2): 37-39. |
| [14] |
肖飞. 基于随机海浪理论的海上浮动平台运动分析[J]. 机械制造与自动化, 2014, 43(6): 156-157+165. DOI:10.3969/j.issn.1671-5276.2014.06.046 |
| [15] |
郭惜久, 程翔. 随机海浪模型仿真[J]. 四川兵工学报, 2010, 31(8): 134-136. |
| [16] |
张泽鹏, 李洋, 徐海升. 四自由度汽车振动模型分析[J]. 时代汽车, 2018(301): 118-119. |
 2024, Vol. 46
2024, Vol. 46
