2. 深海载人装备国家重点实验室,江苏 无锡 214082;
3. 深海技术科学太湖实验室,江苏 无锡 214082;
4. 上海交通大学,上海 200240
2. State Key Laboratory of Deep-Sea Manned Vehicles, Wuxi 214082, China;
3. Taihu Laboratory of Deep-sea Technological Science, Wuxi 214082, China;
4. Shanghai Jiaotong University, Shanghai 200240, China
水下航行器作为一种海洋探测装备,其体积小、隐身性好、机动性、成本低、可快速组网,探测能力强,广泛用于海底科学考察、水域勘察与识别、海洋生物群落调查、水下线缆维修、海底打捞等[1]。
水下航行器模型复杂且非线性,国内外学者对水下航行器操纵仿真研究做了大量工作。Jinmo等[2]根据牛顿第二定律,考虑电缆的干扰,利用动力学建模方法建立了半潜式自主水下机器人的六自由度运动方程。PARK等[3]基于Gertler、Hagen和Feldman的研究,建立了潜艇在大攻角下的动力学模型。PARK等[4]使用计算流体动力学(CFD)模拟了水下航行器的六自由度(6-DOF)自由导航控制,并用测试数据进行了验证。聂为彪等[5]建立了航行器在水平面内的动力学模型,对航行器在水平面内的定常回转和回舵、正弦操舵和Z型操舵等操纵运动进行了预报,仿真结果表明,该水下航行器具有良好的应舵性和操纵性,响应时间较快,能准确预报航行器的操纵性能。李德军等[6]对某深潜器水下空间运动开展仿真研究,采用PID控制方法,定深下的回转运动进行仿真研究,并得出结论,定深状态下的回转直径相对较小,反映出垂向诱导水动力对回转直径的干扰影响。
在水下航行器运动控制技术钟,应用最广的控制算法是PID控制,此方法简单稳定,适用于对控制品质要求不高的水下任务。此外,滑模变结构控制经历50余年的发展,成为自动控制系统的一种典型设计方法,适用于线性和非线性系统。
水下航行器操纵运动仿真是复现和预报水下航行器运动的关键技术。本文建立了水下航行器垂直面航行运动模型,分析了高速航行下的运动特性。为保证高速航行高效稳定,通过首舵和尾舵的组合控制,可实现无纵倾的定深航行运动。在航行自动定深控制采用滑模控制,滑模控制技术的优点是对模型的摄动具有鲁棒性,满足定深航行需求。由于水下航行器航行过程中纵倾变化不大,采用PID经典控制方法可满足控制需求,同时保证了系统的稳定性。
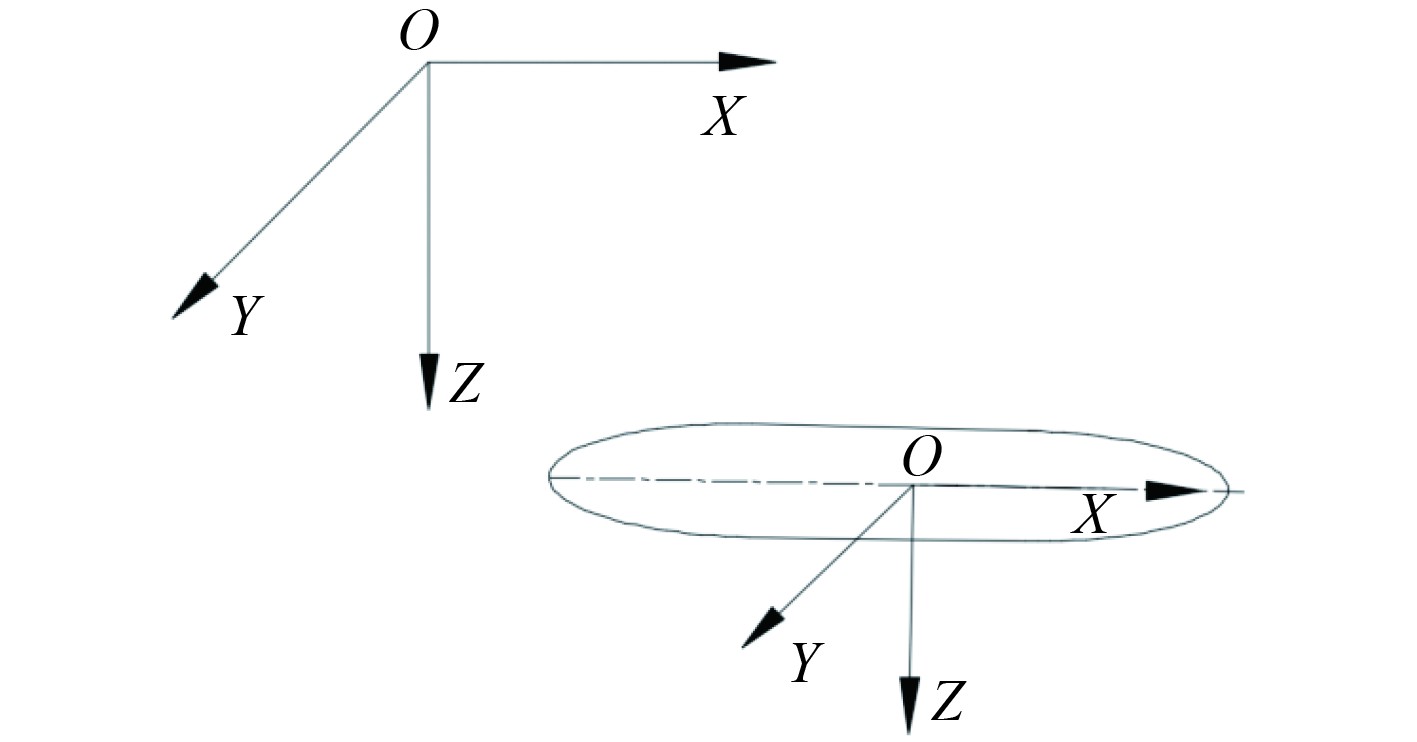
1 水下航行器航行运动模型研究水下无人航行器高速运动时,通常采用通用坐标系,建立2个坐标系:一个是惯性坐标系,其固定于地球,又称地球坐标系;一个是随体坐标系,其固定于水下航行器,2种坐标系均采用右手系[7],如图1所示。
|
图 1 水下航行器运动坐标系示意图 Fig. 1 Schematic diagram of underwater vehicle motion coordinate system |
通过惯性坐标系和随体坐标系的转换,可得水下航行器的垂直面运动学模型,即:
| $ \left[ {\begin{array}{*{20}{c}} {\dot X} \\ {\dot Z} \\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\mathrm{c}}} \theta {{\mathrm{c}}} \psi }&{{\mathrm{s}} \phi {\mathrm{s}} \psi + {{\mathrm{c}}} \phi {\mathrm{s}} \theta {{\mathrm{c}}} \psi }&0 \\ { - {\mathrm{s}} \theta }&{{{\mathrm{c}}} \phi {{\mathrm{c}}} \theta }&0 \\ 0&0&{{{\mathrm{c}}} \phi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u \\ w \\ q \end{array}} \right]。$ | (1) |
其中,s(.)=sin(.),c(.)=cos(.),t(.)=tan(.)。
通过动力学建模,在潜艇六自由度运动方程[8-9]的基础上进行简化,可得适用高速航行下的水下航行器垂直面的纵向、垂向和纵倾运动方程。
纵向方程:
| $ \begin{split} m\left[ {\dot u + wq} \right] =& \frac{1}{2}\rho {L^4}{X_{qq}'}{q^2} + \frac{1}{2}\rho {L^3}\left[ {X_{\dot u}' \dot u + X_{wq}'wq} \right] +\\ &\frac{1}{2}\rho {L^2}\left[ {X_{uu}'{u^2} + X_{ww}'{w^2} + X_{uw}'uw} \right] +\\ &\frac{1}{2}\rho {L^2}{u^2}\left[ {X_{{\delta _b}{\delta _b}}' {\delta}_b^2 + X_{{\delta _s}{\delta _s}}' {\delta}_s^2} \right] + {X_{{T}}} 。\end{split} $ | (2) |
垂向方程:
| $ \begin{split} m\left[ {\dot w - uq} \right] = &\frac{1}{2}\rho {L^4}\left[ {Z_{\dot q}'\dot q + Z_{q\left| q \right|}'q\left| q \right|} \right] + \frac{1}{2}\rho {L^3}\left[ Z_{\dot w}'\dot w + \right.\\ & \left. Z_q'uq + Z_{w\left| q \right|}'w\left| q \right| \right] + \frac{1}{2}\rho {L^2}\left[ Z_0'{u^2} + \right.\\ & \left. Z_w'uw + Z_{\left| w \right|}'u\left| w \right| + Z_{ww}'{w^2} + Z_{w\left| w \right|}'w\left| w \right| \right] +\\ & \frac{1}{2}\rho {L^2}{u^2}\left[ {Z_{{\delta _b}}'{\delta _b} + Z_{{\delta _s}}'{\delta _s}} \right] + {Z_{{T}}} 。\end{split} $ | (3) |
纵倾方程:
| $ \begin{split} {I_y}\dot q =& \frac{1}{2}\rho {L^5}\left[ {M_{\dot q}'\dot q + M_{q\left| q \right|}'q\left| q \right|} \right] + \frac{1}{2}\rho {L^3}\left[ M_w'uw + M_{\left| w \right|}'u\left| w \right| +\right.\\ &\left. M_{ww}'{w^2}{\text{ + }}M_{w\left| w \right|}'w\left| w \right| \right] + \frac{1}{2}\rho {L^3}M_0'{u^2} + \frac{1}{2}\rho {L^4}\times\\ & \left[ {M_{\dot w}'\dot w + M_q'uq + M_{\left| w \right|q}'\left| w \right|q} \right]- \left( {{z_G}W - {z_C}B} \right)\sin \theta + \\ &\frac{1}{2}\rho {L^3}{u^2}\left[ {M_{{\delta _b}}'{\delta _b} + M_{{\delta _s}}'{\delta _s}} \right] + {M_{{T}}}。\\[-15pt] \end{split} $ | (4) |
式中:u、w均为线速度;

|
图 2 CFD计算图 Fig. 2 CFD calculation diagram |
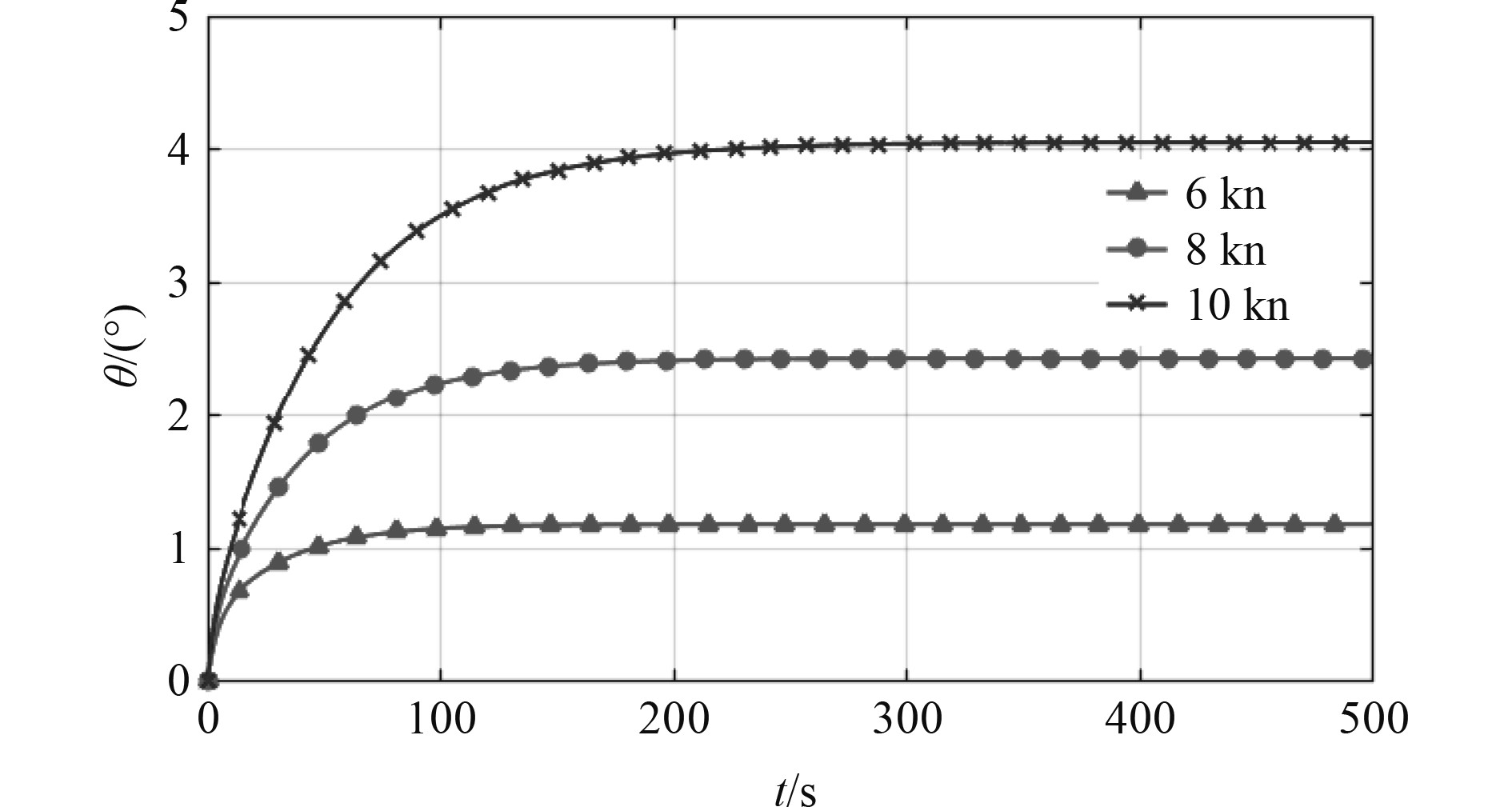
水下航行器高速航行时,对姿态的要求极高,有必要分析高速航行下的水下航行器运动特性。在不同航速下的纵倾变化如图3所示。
|
图 3 不同航速下的纵倾变化 Fig. 3 Pitch change at different speeds |
从仿真结果可看出,在高速航行下,水下航行器会产生一定纵倾,且随着航速的增加,纵倾影响会越大。在6 kn的航速下的纵倾值约1°,反映水下航行器设计的性能良好;在10 kn航速下的纵倾值约4°,由于高速状态放大了水下航行器外形上下轻微不对称的特性,从而产生的垂向水动力及力矩增大。
3 水下航行器运动控制研究仿真技术是一门多学科的综合技术,通过仿真手段可加快控制技术研究和控制系统验证。
滑模控制作为一种控制系统的设计方法,具有极大的灵活性和多样性,适用于非线性系统。在航行过程中,纵倾值不大,取
| $ \left\{ {\begin{array}{*{20}{c}} {{\delta _b}' = \dfrac{{[{{\ddot Z}_d} + \varepsilon {\mathrm{sat}}(s) + ks + C({{\dot Z}_d} - \dot Z)] - F - {F_{\text{3}}}\left( {x,y,z} \right)}}{{\dfrac{1}{2}\rho {L^2}{u^2}Z_{{\delta _b}}'},}}\times\\ {{\delta _b} = {\delta _b}'\left(m - \dfrac{1}{2}\rho {L^3}Z_{\dot w}'\right)} 。\qquad\qquad\qquad\qquad\qquad\qquad\quad \end{array}} \right. $ | (5) |
其中
| $ \begin{split} F =& \frac{1}{2}\rho {L^4}\left[ {Z_{\dot q}'\dot q + Z_{q\left| q \right|}'q\left| q \right|} \right] + \frac{1}{2}\rho {L^3}\left[ Z_q'uq + \right.\\ & \left. Z_{q\left| q \right|}'Z_{w\left| q \right|}'w\left| q \right| \right] + \frac{1}{2}\rho {L^2}\left[ Z_0'{u^2} + \right.\\ & \left.Z_w'uw + Z_{\left| w \right|}'u\left| w \right|{\text{ + }}Z_{ww}'ww + Z_{w\left| w \right|}'w\left| w \right| \right] +\\ & muq + \frac{1}{2}\rho {L^2}{u^2}Z_{{\delta _s}}'{\delta _s} 。\end{split} $ | (6) |
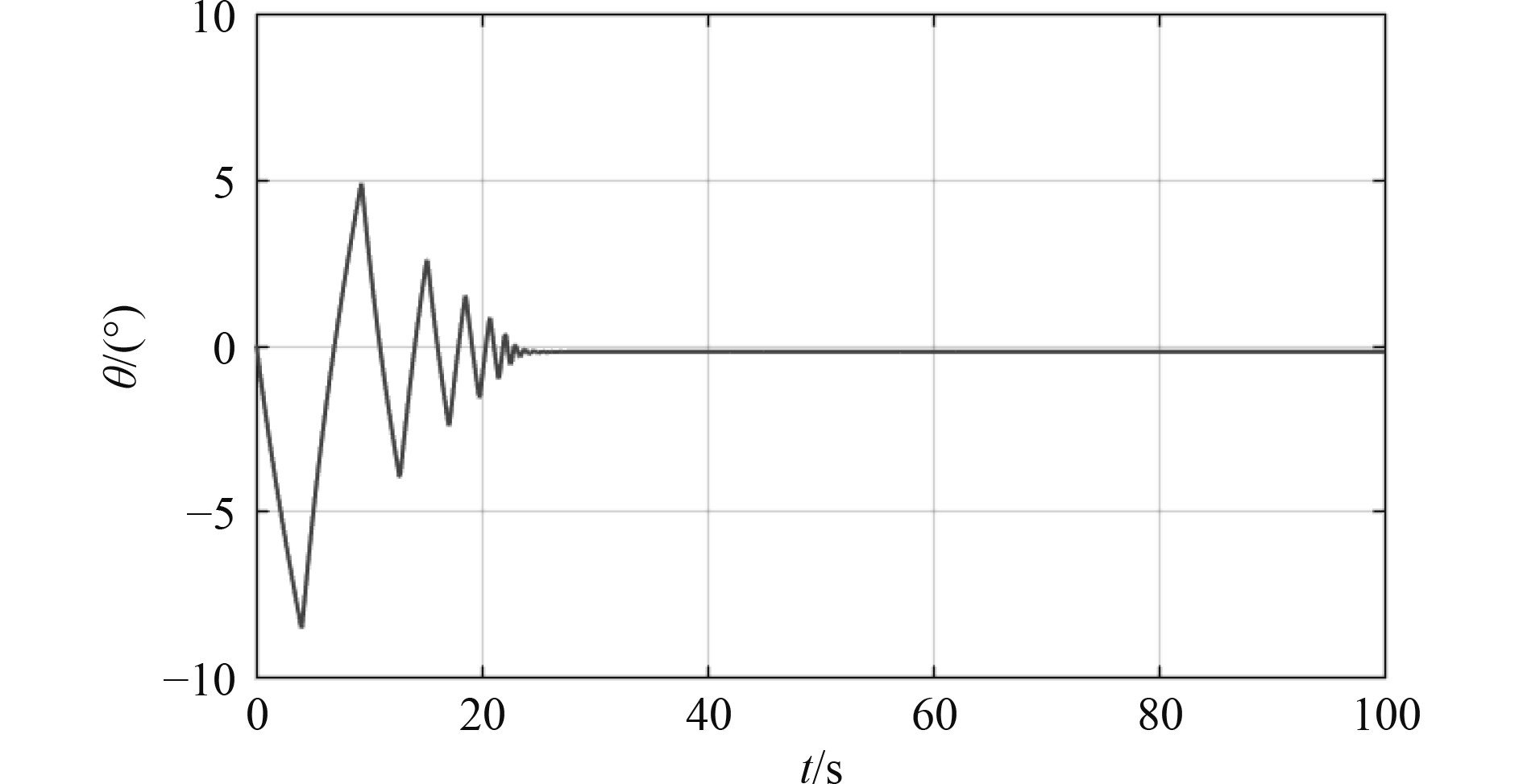
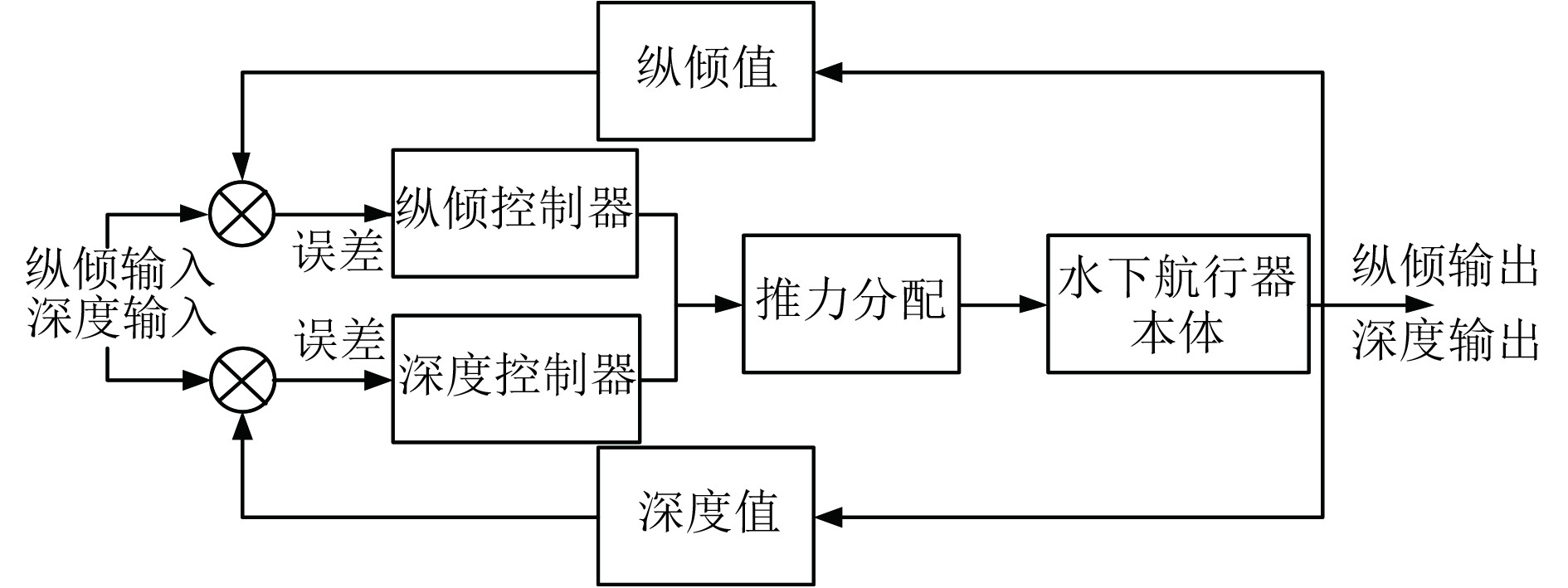
开启自动定深时,纵倾变化如图4所示。从仿真结果可看出,开启自动定深时,纵倾变化较明显,为保证航行由于整个航行过程稳定,需同时开启纵倾控制。考虑到纵倾值不大,采用PID控制纵倾值,保证航行姿态稳定。长距离航行控制结构如图5所示。
|
图 4 自动定深下的纵倾变化 Fig. 4 Pitch change under automatic depth determination |
|
图 5 水下航行器长距离航行控制结构图 Fig. 5 Control structure diagram of underwater vehicle long-distance navigation |
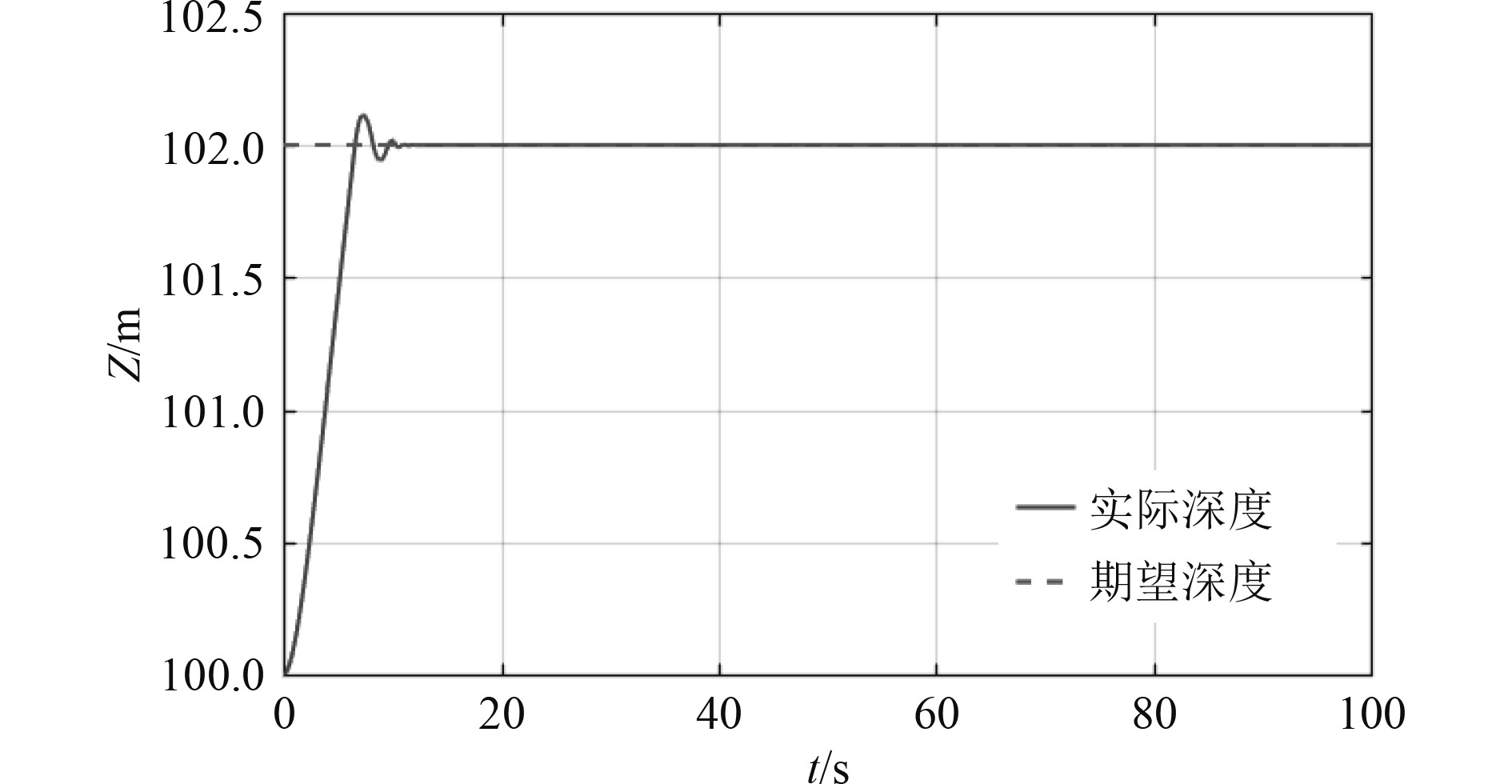
在航行过程中,保持一定深度巡航,深度、纵倾、航速变化曲线如图6~图8所示。
|
图 6 深度变化曲线 Fig. 6 Change curve of depth |
|
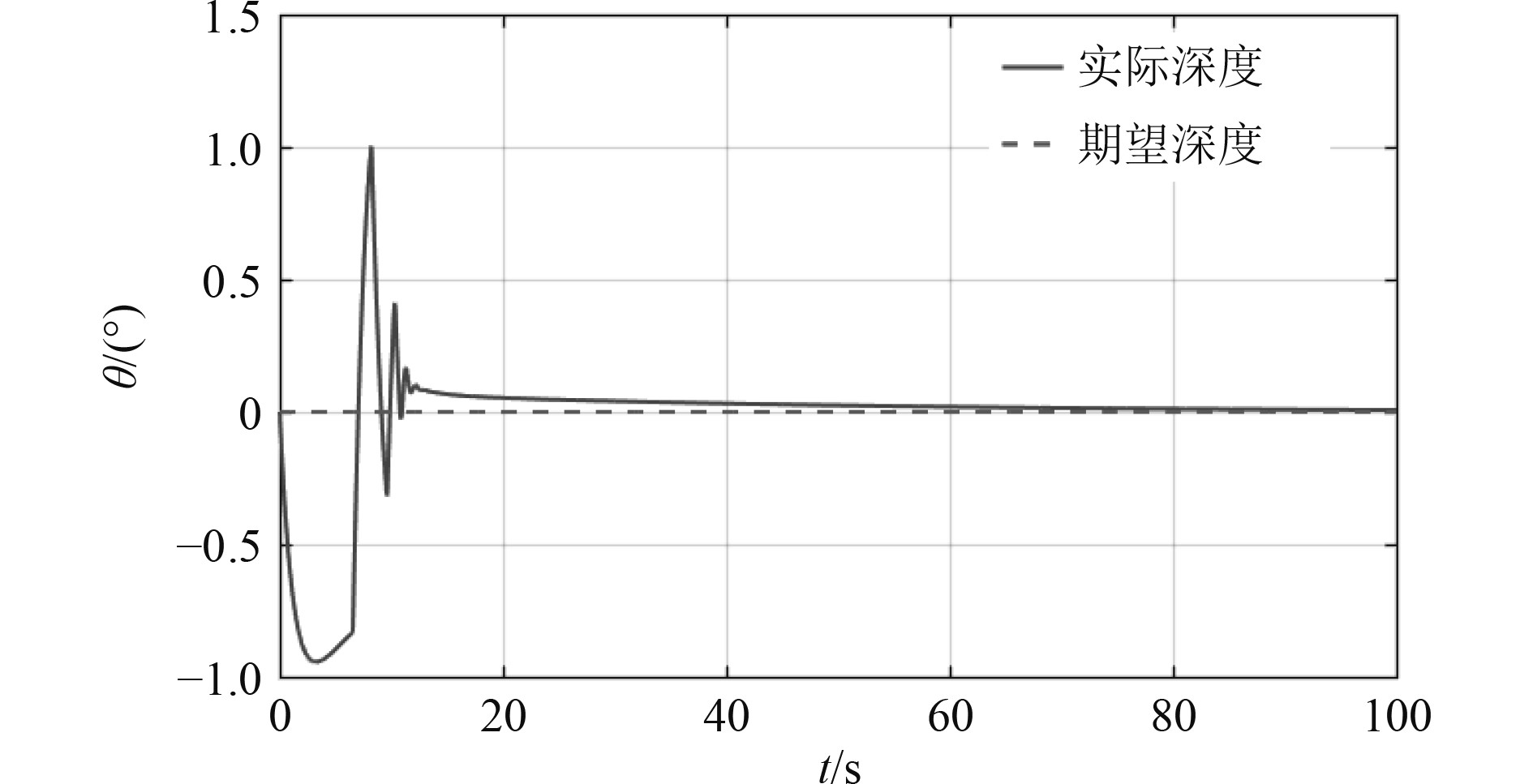
图 7 纵倾变化曲线 Fig. 7 Change curve of pitch |
|
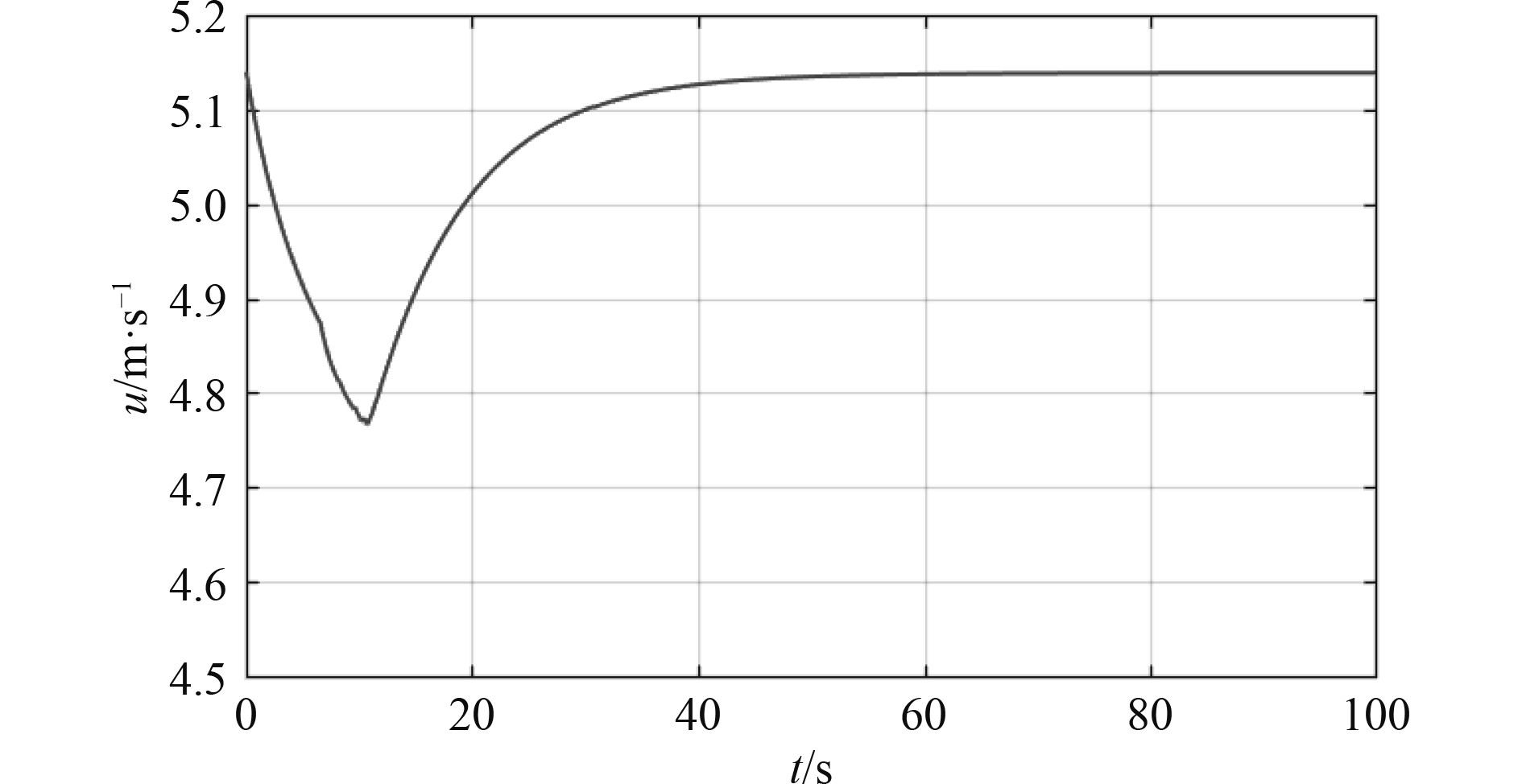
图 8 速度变化曲线 Fig. 8 Change curve of speed |
从仿真结果可看出,深度控制方面,在10 s时到达了期望深度,且很快稳定在期望深度;纵倾控制方面,纵倾角不大,整体在1°范围,精度在0.1°范围内,控制有一定波动调节,表明水下航行器运动模型具有非线性特点,纵倾和深度之间耦合性强。
视景仿真直观展示航行过程,进一步发挥仿真平台的工程分析潜能[11]。本文基于unity3D软件,开发了水下航行器的三维视景仿真平台,为水下航行器控制技术设计验证提供测试环境。通过视景仿真显示(见图9),水下航行器在近海底航行时能保持稳定航行状态。

|
图 9 水下航行器运动视景 Fig. 9 View of underwater vehicle movement |
本文建立了水下航行器垂直面运动模型,提出PID方法控制纵倾和滑模方法控制深度的组合控制策略。通过仿真试验,开展了运动控制仿真研究。基于水下航行器的三维视景仿真平台,直观展示航行过程。研究结果表明,水下航行器能稳定保持固定深度远距离航行,控制策略具有很好的适用性。
| [1] |
朱丹. 美军自主水下航行器发展研究[J]. 指挥控制与仿真, 2020, 42(1): 134-140. |
| [2] |
JINMO Park, NAKWAN Kim. Dynamics modeling of a semi-submersible autonomous underwater vehicle with a towfish towed by a cable[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7(2): 409-425. DOI:10.1515/ijnaoe-2015-0029 |
| [3] |
PARK Jong-Yong, KIM Nakwan, SHIN Yong-Ku. Experimental study on hydrodynamic coefficients for high-incidence-angle maneuver of a submarine[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(1): 100-113. DOI:10.1016/j.ijnaoe.2016.08.003 |
| [4] |
HOWAN Kim, DEV Ranmuthugala, ZHI Quan Leong, et al. Six-DOF simulations of an underwater vehicle undergoing straight line and steady turning manoeuvres[J]. Ocean Engineering, 2018, 150: 102-112. DOI:10.1016/j.oceaneng.2017.12.048 |
| [5] |
聂为彪, 钱治强, 吴铭, 等. 水下航行器横向操纵性运动预报设计与仿真[J]. 舰船科学技术, 2021, 43(S1): 22-26. |
| [6] |
李德军, 张伟, 赵桥生, 等. 深海潜水器运动操纵仿真研究[J]. 舰船科学技术, 2022, 44(8): 69-72. DOI:10.3404/j.issn.1672-7649.2022.08.014 |
| [7] |
魏延辉. UVMS系统控制技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2017.
|
| [8] |
GERTLER M, HAGEN G R. Standard equations of motion for submarine simulation[J]. Standard Equations of Motion for Submarine Simulation, 1967.
|
| [9] |
FELDMAN J P. DTNSRDC revised standard submarine equations of motion[J]. PoëmesEtLégendesKommentar, 1979.
|
| [10] |
马骋, 连琏. 水下运载器操纵控制及模拟仿真技术[M]. 北京: 国防工业出版社, 2009.
|
| [11] |
孙叶义, 杨文山, 周海波. 智能水下航行器动态对接三维视景仿真研究[J]. 舰船科学技术, 2020, 42(23): 47-51. DOI:10.3404/j.issn.1672-7649.2020.12.009 |
 2024, Vol. 46
2024, Vol. 46
