2. 国网烟台供电公司,山东 烟台 264000
2. State Grid Yantai Power Supply Company, Yantai 264000, China
铺缆船在海上航行时,受到风、浪、海流等环境因素的干扰,使船舶偏离指定位置点,降低了工作效率。为了确保船舶平稳运行,需要对其进行实时定位。动力定位(Dynamic Positioning,DP)区别于锚泊定位,系统检测船舶实际与目标位置差值,将其作为控制系统输入,通过调整参数,使船舶沿规划路径向目标位置航行。控制系统是DP船舶的重要组成部分,对于航行稳定,提高工作效率具有重要意义,受到广泛研究[1]。
船舶运动系统较为复杂,经典PID算法控制效果不好。目前常用控制方法有模糊PID控制、滑模控制、反步法控制和李雅普诺夫理论分析等[2-5]。模糊控制方法抗干扰能力强。Wang等[6]在自适应模糊反推控制方法基础上构造了一个高增益观测器来估计速度矢量。Yu等[7]采用直接自适应模糊控制来补偿水下机器人执行器饱和的影响,保证了执行器饱和时系统轨迹跟踪的稳定性。张爱华等[8]在传统PID控制基础上加入自整定模糊算法,减少船舶当前位置与设定点的位置差值。
智能算法对船舶循迹具有的精准的控制能力。Yang等[9]用粒子群算法改进神经网络,对最佳量化因子曲线(BQFQ)进行拟合,提高对MMG模型的控制精度。戈一航等[10]采用麻雀算法对PID进行整定,有效控制机器人对路径的跟踪。张品等[11]在机器人路径寻迹问题采用模糊PID结合改进麻雀算法的控制方法,提高了全向搬运机器人的工作状况。祝亢等[12]为实现对航迹跟踪的精准控制,使用深度确定策略梯度(DDPG)方法对控制器进行离线学习。
仿真实验基于动力定位铺缆船运动数学模型,在风、浪、流作用力下检测船舶实际与目标位置差值,将其作为控制器输入,设计自整定模糊PID结合非洲秃鹫算法的路径跟踪控制器,根据模糊规则自动调整PID参数,通过秃鹫算法的4个阶段寻找最优解,结合Levy飞行策略,提高寻优准确性。通过仿真对AVOA算法进行Kp、Ki、Kd参数整定,优化模糊PID控制进行模拟测试,分析改进后控制方法路径跟踪效果。
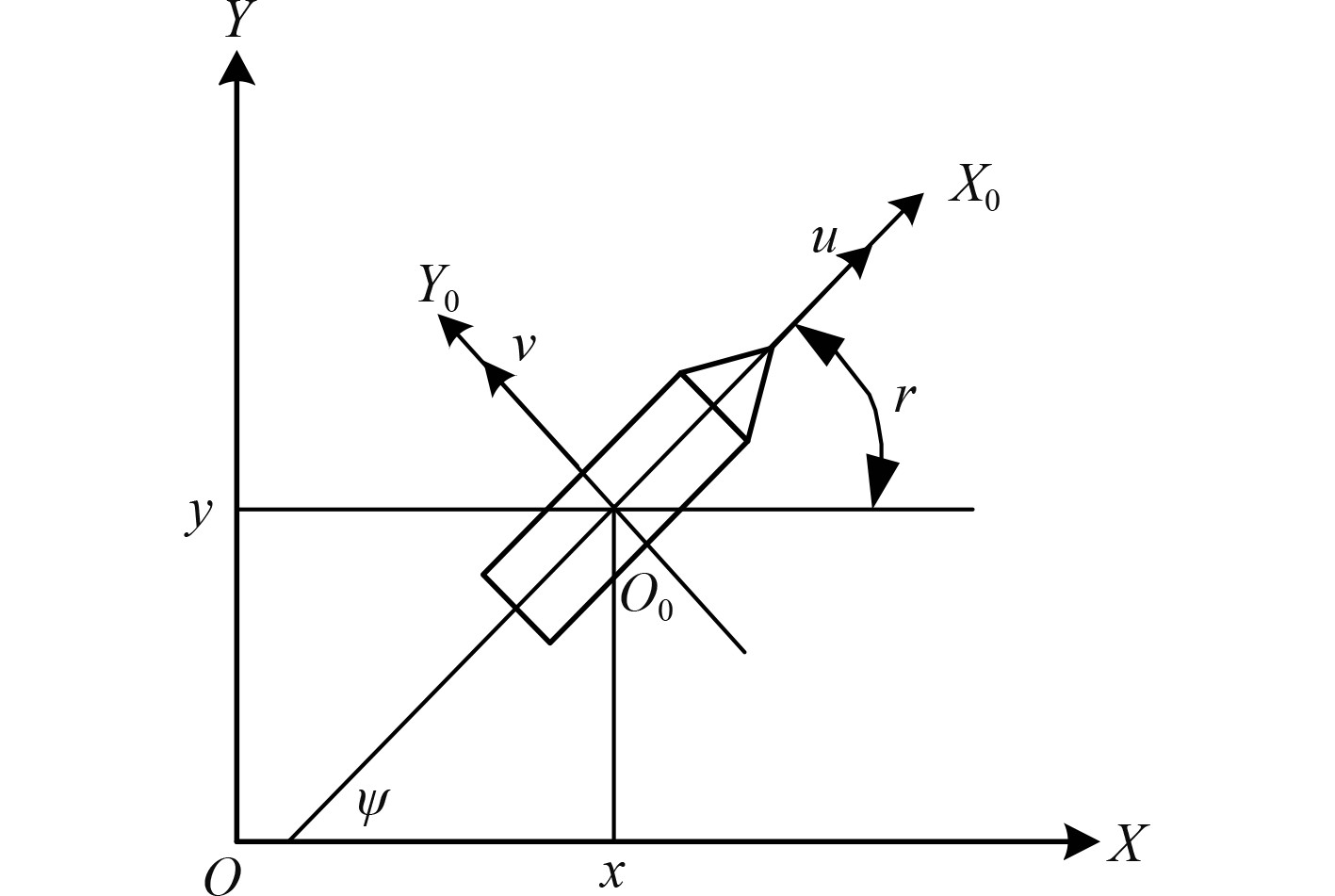
1 运动数学模型 1.1 铺缆船运动数学模型动力定位控制系统模型为Fossen提出的六自由度模型[13]。现有DP船舶控制技术如下:首向保持、定点控制以及航迹跟踪,控制的状态变量为船舶的经、纬度和首向角,即采用纵荡、横荡和首摇3个自由度船舶运动数学模型作为铺缆船运动数学模型,建立大地坐标系O-X-Y和船体坐标系O0-X0-Y0如图1所示,纵荡、横荡和首摇三自由度如表1所示。
|
图 1 船舶平面运动 Fig. 1 Vessel plane motion |
|
|
表 1 自由度名称及表示符号 Tab.1 Names and symbols of degrees of freedom |
铺缆船运动数学模型如下:
| $ \left\{ \begin{gathered} \dot \eta = R(\varphi )V ,\\ M\dot V + DV = \tau + {\tau _{env}}。\\ \end{gathered} \right. $ | (1) |
式中:
| $ {\boldsymbol{R}}(\varphi)=\left[\begin{array}{ccc} \cos \varphi & -\sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{array}\right] 。$ | (2) |
M为船舶系统的惯性矩阵:
| $ {\boldsymbol{M}}=\left[\begin{array}{ccc} m-X_{i} & 0 & 0 \\ 0 & m-Y_{i} & m x_{z}-Y_{i} \\ 0 & m x_{g}-Y_{i} & I_{x}-N_{i} \end{array}\right]。$ | (3) |
其中:m为船舶质量;
| $ {\boldsymbol{D}}=\left[\begin{array}{ccc} -X_{\mathrm{w}} & 0 & 0 \\ 0 & -Y_{\mathrm{v}} & -\mathrm{Y}_{v} \\ 0 & -Y_{v} & -N_{r} \end{array}\right]。$ | (4) |
由于海面环境变化较大,铺缆船在在铺设电缆时会受到风、浪、流等作用力影响,建立环境干扰力数学模型[14]。为便于分析,
| $ {\tau _{env}} = \tau _{env}^{{\rm{wind}}} + \tau _{env}^{{\rm{wave}}} + \tau _{env}^{{\rm{current}}}。$ | (5) |
式中:
风干扰通过前馈方式加入系统,以船体四周平均风载荷为依据,其数学表达式如下:
| $ \tau _{env}^{{\rm{wind}}} = \frac{1}{2}{\rho _a}V_{rw}^2\left[ {\begin{array}{*{20}{c}} {{C_x}({\gamma _w}){A_{Fw}}} \\ {{C_y}({\gamma _w}){A_{Lw}}} \\ {{C_n}({\gamma _w}){A_{Lw}}{L_{OA}}} \end{array}} \right]。$ | (6) |
式中:
考虑规则波对船作用力,采用Daidola提出的浪作用力模型,表达式如下:
| $ \tau _{env}^{{\rm{wave}}} = \frac{1}{2}{\rho _w}{L_{OA}}a_w^2\left[ {\begin{array}{*{20}{c}} {\cos \chi {C_{xw}}(\lambda )} \\ {\sin \chi {C_{yw}}(\lambda )} \\ {{L_{OA}}\sin \chi {C_{nw}}(\lambda )} \end{array}} \right]。$ | (7) |
式中:
由于DP船舶低速行驶,流作用的阻尼力和力矩表达如下:
| $ \tau _{env}^{{\rm{current}}} = \frac{1}{2}{\rho _w}V_{rc}^2\left[ {\begin{array}{*{20}{c}} {{A_{Fc}}{C_x}({\gamma _c})} \\ {{A_{Lc}}{C_y}({\gamma _c})} \\ {{A_{Lc}}{C_n}({\gamma _c}){L_{OA}}} \end{array}} \right] 。$ | (8) |
式中:
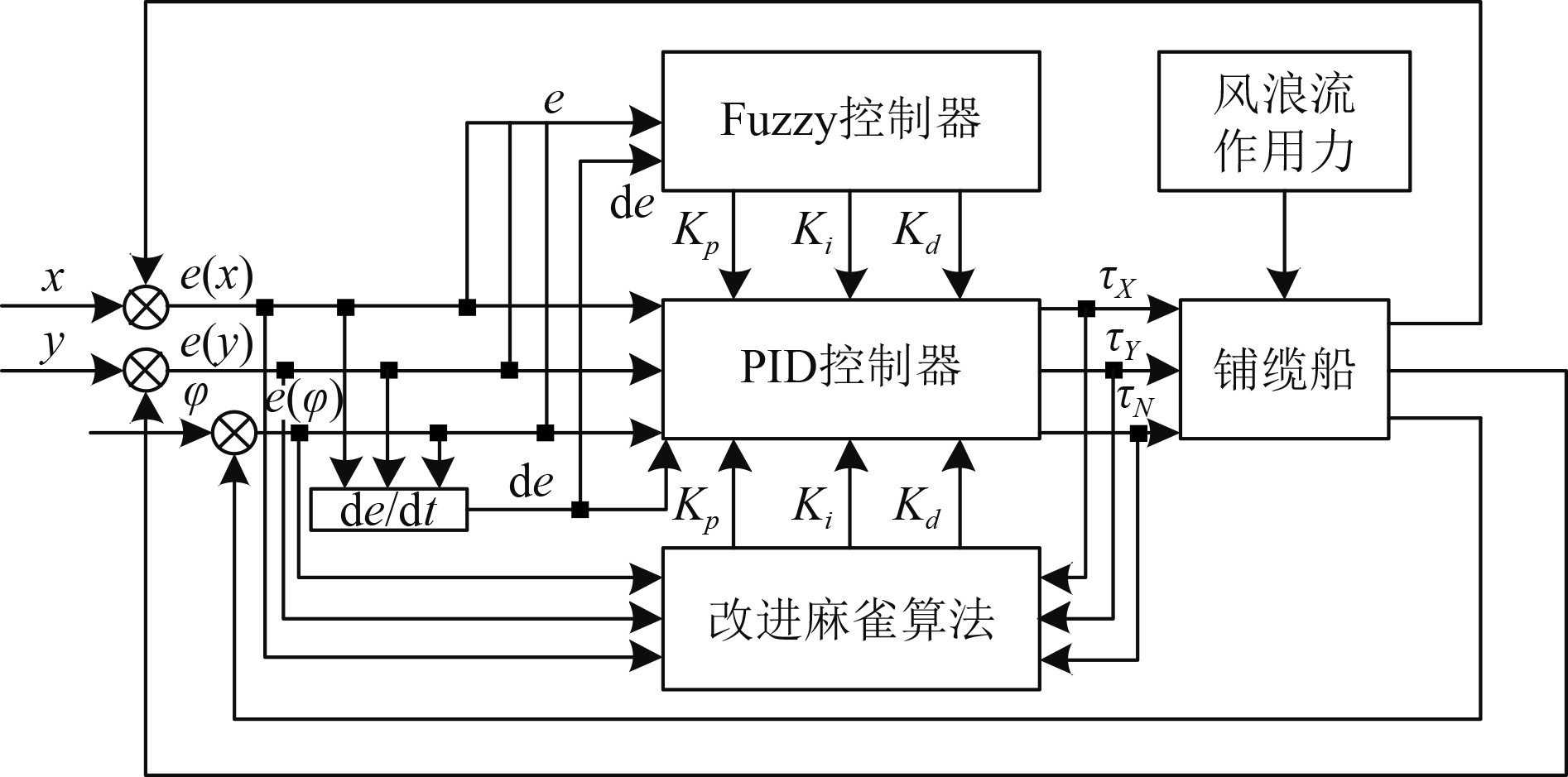
通过系统仿真模拟真实海况,将风、浪、流作用力加载到DP铺缆船运动模型上,计算得出船舶的位置和姿态矢量偏差,并将其输入到控制器中,通过调节参数不断减小船舶位置首向差值,实现船舶寻优定位。控制结构如图2所示。
|
图 2 控制系统结构图 Fig. 2 Control system structure diagram |
PID控制通过反馈信号与实时信号的差值调整参数。设船舶目标与实际位置状态的差值为e,其变化率de,作为PID控制器的输入,调整Kp、Ki、Kd参数,达到控制要求。其控制公式为:
| $ \tau (t) = {K_p}\left[ {e(t) + \frac{1}{{{T_i}}}\int_0^t {e(t){\rm{d}}t} + \frac{{{T_{\rm{d}}}{\rm{d}}e(t)}}{{{\rm{d}}t}}} \right]。$ | (9) |
传递函数为:
| $ g(s) = \frac{{\tau (s)}}{{e(s)}} = {K_p} + \frac{{{K_i}}}{s} + {K_d}s 。$ | (10) |
式中:Kp为比例系数;Ki、Kd分别为积分、微分时间常数。
比例环节反映系统的偏差信号e(t);积分环节消除系统静差;微分环节显现信号变化。e(t)较大时,引入修正信号,产生超前的控制作用。但随着调节精度变高,PID调节产生振荡,动态响应变慢,容易受到外界干扰。因此需要对其进行改进。
2.2 模糊控制器原理将模糊(Fuzzy)算法与PID组合成模糊PID控制器,加强抗干扰和稳定性,控制灵活,精度较高。采用自整定模糊PID控制器,用模糊集合表示控制规则,根据系统反馈做出模糊推理,从而寻求Kp、Ki、Kd的调整变化量ΔKp、ΔKi、ΔKd与e和de间的关系,自动调节参数,达到控制要求。
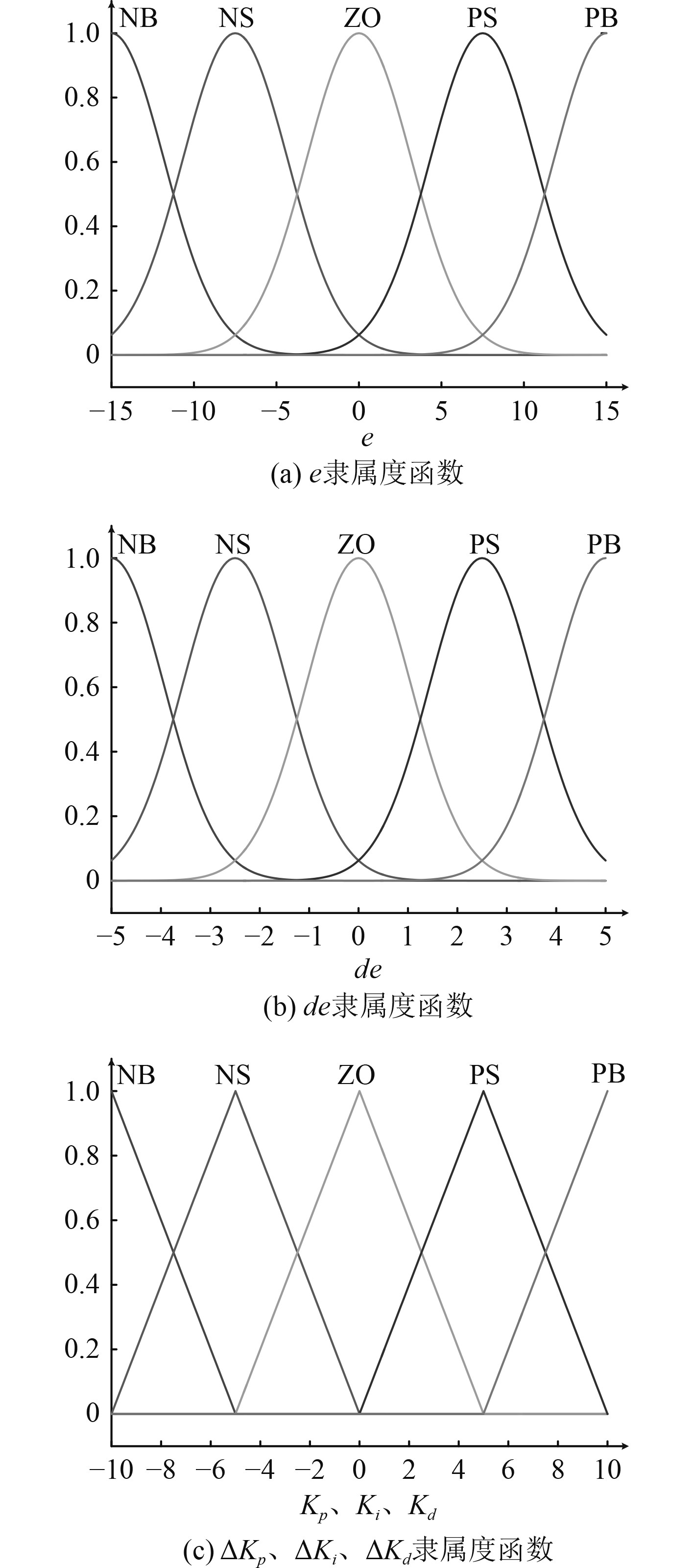
为提高控制精度,分别对横向、纵向和首向3个自由度进行控制。首先进行模糊化,制定模糊规则。控制过程中铺缆船是低速运动,不会导致太大的位置和首向偏差,设e、de和ΔKp、ΔKi、ΔKd三个控制参数的模糊子集和论域如下:
| $ \begin{split}&\Delta {K}_{p}、\Delta {K}_{i}、\Delta {K}_{d}=\left\{PB,PS,ZO,NS,NB\right\}\in \left[-10,10\right],\\& \left\{\begin{array}{l}e=\left\{PB,PS,ZO,NS,NB\right\}\in \left[-15,15\right],\\ {\rm{d}}e=\left\{PB,PS,ZO,NS,NB\right\}\in \left[-5,5\right]。\end{array}\right.\\[-5pt]\end{split} $ | (11) |
隶属度函数分布情况如图3所示。模糊控制器采用离线控制决策,控制规则如表2所示。
|
图 3 隶属度函数 Fig. 3 Affiliation function |
|
|
表 2 模糊控制规则表 Tab.2 Table of fuzzy control rules |
非洲秃鹫算法(AVOA)由Abdollahzadeh等[15]提出,模拟非洲秃鹫的觅食和导航行为。
2.3.1 阶段1:确定任意组最优秃鹫初始种群形成后,计算所有解的适应度,选择最优解作为第一组秃鹫,次优解为第二组秃鹫,其他解朝第一组和第二组移动。在每次适应度迭代中,将重新计算整个总体。
| $ R\left( i \right) = \left\{ \begin{split} & BestVultur{e_1},{\text{ if}}{\text{ }}{p_i} = {L_1} ,\\ &BestVultur{e_2},{\text{ if}}{\text{ }}{p_i} = {L_2}。\\ \end{split} \right. $ | (12) |
式中:R(i)为最佳秃鹫之一;P(i)为秃鹫当前位置矢量;L1和L2为搜索操作之前给定的参数,其值介于0和1之间,且2个参数之和为1。使用轮盘赌法轮获得选择最优解概率,并为每组选择每个最佳解。
| $ p_{i}=\frac{F_{i}}{\sum_{i=1}^{n} F_{i}}。$ | (13) |
式中,Fi为适应度值。
2.3.2 阶段2:秃鹫饥饿率受秃鹫吃饱或饥饿速度的启发,模型如下:
| $ F=\left(2 \times \operatorname{rand}_{1}+1\right) \times Z \times\left(1-\frac{{ Iteration }}{{ {\rm{max}}tercations }}\right)+t 。$ | (14) |
式中:F为饱腹率;Iteration为当前迭代次数;maxiterations表示最大迭代次数;z是介于−1~1的随机数;rand1为介于0~1之间的随机数。当z<0时,秃鹫饥饿,当z=0时,秃鹫饱腹。
当|F|≥1时,秃鹫在不同区域寻找食物,AVOA进入探索阶段;当|F|<1时,秃鹫处于开发模式,在最优位置附近寻找食物。
2.3.3 阶段3:探索在AVOA中,秃鹫基于2种策略检查随机区域,策略通过P1来选择。生成一个介于0和1之间的随机数randP1,当randP1≥P1时,使用式(16);当randF≤P1,使用式(17)。搜索饱腹感区域如下:
| $ P(i+1)=\left\{\begin{split} &\text { Equation(16) } & \text { if } P_{1} \geq { rond }_{P 1},\\ &\text { Equation }(18) & \text { if } P_{1}< { rand }_{\mathrm{P}}。\end{split}\right. $ | (15) |
| $ P({i}+1)=R({i})-D({i}) \times F,$ | (16) |
| $ D({i})=|X \times R({i})-P({i})|。$ | (17) |
式中:P(i+1)为迭代后秃鹫位置矢量;D(i)为当前秃鹫与2组中的最佳秃鹫之一的随机距离;X为秃鹫随机移动位置,采用公式X=2×rand获得,保护食物免受其他秃鹫的伤害。
| $ P(i+1)=R(i)-F+rand_{2} \times\left((u b-l b) \times rand_{3}+l b\right) 。$ | (18) |
式中:lb和ub为变量的上界和下界;rand2 和rand3是介于0和1之间随机数,用于增加随机性系数。当rand3约为1时,随lb添加一个随机运动以增加多样性并搜索不同空间区域。
2.3.4 阶段4:开发当值|F|介于0.5~1之间时,AVOA执行2种不同的旋转飞行和围攻策略。P2用于确定每个策略的选择,其值应介于0和1之间。初始阶段,生成介于0和1之间的随机数randP2。当randP2≥P2,则围攻策略将缓慢实施;当randP2< P2,则执行旋转飞行策略。公式如下:
| $ P(i+1)=\left\{\begin{split} &\text { Equation(20) } ,& \text { if } P_{2} \geqslant \text { rand }_{P 2} ,\\ &\text { Equation(23) } ,& \text { if } P_{2}<\text { rand }_{P 2}。\end{split}\right. $ | (19) |
当|F|≥0.5时,许多秃鹫聚集在同一食物源上会引起严重的冲突。身体强壮的秃鹫获得食物机会更大。身体弱小的秃鹫聚集在强壮秃鹫周围,引发小冲突使其疲劳,从而获取食物。运动模型如下:
| $ P(i+1)=D(f) \times\left(F+r a n d_{4}\right)-d(t) ,$ | (20) |
| $ d(y)=R(i)-P(i)。$ | (21) |
式中:rand4是介于0~1之间的随机数,用于增加随机系数;d(y)为当前秃鹫与2组中最佳秃鹫之一的距离。
秃鹫的旋转飞行用于模拟螺旋运动。在两2个最佳秃鹫中选择一个,与其余秃鹫建立螺旋方程,公式为:
| $ \begin{split} S_{1}=R(i) \times\left(\dfrac{{rand}_{5} \times P_{i}}{2 {\text{π}} }\right) \times \cos (P(i)),\\ S_{2}=R(i) \times\left(\dfrac{r a n d_{5} \times P_{i}}{2 {\text{π}}}\right) \times \cos (P(i)),\end{split} $ | (22) |
| $ P(t+1)=R(f)-\left(S_{1}+S_{2}\right)。$ | (23) |
式中,rand5和 rand6是介于0~1之间的随机数。
当|F|< 0.5时,生成介于0~1之间的随机数randP3。当randP3≥P3时,食物源上会累积几种类型的秃鹫;当randP3<P3时,实施围攻策略。该过程为:
| $ P(i+1)=\left\{\begin{split} \text { Equation }(26) ,& \text { if } P_3 \geqslant\text { rand }_{p 3},\\ \text { Equation }(27),& \text { if } P_{3}<\text { rand }_{p 3}。\end{split}\right. $ | (24) |
标记向食物源移动的所有秃鹫,此时会积累几种不同类型秃鹫。运动模型如下:
| $ \begin{split} & {{{A}}_{{1}}} = BestVulture(i) - \frac{{{{B}}estVultur{e_1}(i){{ \times P}}(i)}}{{{{B}}estVultur{e_1}(i) - {{P}}{{(i)}^2}}}{{ \times F}},\\ & {{{A}}_{{2}}} = BestVulture(i) - \frac{{{{B}}estVultur{e_2}(i){{ \times P}}(i)}}{{{{B}}estVultur{e_2}(i) - {{P}}{{(i)}^2}}}{{ \times F}},\end{split}$ | (25) |
| $ P(t+1)=\frac{A_{1}+A_{2}}{2} 。$ | (26) |
式中:BestVulture1(i)是当前迭代最优秃鹫;BestVulture2(i)是当前迭代中第二组的最佳秃鹫。
这一阶段领头秃鹫变得饥饿和虚弱,其他秃鹫向此位置移动来寻找食物。运动模型如下:
| $ P(i+1)=R(t)-|d(i)| \times F \times L \times levy。$ | (27) |
式中,Levy为飞行机制,用于提高AVOA寻优效率,具体表达式如下:
| $ L e v y=0.01 \times \frac{u \times \sigma}{|v|^{\frac{1}{\beta}}}, \sigma=\left(\dfrac{\Gamma(1+\beta) \times \sin \left(\dfrac{{\text{π}} \beta}{2}\right)}{\Gamma\left(\dfrac{1+\beta}{2}\right) \times \beta \times 2^{\frac{\beta 1}{2}}}\right)^{\frac{1}{\beta}}。$ | (28) |
式中:β为1.5;σ为标准差;µ和v服从正态分布。
| $ \mu \sim N\left(0, \sigma_{\mu}^{2}\right), v \sim N\left(0, \sigma_{v}^{2}\right) 。$ | (29) |
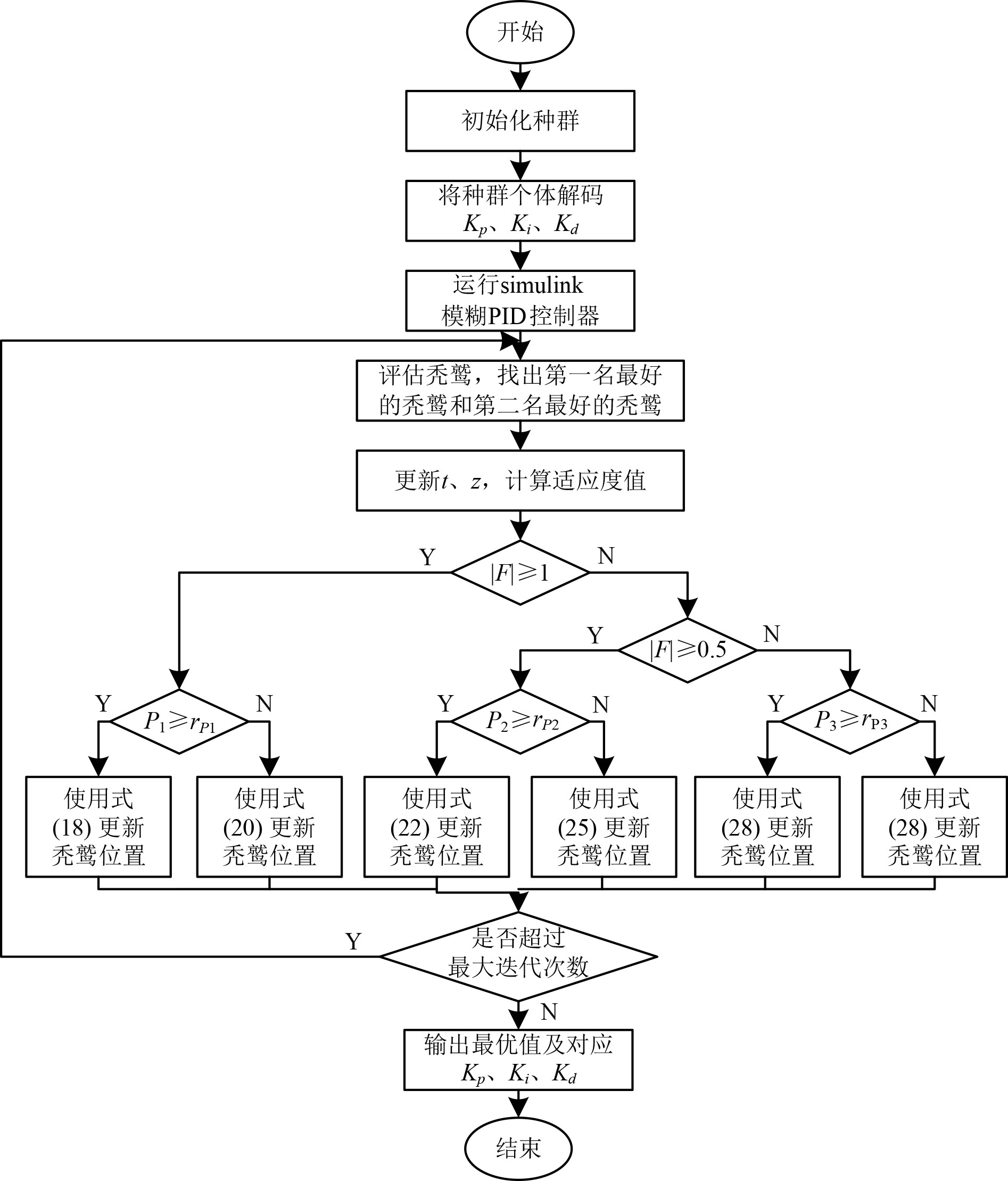
结合模糊控制,算法流程图如图4所示。
|
图 4 算法流程图 Fig. 4 Algorithm flow chart |
为验证AVOA-Fuzzy-PID算法对船舶路径跟踪控制效果,在Matlab2015b环境下利用Simulink搭建船舶控制系统仿真模型。非洲秃鹫算法参数:种群规模30,迭代次数30次。DP铺缆船参数:船长L=76.2 m,质量m=4×106 kg,排水量Δ=6×106 kg。埋设犁质量mp=1.85×104 kg。初始环境状态为:风速4级(7.9 m/s),风向45°;海流流速2 kn以下,流向60°;波浪高1.5 m。设船体坐标系原点与船舶重心重合,其低速模型线性阻尼矩阵D和系统惯性矩阵M如下[16-17]:
| $ {\boldsymbol{D}}=10^{6} \times\left[\begin{array}{ccc} 0.05138 & 0 & 0 \\ 0 & 0.1698 & -1.5081 \\ 0 & -1.5081 & 253 \end{array}\right] ,$ | (30) |
| $ {\boldsymbol{M}}=10^{6} \times\left[\begin{array}{ccc} 4.5096 & 0 & 0 \\ 0 & 7.5608 & -22.68 \\ 0 & -22.68 & 2968.3 \end{array}\right] 。$ | (31) |
为了便于研究,设DP铺缆船在大地坐标系中初始位置:x=0 m,y=0 m,目标位置:x=100 m,y=100 m,循迹轨迹为直线。仿真步骤如下:
步骤1 运行非洲秃鹫算法,种群初始化;
步骤2 将种群个体解码,调用Simulink仿真模型,将算法整定后的Kp、Ki、Kd代入模糊PID控制器,计算出船舶与目标位置距离,规划航行路径;
步骤3 判断是否超过最大迭代次数。若未超过,则返回步骤2;若超过,则终止迭代。通过算法多次迭代,得到船舶最优行驶路径。
将AVOA算法应用于模糊PID控制器能够使得DP铺缆船运动系统具有更强的准确性和快速性。
船舶速度矢量和埋设犁受力变化曲线如图5所示。可以看出,相比Fuzzy-PID,AVOA-Fuzzy-PID控制的船舶速度以及埋设犁所受拉力变化波动较小。其中图5(a)、图5(d)中,DP铺缆船前进速度和埋设犁所受拉力峰值较低,偏差较小。由此可知,AVOA-Fuzzy-PID控制器稳定性较好,精度较高。
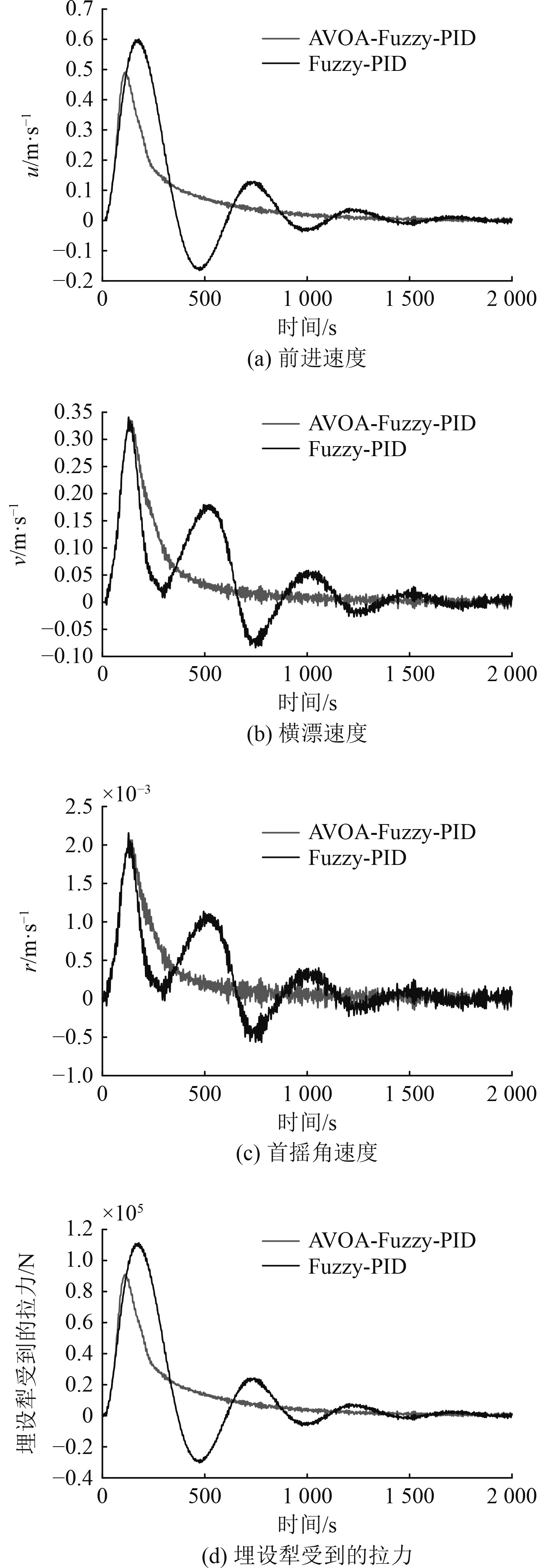
|
图 5 船舶速度矢量变化曲线 Fig. 5 Vessel speed vector variation curve |
DP铺缆船位置角度差值及坐标变化的曲线如图6和图7所示。图6中,Fuzzy-PID控制的横向、纵向峰值为82,AVOA-Fuzzy-PID控制的横向、纵向峰值为65、71,使船舶以更短的距离靠近目标位置。图7中,AVOA-Fuzzy-PID控制船舶的位移和角变跟踪过程平顺迅速。由此可以看出,AVOA-Fuzzy-PID控制以更小的偏差量趋于航迹,快速到达目标设定点。
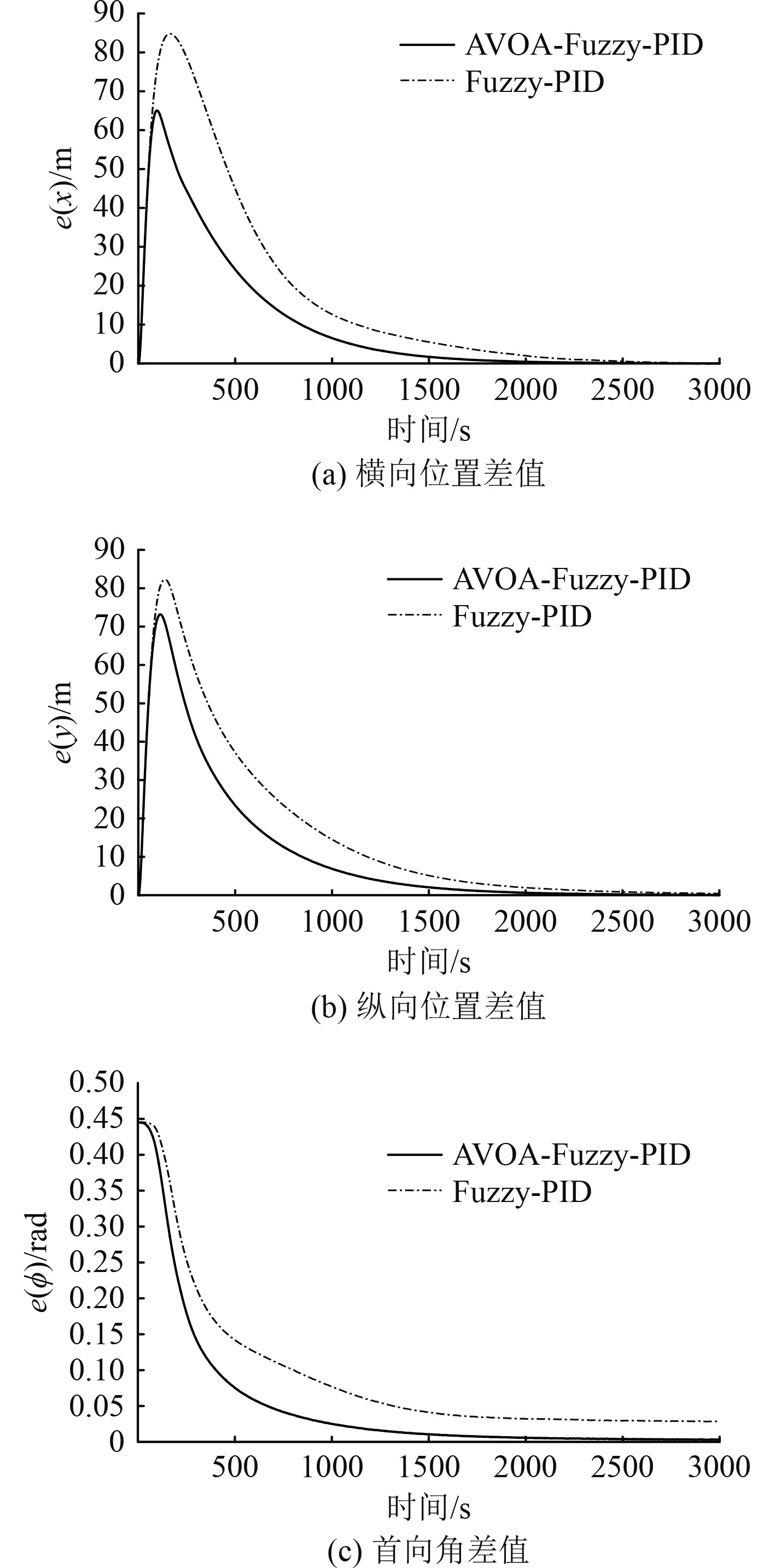
|
图 6 船舶位置角度差值曲线 Fig. 6 Vessel position angle difference curve |
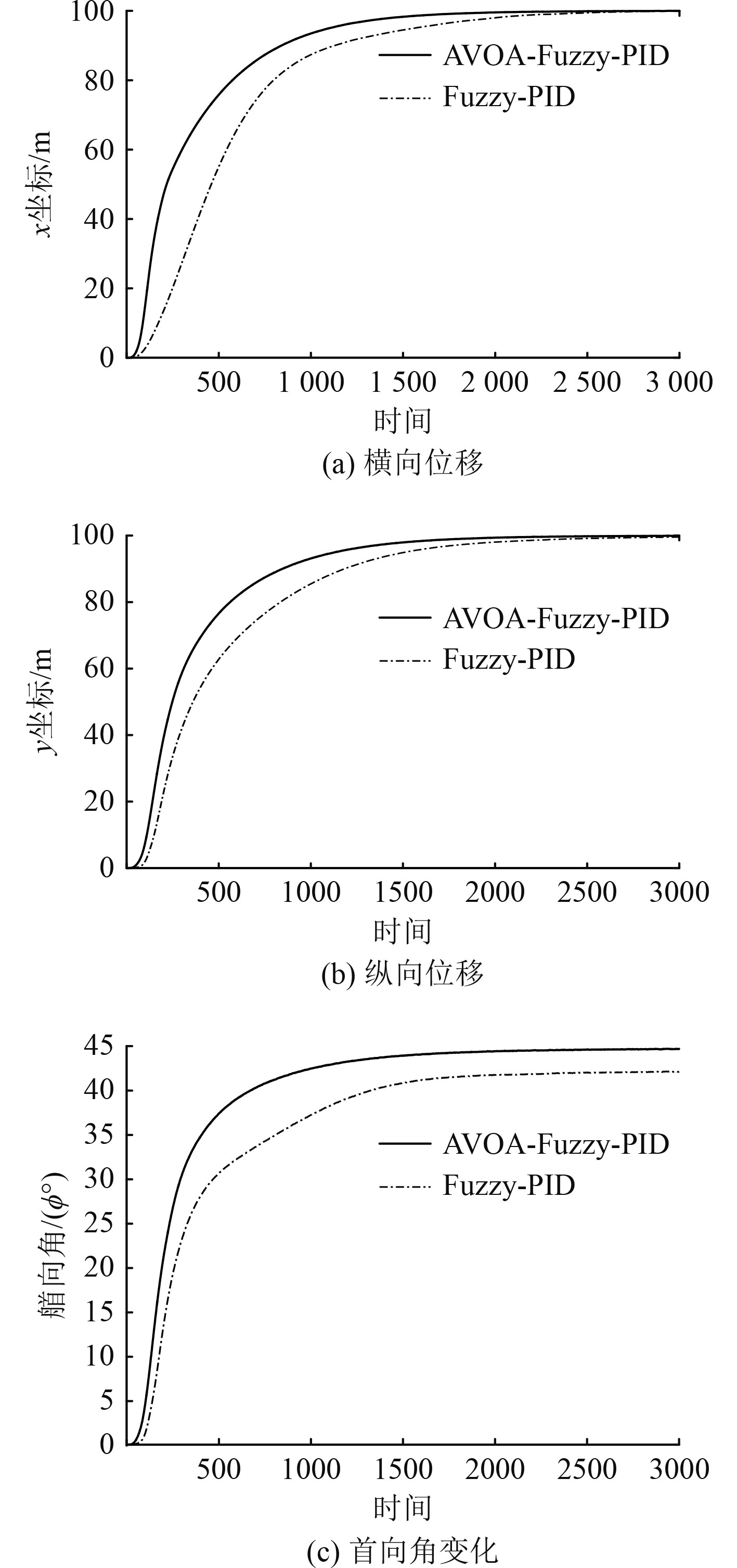
|
图 7 船舶坐标变化曲线 Fig. 7 Vessel coordinate variation curve |
AVOA算法对Kp、Ki、Kd整定如图8所示。可以看出,算法能够在第10~15次迭代完成对Kp、Ki、Kd参数的寻优。
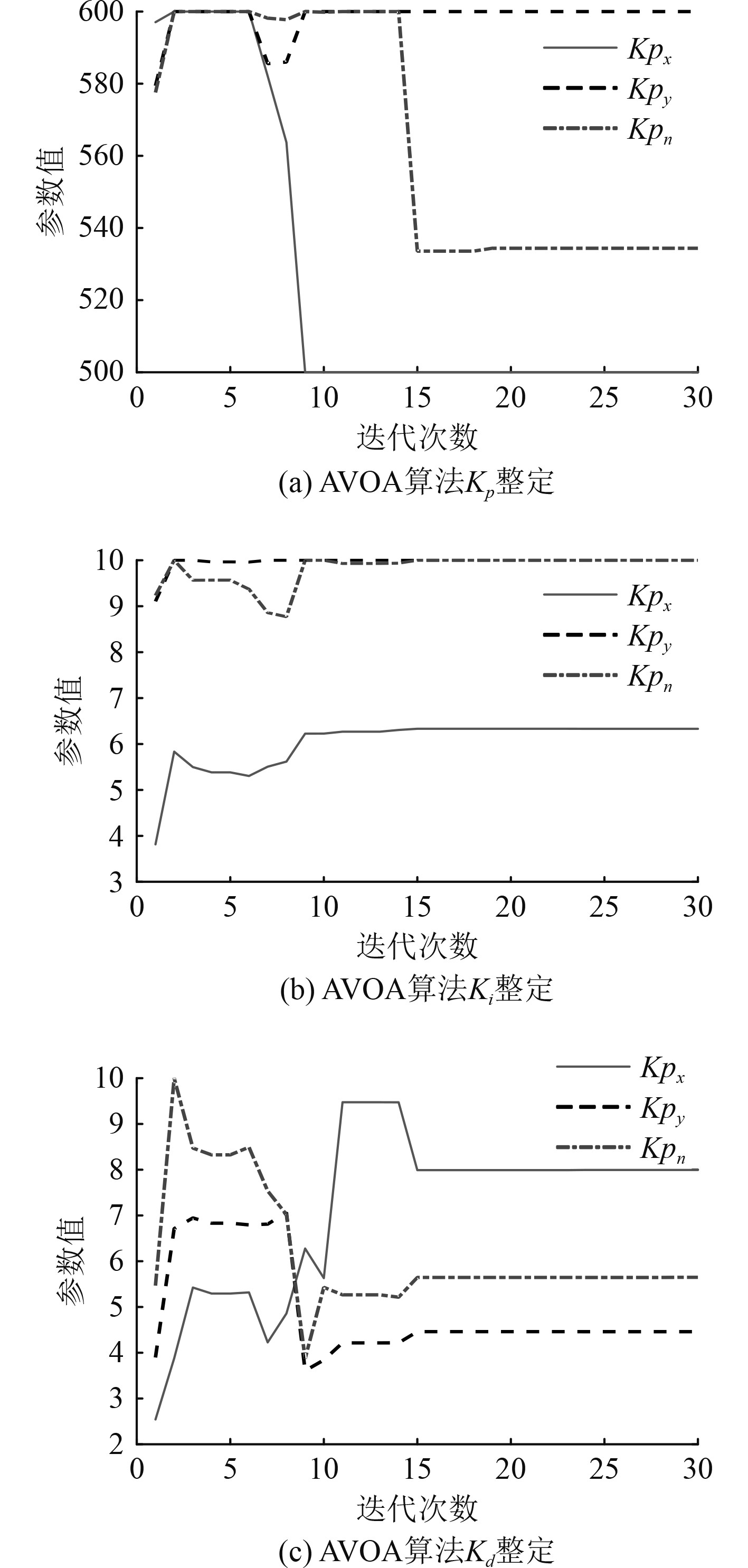
|
图 8 AVOA算法对Kp、Ki、Kd整定 Fig. 8 AVOA algorithm for Kp、Ki、Kd rectification |
PSO、GA、SSA和AVOA算法优化Fuzzy-PID控制器适应度函数曲线如图9所示。可以看出,相较于其他智能算法,AVOA算法寻优精度较高,收敛速度较快,在求解非线性最优化计算问题效果较好。
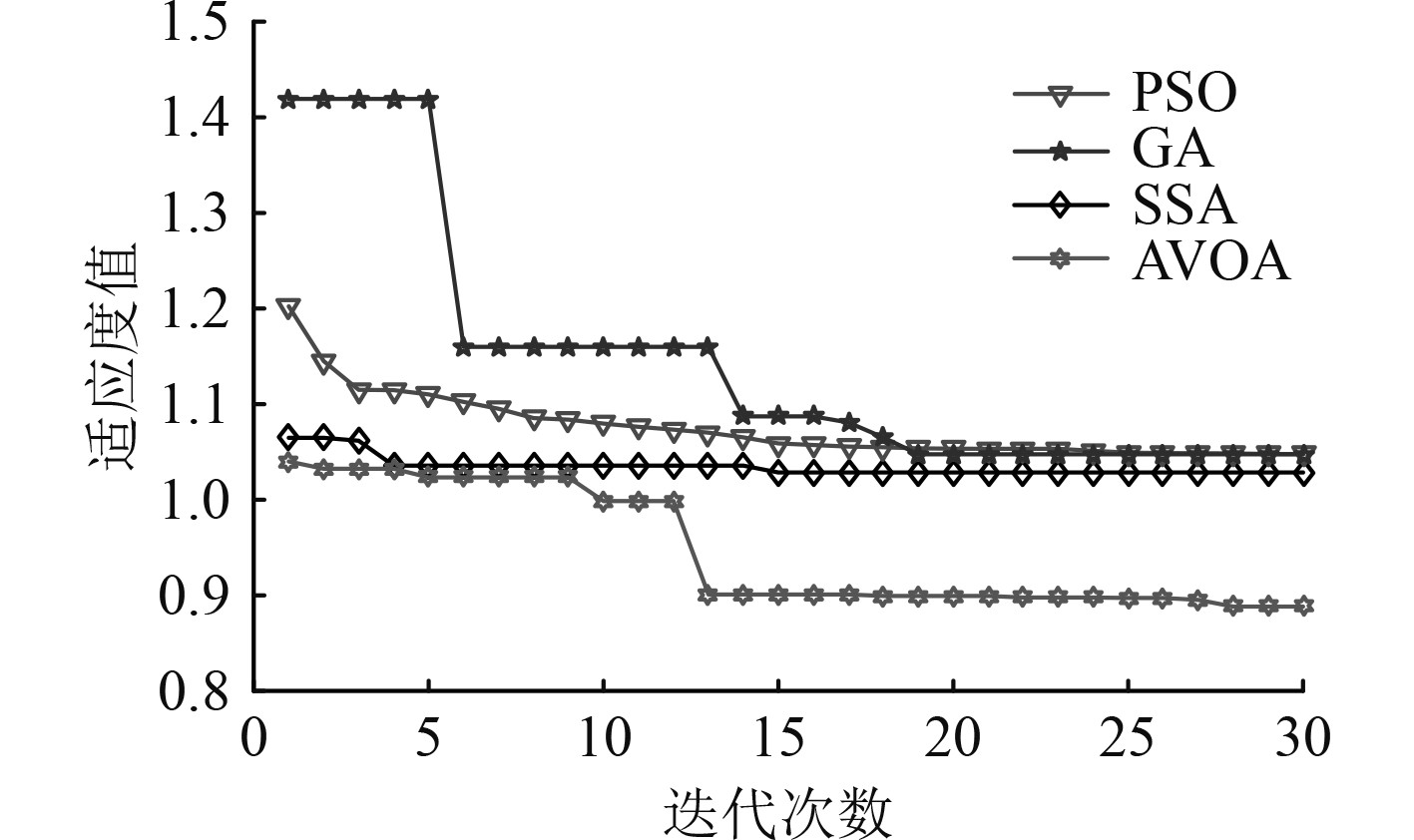
|
图 9 不同算法适应度函数曲线 Fig. 9 Aaptation function curves of different algorithms |
不同算法下铺缆船轨迹变化曲线如图10所示。对比不同算法控制,AVOA-Fuzzy-PID控制船舶沿规划路径行驶的轨迹偏航幅度较小。结合以上仿真结果可以看出,AVOA-Fuzzy-PID总体循迹控制效果较好,能够使DP铺缆船实时行驶路径更靠近期望路径。
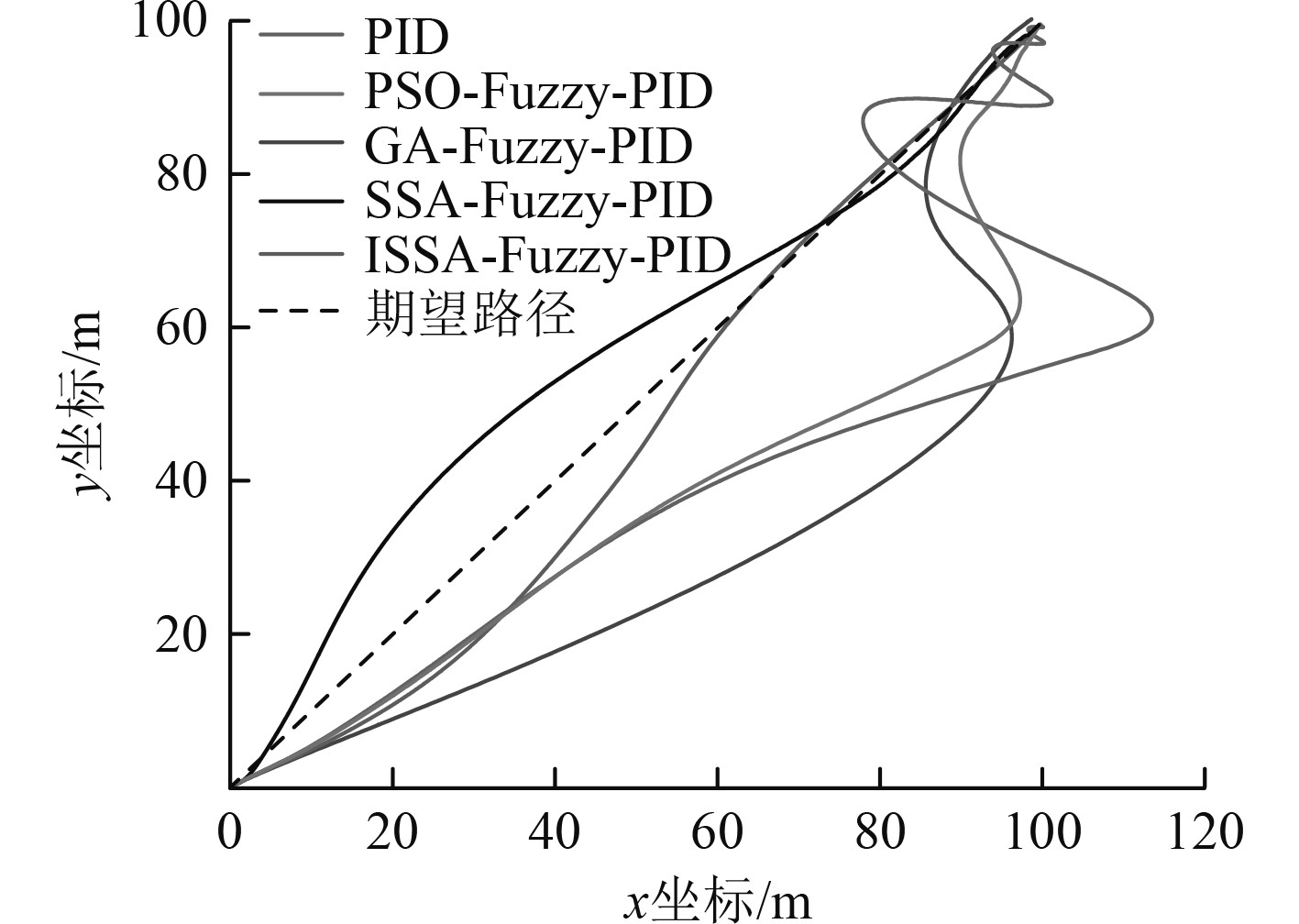
|
图 10 铺缆船轨迹变化 Fig. 10 Variation of the trajectory of cable-laying vessel |
| [1] |
徐海祥, 李超逸, 余文曌, 等. 智能船舶循迹控制方法研究[J]. 华中科技大学学报(自然科学版), 2020, 48(8): 103-8. XU Haixiang, LI Chaoyi, YU Wenju, et al. Research on intelligent ship tracking control method[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(8): 103-8. |
| [2] |
尤冬梅, 孙英培. 非线性船舶模型运动控制中鲁棒神经网络的应用[J]. 舰船科学技术, 2022, 44(12): 161-164. YOU Dongmei, SUN Yingpei. Application of therobust neural network in motion control of nonlinear ship model[J]. Ship Science and Technology, 2022, 44(12): 161-164. DOI:10.3404/j.issn.1672-7649.2022.12.033 |
| [3] |
谢文博, 付明玉, 张健, 等. 动力定位船舶自适应反步逆最优循迹控制[J]. 中国造船, 2013, 54(3): 58-69. XIE Wenbo, FU Mingyu, ZHANG Jian, et al. Adaptive backstepping inverse optimal trajectory control for power positioning ships[J]. China Shipbuilding, 2013, 54(3): 58-69. DOI:10.3969/j.issn.1000-4882.2013.03.008 |
| [4] |
孙豫. 线性变参数系统算法在船舶运动与参数控制的应用[J]. 舰船科学技术, 2022, 44(13): 68-71. SUN Yu. Application of linear variable parameter (LPV) system algorithm in ship motion and parameter control[J]. Ship Science and Technology, 2022, 44(13): 68-71. DOI:10.3404/j.issn.1672-7649.2022.13.016 |
| [5] |
LI, Jia wang. Robust tracking control and stabilization of underactuated ships[J]. Asian Journal of Control, 2018, 20(6): 2143-2153.
|
| [6] |
WANG Y, WANG H, LI M, et al. Adaptive fuzzy controller design for dynamic positioning ship integrating prescribed performance[J]. Ocean Engineering, 2020, 219(9): 107956. |
| [7] |
YU C, XIANG X, ZHANG Q, et al. Adaptive fuzzy trajectory tracking control of an under actuated autonomous underwater vehicle subject to actuator saturation[J]. International Journal of Fuzzy Systems, 2017, 20(1): 269-79. |
| [8] |
张爱华. 铺缆船作业过程中的循迹控制方法的研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [9] |
YANG C, ZOU Z. Straight-line tracking control for underactuated ships based on LOS and adaptive fuzzy method[J]. Computer Systems Science Engineering, 2017, 32(6): 507-13. |
| [10] |
戈一航, 杨光永, 徐天奇, 等. 基于SSA优化PID在移动机器人路径跟踪中的研究[J]. 国外电子测量技术, 2021, 40(9): 64–69. GE Yihang, YANG Guangyonog, XU Tianqi, et al. Research on SSA-based optimized PID for mobile robot path tracking[J]. Foreign electronic measurement technology, 2021, 40(9): 64–69 |
| [11] |
张品, 李长勇. 基于改进模糊PID的全向搬运机器人路径跟踪控制研究[J]. 食品与机械, 2021, 37(6): 114-9+90. ZHANG Pin, LI Changyong. Research on path tracking control of omnidirectional handling robots based on improved fuzzy PID[J]. Food and Machinery, 2021, 37(6): 114-9+90. |
| [12] |
祝亢, 黄珍, 王绪明. 基于深度强化学习的智能船舶航迹跟踪控制[J]. 中国舰船研究, 2021, 16(1): 105-13. ZHU Kang, HUANG Zhen, WANG Xuming. Intelligent ship track tracking control based on deep reinforcement learning[J]. China Ship Research, 2021, 16(1): 105-13. |
| [13] |
FOSSEN T I. A nonlinear unified state-space model for ship maneuvering and control in a seaway[J]. International Journal of Bifurcation Chaos, 2005, 15(09): 2717-2746. DOI:10.1142/S0218127405013691 |
| [14] |
FOSSEN T I. Handbook of marine craft hydrodynamic and motion control[Z]. 2011: 133–183
|
| [15] |
ABDOLLAHZADEH B, GHAREHCHOPOGH F S, MIRJALILI S. African vultures optimization algorithm: a new nature-inspired metaheuristic algorithm for global optimization problems[J]. Computers & Industrial Engineering, 2021: 1.
|
| [16] |
CHENG J, YI J, ZHAO D. Design of a sliding mode controller for trajectory tracking problem of marine vessels[J]. Control Theory Applications Iet, 2007, 1(1): 233-237. DOI:10.1049/iet-cta:20050357 |
| [17] |
冯辉, 胡胜, 余文曌, 等. 基于有限时间引导律的欠驱智能船舶循迹控制[J]. 北京航空航天大学学报, 2021: 1–11. FENG Hui, HU Sheng, YU Wenzhao, et al. Underdriven intelligent ship tracking control based on finite-time bootstrap law[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021: 1–11. |
 2024, Vol. 46
2024, Vol. 46
