随着海洋中油气资源开发规模的不断扩大,采用何种最经济快捷的方法将大量的油气资源从海上运输到陆地上成为重要的研究热点之一[1]。目前最主要的海洋油气运输依旧是远洋运输[2]。如果船舶上的液舱没有全部满载,船舶在航行过程中一旦出现倾斜现象,船舶舱内的液体会出现流动现象,对船舶的稳定性产生一定的影响[3]。因此在船舶的设计以及运动阶段均需要考虑船舶液舱内的液体流动和船体运动的耦合作用[4]。基于势流理论,对液货船船体以及液舱的晃荡运动进行分析,这有助于船舶稳定性设计方法的快速发展。
1 势流理论 1.1 船舶水动力模型本文研究的船舶运动参考坐标系为o-xyz坐标系,假定微幅规则波作为入射波,速度势计算式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\phi _I}\left( {p,t} \right) = {Re} \left( {{\varphi _I}\left( p \right){e^{ - i{\omega _e}t}}} \right)} ,\\ {{\varphi _I}\left( p \right) = \displaystyle\frac{{ig\zeta }}{\omega }{e^{kz}}{e^{ - ik\left( {x\cos \beta - y\sin \beta } \right)}}} 。\end{array}} \right.$ | (1) |
波数k和波浪圆率ω之间满足散色关系,如下式:
| $ v = \frac{{{\omega ^2}}}{g} = k\tanh \left( {kH} \right)。$ | (2) |
阻尼系数的计算式为:
| $ {\mu _{ij}}\left( \omega \right) + \frac{i}{j}{\lambda _{ij}}\left( \omega \right) = \rho \iint\limits_{{S_0}} {{\phi _j}\frac{{\partial {\phi _i}}}{{\partial n}}{\mathrm{d}}s}\text{。} $ | (3) |
基于Haskind理论,将Froude-Krylov力和饶射力进行合并处理,则在没有航速的情况下,船体受到的波浪力计算式为:
| $ {f_{\omega j}} = \rho i{\omega _0}\iint\limits_{{S_0}} {\left( {{\phi _I}\frac{{\partial {\phi _j}}}{{\partial n}} - {\phi _j}\frac{{\partial {\phi _I}}}{{\partial n}}} \right){\mathrm{d}}s}\text{。} $ | (4) |
船体受到波浪的影响而处于摇荡状态的时候,并且操纵力、推进力以及粘性力都不考虑,只考虑影响到摇荡运动的流体作用力,那么船体受到的外力以及外力矩的计算式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_i} = \displaystyle\iint\limits_{{S_0}} {p{n_i}{\mathrm{d}}s}},\\ {{M_i} = \displaystyle\iint\limits_{{S_0}} {p{n_{i + 3}}{\mathrm{d}}s}} 。\end{array}} \right. $ | (5) |
附加质量的表达式为:
| $ f_{ij}^R = - {\mu _{ij}}{\ddot x_j} - {\lambda _{ij}}{\dot x_j}\text{。} $ | (6) |
静恢复力是由于船舶摇荡过程中偏离平衡位置而产生的,如下式:
| $ f_{ij}^S = - {C_{ij}}{x_j}。$ | (7) |
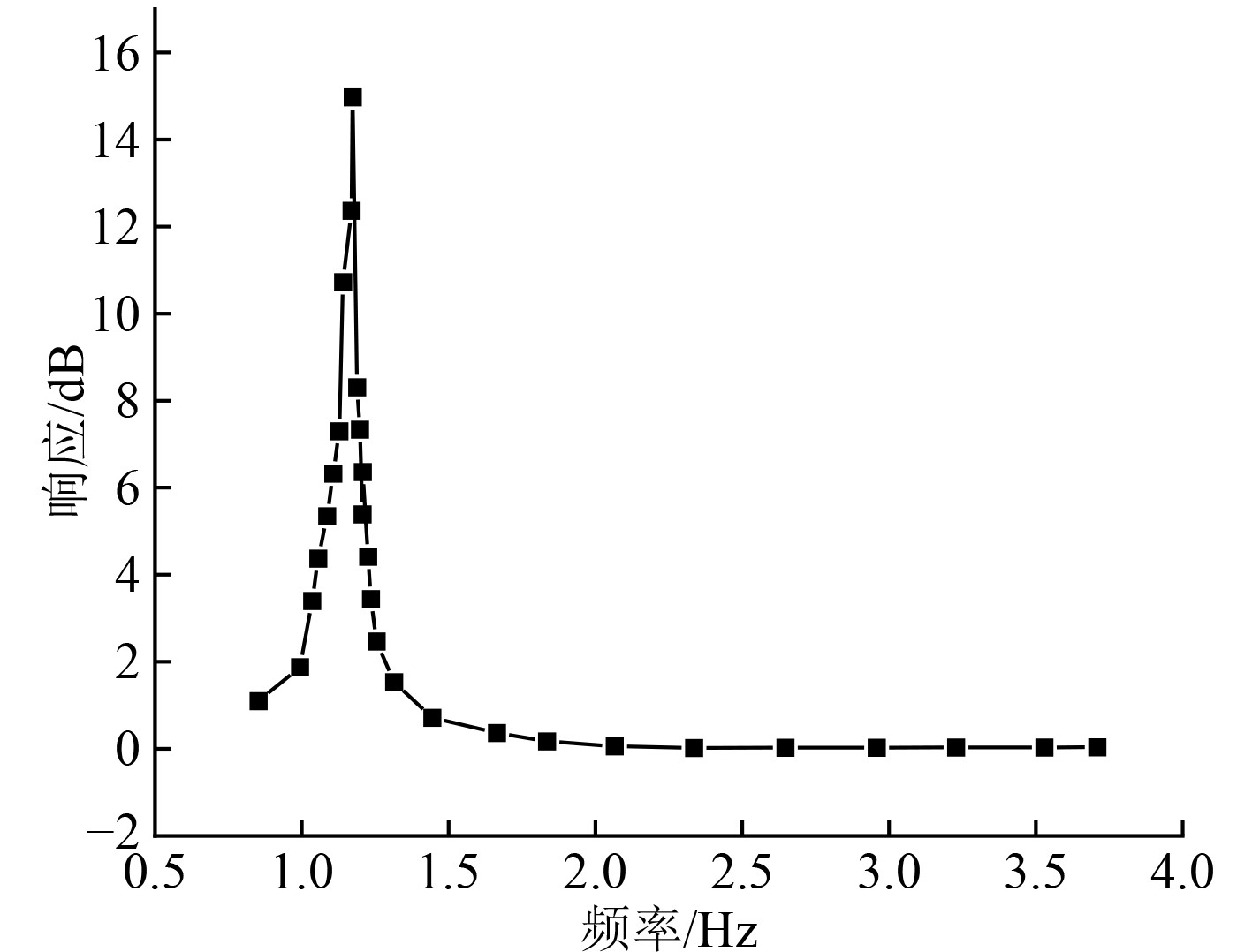
船舶在海面上航行过程中,基于频域的运动方程可以用式(8)表示。频域响应曲线如图1所示。可以发现,船舶最大的响应出现在频率为1.3 Hz附近。
|
图 1 频域响应曲线 Fig. 1 Frequency domain response curve |
| $ \left( {{m_{ij}} + {\mu _{ij}}} \right){\ddot x_j} + {\lambda _{ij}}{x_j} = f_{\omega i}^k + f_{\omega i}^{\mathrm{d}}。$ | (8) |
通过辐射势,获得船舶辐射力的表达式为:
| $ F_{ij}^R\left( t \right) = \left\{ {{\omega ^2}{\mu _{ij}}\left( \omega \right) - i\omega {\lambda _{ij}}\left( \omega \right)} \right\}。$ | (9) |
式中:μij(ω)和λij(ω)均为频域水动力系数,其时域中的表达式为:
| $ {\mu _{ij}}\left( \omega \right) = {\mu _{ij}} - \frac{1}{\omega }\int_0^t {{K_{ij}}\left( \tau \right)\sin \left( {\omega \tau } \right){\mathrm{d}}\tau } \text{,} $ | (10) |
| $ {\lambda _{ij}}\left( \omega \right) = \int_0^t {{K_{ij}}\left( \tau \right)\cos \left( {\omega \tau } \right){\mathrm{d}}\tau } 。$ | (11) |
式中,Kij(τ)为时域下的时延函数,其计算式为:
| $ {K_{ij}}\left( \tau \right) = \frac{2}{{\text{π}} }\int_0^\infty {{B_{ij}}\left( \omega \right)\cos \left( {\omega \tau } \right){\mathrm{d}}\omega } \text{。} $ | (12) |
时域中波浪力的卷积关系计算式为:
| $ {F_W} = \int_0^t {{g_1}\left( \tau \right)\zeta \left( {t - \tau } \right){\mathrm{d}}\tau } 。$ | (13) |
式中,g1(τ)为波浪力脉冲响应函数,计算式为:
| $ {g_1}\left( \tau \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {F\left( \omega \right){e^{i\omega t}}{\mathrm{d}}\omega } 。$ | (14) |
将时域下的水动力参数代入到式(8),则能够获得船舶在时域下的运动方程,如下式:
| $ {F_{iW}}\left( t \right) = \left( {{m_{ij}} + {\mu _{ij}}} \right){\ddot x_j}\left( t \right) + \int_0^t {{K_{ij}}\left( {t - \pi } \right){{\dot x}_j}\left( \tau \right){\mathrm{d}}\tau + {C_{ij}}{x_j}\left( t \right)} 。$ | (15) |
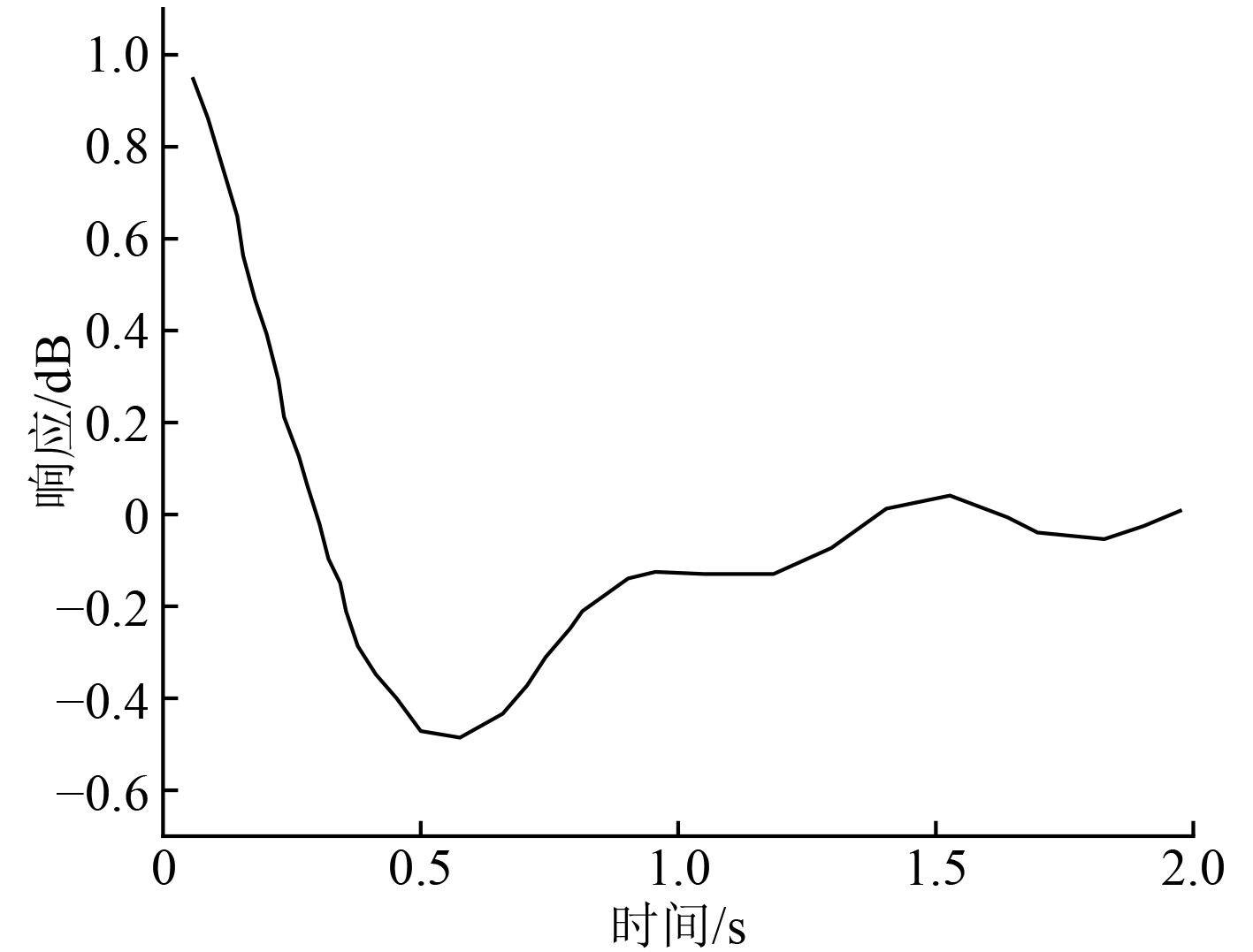
得到的时域下的响应曲线如图2所示,可以看出,时域下的船舶垂荡运动响应先降低,然后逐渐上升。在解算时间上,本文使用的IRF法比直接时域法所消耗的时间要少得多,因此IRF法有着更高的解算效率和精度。
|
图 2 船舶垂荡运动脉冲响应曲线 Fig. 2 Pulse response curve of ship heave motion |
船舶液舱晃荡的时域模拟是研究液舱晃荡和船体耦合运动分析的基础。在解算船舶液舱晃荡和船体耦合运动的过程中,需要把晃荡力考虑进船舶的运动方程[5]。对于没有非线性现象的问题,使用边界元法对船舶液舱晃荡问题进行解算,能够得到精确的结果[6]。流体的控制方程满足下式:
| $ \frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {z^2}}} = 0\text{。} $ | (16) |
船舶在海面上航行过程中其晃荡运动存在6个自由度,因此需要满足一定的边界条件,船舶的自由表面的动力边界条件如式(17)所示,其运动边界条件如式(18)所示[7]。
| $ \frac{{\partial \phi }}{{\partial t}} + \frac{1}{2}{\left| {\nabla \phi } \right|^2} - \left\{ {\vec \Omega \times \vec r} \right\} + \frac{{d\vec V}}{{dt}} \cdot \vec r = 0\text{,} $ | (17) |
| $ {n_z}\frac{{\partial \xi }}{{\partial t}} = \frac{{\partial \phi }}{{\partial n}}。$ | (18) |
以格林定理为基础,可以获得流场中任何一点的速度势,其表达式为:
| $ \alpha \phi \left( P \right) = \frac{1}{{4\pi }}\mathop{{\int \int}\mkern-21mu \bigcirc}\limits_S {\frac{{\partial \phi \left( Q \right)}}{{\partial n}}} G\left( {P,Q} \right) - \frac{{\partial G\left( {P,Q} \right)}}{{\partial n}}\phi \left( Q \right){\mathrm{d}}s\text{。} $ | (19) |
式中,G(P,Q)为三维简单格林函数,该函数的表达式为:
| $ G\left( {P,Q} \right) = \frac{1}{{\sqrt {{{\left( {x - \xi } \right)}^2} + {{\left( {y - \eta } \right)}^2} + {{\left( {z - \zeta } \right)}^2}} }}。$ | (20) |
流体表面上不同时刻的自由面形状和质点速度的解算方法,如下式:
| $ {\phi _{t + \Delta t}} = {\phi _{t - \Delta t}} + 2\Delta t \cdot {\left. {\frac{{\partial \phi }}{{\partial t}}} \right|_t}\text{,} $ | (21) |
| $ {\xi _{t + \Delta t}} = {\xi _{t - \Delta t}} + 2\Delta t \cdot {\left. {\frac{{\partial \xi }}{{\partial t}}} \right|_t}。$ | (22) |
针对每个时间步长,解算得到每个离散点的速度势之后,以式(23)中的拉格朗日方程为基础,则可以得到离散点处的压力。
| $ \frac{P}{\rho } + gz + \frac{{\partial \phi }}{{\partial t}} + \frac{1}{2}{\left| {\nabla \phi } \right|^2} = 0。$ | (23) |
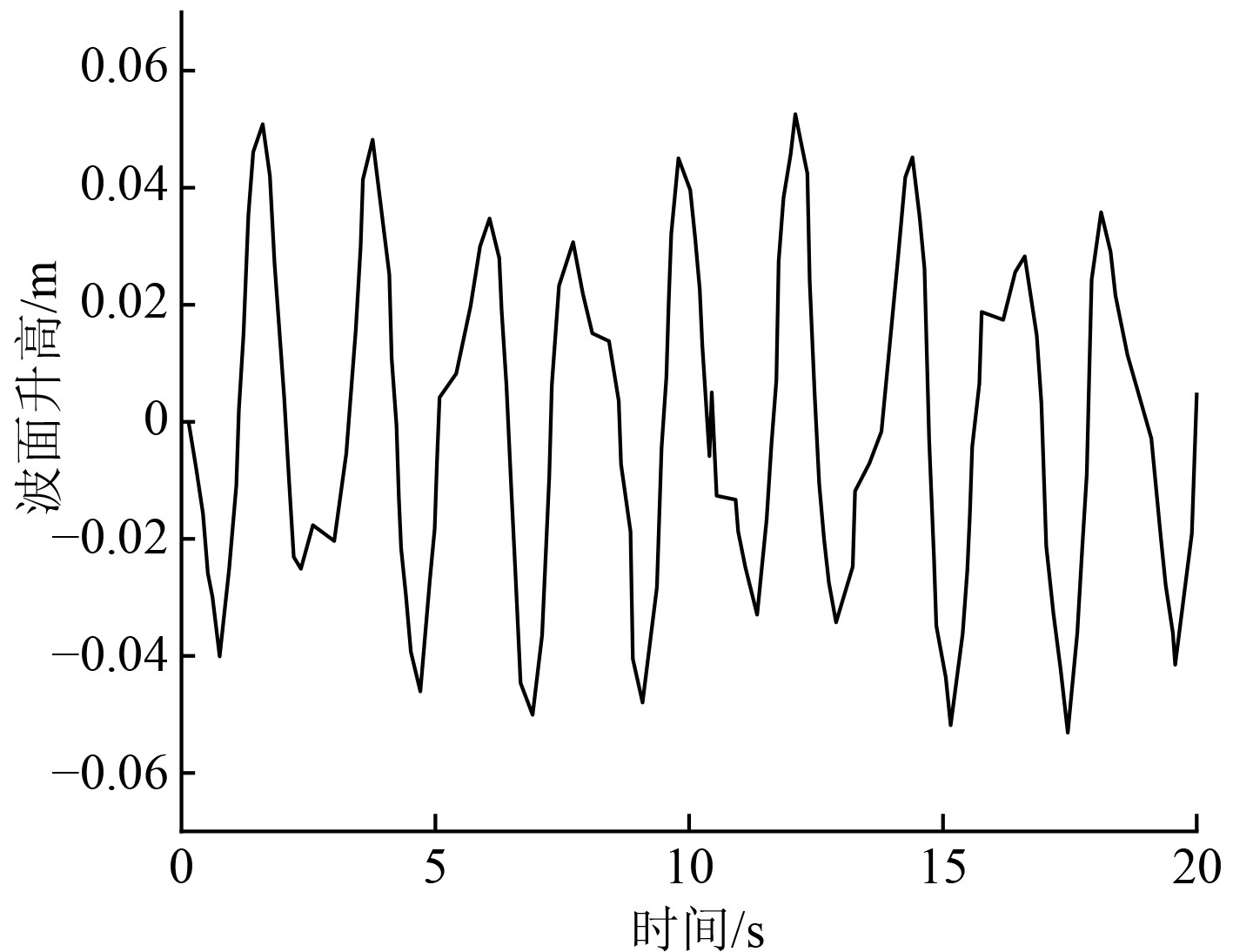
本文对1 m × 1 m × 1 m的方形船舶液舱进行自由面的波形求解,该液舱中有着深度为0.5 m的液体。仿真得到的船舶横摇情况下船舶液舱自由面中心处的波面升高变化曲线,如图3所示。可以看出,横摇状态下船舶液舱自由面的波面会随着海面波浪的变化而上下震荡。
|
图 3 船舶横摇情况下波面升高变化曲线 Fig. 3 Curve of wave surface elevation under ship roll |
液舱模型受到的横荡运动激励如下式:
| $ x = 0.015\sin \left( {2.475t} \right)。$ | (24) |
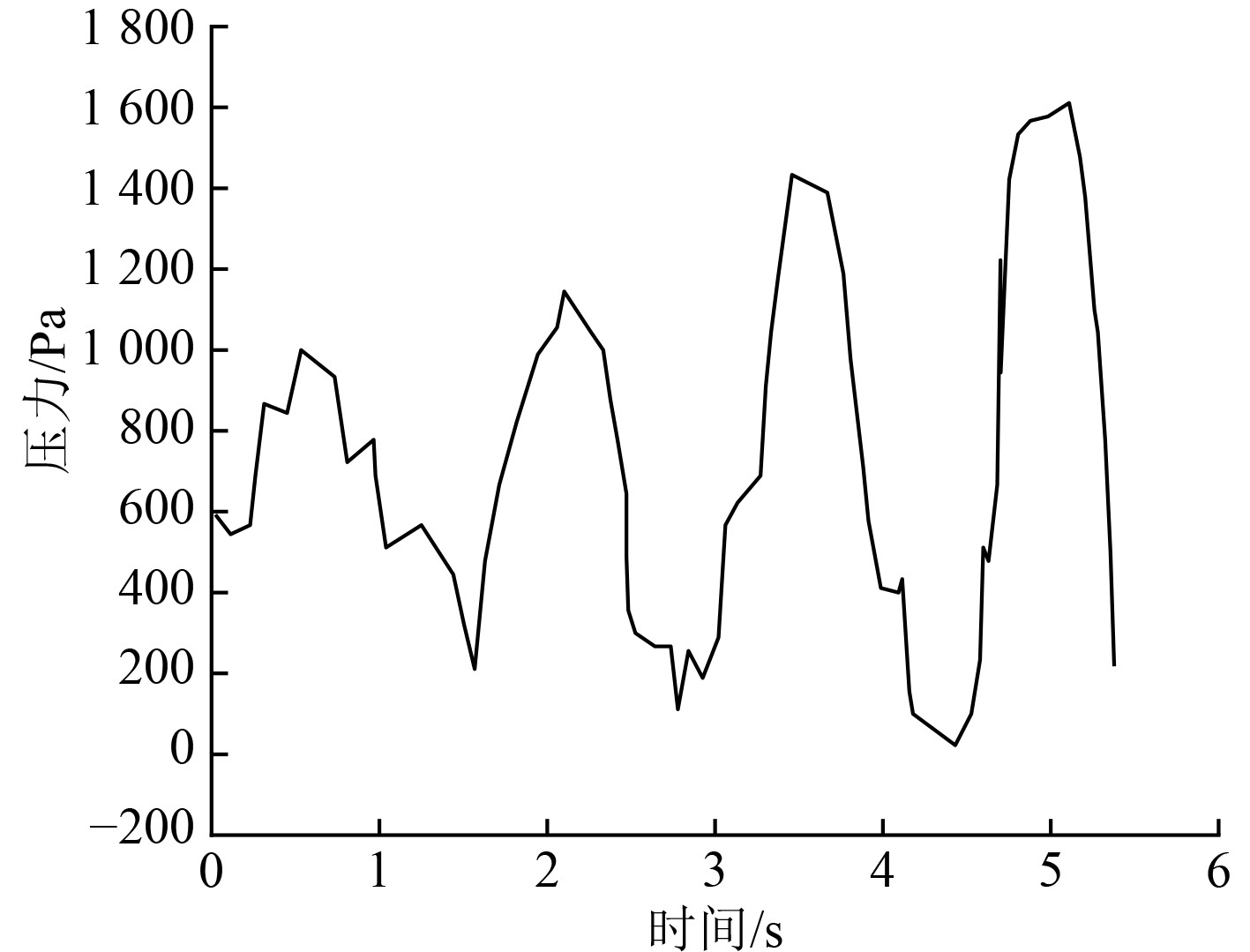
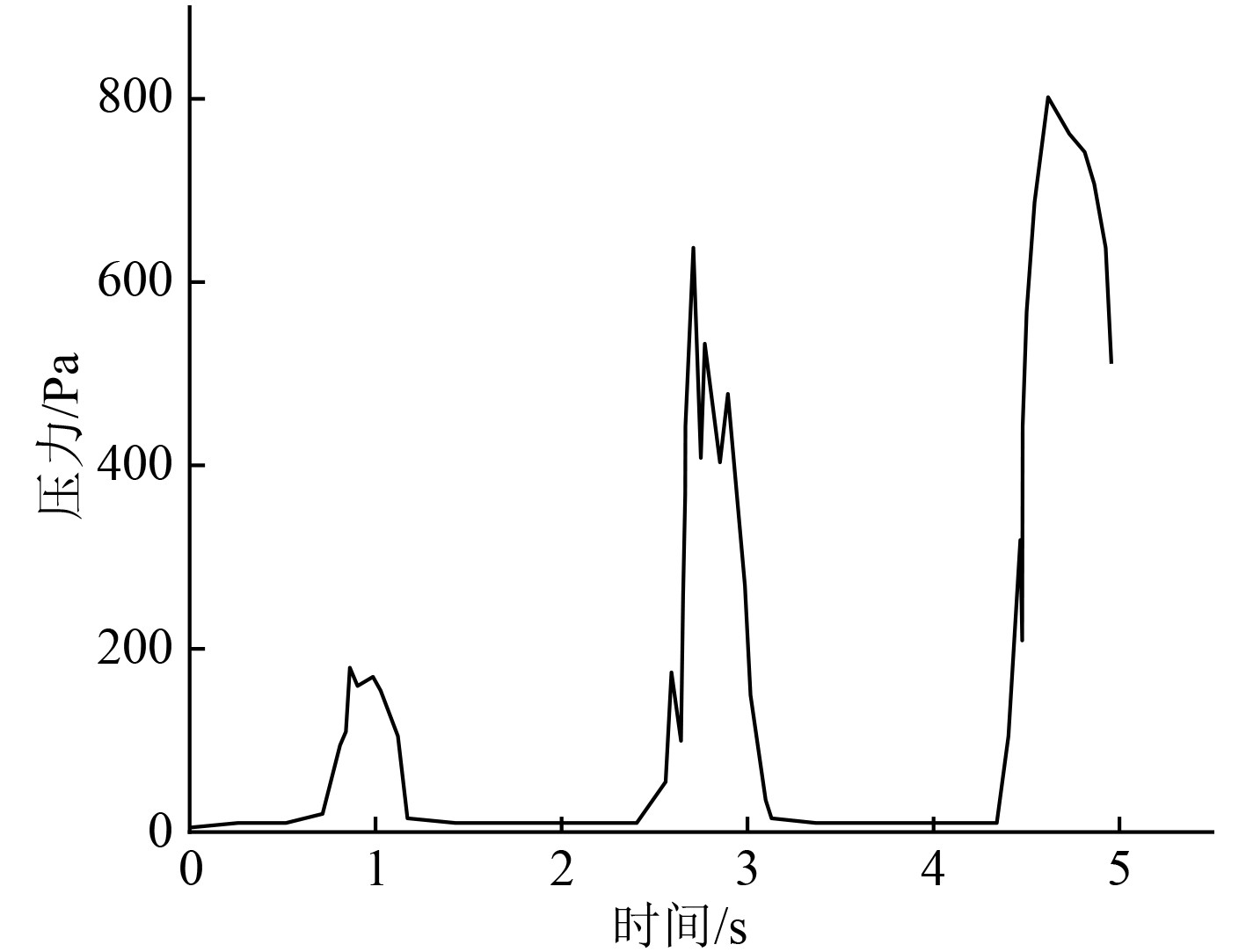
标记船舶液舱模型壁面上的P点和M点,P点距离底面的距离为0.3 m,M点距离底面的距离为0.426 m。仿真得到的船舶液舱模型壁面上的P点和M点处的压力变化曲线分别如图4和图5所示。由图4可以看出,随着时间的推移,船舶液舱模型壁面上的P点受到的压力以500 Pa为中心上下波动。图5显示船舶液舱模型壁面上的M点在1 s、2.8 s以及4.8 s左右受到的压力会突然增大,其余时间受到的压力基本上等于0。
|
图 4 P点压力变化曲线 Fig. 4 P-point pressure change curve |
|
图 5 M点压力变化曲线 Fig. 5 M-point pressure change curve |
采用方形液舱模型,并且与实际的船舶的尺寸比为1∶55,其尺寸如表1所示。
|
|
表 1 船舶模型尺寸 Tab.1 Ship model dimensions |
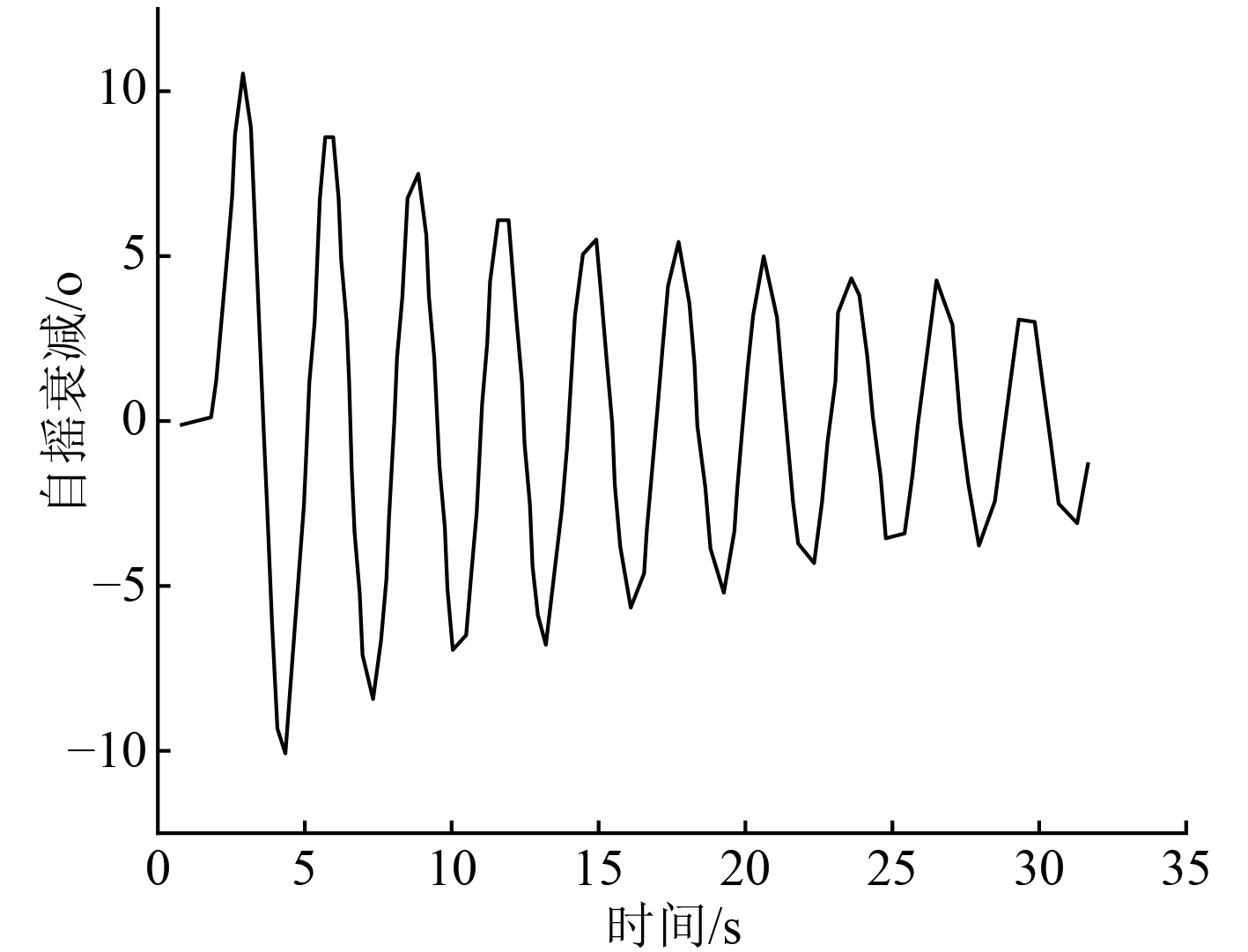
在船舶运动和液舱晃动的耦合运动方程中,船舶的非线性横摇阻尼系数可以船舶模型的自摇衰减曲线为基础,利用最小二乘法获得。自摇衰减曲线如图6所示,可知,船舶的自摇衰减曲线的震荡幅度越来越小。
|
图 6 船舶自摇衰减曲线 Fig. 6 Ship rolling attenuation curve |
以平均幅值ϕam作为横坐标,以幅值差Δϕ作为纵坐标,可以获得船舶的横摇曲线,其表达式为:
| $ \Delta \phi = a{\phi _{am}} + b\phi _{am}^2。$ | (25) |
阻尼力矩和角速度的关系式为:
| $ M\left( {\dot \phi } \right) = - 2N\dot \phi - W\left| {\dot \phi } \right|\dot \phi 。$ | (26) |
式(25)中的系数a、b和式(26)中的系数N、W之间的关系可以用式(27)和式(28)来表示。
| $ a = \frac{{{T_\phi }}}{{2{{I'}_{xx}}}}N\text{,} $ | (27) |
| $ b = \frac{{4W}}{{3{{I'}_{xx}}}}。$ | (28) |
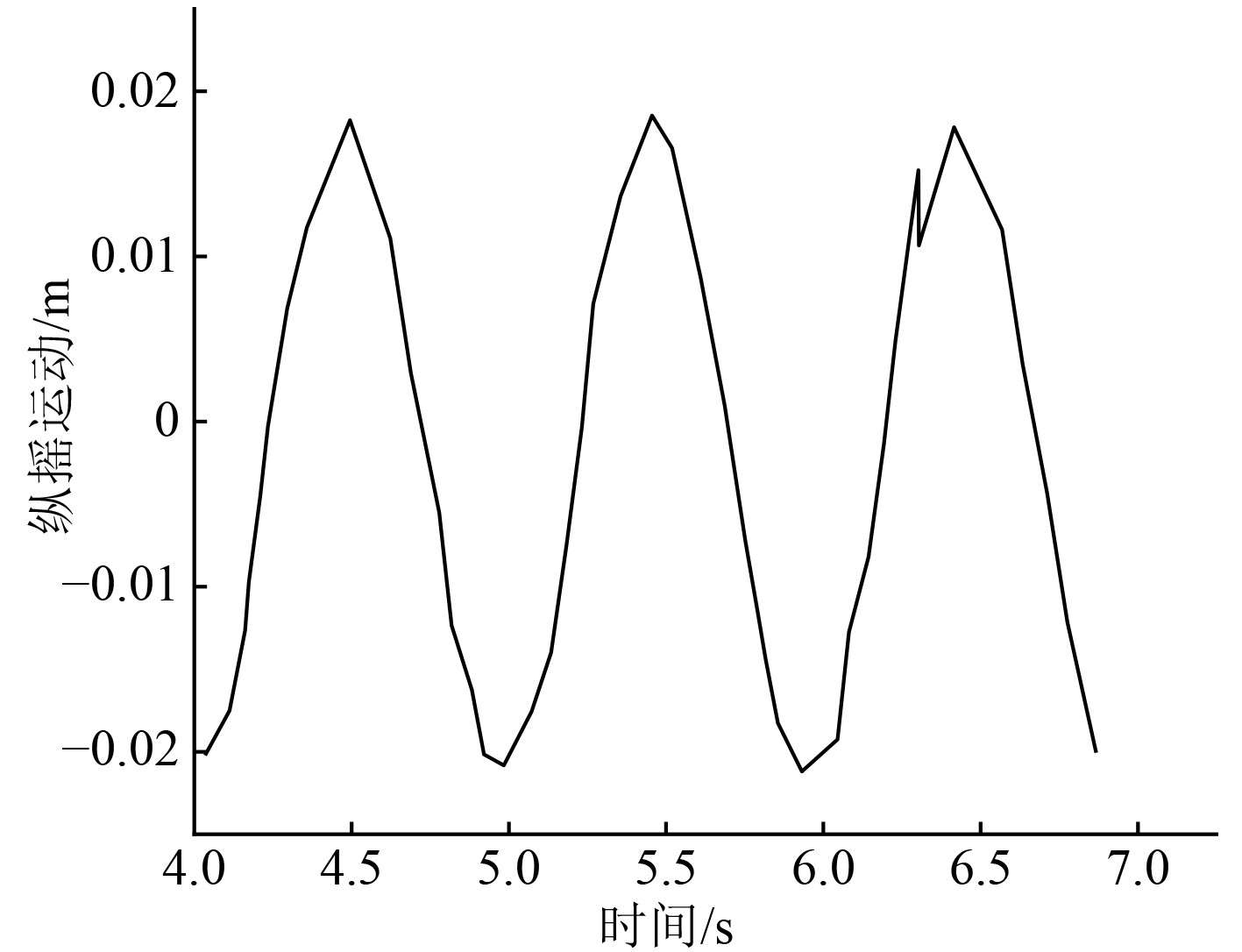
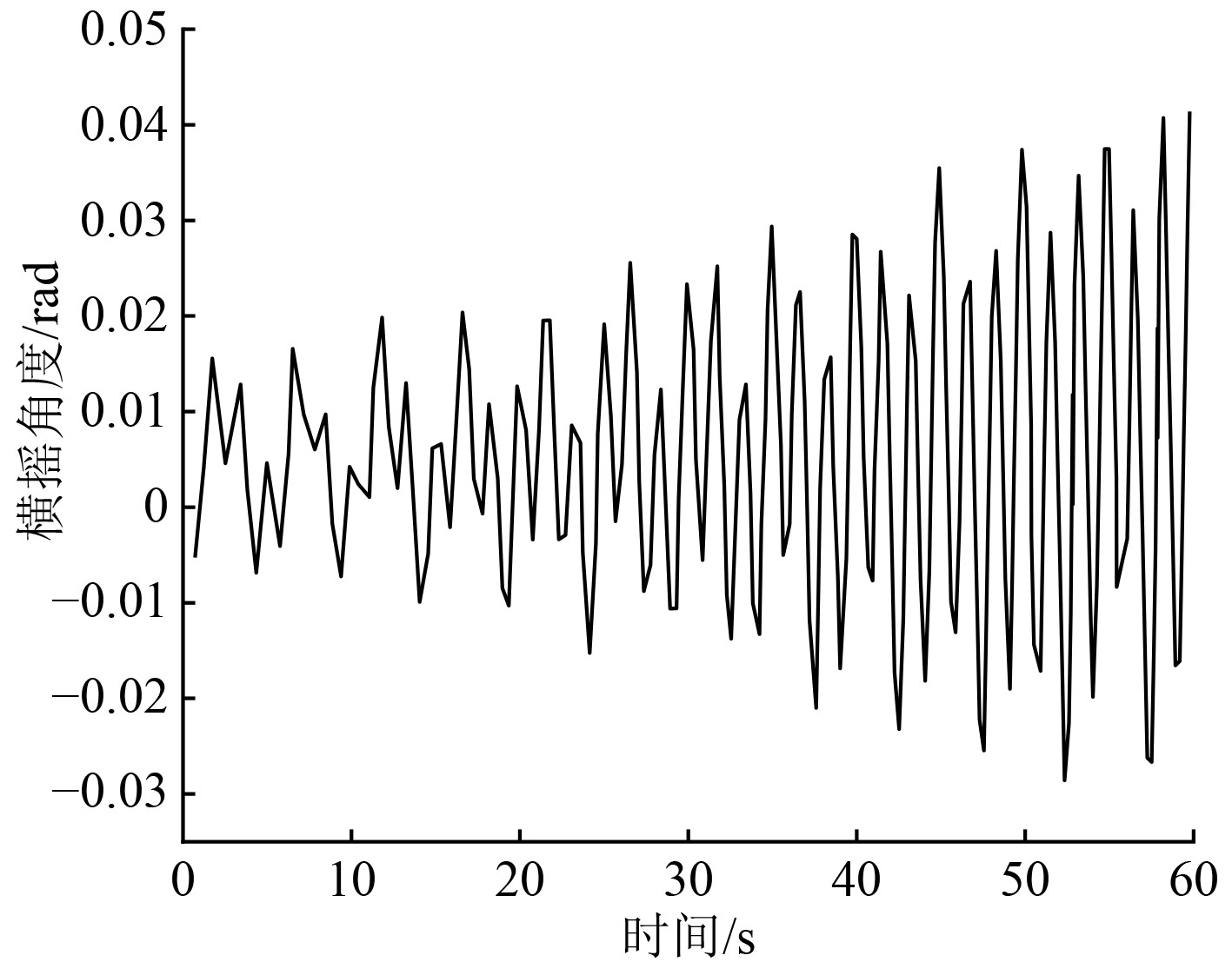
本文对船舶模型加载了横浪和迎浪2种工况下的负载激励,并进行船舶运动和液舱晃荡的耦合运动时域解算分析。图7所示为船舶纵摇运动曲线,可知,船舶纵摇围绕0位置为中心上下波动。图8为的船舶横摇运动曲线,可以看出,随着时间的推移,船舶的横摇运动波幅值越来越大,并且当波动的幅值达到一定的数值之后就无法继续解算了。
|
图 7 迎浪工况下船舶纵摇运动曲线 Fig. 7 Ship pitch motion curve under wave conditions |
|
图 8 横浪情况下船舶横摇运动曲线 Fig. 8 Ship roll motion curve under transverse waves |
随着海洋中油气资源开采力度的加强以及各类液货船舶的广泛应用,船舶上液舱对船舶航行的影响逐渐得到人们的重视。载有液货的船舶在海面上航行的过程中,由于受到海面风浪的影响,船舶上液舱在运动过程中会带动其内部装载的液体也产生晃荡现象,并且船舶上液舱产生的晃荡力会对船体产生一定的影响,严重时会影响到船体的航行姿态。本文以势流理论为基础,研究了液货船船体与液舱晃荡运动,这对我国液货船舶的发展有着积极的促进作用。
| [1] |
骆阳, 朱仁庆, 刘永涛. FPSO与运输船旁靠时液舱晃荡与船舶运动耦合效应分析[J]. 江苏科技大学学报, 2015(29): 307-316. |
| [2] |
王庆丰, 焦经纬, 徐刚, 等. FSRU船舶运动与液舱晃荡的耦合分析[J]. 江苏科技大学学报, 2017(31): 684-688. |
| [3] |
洪亮, 朱仁传, 缪国平, 等. 波浪中船体与液舱晃荡耦合运动的时域数值计算[J]. 哈尔滨工程大学学报, 2012(33): 635-641+647. |
| [4] |
韩旭亮, 谢彬, 朱小松, 等. 大型FLNG液舱晃荡和船体耦合运动研究现状及展望[J]. 中国海上油气, 2017(29): 116-123. |
| [5] |
吴江涛, 陈作钢. 横浪中液舱晃荡与养殖工船耦合运动[J]. 船舶工程, 2021(43): 17-23+47. |
| [6] |
薛米安, 邢建建, 陈亦超, 等. 基于振动台实验的液体晃荡激励参数敏感性研究[J]. 大连理工大学学报, 2019(59): 162-171. |
| [7] |
黄硕, 段文洋, 马庆位, 等. 液舱晃荡及其与船舶耦合运动问题的研究进展[J]. 船舶力学, 2013(17): 1209−1220.
|
 2024, Vol. 46
2024, Vol. 46
