2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 中国船舶及海洋工程设计研究院,上海 200011
2. Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai Jiaotong University, Shanghai 200240, China;
3. Marine Design and Research Institute of China, Shanghai 200011, China
部分船舶如油船、散货船及一些军船由于功能的需求一般采用短上层建筑,短上层建筑几乎不参与船体总纵强度,当短上层建筑船舶发生中拱和中垂弯曲时,上层建筑受到剪切效应影响很大,同时由于短上层建筑和主船体之间结构连接较为复杂,导致力的传递受到影响,其正应力分布规律与一般丰满型上层建筑相比有很大不同,传统船体梁理论不适用于短上层建筑的应力水平评估。
1947年,为研究大型客船上层建筑接二连三的裂缝损坏事故,美国船舶结构委员会通过“威尔逊总统”号实船试验[1]推动了船舶上层建筑理论的进一步探讨研究,1953年,该委员会模型试验得出了不同长度上层建筑下中间横剖面的正应力,试验结果认为正应力呈折线分布[2]。Crawford[3]于1950年提出经典的“双梁理论”,将主船体和上层建筑分离为两根梁,忽略上层建筑中部受到的剪切迟滞影响,对双梁的弯曲变形进行了基础研究。Bleich[4]对上层建筑正应力分布进行了计算,同时对主船体和上层建筑发生弯曲时的弯曲曲率进行了计算,对二者曲率不一致现象进行了详细讨论。1954年,斯曼斯基[5]基于双梁理论,对上层建筑端部和短上层建筑的纵向正应力分布规律进行研究,认为短上层建筑正应力分布符合指数近似公式规律。库尔庙莫夫[6]将短上层建筑的侧壁和顶板视为长折角板条,两长边受到对称的切应力,由弹性力学公式求解可知上层建筑正应力分布符合二次抛物线规律。国内上层建筑强度研究大多起步于有限元计算方法诞生后,关注重点主要是长上层建筑参与总纵强度的问题以及强力上层建筑的设计方法。陈倩等[7]基于有限元方法,对上层建筑参与总纵强度的有效度进行了分析和讨论,并依据有限元计算结果对双梁理论计算公式进行了修正。王西典[8]基于双梁理论以有效度计入强力上层建筑设计,提出了强力上层建筑设计基本流程。2017年,严卫祥等[9]综合分析了不同船型的长上层建筑参与船体总纵强度的有效度,在此基础上建立了主船体和上层建筑的正应力计算理论方法,理论计算结果与有限元计算结果相当符合。于滨等[10]对航母岛式上层建筑的总强度计算方法进行探究,结合有限元计算方法和船体总强度理论提出新的岛式上层建筑总强度计算方法以适用航母等特殊船型的上层建筑。杨斌等[11]以内河邮轮为研究对象,采用简单梁理论、双梁理论和有限元方法计算邮轮纵向应力,提出修正双梁理论公式来评估邮轮的正应力分布规律。
对于丰满长上层建筑船型,国内外学者已经有了较多研究,短上层建筑研究则较为缺少,对短上层建筑的关注点仅限于总强度而忽略了其自身的强度计算,研究短上建的应力分布规律对于其设计十分关键。本文借助有限元法,通过分别改变某油船短上层建筑长度、高度以及其在船体的位置,对比明确了影响短上层建筑正应力分布的最主要因素,进一步在有限元结果和现有理论公式基础上,采用指数函数模型对短上层建筑正应力进行拟合,得出了短上层建筑正应力沿高度分布的计算公式。本文提出的公式可用于设计初期对舰船、油船等拥有较短上层建筑的船舶上建进行正应力估算,以满足结构强度设计要求。
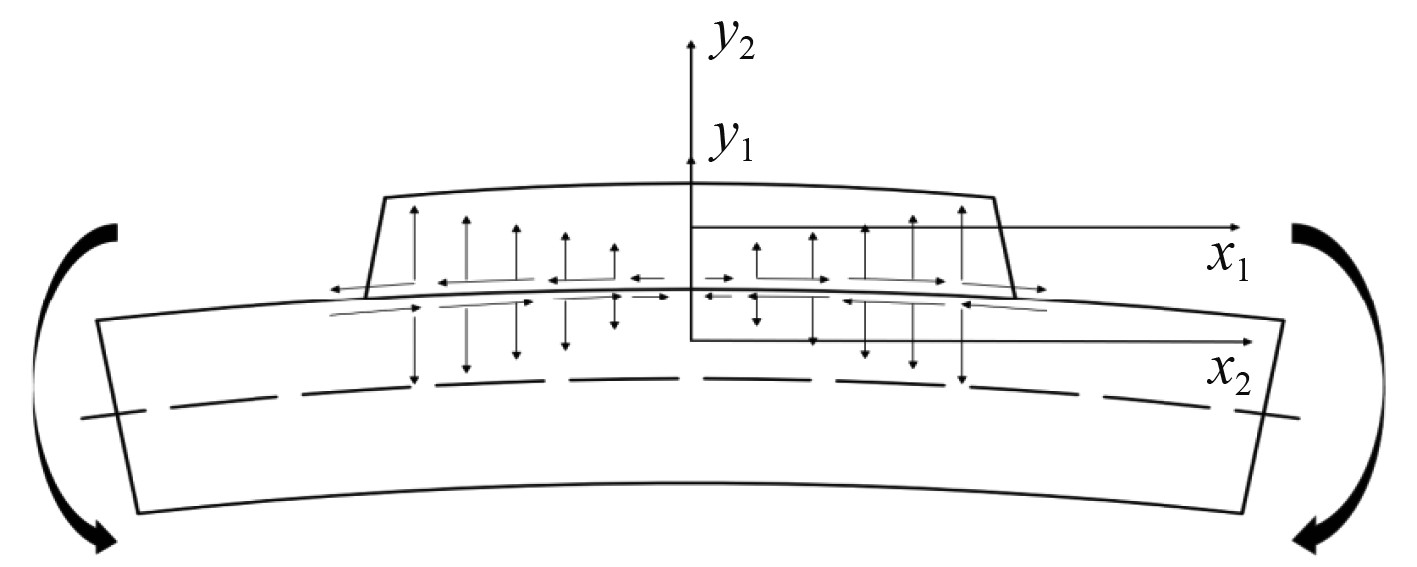
1 船舶上层建筑强度理论在船体发生纵向弯曲时,由于上层建筑和主船体连接方式较为复杂,它们之间力的传递也比较复杂。采用双梁理论分析时,相互作用可分解为上层建筑与主船体相交线处的水平剪力和竖直方向的力[12],船体发生中拱弯曲时,双梁理论受力示意见图1。
|
图 1 双梁理论受力示意图 Fig. 1 Diagram of composite beam theory |
双梁理论将整个船体视为2个互为弹性支座的梁[13],将上层建筑和主船体取分离体后可得2根梁的弯矩方程式为:
| $ {E_1}{I_1}{v_1}^{''}\left( x \right) = \mathop \smallint \nolimits_0^x \mathop \smallint \nolimits_0^x \left( {{p_1} - p} \right){\rm{d}}x{\rm{d}}x + {e_1}\mathop \smallint \nolimits_0^x q\left( x \right){\rm{d}}x,$ | (1) |
| $ {E_2}{I_2}{v_2}^{''}\left( x \right) = \mathop \smallint \nolimits_0^x \mathop \smallint \nolimits_0^x \left( {p + {p_2}} \right){\rm{d}}x{\rm{d}}x + {e_2}\mathop \smallint \nolimits_0^x q\left( x \right){\rm{d}}x 。$ | (2) |
式中:E1、E2均为弹性模量;I1、I2分别为上层建筑和主船体的惯性矩;e1、e2分别为上层建筑和主船体剖面形心到主甲板的距离;p为上层建筑与主船体连接处垂向正应力;p1、p2分别为上层建筑和主船体垂向正应力;q(x)为上层建筑和主船体连接处切应力。
对于丰满上层建筑,一般假设中部不受剪切迟滞效应的影响[14],上层建筑和主船体的正应力分布为:
| $ {\sigma _{x1}} = - \frac{{{M_1}}}{{{I_1}}}{y_1} + \frac{{{Q_1}}}{{{F_1}}},$ | (3) |
| $ {\sigma _{x2}} = - \frac{{{M_2}}}{{{I_2}}}{y_2} + \frac{{{Q_2}}}{{{F_2}}} 。$ | (4) |
式中:σx1和σx2分别为上层建筑和主船体的正应力;M1和M2分别为上层建筑和主船体所受弯矩;y1和y2分别为上层建筑和主船体考察位置到其形心的竖直距离;Q1和Q2分别为上层建筑和主船体所受剪切力;F1和F2分别为上层建筑和主船体横剖面面积。
短上层建筑结构规模很小,上层建筑剖面距离上层建筑端部较近,剪切效应必须考虑,因此正应力不呈线性分布,且精准的应力分布很难获得,斯曼斯基推荐采用指数近似公式求解:
| $ {\sigma _{x1}} = - \frac{{{M_1}}}{{{I_1}}}{y_1} + {\sigma _1}{e^{ - \frac{{{w_s}}}{{{F_1}}}}} 。$ | (5) |
式中:ws为上层建筑考察处到主甲板的横剖面面积;σ1为主甲板正应力,根据主船体平断面公式确定。
库尔庙莫夫利用弹性力学方法将上层建筑的侧壁和甲板各自取为分离体,两边受到对称的剪切应力荷重,由弹性力学公式求解认为q(x)引起的正应力分布呈现二次抛物线分布[15],具体为:
| $ {\sigma _{x1}} = - \frac{{{M_1}}}{{{I_1}}}{y_1} - \frac{{{Q_1}}}{{{F_1}}} + \frac{{Eq}}{{2{k_1}}}[3{\left( {1 - \frac{{2{w_s}}}{{{F_1}}}} \right)^2} - 1]。$ | (6) |
式中:k1为抗剪刚性系数,按Hovgaard的假设[16],k1的计算公式如下:
| $ {k_1} = \frac{{2G{t_1}}}{{{e_1}\left( {1 - \frac{{{t_1}{e_1}}}{{{F_1}}}} \right)}}。$ | (7) |
式中:G为剪切模量;t1为上层建筑甲板厚度。
式(5)和式(6)都反映了短上层建筑正应力沿高度方向不断减小的趋势,不同之处在于斯曼斯基认为正应力的衰减速度符合指数规律,而库尔庙莫夫则认为符合二次函数规律。
2 短上层建筑(甲板室)应力分布数值求解及规律分析由于主船体加上层建筑形成的复杂弹性体结构无法基于理论精确求解,上述对于上层建筑应力的理论解答不可避免要基于各种假定,从而与实船有一定差异,影响计算精度,本文以1艘具有短上建油船为对象,通过改变短上层建筑长度、高度规模,改变短上层建筑在船体的位置,借助数值方法进行总强度分析,基于响应结果总结短上层建筑应力分布规律,同时考察规模和位置的影响。
2.1 短上层建筑(甲板室)多方案有限元模型目标油船为钢质结构,上层建筑每层高度均为2.75 m,其连续性较好,内部结构简单,每层甲板之间以支柱和横舱壁进行连接。根据《钢质海船入级规范》[17]规定:长上层建筑及短上层建筑:长度大于0.15 L,且不小于其高度6倍的上层建筑为长上层建筑,不符合长上层建筑条件的为短上层建筑。该目标船上层建筑(甲板室)符合短上层建筑(甲板室)要求。
设计不同短上层建筑方案列于表1,其中方案1~方案5用于考察短上层建筑长度的影响,方案6和方案7分别用于考察位置和高度的影响。建立7个方案船舶结构有限元模型,网格大小根据纵骨间距平均在800 mm×800 mm。油船方案6短上层建筑有限元模型如图2所示,该模型节点总计约20万个,单元约41万个。
|
|
表 1 油船不同上层建筑方案 Tab.1 Different superstructure schemes of oil tanker |

|
图 2 油船有限元模型 Fig. 2 Finite element model of oil tanker |
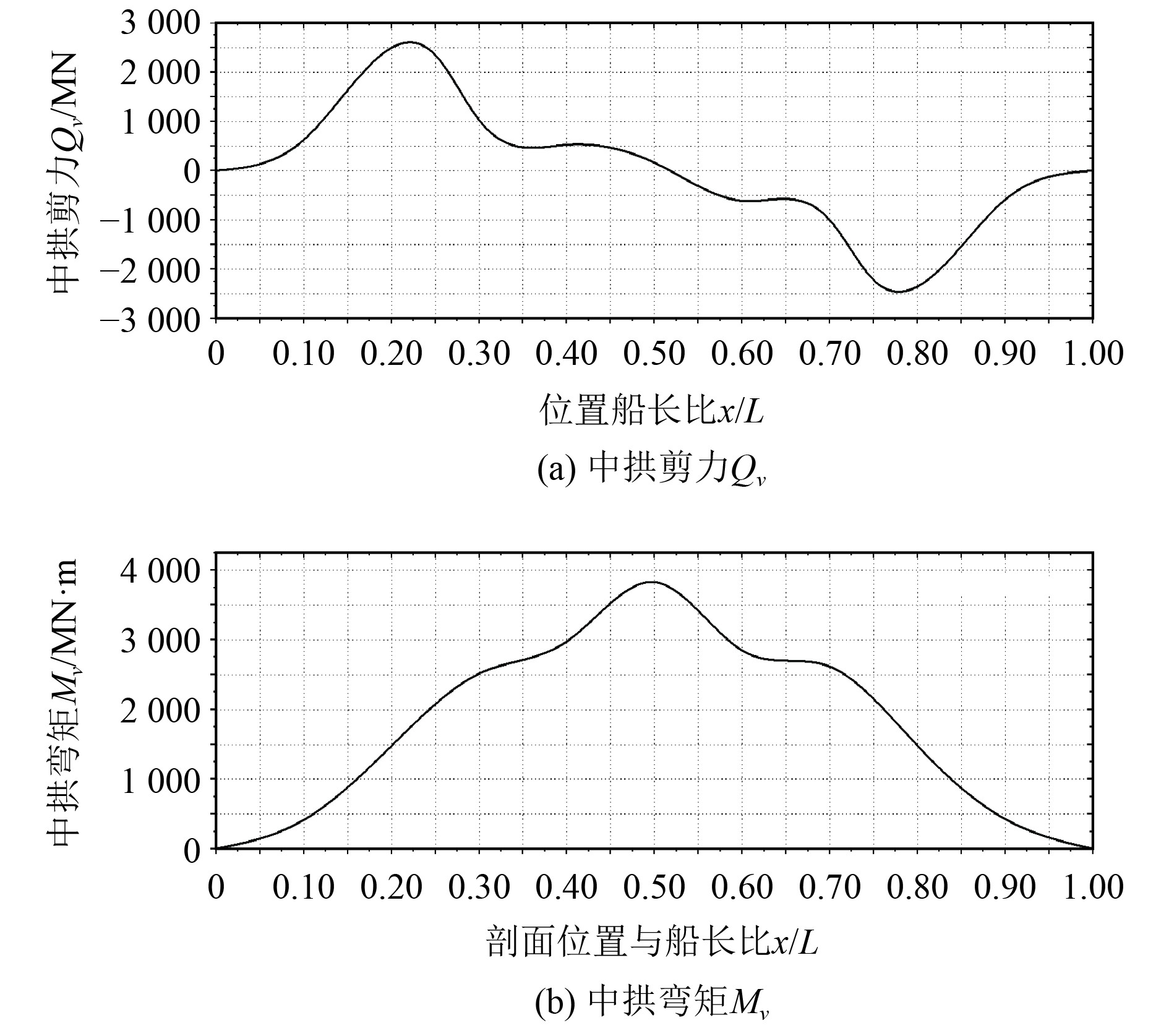
对模型施加约束条件为首垂线与底部外板的交点约束x、y、z方向的线位移,尾垂线与底部外板的交点约束y方向的线位移,尾垂线所在横剖面舷侧外板与干舷甲板的2个交点约束z方向线位移。船体梁载荷根据相关规范确定,沿船长方向分布剪力值Qv和垂向弯矩值Mv如图3所示。在船舶主船体各强框剖面施加剪流节点力[18],使该油船各剖面满足目标载荷要求。
|
图 3 油船目标载荷沿船长分布曲线 Fig. 3 Target load distribution curve of oil tanker along ship length |
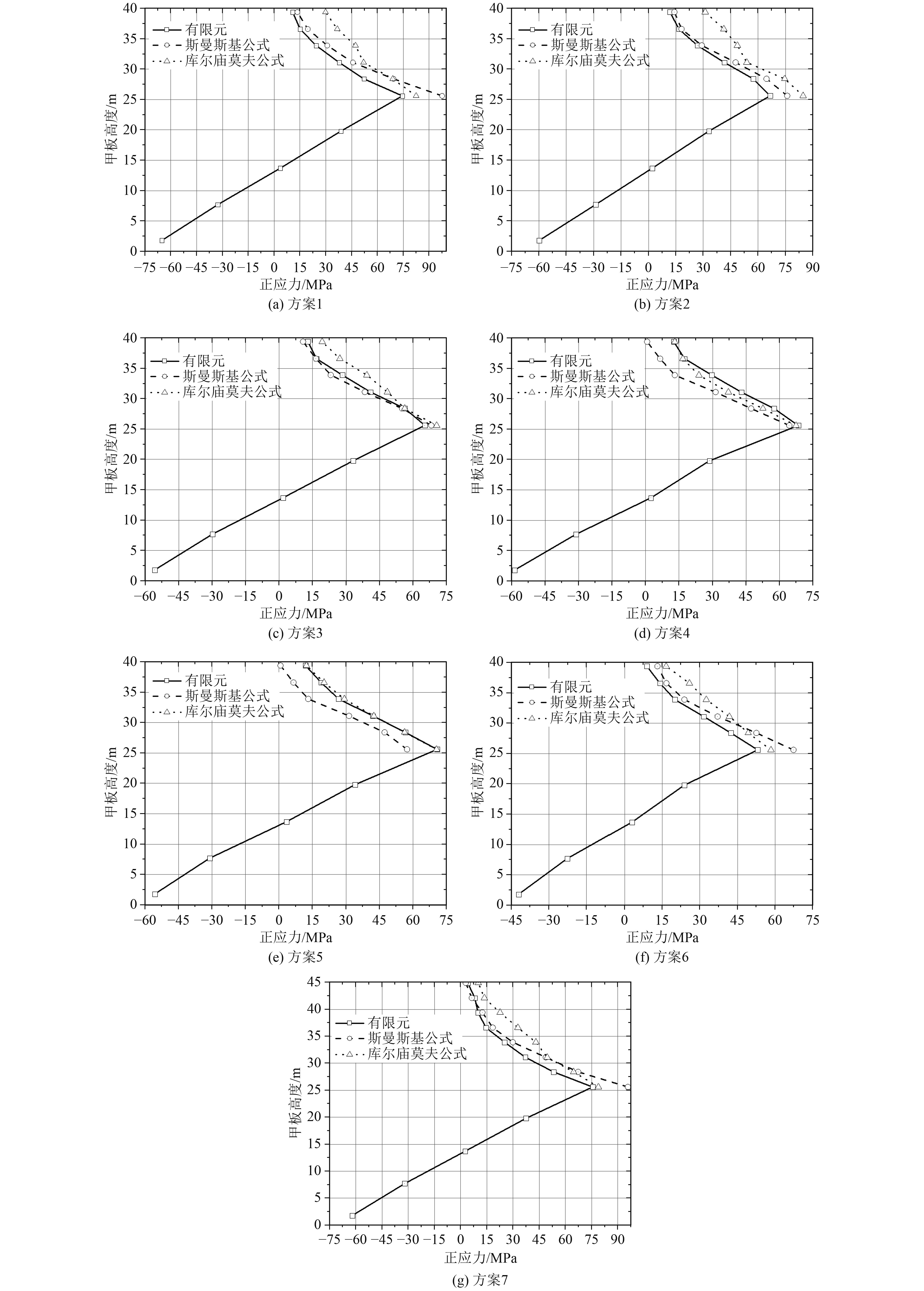
取不同方案上建甲板有限元正应力分布均匀处计算结果见表2,同时采用斯曼斯基公式(表中简记为“斯”)和库尔庙莫夫公式(表中简记为“库”)进行了正应力计算,结果见表3,其中高度为距基线高度。绘制上层建筑中处横剖面各层甲板(包括底板)的数值与理论公式正应力结果沿高度分布曲线如图4所示。
|
|
表 2 不同上层建筑方案正应力有限元计算结果(MPa) Tab.2 Calculation results of normal stress FEM of different superstructure schemes middle section(MPa) |
1)主船体各层甲板正应力有限元计算结果和平断面公式结果基本一致,随高度方向呈线性变化;上层建筑第一层甲板正应力最大,在设计时应着重考虑加强上层建筑第一层甲板和上层建筑第一层甲板与主甲板之间侧壁。
2)船舶短上层建筑正应力沿高度方向不断减小,且不呈现线性分布规律。当上层建筑长度<L/6时,即方案1、方案2和方案3不同长度的上层建筑,方案1和方案2正应力有限元计算结果与斯曼斯基公式结果比较接近,方案3则吻合非常好,此时沿高度方向正应力衰减更符合指数规律;当上层建筑长度增长至L/4左右时,即方案4和方案5,正应力有限元计算结果与库尔庙莫夫公式结果十分接近,正应力沿高度方向衰减趋势符合二次函数规律。
3)对比方案1和方案6发现,尽管由于上层建筑所在位置不同导致应力值差距较大,但二者正应力衰减规律基本一致。
|
|
表 3 不同上层建筑方案正应力理论公式计算结果(MPa) Tab.3 Calculation results of normal stress FEM of different superstructure schemes middle section(MPa) |
|
图 4 上层建筑及主船体甲板正应力沿高度分布曲线 Fig. 4 Normal stress distribution curve of superstructure and mian hull deck along height |
从不同方案计算结果分析可知,对于船舶短上层建筑正应力分布规律影响最大的因素是短上层建筑的长度,随着上层建筑长度逐渐增加,短上层建筑的正应力随高度衰减速度逐渐减缓,对比丰满上层建筑船型可以发现当上层建筑增长到一定长度后,上层建筑正应力随高度增加呈线性增长,而在二者之间理论上存在最理想上层建筑,在船体发生纵向弯曲时上层建筑不发生弯曲,正应力随高度变化几乎不变。
对于给定短上层建筑船中剖面,若其内部结构形式不变,上层建筑正应力衰减规律仅与其长度有关,上述两公式由于没有反映这个规律适用性受限。鉴于明确应力对于上层建筑结构设计十分重要,在此对短上建的正应力分布规律进行研究。为进一步分析长度对于短上层建筑船型正应力分布规律的影响,将方案1~方案5上层建筑甲板正应力进行指数曲线拟合。结合短上层建筑应力理论公式,将短上建正应力分解为线性项和指数项,拟合公式如下:
| $ {\sigma _{x1}} = - a\frac{{{M_1}}}{{{I_1}}}{y_1} + {\sigma _1}{e^{ - b{y_1}}}。$ | (8) |
式中:a、b为待定系数,根据有限元分析结果可知,随着船长增加,正应力衰减速度减缓,因此待定系数a、b可作为衰减系数反映短上层建筑正应力分布规律,适用范围为l/L在1∶9.65~1∶3.22之间的短上层建筑。
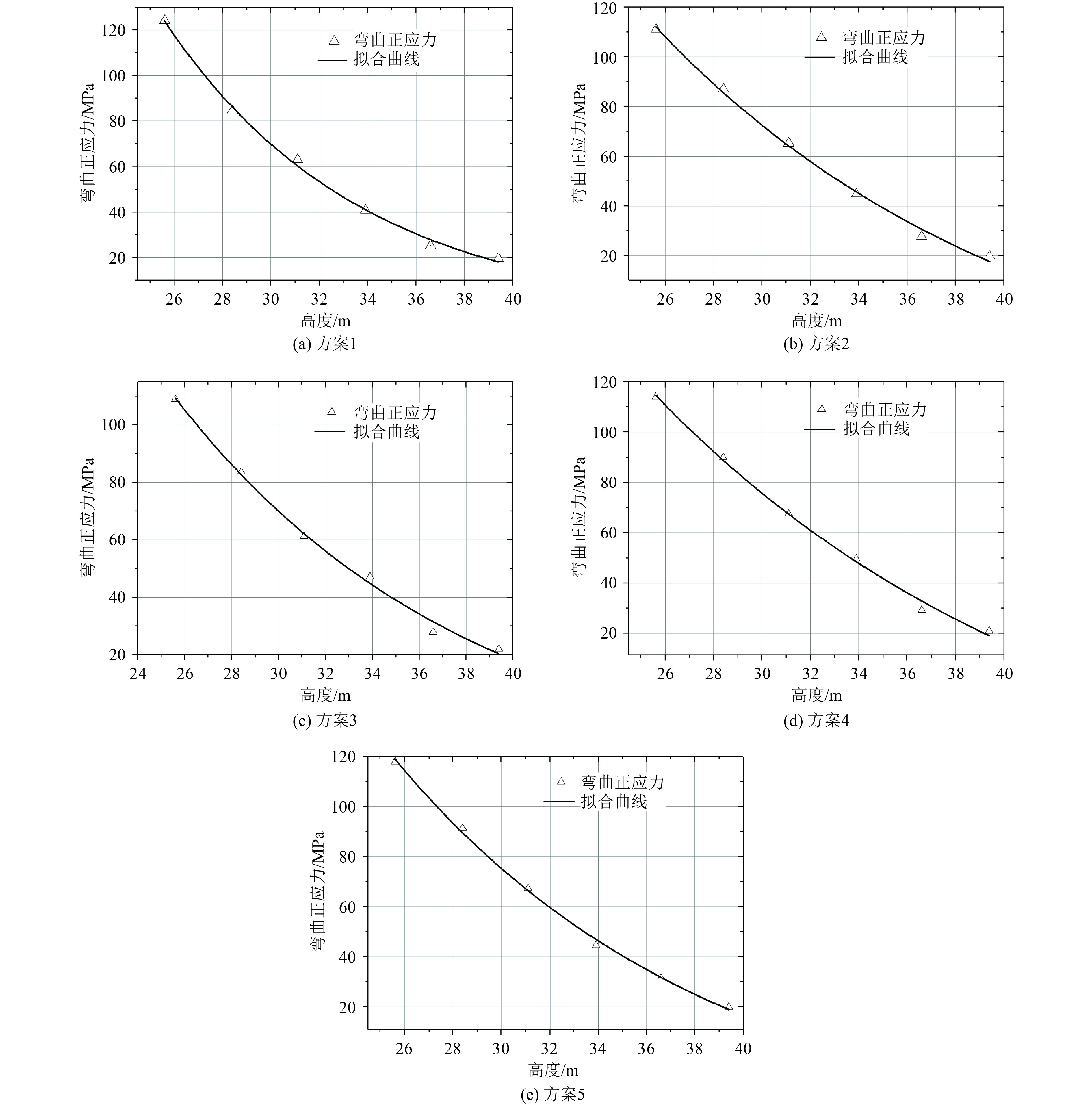
采用式(8)得到各方案下正应力分布计算值和拟合曲线见图5,获得拟合系数见表4。
|
图 5 油船短上层建筑正应力拟合曲线 Fig. 5 Short superstructure of oil tanker normal stress distribution fitting curve |
|
|
表 4 拟合公式系数值 Tab.4 The coefficient value of fit formula |
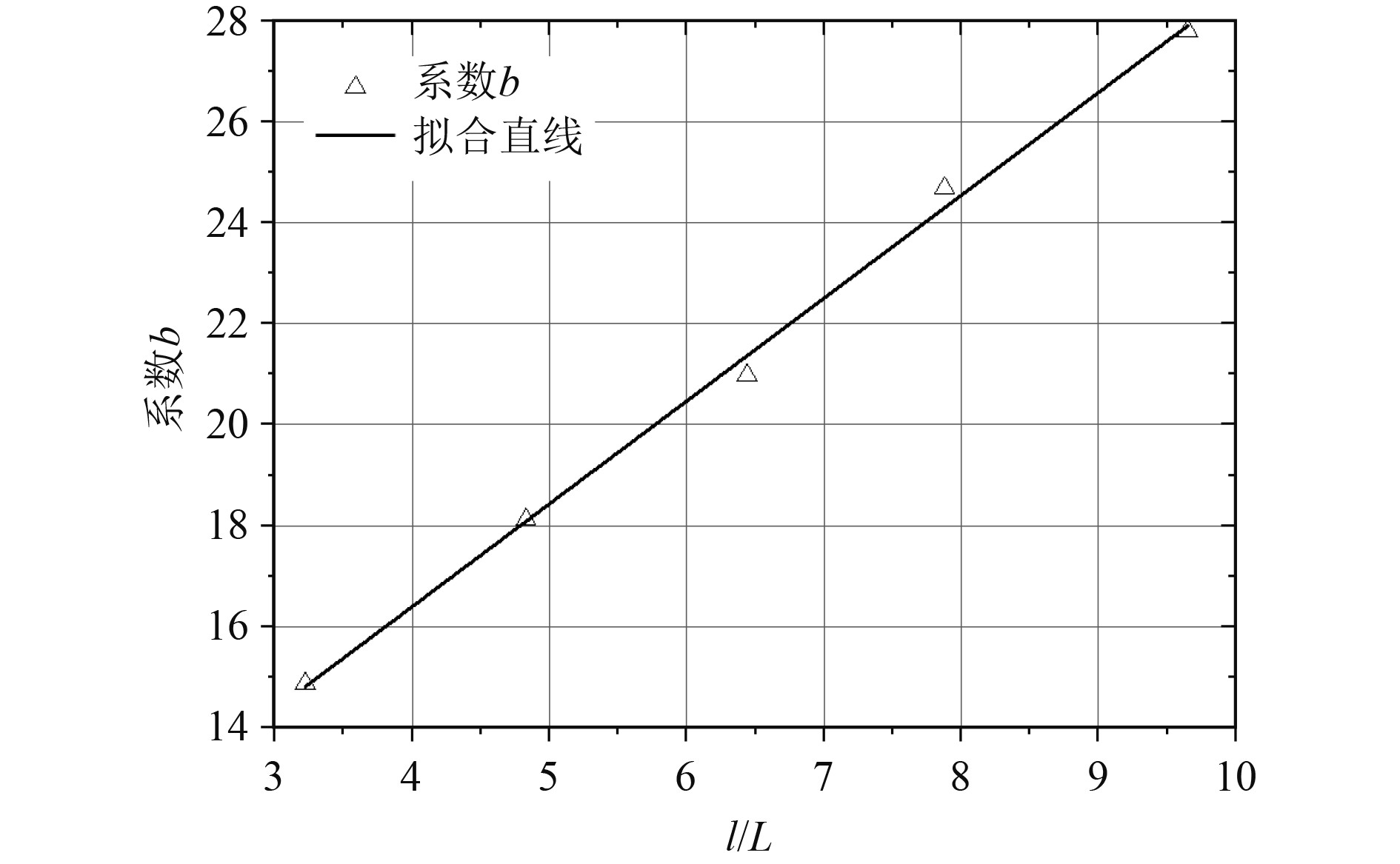
由表4可知,系数a随着短上层建筑的长度变化不大,而系数b随上层建筑长度增加不断变小,这也说明了随着短上层建筑长度增加,其正应力随高度衰减速度逐渐减缓,与2. 2节结果吻合。对系数b再进行直线拟合,得到方程式如式(9),拟合结果见图6。
|
图 6 系数b拟合直线 Fig. 6 Linear fit of coefficient b |
| $ b = 2.04\frac{l}{L} + 8.25 。$ | (9) |
由于系数a的值受短上建长度变化影响不大,可以取为方案1~方案5的均值为a=1.18。则可得到新的短上层建筑正应力计算公式如下:
| $ {\sigma _{x1}} = - 1.18\frac{{{M_1}}}{{{I_1}}}{y_1} + {\sigma _1}{e^{ - (2.04\frac{l}{L} + 8.25){y_1}}}。$ | (10) |
该公式可用于短上建甲板正应力应力计算。
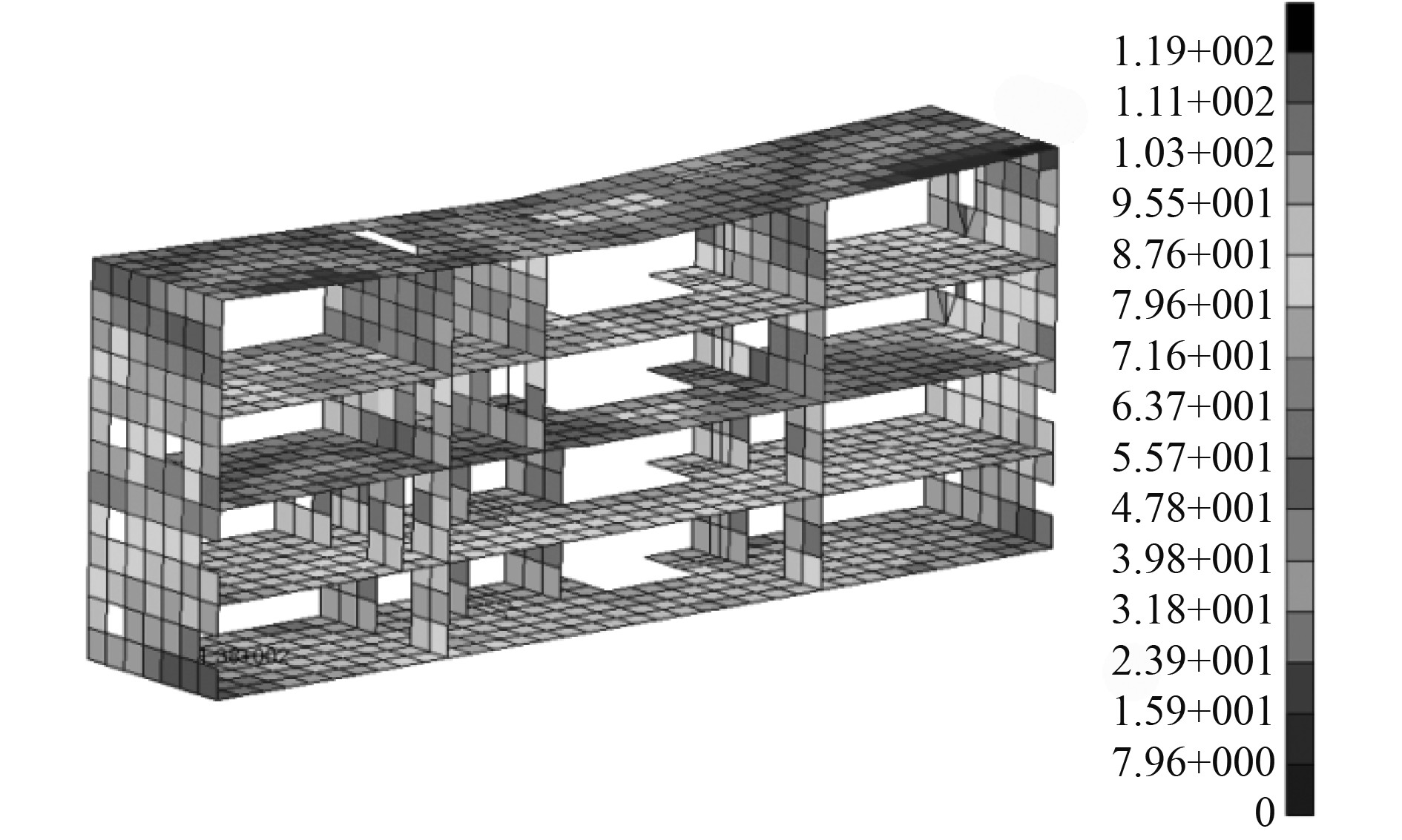
3.2 正应力计算公式验证为了验证新式(10)的有效性,在此设计上层建筑与船长比(l/L)为1∶5. 75的方案8,建立有限元模型见图7,施加剪流节点力载荷进行总强度计算,得到上建中处横剖面正应力云图见图8,将得到甲板正应力与公式计算结果对比见表5,方案8船体上层建筑中处横剖面各层甲板(包括底板)正应力的有限元与理论公式结果沿高度分布曲线如图9所示。

|
图 7 方案8有限元模型 Fig. 7 Finite element model of scheme8 |
|
图 8 方案8上层建筑中部横剖面正应力云图 Fig. 8 Normal stress contour of superstructure middle section of scheme8 |
|
|
表 5 上层建筑正应力拟合公式、有限元和理论公式计算结果(MPa) Tab.5 Calculation results of normal stress fitting formulas, FEM and theoretical formula of superstructure (MPa) |
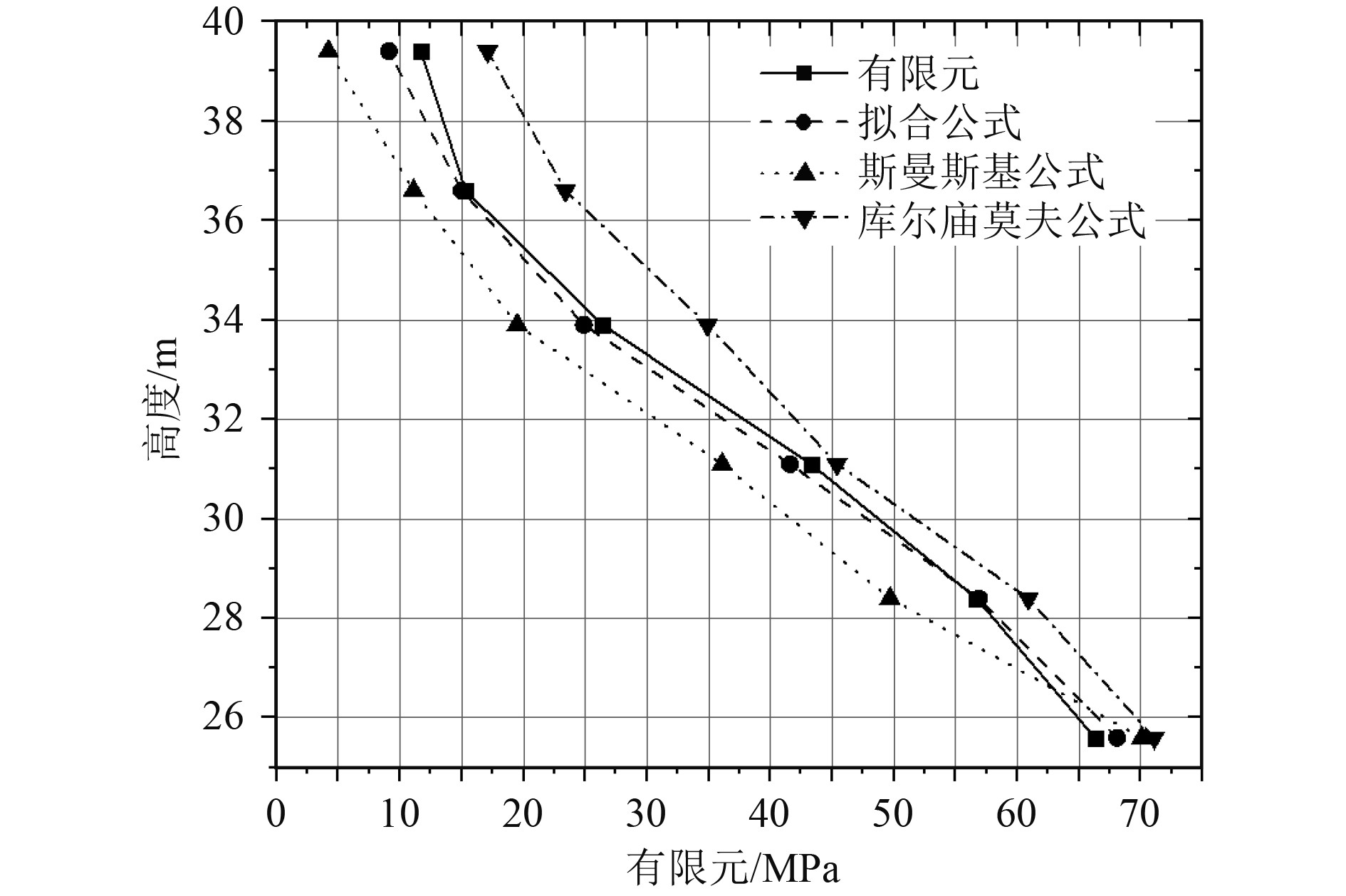
|
图 9 方案8上层建筑甲板正应力沿高度分布曲线 Fig. 9 Normal stress distribution curve of superstructure along height of scheme8 |
为将正应力拟合公式推广到其他短上层建筑船型,对一艘典型的短上层建筑矿砂船进行总强度计算,计算工况、载荷和边界条件等参考前文,矿砂有限元模型见图10,将得到甲板正应力与公式计算结果对比见表6,矿砂船上层建筑中处横剖面各层甲板(包括底板)正应力的有限元与理论公式结果沿高度分布曲线如图11所示。

|
图 10 矿砂船有限元模型 Fig. 10 Finite element model of ore carrier |
|
|
表 6 上层建筑正应力拟合公式、有限元和理论公式计算结果(MPa) Tab.6 Calculation results of normal stress fitting formulas, FEM and theoretical formula of superstructure (MPa) |
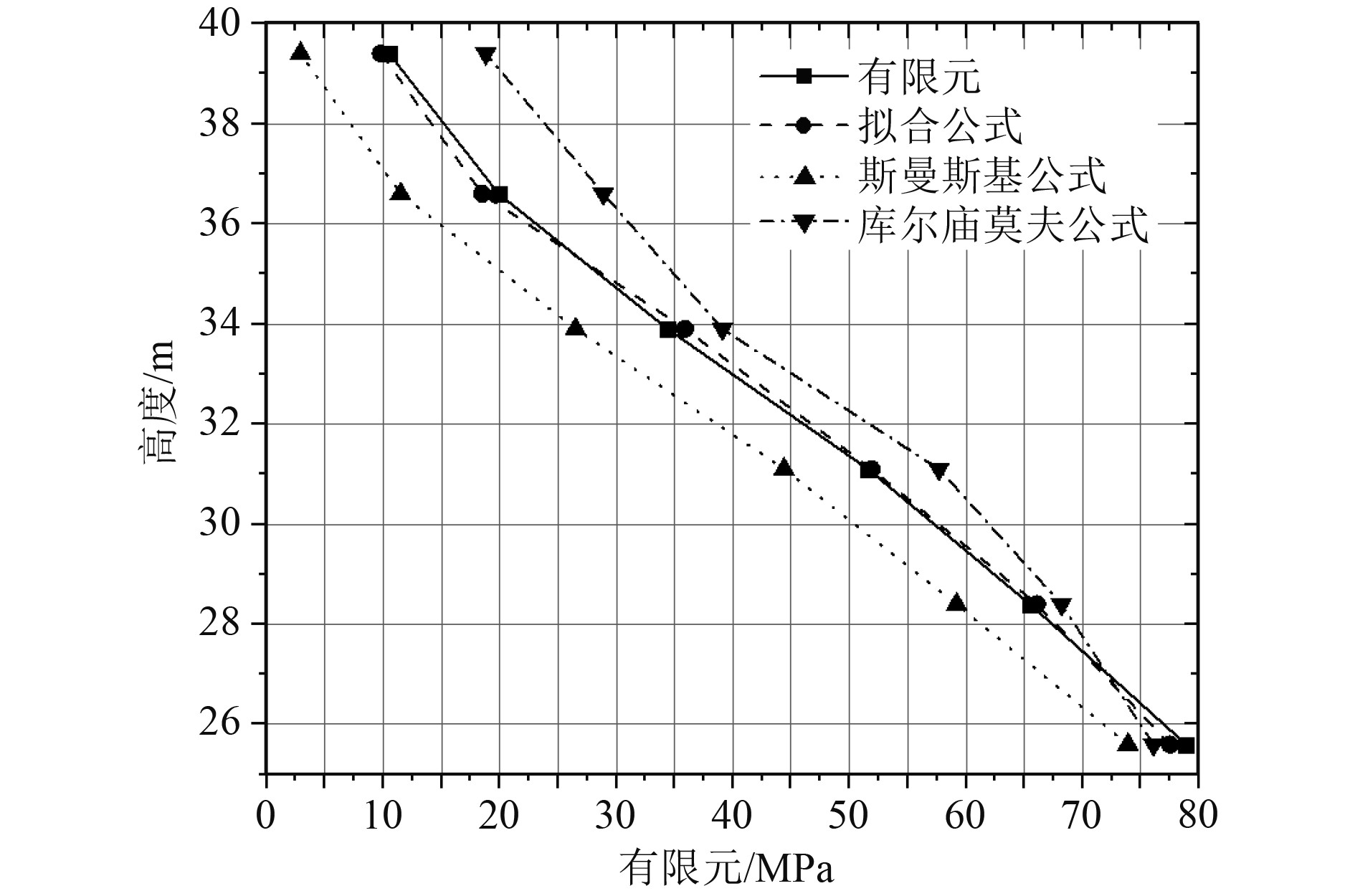
|
图 11 矿砂船上层建筑甲板正应力沿高度分布曲线 Fig. 11 Normal stress distribution curve of superstructure along height of ore carrier |
从方案8和矿砂船验算结果来看,有限元结果和拟合公式计算结果最大误差不超过3 MPa,拟合结果较好,基本符合实际短上建甲板正应力的衰减规律,斯曼斯基指数公式衰减过快,库尔庙莫夫二次函数公式衰减过慢,都会对实际应力评估造成一定偏差,不能很好反应短上建甲板正应力的衰减规律。
4 结 语本文以一艘油船作为研究对象,设计了不同短上层建筑方案,借助有限元法考察了短上建各层甲板的应力分布特点,并拟合得到了短上层建筑沿高度方向的正应力分布公式,得到结论:
1)短上层建筑主船体各层甲板正应力有限元计算结果沿高度方向呈线性变化,符合平断面假定;上层建筑各层甲板正应力有限元计算结果沿高度方向逐渐衰减且不呈线性变化,衰减的速度主要与上层建筑和主船体的长度比呈反比,上层建筑长度增加,正应力沿高度衰减速度逐渐减缓。
2)本文研究发现,短上层建筑正应力衰减规律可用指数函数进行拟合估算,引入衰减系数可反映上层建筑和主船体长度比对正应力分布规律的影响,验证方案对比表明新公式计算结果与有限元计算吻合较好,可以推广。
| [1] |
陆鑫森. 船舶上层建筑的强度问题[J]. 交通大学学报, 1958(3): 186-223. |
| [2] |
CRAWFORD L. Discussion of nonlinear distribution of bending stresses[J]. Applied Mechanics, 1953(9): 438. |
| [3] |
CRAWFORD L. Theory of long ship’s superstructures[J]. Trans. Society of Naval Architects and Marine Engineers, 1950(4): 693. |
| [4] |
BLEICH H H. Nolinear Distribution of bending stressed due to distortion of the cross section[J]. Applied Mechanics, 1953(3): 95−104.
|
| [5] |
Ю. А. Шиманский. Проектирование Прерывистых Свяэей Суловото Корнуса[M]. Сулпромтиэ, 1954.
|
| [6] |
A. A. Кудюмов. Прочностъ Кораоля[M]. Судпромтиз, 1956.
|
| [7] |
陈倩, 张世联, 李源源. 铝合金上层建筑参与船体总纵弯曲的特性研究[J]. 船舶工程, 2011, 33(S2): 21−24+28.
|
| [8] |
王西典. 计入有效度的强力上层建筑设计研究[D]. 上海: 上海交通大学, 2015.
|
| [9] |
严卫祥, 赵文斌, 高峰. 长上层建筑计入船体梁总纵强度研究[J]. 船舶设计通讯, 2017(151): 44-48. |
| [10] |
于滨, 陈志坚, 唐宇航. 岛式上层建筑总强度计算方法[J]. 舰船科学技术, 2019, 41(15): 12-16. |
| [11] |
杨斌, 裴志勇, 吴卫国. 基于修正双梁理论的邮轮应力分布特性研究[J]. 船舶力学, 2022, 26(10): 1503-1513. |
| [12] |
HENDRIK N, PETRI V, PENTTI K. A theory of coupled beams for strength assessment of passenger ships[J]. Marine Structures, 2005(8): 599
|
| [13] |
杨平, 吴凯. 上层建筑对船体总纵弯曲的效应分析[J]. 武汉交通科技大学学报, 1999(1): 34−39.
|
| [14] |
孔超群. 圣维南原理研究工作综述[J]. 上海力学, 1990(3): 35−40.
|
| [15] |
MORSHEDSOLOUK F, KHEDMATI M R. An extension of coupled beam method and its application to study ship's hull-superstructure interaction problems[J]. Latin American Journal of Solids and Structures, 2011(3): 28−33.
|
| [16] |
HOVGAARD. W. A New Theory of the Distribution of Shearing Stresses in Riveted and Welded Connection[J]. T. INA1931(8
|
| [17] |
中国船级社. 钢质海船入级规范[S]. 2021
|
| [18] |
谢心, 吴嘉蒙, 王德禹. 基于剪流分布规律的节点力加载方式在船体结构有限元分析中的应用[J]. 舰船科学技术, 2017, 39(5): 12-17. |
 2024, Vol. 46
2024, Vol. 46
