1. 中国船舶及海洋工程设计研究院,上海 200011;
2. 哈尔滨工程大学 青岛创新发展基地,山东 青岛 266000
收稿日期: 2023-03-14.
基金项目: 国家自然科学基金资助项目(12172098)
作者简介: 陈思远(1994 – ),男,硕士,工程师,研究方向为轻质多功能结构设计及其抗冲击性能
Research on impact resistance of the three-dimensional enhanced double arrow negative Poisson's ratio structure
1. Marine Design and Research Institute of China, Shanghai 200011, China;
2. Qingdao Innovation and Development Base, Harbin Engineering University, Qingdao 266000, China
0 引 言 与传统的多胞结构相比[1 − 3],负泊松比结构具有轻质、孔隙率大、可设计性强和独特的拉胀特性等优点。众多学者对负泊松比结构的拓扑构型设计进行了研究。刘海涛等[4]提出一种泊松比可调控的圆弧星型结构,采用理论分析、数值仿真和试验的方法研究了几何参数对结构等效泊松比的影响规律。韩会龙等[5]利用双向内凹胞元得到一种具有负泊松比效应的蜂窝结构,基于一维应力波理论给出了结构的密实化应变和动态平台应力的经验公式,并与数值模拟结果进行验证,一致性吻合较好。胡章优等[6]设计了不同内凹形式的三角形负泊松比多胞结构,研究不同内凹形式对结构平台应力和能量吸收效率的影响。沈振峰等[7]基于内凹六边形蜂窝设计出一种新型负泊松比内凹蜂窝结构,研究了不同冲击速度下胞元结构对内凹蜂窝的失效模式、冲击应力和能量吸收特性的影响规律。虞科炯等[8]提出一种正弦负泊松比蜂窝结构,通过改变振幅、壁厚和冲击速度研究了对结构平台应力和能量吸收性能的影响。
与此同时,仿生梯度设计思想在负泊松比结构的研究中同样受到了广泛关注,梯度的连续变化可降低结构的初始峰值应力,充分发挥各芯层的优势,改变结构的变形模式,影响能量吸收效率。邓小林等[9]研究了分层梯变负泊松比蜂窝结构在不同冲击速度下的动力学响应,结果发现合理的梯度设计可降低初始峰值应力,提高结构的能量吸收效率。张权等[10]采用数值仿真的方法研究了冲击速度、厚度梯度和角度梯度的星型负泊松比蜂窝结构在动态冲击下的力学响应,研究发现梯度设置影响结构的失效模式和能量吸收。陶晓晓等[11]采用数值模拟方法研究了不同胞元高度、宽度、夹角和壁厚的内凹蜂窝在爆炸冲击载荷下的力学响应,结果发现胞元长度和角度对结构的抗爆防护性能影响较小,胞元高度和壁厚影响较为显著。
鉴于负泊松比结构的初始刚度、强度相对较弱的问题,本文结合仿生梯度设计思想提出一种新型三维增强型双箭头负泊松比结构,采用理论分析和数值模拟的方法研究了梯度设计和冲击速度对其宏观等效泊松比、变形机理、失效模式、平台应力及能量吸收的影响规律。
1 增强型双箭头结构的设计及其理论表征 1.1 增强型双箭头结构设计 本文设计出一种新型增强三维双箭头负泊松比结构,下文简称为“增强型双箭头结构”。在二维双箭头单胞中增加支撑连杆,通过旋转、阵列和堆叠形成增强型双箭头结构,具体设计思想如图1所示,中间支撑连杆可显著提高结构的整体刚度和强度。
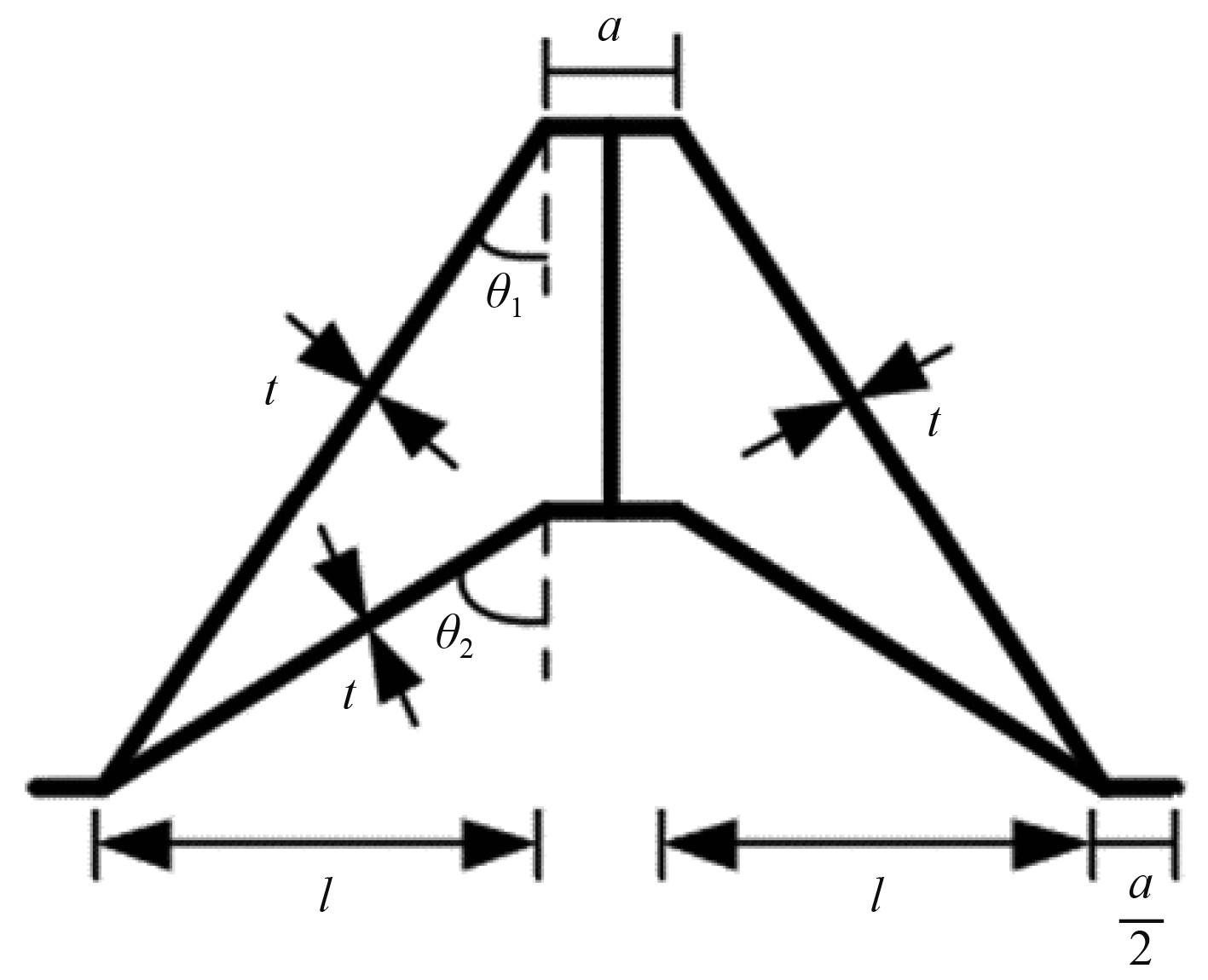
增强型双箭头结构是将二维双箭头增加支撑连杆得到一种新型拉胀结构,其胞元的几何参数如图2所示,其几何参数主要由水平横杆$ a $,倾斜杆与垂向线的夹角$ {\theta }_{1}、{\theta }_{\text{2}} $,倾斜杆厚度$ t $及倾斜杆在水平方向的投影$ l $组成。通过改变$ {\theta }_{1}、{\theta }_{\text{2}} $可形成不同角度梯度的双箭头结构如表1所示。根据多胞结构相对密度推导的定义可知,三维增强型双箭头结构相对密度可表示为:
表 1(Tab. 1)

表 1 不同角度增强型双箭头胞元几何参数
Tab. 1 Different angle enhanced double arrow cell geometry parameters
| 构型 |
Z-AB |
Z-AC |
Z-AD |
| $ l/{\mathrm{mm}} $ |
10 |
10 |
10 |
| $ t/{\mathrm{mm}}$ |
1.2 |
1.2 |
1.2 |
| $ a/{\mathrm{mm}} $ |
2.4 |
2.4 |
2.4 |
| $ ({\theta }_{1},{\theta }_{2}) $ |
(30,45) |
(30,60) |
(30,75) |
| M/kg |
0.559 |
0.561 |
0.565 |
|
表 1 不同角度增强型双箭头胞元几何参数
Tab.1 Different angle enhanced double arrow cell geometry parameters
|
|
$ \Delta \rho = \frac{{\left[ {(2l \cdot \dfrac{{\sin {\theta _1} + \sin {\theta _2}}}{{\sin {\theta _1} \cdot \sin {\theta _2}}} + 3a) + \dfrac{{3l(\tan {\theta _2} - \tan {\theta _1})}}{{4\tan {\theta _1} \cdot \tan {\theta _2}}}} \right] \cdot {t^2}}}{{\dfrac{{l \cdot {{(l + a)}^2} \cdot (\tan {\theta _2} - \tan {\theta _1})}}{{\tan {\theta _1} \cdot \tan {\theta _2}}}}}。$
|
(1) |
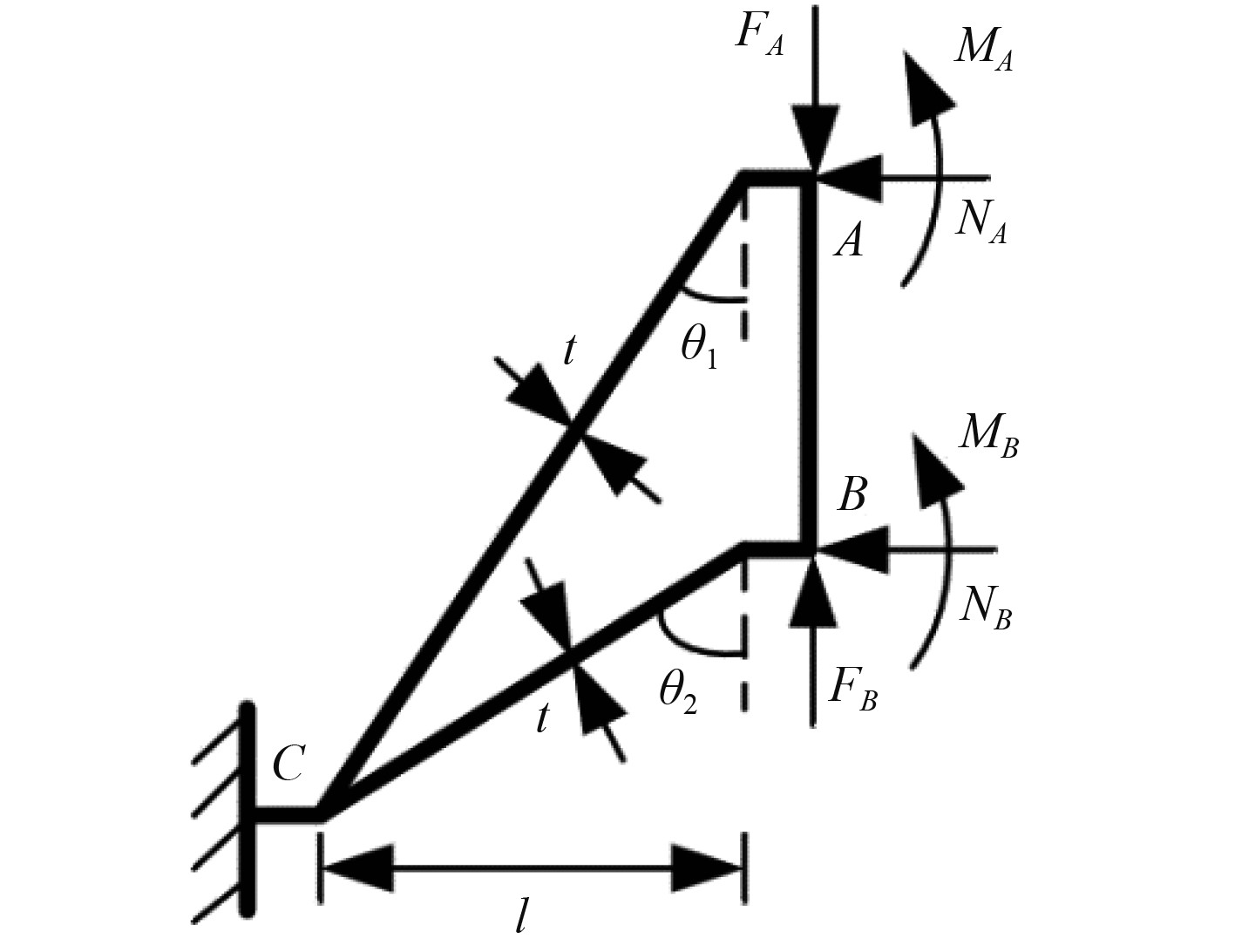
1.2 增强型双箭头结构理论表征 增强型双箭头结构由胞元周期性阵列得到,考虑到结构具有对称性,为简化计算模型,采用二维代表性胞元对其受力分析,如图3所示。假设C点固支,由于A、B点位于结构的对称面上,因此A、B点的转角位移为0,且胞元的变形主要来源于胞元内部,A、B点的水平位移相等。根据此可得,结构的变形协调条件,利用力法正则方程,求出未知力FA、FB和未知力矩MA、MB,采用摩尔积分将得到的未知力和力矩代入可得A、B点的水平和竖直方向的位移,利用定义即可推导得到增强型双箭头结构的宏观泊松比。由于压缩和剪切产生的位移较小可忽略不计,本推导计算中仅考虑弯曲变形产生的位移。
由结构力学知识可知,$ {\delta _{{\text{ii}}}} $表示作用在Xi由Xi=1单独作用时产生的位移;因此由摩尔积分可得式(2)~式(13),其中,E为材料的弹性模量,I为截面对中性轴的惯性矩。
|
$\begin{aligned}
{\delta _{{N_A}{M_A}}} = & \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _1}}} \times l \cdot \cot {\theta _1} \times 1} \right) =\\
& \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{{{l^2}}}{{\sin {\theta _1}}} \cdot \cot {\theta _1}} \right),\end{aligned} $
|
(2) |
|
$\begin{aligned}
{\delta _{{N_A}{F_A}}} =& - \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _1}}} \times l \cdot \cot {\theta _1} \times \frac{2}{3} \cdot l} \right) =\\
& - \frac{1}{{EI}}\left( {\frac{1}{3} \times \frac{{{l^3}}}{{\sin {\theta _1}}} \times \cot {\theta _1}} \right),\end{aligned} $
|
(3) |
|
$\begin{aligned}
{\delta _{{N_A}{N_A}}} =& \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _1}}} \times l \cdot \cot {\theta _1} \times \frac{2}{3} \cdot l \cdot \cot {\theta _1}} \right) =\\
& \frac{1}{{EI}}\left( {\frac{1}{3} \times \frac{{{l^3}}}{{\sin {\theta _1}}} \cdot {{\cot }^2}{\theta _1}} \right) ,\end{aligned}$
|
(4) |
|
$\begin{aligned}
{\delta _{{N_B}{M_B}}} =& \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _2}}} \times l \cdot \cot {\theta _2} \times 1} \right) =\\
& \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{{{l^2}}}{{\sin {\theta _2}}} \cdot \cot {\theta _2}} \right),\end{aligned}$
|
(5) |
|
$\begin{aligned} {\delta _{{N_B}{F_B}}} = &\frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _2}}} \times l \cdot \cot {\theta _2} \times \frac{2}{3}l} \right) = \\
&\frac{1}{{EI}}\left( {\frac{1}{3} \times \frac{{{l^3}}}{{\sin {\theta _2}}} \times \cot {\theta _2}} \right),\end{aligned}$
|
(6) |
|
$\begin{aligned}
{\delta _{{N_B}{N_B}}} = & \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _2}}} \times l \cdot \cot {\theta _2} \times \frac{2}{3} \cdot l \cdot \cot {\theta _2}} \right) =\\
& \frac{1}{{EI}}\left( {\frac{1}{3} \times \frac{{{l^3}}}{{\sin {\theta _2}}} \cdot {{\cot }^2}{\theta _2}} \right),\end{aligned}$
|
(7) |
|
$ {\delta _{{M_A}{M_A}}} = \frac{1}{{EI}}\left( {\frac{l}{{\sin {\theta _1}}} \times 1 \times 1} \right) = \frac{1}{{EI}} \times \frac{l}{{\sin {\theta _1}}} ,$
|
(8) |
|
$ {\delta _{{M_A}{F_A}}} = - \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _1}}} \times l \times 1} \right) = - \frac{1}{{EI}} \times \frac{{{l^2}}}{{2\sin {\theta _1}}},$
|
(9) |
|
$ {\delta _{{M_B}{M_B}}} = \frac{1}{{EI}}\left( {\frac{l}{{\sin {\theta _2}}} \times 1 \times 1} \right) = \frac{1}{{EI}} \times \frac{l}{{\sin {\theta _2}}},$
|
(10) |
|
$ {\delta _{{M_B}{F_B}}} = \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _2}}} \times l \times 1} \right) = \frac{1}{{EI}} \times \frac{{{l^2}}}{{2\sin {\theta _2}}},$
|
(11) |
|
$ {\delta _{{F_A}{F_A}}} = \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _1}}} \times l \times \frac{2}{3} \times l} \right) = \frac{1}{{EI}} \times \frac{1}{3}\frac{{{l^3}}}{{\sin {\theta _1}}},$
|
(12) |
|
$ {\delta _{{F_B}{F_B}}} = \frac{1}{{EI}}\left( {\frac{1}{2} \times \frac{l}{{\sin {\theta _2}}} \times l \times \frac{2}{3}l} \right) = \frac{1}{{EI}} \times \frac{1}{3}\frac{{{l^3}}}{{\sin {\theta _2}}}。$
|
(13) |
基于变形协调条件,可得如下力法正则式(14)~式(16):
|
$\begin{aligned}
& {\delta _{{N_A}{N_A}}}{N_A} + {\delta _{{N_A}{M_A}}}{M_A} + {\delta _{N_A^{}{F_A}}}{F_A} = {\delta _{{N_B}{N_B}}}{N_B} + \\
& {\delta _{{N_B}{M_B}}}{M_B} + {\delta _{{N_B}{F_B}}}{F_B},\end{aligned}$
|
(14) |
|
$ {\delta _{{M_A}{N_A}}}{N_A} + {\delta _{{M_A}{M_A}}}{M_A} + {\delta _{{M_A}{F_A}}}{F_A} = 0,$
|
(15) |
|
$ {\delta _{{M_B}{N_B}}}{N_B} + {\delta _{{M_B}{M_B}}}{M_B} + {\delta _{{M_B}{F_B}}}{F_B} = 0。$
|
(16) |
将式(2)~式(13)计算结果带入力法正则方程推导可得未知力FA、FB和未知力矩MA、MB,利用摩尔积分可得到A点、B点的水平和竖向位移。
|
$ u_y^A = {\delta _{{F_A}{F_A}}}{F_A} + {\delta _{{F_A}{M_A}}}{M_A} + {\delta _{{N_A}{F_A}}}{N_A} ,$
|
(17) |
|
$ u_y^B = {\delta _{{F_B}{F_B}}}{F_B} + {\delta _{{F_B}{M_B}}}{M_B} + {\delta _{{N_B}{F_B}}}{N_B},$
|
(18) |
|
$ {\delta _{{M_B}{N_B}}}{N_B} + {\delta _{{M_B}{M_B}}}{M_B} + {\delta _{{M_B}{F_B}}}{F_B} = 0。$
|
(19) |
将式(17)~式(19)代入可得水平和竖向的应变,根据泊松比的定义,将其代入式(22)可得增强型双箭头结构的等效宏观泊松比。
|
$ {\varepsilon _{\text{y}}} = \frac{{u_y^A + u_y^B}}{{\Delta h}},$
|
(20) |
|
$ {\varepsilon _x} = \frac{{u_x^A}}{l},$
|
(21) |
|
$ {\nu _{xy}} = - \frac{{{\varepsilon _x}}}{{{\varepsilon _y}}}。$
|
(22) |
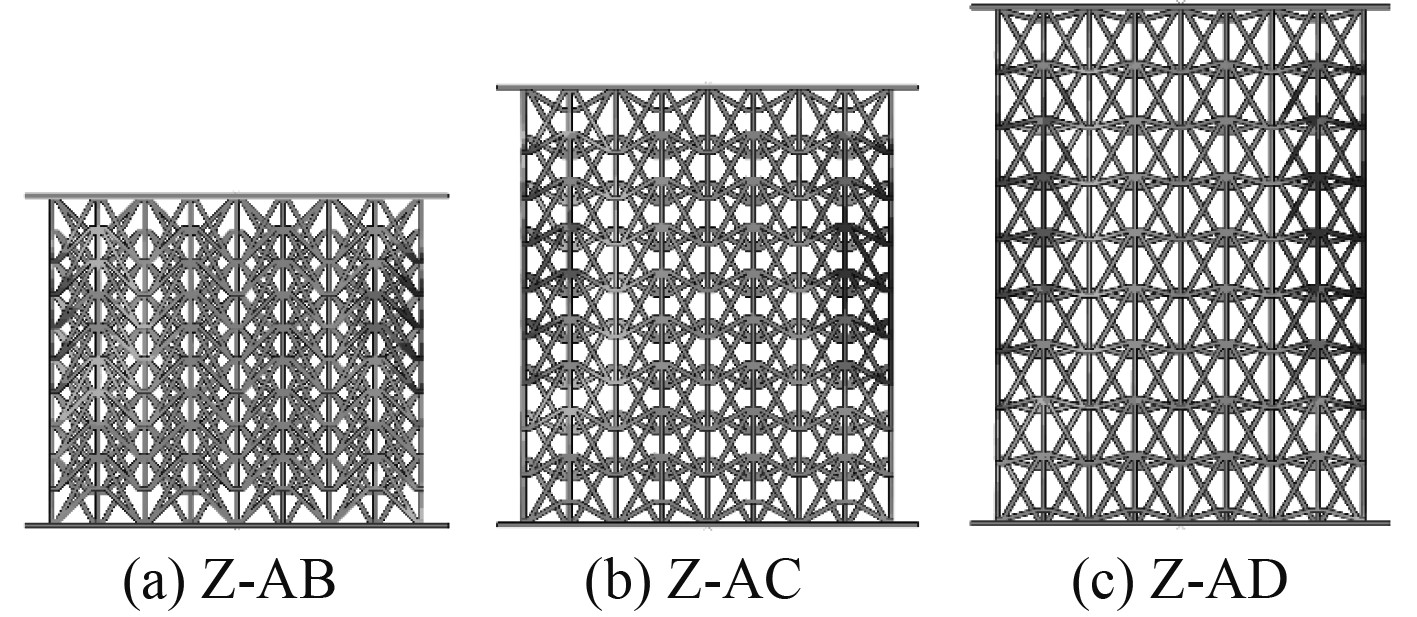
1.3 增强型双箭头结构宏观泊松比的有限元分析 采用Abaqus数值模拟软件计算了增强型双箭头结构在弹性范围内的力学响应,由图4可知在单轴压缩载荷作用下,Z-AB、Z-AC和Z-AD这3种角度梯度的双箭头结构均向内收缩表现出负泊松比效应。在双箭头芯子结构上选取典型参考点输出沿压缩方向和垂直于压缩方向的节点位移,根据定义可计算出双箭头结构的宏观泊松比。角度梯度增强型双箭头结构的宏观泊松比理论分析和数值模拟对比结果如表2所示。由表可知,理论分析能较好预测增强型双箭头结构的负泊松比性质,且随着$ \theta $的增大,宏观泊松比逐渐减小。理论值略大于数值计算结果,因数值计算中模型尺寸是有限的,理论推导基于模型的无限大假设,不受边界效应的影响;而且理论表征中简化了计算模型,忽略了水平横杆对结构宏观泊松比的影响。
表 2(Tab. 2)

表 2 不同构型增强型双箭头结构的宏观泊松比
Tab. 2 Macroscopic Poisson's ratio of different configuration enhanced double arrow structures
| 构型 |
Z-AB |
Z-AC |
Z-AD |
| 理论分析 |
–1.73 |
–1.00 |
–0.46 |
| 数值模拟 |
–1.64 |
–0.92 |
–0.41 |
| 误差/% |
5.20 |
8.00 |
10.87 |
|
表 2 不同构型增强型双箭头结构的宏观泊松比
Tab.2 Macroscopic Poisson's ratio of different configuration enhanced double arrow structures
|
2 速度梯度下增强型双箭头结构动态冲击特性 2.1 有限元模型 采用Abaqus数值仿真软件研究了增强型双箭头结构在不同速度梯度作用下的抗冲击性能,有限元模型如图5所示。其中,增强型三维双箭头芯子位于2块刚性板间,刚性冲击端中心处施加30 kg的集中点质量,并沿竖向设置场速度输出,约束3个方向的旋转自由度,固定端设置固支边界,模拟落锤冲击作用下增强型双箭头结构的力学响应。芯子材料采用45钢,考虑材料的应变率效应,利用Johnson-Cook本构模型进行仿真计算,具体材料参数如表3所示。芯子采用C3D8R单元进行网格划分,经网格收敛性分析可知,网格尺寸取0.6 mm时,可提高仿真计算效率并满足结果的可靠性。考虑到冲击过程中,芯子与刚性板会发生接触碰撞,因此芯子与芯子和芯子与刚性板板间设置为通用接触,芯子与冲击端法向设置为硬接触,切向摩擦系数为0.1。根据增强型双箭头结构的几何尺寸和基体材料,本文选取不同梯度的冲击速度:20 m/s、80 m/s和140 m/s,研究冲击速度对结构变形模式、平台应力和比能量吸收的影响规律。
表 3(Tab. 3)

表 3 45钢Johnson-Cook本构模型材料参数
Tab. 3 45 Steel Johnson-Cook constitutive model material parameters
| $ \begin{gathered} \quad\;\; \rho \\ /{\mathrm{kg}} \cdot {{\mathrm{m}}^{ - 3}} \\ \end{gathered} $ |
$E /{\text{GPa} }$ |
$ \nu $ |
$A /{\text{MPa} }$ |
$B/ {\text{MPa} }$ |
$ n $ |
$ m $ |
${T_m}/K$ |
${T_r}/K$ |
| 7820 |
200 |
0.3 |
507 |
320 |
0.28 |
1.06 |
1783 |
293 |
|
表 3 45钢Johnson-Cook本构模型材料参数
Tab.3 45 Steel Johnson-Cook constitutive model material parameters
|
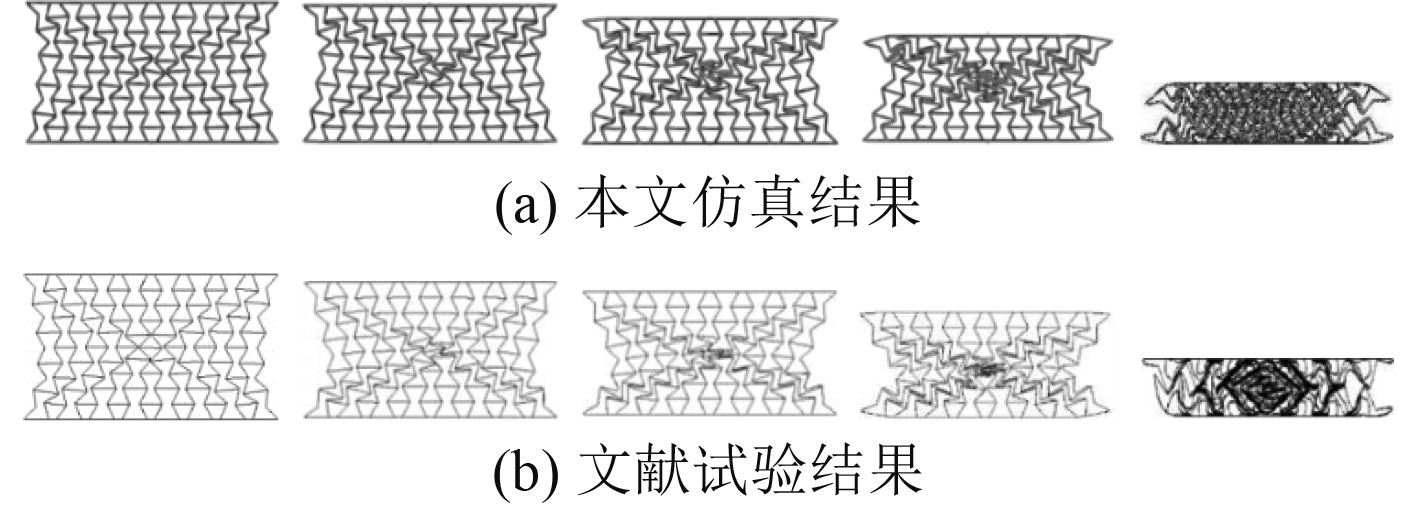
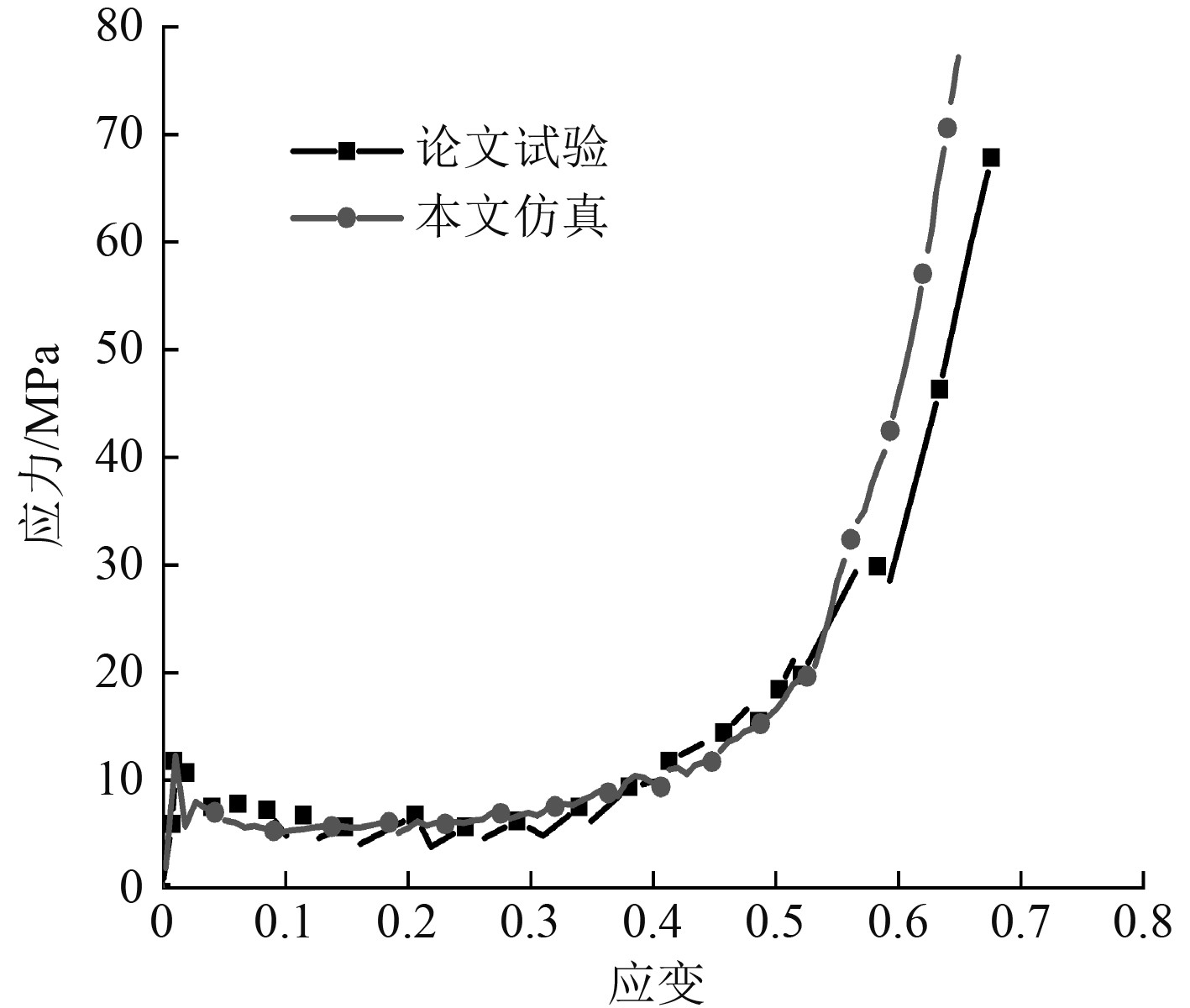
2.2 模型可靠性验证 岑神德等[12]利用数值模拟和试验的方法研究了金属内凹蜂窝在动态冲击下的力学响应。为验证模型的可靠性,本文采用Abaqus软件在相同工况下进行数值模拟计算并与其试验结果对比分析。图6和图7为在5 m/s的落锤冲击作用下,仿真与试验结果的变形模式和应力应变曲线,由图可知,在冲击载荷作用下结构整体向内收缩,呈“X”型变形模式,初始峰值应力和平台应力一致性较好,仿真结果与试验结果吻合较好,验证了数值模型的可靠性。
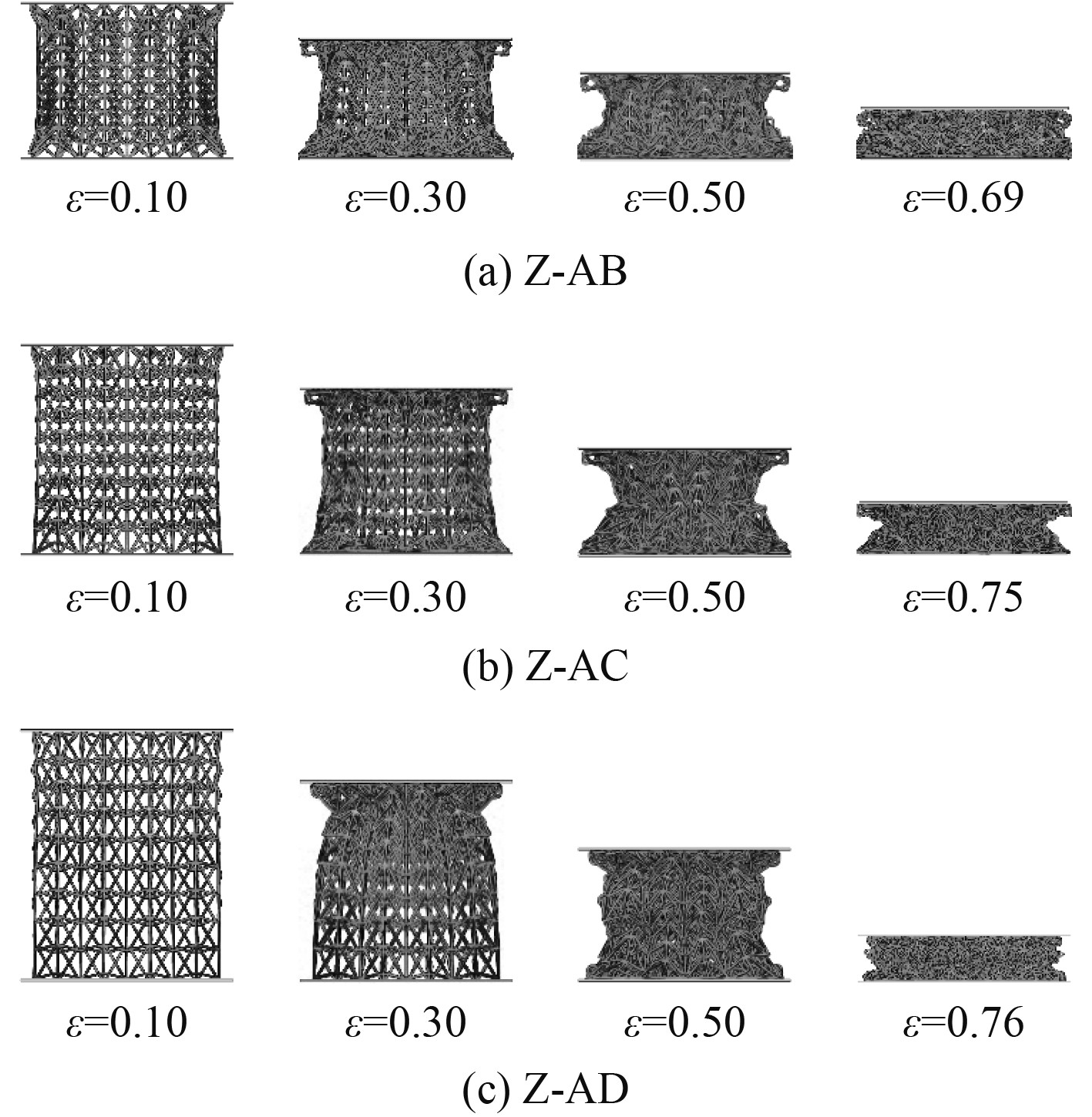
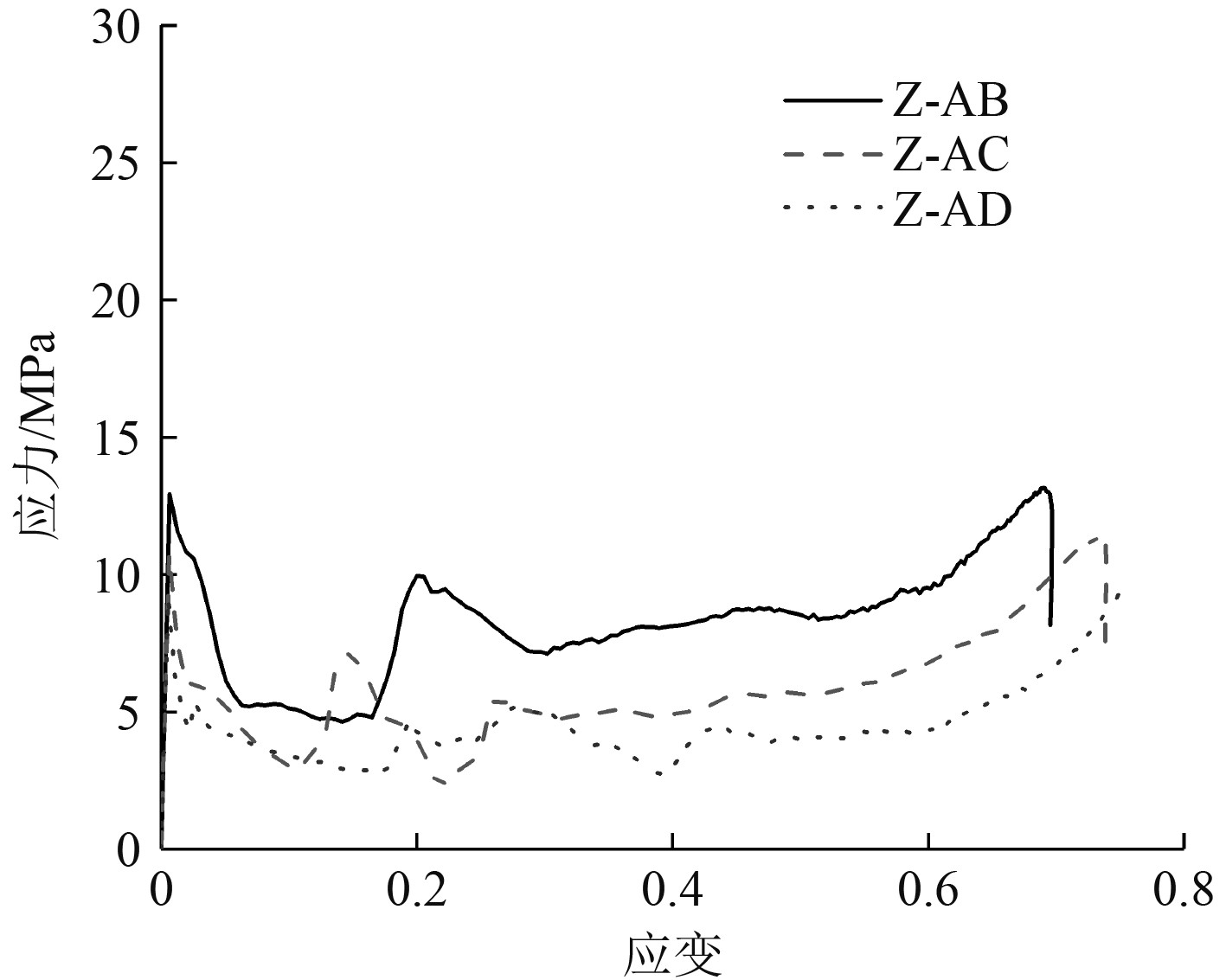
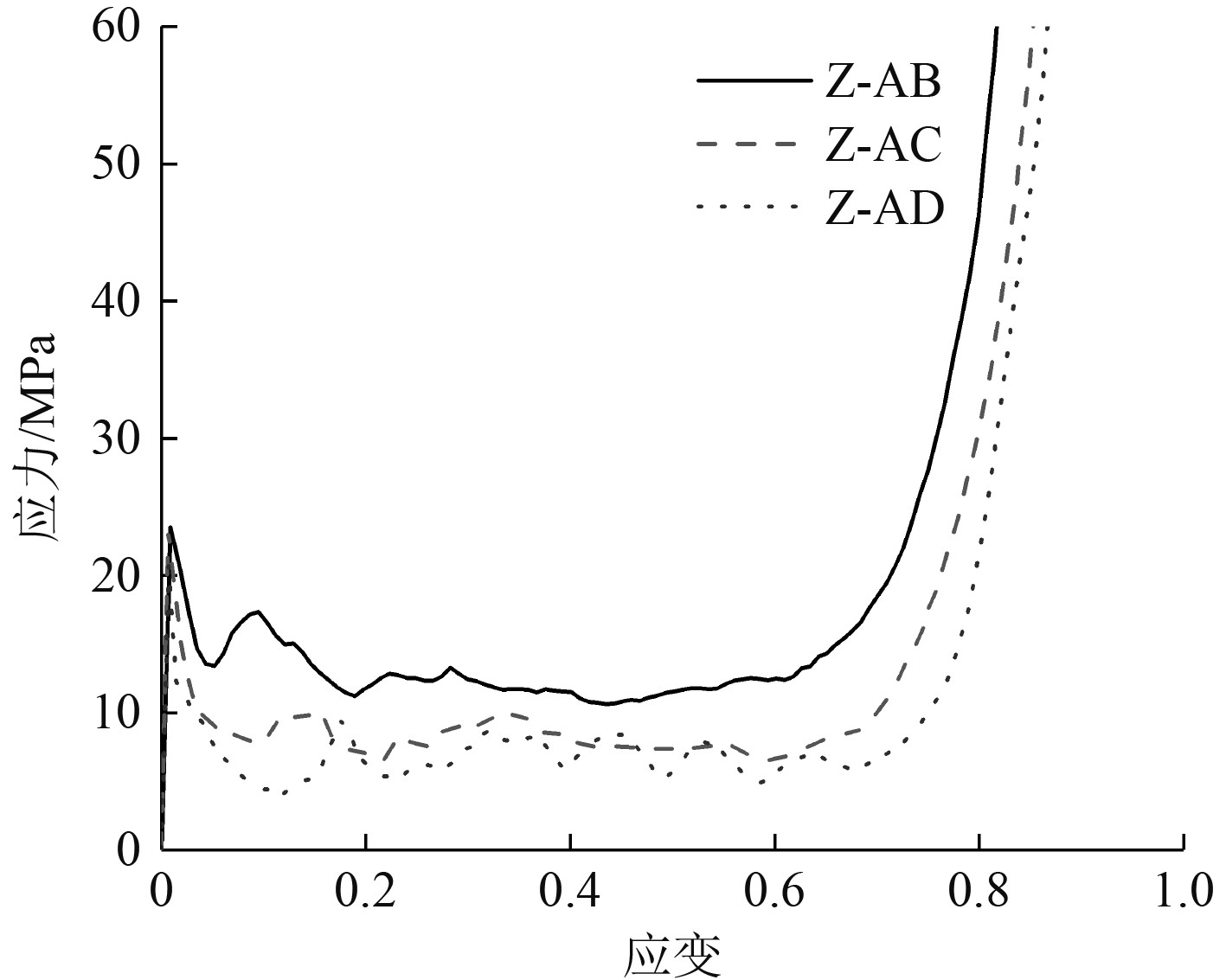
2.3 增强型双箭头结构的变形模式 计算结果表明,增强型双箭头结构在动态冲击过程中会产生向内收缩典型的变形模式。图8所示为在20 m/s冲击速度下,角度梯度增强型双箭头结构的失效模式,可知,在初始阶段,Z-AB、Z-AC和Z-AD在垂直于压缩方向均向中心处收缩,在冲击端和固定端表现出“V”型的变形模式。表现出明显的负泊松比效应。当压缩至$ \varepsilon = 0.50 $时,结构的横向收缩更为显著,结构整体表现出颈缩现象,呈“X”型的变形模式。随着压缩应变的增大,芯子杆发生屈曲失效,结构被压缩密实。图9所示为冲击端的名义应力应变曲线,由图可知,增强型双箭头结构在冲击初始的瞬时出现较高初始峰值应力,此阶段为弹性阶段;随后芯子发生屈曲进入平台阶段,此阶段平台应力表现出稳定波动状态,且低于初始峰值应力;随着结构不断冲击压缩,局部进入密实化,承载能力增强,出现应力平台增强阶段;由于仿真过程中,20 m/s冲击速度能量相对较低,结构未完全压缩密实,未出现密实化阶段。Z-AB表现出较高的平台应力,主要因为Z-AB压缩过程中负泊松比效应较为明显,结构整体向内收缩产生显著的刚度增强效应。
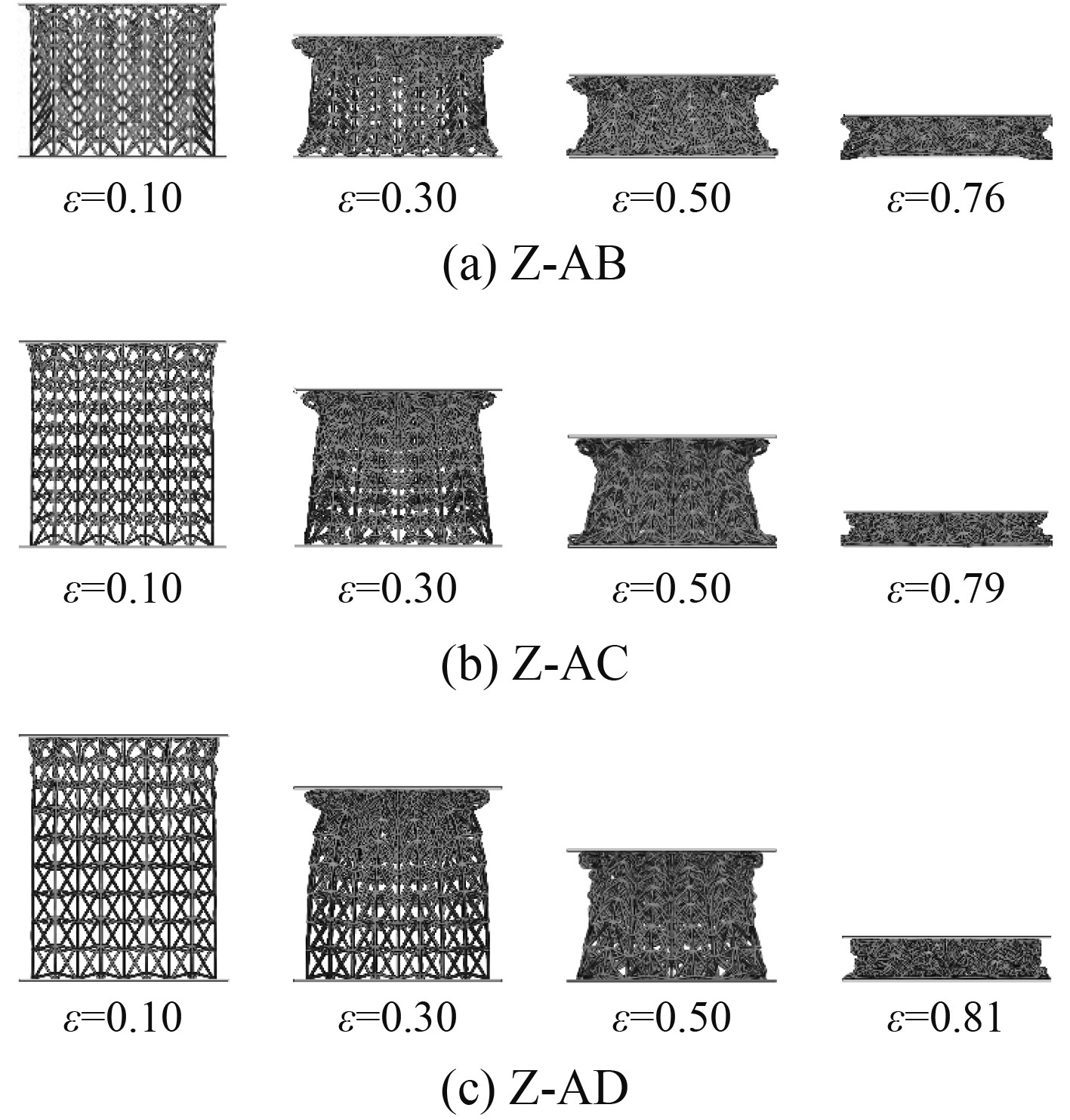
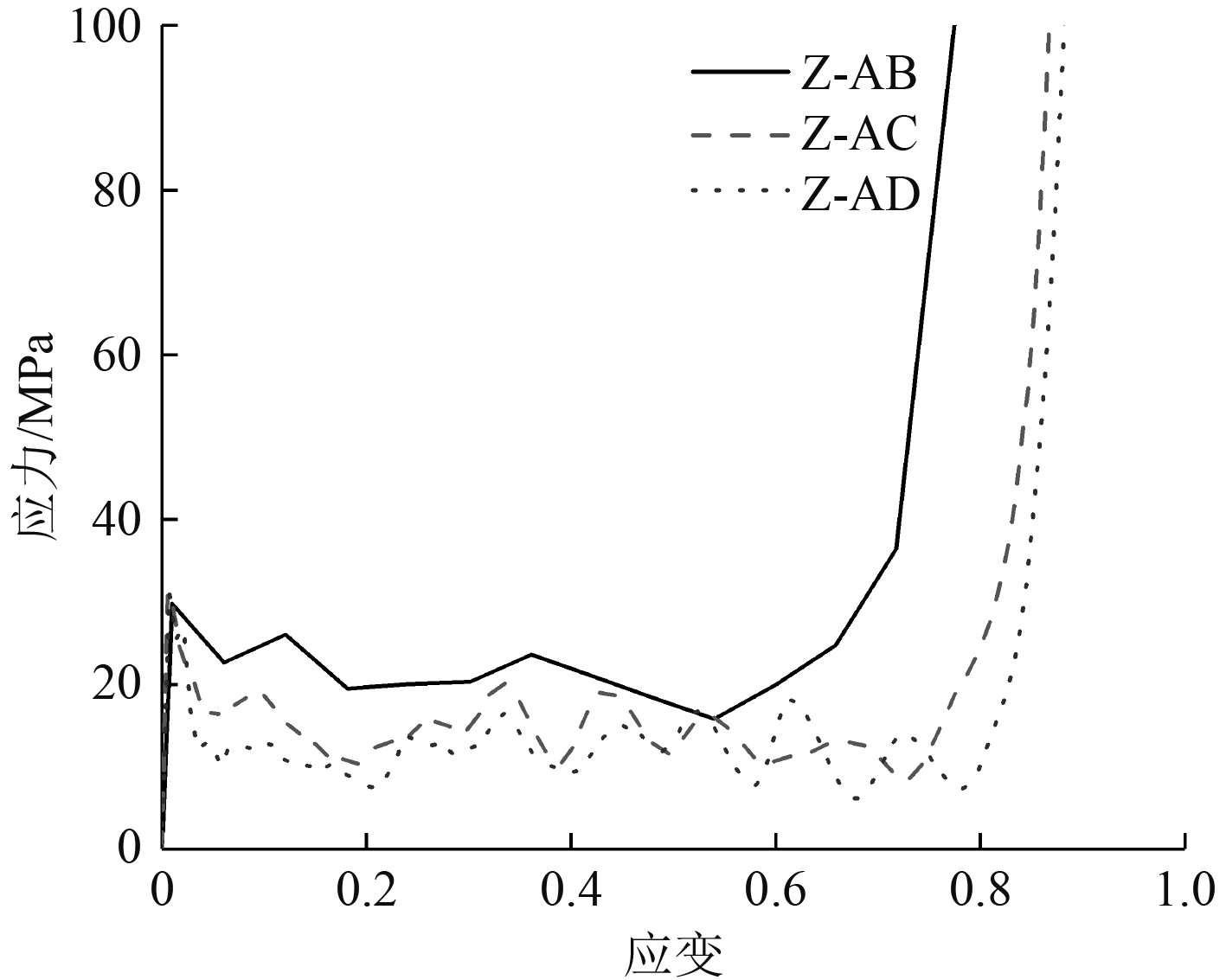
当冲击速度为80 m/s时,增强型双箭头结构的变形模式发生了明显变化,由于微惯性效应,结构在冲击端首先出现局部变形带,由图10可知,冲击端芯子首先出现屈曲失效,向内收缩,呈“V”型的变形模式,随着压缩应变的增大,局部的“V”型由冲击端向固定端逐渐扩展,直至双箭头结构被压缩密实。图11为该冲击速度下的应力应变曲线,可知,不同梯度的增强型双箭头结构均表现出典型的4个阶段、即弹性阶段、平台阶段、应力平台增强阶段和密实化阶段,Z-AB的平台应力明显高于Z-AC和Z-AD,对比结构的失效模式可知,Z-AB初始阶段表现出“V”型失效。随着压缩应变的增大,结构表现出低速冲击作用下的 “X”型变形模式,而Z-AC和Z-AD压缩过程中,由冲地端到固定端一直表现出“V”型失效,“X”型变形模式结构出现较大的宏观负泊松比,结构向内收缩较为明显,力学承载性能发挥充分,故平台应力较大。
由图12可知,随着冲击速度的增大,当冲击速度为140 m/s时,由于微惯性效应增强,惯性效应在变形中占据主导作用,Z-AB、Z-AC和Z-AD这3种梯度增强型双箭头结构变形均主要出现在冲击端,芯子杆件在冲击端屈曲变形,压缩密实,结构整体均表现出从冲击端到固定端逐层失效,呈“I”型变形模式,增强型双箭头结构负泊松比效应消失,表现出与传统多胞结构相似的失效形式。由图13可知,与低速冲击不同,在高速冲击作用下,结构由于逐层发生失效,曲线表现出围绕着平台应力出现震荡,且应力平台增强阶段基本消失。
2.4 增强型双箭头结构动态响应分析 平台应力为衡量多胞结构抗冲击特性的重要指标,增强型双箭头结构的平台应力可表示为:
|
$ {\sigma _p} = \frac{1}{{{\varepsilon _d} - {\varepsilon _{cr}}}}\int_{{\varepsilon _{cr}}}^{{\varepsilon _d}} {\sigma (\varepsilon ){\rm{d}}\varepsilon }。$
|
(23) |
式中:$ {\varepsilon _{cr}} $为屈服应变;$ {\varepsilon _d} $为密室化应变;$ \sigma (\varepsilon ) $为应力随应变的变化曲线。
根据式(23),表4为梯度增强型双箭头结构在不同冲击速度下平台应力的变化规律,当冲击速度相同时,Z-AB结构表现出较高的平台应力,且随着内凹角度的减小,平台应力逐渐降低,主要因为内凹角度越小,芯子杆件长细比越大,芯子易发生屈曲,承载性能为充分发挥,故平台应力越小;相同梯度的增强型双箭头结构,冲击速度越高,结构的平台应力越大,Z-AB、Z-AC和Z-AD随着冲击速度的增大,平台应力增加趋势越明显。可知,增强型双箭头结构的平台应力主要与结构的几何尺寸和冲击速度等参数相关。
表 4(Tab. 4)

表 4 增强型双箭头结构的平台应力
Tab. 4 Platform stresses for enhanced double arrow structures
| 冲击速度/m·s−1 | Z-AB/MPa | Z-AC/MPa | Z-AD/MPa |
| 20 | 7.10 | 5.07 | 4.05 | | 80 | 11.94 | 8.31 | 6.67 | | 140 | 21.05 | 16.13 | 14.60 |
|
表 4 增强型双箭头结构的平台应力
Tab.4 Platform stresses for enhanced double arrow structures
|
对于多胞结构,通常用比吸能(SEA)即结构单位质量所吸收的能量来评价结构的能量吸收,其表达式可表示为:
|
$ {E_m} = \frac{{{E_V}}}{{\Delta \rho \cdot {\rho _s}}} 。$
|
(24) |
其中,$ {E}_{V}={\int }_{{\varepsilon }_{cr}}^{{\varepsilon }_{{{d}}}}\sigma \left(\varepsilon \right){\mathrm{d}} \varepsilon $为单位体积增强型双箭头结构吸收的能量,$ \Delta \rho $为结构的相对密度,$ {\rho }_{s} $为基体材料的密度。
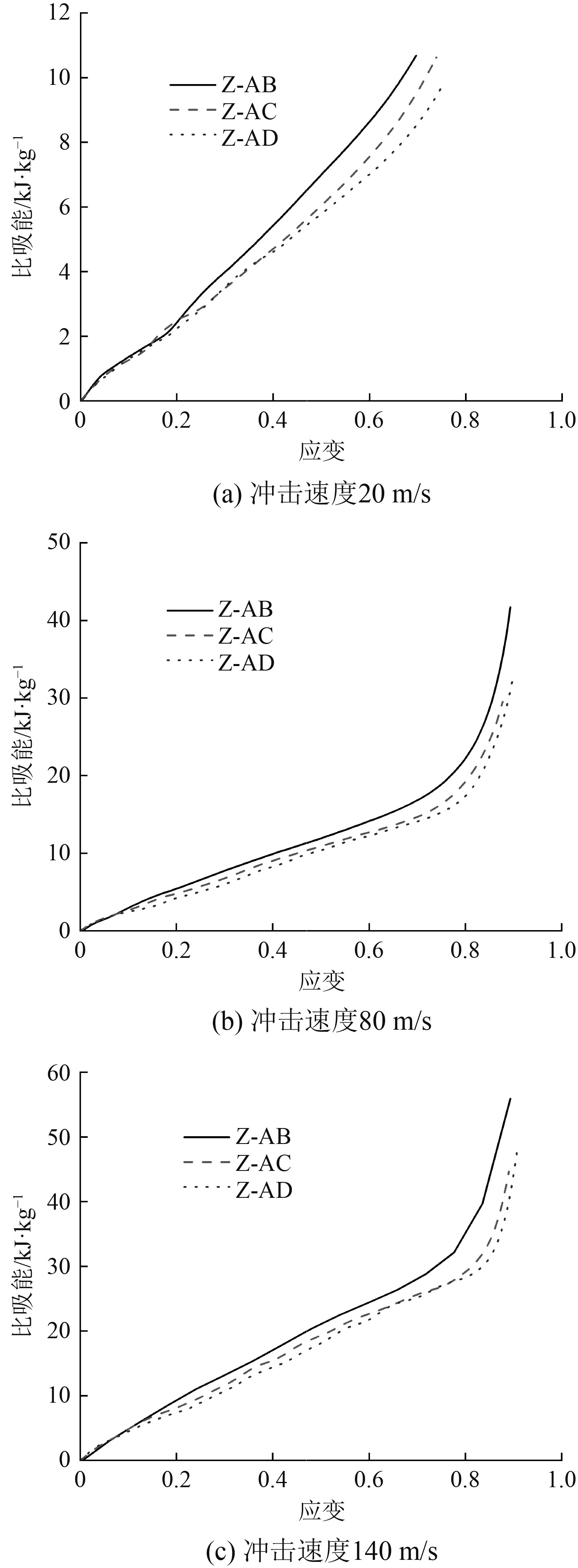
增强型双箭头结构在不同冲击速度下的比吸能情况如图14所示。可知,冲击速度相同时,不同梯度的双箭头结构表现出不同的能量吸收,Z-AB的比能量吸收明显大于Z-AC和Z-AD,主要因为在相同的冲击速度下,Z-AB的宏观负泊松比明显小于Z-AC和Z-AD,结构在动态冲击过程中结构向内收缩,结构的承载能力增强,芯子杆件的抗屈曲能力发挥的较为充分,能量吸收相对较多。相同梯度的增强型双箭头结构,冲击速度越大,结构的比吸能越多,随着冲击速度的增大,惯性效应增强,结构发生由“X”型到“V”型最后“I”型逐层失效的变形模式,不同梯度增强型双箭头结构的比吸能吸收逐渐趋于一致。
3 结 语 1)基于二维双箭头负泊松比结构,通过增加支撑连杆方式设计了新型增强型三维双箭头负泊松比结构,推导了结构的宏观泊松比解析公式,结果发现增加支撑连杆未影响结构的负泊松比效应,且随着$ \theta $的增大,结构的宏观泊松比逐渐减小,理论表征与数值模拟进行验证,结果吻合较好。
2)在动态冲击作用下,Z-AB具有显著的负泊松比效应,平台应力和比吸能均优于Z-AC和Z-AD,表现出优异的力学特性。
3)不同冲击速度下,增强型双箭头结构表现出不同的变形模式。在低速情况下,结构表现出“X”型失效模式,在中速情况下,呈现“V”型失效,高速情况下,呈现“I”型失效的变形模式。
4)随着冲击速度的增大,不同角度梯度增强型双箭头结构的平台应力和比吸能均表现出明显提高。



 2024, Vol. 46
2024, Vol. 46
