0 引　言

深海载人潜水器是深海进入、探测、开发和保护的重要技术手段和装备^[1−2]。载人舱耐压球壳是保证下潜人员及舱内设备免受外界海水巨大压力的耐压结构，为载人潜水器的核心部件^[3]。目前，大深度载人潜水器多选用钛合金耐压球壳形式，其具有结构简单、容重比高、承载能力强、有相同的周向和径向应力值等优点^[4]。其安全可靠性水平对整个载人潜水器能完成设定的任务有决定性影响，开展耐压球壳的安全可靠性研究具有重要意义。

国内学者在耐压球壳可靠性计算分析问题上开展了一些研究，周勇^[5]参考半球弹塑性屈曲载荷参数近似公式，使用改进一次二阶矩法开展了半球壳结构可靠性分析。张磊等^[6]采用Kriging建模和序贯加点相结合的方法开展了耐压球壳结构可靠性计算并开展了载人舱结构优化设计。石佳睿等^[7]在基于有限元计算结果的拟合得到了的耐压球壳临界压力计算公式，在此基础上使用改进一次二阶矩法开展了可靠性和灵敏度分析。需注意的是，其研究方法都在全域失效方程基础上开展，全域的失效方程在对于反映结构失效规律有重要意义，但在针对具体结构失效点附近的精度不高，这可能给最终的可靠性评估结果带来较大误差，因此需开展较为精确的耐压球壳可靠性计算方法研究。

本文在有限元计算结果的基础上基于自适应Kriging方法，获得了耐压球壳在不同载荷下的失效方程，并在此基础上开展了耐压球壳可靠性分析，本文研究结果可为无失效方程结构的可靠性计算提供参考。

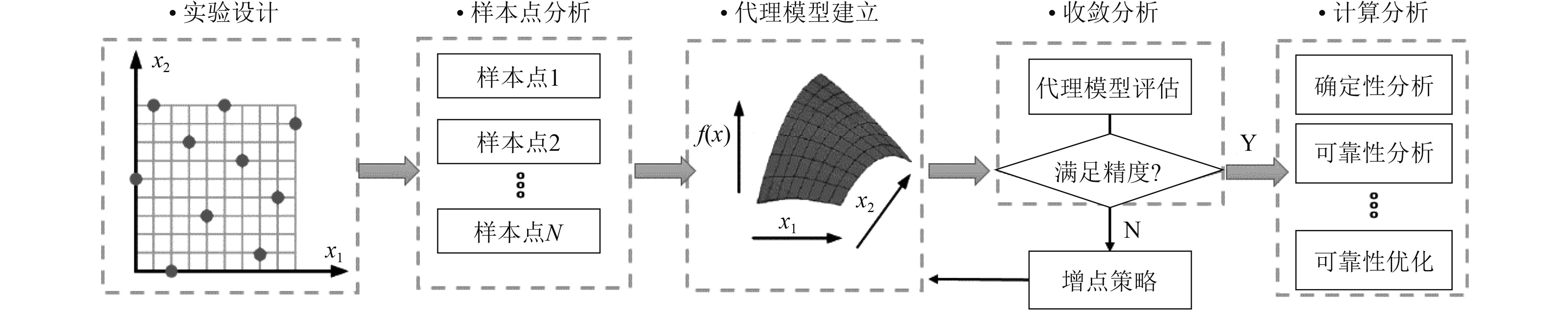
1 代理模型及自适应Kriging方法 1.1 代理模型方法

在可靠性分析中，如果直接采取高精度的仿真模型进行分析与设计将产生巨大的计算成本，促使提出一种以较小计算代价获得研究对象较为准确状态函数的方法，代理模型技术应运而生。所谓代理模型技术^[8]是在保证一定拟合精度的前提下，利用已知模型（仿真分析模型、数值模型或物理模型等）的离散数据以某种合适的代理模型方法进行数据拟合，近似获得一个数学函数模型去替代高耗时分析模型进行需要较大样本量的分析工作。一般使用代理模型方法开展可靠性计算过程，主要包括：实验设计、样本点分析、代理模型建立、收敛分析及在建立的代理模型的基础上开展各类计算分析，代理模型一般的应用模式如图1所示。常用的构建代理模型方法包括响应面法、人工神经网络、径向基函数、Kriging等方法。

1.2 Kriging模型

Kriging模型的思想由南非采矿工程师Krige^[9]于1951年提出，Kriging模型理论形成后，最初应用于地质储量估计，后来发展成一类非常流行的地质统计插值方法。1989年，Sacks教授等^[10]将Kriging理论进一步推广并给出一种较为实用的Kriging算法，使得Kriging模型不仅在地质、气象等自然科学领域得到应用，也在航空航天、船舶等工程领域得到应用和发展。Kriging模型一般可表示为一个含参数的线性回归模型和一个随机分布之和，即：

$ {G_{{\rm{Kriging}}}}\left( {x} \right) = {F}\left( {{\beta },{x}} \right) + {\delta }\left( {x} \right) = {{f}^{\mathrm{T}}}\left( {x} \right){\beta } + {\delta }\left( {x} \right) 。$

(1)

其中，${G_{{\rm{Kriging}}}}\left( {x} \right)$为Kriging模型；$ {x} $为预测样本；${\beta } = {\left[ {{\beta _1},{\beta _2}, \cdots ,{\beta _p}} \right]^{\rm{T}}}$为回归函数的待定系数；${{f}^{\rm{T}}}\left( {x} \right) = {\left[ {{f_1}\left( {x} \right),{f_2}\left( {x} \right), \cdots ,{f_p}\left( {x} \right)} \right]^{\rm{T}}}$为预测样本的基函数；$ p $为基函数的个数，$ {\delta }\left( {x} \right) $为一非参数高斯随机过程，其均值为0，方差为$ {\sigma ^2} $，其协方差矩阵分量可表示为：

$ {\text{Cov}}\left[ {{\delta }\left( {{{x}^{\left( i \right)}}} \right),{\delta }\left( {{{x}^{\left( j \right)}}} \right)} \right] = {\sigma ^2}\left[ {R\left( {{{x}^{\left( i \right)}},{{x}^{\left( j \right)}}} \right)} \right]。$

(2)

对于由$ {n_d} $个n维训练样本组成的样本集（训练集）${x = }{\left[ {{{x}_1},{{x}_2}, \cdots ,{{x}_{{n_d}}}} \right]^{\rm{T}}}$，该样本集对应的响应值为${Z = }{\left[ {G\left( {{{x}_1}} \right),G\left( {{{x}_2}} \right), \cdots ,G\left( {{{x}_{{n_d}}}} \right)} \right]^{\rm{T}}}$，那么预测样本$ {x} $的Kriging模型的预测值和对应的预测偏差（方差）分别分别可表示为

$ {G_{Kriging}}\left( {x} \right) = {\hat \beta } + {{r}^{\rm{T}}}\left( {x} \right){{R}^{ - 1}}\left( {{Z} - {\hat \beta F}} \right)，$

(3)

$\begin{split} \sigma _{Kriging}^2\left( {x} \right) =& {{\hat \sigma} ^2}( 1 - {{r}^{\rm{T}}}\left( {x} \right){{R}^{ - 1}}{r}\left( {x} \right) + \\ & {{u}^{\rm{T}}}\left( {x} \right){{\left( {{{F}^{\rm{T}}}{{R}^{ - 1}}{F}} \right)}^{ - 1}}{u}\left( {x} \right) ) 。\end{split}$

(4)

式中：${F} = {\left[ {1,1, \cdots 1} \right]^{\rm{T}}} \in {\mathbb{R}^{{n_d}}} $，${\hat \beta } = {\left( {{{F}^{\rm{T}}}{{R}^{ - 1}}{F}} \right)^{ - 1}} {{F}^{\rm{T}}}{{R}^{ - 1}}{Z}$，$\hat \sigma =\dfrac{1}{{{n_d}}}{( {{Z} - {\hat \beta F}} )^{\rm{T}}}{{R}^{ - 1}}( {{Z} - {\hat \beta F}} )$，${r}^{\rm{T}}\left( {x} \right) = [ R( {{x},{{x}_1}} ), R( {x}, {{x}_2} ), $$\cdots , R( {{x},{{x}_{{n_d}}}} ) ] $，${{u}^{\mathrm{T}}}({x}) = {{F}^{\rm{T}}}{{R}^{ - 1}}{r}\left( {x} \right) - 1$。

$ {R} $为样本间的相关矩阵，其中$ {R_{ij}} = R( {{{x}_i},{{x}_j}} ) ( i,j = 1, 2, \cdots {n_d}) $。

Kriging模型不仅可以对样本点的函数值进行预测，还能估计预测值的方差，该方差可用于指导加入新的样本点，以提高建立的代理模型的精度。

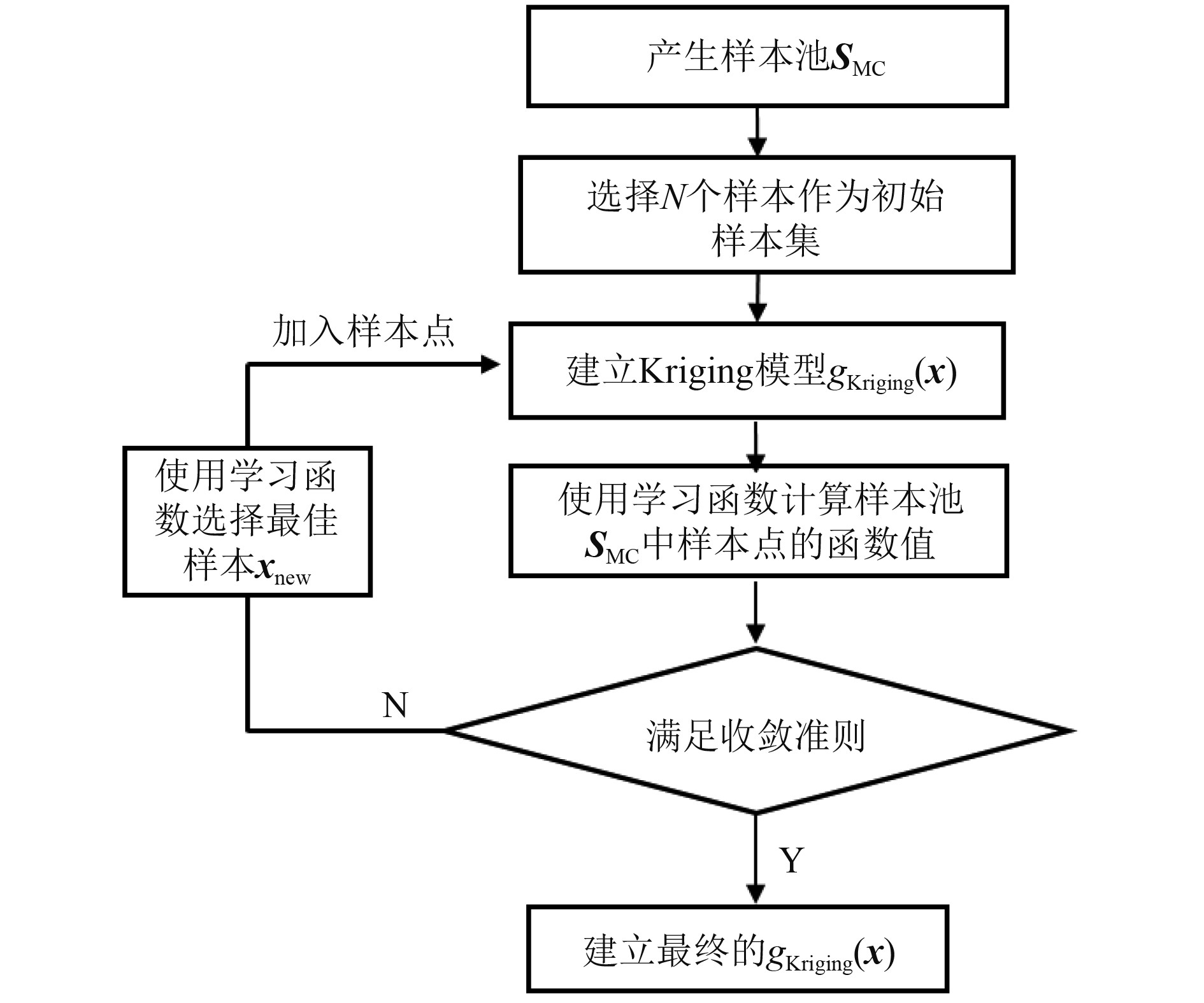
1.3 自适应Kriging

为更高效建立Kriging模型用于开展可靠性分析，已有自适应Kriging方法的提出与应用。自适应Kriging的主要思想是使用学习函数筛选对建立Kriging模型效果最佳的样本点加入训练样本集，并在此基础上不断更新代理模型，其主要流程如图2所示。

ERF（Expected Risk Function）是一种自适应Kriging常用的学习函数，其基本思想是基于预测值符号（正负）不确定性的思想，选择候选样本中符号预测风险最大的样本用于更新实验设计，学习函数ERF一般被定义为：

$ \begin{split} & \text{ERF}\left(x\right)=-\text{sign}\left(\mu_{\hat{G}}\left(x\right)\right)\mu_{\hat{G}}\left(x\right) \\ & \Phi\left(\text{sign}\left(\mu_{\hat{G}}\left(x\right)\right)\frac{\mu_{\hat{G}}\left(x\right)}{\sigma_{\hat{G}}\left(x\right)}\right)+\sigma_{\hat{G}}\left(x\right)\phi\left(\frac{\mu_{\hat{G}}\left(x\right)}{\sigma_{\hat{G}}\left(x\right)}\right)。\end{split} $

(5)

其中，$ \text{sign}(·) $为符号函数，ERF函数值最大的样本点符号被误判的风险最大，候选样本中ERF最大值的样本被识别出来用于更新实验设计并重新生成Kriging模型，ERF值越小，样本符号被误判的概率就越低，文献[11]给出收敛条件建议值为$ \max \left[ {{\text{ERF}}\left( {x} \right)} \right] \leqslant {10^{ - 4}} $。

2 数值算例 2.1 算例1

该算例来源于文献[12]，其本身是一个二维小概率失效问题，包含2个标准正态分布随机变量$ {x_1} $和$ {x_2} $，且$ {x_1} $和$ {x_2} $相互独立，其极限状态函数为：

$ G\left( {x} \right) = 0.5{\left( {{x_1} - 2} \right)^2} - 1.5{\left( {{x_2} - 5} \right)^3} - 3。$

(6)

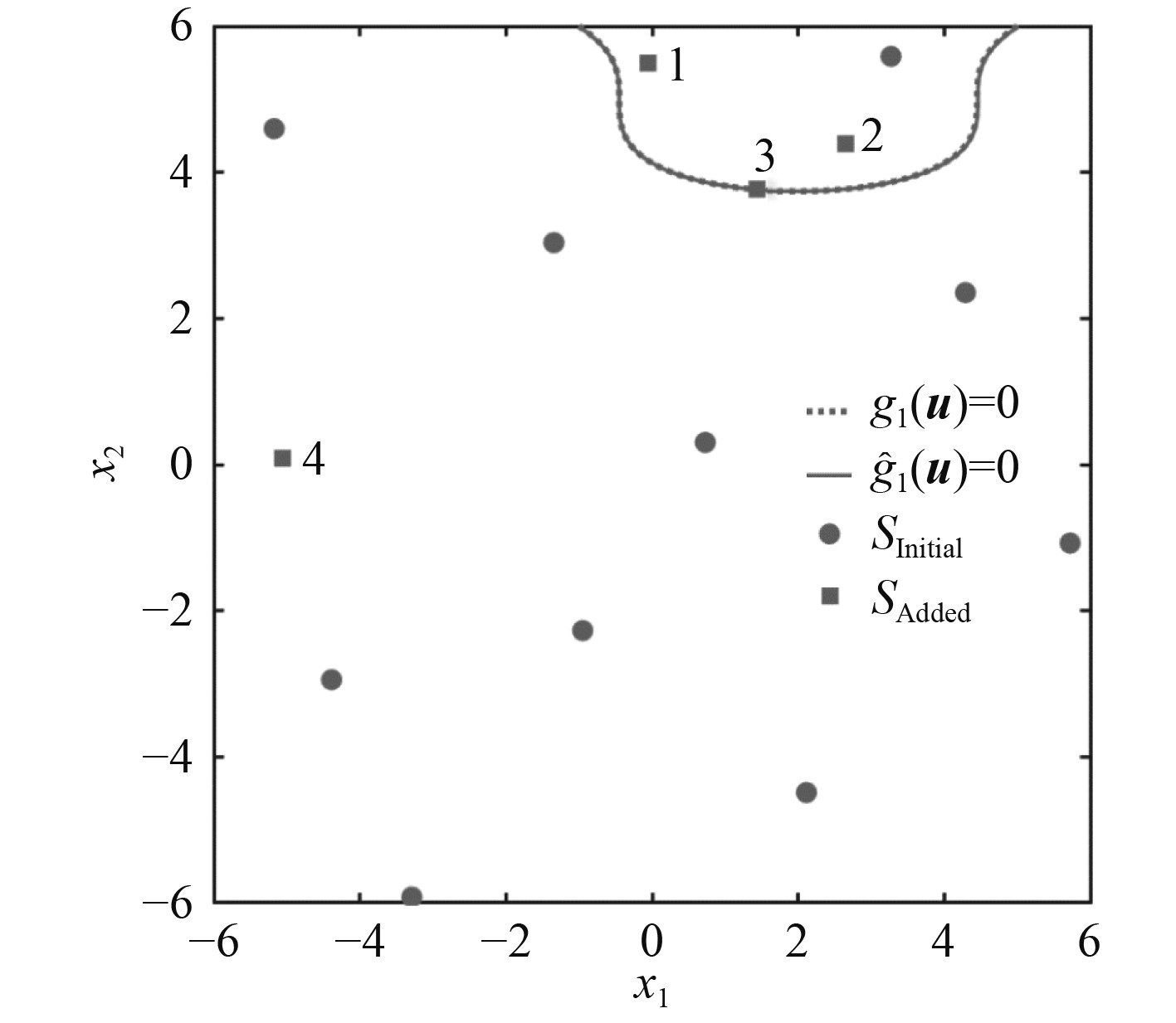
图3所示为算例1的失效边界构建过程，该算例设计了$ 2 \times {10^7} $个候选样本点，使用10个初始样本点，在学习函数的指导下通过加入4个样本点即构建出了极限状态函数，该算例的可靠性计算结果如表1所示。本文使用的自适应Kriging方法与蒙特卡洛法的计算结果一致，调用功能函数次数远小于蒙特卡洛法。

2.2 算例2

该算例来源于文献[13]，其是一个包含6个独立随机变量的单自由度无阻尼弹簧振子模型，系统示意图见图4，该模型极限状态函数为：

$ G\left( {r,m,{c_1},{c_2},{t_1},{F_1}} \right) = 3r - \left| {\frac{{2{F_1}}}{{m\omega _0^2}}\sin \left( {\frac{{{\omega _0}}}{2}t} \right)} \right|。$

(7)

其中，$ {\omega _0} = \sqrt {\left( {{c_1} + {c_2}} \right)/m} $，分布参数如表2所示。

该算例设计了$ 2 \times {10^5} $个候选样本点，使用10个初始样本点，在学习函数的指导下通过加入19个样本点即构建出了极限状态函数，该算例的可靠性计算结果如表3所示。本文使用的自适应Kriging方法与蒙特卡洛法的计算结果一致，调用功能函数次数远小于蒙特卡洛法。

3 耐压球壳可靠性分析

本文研究的耐压球壳设计下潜深度为11 km，主要研究其在计算压力172.5 MPa附近的可靠性指标，该结果可有助于评估结构设计方案的安全可靠性。耐压球壳的变量参数如表4所示。

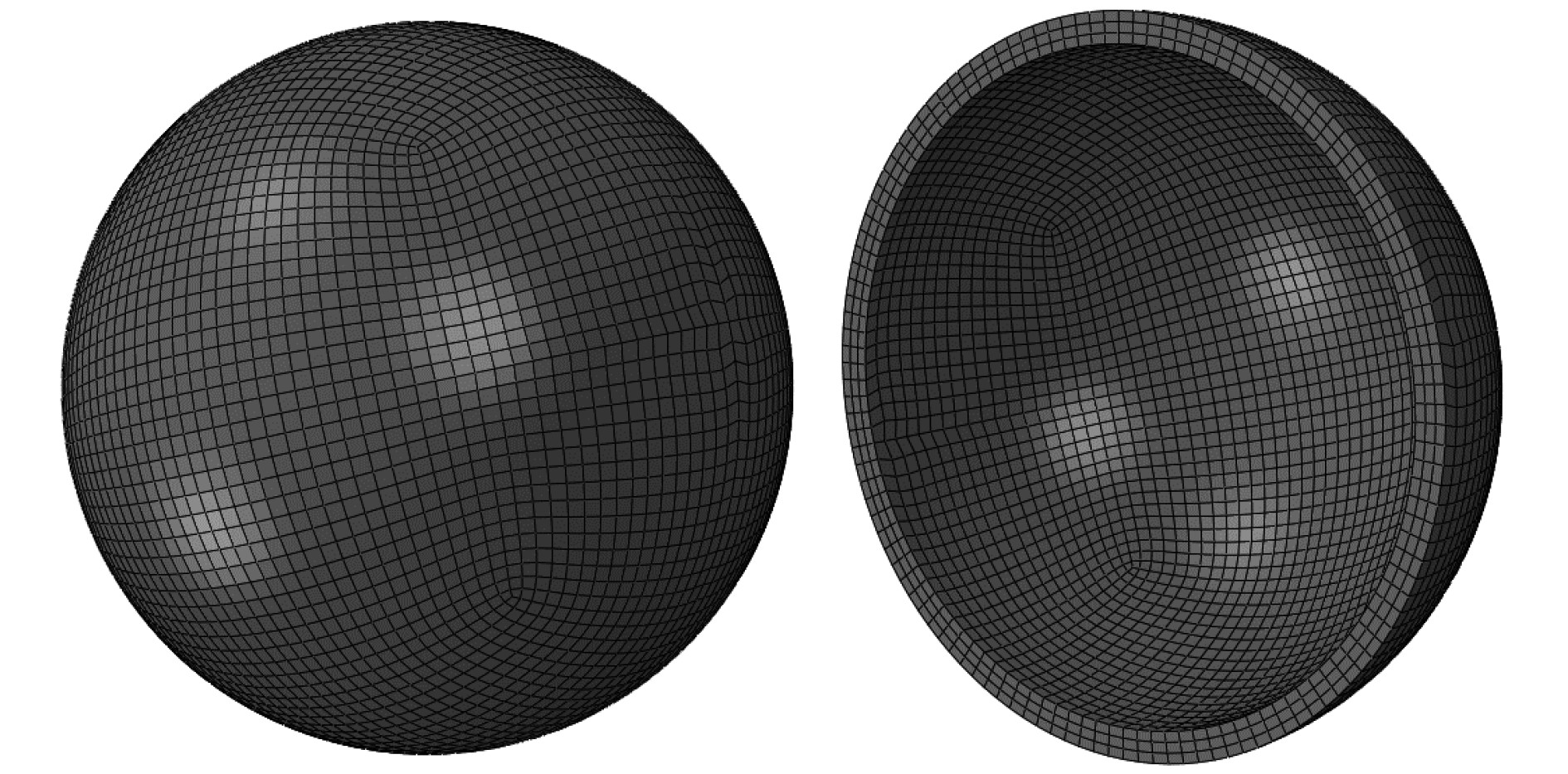
建立代理模型的样本空间范围为各变量的均值加减5倍的标准差，总共的候选样本点为2×10⁵，实验设计方法采用拉丁超立方抽样。按照自适应Kriging方法，选择10个初始样本作为初始样本集，并基于ERF学习函数的计算结果不断更新训练样本集。每个样本点均采用Abaqus有限元软件计算，参数化建模通过宏文件的方式完成，有限元模型如图5所示。结构采用实体单元，单元尺寸大小取为5 mm，球壳厚度方向设置了3层单元。在球壳承载能力计算过程中，首先使用线性有限元获得结构的一阶屈曲模态，将一阶屈曲模态乘以球壳缺陷幅值作为球壳的初始缺陷，然后使用非线性有限元计算结构的承载能力^[14]。

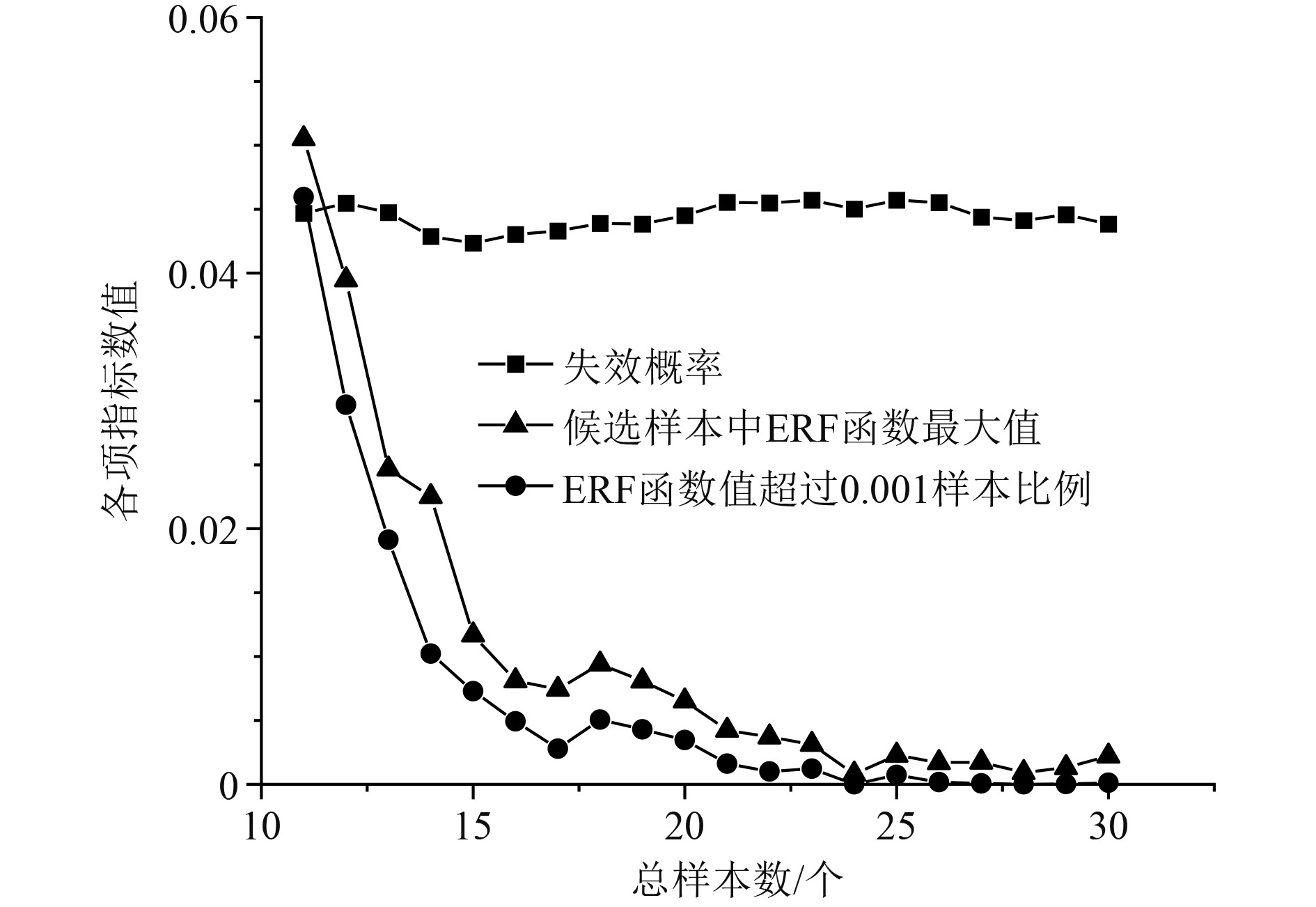
图6所示为外载荷为172.5 MPa下，使用自适应Kriging方法计算该耐压球壳失效概率的过程，表5给出了样本数20后候选样本中的最大值、失效概率的具体数值。随着样本数量的增加，候选样本中ERF函数最大值整体呈下降趋势，说明生成的Kriging模型对于候选样本点的对应响应值的误判概率越来越低。当样本数量超过24后，随着样本数量继续增加，耐压球壳的失效概率、候选样本中ERF函数最大值等指标不再产生明显变化，继续增加样本数对于提高结构失效概率精度无显著意义，因此可认为该耐压球壳的Kriging模型构建过程中收敛条件为$ \max \left[ {{\text{ERF}}\left( {x} \right)} \right] \leqslant 1 \times {10^{ - 3}} $。

表6所示为随机选择的预报值接近172.5 MPa的10个样本点作为验证集的计算结果，对比可发现：验证集Kriging模型计算结果与有限元计算结果最大误差未超过0.5‰，该Kriging模型具有较高的计算精度。需注意的是，本文提出的耐压球壳的Kriging模型构建过程中收敛条件大于文献[11]给出的建议值，其原因可能为，文献[11]给出的收敛条件建议值是基于数值算例给出的，数值算例在候选样本点的响应值为该点响应值的精确解，而本文的响应值是通过有限元软件给出的，其本质上属于近似解，同时由于球壳厚度较厚，本文使用实体单元进行计算分析并将内径设为随机变量，这就导致每次计算时都要重新生成有限元模型，网格尺寸等均会随之变化，在这些因素的共同作用下仍选择文献[11]给出的建议值将不再合适。

在开展172.5 MPa下耐压球壳失效概率计算以外，本文还计算了170 MPa、175 MPa和177.5 MPa下结构失效概率，计算过程中对数据进行了对比，当ERF函数值达到收敛条件$\max \left[ {{\text{ERF}}\left( {x} \right)} \right] \leqslant$1×10⁻³后，再增加样本数耐压结构的失效概率无明显变化，因此可认为收敛条件取为$ \max \left[ {{\text{ERF}}\left( {x} \right)} \right] \leqslant $1×10⁻³是合适的。各个载荷下结构的失效概率如表7所示，对比建立Kriging模型所需样本总数与达到变异值5%^[13]使用抽样法所需的样本数相比，本文提出的基于Kriging的耐压球壳可靠性计算方法具有较高计算效率。

4 结　语

本文使用自适应Kriging方法结合ERF学习函数基于有限元方法建立了耐压球壳结构的失效方程，并在此基础上开展耐压球壳靠性计算，可得如下结论：

1）本文使用的自适应Kriging方法可构建耐压球壳的失效方程并可在此基础上开展可靠性计算，通过验证样本点的对比结果看该方法建立的失效方程具有的较高精度，且与抽样法相比具有较高的计算效率，使用自适应Kriging方法可解决无失效方程结构的可靠性计算问题。

2）在开展自适应方法建立Kriging模型过程中，学习函数的收敛指标应随着计算模型的精度进行适当调整。