0 引　言

海洋开发活动多样化和细致化对船舶定位技术提出了严峻挑战，传统锚泊定位受限于水深和定位精度，无法满足船舶作业的要求。20世纪60年代提出船舶动力定位概念。船舶动力定位系统的核心是控制系统^[1]。由控制器发出控制信号，推进器产生推力和力矩以抵消外界环境干扰，使船舶保持在预期位置、首向，拥有稳定可靠的作业能力。

早期的动力定位大多采用PID控制器。PID控制器算法简单，具有一定的鲁棒性，但由于不能在线调整参数^[2]，面对非线性、时变的对象以及外界干扰过大时无法达到理想的动力定位控制效果。随着计算机信息技术发展，一些学者尝试运用模糊控制解决上述问题。模糊控制在一定程度上模仿人类智能的推理方式，是一种可处理不确定性、非线性和其他不适定问题的有效控制技术。它不依赖于控制对象的精确数学模型，抗干扰能力较强，鲁棒性好，能达到较好的动力定位控制效果。Inoue等^[3]结合模糊控制策略，采用位置及位置偏差作为控制器输入量，以推进器的推力作为输出量，推导出单点系泊动力定位的基本模型并验证控制效果较好。赵国华^[4]提出利用模糊神经算法，通过更新动力定位系统的输出控制量策略，实现水面船舶动力定位控制，可显著减小控制误差。龙洋等^[5]将模糊解耦控制算法应用于动力定位船舶定速航行中，使系统响应性能较好，而且具有一定的鲁棒性。但需指出的是，模糊控制器对于稳态误差的消除能力较弱，无法满足有精度要求的动力定位控制系统。此外，模糊控制在离散化和量化取整时必然带来一定误差，可导致控制系统不稳定。因此，对于非线性、时变、面临较大的干扰且有精度要求的控制对象，单独使用PID或模糊控制都有一定局限性。现有研究表明，将PID和模糊控制结合起来，可起到取长补短效用。例如，张梅红^[6]将模糊PID控制应用于车载自动调平液压系统中获得较高控制精度，且表现出良好的动态响应性能。钱素娟等^[7]将模糊PID控制器应用于电液比例阀控制中，可大幅降低了系统振荡幅度，并提高了电液比例阀的控制精度。陈珊珊^[8]结合模糊控制理论和经典PID方法设计了基于舰船动态过程的PID参数模糊自整定控制器，提高了控制品质并可增强鲁棒性。

需说明的是，现有模糊PID控制并未实现对量化比例因子进行优化，这可能限制模糊PID控制性能发挥。当遇到对船舶定位有严苛要求的工程环境可能无法满足工程要求^[9]。基于某动力定位船舶三自由度运动模型，尝试引入天牛须搜索算法（Beetle Antennae Search algorithm, BAS）设计了一种基于优化算法的模糊PID控制器，通过加入串联补偿解耦算法消除横荡与首摇控制量的相互影响，然后利用Matlab/Simulink对定点定位工况在无干扰和瞬时干扰下的船舶运动响应进行仿真分析，通过与PID、模糊PID对比，探究基于BAS的模糊PID解耦算法在船舶动力定位系统中的应用。

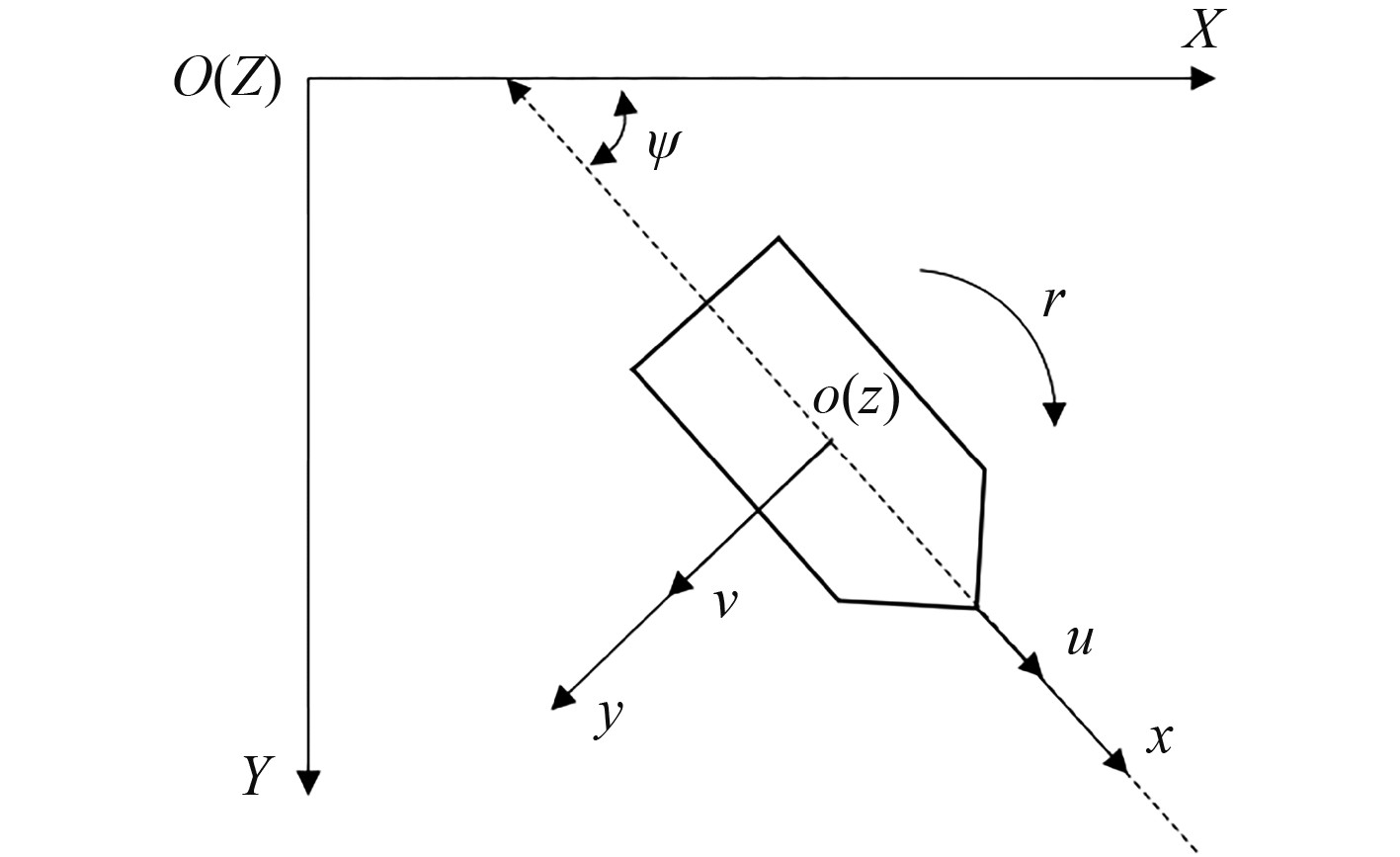
1 动力定位船舶数学模型 1.1 运动学模型

采用图1所示的大地坐标系$ O - XYZ $与随船坐标系$ o - xyz $。对于动力定位船舶，在横摇和纵摇很小的情况下，其运动可简化为3个自由度，即横荡、纵荡和首摇^[5]。动力定位船舶三自由度运动学模型如下：

$ \dot \eta = R\left( \psi \right)\upsilon 。$

(1)

式中：${\mathbf{\eta }} = {\left[ {x,y,\psi } \right]^{\text{T}}}$为船舶在大地坐标系的位置，$\psi $为首向角；坐标转换矩阵$R\left( \psi \right) = [\cos \psi , - \sin \psi ,0;\sin \psi , \cos \psi ,0;0,0,1]$；$\upsilon = {\left[ {u,v,r} \right]^{\text{T}}}$为随船坐标系下的纵荡速度$u$、横荡速度$v$以及首摇角速度$r$。

1.2 动力学模型

对于动力定位船舶，一般只需考虑横荡、纵荡和首摇3个方向低频运动，忽略科氏力，船舶的动力学模型如下^[5]：

$ {\boldsymbol{M}}\dot \upsilon + {\boldsymbol{D}}\upsilon = \tau + \omega。$

(2)

式中：$ {\boldsymbol{M}} $为船舶的惯性矩阵，$ {\boldsymbol{D}} $为阻尼矩阵，$\tau = {[{\tau _x},{\tau _y},{\tau _\psi }]^{\rm{T}}}$为推力（力矩）矩阵，$ {\tau _x} $和$ {\tau _y} $分别为纵荡、横荡方向上的推力，${\tau _\psi }$为首摇推力矩；$\omega = [{\omega _x}, {\omega _y}, {\omega _\psi }]^{\rm{T}}$为环境的干扰力（力矩）矩阵，$ {\omega _x} $和$ {\omega _y} $分别为船舶在纵荡和横荡方向的干扰力，$ {\omega _\psi } $为船舶在首摇方向的干扰力矩。

$ M = \left[ {\begin{array}{*{20}{c}} {m - {X_{\dot u}}}&0&0 \\ 0&{m - {Y_{\dot v}}}&{m{x_G} - {Y_{\dot r}}} \\ 0&{m{x_G} - {N_{\dot v}}}&{{I_z} - {N_{\dot r}}} \end{array}} \right]，$

(3)

$ D = \left[ {\begin{array}{*{20}{c}} { - {X_u}}&0&0 \\ 0&{ - {Y_v}}&{ - {Y_r}} \\ 0&{ - {N_v}}&{ - {N_r}} \end{array}} \right]。$

(4)

式中：$ m $为船舶的质量；$ {I_z} $为船舶的转动惯量；$ {x_G} $为船舶重心与随船坐标系原点之间的距离（一般可假设为0）；$ {X_{\dot u}} $、$ {Y_{\dot v}} $分别为船舶在纵荡、横荡方向的附加质量；$ {N_{\dot r}} $为首摇方向的附加转动惯量；$ {Y_{\dot r}} $、$ {N_{\dot v}} $为船舶横荡与首摇耦合运动引入的附加质量；$ {X_u} $、$ {Y_v} $、$ {Y_r} $、$ {N_v} $、$ {N_r} $分别为船舶在纵荡、横荡、首摇方向上的线性阻尼系数。

2 基于BAS的模糊PID解耦控制算法

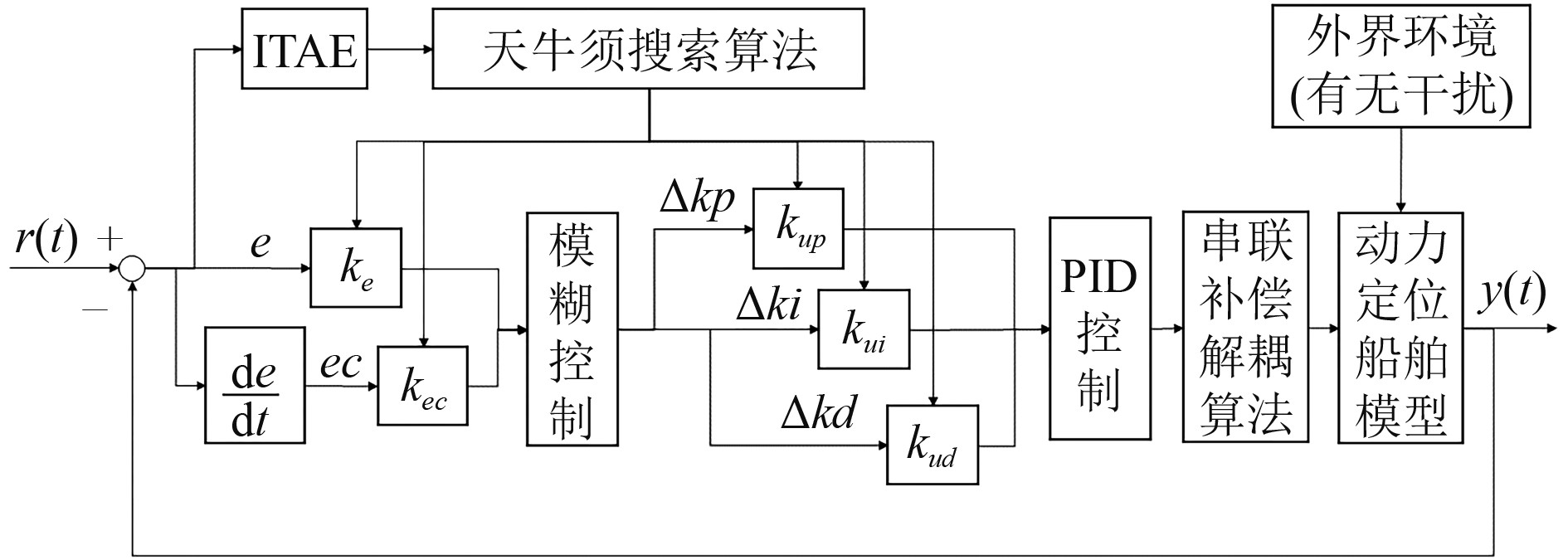
参考动力定位船舶定点定位工作模式，结合串联补偿解耦算法，设计一种基于BAS的模糊PID控制器，进一步优化PID参数的整定，原理如图2所示，其中，r(t)为控制输入，y(t)为实际输出，e为两者的偏差，ec为偏差的变化率，∆kp、∆ki、∆kd为经过模糊控制输出的PID参数调节值。BAS寻优的依据是适应度函数。时间乘绝对误差积分（Integrals of Time-weighted Absolute Error，ITAE）在控制系统静态和动态性能方面都有较好表现，故可选用ITAE为适应度函数^[10]。BAS将每次迭代后的天牛须位置实时代入到适应度函数中进行计算，通过比较适应度函数的值来确定最优位置。这里以船舶纵荡、横荡的ITAE之和为目标函数，通过BAS寻找到其最小值时对应的量化比例因子k_e、k_ec、k_up、k_ui、k_ud等5个参数值，进而实现对模糊PID控制器的优化。

2.1 动力定位解耦控制算法

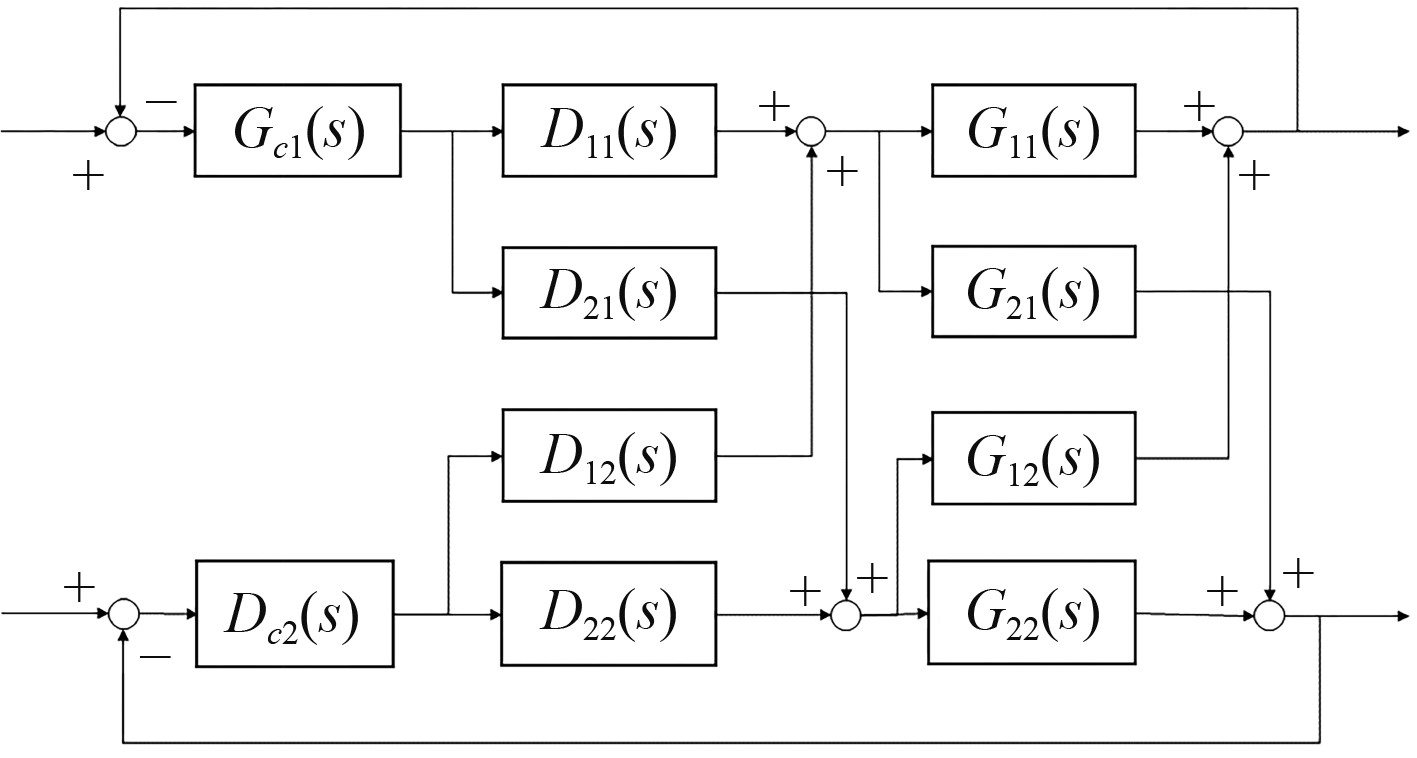
动力定位系统中横荡和首摇耦合可能导致船舶在外界干扰时振荡现象明显，进而无法准确实现定位^[11]。为提高系统控制性能，可采用串联补偿解耦方法实现横荡和首摇的单输入单输出控制^[12]。图3为动力定位系统串联补偿解耦结构图，其中，${G_{c1}}(s)$、${G_{c2}}(s)$分别为横荡与首摇模糊PID控制环节；${D_{11}}(s)$、${D_{12}}(s)$、${D_{21}}(s)$、${D_{22}}(s)$分别为串联补偿解耦环节的传递函数；${G_{11}}(s)$、${G_{12}}(s)$、${G_{21}}(s)$、${G_{22}}(s)$分别为动力定位船舶力与速度的传递函数。

由串联补偿解耦原理可得：

$ \begin{gathered} \left[ {\begin{array}{*{20}{c}} {{G_{11}}(s)}&{{G_{12}}(s)} \\ {{G_{21}}(s)}&{{G_{22}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{D_{11}}(s)}&{{D_{12}}(s)} \\ {{D_{21}}(s)}&{{D_{22}}(s)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{G_{11}}(s)}&0 \\ 0&{{G_{22}}(s)} \end{array}} \right] 。\\ \end{gathered} $

(5)

进而可推导出解耦部分的传递函数为：

$ {D_{11}}(s) = \frac{{{G_{11}}(s){G_{22}}(s)}}{{{G_{11}}(s){G_{22}}(s) - {G_{12}}(s){G_{21}}(s)}} ，$

(6)

$ {D_{12}}(s) = \frac{{ - {G_{12}}(s){G_{22}}(s)}}{{{G_{11}}(s){G_{22}}(s) - {G_{12}}(s){G_{21}}(s)}}，$

(7)

$ {D_{21}}(s) = \frac{{ - {G_{11}}(s){G_{21}}(s)}}{{{G_{11}}(s){G_{22}}(s) - {G_{12}}(s){G_{21}}(s)}} ，$

(8)

$ {D_{22}}(s) = \frac{{{G_{11}}(s){G_{22}}(s)}}{{{G_{11}}(s){G_{22}}(s) - {G_{12}}(s){G_{21}}(s)}}。$

(9)

2.2 模糊PID控制

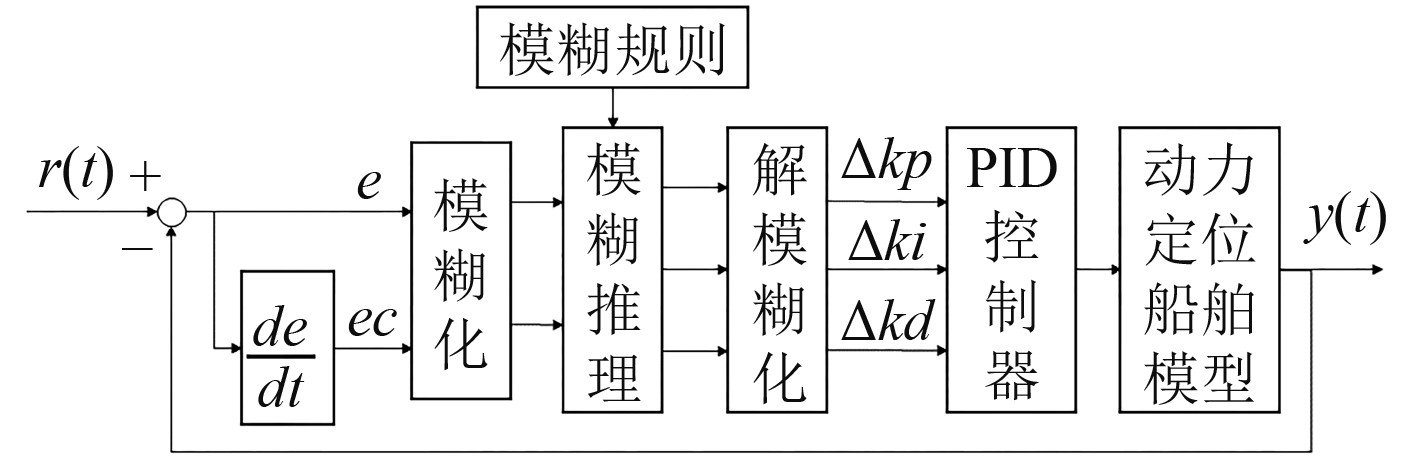
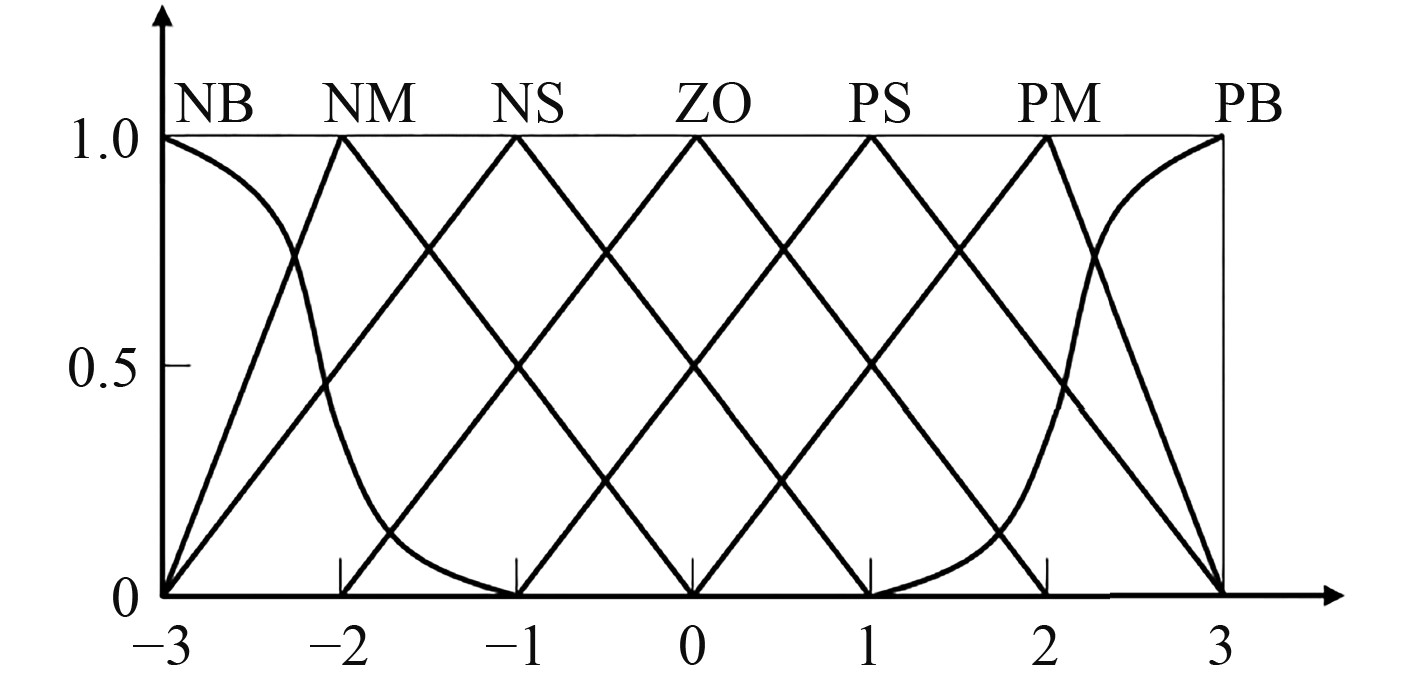
在模糊PID控制中，控制系统根据偏差及偏差变化率的大小，按照设定的模糊规则进行模糊推理和决判，得到相应的控制输出，实现对PID参数实时调整，进而优化对整个系统的控制^[9]。模糊PID控制器结构如图4所示。设置模糊控制输入论域为[−3,3]，输出论域为[−0.2,0.2]，隶属度函数曲线如图5所示，对应的模糊集为{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}。E、EC与∆kp、∆ki、∆kd对应的模糊规则如表1所示。

2.3 天牛须搜索算法

天牛须搜索算法即BAS是由Jiang等^[13]在2017年提出的一种智能优化算法，特点是寻优速度快且搜索能力强。BAS模仿自然界中天牛觅食行为。天牛在觅食过程中，通过2只触角对空气中食物气味进行感知。触角所感知的气味浓度与食物的距离有关，当食物处于天牛左侧时，左触角感知的气味浓度强于右触角感知的气味浓度，天牛根据感知到的浓度差，向着浓度强一侧随机前进。通过一次次迭代，最终找到食物的位置^[14]。

天牛找寻食物过程是BAS寻优步骤，具体描述如下^[14]：

步骤1　个体初始朝向创建：

$ d = \frac{{{\mathrm{rands}}(K,1)}}{{||{\mathrm{rands}}(K,1)||}} 。$

(10)

式中，$ \mathrm{rands}\left(\cdot \right) $为随机函数；$ K $为空间维度。

步骤2　设置步长因子$\xi $。个体的区域搜索能力是由$\xi $决定，为提高天牛的搜索范围，选取较大初始步长，并线性递减步长。公式如下：

$ {\xi _{t + 1}} = {\xi _t} \times eta，{t = 1,...,n} 。$

(11)

式中：$ eta $为递减因子，范围为[0,1]，t为当前迭代数，$ n $为总迭代数。

步骤3　建立天牛左右两触须位置坐标：

$ \left\{ {\begin{array}{*{20}{c}} {{X_r} = {X_t} + {d_0}\dfrac{d}{2}}，\\ {{X_l} = {X_t} - {d_0}\dfrac{d}{2}} 。\end{array}} \right.\begin{array}{*{20}{c}}{(t = 1,...,n)} ，\end{array} $

(12)

式中：$ {X_r} $为右须位置；$ {X_l} $为左须位置；$ {X_t} $为迭代数为t时个体质心的位置；$ {d_0} $为两触须之间的长度。

步骤4　计算适应度函数$f( \cdot )$，即左右气味浓度$f({X_r})$与$f({X_l})$的值。$f( \cdot )$根据需求而定。

步骤5　更新个体的位置，对比两触须适应度值的大小，若$f({X_r}) \gt f({X_l})$，个体向右移动；反之向左移动。其更新公式如下：

$ {X_{t + 1}} = {X_t} + {\xi _t} \cdot d \cdot {\mathrm{sign}}[f({X_r}) - f({X_l})]。$

(13)

式中：$ {\xi _t} $为$ t $次迭代步长因子；$ {\mathrm{sign}}( \cdot ) $为符号函数。

3 仿真分析

基于某动力定位船舶的三自由度模型，采用Matlab/Simulink模拟定点定位工作过程。在无外界干扰和瞬时外界干扰的2种工况下，对PID控制、模糊PID控制以及基于BAS模糊PID控制下的船舶三自由度运动响应进行仿真分析。船舶模型的参数如表2所示，该船模的惯性矩阵和阻尼矩阵^[15]如下式：

$ {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {0.754}&0&0 \\ 0&{1.199}&{0.211} \\ 0&{0.029}&{0.524} \end{array}} \right]，$

(14)

$ {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {0.014}&0&0 \\ 0&{0.102}&{ - 0.024} \\ 0&{0.192}&{0.095} \end{array}} \right]。$

(15)

3.1 程序验证

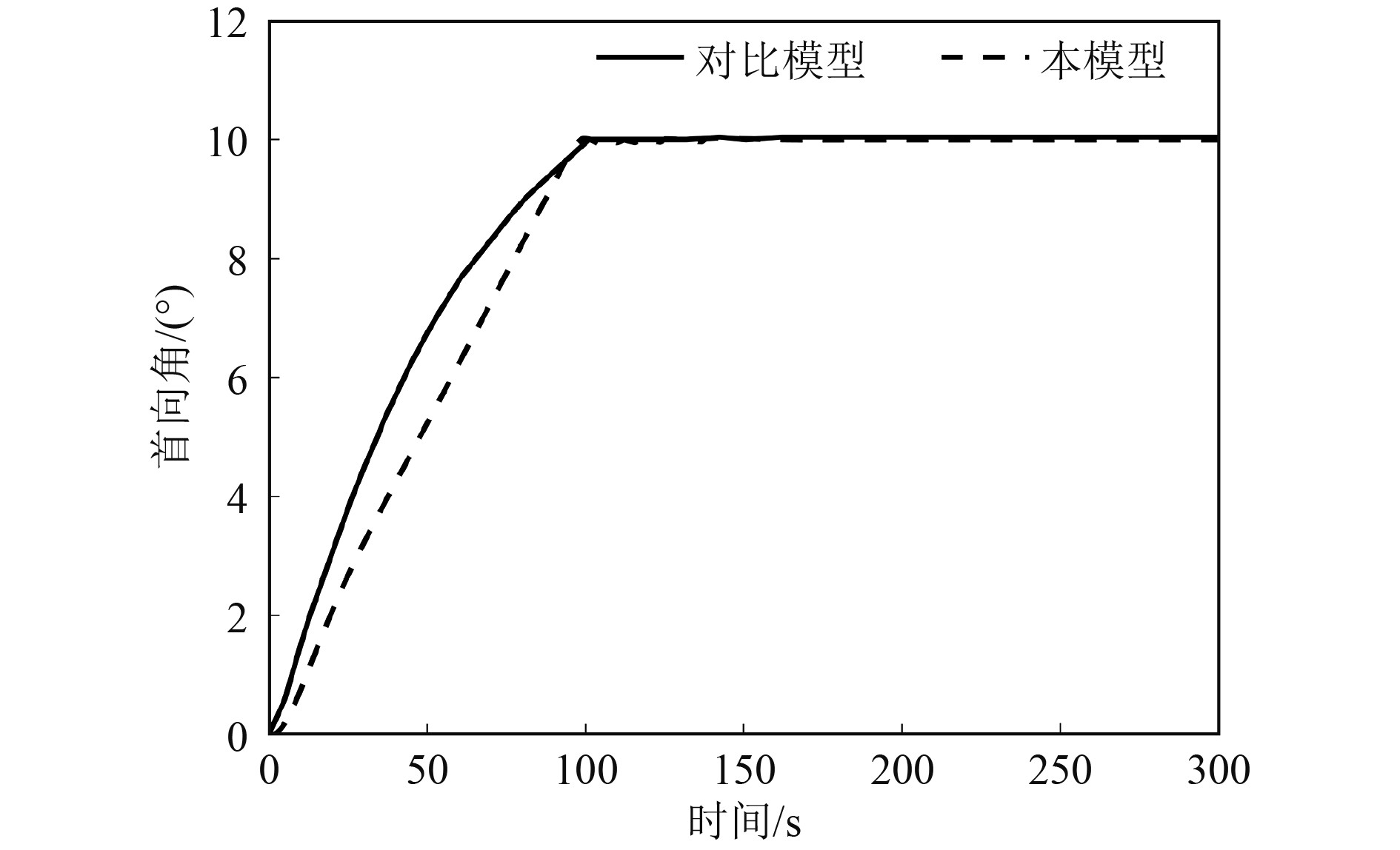
为验证本程序，与邵静林^[16]的仿真结果进行对比（两模型中船模的惯性矩阵和阻尼矩阵相同）。在无干扰工况下，先设置初始首向角为0°，期望的首向角为10°，动力定位船舶的首向角响应如图6所示，可发现，本模型和对比模型皆可在约100 s的时刻到达并稳定在期望首向角。到达阶段曲线略有差异，是二者基于偏差的速度控制不同导致。

3.2 无干扰工况

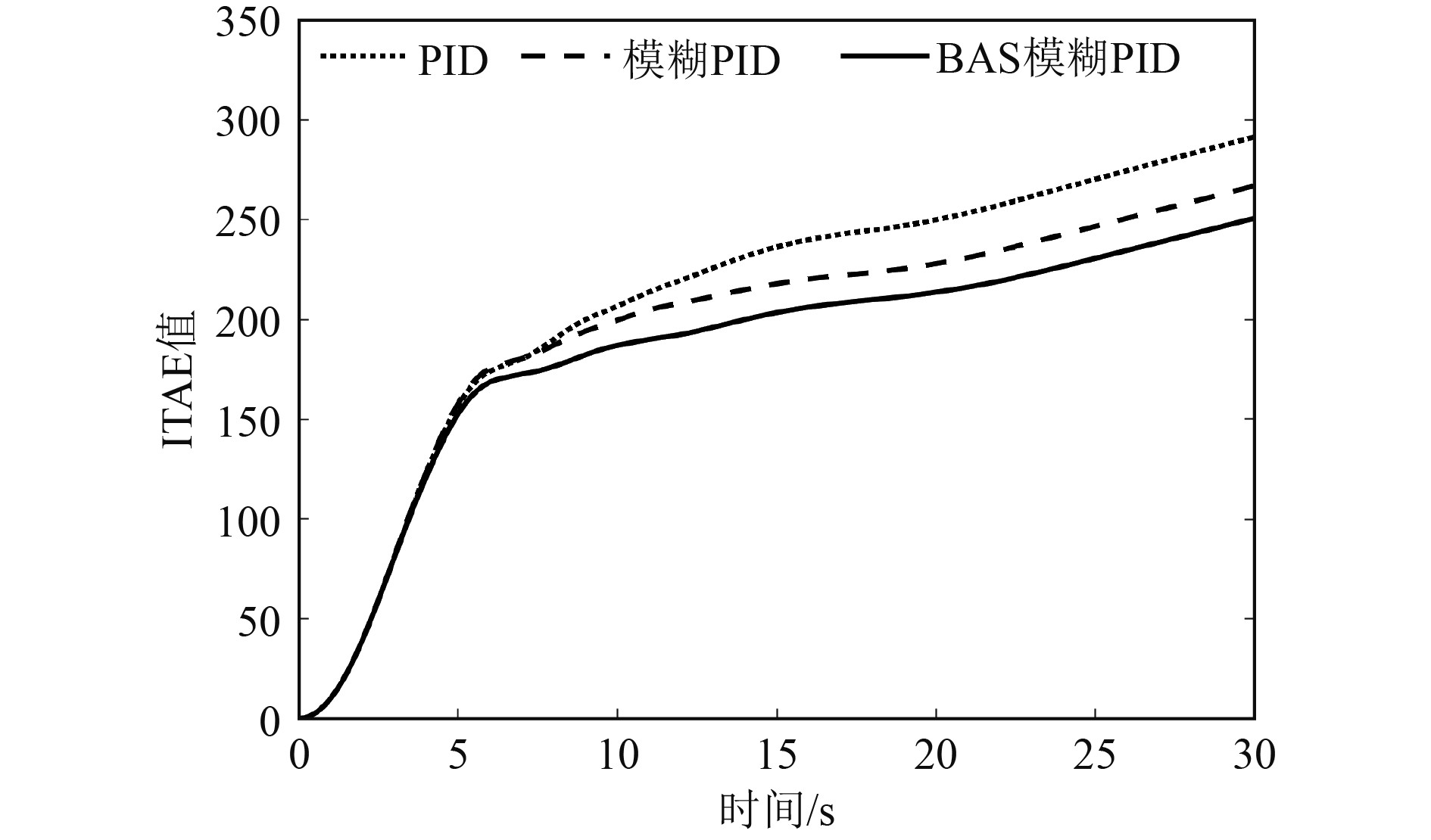
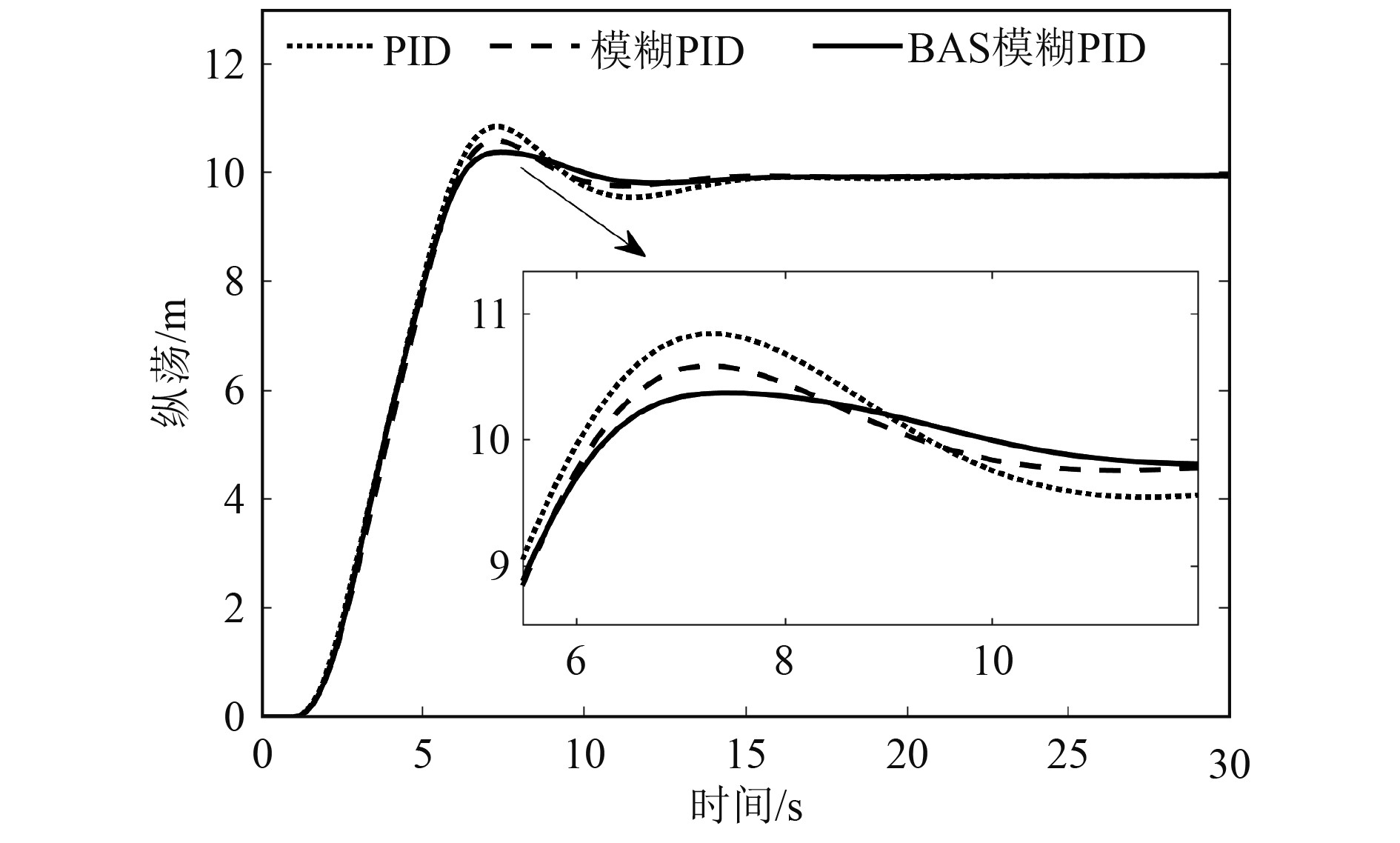
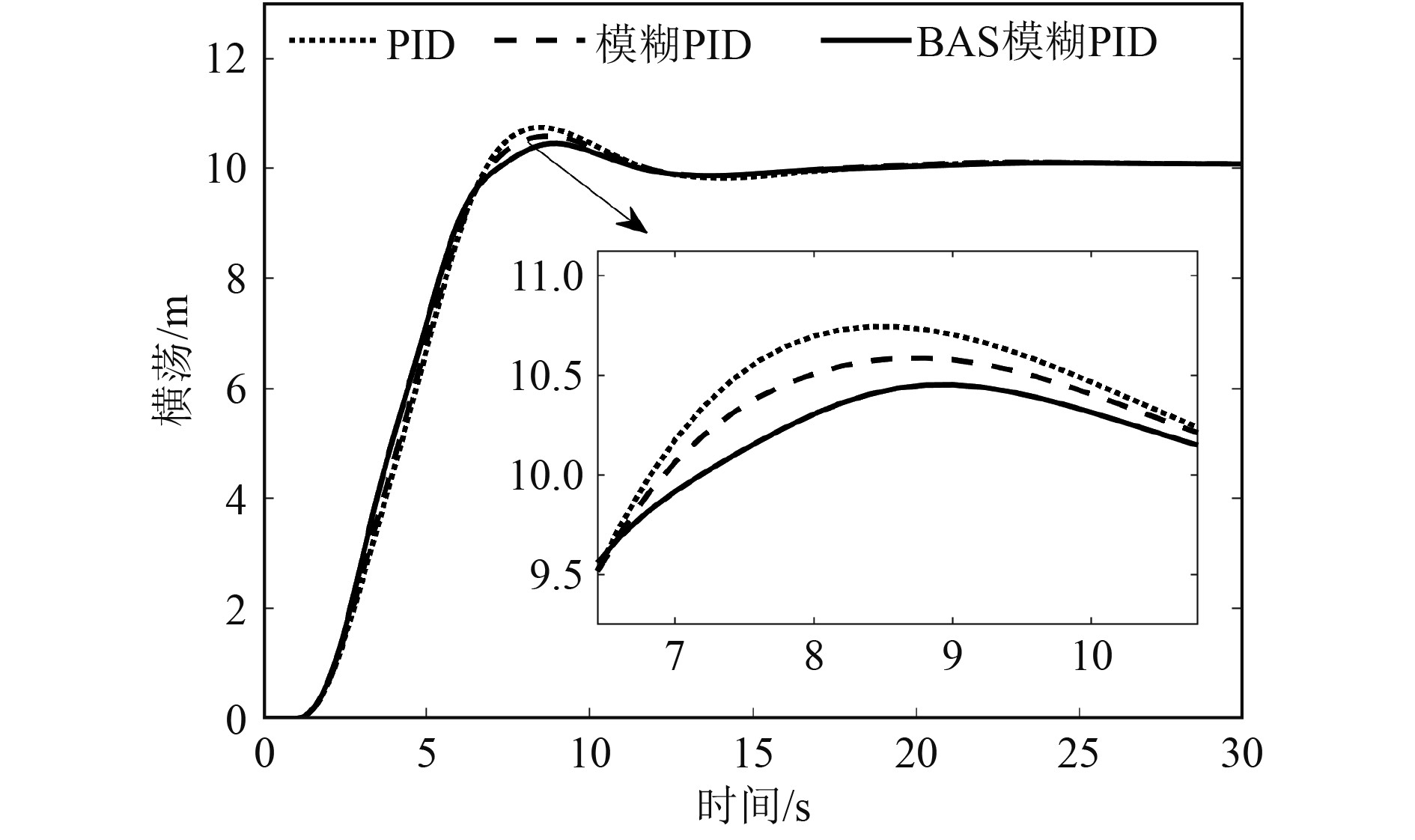
首先设置船舶的初始位置和初始首向分别为[0 m, 0 m, 0°]，设置预期的位置和首向分别为[10 m, 10 m, 0°]，步长为0.2 s。图7为无干扰工况下，动力定位船舶纵荡与横荡的ITAE值。基于BAS的模糊PID控制下ITAE值最小。ITAE值越小表明系统误差越小^[10]，这证明基于BAS模糊PID控制的船舶定位精度最高。图8和图9分别为船舶的纵荡和横荡响应曲线。研究发现，当动力定位船舶采用基于BAS模糊PID控制时，在纵荡与横荡上超调量最小，且纵荡方向在10 s左右就可到达预期值。在传统PID、模糊PID以及基于BAS的模糊PID控制下，船舶的运动响应参数如表3所示。基于BAS的模糊PID在横荡方向上的超调量相对于PID和模糊PID分别减少39.3%和26.4%，在纵荡方向超调量相对于PID和模糊PID分别减少了55.6%和39.9%，且在纵荡方向始终未发生振荡现象。该船舶的首摇响应如图10所示，3种控制策略下的船舶首向可始终保持在[−0.015°, 0.01°]的合理范围内。

3.3 瞬时干扰工况

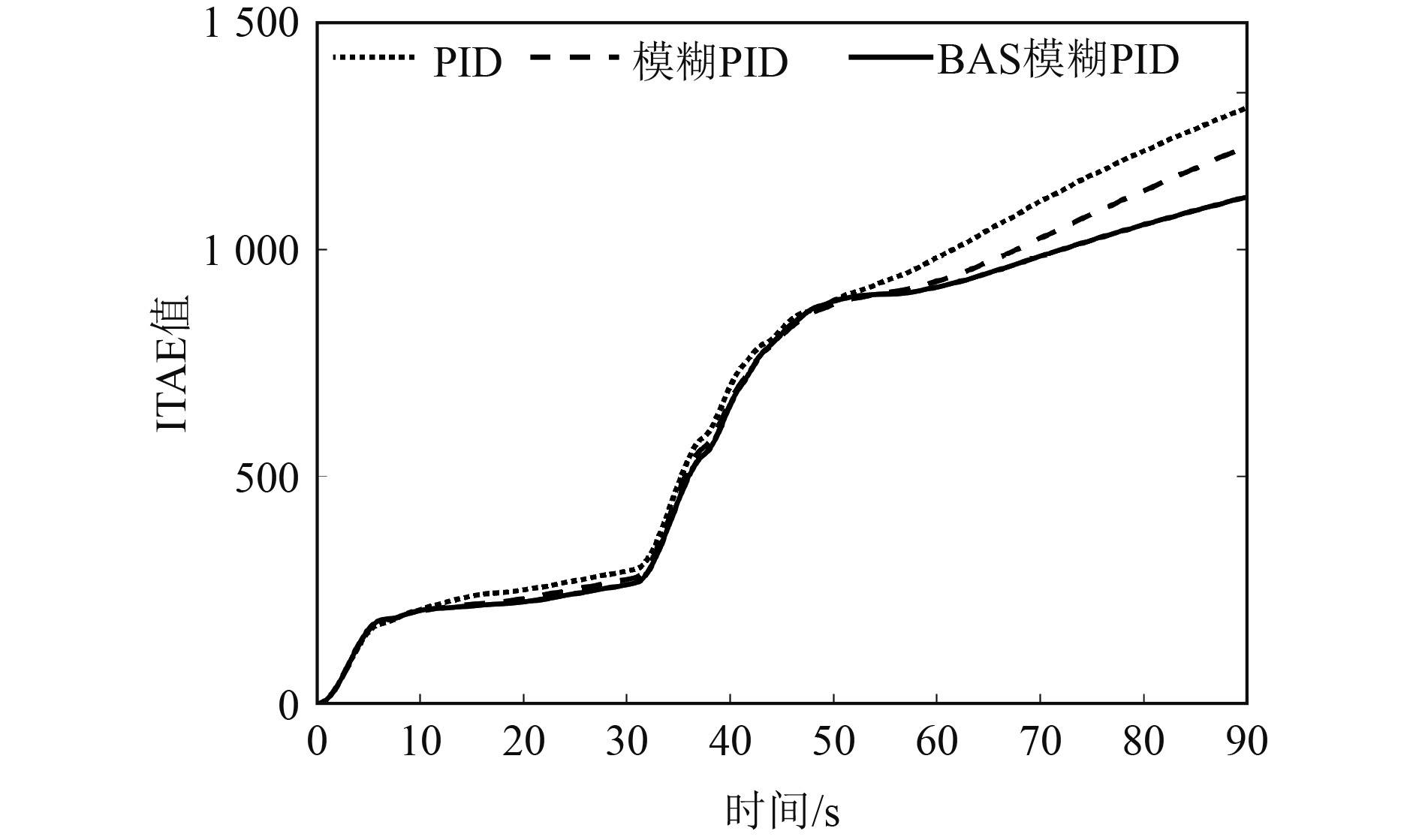
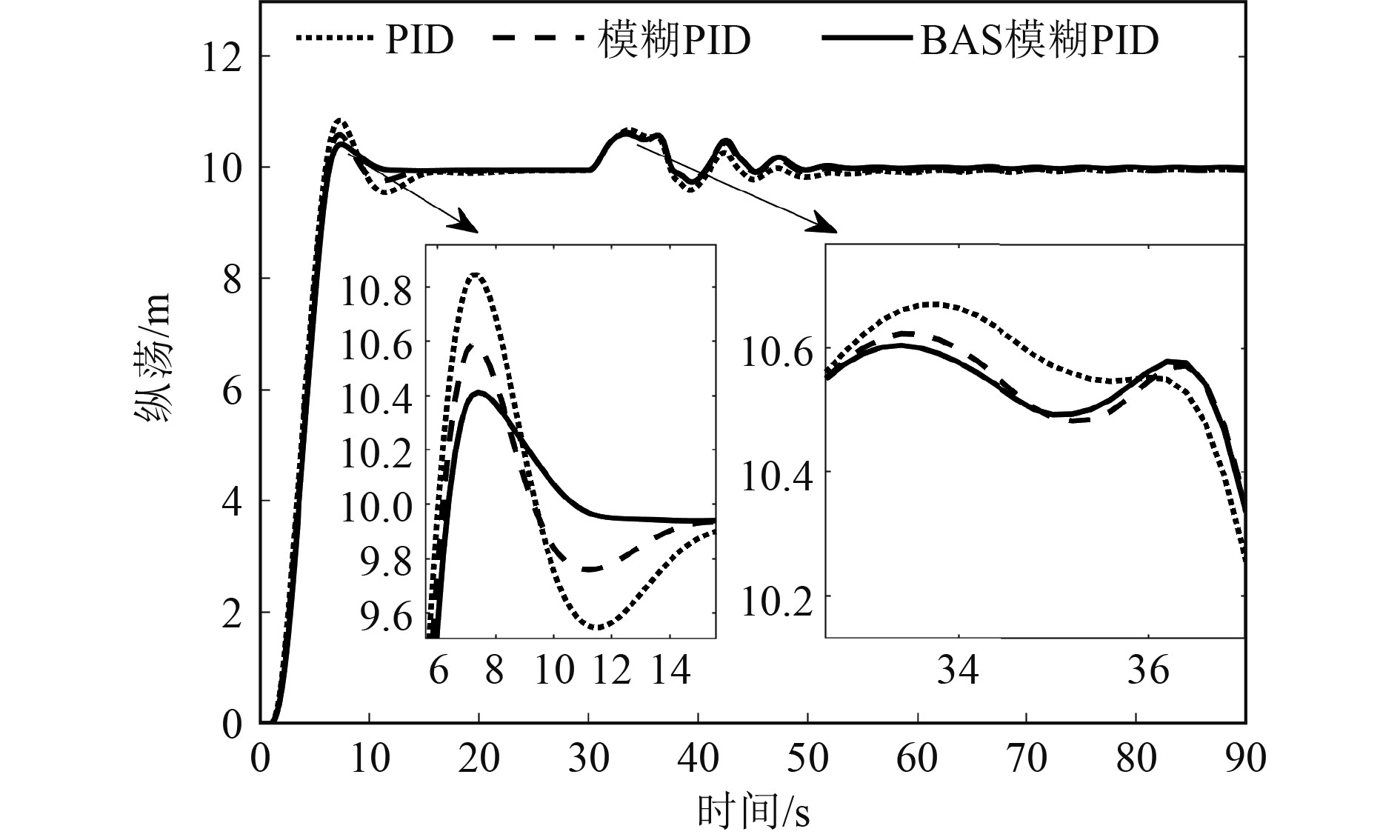
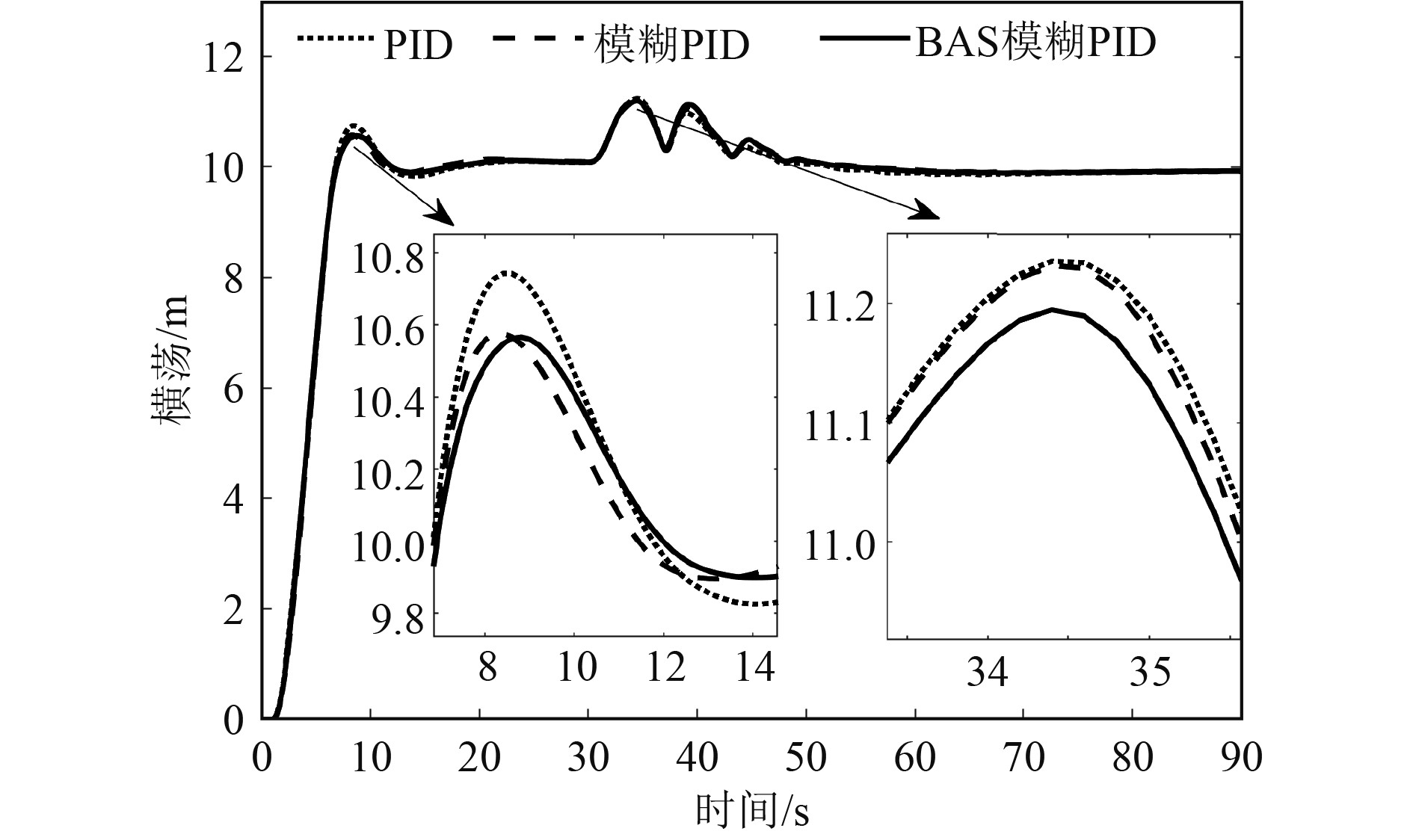
设置初始位置和首向角为[0 m, 0 m, 0°]，预期的位置和首向角分别为[10 m,10 m, 0°]，步长为0.2 s。为研究系统抗干扰能力，模拟船舶在预期位置稳定后受到阵风干扰，设置船舶在30 s时，遭受持续5 s的外界干扰^[17]。依据风载荷计算经验公式^[18]，结合船模参数可设置瞬时干扰为[0.3 kN, 0.3 kN, 0.3 kN·m]。图11为瞬时干扰工况下船舶纵荡与横荡的ITAE之和。在受到瞬时干扰后，基于BAS模糊PID控制下的动力定位船舶的ITAE值最小。这表明船舶受到瞬时干扰后，在基于BAS模糊PID控制的动力定位精度最高。图12和图13分别为船舶纵荡和横荡曲线，表4为船舶响应参数。

1）横荡方向

基于BAS的模糊PID控制下，横荡超调量相对PID控制减少23.8%，相对于模糊PID控制减少1.7%；横荡最大偏离量相对PID控制减少3.3%，相对模糊PID控制减少3.0%；

2）纵荡方向

基于BAS的模糊PID控制下，纵荡超调量相对PID控制减少51.1%，相对于模糊PID控制减少28.8%，且在约11s时就可达预期位置；纵荡最大偏离量相对于PID控制减少了13.9%，相对模糊PID控制则减少7.2%。

3）首摇响应

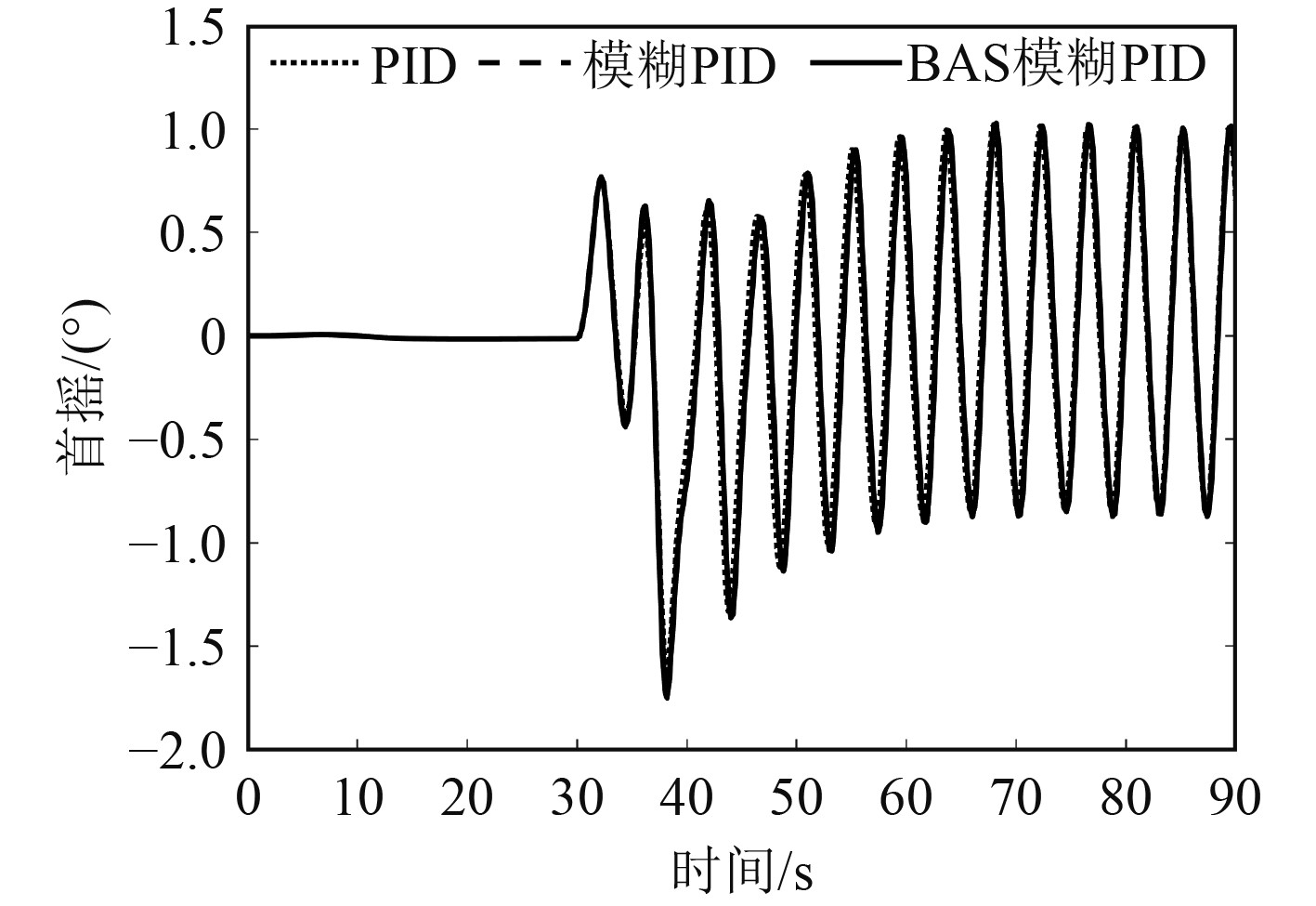
如图14所示，在受到瞬时干扰后，船舶在3种控制策略下首向最大偏离角基本相同，大约在−1.7°，随后保持在[−1°, 1°]可控范围。

4 结　语

将模糊PID应用于船舶动力定位控制系统时，由于无法确保量化比例因子选取到最优值可能限制模糊PID的控制性能发挥。尝试采用天牛须搜索算法，以船舶纵荡与横荡的ITAE之和为目标函数，通过搜索其最小值来确定模糊PID的量化比例因子。

基于动力定位船舶三自由度运动模型，加入串联补偿解耦算法来消除船舶横荡与首摇控制量的相互影响，选取动力定位船舶定点定位工作模式，利用Matlab/Simulink采用传统PID、模糊PID、基于BAS的模糊PID这3种控制器进行仿真分析。研究发现，相比于传统PID控制和模糊PID控制，采用BAS的模糊PID控制尽管在船舶首摇方向没有取得改进效果，但可显著提高船舶纵荡与横荡响应的控制精度，可明显减少纵荡与横荡的超调量以及在受到瞬时干扰时在纵荡和横荡方向的最大偏移量，进而可改善船舶动力定位系统的性能。