高压气动装置作为一种特殊的弹射试验装置在试验室得到广泛应用,它具有弹射参数调节范围广,试验成本低,不涉及火药发射时的安全问题,能够弹射各种形状、尺寸、重量、材料的弹射体等优点。因此,高压气动装置是非常有效和实用的弹射试验设备,可用于测试各种速度、过载状态下的弹射体性能。通过对高压气动装置弹射性能的建模、数值计算与分析,不仅可以为高压气动装置的弹射试验提供参考,还可以为高压气动弹射装置的优化设计、制造提供理论依据[1−2]。
在有些应用中,需要将一定质量的弹射体通过高压气动弹射装置弹射后,在满足最小出筒速度的条件下,尽可能降低弹射过程的最大瞬时过载。本文主要通过数学建模、数值计算方法,分析无缓冲腔、采用缓冲腔、采用多组高速开关阀等3种弹射装置相关参数对弹射体出筒速度、弹射过程最大瞬时过载等的影响,为高压气动弹射装置的优化设计提供依据。
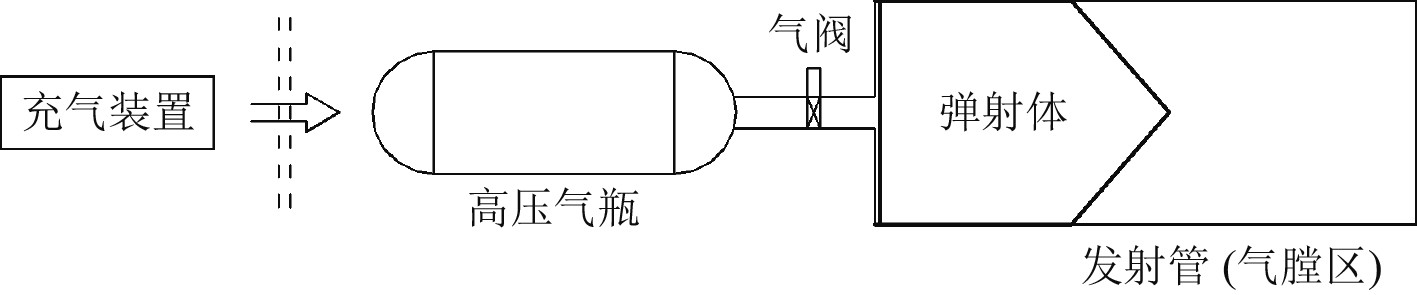
1 工作原理高压气动弹射装置利用瞬间快速释放高压气瓶内压缩空气所产生的动能和冲击压力使弹射体弹射出发射管,其工作原理如图1所示。弹射准备状态:将弹射体装在发射管的起始部,关闭气阀,向高压气瓶充气;弹射状态:打开气阀,压缩空气流经气阀推动弹射体向前运动,弹射体后的气室容积不断增大,压力逐渐降低,同时不断对弹射体加速至发射筒口,弹射体获最大速度完成弹射过程。
|
图 1 高压气动弹射装置工作原理 Fig. 1 Operating principle of high-pressure pneumatics ejection system |
由于气阀开启后,高压气瓶内的压缩空气瞬时膨胀,将对弹射体产生较大冲击,弹射体的最大瞬时过载可能超过其所能承受的范围,因此,需要在高压气动弹射装置中增加缓冲腔,含缓冲腔的高压气动弹射装置工作原理见图2。

|
图 2 含缓冲腔的高压气动弹射装置工作原理 Fig. 2 Operating principle of high-pressure pneumatics ejection system with cushion chamber |
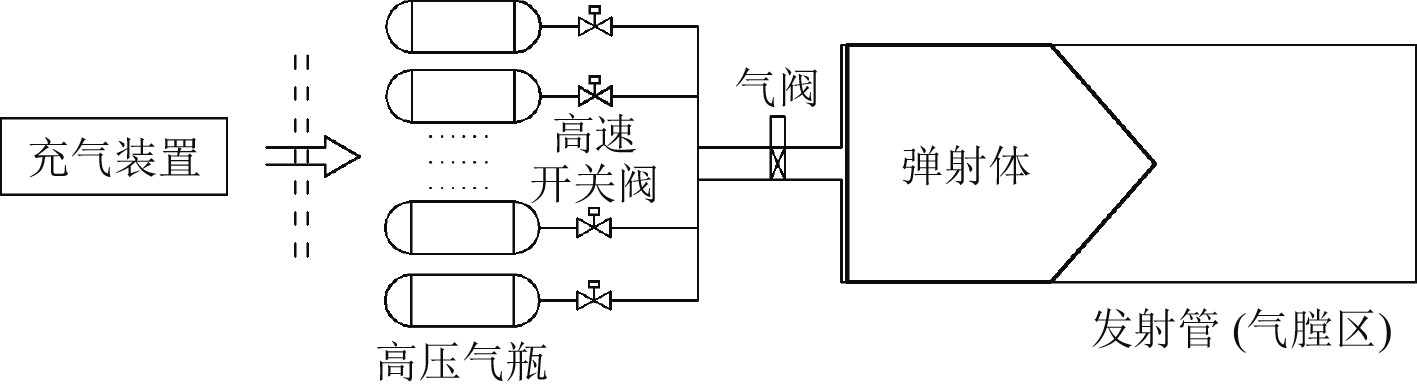
气阀开启后,高压气瓶内压缩空气的瞬时膨胀会对弹射体产生冲击,气瓶容积越大,冲击越大,冲击持续时间越长。当前,技术成熟的毫秒级响应速度的高速开关阀及高频控制系统的出现,可实现将一次大的长时冲击转化为多次小的冲击接力。将大容积的气瓶替换成多组小容积气瓶,并采用多组高速开关阀的高压气动弹射装置工作原理见图3。
|
图 3 采用多组高速开关阀的高压气动弹射装置工作原理 Fig. 3 Operating principle of high-pressure pneumatics ejection system with high-speed on-off valve |
1)工作介质为理想气体,气体流动和弹射体运动是一维轴向运动;
2)压缩气体在工作过程中某一瞬时的压力、密度、温度都均匀分布;
3)忽略气体余容的影响;
4)高压气瓶内压缩气体经高压通道流入气膛区并推动弹射体出膛的过程在短时间完成,故认为是绝热过程,忽略气体与容器及通道壁面热交换;
5)不考虑气体的粘性,忽略通道壁面摩擦;
6)对弹射体弹射运动时的空气阻力、膛壁对弹射体的摩擦阻力修正,修正系数为α;
7)气体比热比(绝热指数k)在整个过程中不随之改变,是定值;
8)气阀阀口在瞬间完全开启。
根据高压气动弹射装置工作原理及相关假设,可联立如下方程:
1)高压气瓶放气方程
| $\begin{aligned} &{Q_1} =\\ & \left\{ \begin{gathered} {A_1}\sqrt {k{{\left( {\frac{2}{{k + 1}}} \right)}^{\frac{{k + 1}}{{k - 1}}}}P_1^{\frac{{k + 1}}{k}}\frac{{{\rho _{10}}}}{{P_{10}^{\frac{1}{k}}}}} \frac{{{P_2}}}{{{P_1}}} < {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}},\\ {A_1}\sqrt {\frac{{2k}}{{k - 1}}P_1^{\frac{{k + 1}}{k}}\frac{{{\rho _{10}}}}{{P_{10}^{\frac{1}{k}}}}\left[ {{{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)}^{\frac{2}{k}}} - {{\left( {\frac{{{P_2}}}{{{P_1}}}} \right)}^{\frac{{k + 1}}{k}}}} \right]} \frac{{{P_2}}}{{{P_1}}} \geqslant {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}},\\ \end{gathered} \right. \end{aligned}$ | (1) |
2)高压气瓶内绝热状态方程
| $ \frac{{{T_{10}}}}{{{T_1}}} = {\left( {\frac{{{P_{10}}}}{{{P_1}}}} \right)^{\frac{{k - 1}}{k}}},$ | (2) |
3)高压气瓶内气体质量守恒方程
| $ {m_1} = {m_0} - \int_0^t {{Q_1}} {\mathrm{d}}t,$ | (3) |
4)缓冲区放气方程
| $\begin{aligned} & {Q_2} = \\ & \left\{ \begin{gathered} {A_2}\sqrt {k{{\left( {\frac{2}{{k + 1}}} \right)}^{\frac{{k + 1}}{{k - 1}}}}P_2^{\frac{{k + 1}}{k}}\frac{{{\rho _{20}}}}{{P_{20}^{\frac{1}{k}}}}} \frac{{{P_3}}}{{{P_2}}} < {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}},\\ {A_2}\sqrt {\frac{{2k}}{{k - 1}}P_2^{\frac{{k + 1}}{k}}\frac{{{\rho _{20}}}}{{P_{20}^{\frac{1}{k}}}}\left[ {{{\left( {\frac{{{P_3}}}{{{P_2}}}} \right)}^{\frac{2}{k}}} - {{\left( {\frac{{{P_3}}}{{{P_2}}}} \right)}^{\frac{{k + 1}}{k}}}} \right]} \frac{{{P_3}}}{{{P_2}}} \geqslant {\left( {\frac{2}{{k + 1}}} \right)^{\frac{k}{{k - 1}}}} ,\end{gathered} \right. \end{aligned}$ | (4) |
5)缓冲区绝热状态方程
| $ \frac{{{T_{20}}}}{{{T_2}}} = {\left( {\frac{{{P_{20}}}}{{{P_2}}}} \right)^{\frac{{k - 1}}{k}}},$ | (5) |
6)缓冲区气体质量守恒方程
| $ {m_2} = {m_{20}} + \int_0^t {{Q_1}} {\mathrm{d}}t - \int_0^t {{Q_2}} {\mathrm{d}}t,$ | (6) |
7)气膛区绝热状态方程
| $ \frac{{{T_{30}}}}{{{T_3}}} = {\left( {\frac{{{P_{30}}}}{{{P_3}}}} \right)^{\frac{{k - 1}}{k}}} ,$ | (7) |
8)气膛区气体质量守恒方程
| $ {m_3} = {m_{30}} + \int_0^t {{Q_2}} {\mathrm{d}}t,$ | (8) |
9)弹射体运动方程
| $ \frac{{{{\mathrm{d}}^2}}}{{{\mathrm{d}}{t^2}}}x = \frac{{{A_3}\left( {{P_3} - {P_{atm}}} \right) - mg}}{{\alpha m}} 。$ | (9) |
结合气体状态方程,联立式(2)、式(3),可得高压气瓶压力与放气质量流量的微分方程:
| $ \frac{\rm{d}}{{{\rm{d}}t}}{P_1} = - k\frac{{{Q_1}}}{{{m_{10}}}}P_{10}^{\frac{1}{k}}P_1^{\frac{{k - 1}}{k}} 。$ | (10) |
结合气体状态方程,联立式(5)、式(6),可得缓冲区压力与质量流量的微分方程:
| $ \frac{{\rm{d}}}{{\rm{d}t}}{P_2} = k\frac{{\left( {{Q_1} - {Q_2}} \right)}}{{{m_{20}}}}P_{20}^{\frac{1}{k}}P_2^{\frac{{k - 1}}{k}} 。$ | (11) |
结合气体状态方程,联立式(7)、式(8),可得气膛区压力与质量流量、弹射体位移的微分方程:
| $ \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}{P_3} = \frac{{k\left[ {\dfrac{{{Q_2}}}{{{A_3}{\rho _{30}}}}P_{30}^{\frac{1}{k}}P_3^{\frac{{k - 1}}{k}} - {P_3}\dfrac{{{\mathrm{d}}x}}{{{\mathrm{d}}t}}} \right]}}{x}。$ | (12) |
式(1) 、式(4) 、式(9)~式(12)联立,即为高压气动弹射装置的内弹道模型,在给定高压气瓶压力、容积、气阀通径、缓冲腔尺寸、节流孔板通径等的参数后,即可计算出任意时刻弹射体的位移、速度、加速度。
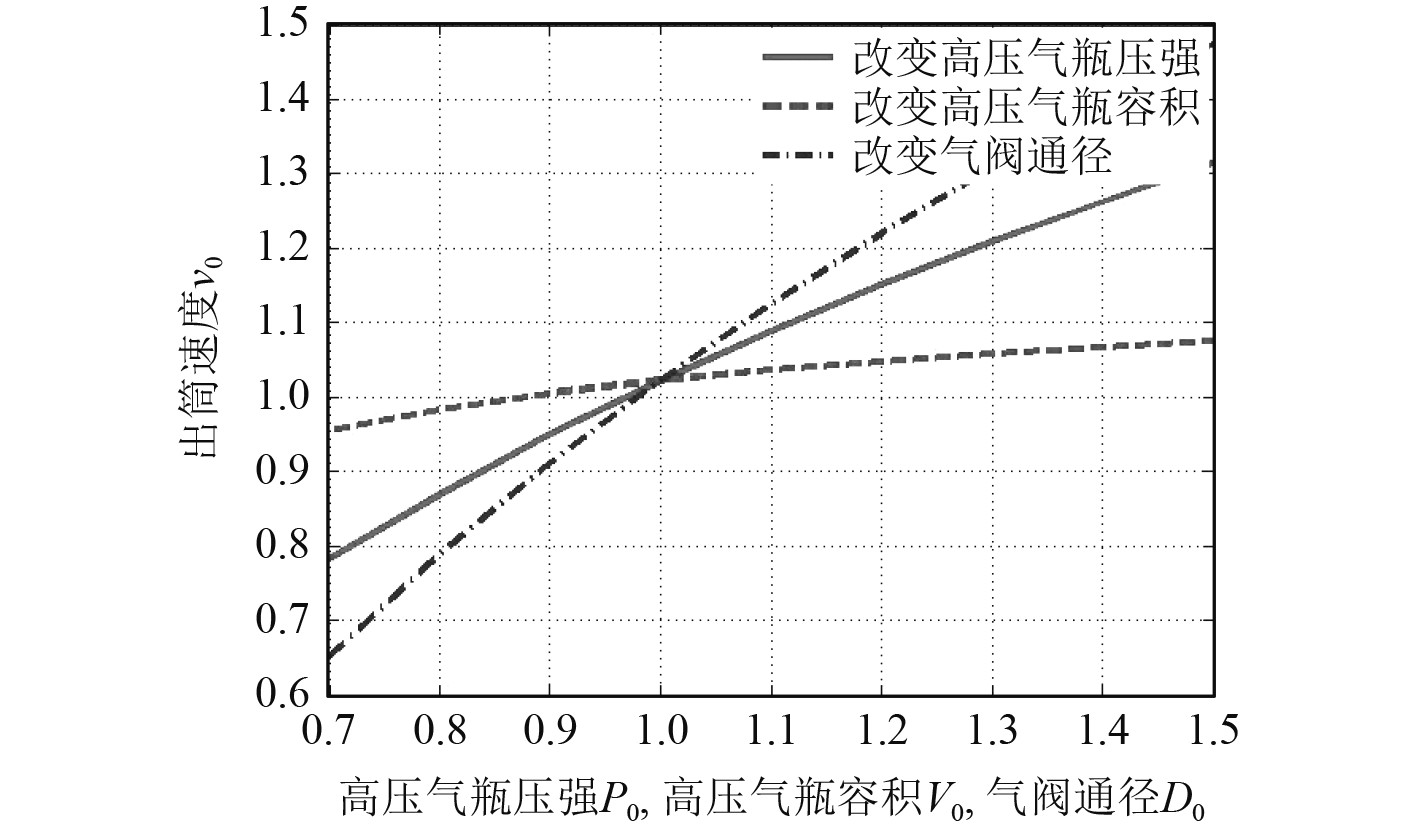
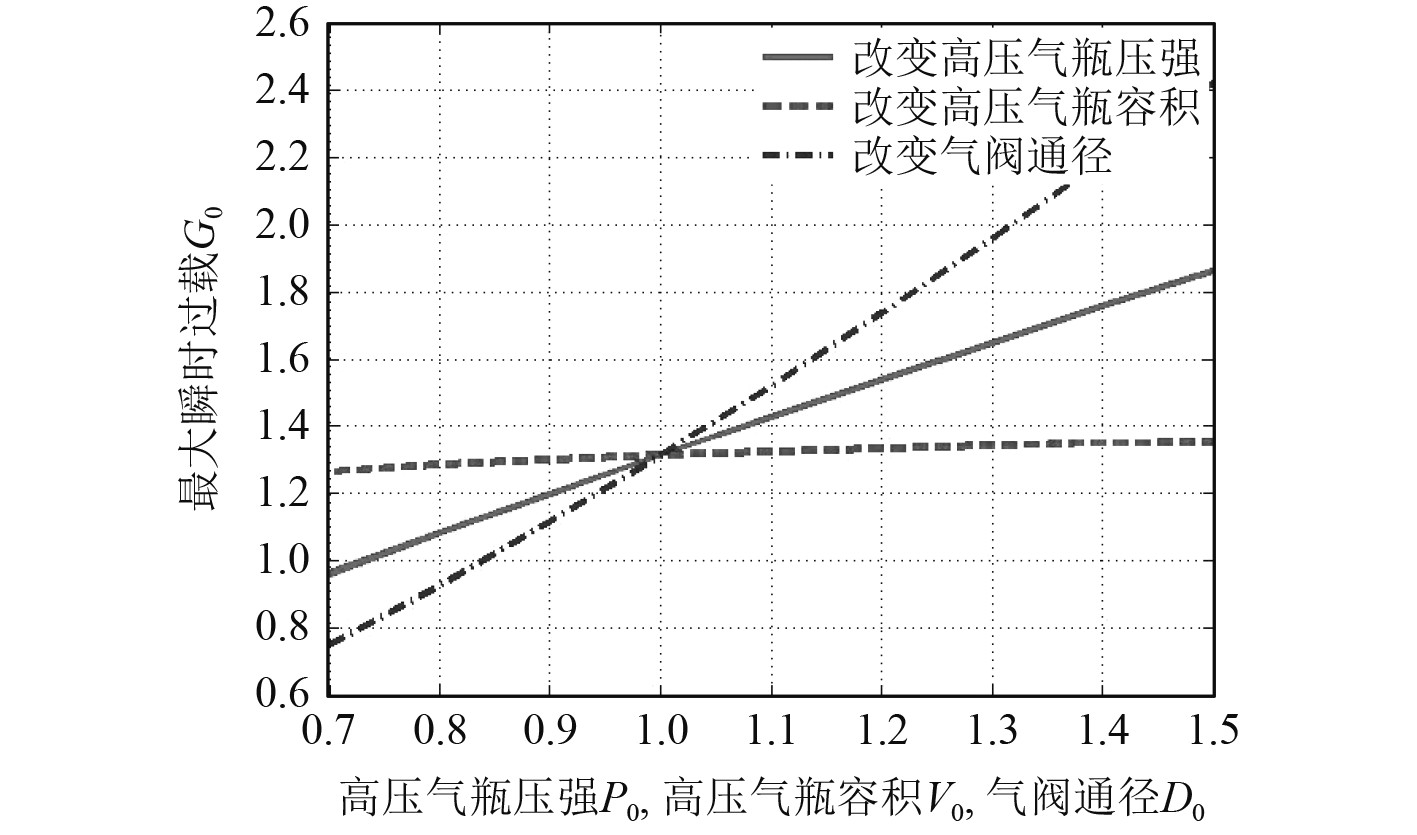
3 计算与分析 3.1 主要参数影响分析在没有采用缓冲腔的情况下,依次改变高压气动弹射装置的高压气瓶压强、高压气瓶容积、气阀通径等3个主要设计参数,弹射体出筒速度、最大瞬时过载计算结果如图4和图5所示。
|
图 4 高压气瓶压强、高压气瓶容积、气阀通径对弹射体出筒速度的影响 Fig. 4 Impacts of tank pressure, tank volume, and latus rectum of air valve on leaving velocity |
|
图 5 高压气瓶压强、高压气瓶容积、气阀通径对弹射体最大瞬时过载的影响 Fig. 5 Impacts of tank pressure, tank volume, and latus rectum of air valve on max-overload |
分析可知:1)随着高压气瓶压强、高压气瓶容积、气阀通径的增加,弹射体的出筒速度和最大瞬时过载均增加;2)气阀通径对出筒速度、最大瞬时过载影响最大,高压气瓶压强次之,高压气瓶容积的影响最小;3)仅通过改变高压气瓶压强、高压气瓶容积、气阀通径等主要参数,很难设计出满足“保证最小出筒速度,降低最大瞬时过载”要求的高压气动弹射装置。
3.2 缓冲腔的影响分析采用缓冲腔前后,依次改变高压气动弹射装置的高压气瓶压强、高压气瓶容积、气阀通径等3个主要设计参数,弹射体出筒速度、最大瞬时过载计算结果对比如图6~图11所示。
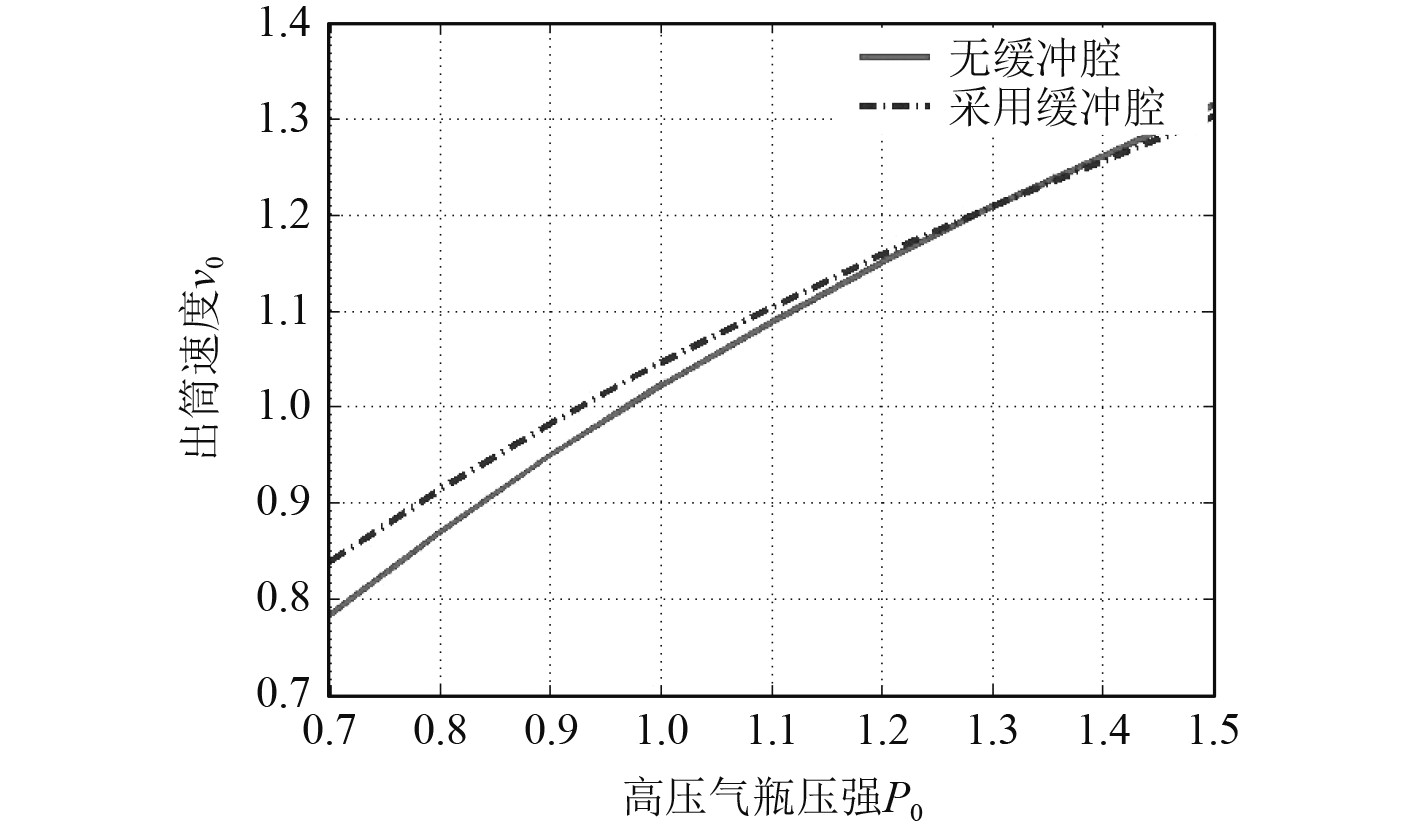
|
图 6 采用缓冲腔前后高压气瓶压强对出筒速度的影响 Fig. 6 Impacts of tank pressure on leaving velocity in systems with and without cushion chamber |
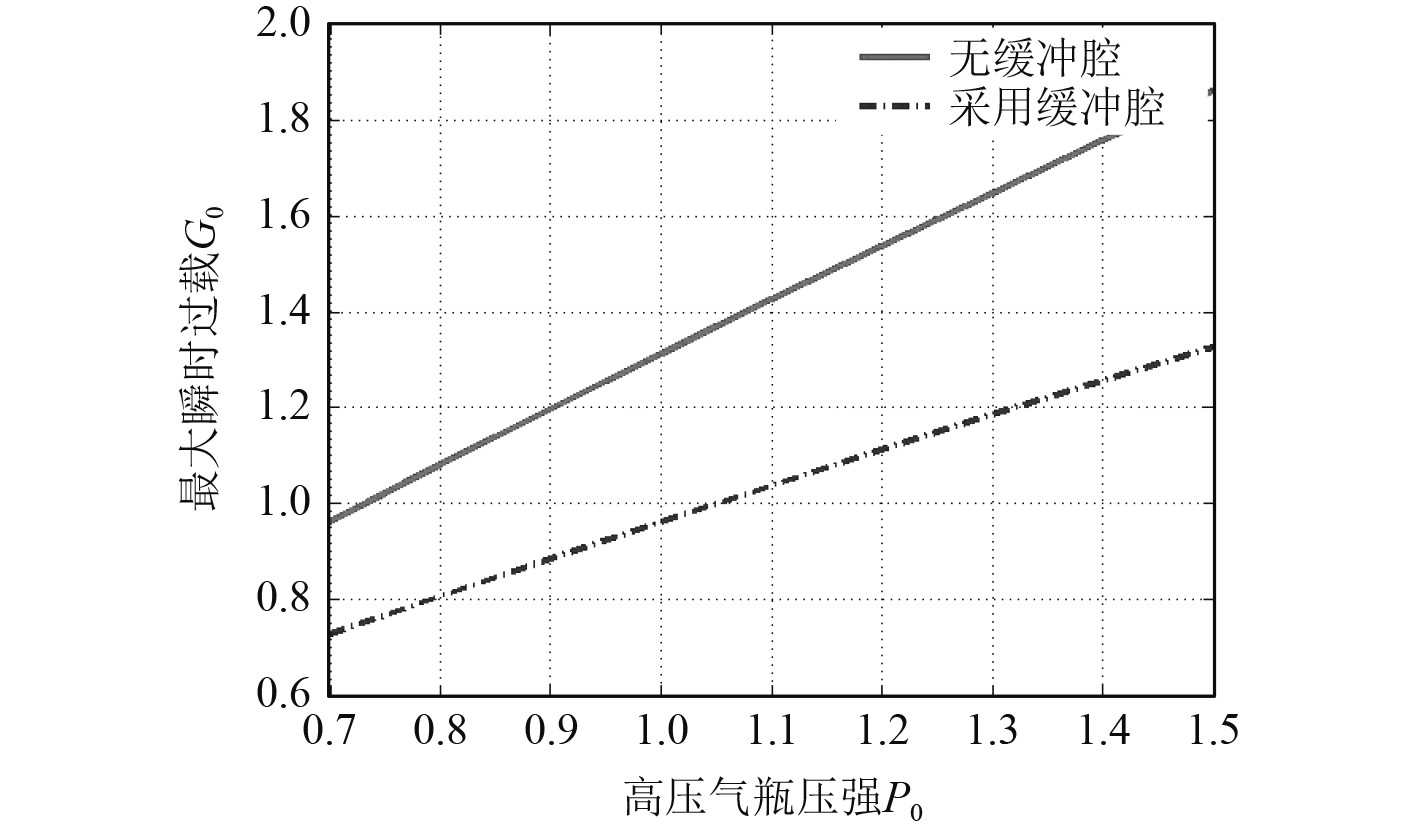
|
图 7 采用缓冲腔前后高压气瓶压强对最大瞬时过载的影响 Fig. 7 Impacts of tank pressure on max-overload in systems with and without cushion chamber |
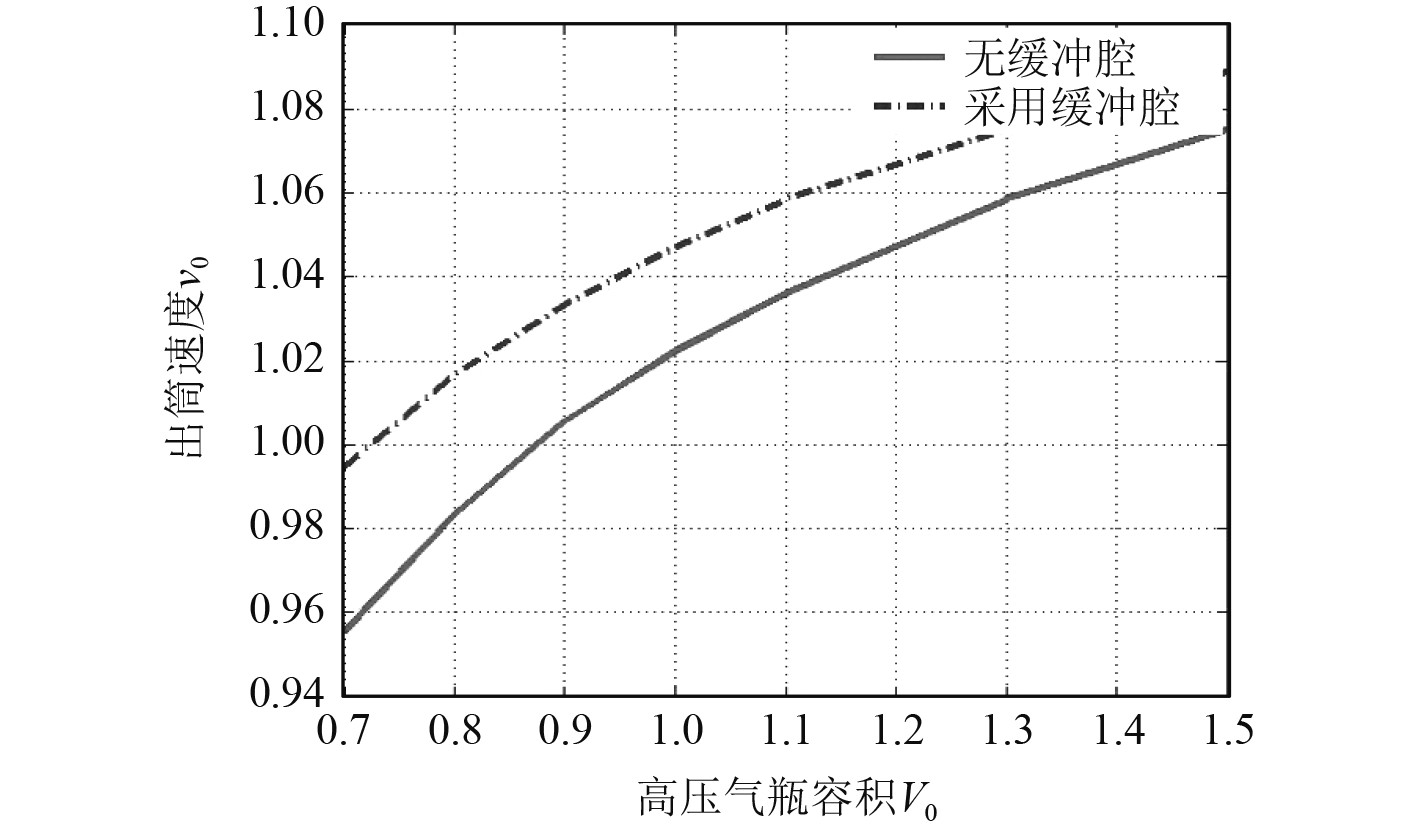
|
图 8 采用缓冲腔前后高压气瓶容积对出筒速度的影响 Fig. 8 Impacts of tank volume on leaving velocity in systems with and without cushion chamber |
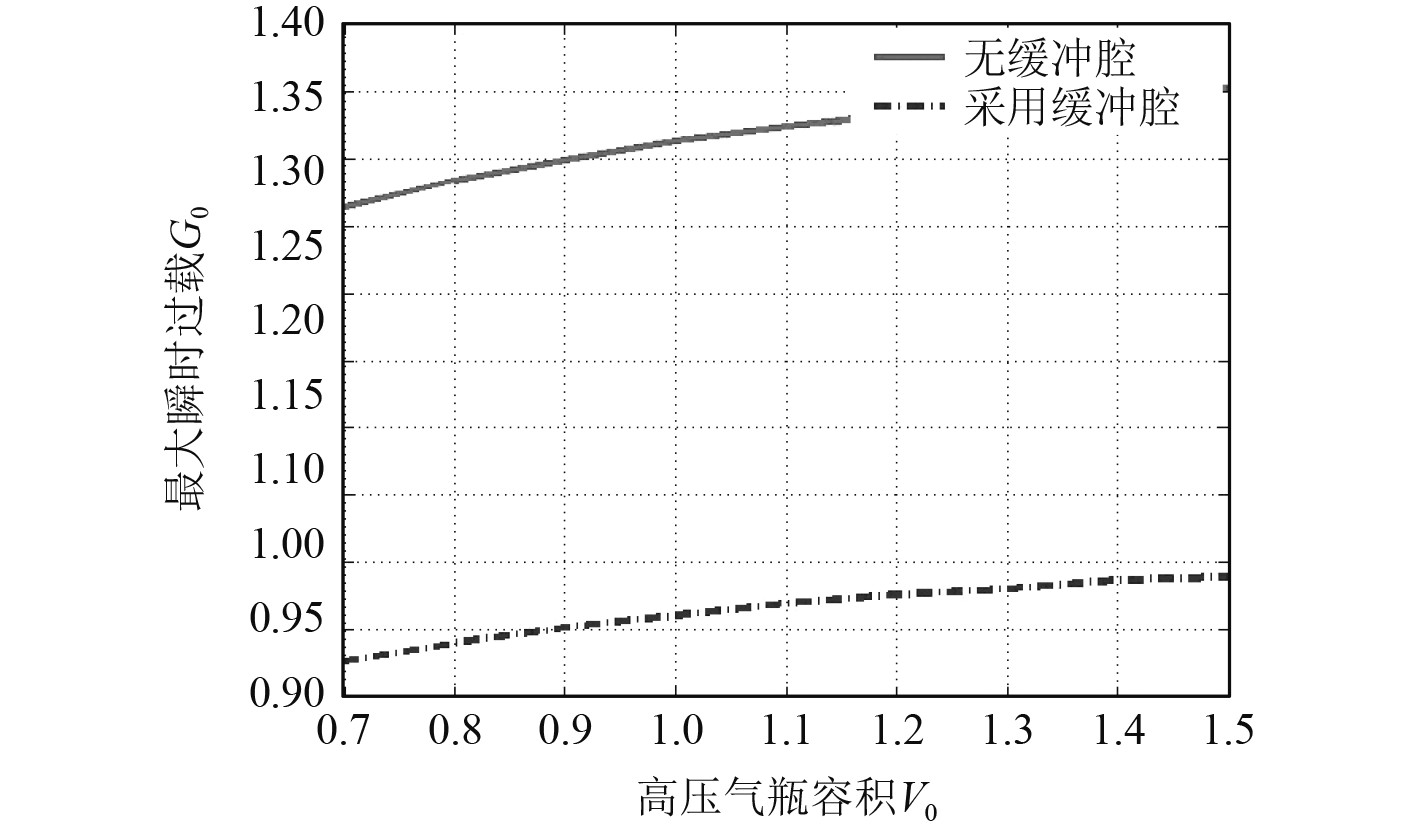
|
图 9 采用缓冲腔前后高压气瓶容积对最大瞬时过载的影响 Fig. 9 Impacts of tank volume on max-overload in systems with and without cushion chamber |
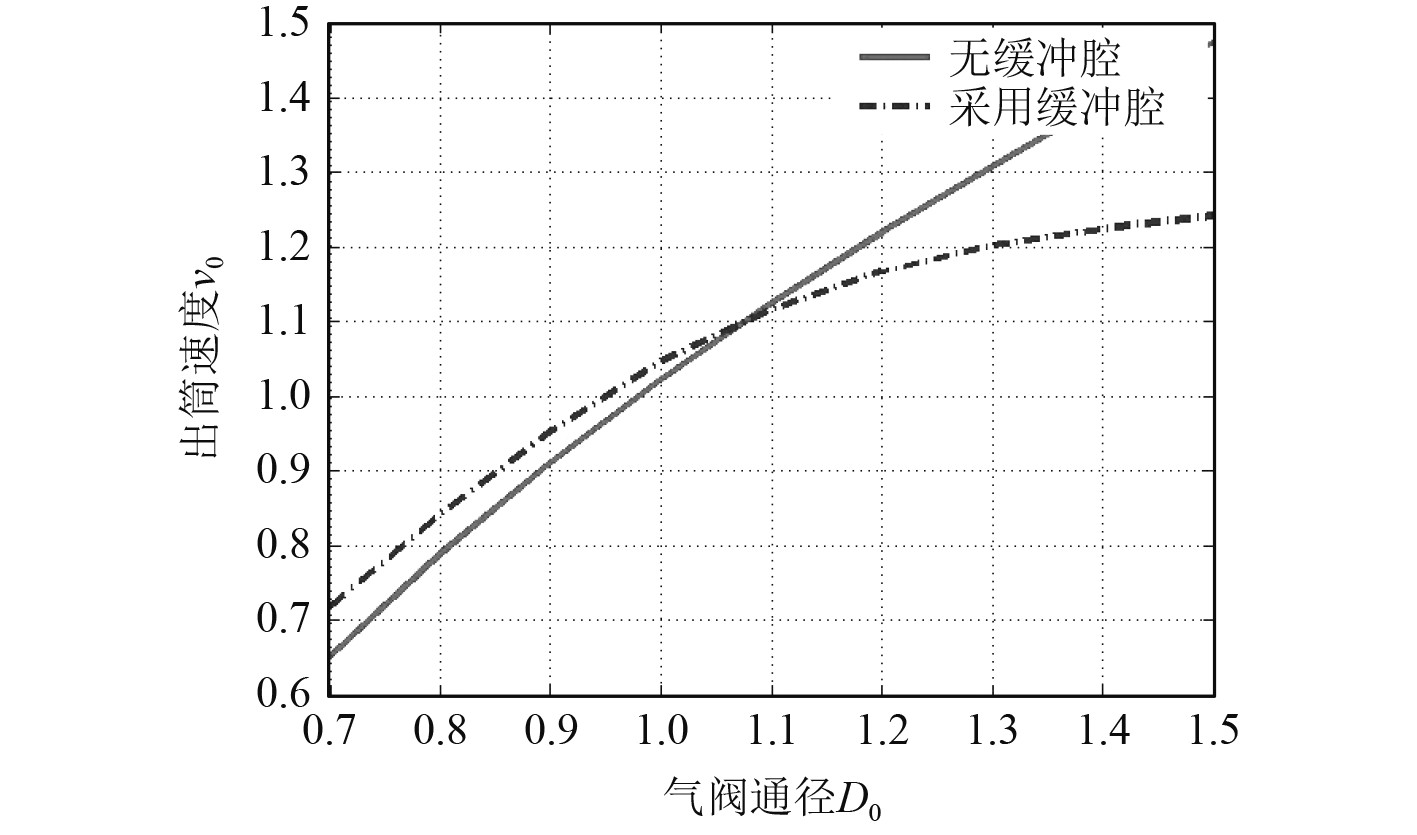
|
图 10 采用缓冲腔前后气阀通径对出筒速度的影响 Fig. 10 Impacts of latus rectum of air valve on leaving velocity in systems with and without cushion chamber |
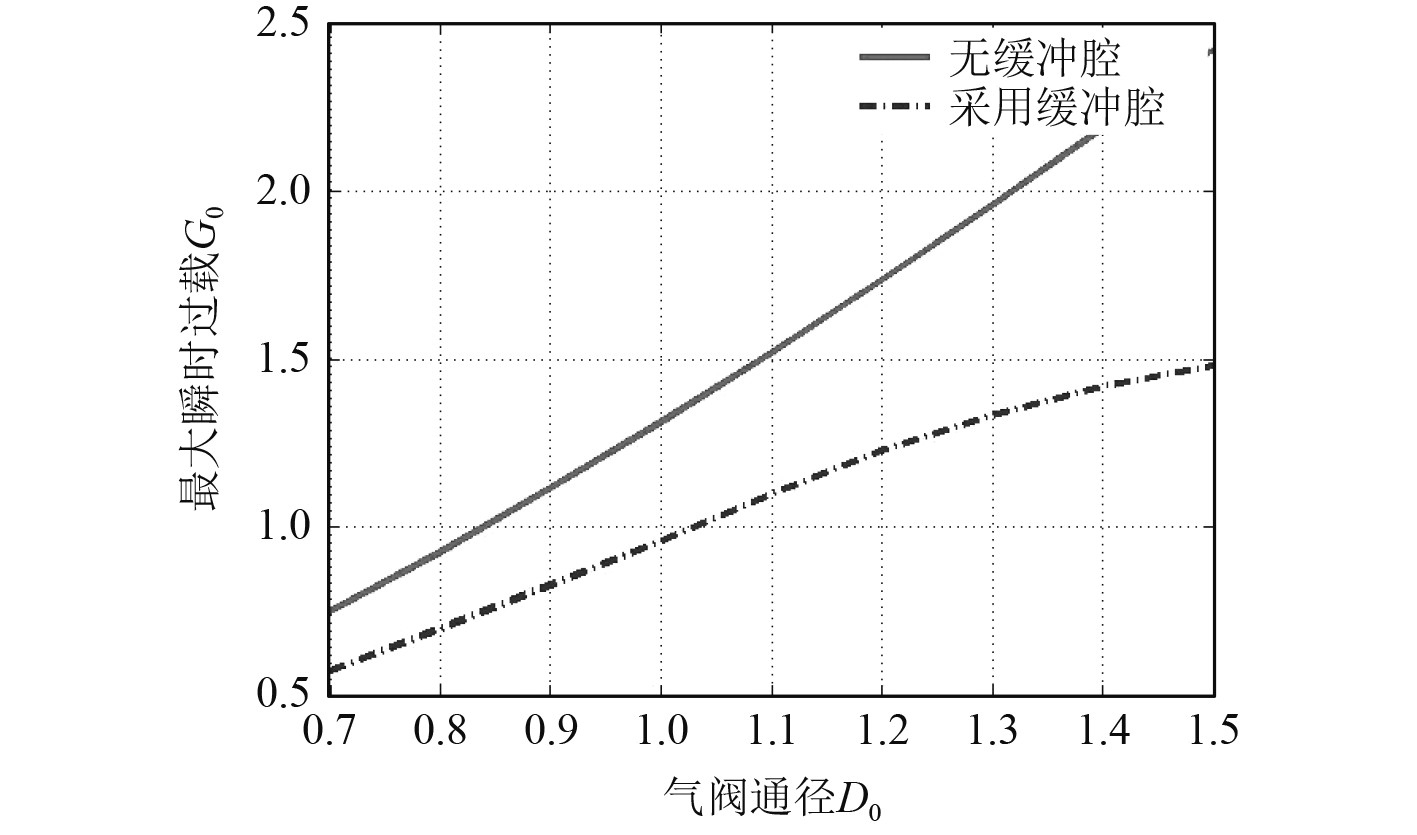
|
图 11 采用缓冲腔前后气阀通径对最大瞬时过载的影响 Fig. 11 Impacts of latus rectum of air valve on max-overload in systems with and without cushion chamber |
分析可知:1)同等参数条件下,采用缓冲腔可降低弹射体的最大瞬时过载;2)特定参数条件下,采用缓冲腔可提高弹射体的出筒速度;3)由于缓冲腔相关参数的影响,部分高压气动弹射装置设计方案无法提高出筒速度。
在高压气动弹射装置的高压气瓶压强为P0、高压气瓶容积为V0、气阀通径为D0情况下,采用缓冲腔后,通过改变缓冲腔节流孔板通径Dj,弹射体的弹射性能如表1所示。
|
|
表 1 不同缓冲腔节流孔板通径对弹射性能的影响 Tab.1 Impacts of latus rectum of throttle orifice on ejection performance |
分析可知:随着缓冲腔节流孔板通径的增加,弹射体出筒时间逐渐减小,出筒速度逐渐增大,最大瞬时过载逐渐增大。表1中第4组设计参数较优,初步满足 “保证最小出筒速度,降低最大瞬时过载”要求。
基于表1中第4组设计参数(高压气动弹射装置的高压气瓶压强为P0、高压气瓶容积为V0、气阀通径为D0,缓冲腔节流孔板通径为Dj0),采用缓冲腔前后弹射过程中的高压气体的质量流量对比见图12。
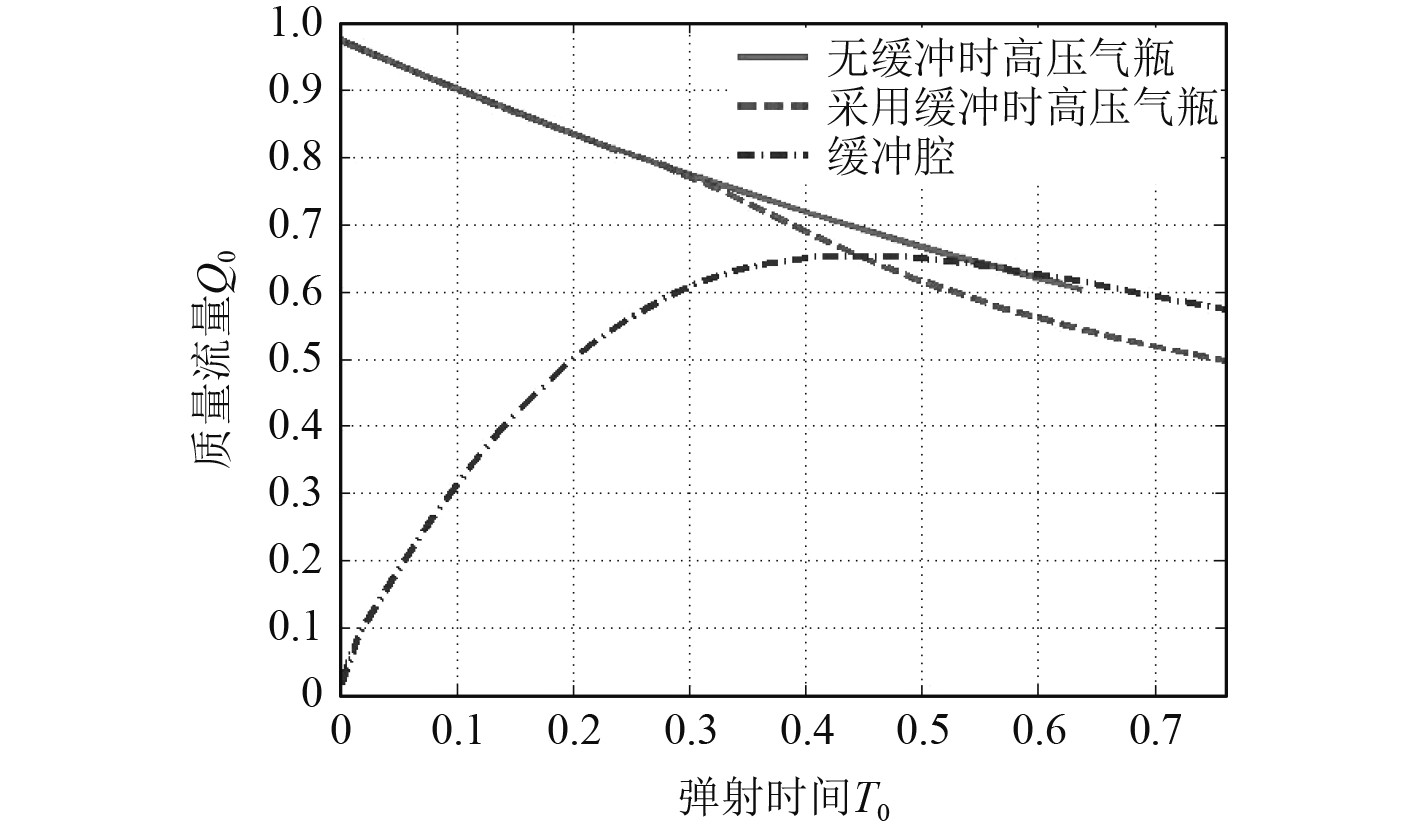
|
图 12 采用缓冲腔前后高压空气质量流量 Fig. 12 Mass flow in systems with and without cushion chamber |
可知,无缓冲腔时,高压气瓶直接放气推动弹射体运动;采用缓冲腔后,高压气瓶内压缩空气瞬时膨胀的过程被缓冲腔迟滞,先给缓冲腔充气,同时通过缓冲腔放气推动弹射体运动;由于缓冲腔的迟滞作用,一方面可以减小弹射体受到的瞬时冲击,另一方面可以使得弹射体加速过程变得平缓,从而达到降低弹射体最大瞬时过载、延长弹射时间、提高出筒速度的目的。
3.3 多组高速开关阀的影响分析基于表1中第4组设计参数,设计采用多组高速开关阀的高压气动弹射装置:小容积气瓶数量为9、小容积高压气瓶压强为P0,小容积高压气瓶容积均为V0/9,高速开关阀及气阀通径均为D0,高速开关阀依次开启时间点分别为0、0.1T0、0.2T0、…、0.8T0。便于对比,与表1中第4组设计参数相同的不含缓冲腔的仿真结果一并给出。无缓冲腔、采用缓冲腔、采用多组高速开关阀等3种弹射装置典型设计参数条件下弹射性能对比如图13和表2所示。
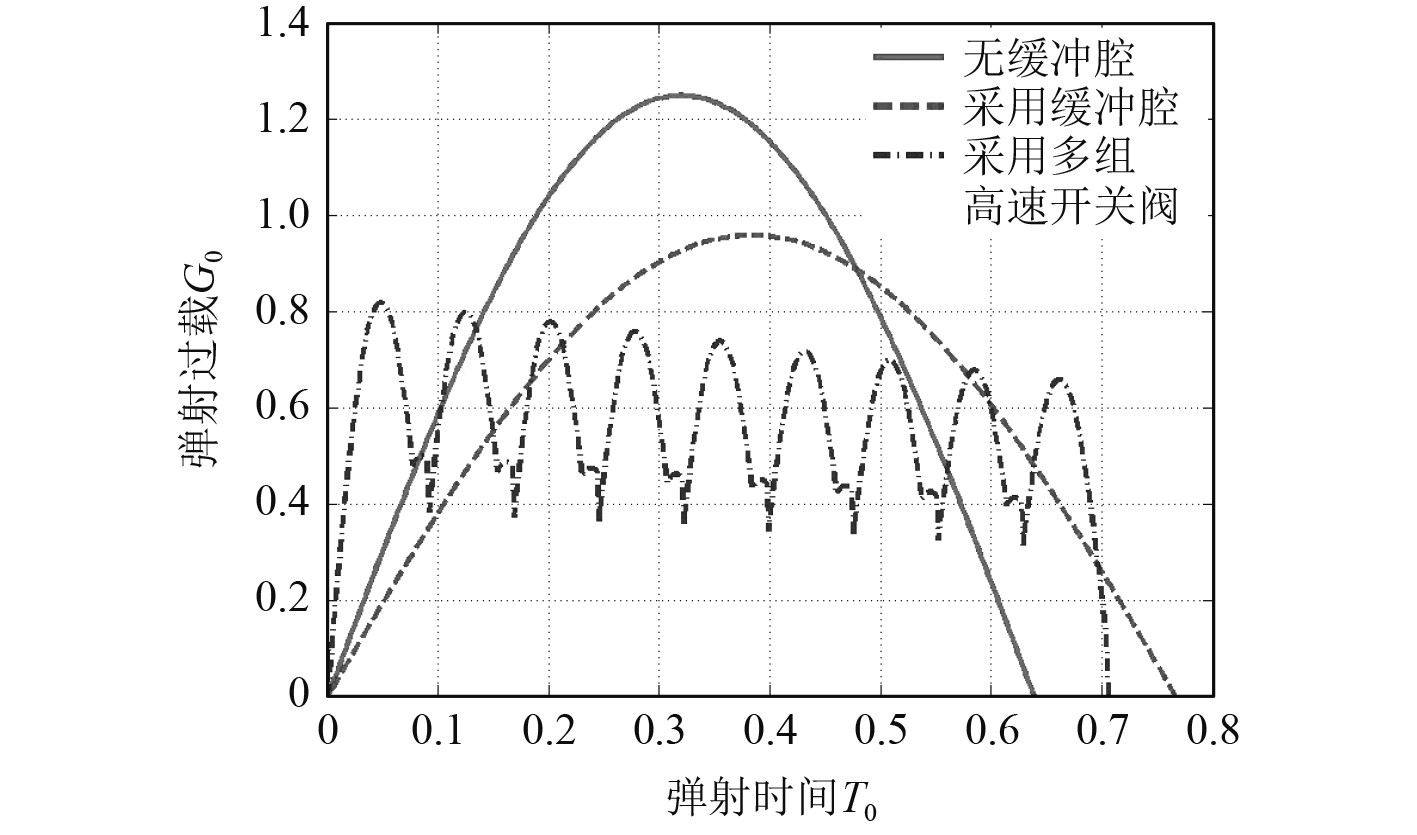
|
图 13 各弹射方案对弹射过载的影响 Fig. 13 Impacts of various ejection schemes on max-overload |
|
|
表 2 3种弹射装置典型设计参数条件下弹射性能对比 Tab.2 Comparison of ejection performance of three ejection devices under typical design parameters |
分析可知:1)相对于采用缓冲腔,采用多组高速开关阀的弹射装置在不明显降低出筒速度的情况下可显著降低最大瞬时过载;2)参数选择恰当的情况下,采用多组高速开关阀的弹射装置性能最优,采用缓冲腔的次之,无缓冲腔的方案弹射性能不理想。
采用多组高速开关阀的弹射装置需要设计、优化的参数较多,包括但不限于选择不同容积的气瓶、不同压力的气瓶、不同通径的高速开关阀、高速开关阀的开启时序也可交错。此外,可以预见:采用缓冲腔的同时,也采用多组高速开关阀的弹射装置弹射性能会更一步提升,不过工程上需要综合评估相应投入与产出。
4 结 语通过分析,可得出以下结论:1)不采用缓冲腔、不采用多组高速开关阀的情况下,仅通过改变高压气瓶压强、高压气瓶容积、气阀通径等主要参数,很难设计出满足“保证最小出筒速度,降低最大瞬时过载”要求的高压气动弹射装置;2)参数选择恰当的情况下,采用多组高速开关阀的弹射装置性能最优,采用缓冲腔的次之,无缓冲腔的方案弹射性能不理想。
本文验证了缓冲腔、多组高速开关阀对高压气动弹射装置的缓冲作用,可为高压气动弹射装置的优化设计、制造及弹射试验提供参考。
| [1] |
赵希欣, 高元楼. 一种气体炮的建模与分析[J]. 液压气动与密封, 2012(10): 43-44. |
| [2] |
胡艳岭. 气动枪械发射原理有关问题的研究[D]. 南京: 南京理工大学, 2008.
|
| [3] |
仲伟君, 赵晓利, 齐杏林. 气体炮内弹道建模与发射环境模拟研究[J]. 动力学与控制学报, 2005, 3(1): 62-66. DOI:10.3969/j.issn.1672-6553.2005.01.013 |
| [4] |
赵俊利, 曹锋. 气体炮实用内弹道方程及应用[J]. 火炮发射与控制学报, 2003(3): 48-51. |
| [5] |
赵俊利, 高跃飞. 气体炮实用内弹道技术研究[J]. 太原理工大学学报, 2003, 34(3): 288-290. |
| [6] |
夏正友, 张河, 陈家安. 一种非火药驱动气体炮内弹道模及发射诸元协调[J]. 爆炸与冲击, 1999, 19(2): 146-150. |
 2024, Vol. 46
2024, Vol. 46
