2. 华侨大学,福建 泉州 362000;
3. 大数据与人工智能福建省高校重点实验室,福建 泉州 362332
2. Huaqiao University, Quanzhou 362000, China;
3. Key Laboratory of Big Data and Artificial Intelligence in University of Fujian Province, Quanzhou 362332, China
舰船领域大量应用混沌保密通信系统,基于混沌信号的复杂性和类似噪声的特性,通过信息加密传输的通信方式保障其信息传输安全[1,2]。舰船混沌保密通信系统将混沌信号视为载波,并通过将待传输信息信号以隐藏或叠加的方式作用于混沌信号的隐藏形式,避免攻击者从中获取信息内容[3,4]。
针对舰船混沌保密通信系统的研究有很多,王飞等[5]在舰船保密通信系统中应用半导体激光器,通过半导体激光器发射的激光获取混沌动力,结合其延迟速率方程,设置用于同步的混沌载波;依据发送与接收两端信息的同步误差,并与接收端信息比较,得到解密信息。董武等[6]研究基于有限时间理论的舰船混沌保密通信系统,利用混沌掩盖方式实现保密通信,有效利用组合同步控制方法,在信号解调过程中进行同步控制。以上研究存在一些缺点和不足之处:如对硬件的依赖性强和缺少环境适应性,这些因素可能会对信号的传输质量和同步造成干扰,从而影响保密通信的效果。为此本文设计了基于神经网络的舰船混沌保密通信系统,助力更好实现舰船信息安全通信。
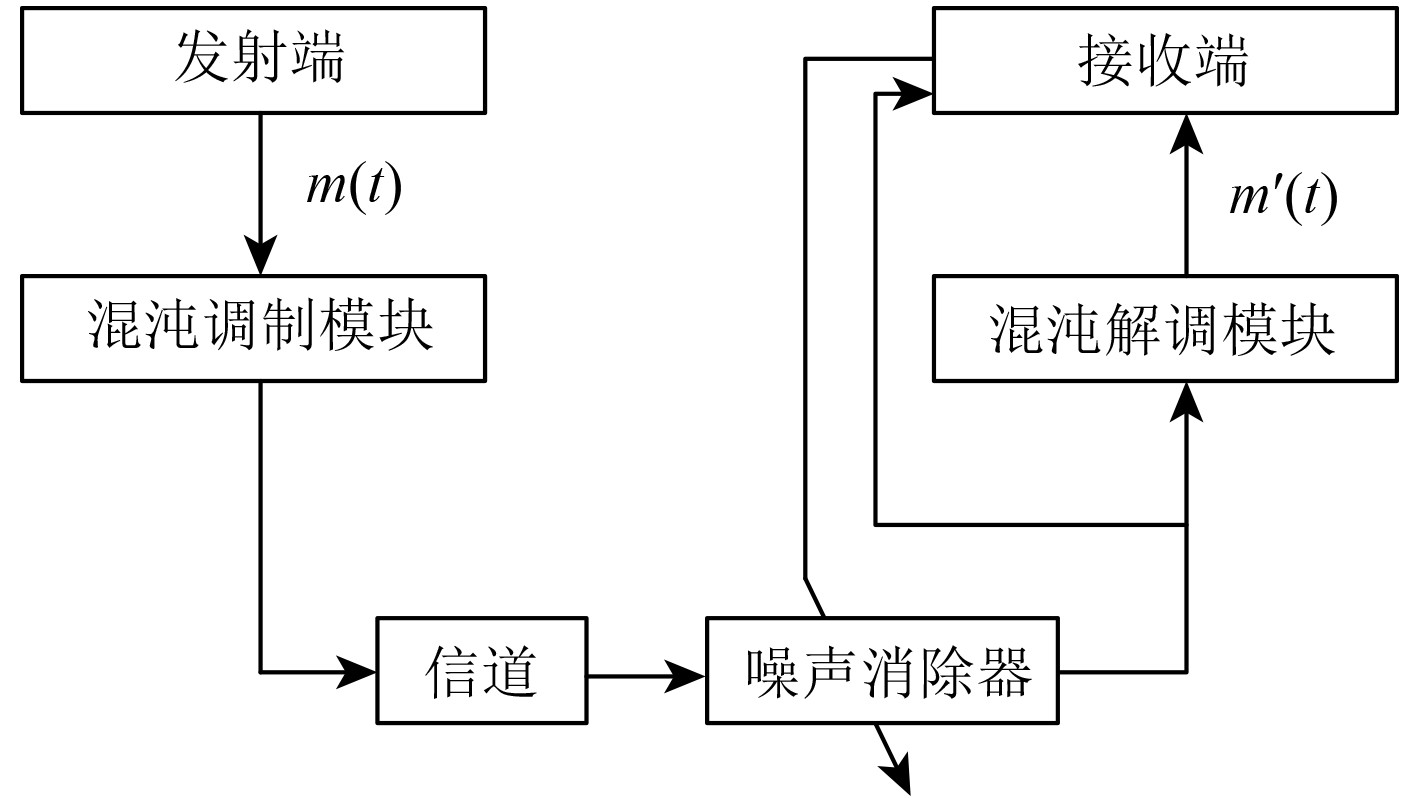
1 舰船混沌保密通信系统 1.1 舰船混沌保密通信系统一般模型图1为舰船混沌同步保密通信系统,利用混沌系统的特性将需要传输的舰船信息信号隐藏或叠加到混沌载波中,通过特定的调制方式将信息信号转化为混沌信号的形式进行传输。混沌解调模块的作用是在接收端接收到含有噪声的加密舰船信息信号后,通过对接收到的混沌信号进行解调和同步处理,恢复出原始的舰船信息信号。
|
图 1 舰船混沌同步保密通信系统一般模型 Fig. 1 General model of ship chaotic synchronous secure communication system |
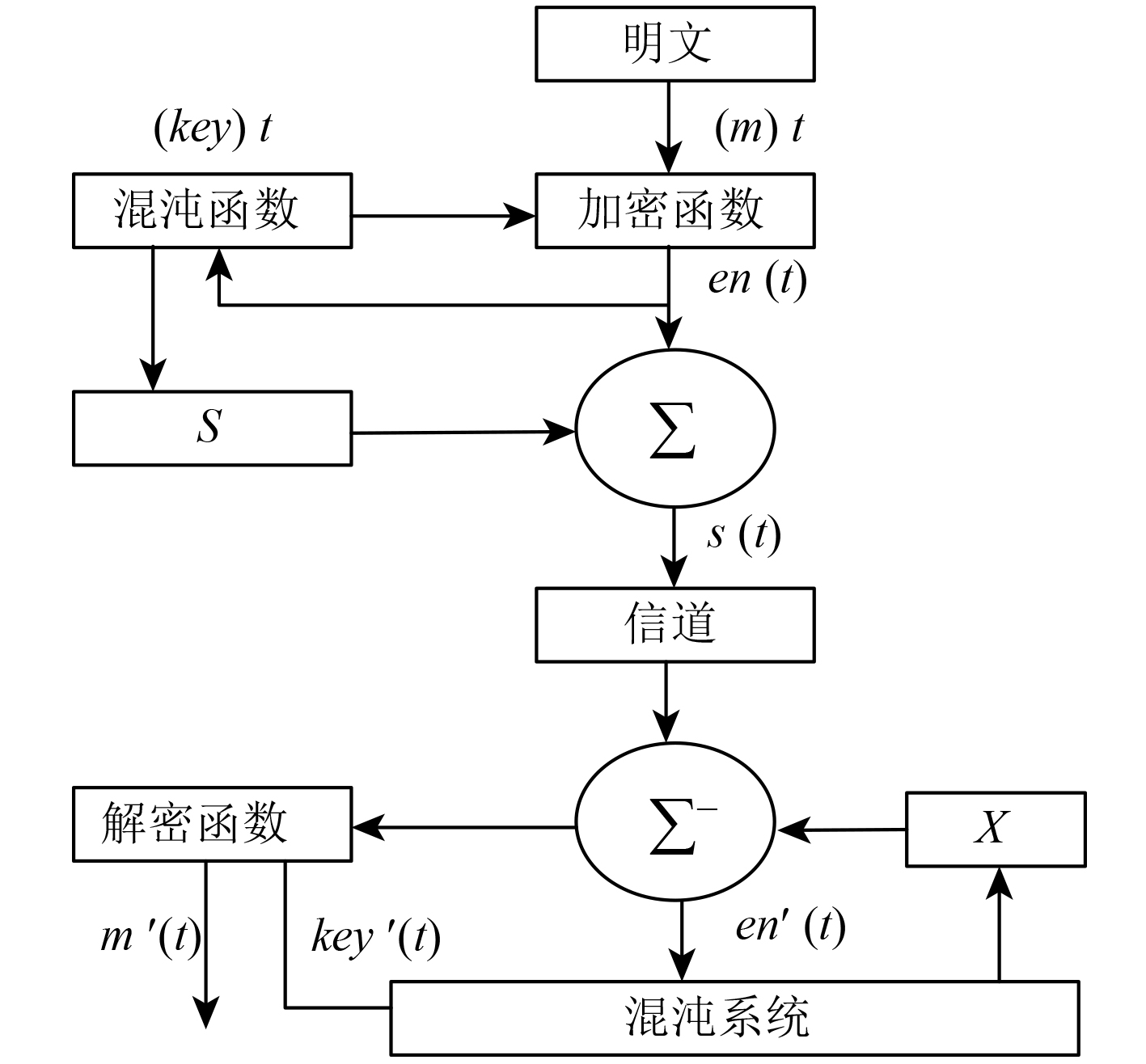
混沌解调模块则利用解密函数从接收到的混沌信号中提取出隐藏信息。具体的混沌保密过程见图2。
|
图 2 混沌保密过程 Fig. 2 Chaos security process |
假设存在一个包含输入层、隐含层、输出层节点数分别为3、
| $ g(k) = \sum\limits_{j = 1}^Q {{\omega _j}\phi \left( {\left\| {X - {C_i}} \right\|} \right)} + {\omega _0} 。$ | (1) |
式中:
设定性能指标函数为:
| $ {J_1} = 0.5{\left[ {g(k) - m(k + 1)} \right]^2}。$ | (2) |
采用梯度下降法通过在线训练的方式对网络的权值
| $ \Delta {\omega _j}(k) = - {\eta _1}\frac{{\partial {J_1}}}{{\partial {\omega _j}(k)}} = - {\eta _1}\left[ {g(k) - m(k + 1)} \right]\phi (x),$ | (3) |
依据式(3)得到式(4):
| $ {\omega _j}(k + 1) = {\omega _j}(k) + \Delta {\omega _j}(k) + a\left( {{\omega _j}(k) - {\omega _j}(k - 1)} \right)。$ | (4) |
其中,
同步控制器的作用为完成舰船混沌同步保密通信系统发射端与接收端信息的同步控制。舰船混沌保密通信系统的发射端数学表达为:
| $ \dot x = {\boldsymbol{A}}x + f(x)。$ | (5) |
式中,
舰船混沌保密通信系统的接收端数学表达为:
| $ \dot y = {\boldsymbol{A}}y + f(y) + u(t),$ | (6) |
式中:
将合理有效的控制器输出
| $ \mathop {\lim }\limits_{t \to \infty } \left\| {y - x} \right\| = 0 。$ | (7) |
将误差定义为
| $ \dot e = \dot y - \dot x = {\boldsymbol{A}}e + f(y) - f(x) + u(t)。$ | (8) |
依据RBF神经网络可通过理想权值以任意精度逼近任意非线性函数的万能逼近能力,设计一个基于RBFNN的同步控制器,RBF神经网络同步控制时权值向量为:
| $ W = {\left( {{w_1},{w_2}, \cdots ,{w_n}} \right)^{\mathrm{T}}}。$ | (9) |
其中,
RBF神经网络同步控制输出表达式为:
| $ u(X)' = {W^{\mathrm{T}}}\phi (X),$ | (10) |
此时,RBF神经网络最优权值表达式为:
| $ W' = \arg \mathop {\min }\limits_{W \in {\Omega _F}} \left[ {\mathop {\sup }\limits_{e \in {S_e}} \left| {u'(X,W) - u(X)} \right|} \right]。$ | (11) |
式中:
在RBF神经网络最优权值
| $ u(X) = {W^{\mathrm{T}}}\phi (X) + \lambda。$ | (12) |
RBF神经网络逼近的误差值,且
将最优逼近结果引入式(8),得到最终系统发送端与接收端的同步控制误差为:
| $ \dot e = \dot y - \dot x = {\boldsymbol{A}}e + f(y) - f(x) + {W^{\mathrm{T}}}\phi (X) + \lambda 。$ | (13) |
通过RBFNN控制器获取与原始舰船信息信号无限接近的同步解调舰船信息信号,实现舰船混沌保密通信。
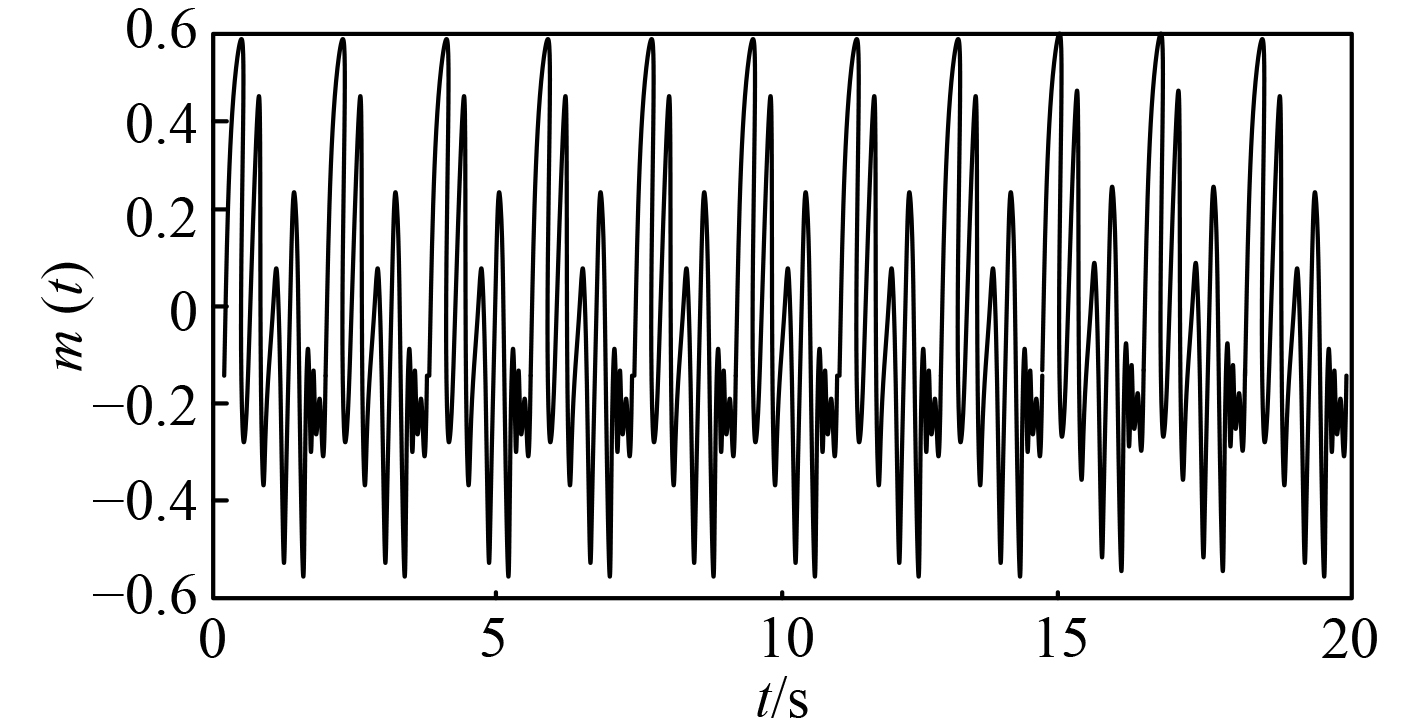
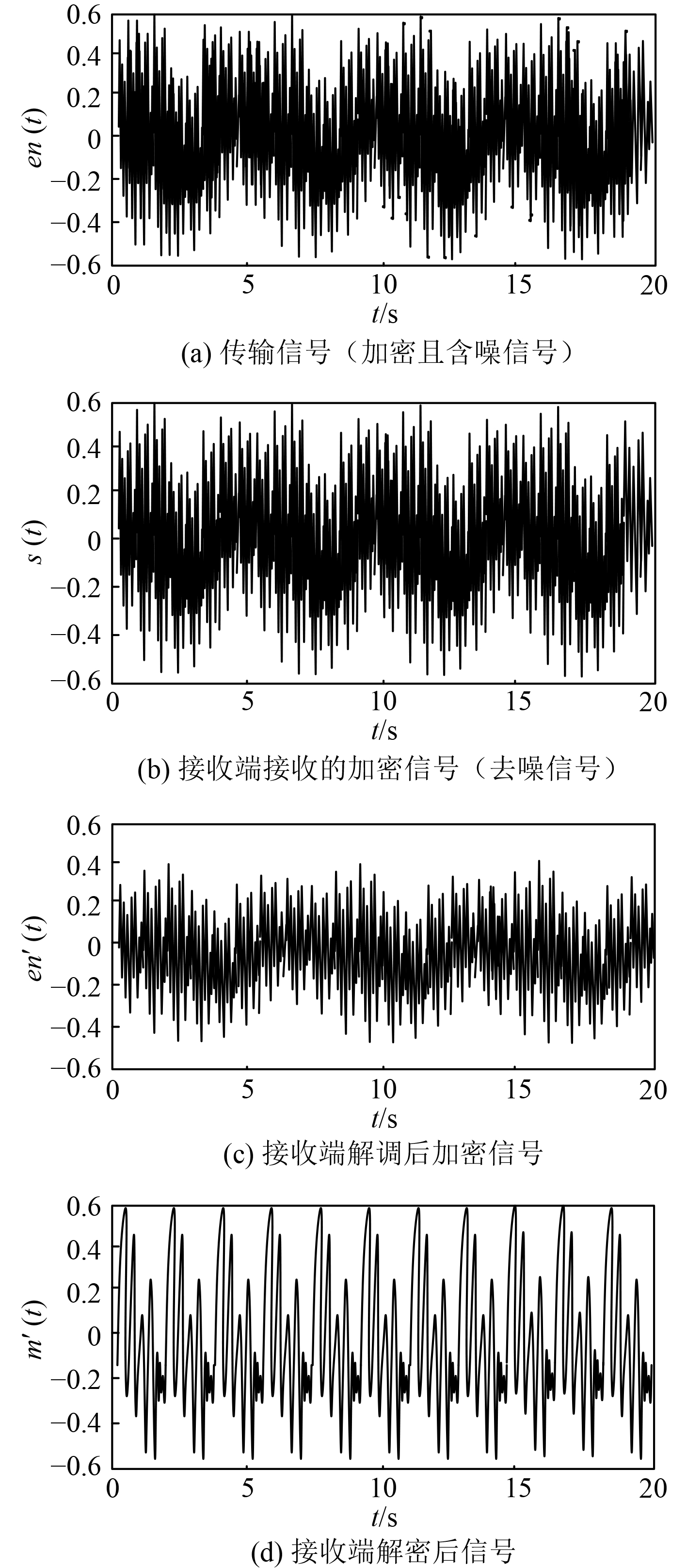
2 实验结果与分析以图3模拟信号为例,进行本文混沌保密通信系统的加密、调制、去噪、解调效果验证,混沌保密通信仿真结果见图4。综合分析图3和图4可知,图4(a)为图3 所示原始信号经加密函数加密后获取的加密信号,并将其通过信道进行传输,可知,加密后有效掩盖了信号中有用信息,达到了原始信号加密目的,这证明本文系统在保护原始信号内容方面起到了显著作用,同时加密信号中含有大量来源于信道传输过程中的各种干扰因素产生的噪声,使得信息图中出现重影及噪声干扰产生的波动。图4(b)为接收端接收到的信息,在信号接收过程中,由于本文在信道传输信号过程引入了噪声消除器可有效去除噪声干扰,获取较为纯净的信号,避免噪声的存在导致信号解调误差或不确定性。图4(c)为经接收端同步解调后得到的加密信号,结合解密函数对其进行解密后得到图4(d)所示的解密信号,对比图4(d)与图3发现,解密后的信号与原始信号一致,说明本文系统可有效完成信号的加密、调制、去噪、解调,且可在接收端实现高精度的信号还原。
|
图 3 发送端发送信号(原始信号) Fig. 3 Signal sent by the sender (original signal) |
|
图 4 混沌保密通信仿真结果 Fig. 4 Simulation results of chaotic secure communication |
以模拟信号
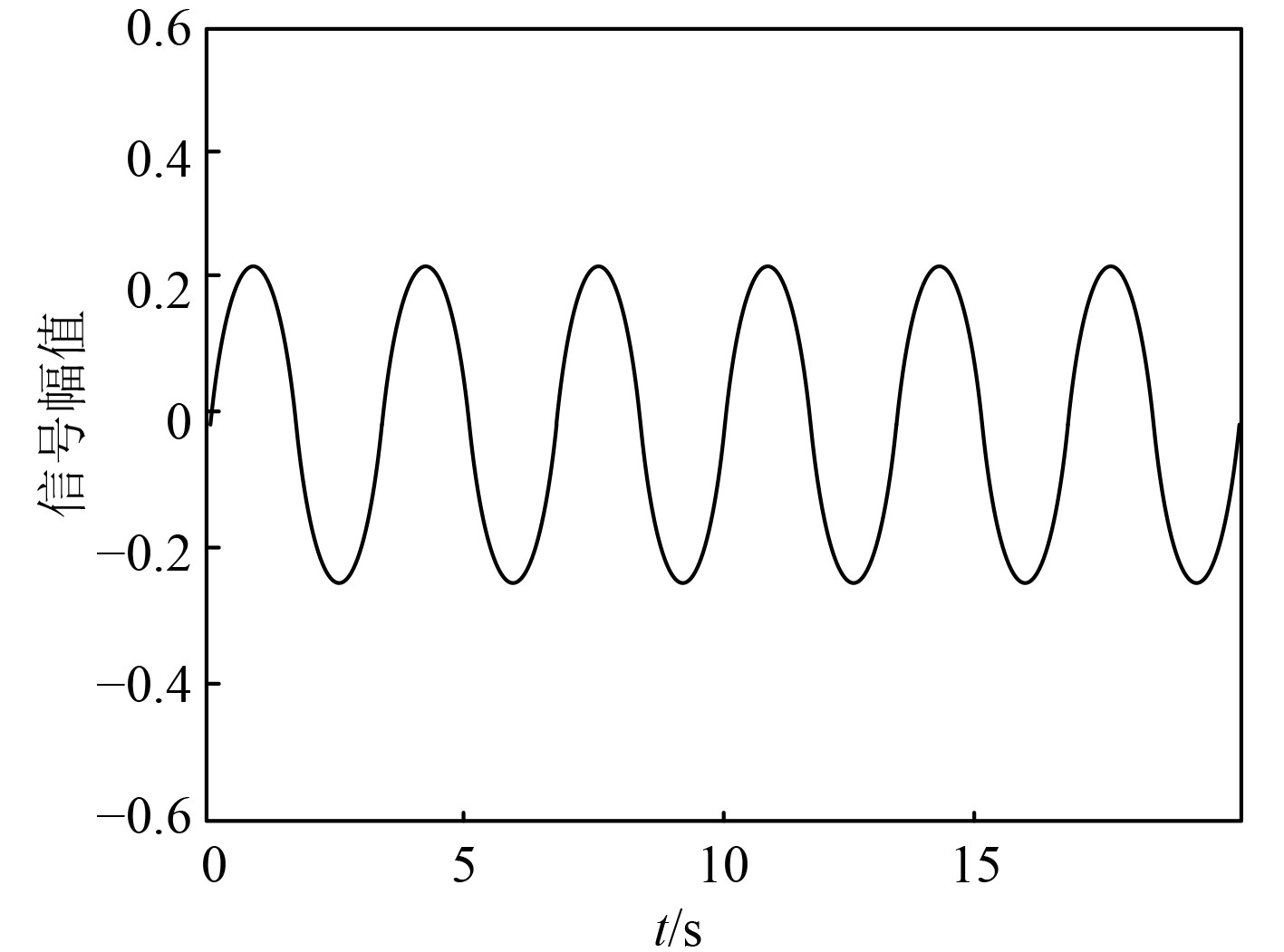
|
图 5 模拟信号 Fig. 5 Analog signal |
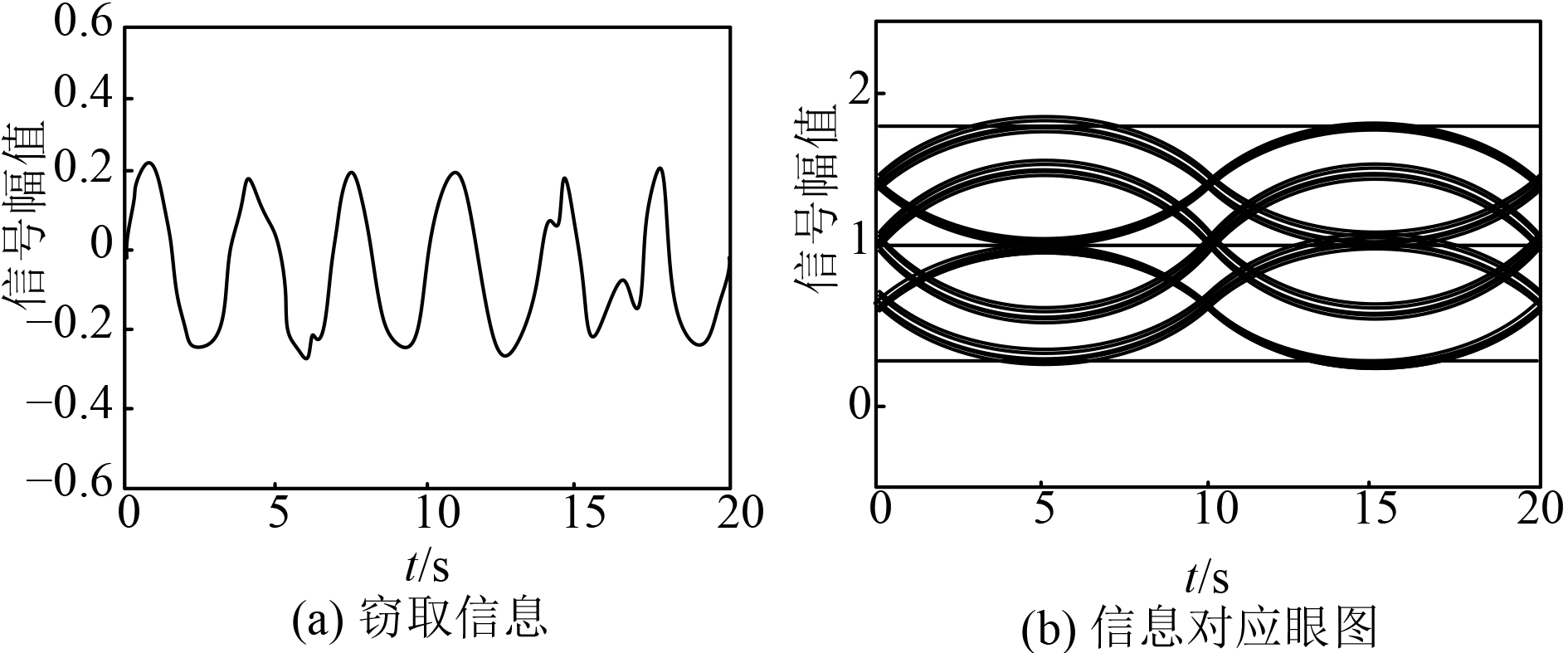
|
图 6 有限时间理论系统应用后 Fig. 6 After the application of finite time theory system |
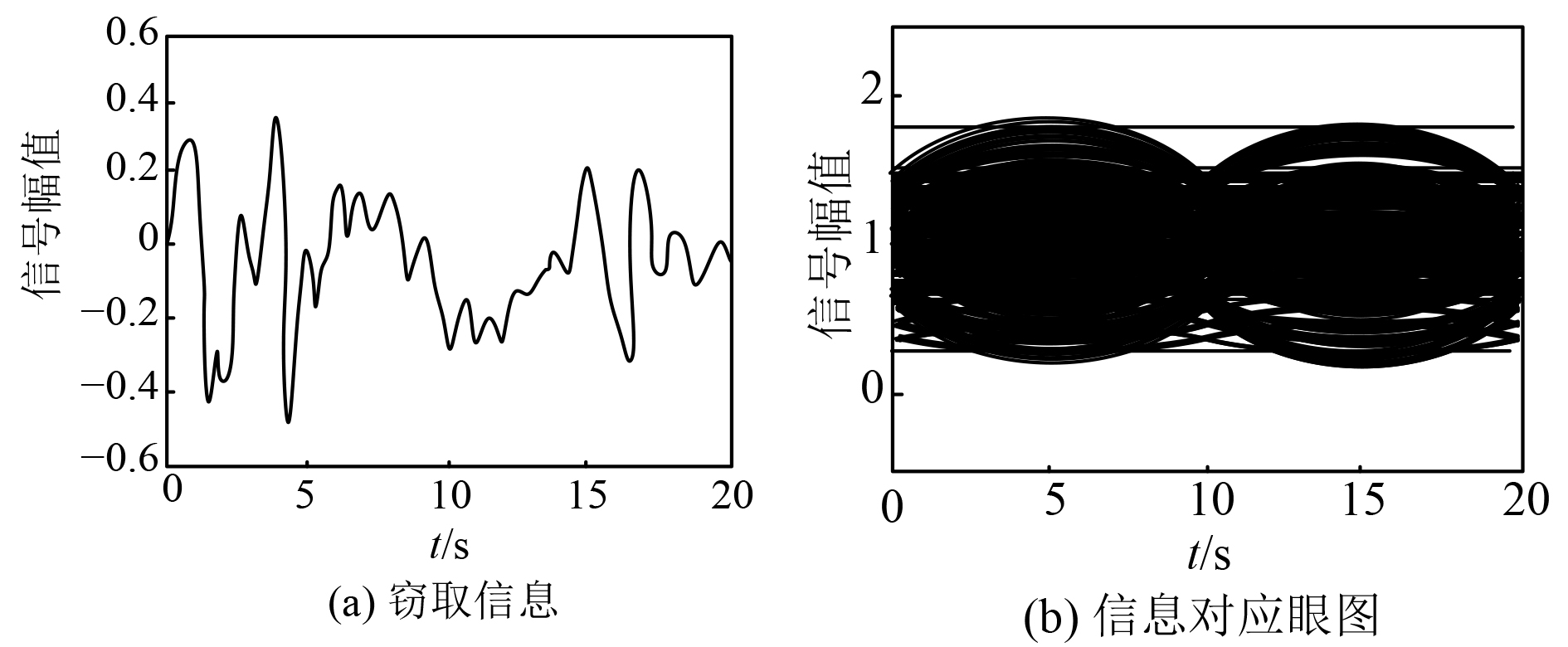
|
图 7 本文系统应用后 Fig. 7 After the application of the system in this article |
本文有效利用RBFNN的优势并引入噪声消除器有效解决了现有舰船保密通信系统的难题,并通过仿真实验分析证明了本文系统在信号的加密、调制、去噪、解调过程中的应用效果。
| [1] |
钟东洲, 徐喆, 赵可可, 等. 基于光学储备池计算的高速混沌保密通信的研究[J]. 光子学报, 2022, 51(4): 100-115. ZHONG Dong-zhou, XU Zhe, ZHAO Ke-ke, et al. Exploring of chaotic secure communications with high-speed using optical reservoir computers[J]. Acta Photonica Sinica, 2022, 51(4): 100-115. |
| [2] |
刘劲杨, 周雪芳, 毕美华, 等. 光混沌保密通信系统在Matlab与OptiSystem中的协同实现[J]. 光电工程, 2021, 48(9): 43-51. LIU Jin-yang, ZHOU Xue-fang, BI Mei-hua, et al. Co-simulation of optical chaotic secure communication systems in Matlab and OptiSystem[J]. Opto-Electronic Engineering, 2021, 48(9): 43-51. |
| [3] |
张小卉, 张顺亮, 李博文. 适用于保密容量为负情形的基于混沌序列的polar码加密方案[J]. 通信学报, 2020, 41(10): 130-138. ZHANG Xiao-hui, ZHANG Shun-liang, LI Bo-wen. Chaotic sequence based polar code encrypted scheme in negative secrecy capacity case[J]. Journal on Communications, 2020, 41(10): 130-138. |
| [4] |
郭锐强, 李珉, 吴君鹏, 等. 基于差分混沌键控的空间光通信系统及其保密性分析[J]. 红外与激光工程, 2020, 49(S1): 225-232. GUO Rui-qiang, LI Min, WU Jun-peng, et al. Space optical communication systems based on differential chaotic keying and its security analysis[J]. Infrared and Laser Engineering, 2020, 49(S1): 225-232. |
| [5] |
王飞, 周雪芳. 一种基于半导体激光器光混沌的双向通信系统[J]. 光通信技术, 2023, 47(3): 52-55. WANG Fei, ZHOU Xue-fang. Bidirectional communication system based on semiconductor laser optical chaos[J]. Optical Communication Technology, 2023, 47(3): 52-55. |
| [6] |
董武, 王聪, 张宏立, 等. 异构超混沌系统有限时间组合-组合同步及应用[J]. 系统仿真学报, 2023, 35(7): 1590-1601. DONG Wu , WANG Cong , ZHANG Hong-li, et al. Finite-time combination synchronization of hyperchaotic systems with different structures and its application[J]. Journal of System Simulation, 2023, 35(7): 1590-1601. |
 2024, Vol. 46
2024, Vol. 46
