0 引　言

同态加密方法是一种突破性的数学加密方法，其允许在加密状态下对密文进行计算，而无需事先解密数据，具备很强的安全性和隐私性。这种特性，使其在网络安全、云计算安全和金融安全等民用领域，以及军事通信、网络和指挥控制系统等军用领域得到了广泛应用。尤其是在传递关键军事指令时，采用同态加密方法加密指令，可确保被授权的人员能在加密的状态下理解并执行这些指令，并使军事指挥控制系统的安全性得到显著提高。目前，采用的同态加密方法主要分成部分同态加密和全部同态加密，较为先进的方法有BFV^[1-2]、CKKS^[3]、BGV^[4]和GSW^[5]。这些方法虽已将开销较低，但在控制理论的应用中还处于起步阶段，当前在控制和决策应用依然是以线性加密控制方案为主。

在控制领域二次规划为一种常见问题，有同态加密需求的情况下，求解此类任务就要面对迭代方法（梯度下降）和同态加密电路乘法深度限制的问题。为解决这一问题，本文在实践应用中采用梯度下降和加速梯度下降算法，以同态加密的方式求解二次规划。本文具体讨论的问题如下：

1）在CKKS方法框架下，选取适当的步长以确保底层算法的收敛性；

2）通过改进同态加密矩阵乘法，在乘法深度方面提升效率；

3）通过计算分析，权衡梯度下降和加速梯度下降算法的适用范围。

由于可用同态加密方案允许执行的操作存在固有限制，本文重点关注无约束二次问题。

1 无约束二次规划的下降算法

二次规划是一个极为成功的算法工具，可对许多生活场景中遇到的问题进行建模。这种无约束的二次规划具有封闭形式的解决方案，但它需要矩阵的求逆，该过程涉及除加法和乘法之外的其他操作，因此对其在同态加密中的实现提出了挑战。还有一种解法，就是使用梯度下降的方式来解决二次规划问题。这是一类迭代算法，提供了一种简单方法，如式（1）来最小化可导函数。

$ \mathop {\min }\limits_{_{x \in {{R}^n}}} f(x)。$

(1)

从初始估计开始，迭代更新：

$ {x_{t + 1}} = {x_t} - \eta \nabla f({x_t}) 。$

(2)

式中：$ \nabla f({x_t}) $为在$ {x_t} $处计算的$ f $梯度；$ \eta $为步长，直到解达到所需的容差。特别是对于二次规划的场景，梯度采用线性的方法$ \nabla f(x) = Qx + p $。

此类方法的收敛情况与解空间的维数n没有关系。这一特性使它们对于非常高维度的优化具有极大优势。然而，收敛性与步长η密切相关，如果太小，算法可能需要很长时间才能收敛，如果太高，算法可能会发散。并且目标函数的平滑度或强凸性等属性在选择η和收敛速度更快的算法时，发挥着相关作用。加速梯度下降和梯度下降方法^[6]对于平滑和强凸二次函数都以指数方式快速收敛（见表1）。

表1中$ R = \left\| {{x_1} - {x^*}} \right\| $为初始估计到最优值的距离。迭代次数直接从固定容差（就距最优值的距离而言）的收敛速度ϵ中得出。

2 同态加密算法

同态加密方案已使用不同方法完成。BFV和BGV执行整数模运算，而CKKS实现近似定点算术。这些方案的安全性是建立在带错误的环学习问题的基础上，是一个以区分随机线性方程为目标的带错学习问题的变体，这些方程受到少量扰动来自均匀的噪声^[7]。

CKKS方案^[8]通常被认为是对实数和复数执行近似同态加密计算的最有效方法^[9]。它可以被认为是一个噪声通道^[10]，一个简单的加密/解密过程会给原始消息添加噪声。该方案中，明文和密文空间$R[{Z_q}]$和$R[C]$利用整数多项式环的结构来完成。该多项式环与规范嵌入变换相结合，对${C^N}$中的向量进行编码-解码的往返交替复多项式$R[C]$的环。要对消息$x \in R[C]$进行编码，可应用逆嵌入变换来得到$\mu = {\sigma ^{ - 1}}(x) \in R[C]$，然后将$\mu $按因子$ \Delta = {2^p} $缩放并四舍五入以获得纯文本$m = [\Delta \cdot \mu ] \in R[{Z_q}]$。

综上可认为CKKS方案是最适合应用梯度下降或加速梯度下降的同态加密方案。因其步长η可以足够小，使得梯度下降算法能够收敛^[11-12]。

3 同态加密梯度下降算法

同态加密下降算法与普通下降算法相比，仍以迭代的方式运行，其区别在于将迭代密文而不是纯文本。针对加速梯度下降和梯度下降算法在同态加密过程中的应用，与通常的加速梯度下降和梯度下降算法非常相似，区别仅在于使用了同态加密算数运算和特殊的MMULT矩阵乘法。

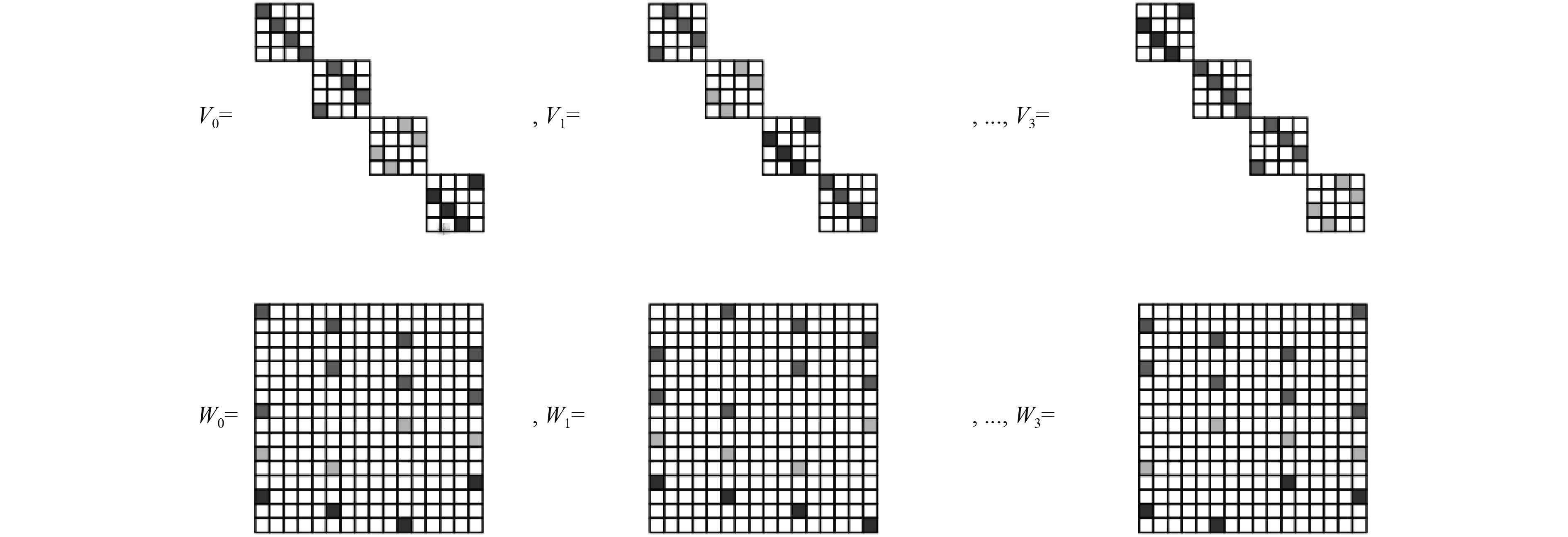
在迭代密文时有2个步骤需格外注意，分别是停止条件和矩阵乘法过程。矩阵乘法过程与噪声水平相关，而噪声水平随乘法深度呈指数增长。当前已有学者提出了一种全同态矩阵乘法算法（Halevi-Shoup 方法）来以更有效的方式执行这些运算^[13]。这种方法提出了一种新矩阵乘法方案（JKLS），该方案允许进行加密矩阵乘法，每个矩阵仅适用一个密文，遵循行排序编码$ A \to a $。虽然应用方便，但JKLS算法仍需2次明文与密文的乘法运算。本文对此做了部分改进，将明文与密文的乘法运算减少了一次。在该算法的基础上，本文将矩阵$ {{\boldsymbol{V}}_k} $和$ {{\boldsymbol{W}}_k} $分别对行编码矩阵A和B进行排列，使得所知的矩阵乘法算法可通过逐元素乘法和加法来实现，具体如下式：

$ {V_k}(d \cdot i + j,l) = \left\{ {\begin{split} 1，{l = d \cdot i + {{[i + j + k]}_d}}，\\ 0，{l \ne d \cdot i + {{[i + j + k]}_d}}。\end{split}} \right. $

(3)

$ {W_k}(d \cdot i + j,l) = \left\{ {\begin{split} 1，{l = d \cdot {{[i + j + k]}_d} + j}，\\ 0，{l \ne d \cdot {{[i + j + k]}_d} + j}。\end{split}} \right. $

(4)

其中，[ ]_d为对d取模运算，示例如图1所示。

对于停止条件直接确定一个加密值是否大于另一个加密值不可行。当前虽然有一些方法可在同态加密过程中实现停止规则，但实现方法仍然十分复杂。

考虑到实际应用中在同态加密过程中实现停止规则的计算压力，本文对加速梯度下降算法做出了一些修改，以便降低算法复杂度。

1）不指定容差ε，而是固定迭代次数N。通过给定的迭代次数N和算法的收敛速度推断出可达到的容差ε；

2）引入初始估计x₀。

4 数值分析

同态加密资源需求与加密电路的容量成正比。电路的容量增加，每次算术运算所需的计算存储器和计算能力也会增加。考虑到计算资源和Microsoft SEAL的参数，在CKKS方案中，本文可实现的最大电路的乘法深度为18。在每次迭代中，加速梯度下降和梯度下降的乘法深度分别为3和2，导致加速梯度下降和梯度下降的上限分别为6次和9次迭代。

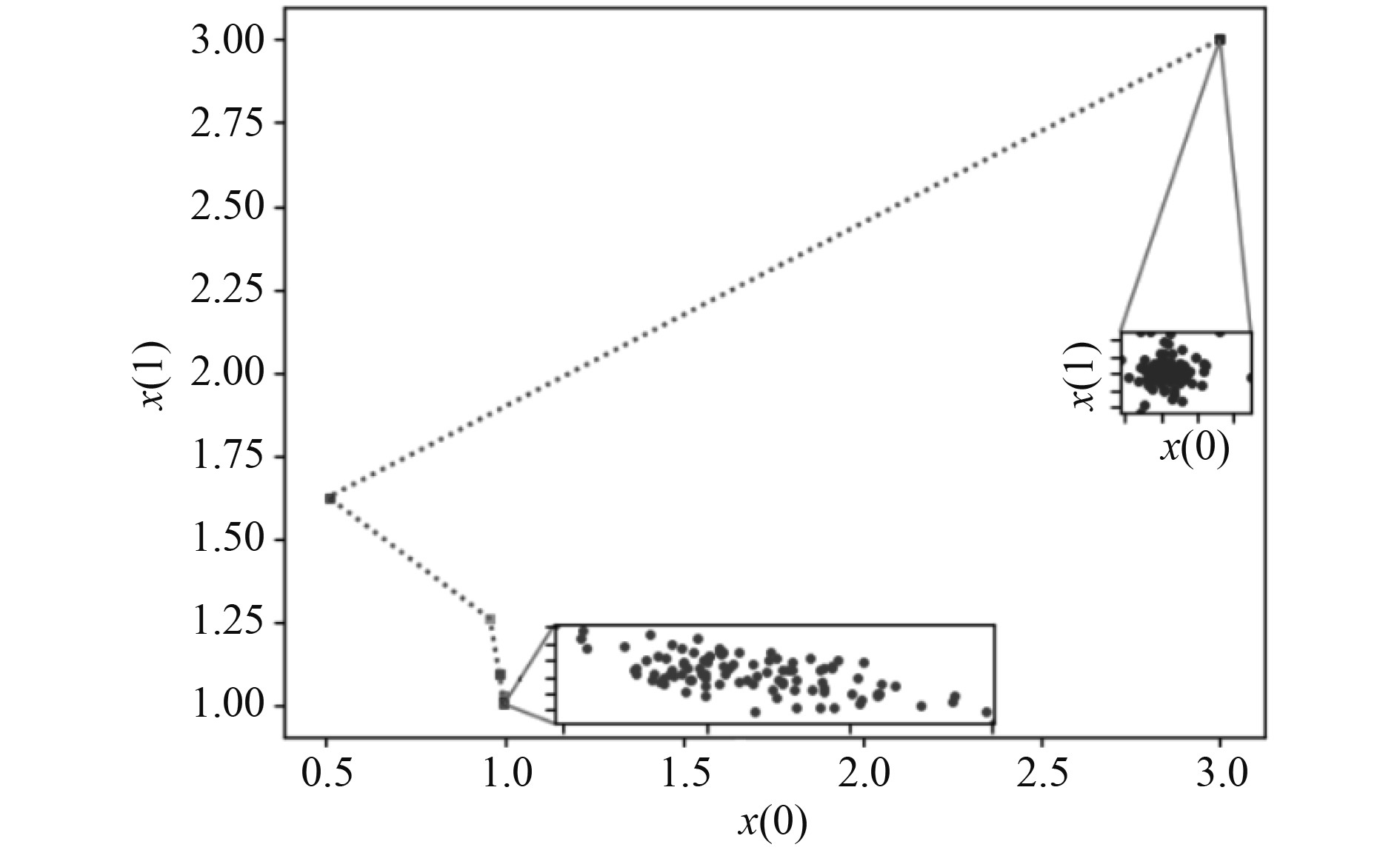
首先，对同一矩阵Q运行具有初始条件$ {x_0} \ne {x^*} $的2种算法，并且会在每一次迭代的时候解密结果。图2显示每一次迭代过程中，解决方案朝着最优方向靠拢。

图2中进行同态加密加速梯度下降算法解密重复100次，使用2×2矩阵，且$ \kappa = 2 $，最优值$ {x^*} = (1,1) $，初始值$ {x_0} = (3,3) $。对于同态加密梯度下降算法结果相近。

从结果来看，加速梯度下降表现出优异的收敛速度，它可以用更少的迭代来满足给定的收敛容差。然而，在加密的情况下，加密电路允许的深度所施加计算限制会带来一种权衡，因为与梯度下降相比加速梯度下降涉及更多算术运算。因此，在计算上可能满足给定容差所需的迭代次数。本文在数值上研究了这种权衡，并表明首选方法取决于二次矩阵Q的条件数$ \kappa $。

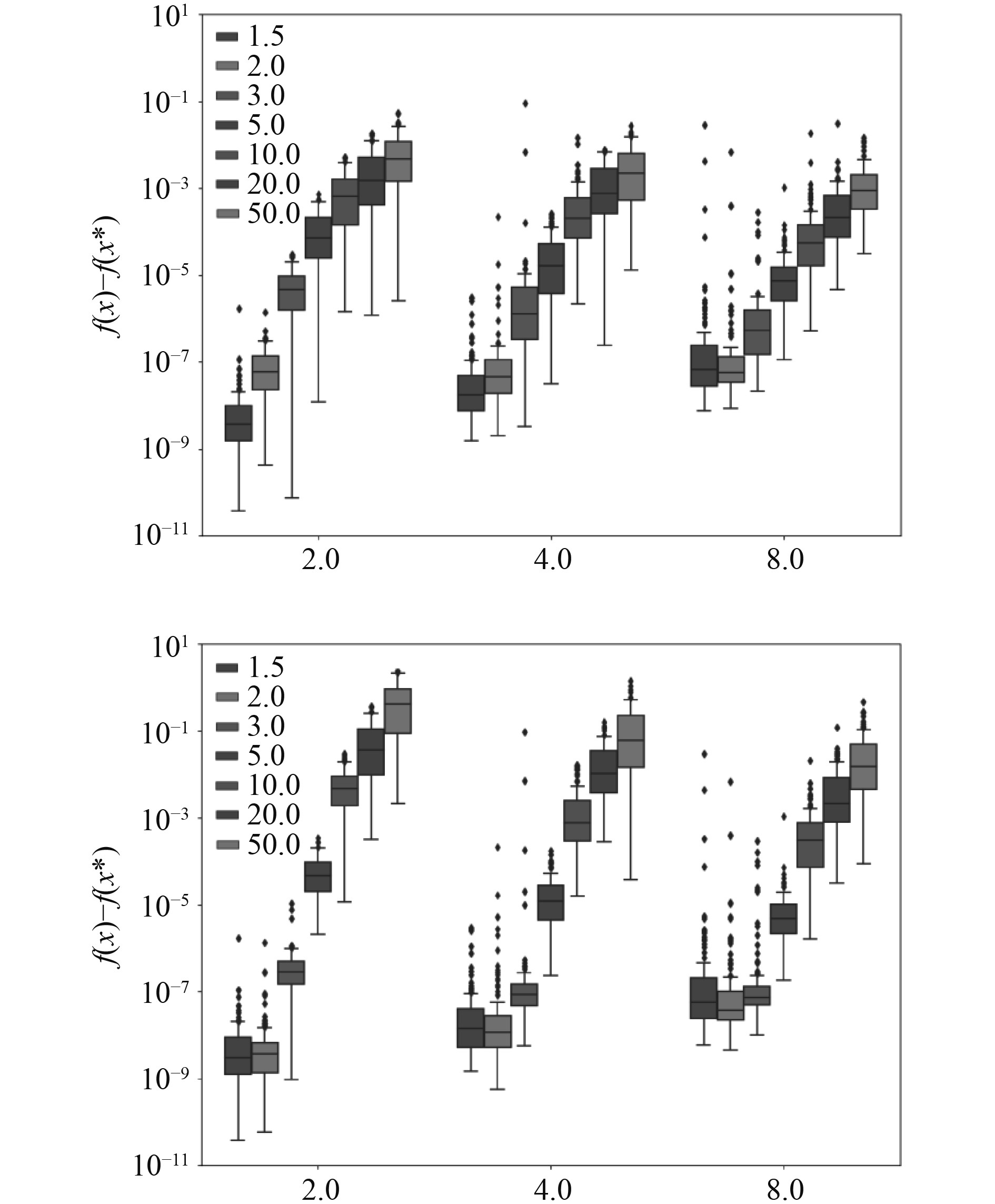
为了在数值上分析这种权衡，生成条件数范围从1.5～50的二次规划实例。为了收集$ \kappa $影响的数值统计，对于每个$ \kappa = 2 $，生成100组随机生成对称的维度为2、4和8的正定矩阵Q及相关随机向量$ p $。通过同态加密梯度下降算法和同态加密加速梯度下降算法方法求解每个二次规划实例，初始条件为$ {x_0} $，使得$ {\left\| {{x_0} - {x^*}} \right\|_2} = 1 $。图3说明了容差对于具有不同维度矩阵，不同条件数$ \kappa $（颜色代码）值在使用加速梯度下降（顶部）和梯度下降（底部）算法时，返回的解$x$与最优成本$f\left( {{x^*}} \right)$的最优差距。

表2为图3中的重要观察结果，表中数字表示对应不同矩阵Q进行100次运算的中值容忍水平。结果表明，额外的迭代可令梯度下降方法更为优秀，并在$ \kappa \leqslant 5 $时实现更好的容差值。然而，在$ \kappa > 5 $（如表2所示）的情况下，加速梯度下降方法的性能比梯度下降方法更好。这表明，在处理具有高$ \kappa $值的矩阵时，乘法深度的限制是一个主要问题。

5 结　语

本文研究、实现和分析了梯度和加速梯度下降算法，以同态加密方式解决二次规划问题。对不同的加密方案做了评估，然后对加密方法做了一定改善。证明了目标函数二次项矩阵的条件数在确定首选算法方面起着重要作用。对于较高的条件数值，首选加速梯度下降，因为即使执行较少迭代，它也能更快地收敛到解。而对于矩阵条件数较低的值，由于额外的迭代，梯度下降算法表现更好。此外，本文提出的改进同态加密矩阵乘法算法，在乘法深度方面更加高效。这些观察结果已通过数值研究得到验证。

然而，给予同态加密的二次规划仍然存在许多突出挑战。例如，考虑到投影到约束集中需额外操作，解决约束问题通常是一个挑战。为了解决这些问题，进一步的工作应集中在优化乘法深度上，或许还可探索在同态加密方案中编码矩阵的替代方法。