在船体曲面设计过程中,需以船舶的静动力性能为基础进行反复修正,并且每次对船体曲面的调整都会改变船舶的水面运动性能,接着基于流体力学理论分析船舶的水面运动性能,通过反复的修改以及分析,最终能得到满足船舶水面运动性能的曲面[1]。进行船型优化改进时,船舶水面运动性能以数值模拟技术为基础进行分析,该方法在构建船体模型的过程中,效率比较低[2]。和传统的船舶建模方法相比较,NURBS曲面理论在修改及控制船舶曲面方面比较灵活,船舶曲面以NURBS理论为基础进行设计修改,可最大限度提升船舶的设计效率[3]。利用NURBS曲线设计方法将船舶的几何模型及网格模型统一在一起,这样可迅速地将NURBS设计的船舶曲面直接转换成网格模型,然后再进行数值模拟分析,能避开船舶在设计过程中的重复性工作,从而可给船舶的型体设计打下坚实基础[4]。本文基于NURBS曲面理论,研究了船舶主体模型的CAD建模方法,这有助于我国船舶结构设计方法的快速提升。
1 NURBS曲面理论 1.1 NURBS曲线曲面的表达B样条基函数存在多种形式的定义,由于De Boor-Cox-Mansfield基函数在计算机上较容易实现,因此本文采用该类型的基函数递推公式[5]。假设存在非递减数列,如下式:
| $ {U^{'}} = \left\{ {{u_0}} \right., \cdots ,\left. {{u_n}} \right\},{u_i} \leqslant {u_n} \text{,} $ | (1) |
式中:un为节点,基于式(1)可得到B样条基函数的表达式,如式(2)。
| $ \left\{ {\begin{array}{*{20}{l}} {{B_{i,0}} = \left\{ {\begin{split} &{1,}\quad{{u_i} \leqslant u \leqslant {u_{i + 1}}},\\& {0,}\quad{\rm{others}} ,\end{split}} \right.} \\ {{B_{i,p}}\left( u \right) = \displaystyle\frac{{u - {u_i}}}{{{u_{i + p}} - {u_i}}}{B_{i,p - 1}}\left( u \right) + \displaystyle\frac{{{u_{i + p + 1}} - u}}{{{u_{i + p + 1}} - {u_{i + 1}}}}{B_{i + 1,p - 1}}\left( u \right)} \text{。} \end{array}} \right. $ | (2) |
假设存在控制定点数列Vi,并且B样条的次数为p次,那么基于式(1)可得到p次的B样条曲线,如下式(3):
| $ {C_i}\left( u \right) = \sum\limits_{i = 0}^p {{B_{j,p}}\left( u \right){V_{i + j}}} \text{。} $ | (3) |
在B样条曲线实际应用的过程中,一般为已知测量数据,需构建出一条通过已有测量数据的B样条曲线,即通过给定的测量数据求解出B样条曲线,满足下式:
| $ \left\{ {\begin{array}{*{20}{l}} {{V_0} = {P_0}} ,\\ {{V_{n + 2}} = {P_n}} 。\end{array}} \right. $ | (4) |
和B样条曲线受到单参数控制相比,B样条曲面会受到2个参数的控制。假设Vi,j为控制顶点,并且B样条曲面的2个控制参数方向分别为U和W,分别如式(5)和式(6)所示,B样条曲面的定义如式(7)所示。
| $ U = \left\{ {\underbrace {0,...,0}_{p + 1},{u_{p + 1}},...,{u_n},\underbrace {1,...,1}_{p + 1}} \right\}\text{,} $ | (5) |
| $ W = \left\{ {\underbrace {0,...,0}_{q + 1},{w_{q + 1}},...,{w_m},\underbrace {1,...,1}_{q + 1}} \right\}\text{,} $ | (6) |
| $ S\left( {u,w} \right) = \sum\limits_{i = 0}^n {\sum\limits_{j = 0}^m {{B_{i,p}}\left( u \right){B_{j,q}}\left( w \right){V_{i,j}}} } \text{。} $ | (7) |
式中:u和w均为3次基函数。非均匀p次有理NURBS曲线,如式(8)所示。
| $ C\left( u \right) = \sum\limits_{i = 0}^n {{V_i}{R_{i,p}}\left( u \right)} \text{,} $ | (8) |
Ri,p(u)的表达式,如式9所示,表示p次有理基函数。
| $ {R_{i,p}}\left( u \right) = \frac{{{W_i}{B_{i,p}}\left( u \right)}}{{\sum\limits_{j = 0}^n {{W_j}{B_{j,p}}\left( u \right)} }}\text{。} $ | (9) |
非均匀u向p次w向q次有理NURBS曲面可用式(10)表示。
| $ S'\left( {u,w} \right) = \frac{{\sum\limits_{i = 0}^n {\sum\limits_{j = 0}^m {{B_{i,p}}\left( u \right){B_{j,p}}\left( w \right){W_{i,j}}{V_{i,j}}} } }}{{\sum\limits_{i = 0}^n {\sum\limits_{j = 0}^m {{B_{i,p}}\left( u \right){B_{j,q}}\left( w \right){W_{i,j}}} } }}\text{,} $ | (10) |
式中,Wi,j为B样条基函数,其表达式如下。
| $ {W_{i,j}} = \left\{ {{w_0},...,{w_{m + q + 1}}} \right\}\text{。} $ | (11) |
假定存在一个弹性样条,并且该样条经过了给定的型值点,其应变能表达式为:
| $ A = \frac{1}{2}{\left( {EI} \right)^2}\int_0^L {{{\left| {k\left( s \right)} \right|}^2}{\mathrm{d}}s} \text{。} $ | (12) |
一般情况下应变能A越小,表明曲线越光顺,即曲线的总曲率越小,当应变能A=0的时候,此时的曲线为一条直线。由于式(12)的解算十分繁琐,因此一般使用近似的能量模型来计算,为了降低计算难度,通常使用曲线的二阶导数来代替样条的曲率,则样条曲线的能量模型可表示为:
| $ {E_c} = \int_0^b {{{\left| {C''\left( u \right)} \right|}^2}{\mathrm{d}}u} \text{。} $ | (13) |
从式(13)可知,样条曲线越光滑,其能量值就越小。曲线偏离程度的约束可表示为:
| $ {T_C} = \sum\limits_{l = 0}^{n + 2} {{{\left( {V_l^* - {V_l}} \right)}^2} \lt \varepsilon } \text{。} $ | (14) |
式中,ε为容差。在满足曲线偏离约束条件的情况下,以最小的曲线应变能为目标,则可构建出优化方程,即通过式(13)和式(14)可获得曲线的光顺模型。此时,存在有约束条件的规划问题,一般会将有约束的转变成无约束的问题进行解算,然后使用惩罚函数对优化方程进行求解,如下式:
| $ {F_C} = \alpha \cdot \int_a^b {{{\left| {C''\left( u \right)} \right|}^2}du + \sum\limits_{l = 0}^{n + 2} {\gamma {{\left( {V_l^* - {V_l}} \right)}^2}} } \text{。} $ | (15) |
式(15)的求解目标是计算FC的极小值,计算方法如式(16)所示。对式(16)进行解算,则可获得光顺之后的B样条曲线。
| $ \frac{{\partial {F_C}}}{{\partial V_l^*}} = 0\text{。} $ | (16) |
剪力跃度平方和的表达式,如式(17)所示。剪力跃度平方和越小,曲率变化就会越均匀。
| $ {D_C} = {\sum\limits_{l = 0}^{n - 2} {\left| {\frac{{{k_{l + 2}} - {k_{l + 1}}}}{{{l_{l + 1}}}} - \frac{{{k_{l + 1}} - {k_l}}}{{{l_l}}}} \right|} ^2}\text{。} $ | (17) |
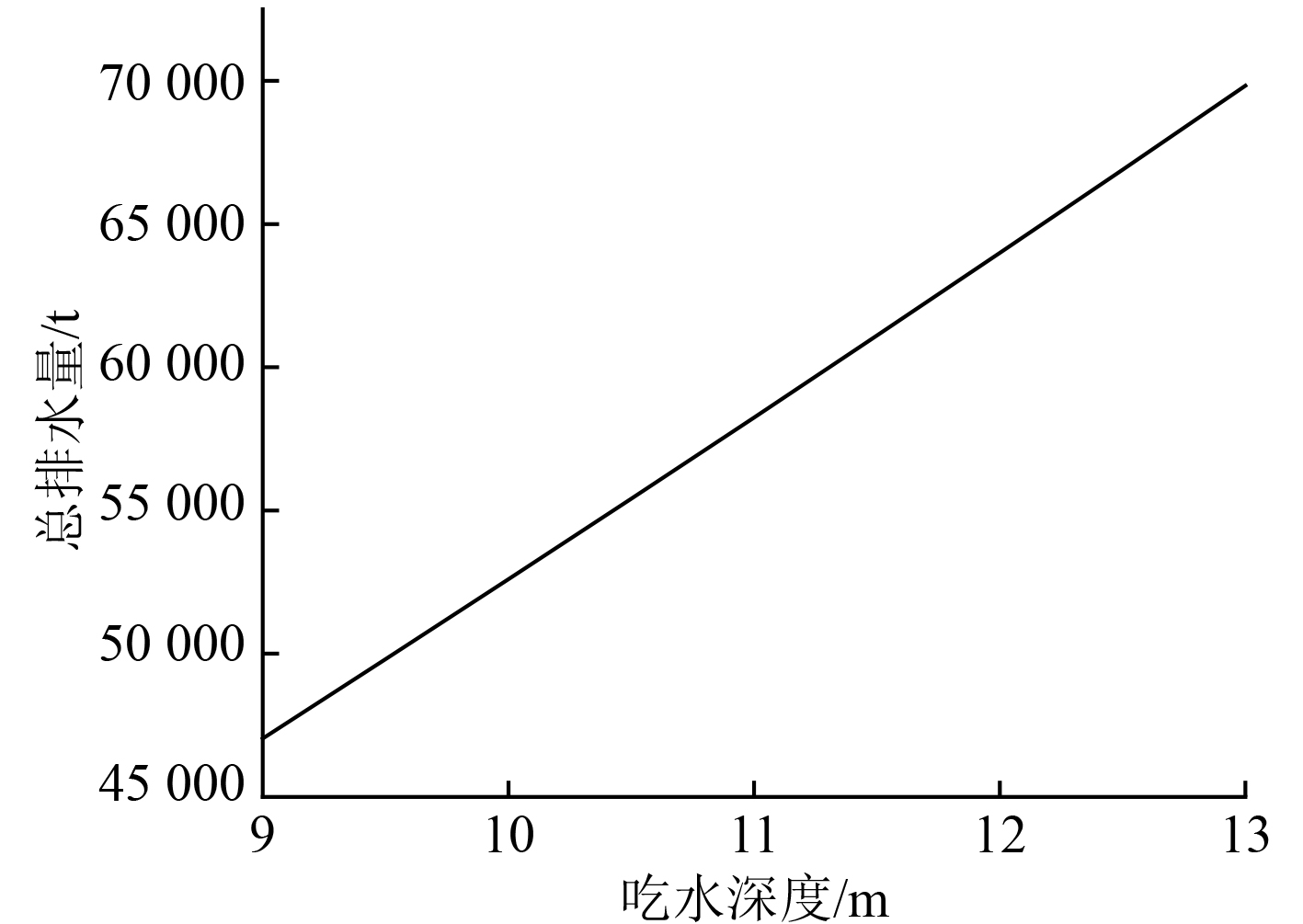
一般情况下,使用二维积分的方法对船舶的水面静水力进行求解,二维积分法主要是梯形法等,虽然二维积分计算方法的原理相对比较简单,但求解的过程十分复杂,并且其求解精度低[6]。随着船舶三维设计方法的推广,船舶利用三维计算的方法进行静水力求解。船舶的静水力曲线在解算过程中,涉及到的参数主要有船长、最大吃水、附体系数等[7]。船舶的排水量随吃水深度的变化曲线,如图1所示。可以看出,船舶的排水量和吃水深度是呈线性关系。
|
图 1 船舶排水量随吃水深度变化曲线 Fig. 1 Curve of ship displacement variation with draft depth |
在船舶吃水深度为11.5 m的情况下,采用三维设计方法对船舶的静水力进行计算,计算结果和船舶原有结果如表1所示。可知,三维模型解算方法得到的剖面参数和船舶原有的数值十分接近,但得到的方形参数和棱形参数都比原有的数值要大一些。
|
|
表 1 船舶静水力计算结果 Tab.1 Ship hydrostatic calculation results |
在对船舶静稳性力臂的解算过程中,采用的是等排水量的方法,通过船舶的三维实体模型可获得等体积倾斜水线,利用这个倾斜水线可对船舶的三维模型进行切割,获得水线下方的实体模型,接着利用内置函数获得切割实体的体积心,然后利用式(18)可对船舶的静稳性力臂进行解算。
| $ l = {y_B}\cos \phi + {z_B}\sin \phi - {z_G}\cos \phi \text{。} $ | (18) |
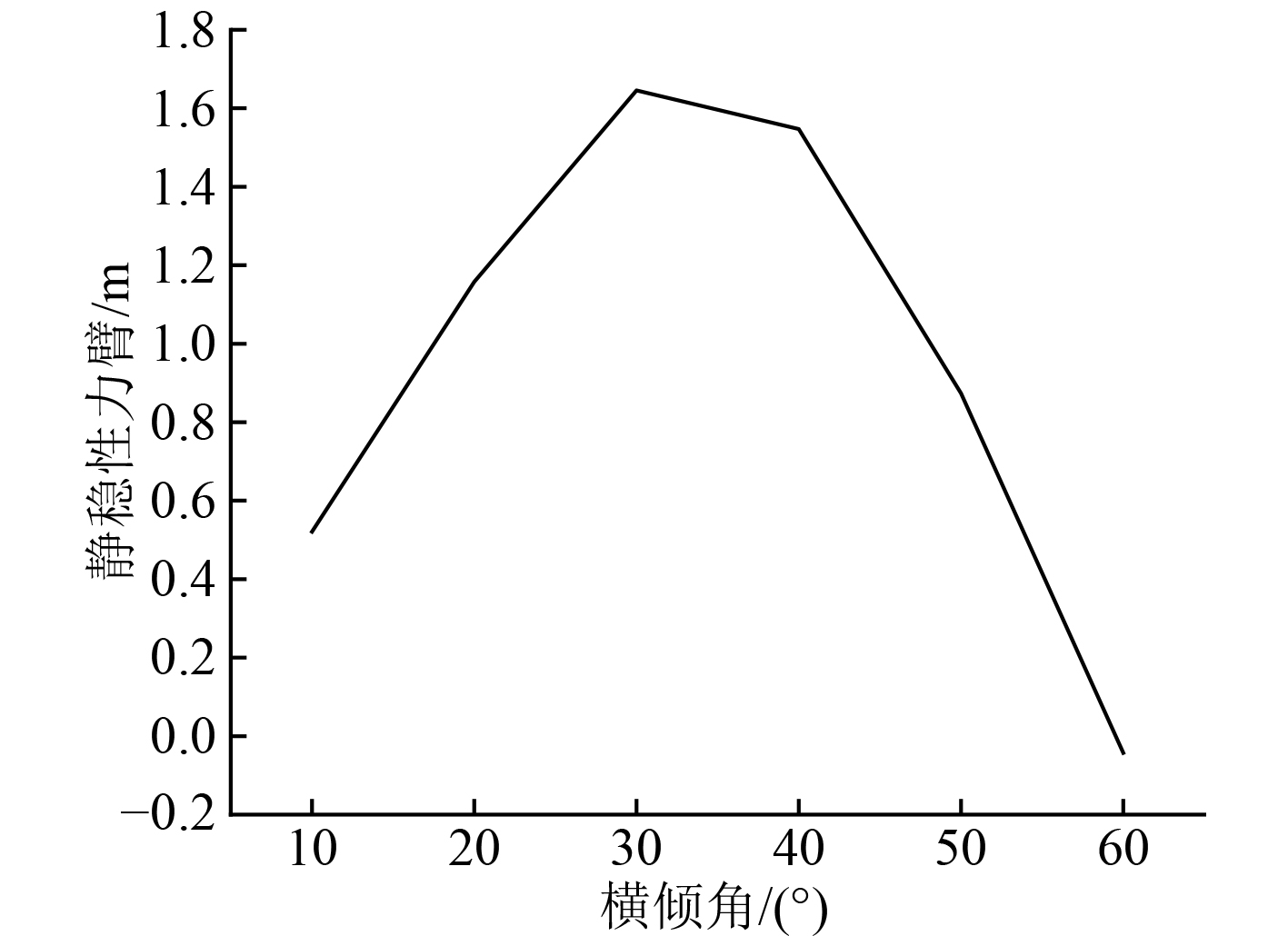
在解算过程中,设置纵倾角为0.53°,图2为船舶静稳性力臂的变化曲线。可知,船舶静稳性力臂的最大值出现在横倾角等于30°的地方。船舶三维模型需满足稳性衡准数,其表达式如式(19)所示;当宽深比大于2的情况下,横倾角的减小值如式(20)所示。
|
图 2 静稳性力臂的变化曲线 Fig. 2 The variation curve of static stability force arm |
| $ K = \frac{{{l_q}}}{{{l_f}}} \geqslant 1\text{,} $ | (19) |
| $ \Delta \theta = 20\left( {\frac{B}{D} - 2} \right) \cdot \left( {k - 1} \right)\text{。} $ | (20) |
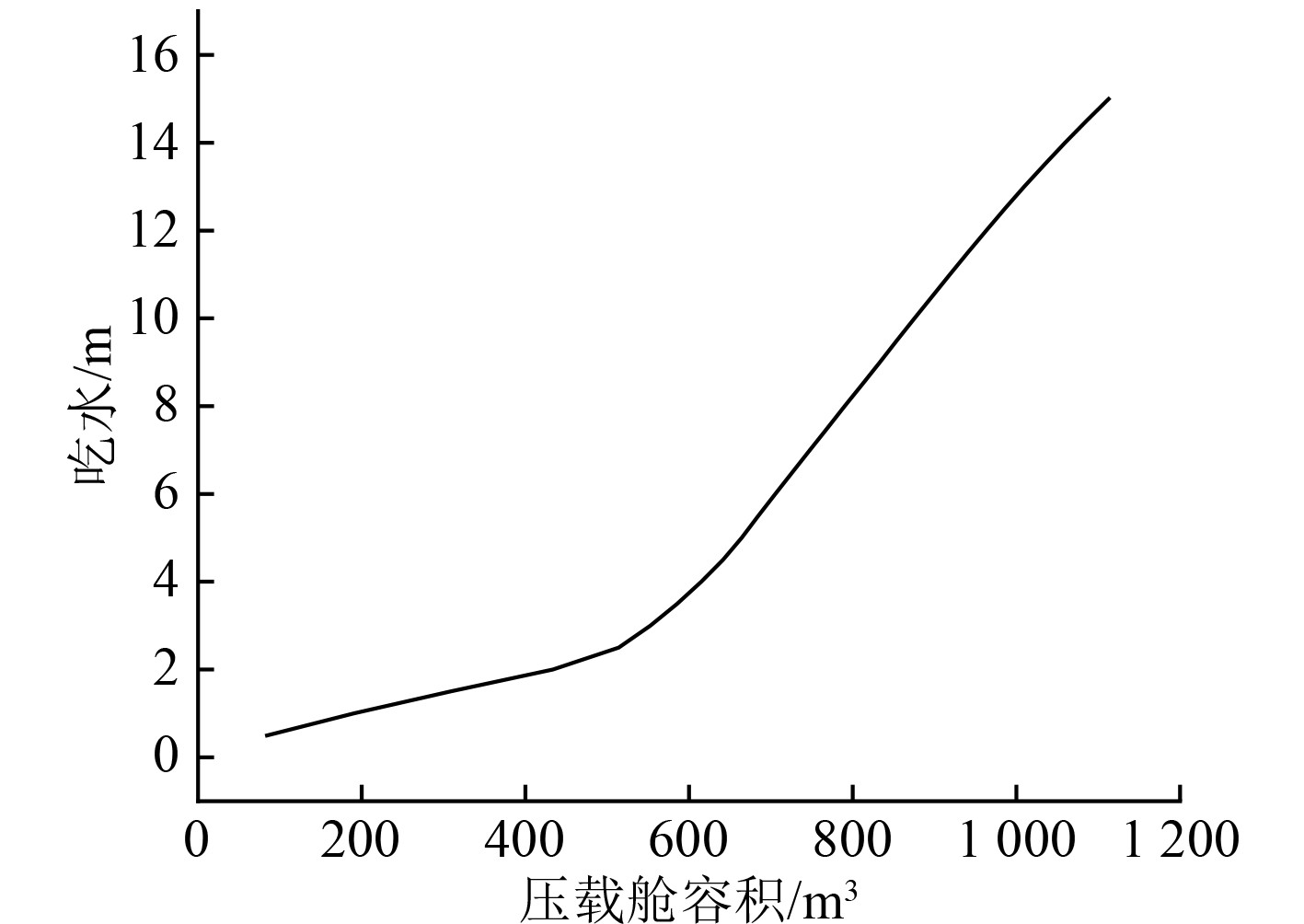
式中:船舶宽/深比的最大值取2.5;稳性衡准数K的最大值取1.5。船舶吃水深度随压载舱容积变化曲线,如图3所示,可知,随着船舶压载舱容积的增大,船舶的吃水深度先缓慢上升,当压载舱容积大于600 m3的时候,船舶吃水深度的增长率会突然变大。
|
图 3 船舶吃水深度随压载舱容积变化曲线 Fig. 3 The curve of ship's draft depth changing with the volume of ballast tanks |
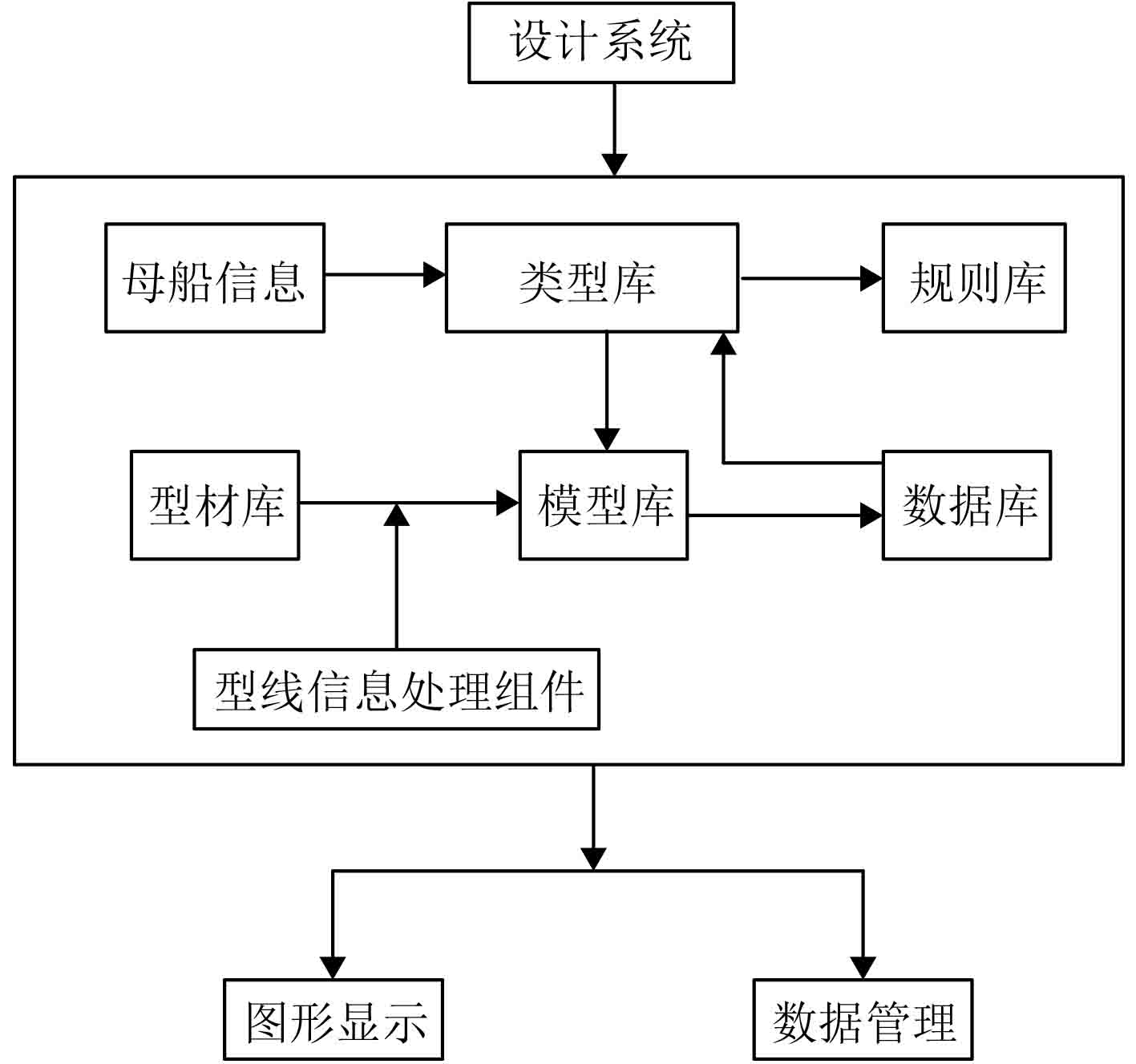
基于船舶结构的设计思路,对船舶的结构执行细化封装,然后基于模块化的思路分解船体结构,并构造出船舶模型库,利用该船舶模型库可快速建模,接着利用类型库存储船舶的设计经验,最终实现船体模型的快速建立以及修改。本文提出的快速建模系统结构图,如图4所示。
|
图 4 快速建模系统结构图 Fig. 4 Quick modeling system architecture diagram |
图4中类型库的任务是对船舶的基本类型进行构建,规则库的目标是生成船舶结构设计参数并提供给模型库,型材库的主要任务是基于标准的型材对其参数进行建立,船舶构件的拓扑信息存储在数据库中。对船舶曲面模型进行构建是船舶结构设计的前提,船舶形状曲线是通过船舶的型线信息处理组件得到的,并用于船舶的构建设计,最后以该形状曲线为基础对船舶构件的轮廓线进行绘制,得到船舶构件的三维结构模型。图4中各种类型的库结构均为可扩展的,新的船型结构以及标准可以随时添加进去。
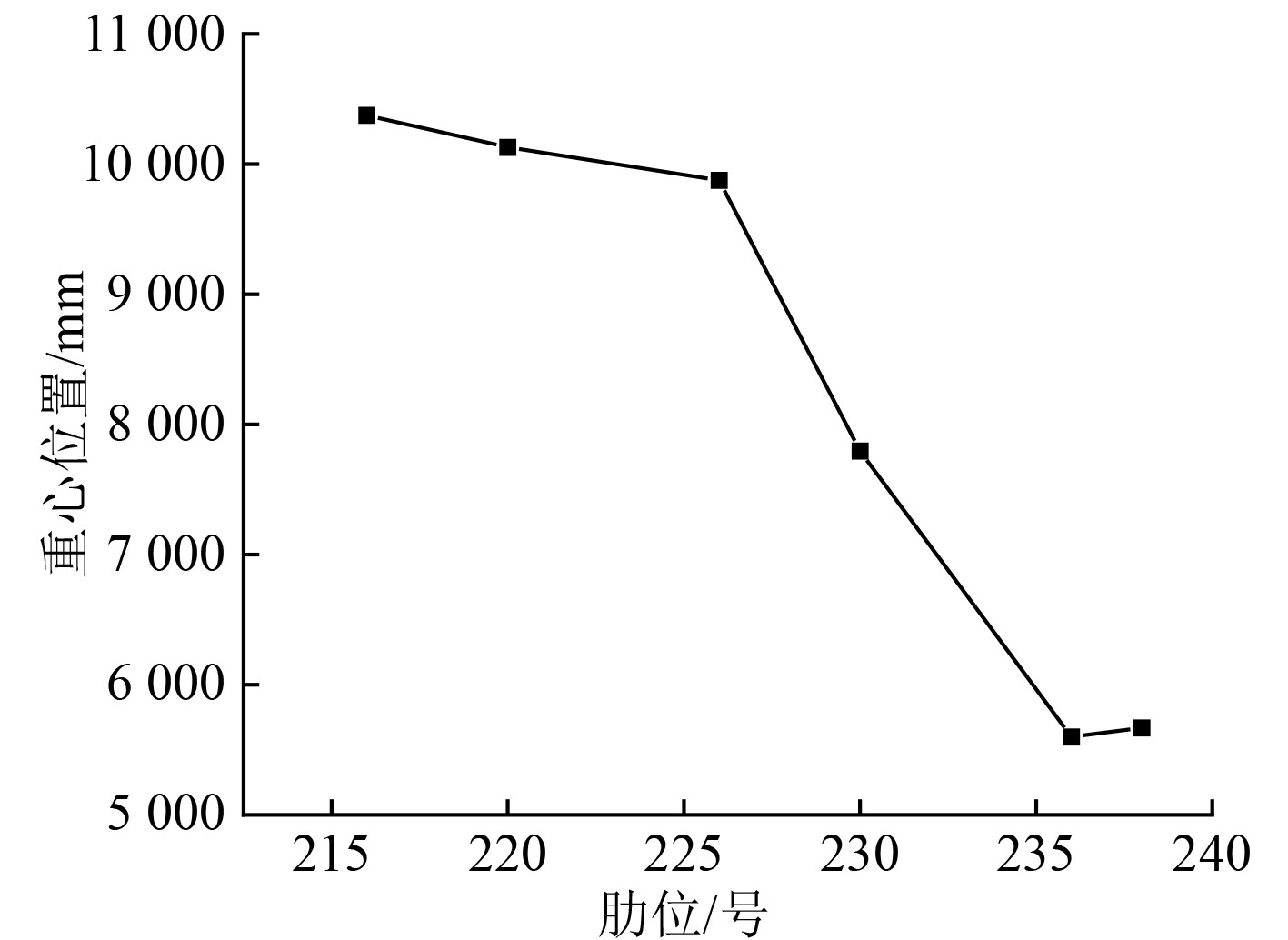
在船舶的船体结构设计过程中,最复杂困难的设计工作是船体结构重心位置的确定。本文在一定的间距下,对船舶的重心位置进行计算,最终可获得不同分段肋位上的重心位置,不同肋位上重心位置的变化曲线,如图5所示。可知,肋位号越大,表示距离船舶几何中心越远,纵坐标重心位置是以船舶底部为基准的垂直距离,因此距离船舶几何中心越远,其重心位置越低。
|
图 5 不同肋位上重心位置的变化曲线 Fig. 5 The variation curve of the center of gravity position on different rib positions |
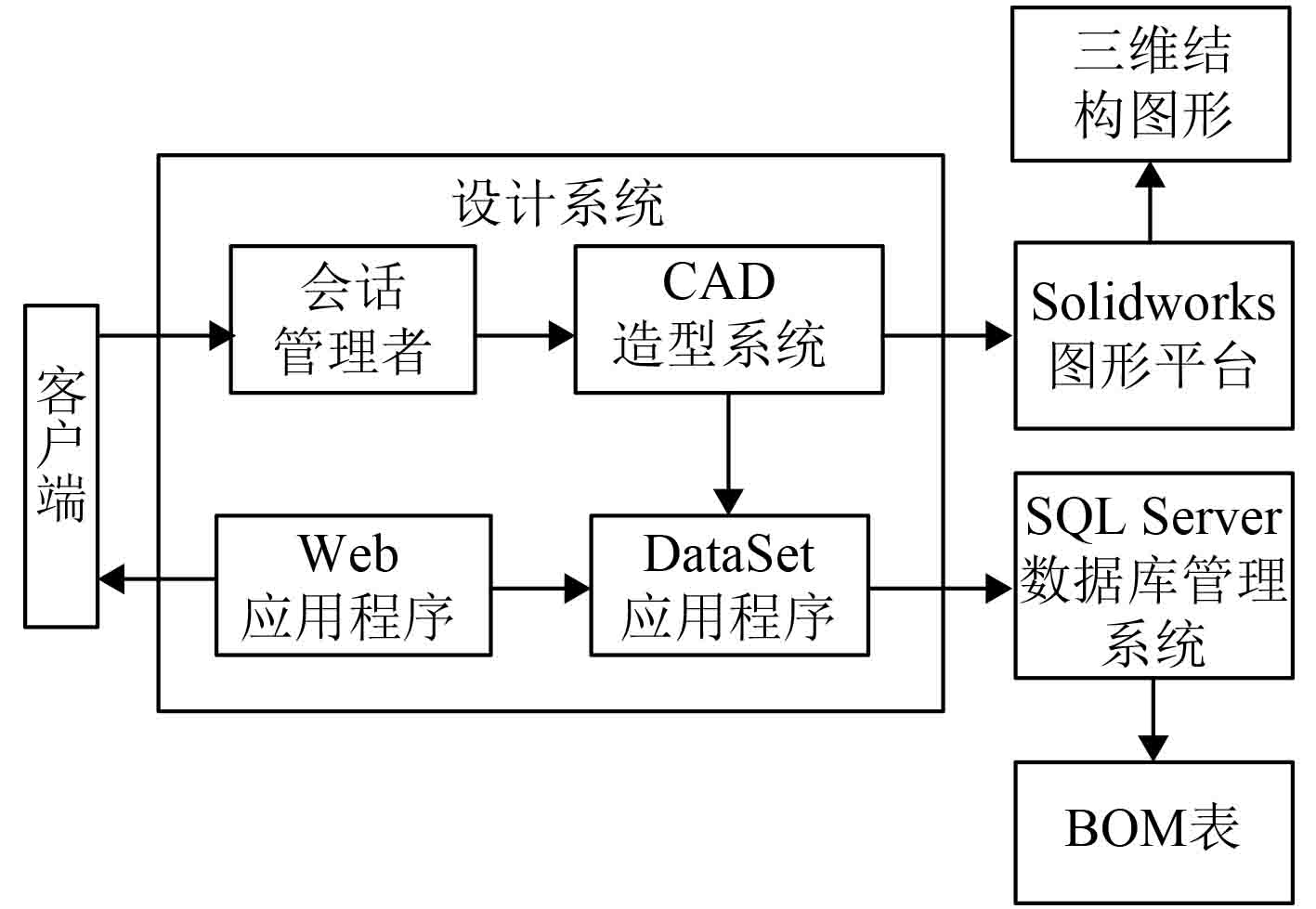
在数字化的设计过程中,虚拟化为其最重要的特征,主要的工作方式是程序化,采用模块化技术自动对相关设计任务进行批量操作,这样可极大提升工作效率。本文图形平台采用solidworks,数据库采用SQL Server,该数据库主要是用于用户端的数据显示任务,同时对ODBC数据库进行构建,然后将设计的结果显示到接口界面上,并将船体模型的设计以及建造信息存储到数据库中,其系统结构如图6所示。
|
图 6 船舶模型系统开发平台 Fig. 6 Ship model system development platform |
NURBS曲面理论凭借其优良特性,被采纳为计算机处理曲面形状的工业标准,因此很多CAD建模软件均支持NURBS曲面理论的建模方法。NURBS曲面理论在船体曲线曲面设计方面存在很多长处。在船舶结构的设计过程中,通过NURBS工具对船体的曲面进行插值计算以及边界处理,可获得基于NURBS表达式的船舶曲面设计,最后利用数值分析的方法,以确定船舶曲面的水动力性能,极大提升了船舶结构的设计效率。
| [1] |
杨广全, 李思益, 曹西京. CAGO中的NURBS曲面—理论与应用[J]. 西北轻工业学院学报, 2001(19): 62-65. |
| [2] |
张礼林, 王国瑾. 带B样条曲率线的NURBS曲面设计[J]. 计算机辅助设计与图形学学报, 2018(30): 1692-1698. |
| [3] |
肖建华, 马成, 朱兆宇, 等. 基于方形压头的双曲率船体外板分段成形设计[J]. 武汉理工大学学报, 2023(45): 110-117. DOI:10.3963/j.issn.1671-4431.2023.09.017 |
| [4] |
郎爱蕾, 马文魁, 郑燕. 基于序列二次规划算法的NURBS曲面轮廓度误差评定[J]. 信息与电脑, 2021(20): 22-25. DOI:10.3969/j.issn.1003-9767.2021.20.008 |
| [5] |
曹拓, 付松, 何思远. 基于自适应变步长欧拉法的NURBS曲面爬行波寻迹算法[J]. 电子技术应用, 2018(44): 19-23. |
| [6] |
刘瀛昊, 佟福山, 高良田. 极地破冰船的快速性优化设计[J]. 计算机仿真, 2016(33): 405-409. DOI:10.3969/j.issn.1006-9348.2016.11.088 |
| [7] |
张凯, 谢承福, 涂跃红, 等. FORAN软件在船舶总体设计中的应用[J]. 中国舰船研究, 2009(4): 76-80. DOI:10.3969/j.issn.1673-3185.2009.04.016 |
 2024, Vol. 46
2024, Vol. 46
