2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
为满足日益增加的能源需求,海洋油气开发比例逐步增加[1]。海洋平台是油气开发过程中的关键装备之一[2],其营运条件较为恶劣,常受到复杂载荷作用及海水腐蚀[3],立柱和腿柱等支撑结构健康程度十分重要[4]。结构健康监测系统通过测量结构在受到载荷前后的响应,分析结构损伤程度及位置,可对风险进行预报及评估[5]。而形状感测能够考虑复杂结构和边界条件,具备足够灵敏度保障实时监视,为海洋结构物健康监测技术提供了新的方向[6]。
目前,变形重构方法主要有模态法[7]、Ko位移理论[8]和逆有限元法[9],其中逆有限元法具有广泛的应用前景,该方法既能重建静态响应也可重建动态响应,对复杂结构的变形重构具有较强兼容性。较多学者通过不同理论方法实现了逆有限元变形重构,Tessler[10]基于Mindlin厚板理论和最小二乘变分原理为基础,实现了板壳结构的形状感测。Gherlone等[11]基于Timoshenko梁理论,采用插值函数推导不同载荷的逆有限元单元,通过实验验证方法的准确性。部分学者提出不同类型传感器监测方法并对模型结构进行验证。Ding等[12]提出了基于FBG的螺旋桨轴系应变-变形重构系统,相较于传统接触式测量方法,可提升复杂结构的重构精度。He等[13]分别利用LDV及应变片测得试验数据,计算加速度导出位移(ADD)和应变导出位移(SDD),确定修正因子得到准确中性轴位置,可提升动载荷作用下结构的重构精度。也有部分学者提出对传感器位置优化进行研究。赵飞飞等[14]将鲁棒性及精确性作为目标,采用多目标粒子群优化算法,在仿真与试验中均可实现重构精度误差在3%以内。贾连徽等[15]根据船体结构高应力部位和海况信息建立了船体结构应力测点选取方法,可有效提升船舶适航能力。蔡智恒等[16]提出一种两步序列应变传感器布局方法,优先满足初始传感器数量少、求解效率高等条件,其次考虑信息冗余度和重构精度,布局结果优于误差估计最小方法。以上研究对逆有限元变形重构有着重要的参考价值,但之前的研究侧重于典型结构逆有限元方法的实现,在工程应用中测点位置及试验误差分析研究较少且缺乏系统性。
基于上述背景,本文提出一种应用于海洋平台立柱的逆有限元变形重构方法。首先,建立Timoshenko梁模型并进行受力分析,得出立柱内部本构关系,再以最小二乘理论,对结构表面进行离散,推导应变场与位移场函数关系。利用该方法将有限元仿真应变结果作为输入条件,分别讨论在均布载荷和集中载荷作用下,不同提取方法及对重构精度的影响。以海洋平台立柱为实验对象,将试验测试应变结果作为输入条件,讨论在集中载荷作用下,不同工况类型对重构精度的影响。最后,在试验过程中,讨论了位置偏差及噪声信号对重构精度的影响规律,为后续海洋结构物健康监测研究提供参考。
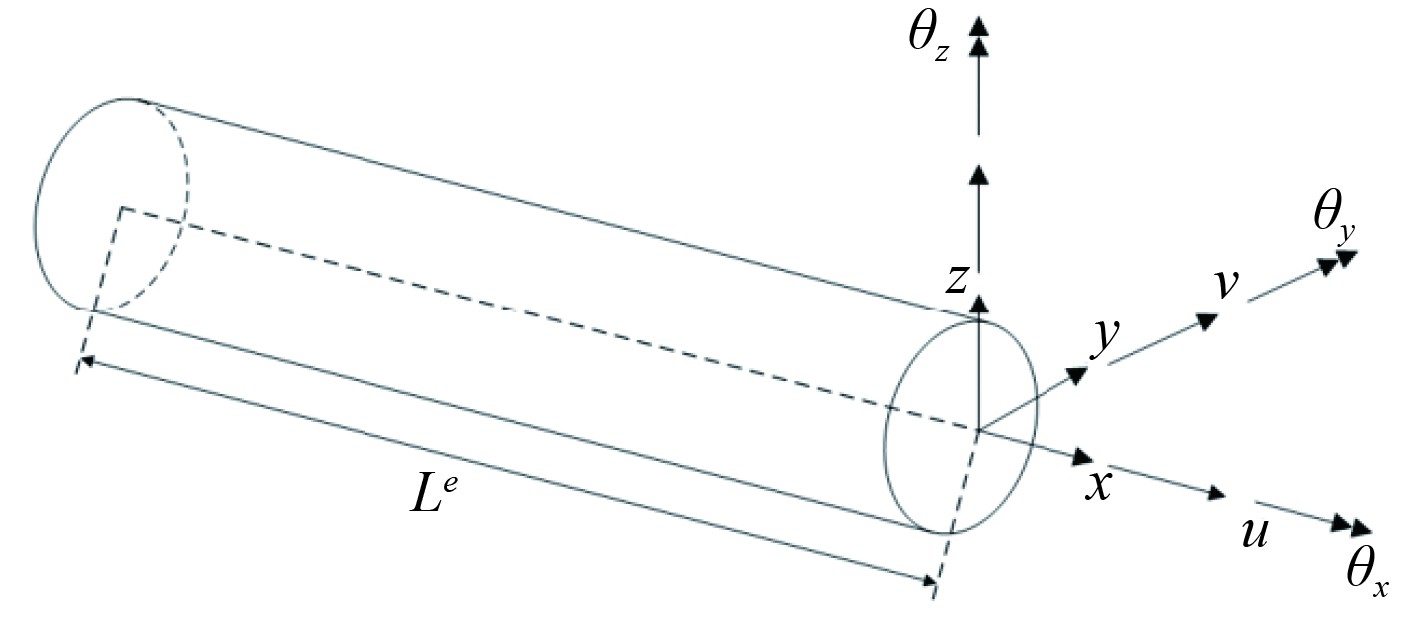
1 逆有限梁单元理论 1.1 Timoshenko 梁理论在笛卡尔直角坐标系中,建立等截面梁结构。如图1所示,以截面中心为原点O,沿轴方向为x,径向为y、周向为z。
|
图 1 悬臂圆柱梁结构示意 Fig. 1 Cantilever cylindrical beam structure |
梁单元具有6个自由度,分别为u、v、w三个平移分量以及
| $ \begin{gathered} {u_x}(x,y,z) = u(x) + z{\theta _y}(x) - y{\theta _z}(x) ,\\ {u_y}(x,y,z) = v(x) - z{\theta _x}(x) ,\\ {u_z}(x,y,z) = w(x) + y{\theta _x}(x)。\end{gathered} $ | (1) |
截面应变可具体如式(2),则可定义理论截面应变为
| $ \begin{gathered} {e_1}(x) = \frac{{\partial u(x)}}{{\partial x}}{\text{ ,}}{e_4}(x) = \frac{{\partial w(x)}}{{\partial x}} + {\theta _y}(x) ,\\ {e_2}(x) = \frac{{\partial {\theta _y}(x)}}{{\partial x}},{e_5}(x) = \frac{{\partial v(x)}}{{\partial x}} - {\theta _z}(x) ,\\ {e_3}(x) = - \frac{{\partial {\theta _z}(x)}}{{\partial x}},{e_6}(x) = \frac{{\partial {\theta _x}(x)}}{{\partial x}}。\\ \end{gathered} $ | (2) |
根据式(1)对x、y求偏导,结合式(2),可得中心轴应变与位移的关系,即
| $ \begin{gathered} {\varepsilon _x}(x,y,z) = {e_1}(x) + z{e_2}(x) + y{e_3}(x) ,\\ {\gamma _{xz}}(x,y) = {e_4}(x) + y{e_6}(x) ,\\ {\gamma _{xy}}(x,z) = {e_5}(x) - z{e_6}(x)。\\ \end{gathered} $ | (3) |
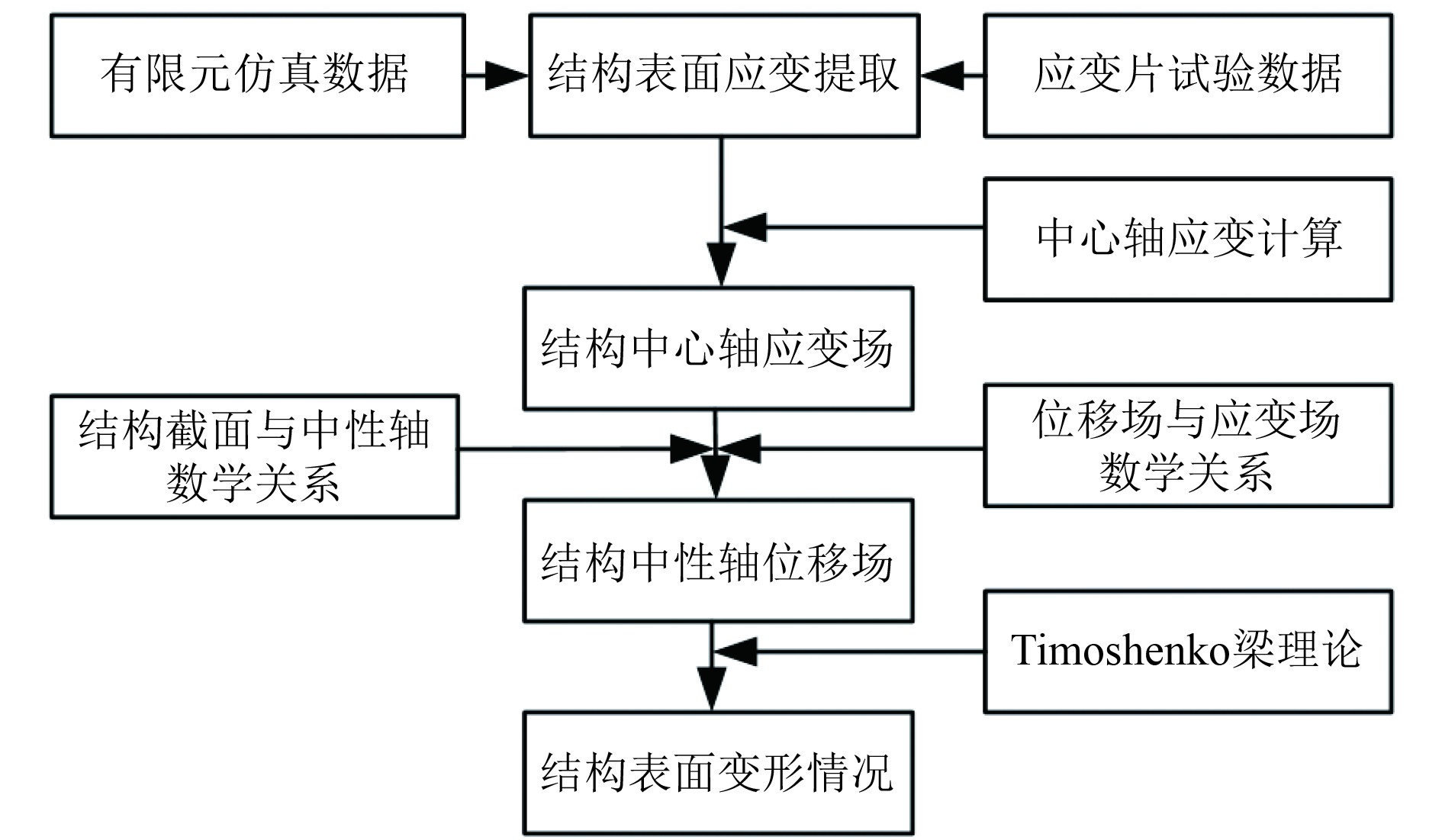
通过试验测试或有限元仿真提取表面应变来计算中心轴应变,通过式(3)可知中心轴位移场,从而通过式(1)计算结构表面变形情况,具体流程如图2所示。
|
图 2 IFEM梁结构模拟流程 Fig. 2 IFEM beam structure simulation process |
在逆有限元仿真过程中,悬臂梁结构存在以下本构关系:
| $ \begin{gathered} N = {A_x}{e_1}{\text{ }}{{{M}}_x} = {J_x}{e_6} ,\\ {Q_y} = {G_y}{e_5}{\text{ }}{{{M}}_y} = {D_x}{e_2},{\text{ }} \\ {Q_z} = {G_y}{e_4}{\text{ }}{{{M}}_z} = {D_x}{e_3} 。\\ \end{gathered} $ | (4) |
式中:N,Qy,Qz为集中载荷;Mx,My,Mz为弯矩;Ax=EA为X方向刚度;Gy=
通过获取悬臂梁表面应变信息可重构出该结构变形情况,需得到位移场与应变场数学关系。根据最小二乘理论,通过将悬臂梁结构离散,则可用无量纲参数及分量形式表示:
| $ {\varPhi }^{e}\left(u\right)\equiv w·\varPhi 。$ | (5) |
无量纲参数
| $ \varPhi _k^e = \frac{{{L^e}}}{n}\sum\limits_{i = 1}^n {{{\left[ {{e_k}\left( {{x_i}} \right) - e_k^{\varepsilon i}} \right]}^2}} {\text{ }}\left( {k = 1, \ldots 6} \right)。$ | (6) |
其中:Le为悬臂梁长度;n为所提取截面应变信息个数;xi为各点所对应轴向坐标;
悬臂梁位移向量u可通过位移型函数N(x)及结点位移ue表示:
| $ {\boldsymbol{u}} = {\boldsymbol{N}}\left( x \right){{\boldsymbol{u}}^e} 。$ | (7) |
将悬臂梁最小二乘函数
| $ {{\boldsymbol{k}}^e}{{\boldsymbol{u}}^e} = {{\boldsymbol{f}}^e},$ | (8) |
其中:
对于复杂结构而言,为求解整体结构位移,需将离散形式的各个刚度矩阵方程进行组合,则整体刚度矩阵如式(9)所示,在引入边界条件后,则节点位移可表示为式(10)。
| $ {\boldsymbol{KU}} = {\boldsymbol{F}} ,$ | (9) |
| $ {\boldsymbol{U}} = {{\boldsymbol{K}}^{ - 1}}{\boldsymbol{F}}。$ | (10) |
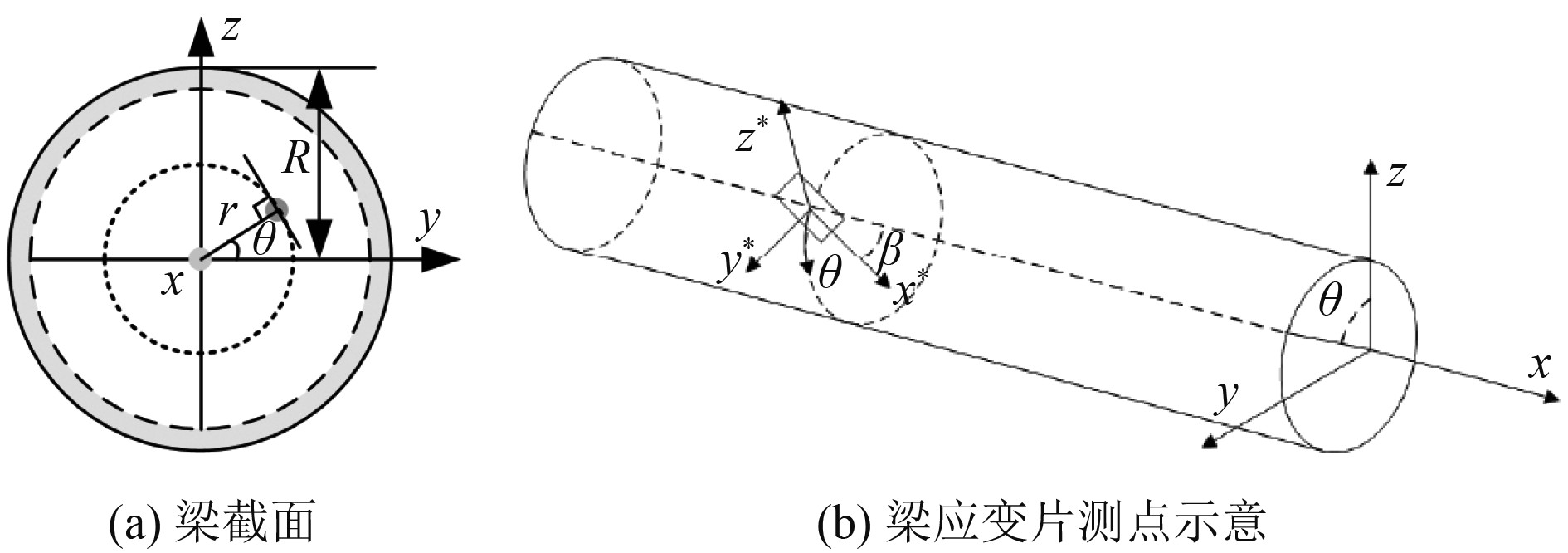
以中性轴与悬臂梁截面交点X为坐标系原点建立坐标系,其中θ为截面所处位置与Y轴夹角,R为悬臂梁半径,r为任意截面距离,如图3所示。
|
图 3 梁单元截面示意 Fig. 3 Cross section of beam element |
在只考虑正应力
| $ \left\{ \begin{gathered} {\varepsilon _x} = \frac{{{\sigma _x}}}{E} ,\\ {\varepsilon _\theta } = - \frac{v}{E}{\sigma _x} = - v{\varepsilon _x},\\ {\gamma _{x\theta }} = \frac{{{\tau _{x\theta }}}}{G} 。\\ \end{gathered} \right. $ | (11) |
其中:ν为泊松比;
如图3(b)所示,应变片所在位置的线应变与表面应变
| $ {\varepsilon _\beta } = {\varepsilon _x}{\cos ^2}\beta + {\gamma _{x\theta }}\sin \beta \cos \beta + {\varepsilon _\theta }{\sin ^2}\beta,$ | (12) |
结合式(11)和式(12)可转化为:
| $ {\varepsilon _\beta } = {\varepsilon _x}({\cos ^2}\beta - v{\sin ^2}\beta ) + {\gamma _{x\theta }}\sin \beta \cos \beta ,$ | (13) |
当r=R时,结合切应变几何关系,可得:
| $ {\gamma _{x\theta }} = {e_4}\cos \theta - {e_5}\sin \theta + {e_6}R ,$ | (14) |
结合式(3)和式(14),可得:
| $\begin{aligned}[b] & {{\varepsilon }_{{{x}^{*}}}}\left( {{x_i},\theta ,\beta } \right) =\\ & {e_1}({x_i})({\cos ^2}\beta - v{\sin ^2}\beta ) + {e_2}({x_i})({\cos ^2}\beta - v{\sin ^2}\beta )\sin \theta {R_{ext}} + \\ & {e_3}({x_i})({\cos ^2}\beta - v{\sin ^2}\beta )\cos \theta {R_{ext}} + {e_4}({x_i})\cos \beta \sin \beta \cos \theta - \\ & {e_5}({x_i})\cos \beta \sin \beta \sin \theta + {e_6}({x_i})\cos \beta \sin \beta {R_{ext}} ,\end{aligned}$ | (15) |
在悬臂梁单元内,载荷与弯矩可表示为:
| $ {Q}_{y}=\frac{\partial {M}_{z}}{\partial x},{Q}_{z}=\frac{\partial {M}_{y}}{\partial x},$ | (16) |
通过式(4)和式(16),其中
| $ \begin{gathered} {e_2} = {m_1}{e_4}x + {c_1},\\ {e_3} = {m_2}{e_5}x + {c_2}。\\ \end{gathered} $ | (17) |
当作用在梁上为集中载荷时,e1、e4、e5、e6为常数,e2、e3为一次函数关系,可得:
| $ \begin{split} & {e_1}\left( x \right) = {a_1},{e_2}\left( x \right) = {m_1}{a_4}x + {a_2},{e_3}\left( x \right) = {m_2}{a_5}x + {a_3},\\ & {e_4}\left( x \right) = {a_4},{e_5}\left( x \right) = {a_5},{e_6}\left( x \right) = {a_6} ,\\[-1pt] \end{split} $ | (18) |
其向量形式可表示为:
| $ {{{\boldsymbol{e}}}^{\boldsymbol{\varepsilon}} }\left( {\boldsymbol{x}} \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&1&0&{{m_1}x}&0&0 \\ 0&0&1&0&{{m_2}x}&0 \\ 0&0&0&1&0&0 \\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \\ {{a_3}} \\ {{a_4}} \\ {{a_5}} \\ {{a_6}} \end{array}} \right] = {{{T_1}}}\left( x \right){{{p_1}}} $ | (19) |
由此可以得到受集中载荷作用下梁单元任意截面处的应变:
| $ \begin{split}{{{\boldsymbol{e}}}^{\boldsymbol{\varepsilon}} }\left( {{{\boldsymbol{x}}_{\boldsymbol{j}}}} \right) = {T_1}\left( {{x_j}} \right){\left( {{T}\left( {{x_i},{\theta _i},{\beta _i}} \right) * {{e}^\varepsilon }\left( {{x_i}} \right)} \right)^{ - 1}}{{\varepsilon }_{{{x}^{*}}}}\left( {{x_i},{\theta _i},{\beta _i}} \right)。\;\;\;\;\\[-2pt] \end{split}$ | (20) |
由式(20)可知,在集中载荷作用时,需提取6个表面可推导梁单元任意截面应变。
当作用在梁上为均布载荷时,e1、e6为常数,e4、e5为一次函数关系,e2、e3为二次函数关系,由式(18)进一步可得:
| $\begin{split} & {e_1}\left( x \right) = {a_1},{e_2}\left( x \right) =\\ & {m_1}{b_4}{x^2} + {m_1}{a_4}x + {a_2},{e_3}\left( x \right) = {m_2}{b_5}{x^2} + {m_2}{a_5}x + {a_3},\\ & {e_4}\left( x \right) = {b_4}x + {a_4},{e_5}\left( x \right) = {b_5}x + {a_5},{e_6}\left( x \right) = {a_6} ,\\[-4pt] \end{split} $ | (21) |
其向量形式可表示为:
| $\begin{aligned} {{{\boldsymbol{e}}}^{\boldsymbol{\varepsilon}} }\left( {\boldsymbol{x}} \right) =\\& \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0 \\ 0&1&0&{{m_1}x}&0&0&{{m_1}{x^2}}&0 \\ 0&0&1&0&{{m_2}x}&0&0&{{m_2}{x^2}} \\ 0&0&0&1&0&0&x&0 \\ 0&0&0&0&1&0&0&x \\ 0&0&0&0&0&1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}} \\[-1pt] {{a_2}} \\[-1pt] {{a_3}} \\[-1pt] {{a_4}} \\[-1pt] {{a_5}} \\[-1pt] {{a_6}} \\[-1pt] {{b_4}} \\[-1pt] {{b_5}} \end{array}} \right] = \qquad\qquad\qquad\qquad\\& {T_2}\left( x \right){p_2}。\end{aligned}$ | (22) |
可得到均布载荷作用下梁单元任意截面应变:
| $ {{{\boldsymbol{e}}}^{\boldsymbol{\varepsilon}} }\left( {{{\boldsymbol{x}}_{\boldsymbol{j}}}} \right) = {T_2}\left( {{x_j}} \right){\left( {{T}\left( {{x_i},{\theta _i},{\beta _i}} \right) * {{e}^\varepsilon }\left( {{x_i}} \right)} \right)^{ - 1}}{{\varepsilon }_{{{x}^{*}}}}\left( {{x_i},{\theta _i},{\beta _i}} \right) 。$ | (23) |
由式(23)可知,在均布载荷作用时,需提取8个表面可推导梁单元任意截面应变。
2 IFEM位移重构结果分析 2.1 计算模型及应变测点方案在Ansys16.0中建立悬臂梁结构,长度为1000 mm,半径为50 mm,单元类型为Beam188单元,弹性模量

|
图 4 悬臂梁有限元模型加载方式 Fig. 4 Cantilever beam finite element model loading method |
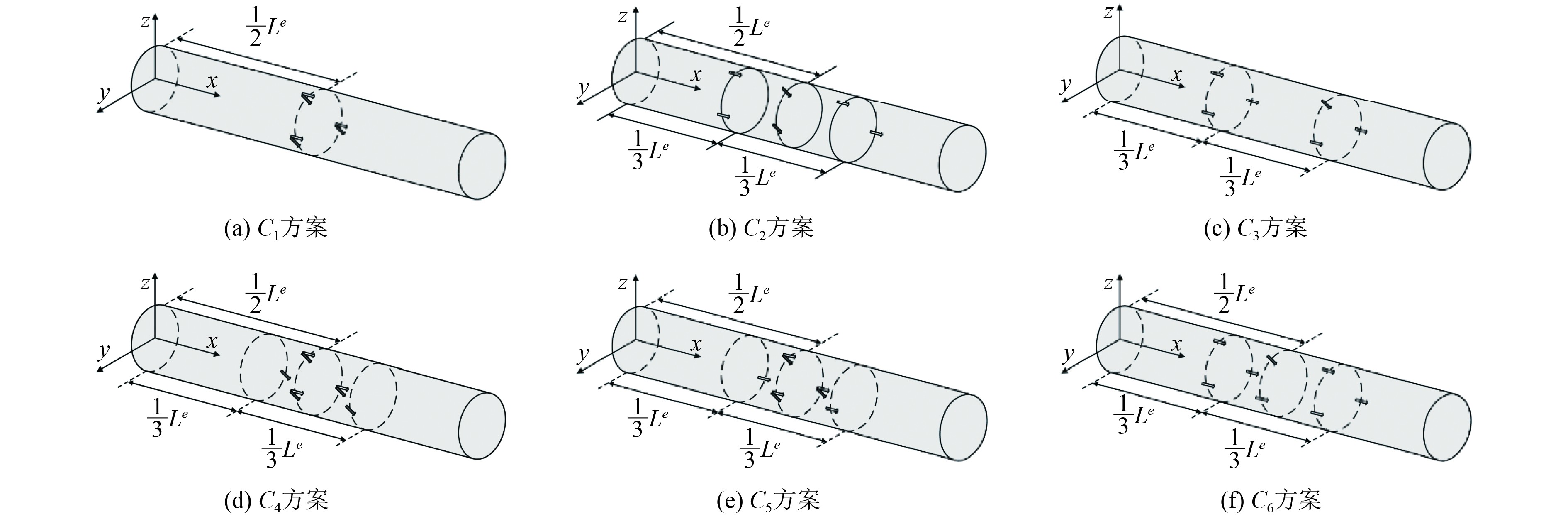
针对不同载荷形式,设计6种应变提取方案,其中C1、C2、C3为集中载荷工况,C4、C5、C6为均布载荷工况,如图5所示。
|
图 5 悬臂梁模型有限元应变信息提取方案 Fig. 5 Extraction scheme of Finite Element strain information of cantilever beam model |
由式(20)可知,集中载荷作用时,需采集6个位置的表面应变数据。均布载荷作用时,需要8个位置的表面应变数据,通过坐标(α,β)描述测点信息。其中α为应变片粘贴位置圆周角,β为应变片粘贴方向与轴向夹角,具体测点位置如表1所示。
|
|
表 1 悬臂梁有限元模型提取位置 Tab.1 Cantilever beam finite element model extraction location |
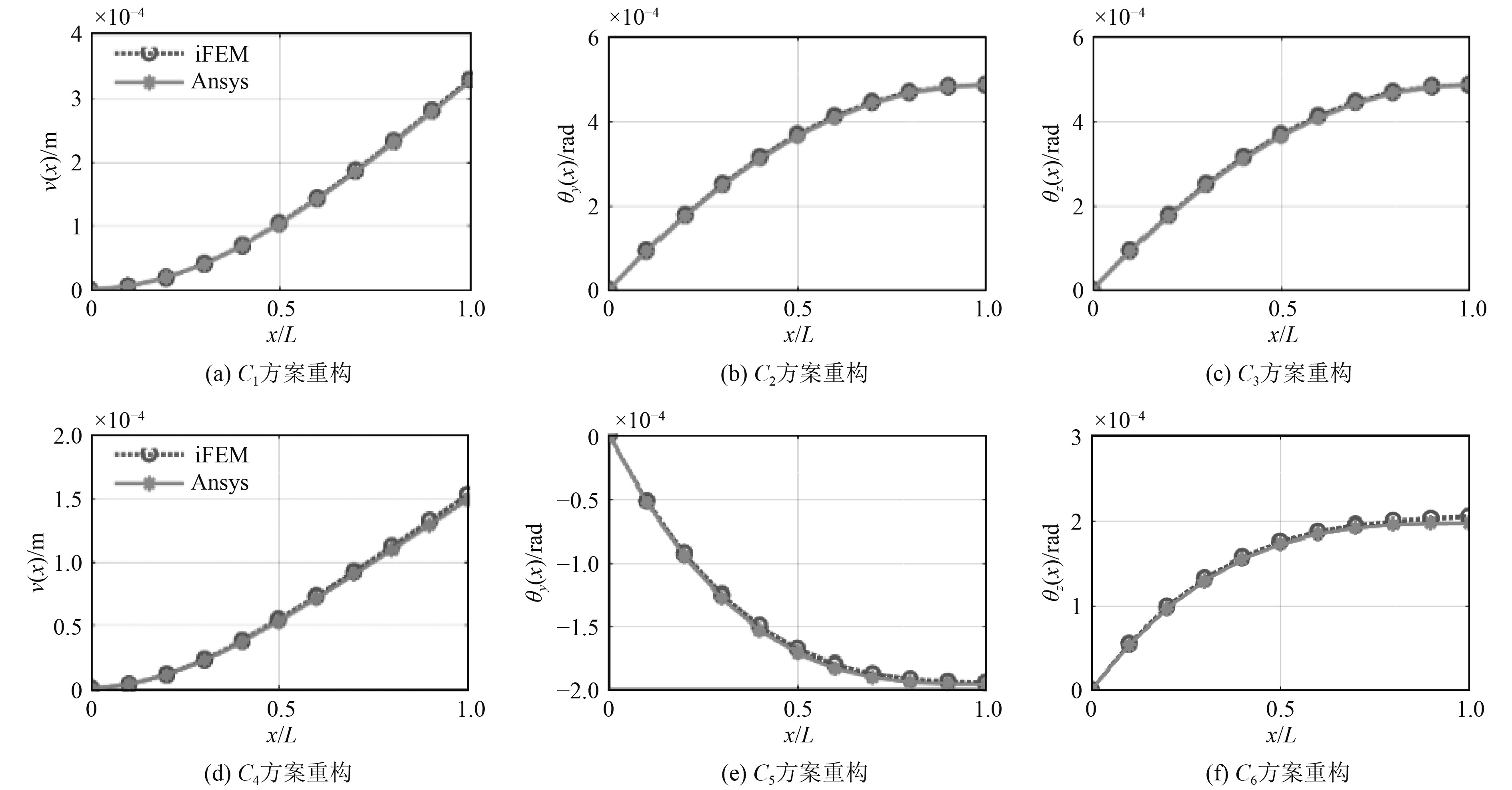
将Ansys提取的表面应变转换为单元的截面应变,代入IFEM刚度方程计算中间节点位移,通过插值形函数重构其他插值点的位移。将有限元分析计算位移与逆有限元重构位移进行对比,结果如图6所示:
|
图 6 有限元与IFEM位移结果对比 Fig. 6 Comparison of FEM and IFEM displacement results |
方案C1和方案C4重构位移与数值计算结果趋势一致。IFEM在梁结构不同载荷作用时,均具有适用性。为直观描述重构精度,将均方误差(RMS)作为评价指标:
| $ {{RMS}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^n {{{\left( {{\delta ^{iFEM}}(x) - {\delta ^{Ansys}}(x)} \right)}^2}} }}{n}} 。$ | (24) |
其中:
由表2可知,集中载荷作用时C3重构精度较高,因β=45°的表面应变需几何关系转化,增加迭算法代误差。在工程应用中,应尽量减少β=45°提取方向的表面应变,但此类型表面应变应不少于1个。
|
|
表 2 IFEM位移重构均方根误差结果 Tab.2 IFEM displacement reconstruction RMSE results |
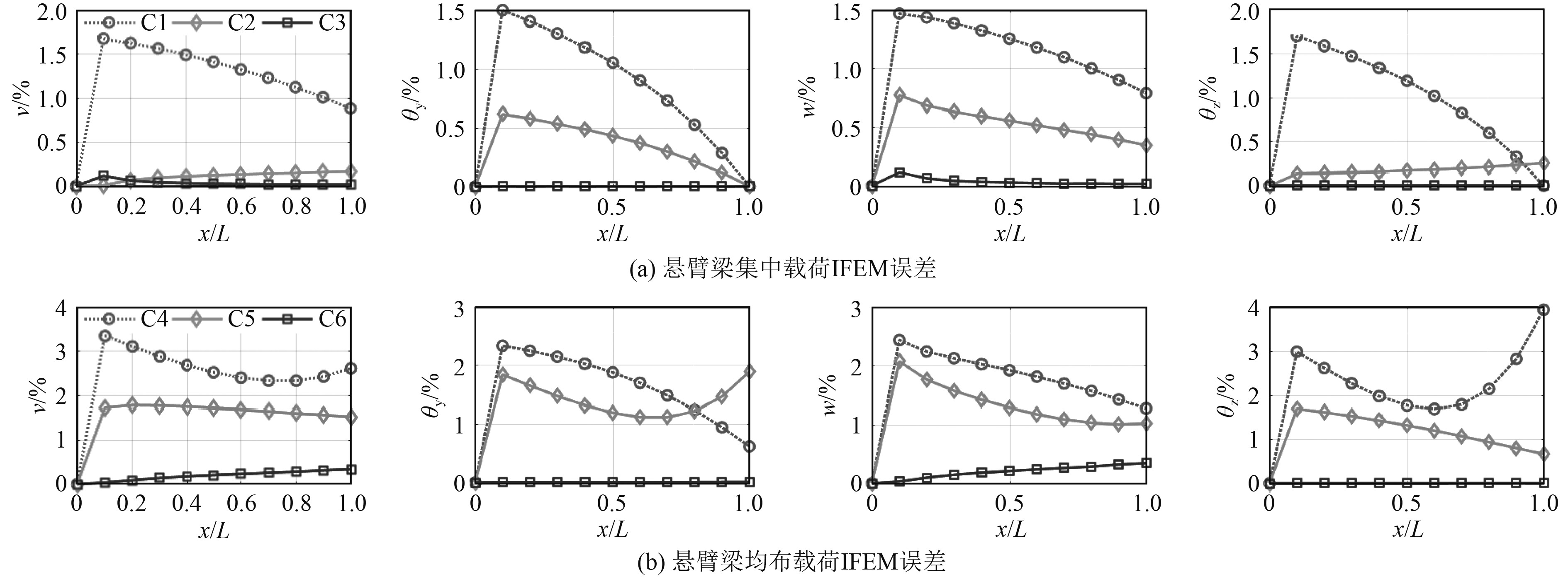
均布载荷作用时C6重构精度较高,其中β=45°的测点数量较少。无论对于集中载荷加载还是均布载荷加载,都应减少该类测点数量。将各方案的重构位移的相对误差进行对比分析,结果如图7所示。
|
图 7 悬臂梁结构不同载荷下误差分析 Fig. 7 Error analysis of cantilever beam structure under different loads |
集中载荷作用时,3种方案的相对误差最大不超过2%,方案C3的相对误差不超过0.5%,重构精度相对较高。均布载荷作用时,方案C6的重构效果最好,重构位移相对误差不超过1%。
2.3 试验与IFEM对比分析本试验台架为不锈钢(304L)薄壁立柱结构,长度Le =1000 mm,半径r =50 mm,厚度为H =4 mm,密度ρ =7.85×103 kg/m3,杨氏模量E =1.71×1011 Pa,泊松比ν =0.33,共有7个应变测点和10个位移测点,载荷施加形式为集中载荷。
如图8(a)所示,应变测点分别位于1/5Le、1/3Le、2/5Le、1/2Le、3/5Le、2/3Le和4/5Le处,每个测点设置3个应变片,0°处布置三向应变片,120°和–120°处布置单向应变片。其中1/2Le处的3个应变测量点均为三向应变片。激光位移传感器间隔1/10Le布置垂直于悬臂梁。
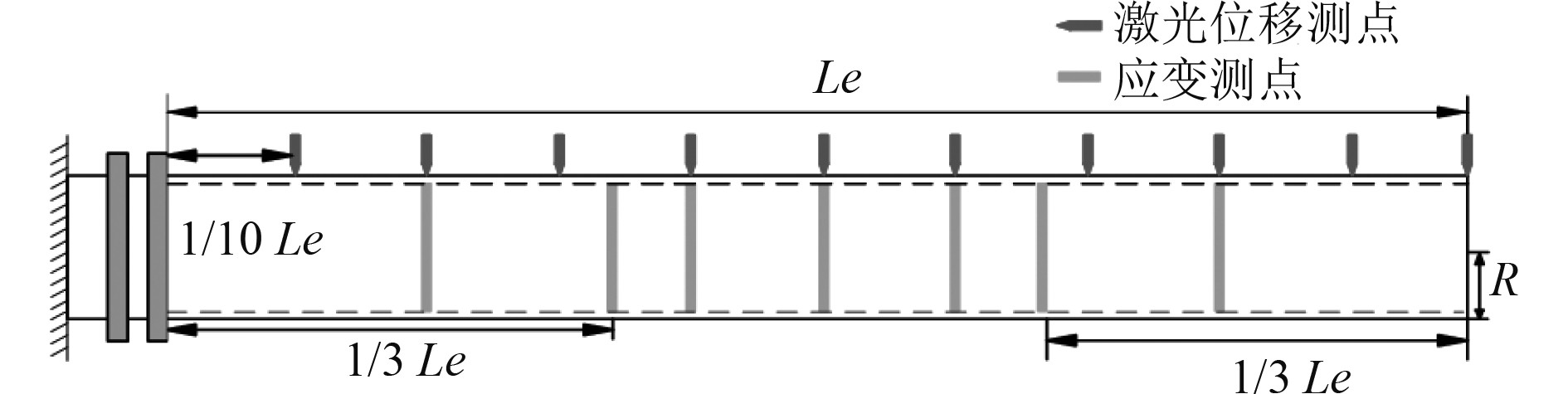
|
图 8 海洋平台立柱试验台架 Fig. 8 Offshore platform column test bench |
根据测点位置及载荷类型,设计20种应变测试方案。通过安装3种砝码模拟5种加载状态,分别为:
|
|
表 3 结构应变测点位置 Tab.3 Structure strain measuring point position |
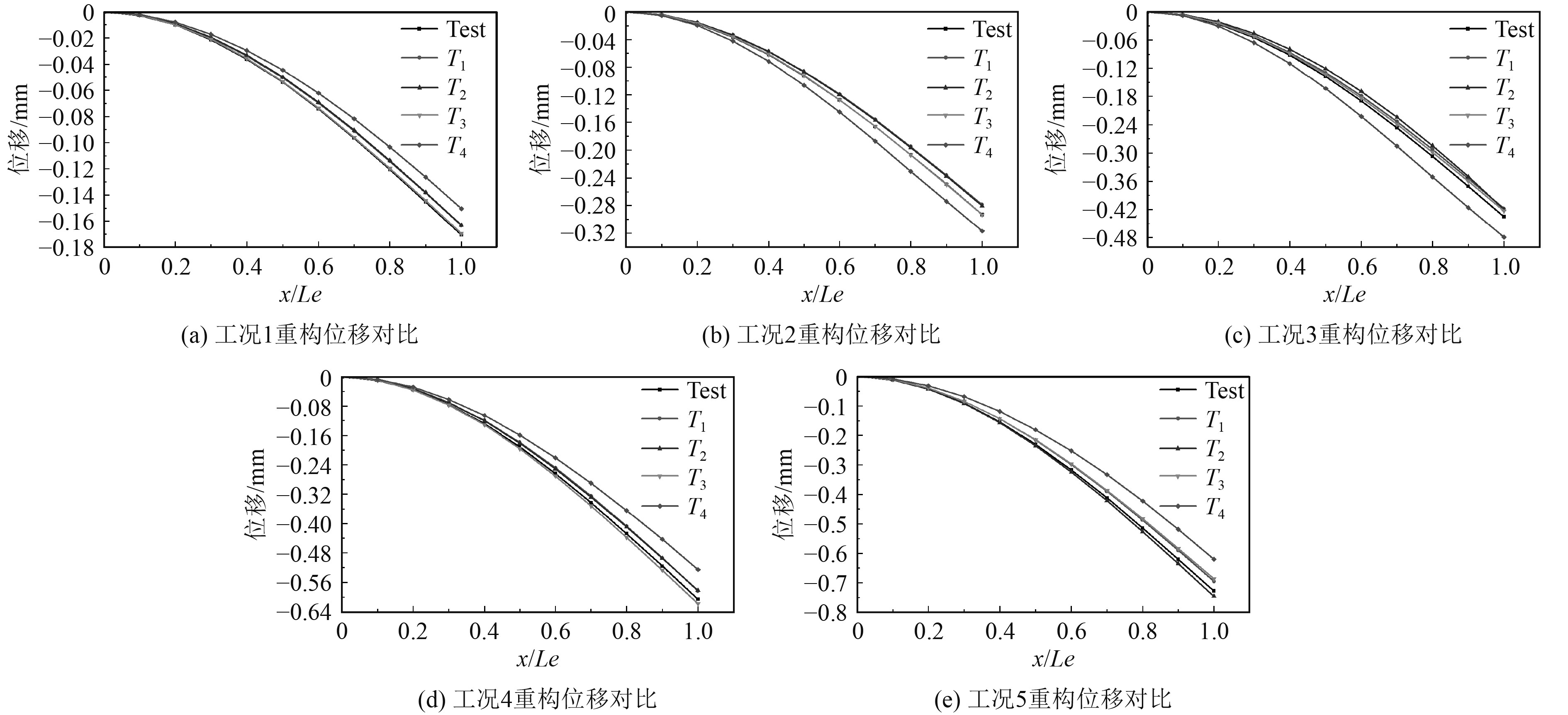
针对每一种工况,将不同测点方案的重构位移与实测位移进行对比分析。其中Test为激光位移传感器所测位移,T1、T2、T3、T4为IFEM重构位移,如图9所示。
|
图 9 试验与仿真重构位移对比 Fig. 9 Comparison of experimental and simulated reconstructed displacements |
可以看出,各方案重构位移与激光位移传感器实测位移趋势一致,T3测点方案的重构精度最高,最大的相对偏差为9.7%。T1和T2测点方案的重构精度较低,测点靠近约束端,应变数值较小,对重构精度影响较大。T4测点方案的重构精度较低,主要为安装45°的应变片较多,布置该类应变片较容易出现角度偏差。
3 应变片测量对重构精度分析逆有限元的试验误差来源主要由两部分组成:1)逆有限单元划分数量和单元形函数引起的算法误差2)测点位置选取和测量不准确性引起的系统误差。仿真和试验采用单元数量及形函数一致,仿真试验误差较小,而试验重构精度较低。主要原因为测量点位置以及应变传感器的测量误差,分别就测量点位置和应变传感器测量误差进行分析,探究逆有限元重构误差的主要影响因素。
3.1 位置偏差对重构精度的影响应变片试验位置与设计位置存在一定偏差,主要为轴向偏差、周向偏差以及混合偏差。根据应变片粘贴经验,轴向位置偏差为±5 mm、±10 mm和±15 mm,周向位置偏差为±3°和±6°,混合偏差中周向偏差为±3°,轴向位置偏差为±5 mm和±10 mm。
由表4可知,轴向位置发生±15mm偏差,重构位移最大相对误差不超过5%。90%以上的重构结果的相对偏差在3%左右,满足实际工程的需求,进而表明轴向偏差不是误差的主要因素。
|
|
表 4 轴向位置偏差相对误差累积频率 Tab.4 Axial position deviation relative error cumulative frequency |
由表5可知,周向位置偏差在±3°之间,最大相对误差不超过6%,90%的重构位移相对误差在5%左右。周向位置偏差在±6°之间,最大相对误差达到10%。相比于轴向偏差影响,周向偏差影响较大。
|
|
表 5 周向位置偏差相对误差累积频率 Tab.5 Circumferential position deviation relative error cumulative frequency |
由表6可知,当轴向位置发生±5 mm偏差和周向位置发生±3°偏差时,94%重构结果的相对误差在5%,相比于仅发生周向角位置±3°偏差,其重构精度较高。在周向偏差的基础上,再出现轴向位置偏差时,提取位置与准确位置可能相同,使重构结果较好。±5 mm、±10 mm轴向偏差对混合偏差影响较小,进而表明周向偏差是主要因素。
|
|
表 6 混合偏差位移重构相对误差累积频率 Tab.6 Hybrid Deviation Displacement Reconstruction Relative Error Cumulative Frequency |
应变片测量中可能存在实验环境或者采集系统引起的测量误差。为模拟这种测量误差,在应变信息中加入随机正态分布的噪声信号,分别为标准差3%、5%和7%的正态分布噪声信号,研究噪声信号对重构精度的影响。
从表7可知,添加3%的噪声信号时,98.1%的重构结果的相对误差在4%。添加5%噪声信号时,98.8%的重构结果的相对误差在6%左右。随着噪声信号增加,重构位移的相对误差也在增加,当噪声信号为7%时,重构结果的最大相对误差达到10%。
|
|
表 7 噪声信号相对误差的累积频率 Tab.7 Cumulative frequency of the relative error of the noise signal |
当噪声信号超过5%,对重构结果的精度有较大影响。在实验过程中,应尽量提高数据的信噪比,提取应变的位置应当尽量靠近中部位置,同时也验证了在实验中T3方案重构精度较高的原因。
4 结 语本文基于逆有限元理论提出一种结构变形重构方法,通过建立Timoshenko梁模型,推导了位移场与应变场函数关系,分别提取有限元仿真与试验测试应变结果作为输入条件,重构结构变形探究该算法的准确性。结合工程应用背景,分析应变片安装误差及信号噪声对该方法精度的影响,主要结论如下:
1)提出的结构变形重构方法在有限元和试验测试中均呈现较高精度。对多种工况及布置方案进行分析,有限元仿真中C3、C6方案最大误差为2%,试验测试T3方案最大误差为3%,该方法可为海洋结构物健康监测提供参考。
2)对于不同载荷形式的立柱结构,因β=45°的表面应变需几何关系转化,增加迭算法代误差。可增加0°或90°方向测点,但至少保留1个β=45°应变测点,可提高逆有限元算法精度。
3)立柱结构试验过程中,轴向偏差不是主要误差因素,周向偏差及噪声信号对重构精度影响较大。针对薄壁柱型位移重构研究,周向位置偏差应在±3°范围内,提取位置尽可能靠近中部位置。
| [1] |
李永胜, 王纬波, 陶沙, 等. 海洋平台结构振动超标分析方法研究[J]. 舰船科学技术, 2021, 43(15): 99-104. |
| [2] |
董科, 李友龙. 半潜式海洋平台受浮冰撞击作用损伤分析[J]. 舰船科学技术, 2018, 40(1): 57-61. |
| [3] |
马栋梁, 王德禹. 基于加速度和卷积神经网络的船体板裂纹损伤检测[J]. 船舶力学, 2022, 26(8): 1180-1188. |
| [4] |
张大朋, 白勇, 朱克强. UKF-PID模式下动力定位海洋平台-立管系统的动力学分析[J]. 应用力学学报, 2022, 39(2): 312-323. |
| [5] |
汪雪良, 朱全华, 张涛, 等. 船舶结构监测技术研究进展[J]. 船舶力学, 2022, 26(8): 1246-1253. |
| [6] |
黄辉. 基于逆有限元方法的板梁结构变形重构的研究[D]. 武汉: 华中科技大学, 2021.
|
| [7] |
FOSS G C, HAUGSE E D. Using modal test results to develop strain to displacement transformations[C]//Proceedings of the 13th international modal analysis conference. 1995, 2460: 112.
|
| [8] |
KO W L, RICHARDS W L, FLEISCHER V T, Applications of KO displacement theory to the deformed shape predictions of the doubly-tapered ikhana wing number [R]. California: Dryden Flight Research Center, 2009.
|
| [9] |
吴懋琦, 谭述君, 高飞雄. 基于绝对节点坐标法的平面梁有限变形下变形重构[J]. 力学学报, 2021, 53(10): 2776-2789. |
| [10] |
TESSLER A. A variational principle for reconstruction of elastic deformations in shear deformable plates and shells[M]. National aeronautics and space administration, langley research center, 2003.
|
| [11] |
GHERLONE M, CERRACCHIO P, MATTONE M, et al. An inverse finite element method for beam shape sensing: theoretical framework and experimental validation[J]. Smart Materials and Structures, 2014, 23(4): 045027. DOI:10.1088/0964-1726/23/4/045027 |
| [12] |
DING G, YAN X, GAO X, et al. Reconstruction of propeller deformation based on FBG sensor network[J]. Ocean Engineering, 2022, 249: 110884. DOI:10.1016/j.oceaneng.2022.110884 |
| [13] |
HE W, LIU P, CHENG H, et al. Displacement reconstruction of beams subjected to moving load using data fusion of acceleration and strain response[J]. Engineering Structures, 2022, 268: 114693. DOI:10.1016/j.engstruct.2022.114693 |
| [14] |
赵飞飞, 曹开拓, 保宏, 等. Timoshenko梁的变形场重构及传感器位置优化[J]. 机械工程学报, 2020, 56(20): 1-11. |
| [15] |
贾连徽, 任慧龙, 孙树政, 等. 船体结构应力监测点的选取方法研究[J]. 船舶力学, 2013, 17(4): 389-397. |
| [16] |
蔡智恒, 周金柱, 唐宝富, 等. 面向结构形变重构的应变传感器优化布局[J]. 振动与冲击, 2019, 38(14): 83-88+124. DOI:10.13465/j.cnki.jvs.2019.14.012 |
 2024, Vol. 46
2024, Vol. 46
