随着全球能源消耗的持续上升和世界各国对环境问题的日益关注,承担着90%国际贸易量的航运业面临着提高可持续性发展的压力,尤其是以石油为燃料的船舶产生的废气排放,已经成为当前大气污染物排放中的关键部分。液化天然气(Liquefied Natural Gas,LNG)因其二氧化碳排放率低、热值高、经济环保等优点而备受关注[1]。因此,LNG作为船舶从传统燃料向低碳可替代能源过渡的中间资源,必将掀起一股发展热潮。常压下,LNG的存储温度为−162℃,处于深冷状态,因此需经过加压、气化、调温、调压等步骤再供给用户端[2],在这一过程中,传统换热器在设备体积、重量、稳定性、换热效率等方面通常无法满足海上船舶LNG储运工艺的技术要求,且易受液体晃动的影响。因此,研究高效率的换热器对LNG的高效利用具有重要意义[3]。由扩散焊接技术制造而成的印制板式换热器(Printed Circuit Heat Exchanger,PCHE)[4]是一种高效紧凑型微通道换热器,在晃荡、高压、交变应力等方面具有很好的优越性,故常被应用于浮式LNG接收站热交换设备中[5]。
PCHE作为新兴的换热器,在LNG领域应用不是特别广泛,主要用于浮式储存与再气化装置(Floating Storage and Regasification Units,SUFR),许多学者对LNG在PCHE内部的流动和换热进行了大量研究。谢丽懿等[6]分析总结了PCHE在SUFR中的应用现状和前景,并对PCHE内部流道的选型和应对海上晃动条件引起的传热恶化等问题提出了相关措施。贾丹丹[7]以超临界LNG为工质,研究了PCHE内不同弯曲角度微流道内的流动与换热特性,结果表明当流道的弯曲角度为15°时换热器具有更好的换热能力及较小的压降。Cui等[8] 以超临界CO2作为工作流体,在NACA0020翼型翅片结构的基础上提出了2种新型翅片结构。结果显示新型翅片PCHE能够获得较小的压降和较大的j因子,热工水力性能较好。同时,刘贵军等[9]在Z字形流道的 PCHE中也研究了超临界CO2的热工水力特性,结果表明,加速核心区域在流体转弯处靠近外侧壁,并且在转弯处下游出现较大压降。为强化LNG在 PCHE 中的换热性能,提出了周期性波动通道,Aneesh等[10]以氦气作为工质,对PCHE周期性微通道内的局部流动和传热特性进行了研究,在此基础上,拓展分析了三角型、梯型和正弦型3种通道对PCHE流动换热性能的影响。结果表明梯型通道PCHE换热性能最好。此外,何雅玲等[11]根据场协同原理,研究了正弦型错列微通道内超临界LNG 的局部换热特性并提出了场协同率,将其与性能评价指标PEC进行对比分析。同时,Bai等[12]在正弦波微通道中研究了超临界 LNG在不同热流密度和操作压力时下的流动和传热性能,得到了超临界 LNG 在正弦波微通道中的流动和换热机理。可知,将 PCHE作为LNG气化器时的换热过程涉及微流道流动、超临界流体物性的变化等问题,影响换热的因素非常复杂,且近年来针对PCHE研究的主要方向是通过改变通道形状和流道结构来优化换热器的热工水利性能,但工质多以超临界LNG、超临界CO2和氦为主。但很少涉及LNG在亚临界状态下的沸腾相变换热,并且工质在微小通道内的沸腾规律明显异于常规通道[13],因此对LNG在微小通道中沸腾流动与换热过程的研究显得尤为重要。
因此,本文对常压LNG在PCHE微小通道内的流动沸腾过程进行数值仿真分析,通过改变微小通道的直径来研究沸腾流动过程中的流型转变规律及对应换热性能,获得努塞尔特数Nu和范宁摩擦因子f的变化趋势,并对不同流型转变过程中的流场分布情况展开分析。同时也定量分析了质量通量对流型分布和流动换热的影响。研究成果可为常压LNG在PCHE微小通道中的流型变化规律和换热性能提供参考。
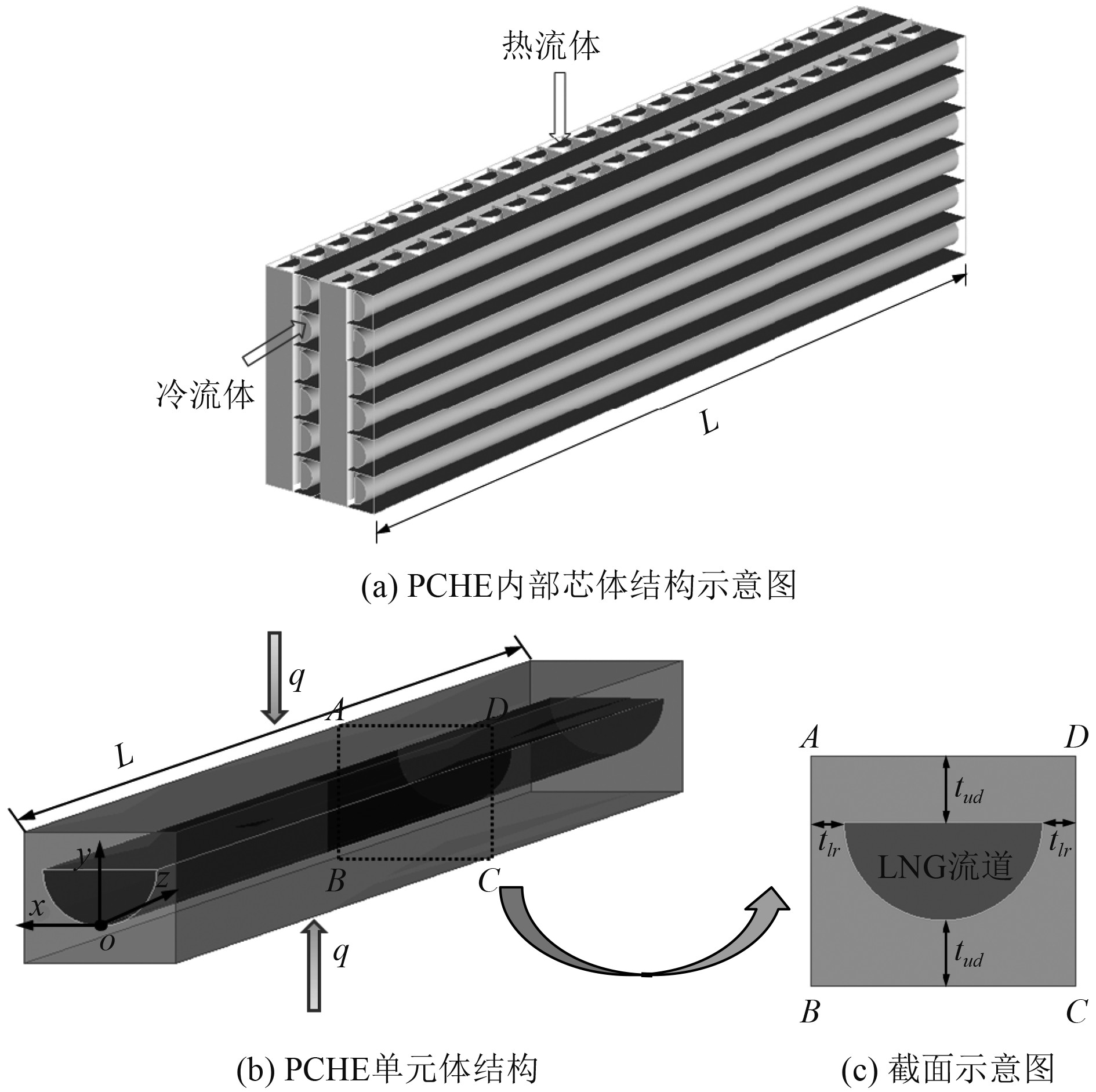
1 模型建立 1.1 物理模型和边界条件图1(a)为PCHE的内部芯体的结构示意图,由于PCHE的核心是由许多相同的半圆形微小通道组成,为了减少计算量,选取PCHE冷流体侧的单个水平通道单元进行研究,如图1(b)所示。为了探究管径对微小通道内流动沸腾的影响,本文建立了1 mm、1.5 mm、2 mm和2.5 mm共4种不同通道直径的三维物理模型,用Fluent软件对其进行数值模拟。所有通道轴向长度L均为80 mm且z方向为流体的流动方向,上下壁厚tud均为0.5 mm,左右壁厚tlr均为0.25 mm,ABCD截面形状如图1(c)所示,为便于描述,建立如图1(b)所示的坐标系。不同管径通道的具体尺寸如表1所示。
|
图 1 微小通道结构示意图 Fig. 1 Schematic diagram of mini-channel structure |
|
|
表 1 不同直径通道的尺寸 Tab.1 List of channel dimensions |
PCHE 选取Fluent 中的不锈钢作为固体材料,沸腾换热的工质为LNG。本文上下加热壁面为第二类边界条件,即给定热流密q,如图1(b)所示,左右2个壁面为绝热边界,进口边界为质量通量进口,进口温度Tin设置为109.51K,出口边界为自由出流,湍流模型采用k-ε湍流模型。
1.2 数学模型本文中多相流模型选用流体体积模型(VOF)[14],该模型是一种在固定欧拉网格下的表面跟踪方法,有利于获得气液界面位置和形状的变化,基于VOF的控制方程如下:
1)连续性方程
| $ \nabla \cdot \left( {{\alpha _v}} \right.{\rho _v}\overrightarrow {{u_v}} ) = {S_v},$ | (1) |
| $ \nabla \cdot \left( {{\alpha _l}} \right.{\rho _l}\overrightarrow {{u_l}} ) = {S_l}。$ | (2) |
式中:
本文LNG被定义为第一相,而天然气(Natural Gas,NG)是第二相,通过求解式(1)或式(2)中的任意一个,其他相的体积分数可由下式计算:
| $ {\alpha _v} + {\alpha _l} = 1 。$ | (3) |
2)动量方程
| $ \nabla (\rho \overrightarrow u \overrightarrow u ) = \nabla [\mu (\nabla \overrightarrow u + \nabla {\overrightarrow u ^T}] - \nabla p + \rho \overrightarrow g + \overrightarrow {{F_\sigma }},$ | (4) |
| $ \rho = {\alpha _l}{\rho _l} + {\alpha _v}{\rho _v} ,$ | (5) |
| $ \mu = {\alpha _l}{\mu _l} + {\alpha _v}{\mu _v}。$ | (6) |
式中:
3)能量方程
| $ \nabla \cdot [\overrightarrow u (\rho E + p)] = \nabla \cdot ({k_e}\nabla T) + {S_E} ,$ | (7) |
| $ E = \frac{{{\alpha _v}{\rho _v}{E_v} + {\alpha _l}{\rho _l}{E_l}}}{{{\alpha _v}{\rho _v} + {\alpha _l}{\rho _l}}} ,$ | (8) |
| $ {k_e} = {\alpha _v}{k_v} + {\alpha _l}{k_l} 。$ | (9) |
式中:
本文通过加载用户自定义函数(User-defined Function,UDF)来考虑控制方程中的源项,源项通过加入不同的计算子模型来模拟气液界面两相的变化,该模型是基于气体动力学理论的传质相变模型,式(1)和式(2)中的质量源项具体计算公式如下:
气体质量源项
| $ \begin{split} & {S}_{v}={\beta }_{e}{\alpha }_{l}{\rho }_{l}\dfrac{(T-{T}_{s})}{{T}_{s}},T>{T}_{s},\\ & {S}_{v}={\beta }_{c}{\alpha }_{v}{\rho }_{v}\dfrac{(T-{T}_{s})}{{T}_{s}},T<{T}_{s}。\end{split} $ | (10) |
液体质量源项
| $ \begin{split} & {S}_{l}={\beta }_{e}{\alpha }_{l}{\rho }_{l}\dfrac{({T}_{s}-T)}{{T}_{s}},T>{T}_{s},\\ & {S}_{l}={\beta }_{c}{\alpha }_{v}{\rho }_{v}\dfrac{({T}_{s}-T)}{{T}_{s}},T<{T}_{s}。\end{split} $ | (11) |
式中:
| $ {S_E} = {h_{lv}}{S_i} 。$ | (12) |
表面张力是维持气泡生长的作用力,其在数学模型中体现为动量方程中施加在控制体表面的外力,即式(4)中的
| $ \overrightarrow {{F_\sigma }} = \sigma \dfrac{{{\alpha _l}{\rho _l}{k_l}\nabla {\alpha _l} + {\alpha _v}{\rho _v}{k_v}\nabla {\alpha _v}}}{{\dfrac{1}{2}({\rho _l} + {\rho _v})}} 。$ | (13) |
式中:
| $ {k_l} = \nabla \cdot \frac{{\nabla {\alpha _l}}}{{\left| {\nabla {\alpha _l}} \right|}} ,$ | (14) |
| $ {k_v} = \nabla \cdot \frac{{\nabla {\alpha _v}}}{{\left| {\nabla {\alpha _v}} \right|}}。$ | (15) |
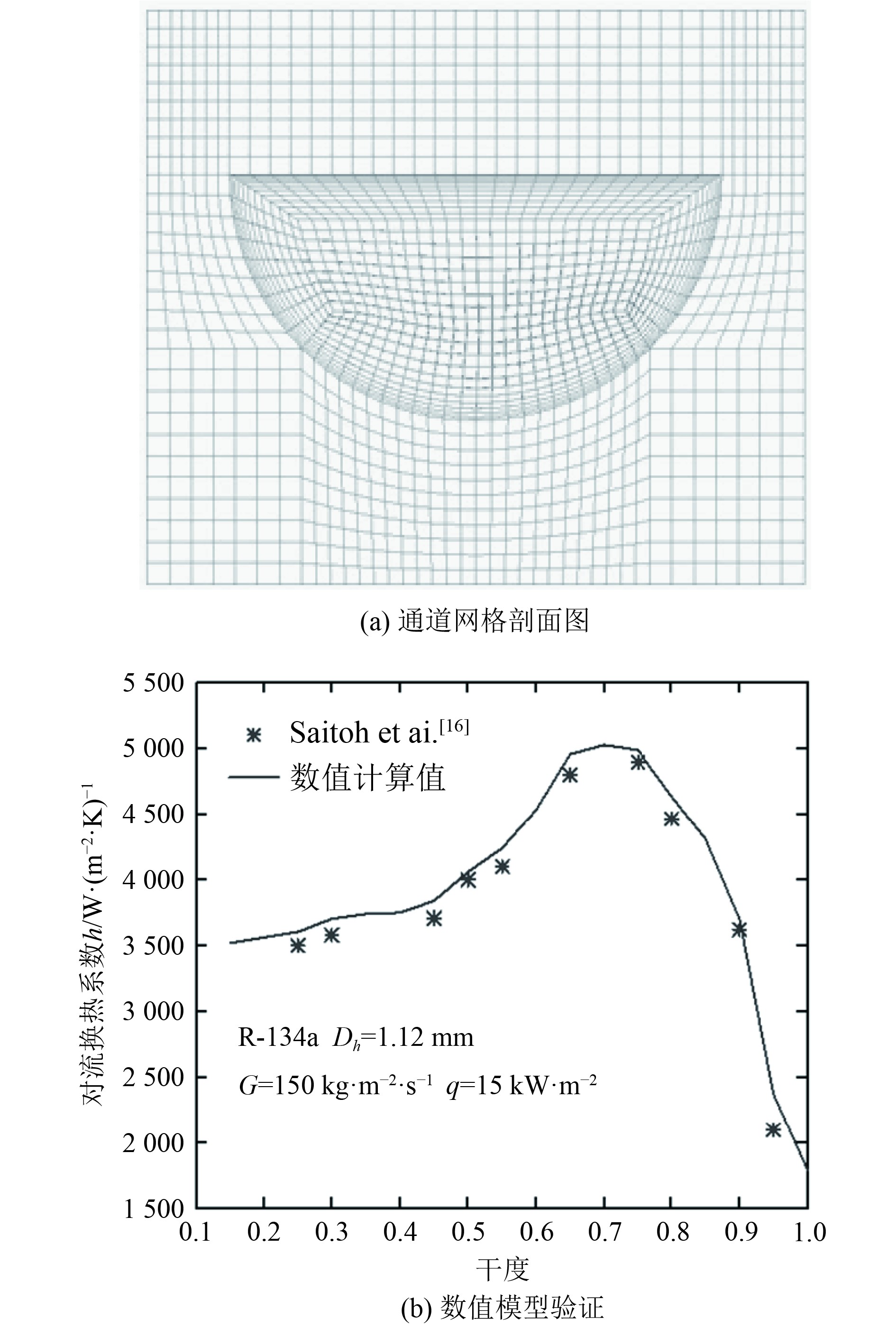
本文研究过程为相变过程,为更好地获得壁面附近气泡的生成与脱离,采用六面体结构化网格,如图2(a)所示。为方便描述,考虑了直径为1.5 mm的微小通道。在通道内的近壁处设置边界层网格,并将y+控制在1以下。划分了6组网格数对网格进行无关性验证,结果如表2所示,可以发现当网格数在2.23×106后进一步增加时,模拟的出口温度随网格数的增加变化不大。因此,选择2.23×106的网格进行后续的数值研究。
|
图 2 网格剖面图和数值模型验证 Fig. 2 Sectional view channel mesh and numerical model validation |
|
|
表 2 网格独立性验证 Tab.2 Grid independence |
图2(b)为在数值计算之前,对选用的数值模型以及编写的相变UDF进行校核的结果。本文根据Saitoh等[16]提出的模型进行验证,该物理模型为水力直径Dh=1.12 mm的水平微小通道,选用的工质为R-134a,操作条件质量通量G=150 kg/m2·s,热通量q=1.5 kW/m2本文用R-134a进行数值模拟,并与文献中的局部对流换热系数结果进行了比较。经计算得出,2个结果之间的最大偏差为6.1%,因此,所采用的数值模型和方法能够应用于后续的数值研究。
1.4 数值模型验证评价换热性能的2个关键指标是流体的换热性能和压降特性。本文衡量换热性能的参数使用努塞尔数
| $ Nu = \frac{{h{D_h}}}{k} 。$ | (16) |
式中:
本文采用范宁摩擦因子
| $ f = \frac{{\nabla {p_f}}}{{2{\rho _{{\mathrm{out}}}}{v_{{\mathrm{out}}}}^2}}\left(\frac{{{D_h}}}{L}\right)。$ | (17) |
式中:
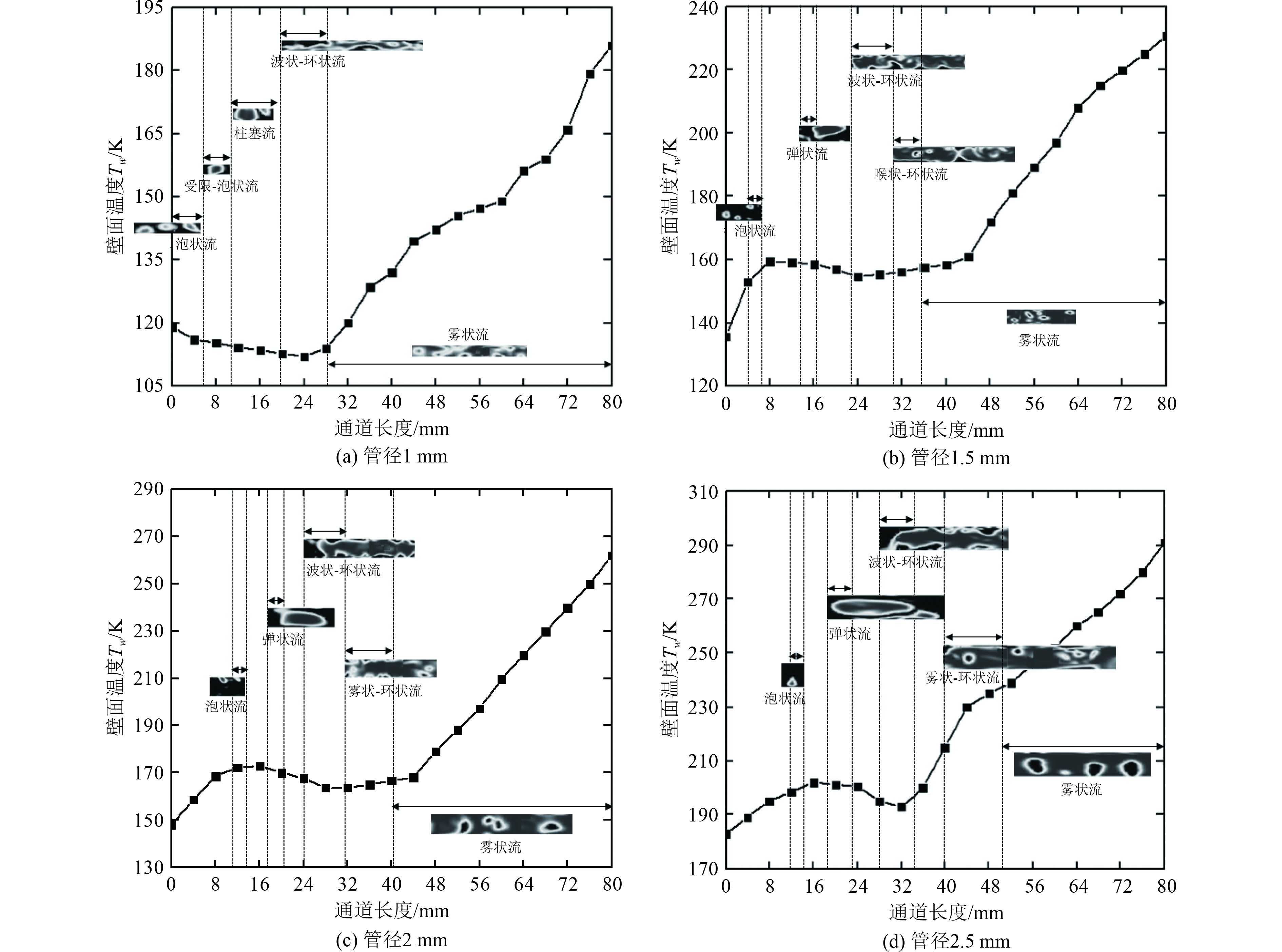
图3为vin=0.52 m/s、P =0.1 MPa时直径为1 mm、1.5 mm、2 mm和2.5 mm通道内的流型分布及对应的温度变化趋势。由于流动速度的增加导致液体和蒸汽速度不同,从而使流体的流动形态发生了一系列的变化。过冷的液体进入通道,当流体温度达到饱和温度时,流动状态从过冷转变为饱和流动沸腾,并沿流动方向产生小气泡形成泡状流,由于气泡的合并和液体蒸发,气泡尺寸增大,随后形成弹状流和波状-环状流等流型。由图3(b)~图3(d)可以看出1.5 mm、2 mm和2.5 mm通道均出现了泡状流、弹状流、波状-环状流、过渡流和雾状流。其中,1.5 mm通道中出现的过渡流是喉状-环状流,2 mm和2.5 mm通道中出现的过渡流是雾状-环状流,前者是由沿轴向延伸的2个连的蒸汽段塞倾向于穿过液膜而形成,后者是由于汽芯的高速运动使液膜破裂而形成的。然而对于图3(a),直径为1 mm的通道没有观察到过渡流,且出现的泡状流很容易转化为受限-泡状流,然后发展为柱塞流,这是由于在直径较小的通道中气泡形成的空间有限,很快受到壁面的限制。同时,在直径为1 mm的通道中形成的气泡狭长而呈现椭圆形,在z=1 mm处开始形成气泡,而处于同一位置(z=1 mm)的其他管径通道仍处于单相流状态,而在直径为1.5 mm、2 mm和2.5 mm的通道中,大部分气泡呈球形。此外,弹状流区域的范围随着通道直径的增加而增加,其中直径为2.5 mm通道中可形成长度高达6 mm的拉长弹状流,表3给出了弹状流长度占通道长度的百分比。并且1 mm通道内的雾状流是混沌的,而1.5 mm、2 mm和2.5 mm通道内的雾状流具有明显的气液界面,液滴尺寸也随通道直径的增大而增大,可以发现2.5 mm通道中的液滴基本呈规则的球状。除此之外,观察到壁面温度并非一直呈上升趋势,可以发现其在两相区域有降低的过程,这是由于传热模式发生了改变,即由单相强制对流换热转变为两相流动沸腾换热,由于靠近壁面的液膜蒸发,导致气泡不断从壁面带走热量,因此,壁面温度降低。
|
图 3 不同管径下的流型分布与壁面温度的变化趋势 Fig. 3 Flow pattern distribution and variation trend of wall temperature for different channel diameters |
|
|
表 3 弹状流长度占通道长度的百分比 Tab.3 Proportion of slugs |
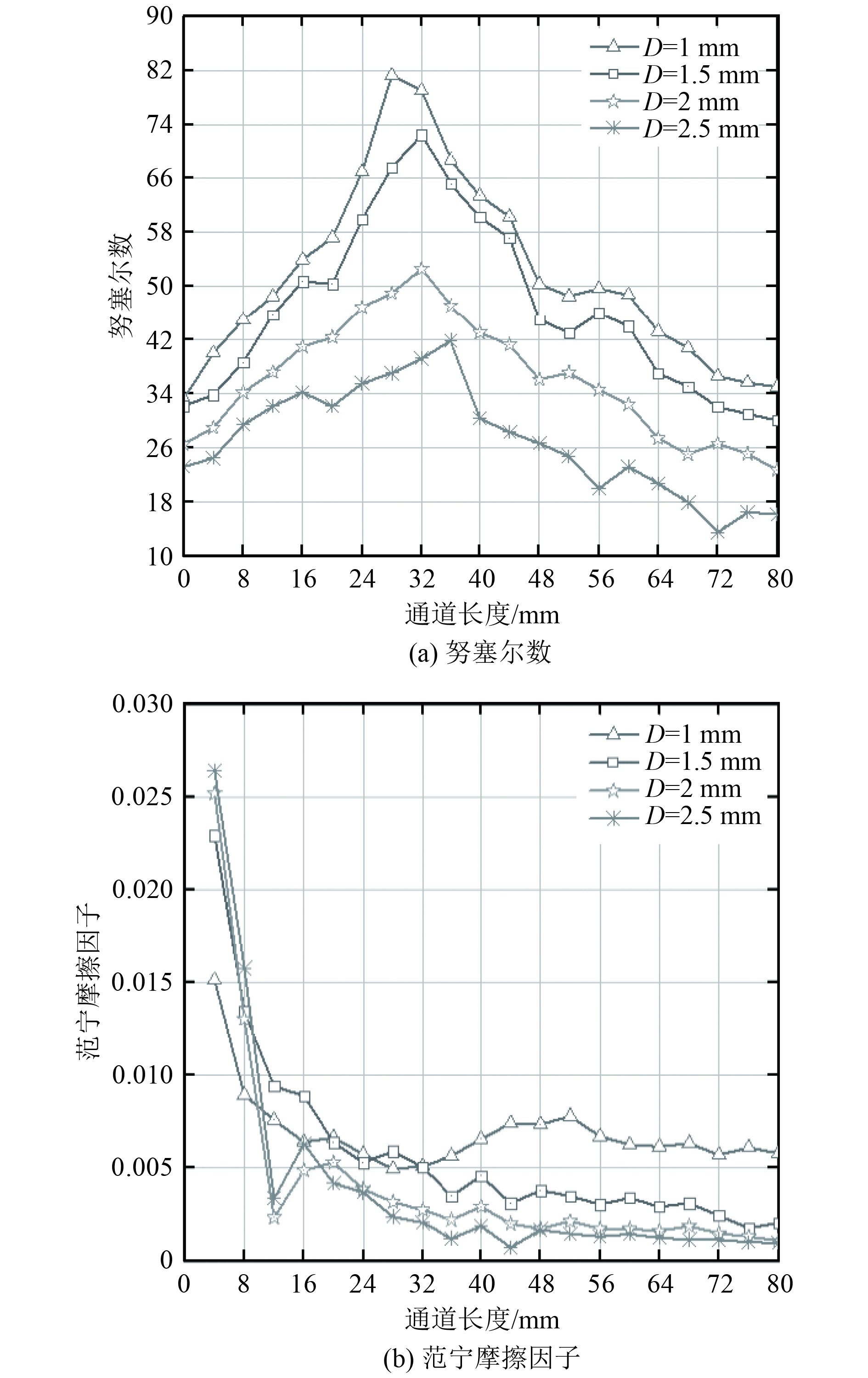
图4为4种不同通道直径下的努塞尔数和范宁摩擦因子的变化。由图4(a)可知,泡状流、弹状流和波状-环状流区域的努塞尔数均有增大,并在波状-环状流区域达到最大值,这是由于壁面在达到了足够的过热度时,壁面上开始产生气泡,而气泡的生长会产生扰动并破坏边界层,换热能力增强,随着气泡的进一步长大,气泡之间便相互影响而形成弹状流,此时,更加剧烈的气泡扰动会导致换热能力进一步提高,随后在波状-环流区域达到最高的换热能力,且经过计算发现与1 mm的通道相比,通道直径每增加0.5 mm、1 mm和1.5 mm,最大换热系数分别降低了11.7%、17.5%和24.6%。随后,在过渡流和雾状流区域的努塞尔数迅速下降,这是由于此时通道大部分面积被气相占据,属于单相区为显热换热,工质温度沿程升高,因此,换热能力急剧下降。随着管径的减小,努塞尔数显著增加,由于管径越小,壁面产生气泡的速率越大,导致气泡不断从壁面带走热量,因此,流体与壁面之间的换热能力越强。此外,值得注意的是自受限-泡状流形成以来,气泡在轴向迅速增长,带走更多的热量有利于降低壁温,最终改善了换热性能,因此,这也是直径为1 mm的通道最先出现转折点的原因。但较小管径也带来了更大压降,2.5 mm管径通道的压降为806 Pa,而1 mm管径通道的压降达到了1616 Pa。范宁摩擦系数沿着流动方向减小,如图4(b)所示,这是由于范宁摩擦系数与速度和密度成反比,而速度的增加速率较大,导致范宁摩擦系数沿着流动方向减小。
|
图 4 管径对流动换热性能的影响 Fig. 4 Effect of channel diameter on flow heat transfer performance |
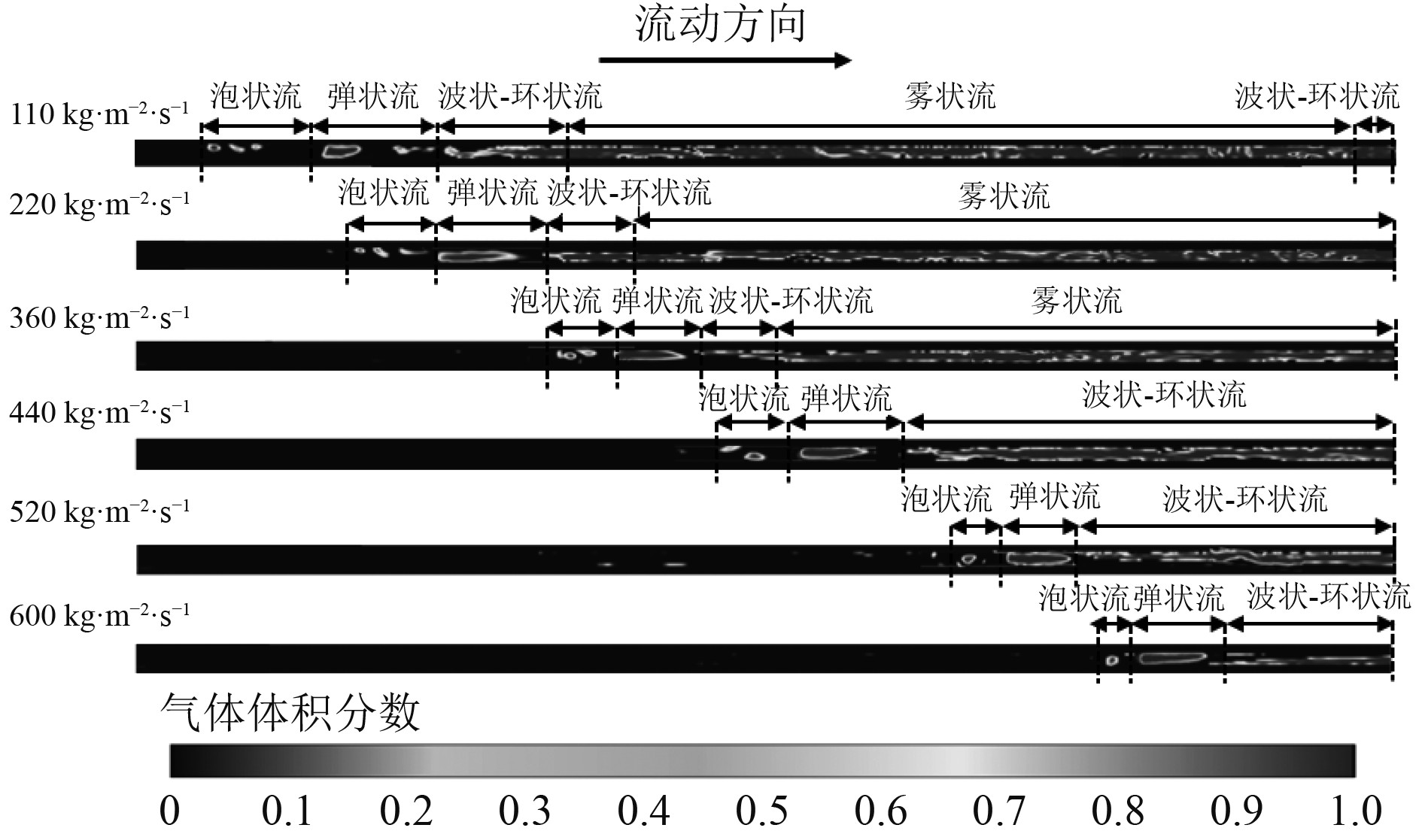
图5为1.5 mm通道在q=154.3 kW/m2、P =0.1 MPa时的流型分布及对应的换热特性。可以观察到每个质量通量工况下都出现了泡状流和弹状流,并成为了高质量通量下的主要流型。而在低质量通量下(G=110 220 kg/m2·s和360 kg/m2·s),出现了雾状流和光滑-环状流,且光滑环状流仅在G=110 kg/m2·s时出现。
|
图 5 不同质量流量下的流型分布 Fig. 5 Flow pattern distribution and variation trend of wall temperature for different mass fluxes |
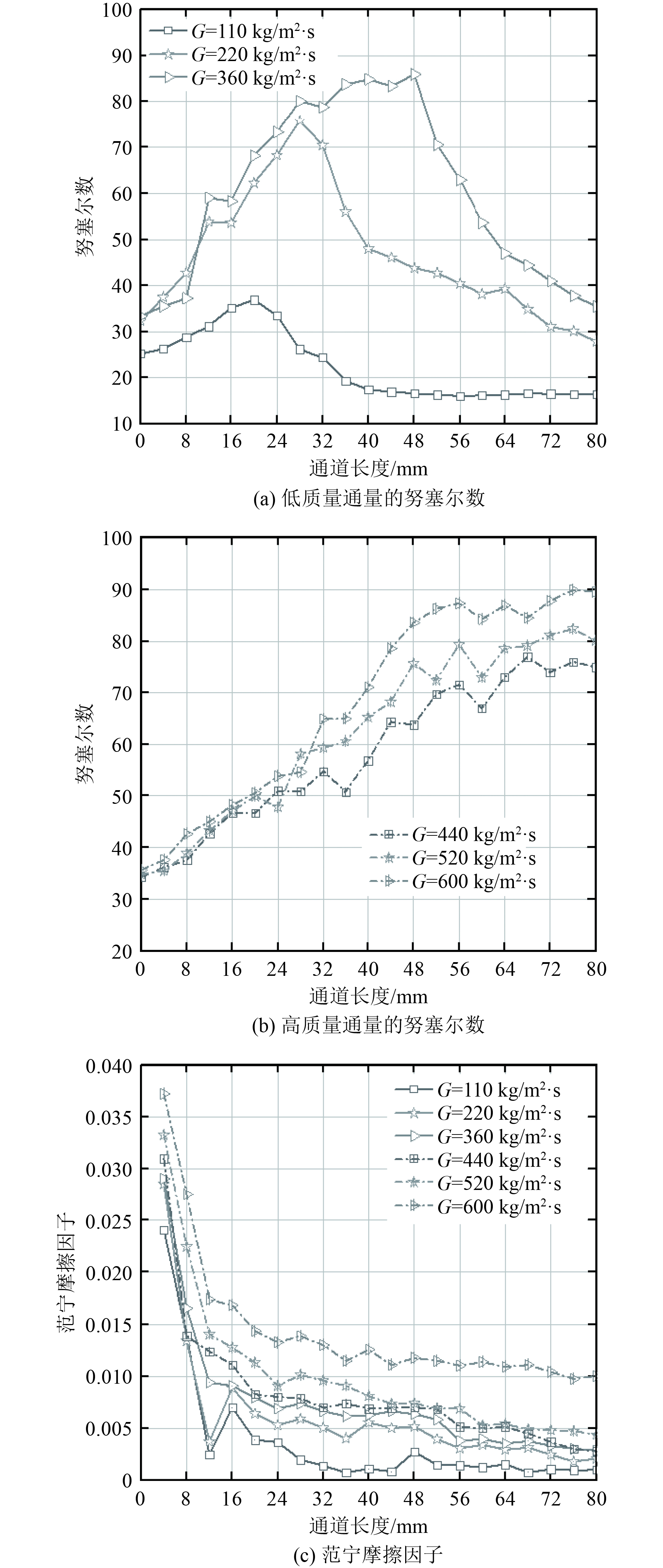
图6所示为努塞尔数和范宁摩擦因子随质量通量的变化曲线。在低质量通量下(≤360 kg/m2·s),努塞尔数沿通道长度方向先增大后急剧减小,分析可知这是由于流型的转变引起的。此外,可以观察到,随着质量通量的增加,努塞尔数曲线的峰值向后移动,这是因为流型的转变延迟,如图5所示。然而在高质量通量下(≥440 kg/m2·s),随着质量通量的增加,由于流型处于泡状流到波状-环状流之间,因此,努塞尔数呈现持续增加的趋势,换热性能逐渐增加。由图6(c)可知,范宁摩擦因子随着LNG质量通量的增加而增加。这是由于质量通量的增加导致气液两相流速增加,从而产生更大的摩擦力,进而导致流动阻力增加。
|
图 6 质量通量对流动换热性能的影响 Fig. 6 Effect of mass flux on flow heat transfer performance |
1)直径为1 mm的通道,沿着流动方向依次出现泡状流、受限-泡状流、柱塞流、波状-环状流和雾状流,然而,在直径大于1 mm的通道中,没有观察到受限-泡状流和柱塞流。且流型随着通道直径的减小而转变加快;当通道直径从2.5 mm减小到1 mm时,换热系数提高了24.6%,但压降增加了2倍。
2)综合分析流型的转变规律和对应的温度分布,证明加热壁上泡状流、弹状流和波状-环状流的形成通过减小温差,从而促进了换热。并在波状-环状流区域达到最大值。
3)随着质量流量的增加,单相流区域随着扩大,从而延缓了流型的转变;并且由于低质量流量和高质量流量工况下流型种类不同,导致换热系数的变化趋势不同。
| [1] |
YOUSEFI A, BIROUK M. Investigation of natural gas energy fraction and injection timing on the performance and emissions of a dual-fuel engine with pre-combustion chamber under low engine load[J]. Applied Energy, 2017, 189: 492-505. DOI:10.1016/j.apenergy.2016.12.046 |
| [2] |
胡国强. LNG动力船供气系统设计与换热器研究[D]. 上海: 上海交通大学, 2020.
|
| [3] |
赵星霖, 王平阳, 黄佳卉. 带有横向微槽道的超临界LNG紧凑式换热器换热强化模拟研究[J]. 低温工程, 2020(6): 1−8.
|
| [4] |
KIM I H, NO H C, Physical model development and optimal design of PCHE[J]. Intermediate heat exchangers in HTGRs, Nuclear Engineering and Design, 2012, 1: 243−250.
|
| [5] |
路达, 张引弟, 吕国政, 等. 错列正弦型微通道中超临界LNG流动与换热分析[J]. 低温工程, 2021(4): 47-53. DOI:10.3969/j.issn.1000-6516.2021.04.009 |
| [6] |
谢丽懿, 李智强, 丁国. FLNG用印刷板路换热器技术特点及发展趋势[J]. 化工学报, 2019, 70(11): 4101-4112. |
| [7] |
贾丹丹. 印刷板式换热器强化换热理论分析与实验研究[D]. 镇江: 江苏科技大学, 2017.
|
| [8] |
CUI X, GUO J, HUAI X, et al. Numerical study on novel airfoil fins for printed circuit heat exchanger using supercritical CO2[J]. International Journal of Heat and Mass Transfer, 2018, 121: 354-366. DOI:10.1016/j.ijheatmasstransfer.2018.01.015 |
| [9] |
刘贵军, 陈德奇, 胡练, 等. 基于CFD方法的PCHE窄小流道内超临界CO2流动传热特性数值研究[J]. 核动力工程, 2019, 40(3): 12-16. |
| [10] |
ANEESH A M, SHARMA A, SRIVASTAVA A, et al. Effects of wavy channel configurations on thermal-hydraulic characteristics of printed circuit heat exchanger[J]. International Journal of Heat and Mass Transfer, 2018, 118: 304-315. DOI:10.1016/j.ijheatmasstransfer.2017.10.111 |
| [11] |
何雅玲, 雷勇刚, 田丽婷, 等. 高效低阻强化换热技术的三场协同性探讨[J]. 工程热物理学报, 2009, 30(11): 1904-1906. DOI:10.3321/j.issn:0253-231X.2009.11.028 |
| [12] |
BAI Junhua, PAN Jie, HE Xiaoru, et al. Numerical investigation on thermal hydraulic performance of supercritical LNG in sinusoidal wavy channel based printed circuit vaporizer[J]. Applied Thermal Engineering, 2020(175): 2271-2281. |
| [13] |
KANDLIKAR S G, GRANDE W J, evolution of microchannel flow passages--thermohydraulic performance and fabrication technology[J]. Heat Transfer Engineering,2003, 24(1): 3−17.
|
| [14] |
HIRJ C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201−225.
|
| [15] |
BRACKBILL JU, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics. 1992, 100: 335−354.
|
| [16] |
SAITOH S, DAIGUJI H, HIHARA E, Correlation for boiling heat transfer of R-134a in horizontal tubes including effect of tube diameter[J]. International Journal of Heat and Mass Transfer, 2007, 50(25−26): 5215−5225.
|
 2024, Vol. 46
2024, Vol. 46



