近年来,无人船的相关应用和研究得到了越来越多的关注。其中除了广泛应用于现代化军事战争外,无人船在搜救、商业、科研等方面的应用也越来越多。无人船的路径跟踪问题是无人船规划控制问题中重要的一部分,路径跟踪问题是指无人船根据路径的相关几何性质完成位置跟踪的过程。
在无人船的导航算法方面,Lefeber等[1]采用LOS算法获取船舶运动过程的期望航向,并基于期望航向和航迹偏差的取值作为算法输入从而控制航向,使船舶收敛到期望路径;Fossen等[2]以LOS算法为基础,开展了一系列有关欠驱动船舶轨迹追踪控制的研究,提出了轨迹追踪控制算法;韩鹏等[3]在LOS导航中引入了自适应接纳圆,使得LOS导航在拐点处具有更高的跟踪精度。
在无人船的控制算法领域,1922年,Sperry等[4]第一次将PID控制器与船舶运动控制相结合,使之控制船舶的自动转向,并取得了一定的效果。后来Sugimoto等[5]基于传统PID控制做出了优化,将自适应的思想融入其中,提出了自适应PID控制。张旋武[6]提出基于DDPG的PID航向控制器参数优化方法,有效提高了PID控制的抗干扰能力。
前述研究方法存在2个问题:一是在不确定的水环境下不能实时准确的描述船体的运动状态,二是部分算法复杂度相对较高,系统的实时性不能完全得到保证。为了解决上述问题,本文基于无人船船体运动模型和海洋环境风、浪、流的数学模型,采用LOS导航算法和模糊PID控制器组合的算法解决无人船的路径跟踪问题。
1 无人船运动模型 1.1 船体运动模型船舶运动是在三维空间的六自由度运动,如表1所示。
|
|
表 1 六自由度运动名称 Tab.1 Name of six-degree-of-freedom motion |
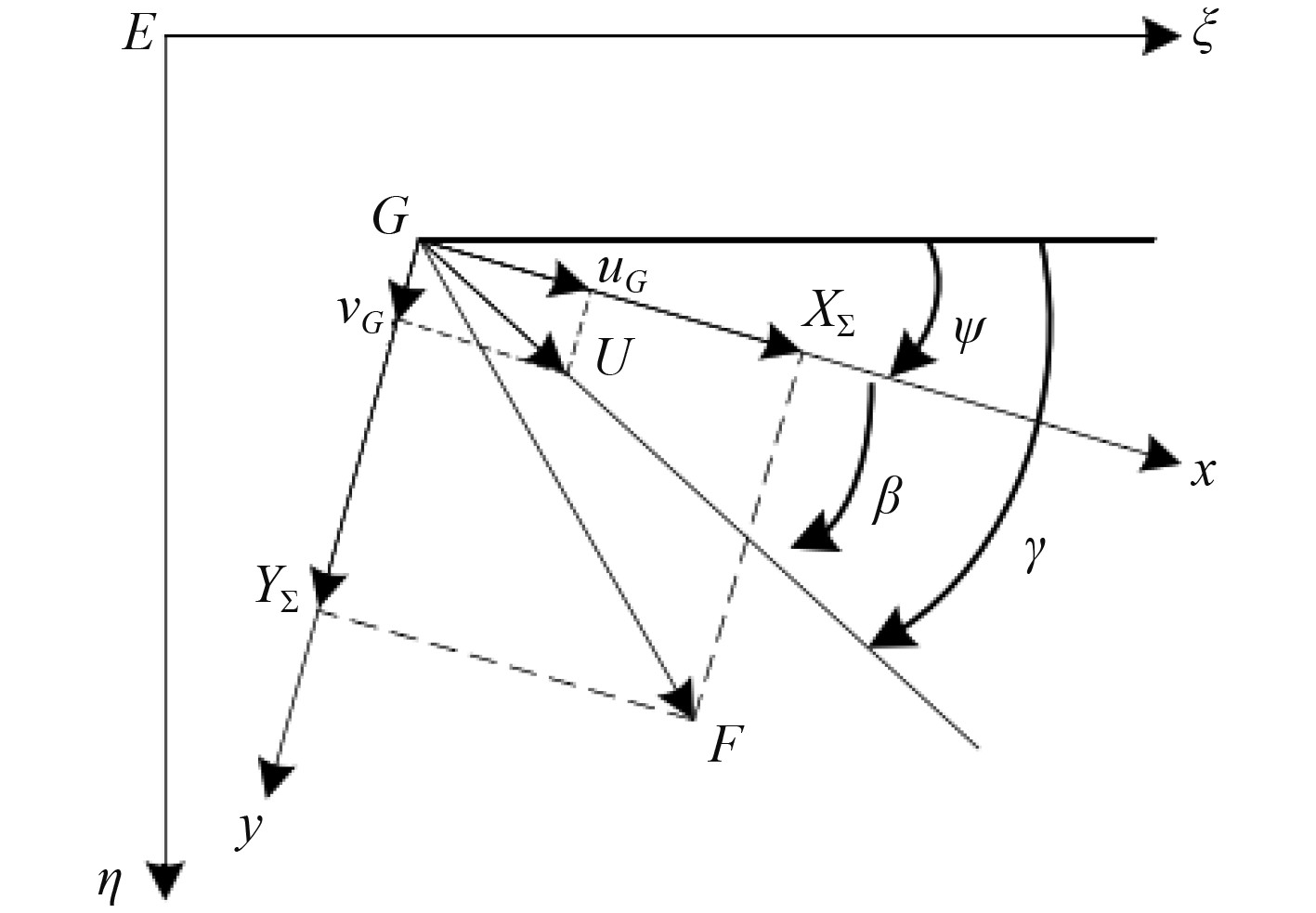
船舶的六自由度运动可以大致分为两类,一类为船舶低频运动,包括纵荡、横荡、首摇,其可以直接改变船舶的总体运动状态,表示为船舶的航行方向、垂直航行方向上的移动和船舶航向的转动。另一类运动为船舶高频运动,包括横摇、纵摇和垂荡,表现为船舶在运动过程中的震荡,不会影响船舶的平均位置变化,因此在对船舶运动控制进行模拟的时候通常可以忽略这部分的运动。水平面运动坐标系如图1所示。
|
图 1 水平面运动坐标系 Fig. 1 Motion coordinate system of horizontal |
静坐标系与动坐标系之间的旋转矩阵表示为:
| ${\scriptsize T = \left[ \begin{gathered} \cos \psi \cos \theta {\text{ cos}}\psi {\text{sin}}\theta {\text{sin}}\phi - \sin \psi \cos \phi {\text{ }}\cos \psi \sin \theta \cos \phi + \sin \psi \sin \phi {\text{ }} \\ \sin \psi \cos \theta {\text{ sin}}\psi {\text{sin}}\theta {\text{sin}}\phi {\text{ + cos}}\psi {\text{cos}}\phi {\text{ }}\sin \psi \sin \theta \cos \phi - \cos \psi \sin \phi \\ {\text{ }} - \sin \theta {\text{ }}\cos \theta \sin \phi {\text{ }}\cos \theta \cos \phi \\ \end{gathered} \right]。} $ | (1) |
只考虑纵荡、横荡、首摇等水平面内的运动,忽略横摇、纵摇和垂荡等运动,可以将旋转矩阵简化为:
| $ R(\psi ) = \left[ \begin{array}{cccccccccccccc} \cos \psi & - {\text{sin}}\psi & 0 \\ \sin \psi& {\text{ cos}}\psi & {\text{ 0}} \\ 0 & 0 & 1 \end{array} \right],$ | (2) |
动静坐标系速度关系:
| $ \dot \xi = u\cos \psi - v\sin \psi ,$ | (3) |
| $ \dot \eta = u\sin \psi + v{\text{cos}}\psi ,$ | (4) |
动静坐标系角速度关系:
| $ \dot \psi = r。$ | (5) |
只考虑水平面上3个自由度时,坐标系原点与重心不重合时的船舶水平面运动方程可以表示为:
| $ \begin{split} & m\left[ {\dot u - vr - {x_G}{r^2} - {y_G}\dot r} \right] = X = {X_H} + {X_E} + {X_T} ,\\ & m\left[ {\dot v + ur - {y_G}{r^2} + {x_G}\dot r} \right] = Y = {Y_H} + {Y_E} + {Y_T},\\ & {I_z}\dot r + m\left[ {{x_G}(\dot v + ur) - {y_G}(\dot u - vr)} \right] = N = {N_H} + {N_E} + {N_T} 。\end{split} $ | (6) |
式中:
船舶在水平面上运动的水动力表示为船舶运动状态的函数:
| $ G = G(u,v,r,\dot u,\dot v,\dot r)。$ | (7) |
其中,G可通过直航工作点下的泰勒级数展开来进行计算。假设选定的展开点是船舶沿X轴方向的匀速直线航行,则有:
| $ u = U{\text{ }}v = r = \dot u = \dot v = \dot r = 0。$ | (8) |
在船舶直航工作点下将纵向、横向水动力以及偏航力矩进行三阶泰勒展开,保留三次项可得轴向力、横向力、偏航力矩的方程:
| $ \begin{split} (m - {X_{\dot u}})\dot u =& {X_u}u + {X_{uu}}{u^2} + {X_{uuu}}{u^3} + {X_{vv}}{v^2} + {X_{rr}}{r^2} +\\ & {X_{vr}}vr + {X_E} + {X_T},\end{split} $ | (9) |
| $ \begin{split} (m - {Y_{\dot v}})\dot v + (m{x_G} - {Y_{\dot r}})\dot r = & {Y_v}v + {Y_r}r + {Y_{vvv}}{v^3} + {Y_{vvr}}{v^2}r +\\ & {Y_{uv}}uv + {Y_{ur}}ur + {Y_E} + {Y_T},\\[-1pt] \end{split} $ | (10) |
| $ \begin{split} &(m{x_G} - {N_{\dot v}})\dot v + ({I_z} - {N_{\dot r}})\dot r = {N_v}v + {N_r}r + {N_{vvv}}{v^3} +\\ & {N_{vvr}}{v^2}r + {N_{uv}}uv + {N_{ur}}ur + {N_E} + {N_T}。\end{split} $ | (11) |
根据上述方程求解可得:
| $ \begin{split} & {f_m} = (m - {Y_{\dot v}})({I_z} - {N_{\dot r}}) - (m{x_G} - {Y_{\dot r}})(m{x_G} - {N_{\dot v}}) ,\\ & {f_x} = {X_u}u + {X_{uu}}{u^2} + {X_{uuu}}{u^3} + {X_{vv}}{v^2} + {X_{rr}}{r^2} + {X_{vr}}vr + {X_E} + {X_T},\\ & {f_y} = {Y_v}v + {Y_r}r + {Y_{vvv}}{v^3} + {Y_{vvr}}{v^2}r + {Y_{uv}}uv + {Y_{ur}}ur + {Y_E} + {Y_T},\\ & {f_n} = {N_v}v + {N_r}r + {N_{vvv}}{v^3} + {N_{vvr}}{v^2}r + {N_{uv}}uv + \\ & \qquad {N_{ur}}ur + {N_E} + {N_T}。\\[-1pt] \end{split} $ | (12) |
| $ \begin{split} & \dot u = {f_x}/(m - {X_{\dot u}}),{\text{ }}\; \dot \xi = u\cos \psi - v\sin \psi,\\ & {\text{ }}\dot v = {f_y} \cdot ({I_z} - {N_{\dot r}})/{f_m} - {f_n} \cdot (m{x_G} - {Y_{\dot r}})/{f_m},\\ & \dot \eta = u\sin \psi + v{\text{cos}}\psi,{\text{ }} \\ & \dot r = {f_n} \cdot (m - {Y_{\dot v}})/{f_m} - {f_y} \cdot (m{x_G} - {N_{\dot v}})/{f_m},{\text{ }}\; \dot \psi = r 。\end{split} $ | (13) |
海洋环境中风、浪、流分别会产生海风干扰力、海浪干扰力和海流干扰力,其数学模型如下:
1)海风干扰力
绝对风是指在大地坐标系内测量到的风。
| $ \begin{split} & {u_R} = {V_T}\cos ({\psi _T} - \psi ) + u,\\ & {v_R} = {V_T}\sin ({\psi _T} - \psi ) - v 。\end{split} $ | (14) |
式中:
相对风向角(风舷角)
| $ {\alpha _R} = \left\{ \begin{split} & \arctan \dfrac{{{v_R}}}{{{u_R}}} - {\text{π}} {{\mathrm{sgn}}} ({v_R}),\qquad {u_R} \geqslant 0 ,\\ & {\text{ }}\arctan \dfrac{{{v_R}}}{{{u_R}}},\qquad {u_R} \lt 0。\end{split} \right. $ | (15) |
相对风速可以通过绝对风速和船速计算得到,计算式为:
| $ V_R^2 = V_T^2 + {V^2} + 2{V_T}V\cos ({\psi _T} - \beta )。$ | (16) |
式中:
作用在船体上的平均风力和力矩的计算式为:
| $ \left\{ \begin{gathered} {X_{wind}} = \frac{1}{2}{C_X}({\alpha _R}){\rho _a}V_R^2{A_T} ,\\ {Y_{wind}} = \frac{1}{2}{C_Y}({\alpha _R}){\rho _a}V_R^2{A_L},\\ {N_{wind}} = \frac{1}{2}{C_N}({\alpha _R}){\rho _a}V_R^2{A_L}L 。\end{gathered} \right. $ | (17) |
式中:
风力和风力矩系数的近似估算常用的方法是Isherwood在1972年提出的Isherwood经验公式。其基于以往大量的船模风洞试验结果,运用多元回归技术对试验结果进行处理分析,得到了以下系数经验公式:
| $ \begin{split} & {C_X} = {A_0} + {A_1}\frac{{2{A_L}}}{{{L^2}}} + {A_2}\frac{{2{A_T}}}{{{B^2}}} + {A_3}\frac{L}{B} + {A_4}\frac{S}{L} + {A_5}\frac{C}{L} + {A_6}M, \\ & {C_Y} = - \left( {B_0} + {B_1}\frac{{2{A_L}}}{{{L^2}}} + {B_2}\frac{{2{A_T}}}{{{B^2}}} + {B_3}\frac{L}{B} + {B_4}\frac{S}{L} +\right.\\ & \qquad\left.{B_5}\frac{C}{L} + {B_6}\frac{{{A_{SS}}}}{{{A_L}}} \right), \\ & {C_N} = - \left( {{C_0} + {C_1}\frac{{2{A_L}}}{{{L^2}}} + {C_2}\frac{{2{A_T}}}{{{B^2}}} + {C_3}\frac{L}{B} + {C_4}\frac{S}{L} + {C_5}\frac{C}{L}} \right)。\\[-1pt] \end{split} $ | (18) |
2)海流干扰力
海水通常并非静止不动,海流的大小对船舶运动也有较大的影响。海流一般由潮汐、重力、海水密度变化等因素导致,随气候变化、地理位置变化等发生改变。
将运动方程中的船舶运动参数处理成与海流的相对运动参数。设固定坐标系中的流速为
| $ \left\{ \begin{gathered} {u_c} = {V_c}\cos ({\psi _c} - \psi ),\\ {v_c} = {V_c}\sin ({\psi _c} - \psi ) 。\end{gathered} \right. $ | (19) |
计算相对水流的速度:
| $ \left\{ \begin{gathered} {u_r} = u - {u_c} ,\\ {v_r} = v - {v_c}。\end{gathered} \right. $ | (20) |
结合式(19)和式(20)求导得加速度:
| $ \left\{ \begin{gathered} {{\dot u}_r} = \dot u - {V_c}r\sin ({\psi _c} - \psi ) = \dot u - r{v_c},\\ {{\dot v}_r} = \dot v + {V_c}r\cos ({\psi _c} - \psi ) = \dot v + r{u_c}。\end{gathered} \right. $ | (21) |
式中,r为首摇角速度。
通过上述公式可以得到船舶在海流干扰下的相对速度和相对加速度。从而在数学模型的角度上运用船舶在水流中的相对运动参数替代原有的船舶在静水中的运动参数,使数学模型中加入了海流对船舶运动的影响。
3)海浪干扰力
海浪造成的干扰力主要包括一阶波浪力和二阶波浪力。一阶波浪力即高频波浪干扰力,对船舶横向和纵向的旋转运动影响较大,容易造成船舶大纵摇大垂荡运动,二阶波浪力则会直接影响船舶的运动轨迹以及航向,对船舶的运动状态影响更明显。
波浪漂移力和力矩可以表达为:
| $ \left\{ \begin{gathered} {X_{wave}} = \frac{1}{2}\rho ghL\zeta _D^2{C_{XD}}(\lambda )\cos \chi,\\ {Y_{wave}} = \frac{1}{2}\rho ghL\zeta _D^2{C_{YD}}(\lambda )\sin \chi,\\ {N_{wave}} = \frac{1}{2}\rho ghL\zeta _D^2{C_{ND}}(\lambda )\sin \chi 。\end{gathered} \right. $ | (22) |
波浪力和力矩系数的公式可以表示为:
| $ \begin{split} & {C_{XD}}(\lambda ) = 0.05 - 0.2\left( {\frac{\lambda }{L}} \right) + 0.75{\left( {\frac{\lambda }{L}} \right)^2} - 0.51{\left( {\frac{\lambda }{L}} \right)^3},\\ & {C_{YD}}(\lambda ) = 0.46 - 6.83\left( {\frac{\lambda }{L}} \right) - 15.65{\left( {\frac{\lambda }{L}} \right)^2} + 8.84{\left( {\frac{\lambda }{L}} \right)^3},\\ & {C_{ND}}(\lambda ) = - 0.11 + 0.68\left( {\frac{\lambda }{L}} \right) - 0.79{\left( {\frac{\lambda }{L}} \right)^2} + 0.21{\left( {\frac{\lambda }{L}} \right)^3}。\end{split} $ | (23) |
在实际计算过程中,波高与风速的关系可以参考表2中经验参数:
|
|
表 2 波高和风速对照表 Tab.2 Comparison table of wave height and wind speed |
路径跟随问题是指已通过路径规划方法获取目标路径之后,利用一些算法和控制方法实现无人船沿着目标路径航行的过程。本文通过LOS导航和传统PID控制的方式解决无人船的路径跟随问题。首先LOS导航算法根据目标路径计算出无人船的目标航向,之后通过PID控制获得无人船的航行舵角从而操纵无人船的运动。整理过程如图2所示。

|
图 2 路径跟随架构图 Fig. 2 The framework of path following |
LOS导航算法是一种常见的路径跟随控制算法。无人水面船的运动过程主要为三自由度运动,即横向位置、纵向位置、首摇角的变化,而本文根据LOS导航算法,假设无人船运动过程中速度大小保持不变,将目标路径上的某点方向作为LOS航向,即可将三自由度的运动问题转化为一自由度的航向控制问题。
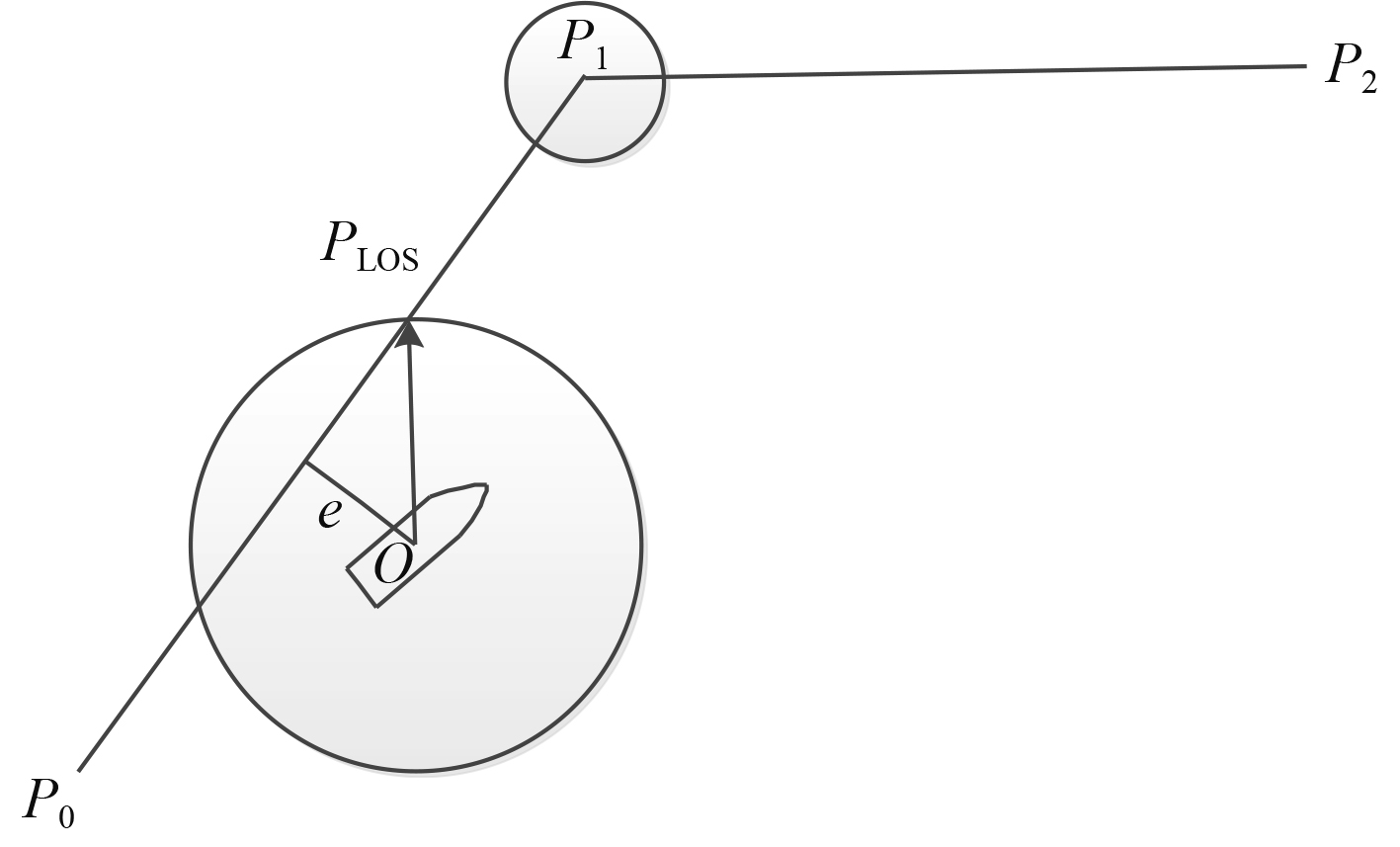
假设路径规划得到的目标路径为P0P1P2,无人船当前位置为O,如图3所示。
|
图 3 LOS导航示意图 Fig. 3 The schematic diagram of LOS navigation |
目标航向控制问题即可转化为目标点PLOS的坐标求解问题。本文以无人船位置为圆心、R为半径的圆与目标路径P0P1P2的交点中靠近下一目标点的一个作为目标点PLOS,则有:
| $ \left\{\begin{aligned} & ({{x}}_{{\mathrm{LOS}}}{-x})^{2}+({{y}}_{{\mathrm{LOS}}}{-y})^{2}={R}^{2},\\ & \mathrm{tan}{\phi }_{d}=\frac{{{y}}_{{\mathrm{LOS}}}{-y}}{{{x}}_{{\mathrm{LOS}}}{-x}}。\end{aligned}\right. $ | (24) |
式中:xLOS、yLOS为PLOS的坐标值;x、y为O点坐标值;
对于R的取值,一方面在无人船偏移量较大时要保证圆与路径有交点,一方面要在无人船偏移量较小时避免目标点过远导致结果受环境影响大,综合考虑本文取R大小为:
| $ {R_{LOS}} = \left\{ {\begin{split} & {3L,\left| e \right| \leqslant 3L},\\ & {e + L,\left| e \right| \gt 3L} 。\end{split}} \right. $ | (25) |
式中:e为无人船相对于目标路径的横向偏移量;L为船长。
另外对于路径转折处,如果仍用相同的方式选取目标点PLOS会导致转向突然,舵角变化率过大,运动不平滑,因此采用接纳圆的方式引导无人船转向。当无人船进入距目标路径转折点R0的范围内时开始进行路径切换。即当
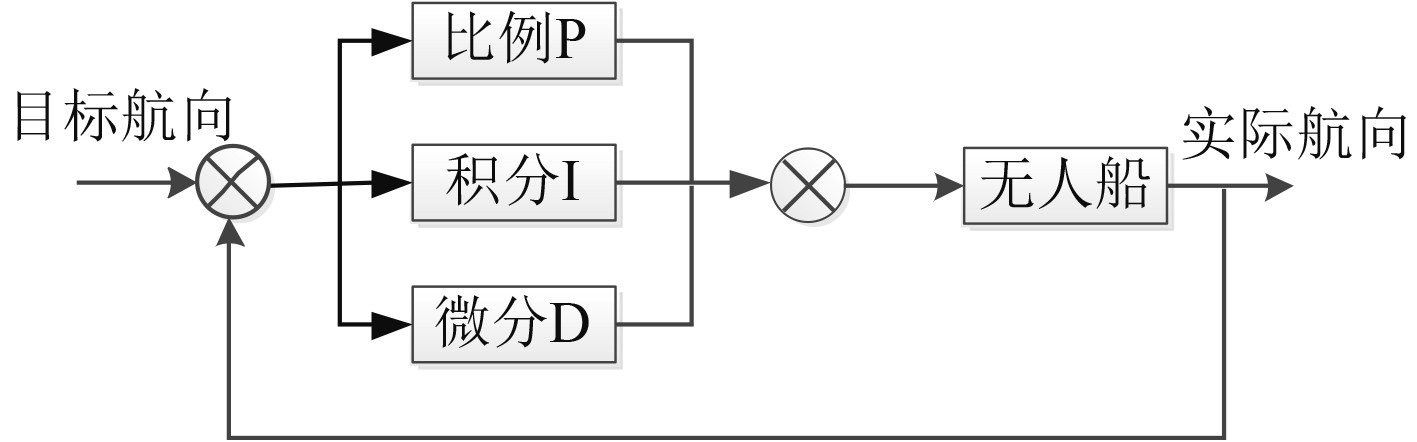
PID控制器方法理论简单、可操作性强,广泛应用于无人船的轨迹控制中。经典PID控制器原理如图4所示。
|
图 4 经典PID控制器原理图 Fig. 4 The schematic diagram of classic PID controller |
根据LOS导航算法得到目标航向
| $ \delta = {K_p}\Delta \varphi + {K_i}\int {\Delta \varphi {\mathrm{d}}t + } {K_d}\frac{{{\mathrm{d}}\Delta \varphi }}{{{\mathrm{d}}t}}。$ | (26) |
式中:
比例系数
积分系数
微分系数
因此合理选取
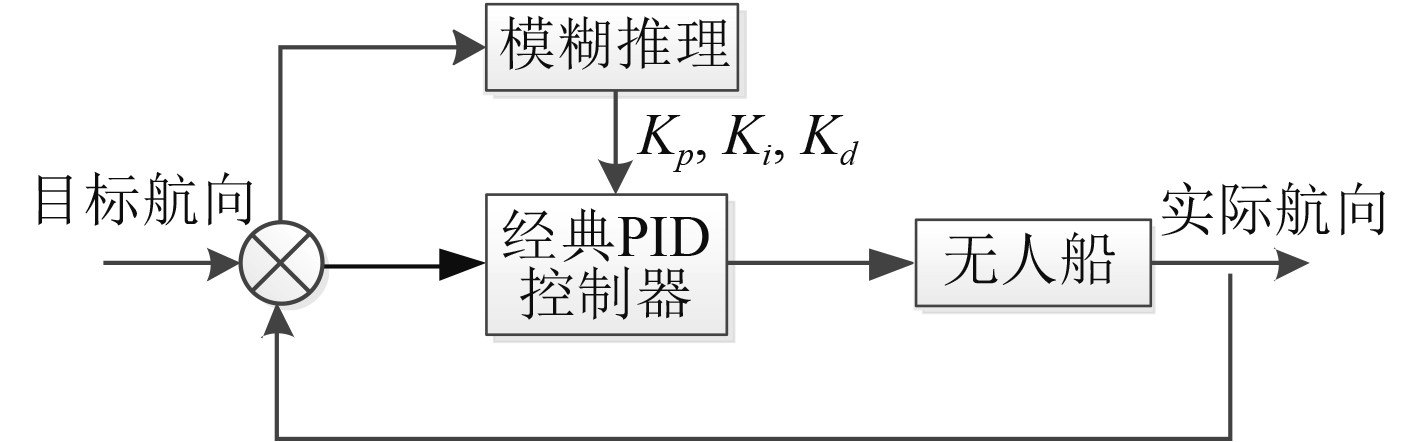
模糊控制是利用模糊规则推理,调节控制器参数的一种控制方法。模糊PID控制可以完善PID控制的自适应性能,根据控制要求对PID控制参数
|
图 5 模糊PID控制器原理图 Fig. 5 The schematic diagram of fuzzy PID controller |
模糊推理的规则大致如下:
1)当
2)当
3)当
通过上述规则可以根据无人船在航行过程中的实际运动状态以及目标航向/航迹调整PID控制器的参数,从而提高控制精度。
3 仿真结果分析针对LOS导航导航算法和模糊PID控制器设计本文进行了如下仿真:
1)无接纳圆LOS导航算法+经典PID控制轨迹跟踪仿真。目标路径为夹角90°的折线路径,从图可以看出在转角处没有接纳圆的时候转向不平滑,会有较大的超调和波动,但一段时间后也能完成路径跟踪目标,转向部分有较大的偏移量。
2)有接纳圆LOS导航算法+经典PID控制轨迹跟踪仿真。对比图7可知,转向处增加接纳圆后会根据接纳圆的引导提前转向,从而使得转向过程更平滑,横向偏移量减小。
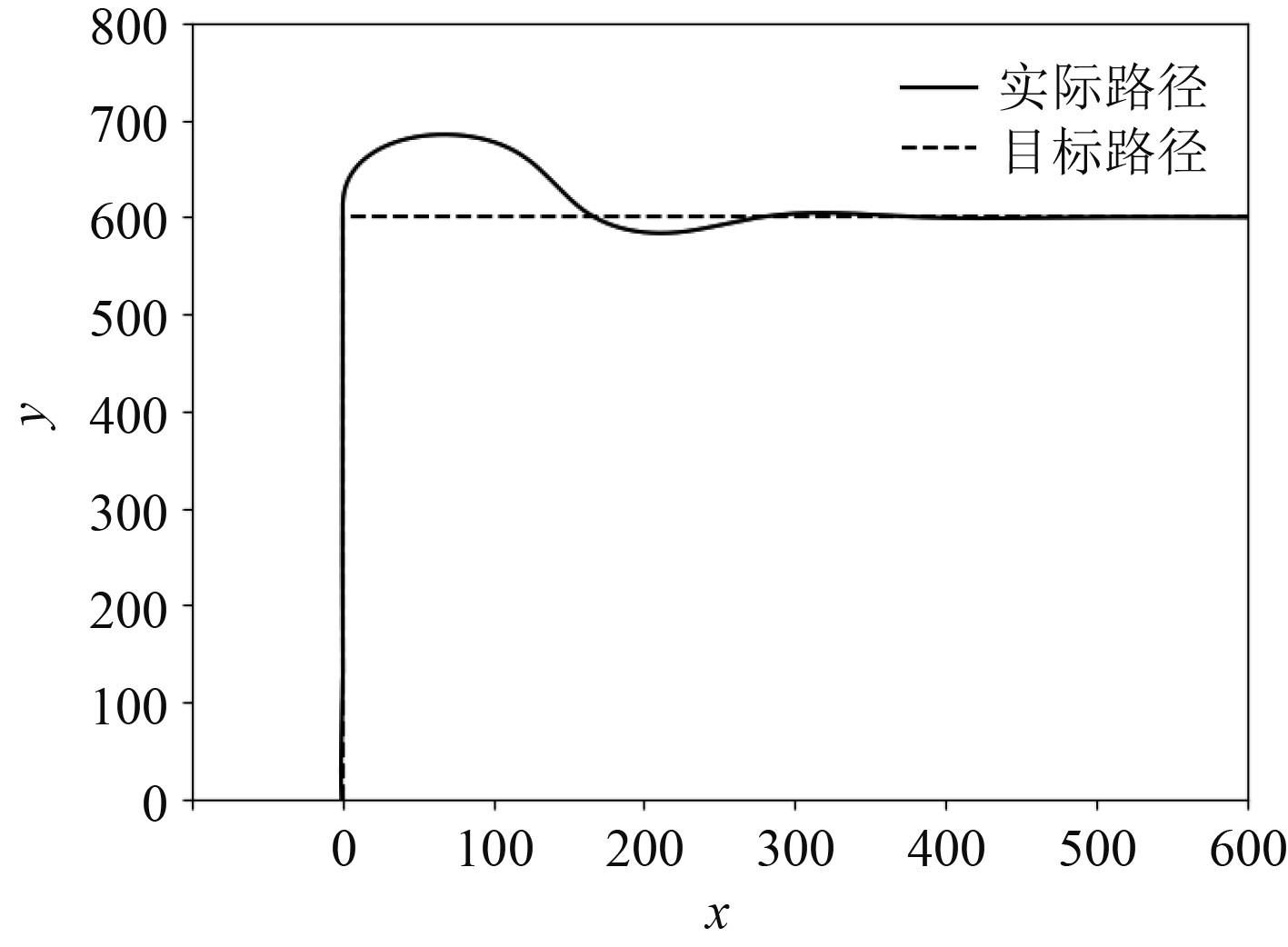
|
图 6 无接纳圆轨迹跟踪仿真结果 Fig. 6 Simulation results of trajectory tracking without acceptance circle |
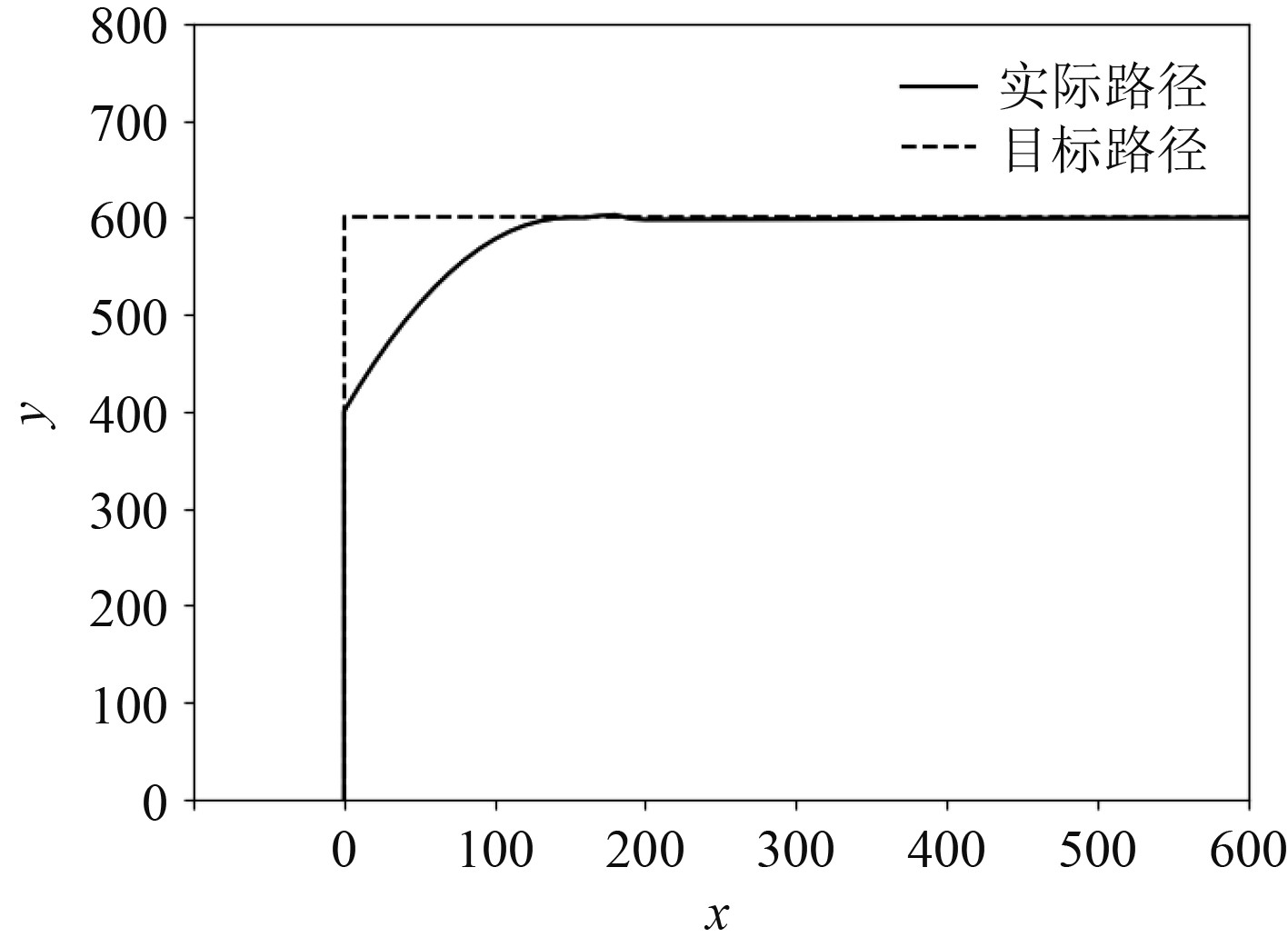
|
图 7 有接纳圆经典PID控制轨迹跟踪仿真结果 Fig. 7 Simulation results of classic PID control trajectory tracking with acceptance circle |
3)有接纳圆LOS导航算法+模糊PID控制轨迹跟踪仿真。在使用模糊PID控制后,无人船可以根据航行状态实时改变PID参数大小,从而改善控制器精度,对比图7和图8可知,控制过程的横向偏移量有了明显减少。
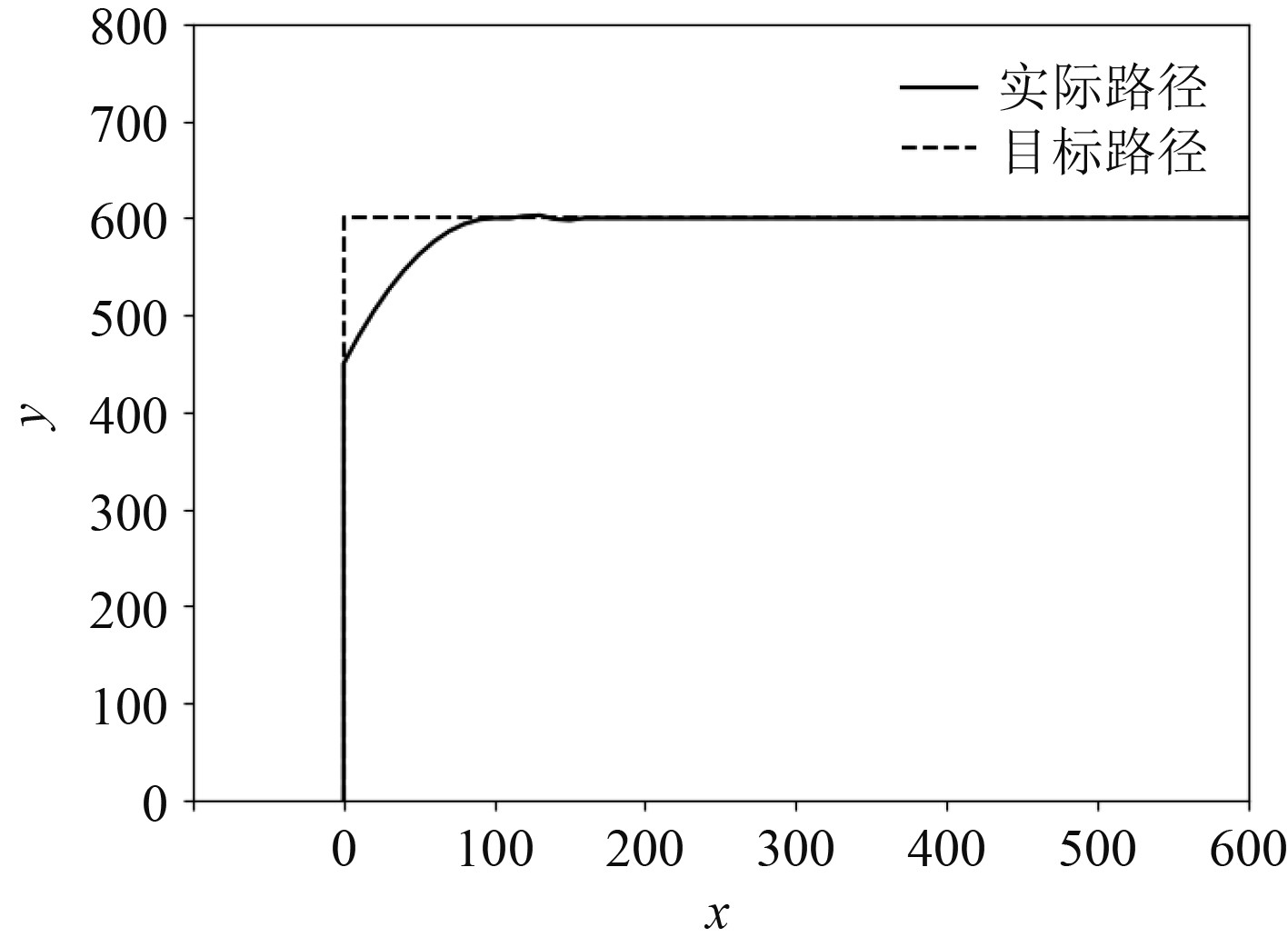
|
图 8 有接纳圆模糊PID控制轨迹跟踪仿真结果 Fig. 8 Simulation results of fuzzy PID control trajectory tracking with acceptance circle |
上述仿真结果表明采用有接纳圆的LOS导航算法和模糊PID控制器的路径跟踪控制算法能够明显提高无人船的路径跟踪响应性能,使得跟踪路径更平滑。
4 结 语针对无人船的路径跟踪控制问题,本文采用了LOS导航算法将问题转化为航向跟踪问题,并基于模糊PID控制器对无人船的航行进行控制。本文进行了无接纳圆、经典PID控制器等对照组的设计,验证了基于模糊PID控制器的LOS导航算法路径跟踪精度高、横向偏移量小、跟踪路径更平滑的特点。
| [1] |
LEFEBER E, PETTERSEN K Y, NIJMEIJER H. Tracking control of an underactuated ship[J]. IEEE Transactions on Control Systems Technology, 2003, 11(1): 52-61. DOI:10.1109/TCST.2002.806465 |
| [2] |
FOSSEN T I, LEKKAS A M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents[J]. International Journal of Adaptive Control and Signal Processing, 2017, 31(4): 445-463. DOI:10.1002/acs.2550 |
| [3] |
韩鹏, 刘志林, 周泽, 等. 基于LOS法的自航模航迹跟踪控制算法实现[J]. 应用科技, 2018, 45(3): 66-70. |
| [4] |
SPERRY E. Directional stability of automatically steered bodies. Journal of American Society of Naval Engineers, 1922, 42(1): 2−13
|
| [5] |
SUGIMOTO A. A new autopilot system with condition adaptivity. Proceedings 5th ship Control systems symposium, Annapolis, Maryland, USA, 1978, 105−111
|
| [6] |
张旋武. 基于强化学习的无人船路径跟随控制[D]. 武汉: 武汉理工大学, 2021.
|
| [7] |
李超. 基于CMAC的无人船模糊PID航迹控制技术研究[D]. 武汉: 湖北工业大学, 2019.
|
| [8] |
柳晨光. 基于预测控制的无人船运动控制方法研究[D]. 武汉: 武汉理工大学, 2019.
|
| [9] |
刘陆. 欠驱动无人船的路径跟踪与协同控制[D]. 大连: 大连海事大学, 2018.
|
| [10] |
秦晋盟. 无人船路径跟踪滑模控制研究[D]. 大连: 大连海事大学, 2021.
|
| [11] |
张薇. 船舶运动智能PID控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [12] |
王艳. 无人船建模及路径跟踪控制[D]. 杭州: 浙江大学, 2020.
|
 2024, Vol. 46
2024, Vol. 46
