随着船舶永磁同步电机在船舶推进系统中的广泛应用,对于船舶永磁同步电机的控制性能有了更高的要求[1]。然而在船舶永磁同步电机运行中,转动惯量会受到无法预知的因素影响,如负载扰动、参数变化等,这些外部扰动的变化会影响船舶推进系统的控制性能[2]。
对于船舶推进系统,需要在线调整控制器参数,使系统具有良好的运行状态。转动惯量是速度环PI控制器的基本设计参数,所以根据运行工况实时调整转动惯量,能够有效抑制系统出现超调和振荡的情况[3]。负载转矩的突变会导致转速瞬间的跌落或上升,因此需要对负载转矩观测,并作为电流补偿,使得系统具备抗扰动性能。转动惯量辨识和负载转矩观测是提高船舶推进系统性能的重点研究问题。
惯量辨识的方法通常分为在线和离线两大类。常见的离线惯量辨识方法为加减法[4],先是规划三角波速度指令,根据转速反馈和转矩反馈计算得到惯量值,这种方法得到的辨识值精度高,但是在工况复杂的情况下,系统的诸多参数发生变化,采用离线惯量辨识不能反映惯量的动态变化。因此,诸多学者结合系统辨识理论,提出在线惯量辨识方法,主要有最小二乘法、模型参考自适应法、扩展卡尔曼滤波算法、人工智能算法、梯度算法等。
文献[5]提出一种基于惯量辨识的自适应扰动观测器,解决了辨识中参数耦合引起的波动问题。文献[6]采用递推最小二乘法对多参数同时辨识,但辨识参数稳定性有待提高。文献[7]提出一种变周期最小二乘法对转动惯量在线辨识,解决了在低加速度下的辨识问题,提高算法的适用范围。文献[8]提出在线辨识转动惯量的扰动观测器,并把辨识的转动惯量和负载转矩作用到速度控制器中,但辨识精度有待提升。文献[9]用蚁群算法同时辨识转动惯量和负载转矩,但算法运行量大,收敛速度不快。
上述文献对惯量辨识算法都有所优化,仍存在船舶推进系统在复杂工况下辨识的惯量误差较大和无法收敛,其难点在于惯量辨识需要观测实时的负载,负载的观测又需要实际的惯量[10-11]。为此本文提出梯度校正法与扩展卡尔曼滤波器(Extended Kalman -Filter, EKF)结合的在线惯量辨识算法,采用后向差分法对电机的运动方程离散化,将梯度校正法用于此模型[12]。在惯量辨识的同时需要获取负载转矩,利用扩展卡尔曼滤波器把负载转矩当成状态变量实现参数估计。对存在负载扰动的工况,可以有效解决转动惯量和负载转矩的耦合问题,具有收敛速度快、精度高、抗扰动性好等特点,仿真和实验验证了算法的有效性[13]。
1 PMSM的数学模型在同步旋转坐标系
| $ \left\{ \begin{gathered} {u_d} = R{i_d} + {L_d}\frac{{\rm{d}}}{{{\rm{d}}t}}{i_d} - {\omega _e}{L_q}{i_q},\\ {u_q} = R{i_q} + {L_q}\frac{{\rm{d}}}{{{\rm{d}}t}}{i_q} + {\omega _e}({L_d}{i_d} + {\psi _f}) 。\\ \end{gathered} \right. $ | (1) |
式中:
PMSM的电磁转矩方程为:
| $ {T_e} = \frac{3}{2}{P_n}{i_q}[{i_d}({L_d} - {L_q}) + {\psi _f}]。$ | (2) |
式中:
对于表贴式三相PMSM,定子电感满足
| $ {T_e} = \frac{3}{2}{P_n}{i_q}{\psi _f} = {K_t}{i_q},$ | (3) |
式中,
电机的机械运动方程为:
| $ J\frac{{{\rm{d}}{\omega _m}}}{{{\rm{d}}t}} = {T_e} - {T_L} - B{\omega _m}。$ | (4) |
式中:
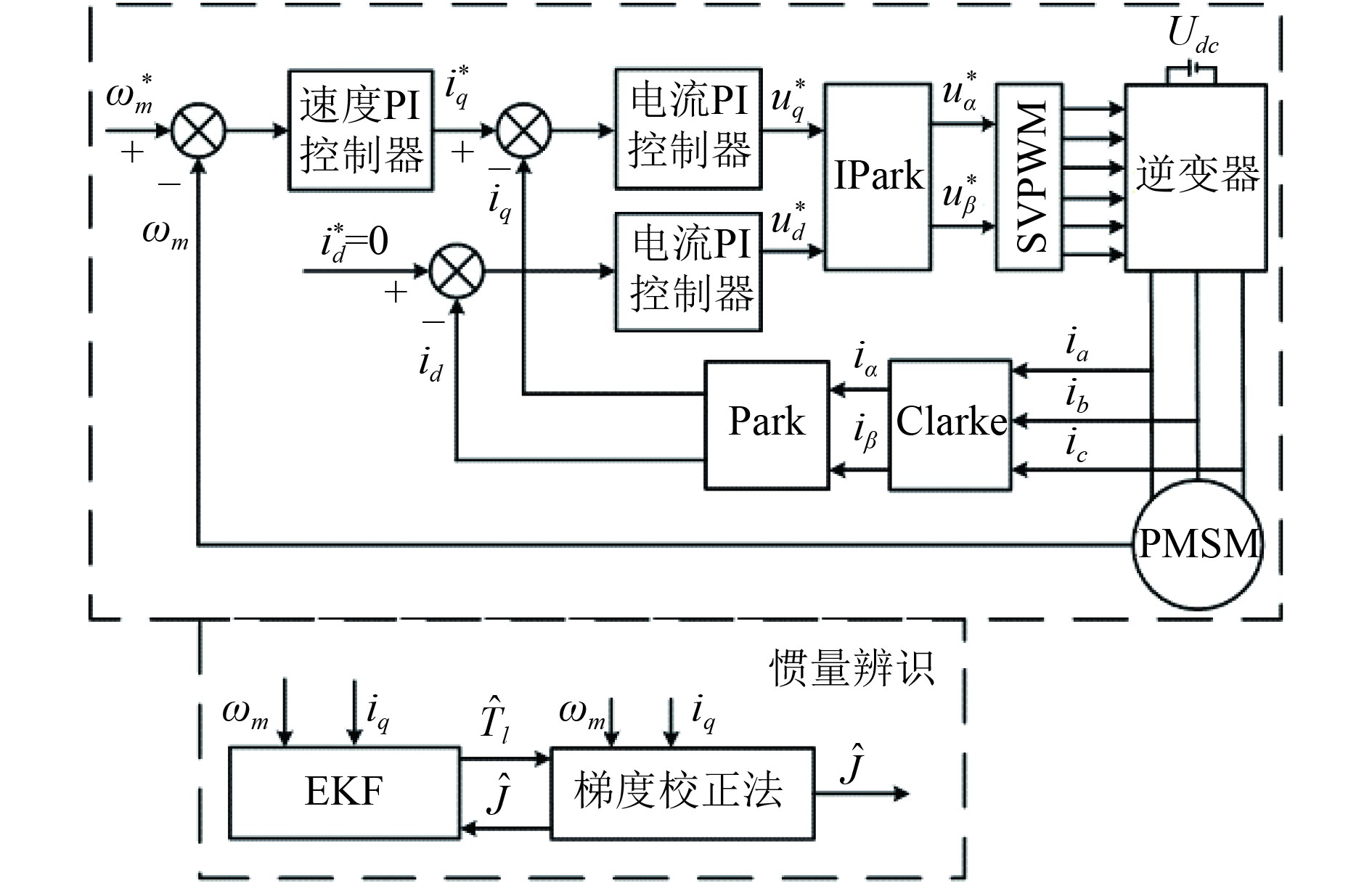
基于梯度校正法与扩展卡尔曼滤波器的惯量辨识框图分为两部分,如图1所示。第一部分是船舶永磁同步电机推进系统矢量控制模块,图中
|
图 1 船舶推进系统惯量辨识框图 Fig. 1 Block diagram of inertia identification of ship propulsion system |
第二部分为惯量辨识模块,由电机运动方程可知,转动惯量和负载转矩存在强耦合关系。因此把梯度校正法与扩展卡尔曼滤波器结合对转动惯量进行辨识,速度反馈
梯度校正法的基本思想是:沿准则函数的负梯度方向,逐步修正模型参数估计值,直至准则函数达到最小值,对于
设梯度校正法中的准则函数为:
| $ J(\theta ) = \frac{1}{2}{\left[ {y(k) - {\varphi ^{\rm{T}}}(k)\widehat \theta (k - 1)} \right]^2} 。$ | (5) |
沿
| $ \widehat \theta (k) = \widehat \theta (k - 1) - {\boldsymbol{R}}({\boldsymbol{k}})grad{\left. {[J(\theta )]} \right|_{\widehat \theta (k)}} 。$ | (6) |
式中,
| $ {\rm{grad}}{\left. {[J(\theta )]} \right|_{\widehat \theta (k)}} = - [y(k) - {\varphi ^{\rm{T}}}(k)\widehat \theta (k - 1)]\varphi (k) ,$ | (7) |
得到梯度校正法的递推公式:
| $ \widehat \theta (k) = \widehat \theta (k - 1) + R(k)\varphi (k)[y(k) - {\varphi ^{\rm{T}}}(k)\widehat \theta (k - 1)] 。$ | (8) |
式中:
根据
| $ R(k)=\frac{1}{{\displaystyle \sum _{i=1}^{N}{\Lambda }_{i}(k){\phi }_{i}^{2}(k)}}\cdot {\rm{diag}}[{\Lambda }_{1}(k)\text{,}{\Lambda }_{2}(k)\text{,}\cdots \text{,}{\Lambda }_{N}(k)],$ | (9) |
式中,一般选择
| $ \widehat \theta (k) = \widehat \theta (k - 1) + \frac{{\varphi (k)}}{{{\varphi ^{\rm{T}}}(k)\varphi (k)}} \cdot [y(k) - {\varphi ^{\rm{T}}}(k)\widehat \theta (k - 1)] 。$ | (10) |
为了避免
| $ \widehat \theta (k) = \widehat \theta (k - 1) + \frac{{\alpha \varphi (k)}}{{\lambda + {\varphi ^T}(k)\varphi (k)}} \cdot [y(k) - {\varphi ^T}(k)\widehat \theta (k - 1)]。$ | (11) |
式中:
对式(4)进行离散化,并忽略黏性阻尼系数
| $ {\omega _m}(k) - {\omega _m}(k - 1) = \frac{{{T_s}}}{J} \cdot ({T_e}(k) - {T_L}(k)),$ | (12) |
根据式(12)将
| $ \begin{aligned} &{\omega _m}(k) - 2{\omega _m}(k - 1) + {\omega _m}(k - 2) = \frac{{{T_s}}}{J} \cdot \\ &[{T_e}(k) - {T_e}(k - 1) - {T_L}(k) + {T_L}(k - 1)]。\end{aligned}$ | (13) |
式中:
将式(13)代入式(11),可得:
| $\begin{aligned} & \widehat \theta (k) = \widehat \theta (k - 1) + \frac{{\alpha \varphi (k)}}{{\lambda + {\varphi ^{\rm{T}}}(k)\varphi (k)}} \cdot \\ & [{\omega _m}(k) - 2{\omega _m}(k - 1) + {\omega _m}(k - 2) - {\varphi ^{\rm{T}}}(k)\widehat \theta (k - 1)] 。\end{aligned}$ | (14) |
式中:
负载转矩扰动影响速度的稳定性,因此需要对负载转矩实时观测,并把负载转矩作为电流前馈补偿。因船舶推进系统是非线性的,
电机负载转矩的变化率对于船舶推进系统的采样率来说变化缓慢,可认为导数为0,即
| $ \frac{{{\rm{d}}{T_L}}}{{{\rm{d}}t}} = 0。$ | (15) |
根据式(4)和式(15),构建PMSM的状态方程为:
| $ \left[\begin{array}{c}\stackrel{·}{{\omega }_{m}}\\ \stackrel{·}{{T}_{L}}\end{array}\right]=\left[\begin{array}{cc}-\frac{B}{J}& -\frac{1}{J}\\ 0& 0\end{array}\right]\left[\begin{array}{c}\omega {}_{m}\\ {T}_{L}\end{array}\right]+\left[\begin{array}{c}\dfrac{{K}_{t}}{J}\\ 0\end{array}\right]{i}_{q} 。$ | (16) |
系统的状态方程和测量方程描述如下:
| $ \Bigg\{\begin{array}{l}\stackrel{·}x{(t)}=f[x(t)]+Bu(t)+w(t),\\ y(t)=h[x(t)]+v(t)。\end{array} $ | (17) |
式中:
对
| $ F[x(t)] = {\left. {\dfrac{{\delta f}}{{\delta x}}} \right|_{x = x(t)}} = \left[ {\begin{array}{*{20}{c}} {{{ - }}\dfrac{{{B}}}{{{J}}}}&{{{ - }}\dfrac{{{1}}}{{{J}}}} \\ {{0}}&{{0}} \end{array}} \right],$ | (18) |
| $ H[x(t)] = {\left. {\frac{{\delta h}}{{\delta x}}} \right|_{x = x(t)}} = \left[ {\begin{array}{*{20}{c}} {{1}}&{{0}} \end{array}} \right]。$ | (19) |
式(17)为非线性方程,设采样周期为
| $ \left\{ \begin{gathered} x(k + 1) = {A_k}x(k) + {B_k}u(k) + w(k),\\ y(k) = {H_k}x(k) + v(k) 。\\ \end{gathered} \right. $ | (20) |
式中:
| $ \left\{ \begin{gathered} \cos (w) = E\left\{ {w{w^{\rm{T}}}} \right\} = Q = \left[ {\begin{array}{*{20}{c}} {{{{q}}_{{w}}}}&{{0}} \\ {{0}}&{{{{q}}_{{{{T}}_{{L}}}}}} \end{array}} \right],\\ \cos (v) = E\left\{ {v{v^{\rm{T}}}} \right\} = R 。\qquad\qquad\qquad\quad\\ \end{gathered} \right. $ | (21) |
式中,
利用
步骤1 状态预测
| $ \widetilde x(k + 1) = \widehat x(k) + {T_s}[f(\widehat x(k)) + B(k)u(k)]。$ | (22) |
步骤2 先验估计协方差矩阵
| $ \widetilde p(k + 1) = F(k)\widehat p(k + 1)F{(k)^{\rm{T}}} + Q。$ | (23) |
步骤3 增益矩阵
| $ K(k + 1) = \widetilde p(k + 1){H^T}{[H\widetilde p(k + 1){H^T} + R]^{ - 1}}。$ | (24) |
步骤4 后验估计
| $ \widehat x(k + 1) = \widetilde x(k + 1) + K(k + 1)[y(k + 1) - \widetilde y(k + 1)]。$ | (25) |
步骤5 后验估计协方差矩阵
| $ \widehat p(k + 1) = \widetilde p(k + 1) - K(k + 1)H\widetilde p(k + 1)。$ | (26) |
为分析梯度校正法和
|
|
表 1 电机参数 Tab.1 The motor parameters |
由电机的机械运动方程可知,当电机的速度变化率
为测试在定惯量的情况下可调参数
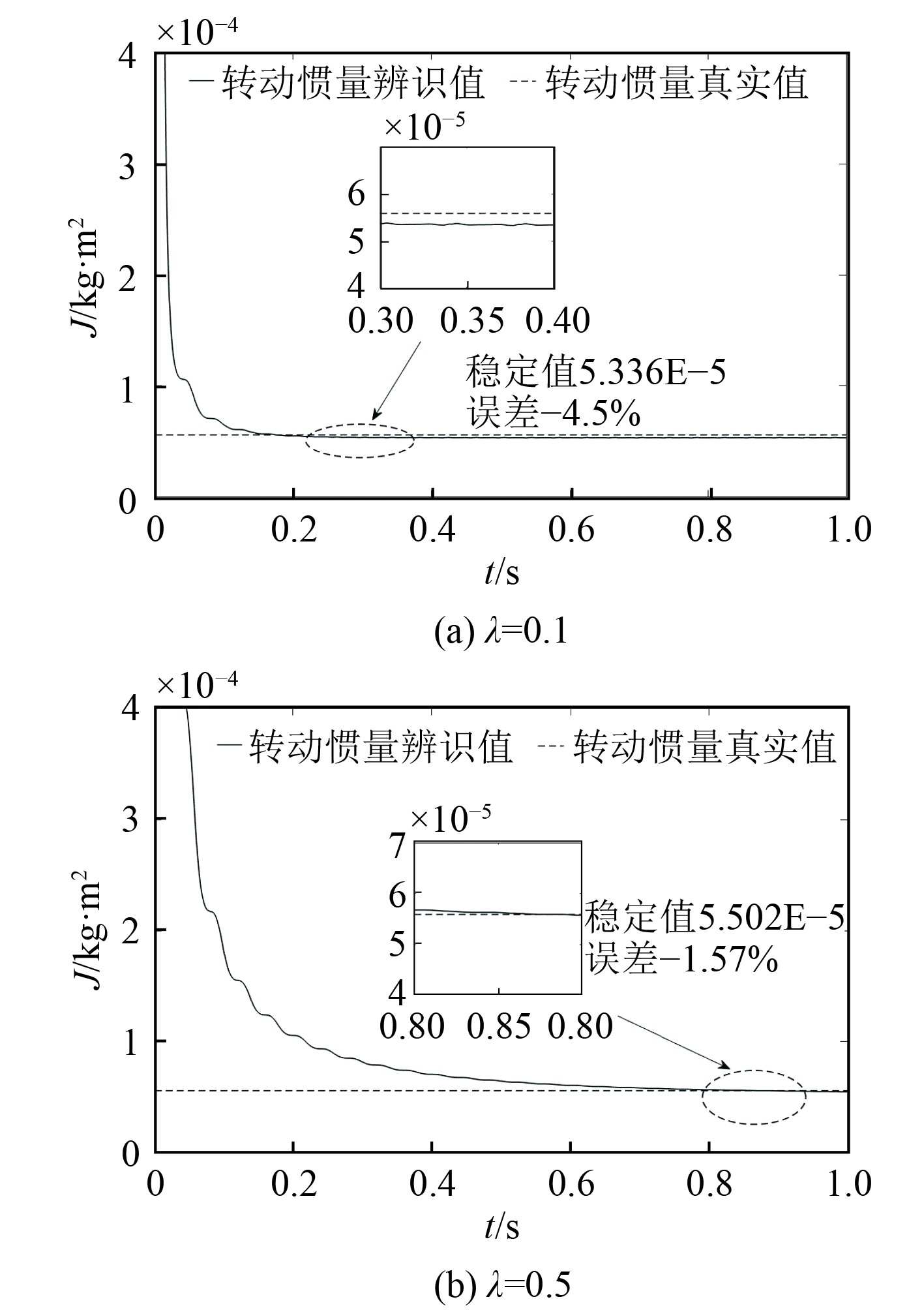
保持
|
图 2
|
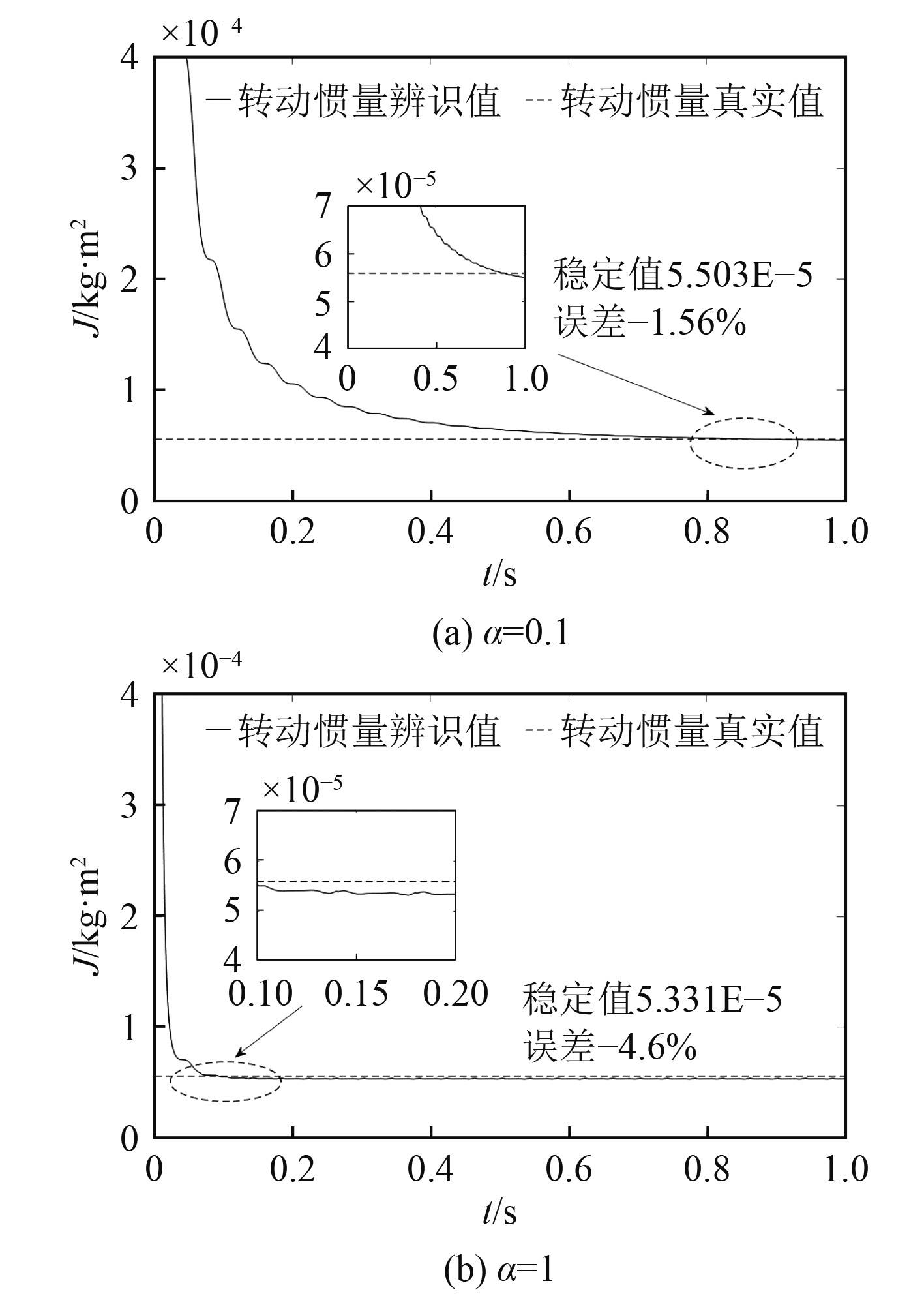
选择
|
图 3
|
通过分析曲线的辨识精度和收敛时间,当
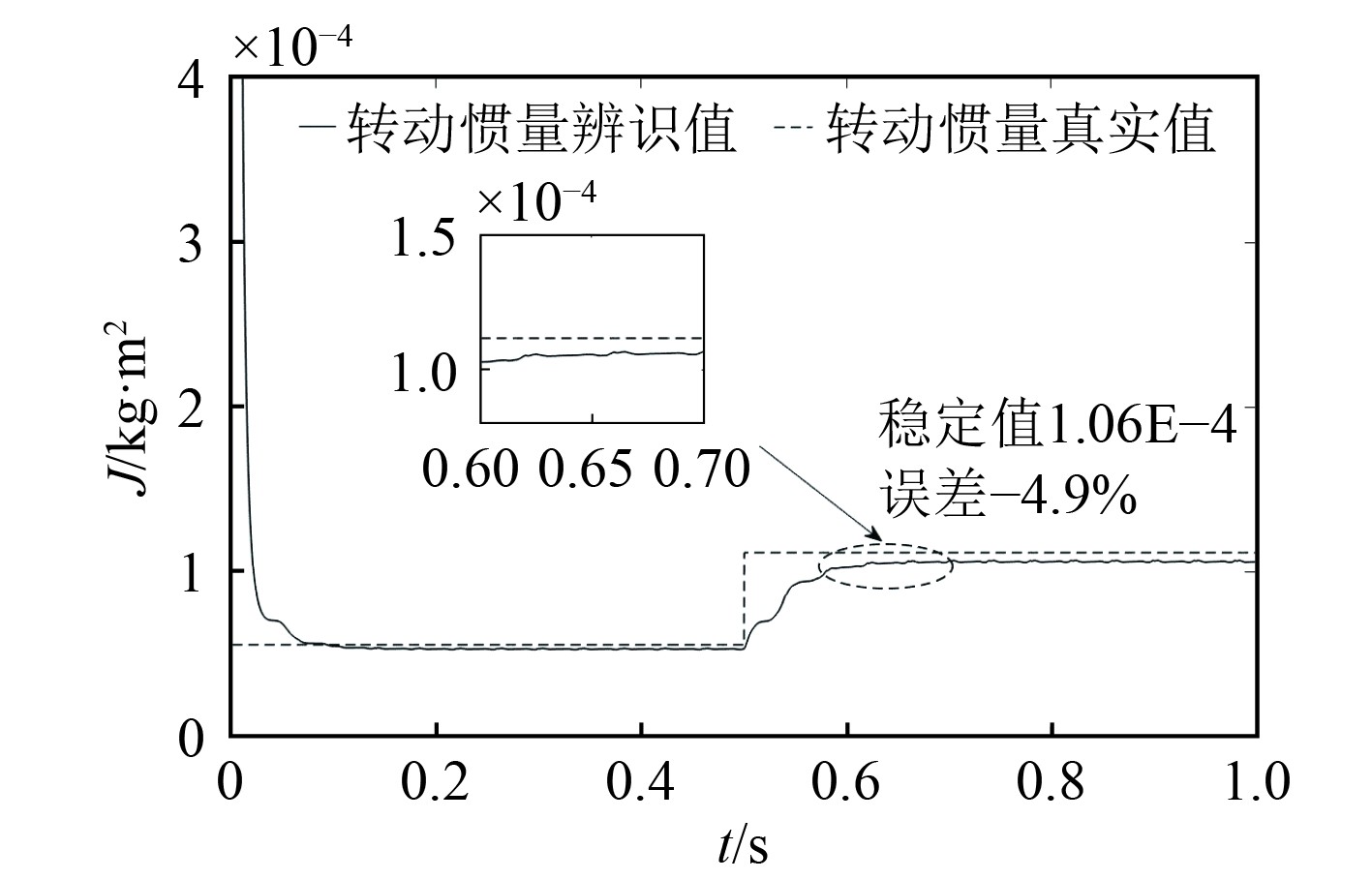
在
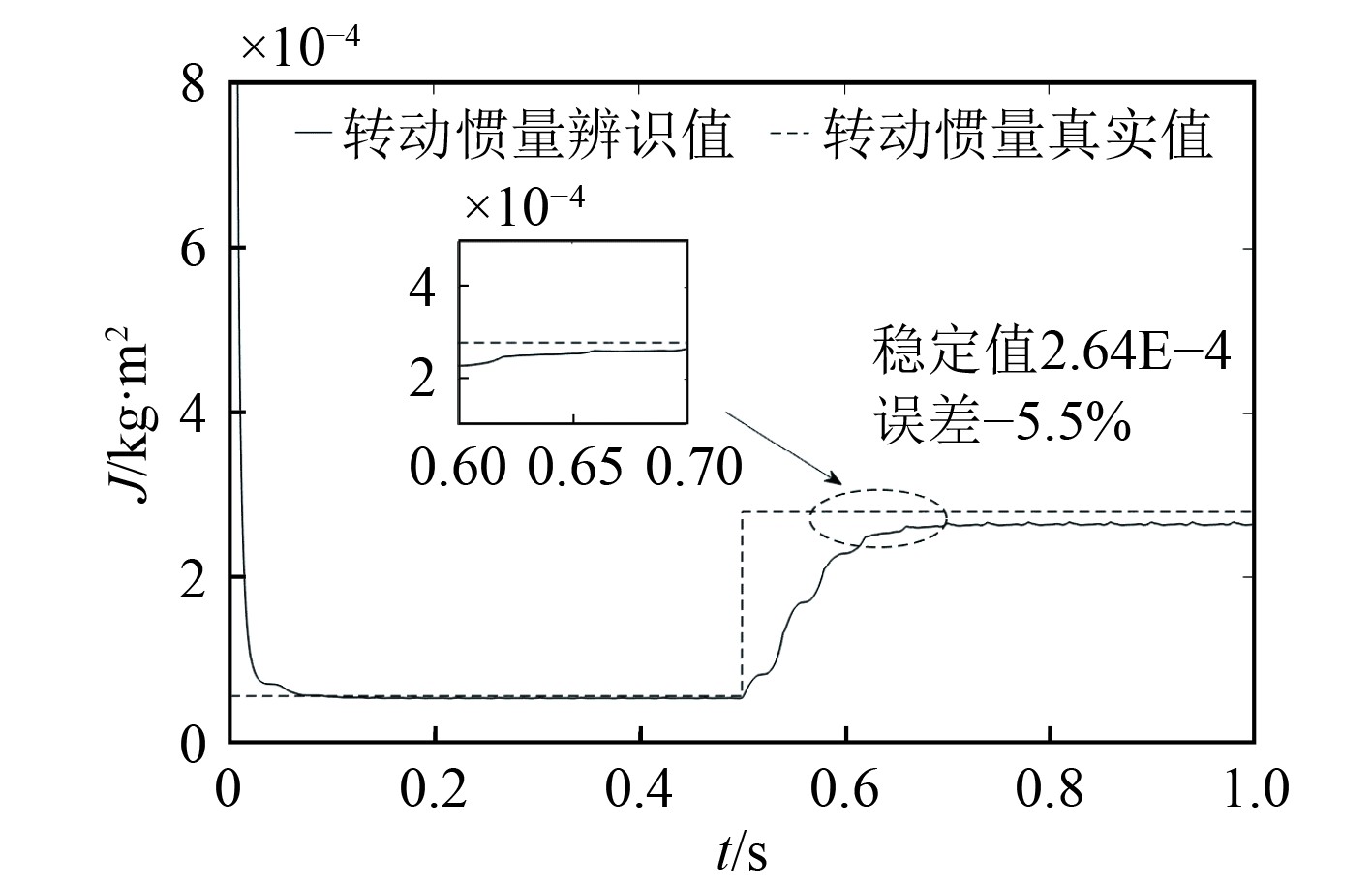
从图4和图5可知,随着转动惯量变化越大,收敛时间变长,辨识精度变低,误差值也变大,可以看出负载惯量从
|
图 4 突加1倍惯量的仿真效果 Fig. 4 The simulation effect of adding 1 times of inertia suddenly |
|
图 5 突加4倍惯量的仿真效果 Fig. 5 The simulation effect of adding 4 times of inertia suddenly |
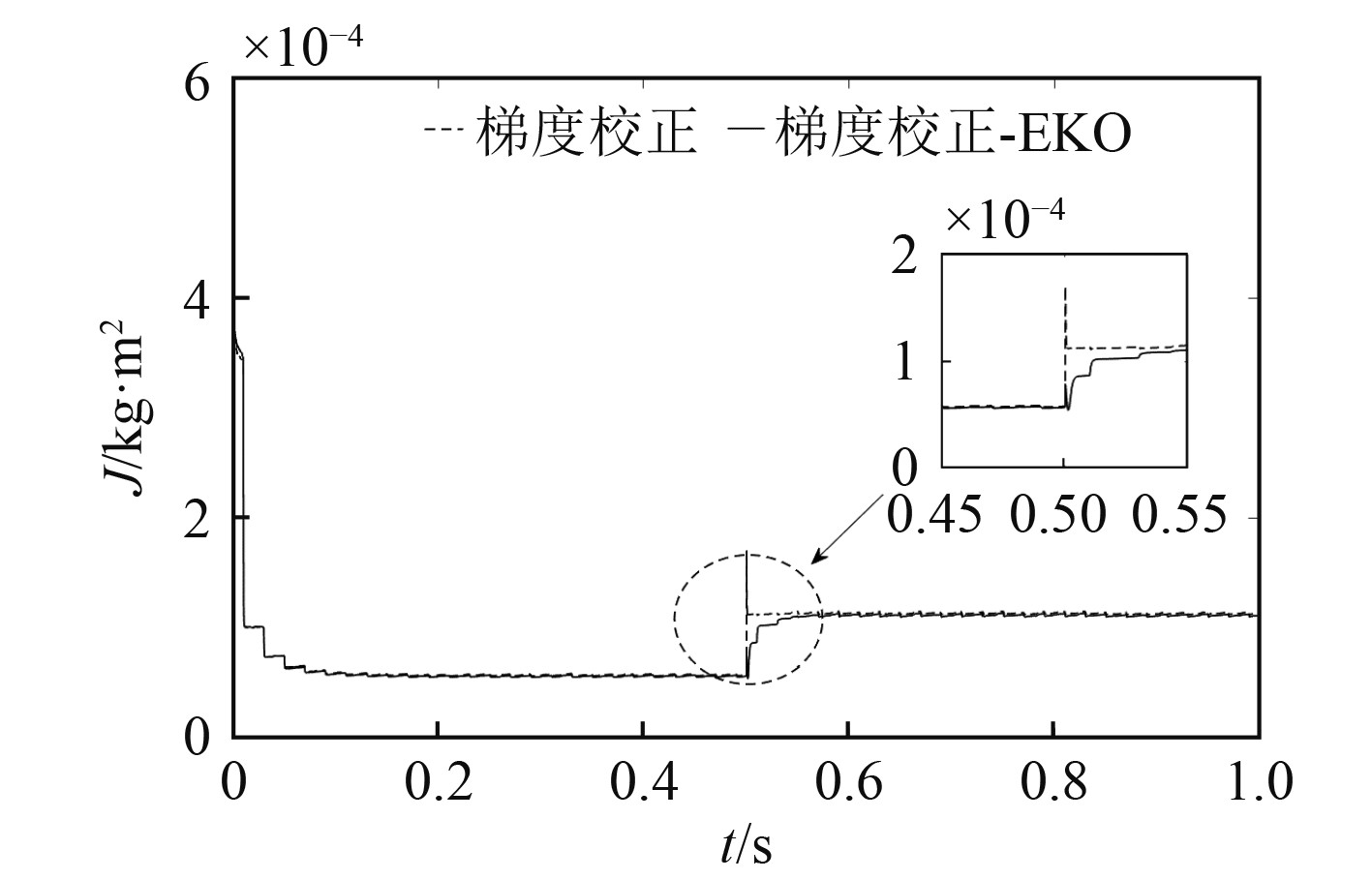
对存在扰动的工况,即电机转动惯量和负载转矩同时变化,当电机空载运行,在
|
图 6 参数突变的辨识结果 Fig. 6 Identification results of parameter mutation |
可以看出,传统梯度校正法在负载突变时,会导致转动惯量明显突变上升到很大的值。相反,本文算法在突加负载时没有突变,逐渐跟随上理论辨识值,稳定后辨识误差也小于传统算法。本文算法改善了动态辨识效果,提高算法的自适应能力。
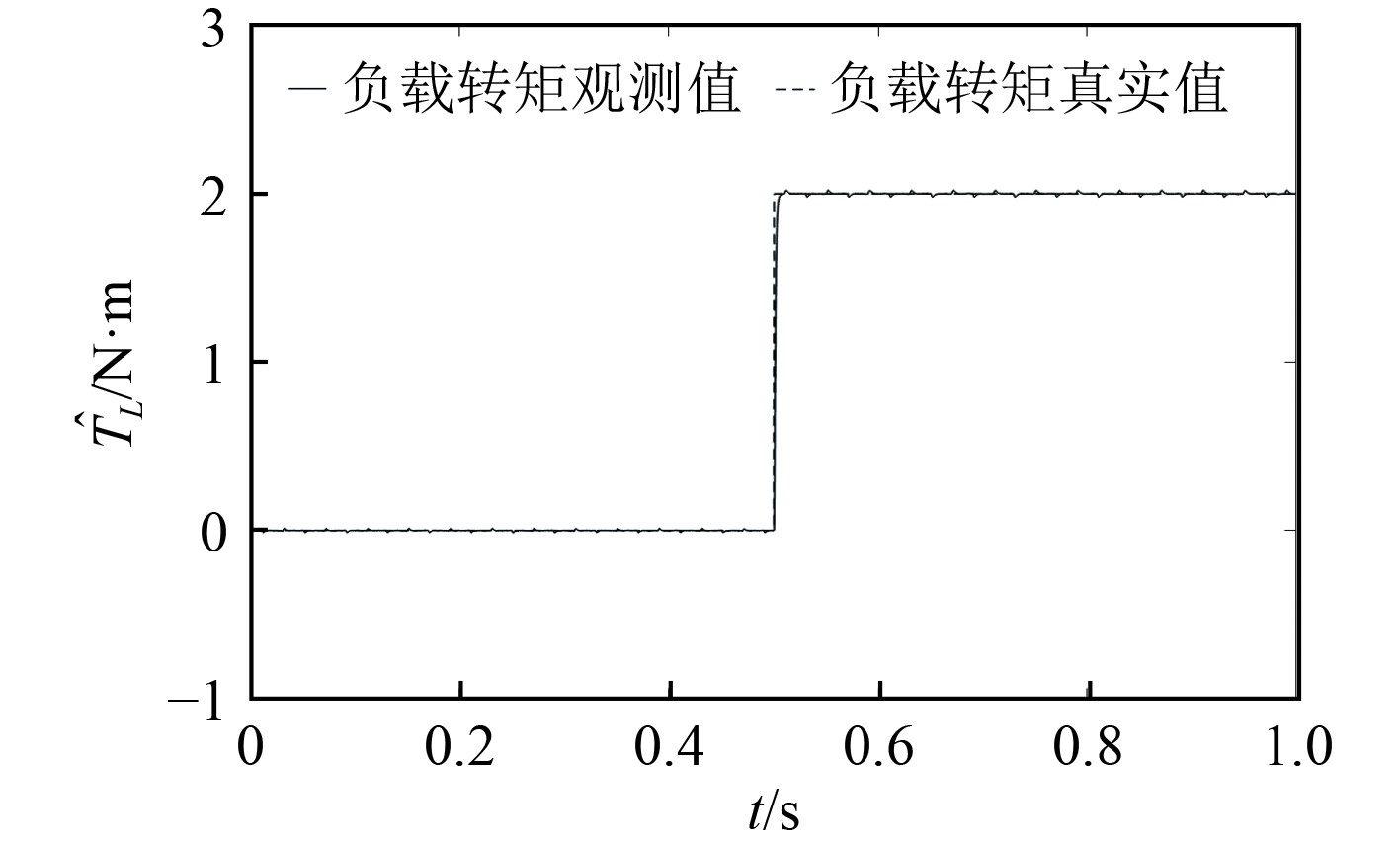
根据调试经验,将EKF的协方差矩阵设为
|
图 7 负载转矩观测值 Fig. 7 Observed load torque |
可知,在空载工况下,观测值很快就能收敛,误差较小;在带载工况下,观测值需经过短时间的波动才收敛到真实值,误差值在
为验证算法的有效性,进行在线惯量辨识实验,其电机转子惯量约为
分别在空载和带负载的工况下测试算法的辨识性能,考虑速度和转矩电流的周期比辨识周期小,经过实验调试,辨识周期取
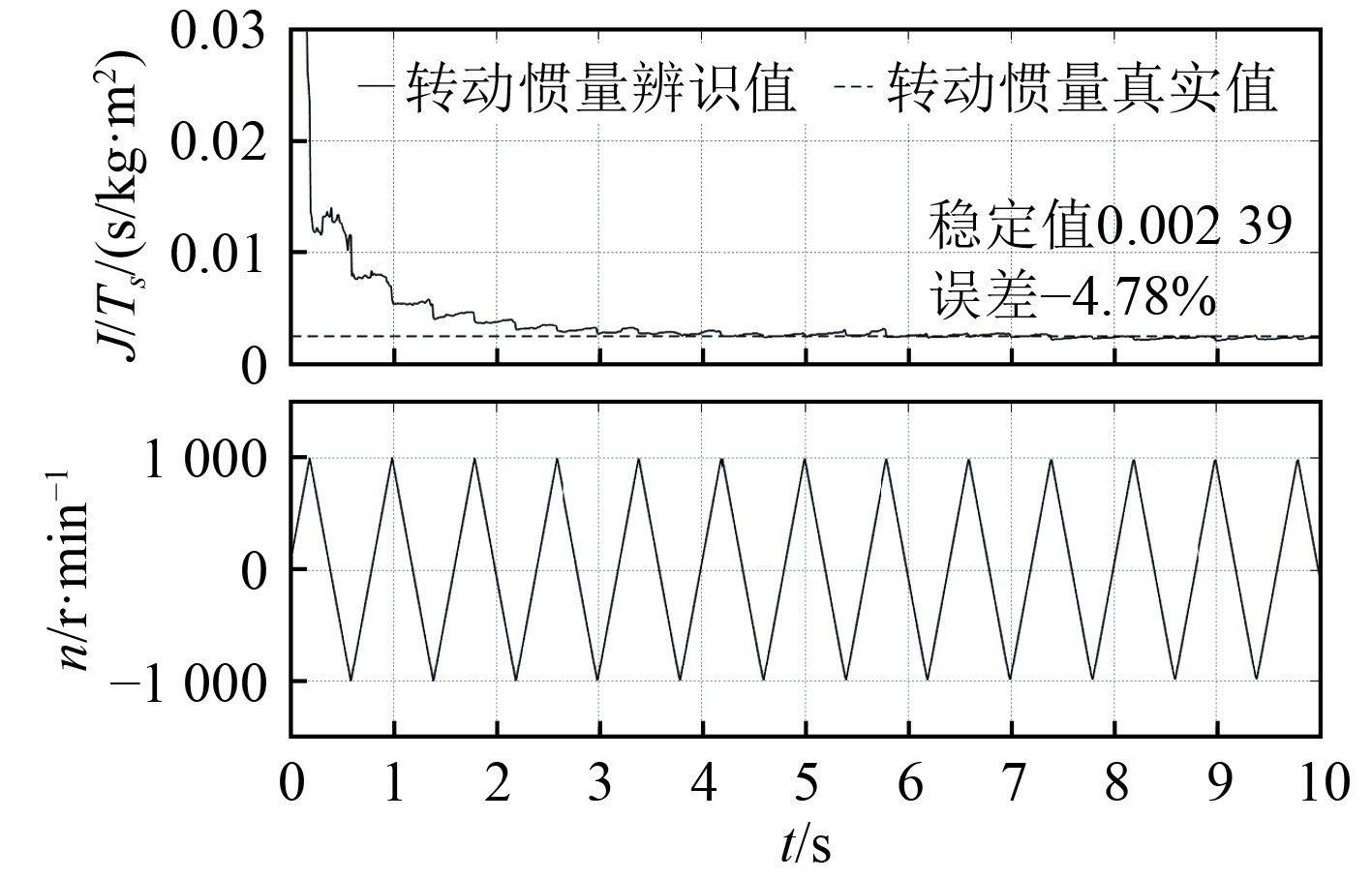
在空载条件下,转动惯量理论辨识值为J/Ts=
|
图 8 空载条件下辨识值 Fig. 8 Identification value under no-load condition |
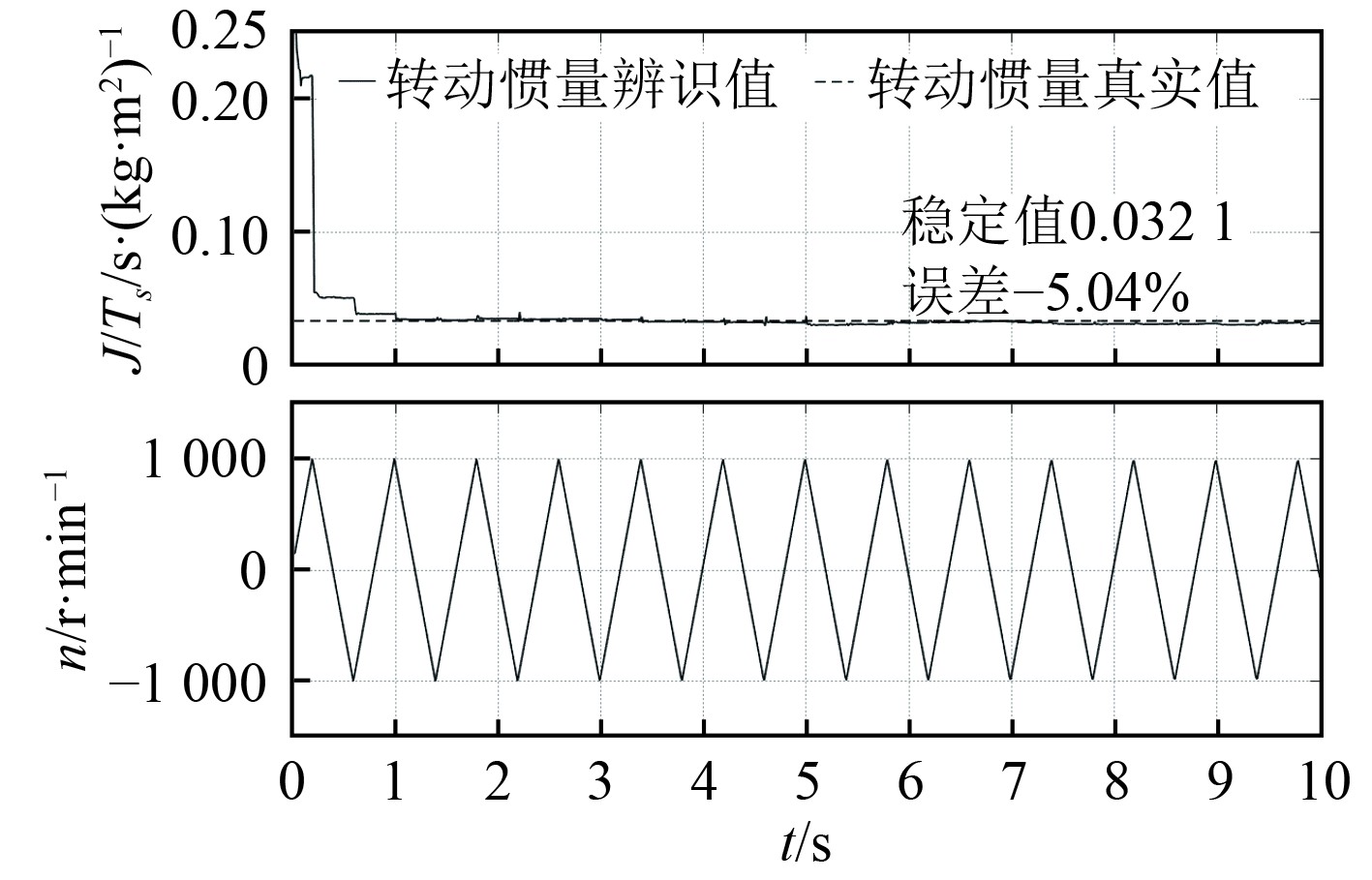
图9为带负载的工况,转动惯量理论辨识值为
|
图 9 带载条件下辨识值 Fig. 9 Identification value under load condition |
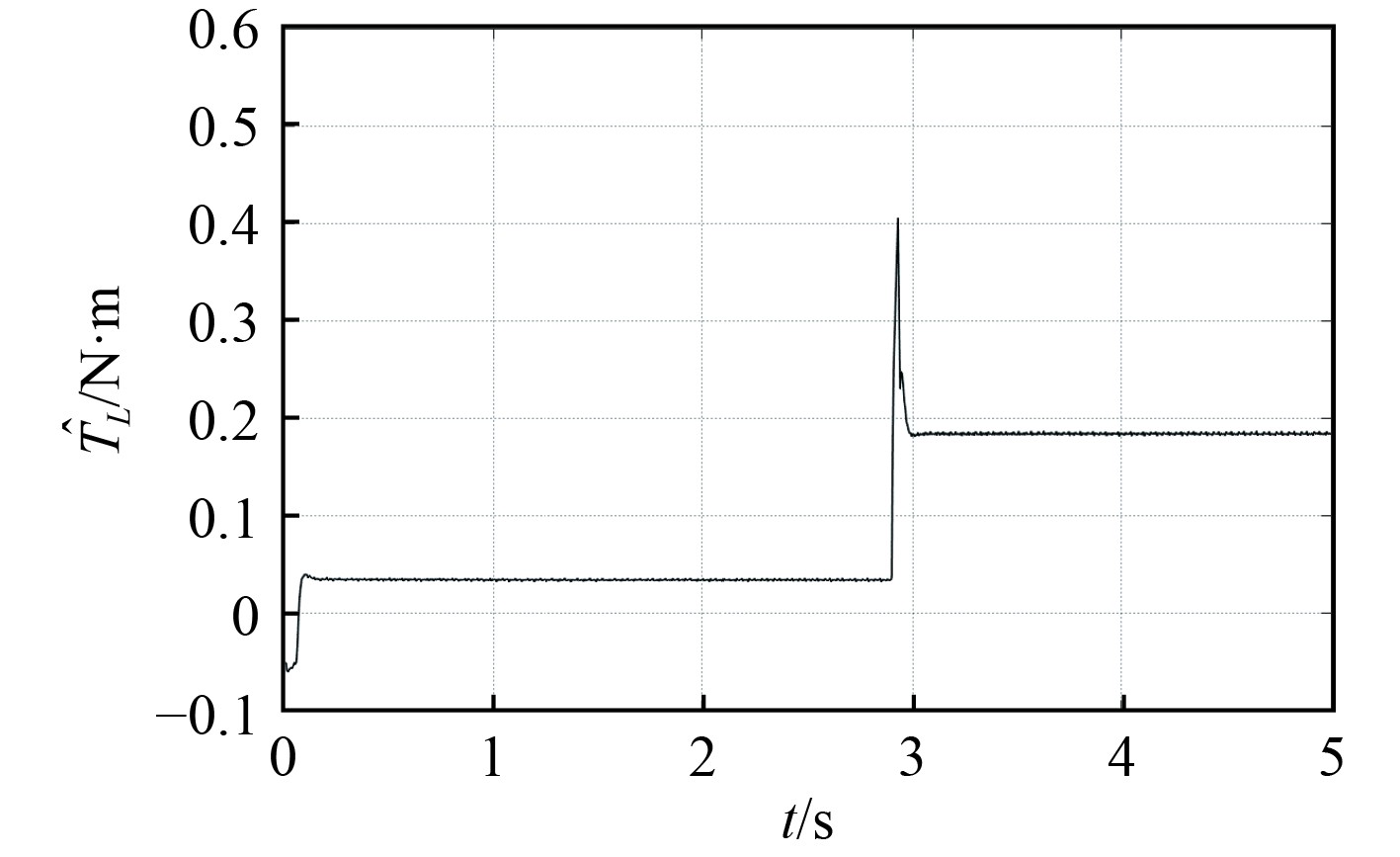
为验证
|
图 10 负载转矩观测值 Fig. 10 Observed load torque |
本文针对船舶永磁同步电机转动惯量和负载转矩存在的扰动问题,提出梯度校正法与扩展卡尔曼滤波器结合的在线惯量辨识方法,很好解决了转动惯量和负载转矩之间因耦合问题导致惯量辨识误差大的问题。通过对梯度校正法选择合适的可调参数,对于定惯量和变惯量的工况,提高了算法的辨识效果。相比传统算法,本文算法在负载转矩阶跃工况下有较好的自适应能力。此外,利用扩展卡尔曼滤波器对负载转矩实时观测,并作为电流前馈补偿。提高了船舶推进系统对负载转矩的抗扰动性能。仿真和实验验证了算法的有效性。
| [1] |
TAMI R, BOUTAT D, ZHENG G, et al. Rotor speed, load torque and parameters estimations of a permanent magnet synchronous motor using extended observer forms[J]. IET Control Theory & Applications, 2017, 11(9): 1485-1492. |
| [2] |
王璨, 杨明, 栾添瑞, 等. 双惯量弹性伺服系统外部机械参数辨识综述[J]. 中国电机工程学报, 2016, 36(3): 804–817.
|
| [3] |
吴春, 郑露华, 支恩. 基于三角函数正交特性的永磁伺服系统机械参数辨识方法[J]. 中国电机工程报, 2022, 42(4): 1617–1625.
|
| [4] |
KIM S. Moment of inertia and friction torque coefficient identification in a servo drive system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 60-70. DOI:10.1109/TIE.2018.2826456 |
| [5] |
陈炜, 郭照升, 夏长亮, 等. 基于转动惯量辨识的交流伺服系统自适应扰动观测器设计[J]. 电工技术学报, 2016, 31(16): 3–4, 42.
|
| [6] |
荀倩, 王培良, 李祖欣, 等. 基于递推最小二乘法的永磁伺服系统参数辨识[J]. 电工技术学报, 2016, 31(17): 161-169. XUN Q, WANG P L, LI Z X, et al. Parameter identification of permanent magnet servo system based on recursive least square method[J]. Transactions of Electrical Technology, 2016, 31(17): 161-169. |
| [7] |
杨明, 屈婉莹, 陈扬洋, 等. 基于变周期递推最小二乘法与卡尔曼观测器的伺服系统在线惯量辨识[J]. 电工技术学报, 2018, 33(S2): 367–376.
|
| [8] |
侯利民, 徐越, 何佩宇, 等. 辨识转动惯量扰动观测器的PMSM滑模控制[J]. 电机与控制学报, 2020, 24(9): 165–172.
|
| [9] |
王少威, 万山明, 周理兵, 等. 利用蚁群算法辨识PMSM伺服系统负载转矩和转动惯量[J]. 电工技术学报, 2011, 26(6): 18–25.
|
| [10] |
CHEN Yang yang, YANG, Ming, JIANG Long, et al. A moderate online servo controller parameter self-tuning method via variable period inertia identification. IEEE Transactions on power Electronics, 2019, 34(12), 12165–1180.
|
| [11] |
季画, 王爽, 黄苏融. 永磁同步电机转动惯量的自适应辨识方法研究[J]. 华中科技大学学报(自然科学版), 2015, 43-(S1): 122–126.
|
| [12] |
NIU Li, XU Dian guo, YANG Ming, et al. On-line inertia identification algorithm for pi parameters optimization in speed loop[J]. IEE. E Transactions on Power Electronics, 2015, 30(2): 849-859. DOI:10.1109/TPEL.2014.2307061 |
| [13] |
梁骄雁, 胡育文, 鲁文其. 基于梯度算法的永磁伺服系统惯量辨识性能研究[J]. 航空学报, 2011, 32(3): 488–496.
|
 2024, Vol. 46
2024, Vol. 46
