主动声呐进行目标探测的过程中,受到海洋背景噪声以及混响信号的干扰较大,尤其是在浅海环境下混响是主要的背景干扰。而且混响形成机理复杂,在时频域都与目标回波具有极强的耦合性,导致信混分离困难,限制了目标探测的性能,这更使得在强海水混响背景下,水中探测受到极大的限制[1-2]。
近年来,国内外大量学者进行混响抑制技术的研究,并取得了大量研究成果。Cox等[3]通过海洋实验证明了几何梳状谱信号在浅海混响条件下有着较好的检测信号的能力。姚东明等[4]基于几何梳状谱信号改进了设计方法,提出了三元组对几何梳状谱信号,相比SFM和GC信号提高了发射效率。S Kay等[5]采用AR预白化处理方法,在满足一定条件下,将混响滤波成白噪声,从而进行匹配滤波获得较高的增益,更有效地对目标回波进行检测;舒象兰等[6]在预白化的基础上,将接收信号进行二分奇异值分解,从而达到更好的混响抑制效果;张宗堂等[7]利用LFM信号在FRFT域的聚集性,将截取后的接收信号与发射信号进行峰值匹配从而提取回波信号起始位置,但是该方法在信混比低于−10.4 dB时便不再适用;石亚莉[8]利用滑动窗对接收到的信号进分数阶傅里叶变换旋转角度扫描,并以此确定目标所在段,但是该方法需要在时频二维进行搜索滤波,大大增加了计算量。
基于匹配滤波器的频域自适应线谱增强(FDAMF)较传统的匹配滤波器(MF)抗噪性能更好,在低信噪比下检测能力更强,更加适用于工程应用[9]。但是,在强混响背景下该检测器检测性能急剧下降,未能实现目标有效检测。分数阶傅里叶变换(FRFT)是一种新兴的时频分析工具,它不同于传统的傅里叶变换,在分数阶傅里叶变换域选取合适的分数阶数时,线性调频信号将表现为冲激信号[10 − 12]。本文正是利用线性调频信号在FRFT域的聚集性,将分数阶傅里叶变换与FDAMF技术相结合,从而实现低信混比下的目标检测。
1 分数阶傅里叶变换
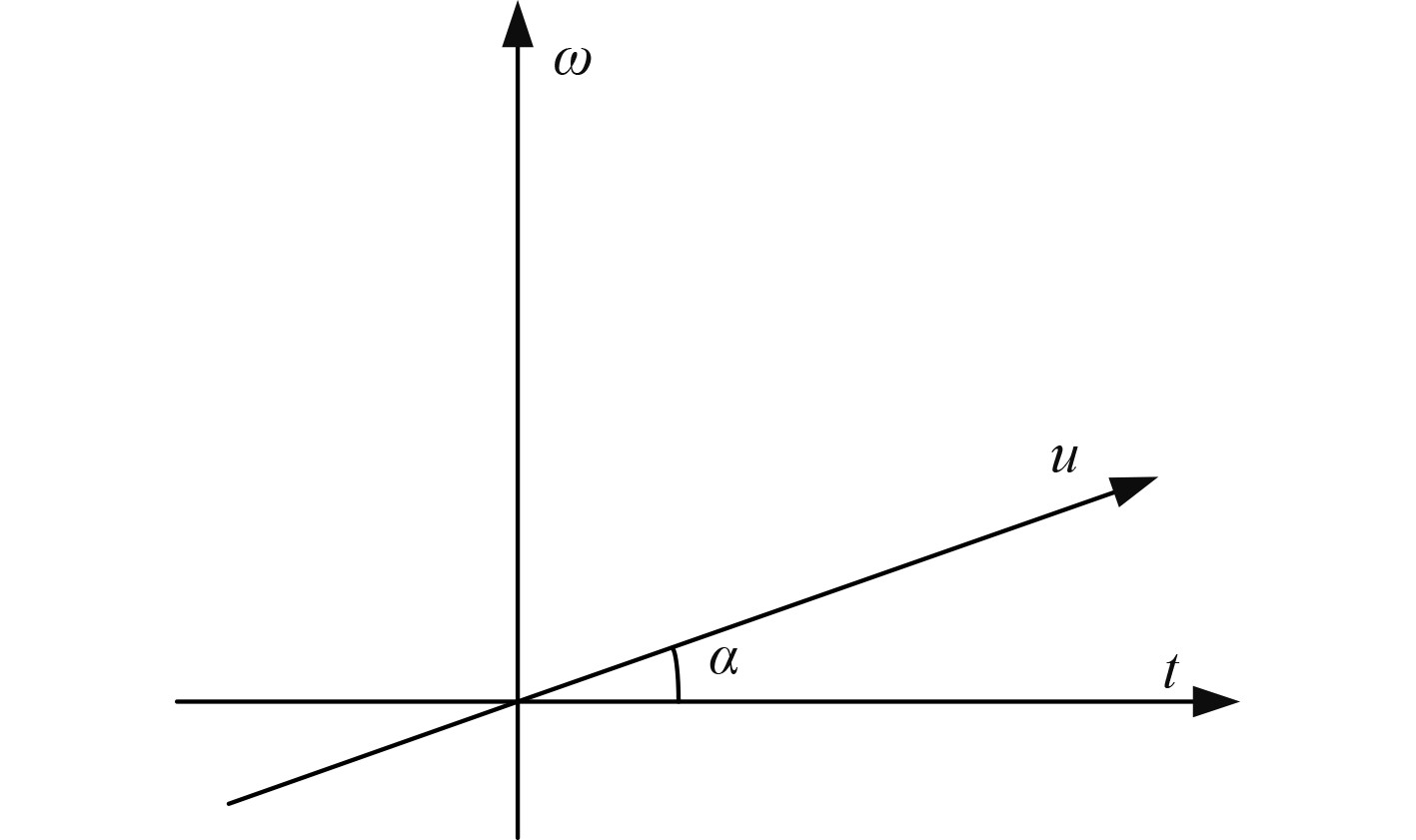
|
图 1 分数阶傅里叶变换示意图 Fig. 1 Schematic diagram of the fractional Fourier transform |
时域信号
| $ {X_p}(u) = {F_p}[x(t)] = \int_{ - \infty }^\infty {x(t){K_p}} (t,u){\mathrm{d}}t。$ | (1) |
式中:
| $\begin{split}& {K_p}(t,u) =\\ &\left\{ \begin{array}{l} {\sqrt {(1 - j\cot \alpha )} {e^{j\text{π} [({t^2} + {u^2})\cot \alpha - 2tu\csc \alpha ]}}},{\alpha \ne n\text{π} } ,\\ {\delta (t - u)},{\alpha = 2n\text{π} },\\ {\delta (t + u)},{\alpha = (2n \pm 1)\text{π} }。\end{array} \right. \end{split}$ | (2) |
式中,
即
| $\begin{split} &{X_p}(u) =\\ & \left\{ {\begin{array}{l} {\int_{ - \infty }^\infty {x(t)\sqrt {(1 - j\cot \alpha )} {e^{j\text{π}[({t^2} + {u^2})\cot \alpha - 2tu\csc \alpha ]}}} },{\alpha \ne n\text{π} },\\ {x(t)},{\alpha = 2n\pi },\\ {x( - t)},{\alpha = (2n \pm 1)\text{π}} 。\end{array}} \right. \\[-1pt]\end{split}$ | (3) |
FRFT是一种广义的傅里叶变换,可以解释为将信号的时频平面旋转任意角度
FRFT的逆变换定义为:
| $ x(t) = \int_{ - \infty }^\infty {{X_p}(u){K_{ - p}}} (t,u){\rm{d}}u 。$ | (4) |
设LFM信号中心频率为6 kHz,带宽2 kHz,采样频率60 kHz,脉宽30 ms。该信号经过分数阶傅里叶变换仿真,在分数阶域上的分布如图2所示。
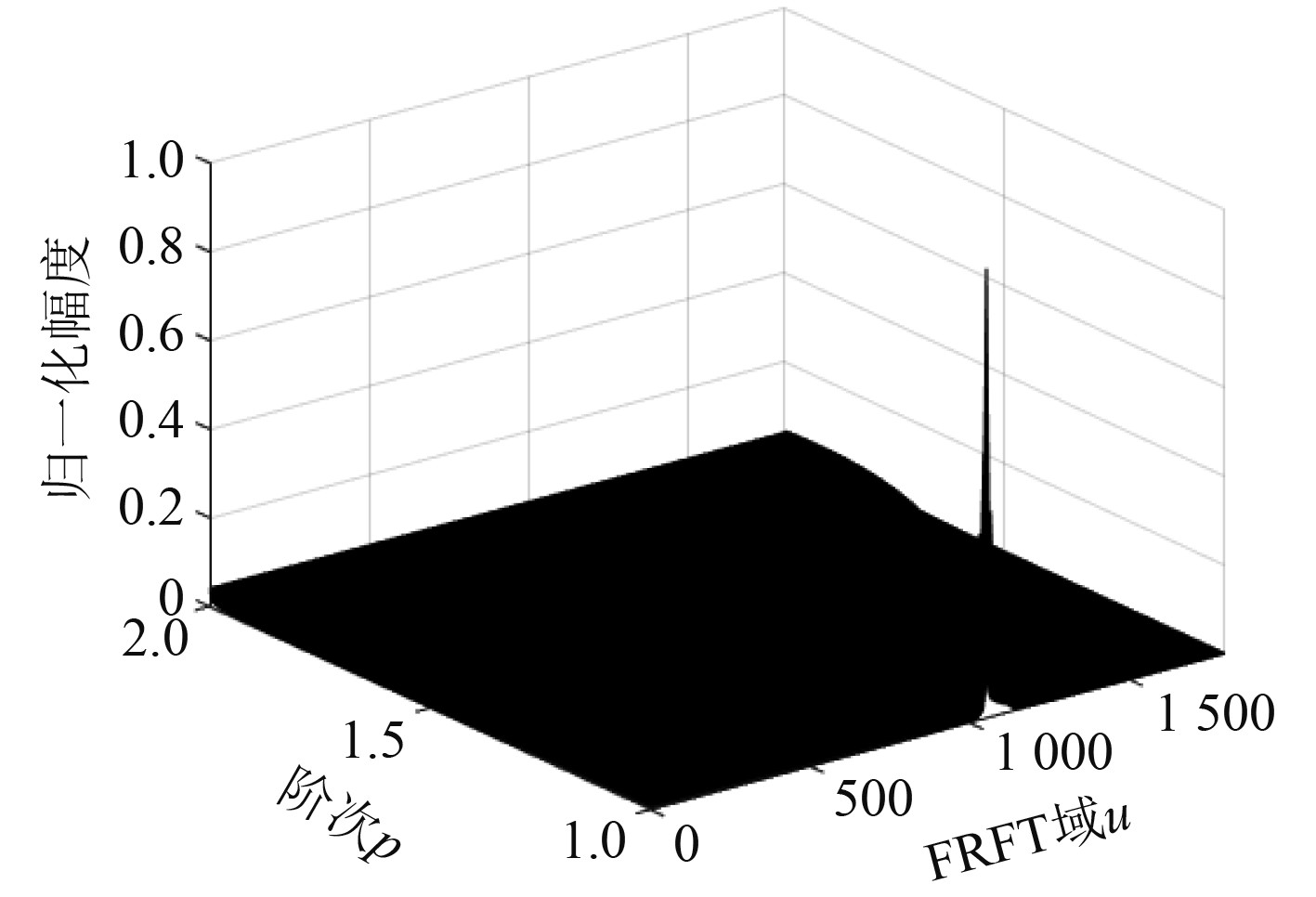
|
图 2 原始信号分数阶傅里叶变换图 Fig. 2 Fractional Fourier transform diagram of the original signal |
频域自适应匹配滤波器(FDAMF)将自适应线谱增强器(ALE)与匹配滤波器相结合,可显著提升主动声呐的检测性能。
设匹配滤波器输入的时域信号为,
| $ x(t) = s(t) + n(t) 。$ | (5) |
式中:
| $ X(\omega ) = S(\omega ) + N(\omega )。$ | (6) |
式中:
对信号进行频域匹配滤波后得到的输出
| $ Y(\omega)=H(\omega)X(\omega)=H(\omega)S(\omega)+H(\omega)N(\omega)。$ | (7) |
若在
| $ H(\omega)=kS^*(\omega)e^{-j\omega t_0}。$ | (8) |
有:
| $\begin{split} Y(\omega)=& kS(\omega)S^*(\omega)e^{-j \omega t_0}+kN(\omega)S^*(\omega)e^{-j \omega t_0}=\\& k|S(\omega)|^2 e^{-j \omega t_0}+kN(\omega)S^*(\omega)e^{-j \omega t_0} 。\end{split}$ | (9) |
可以看出,目标信号在频域经过匹配滤波后的输出
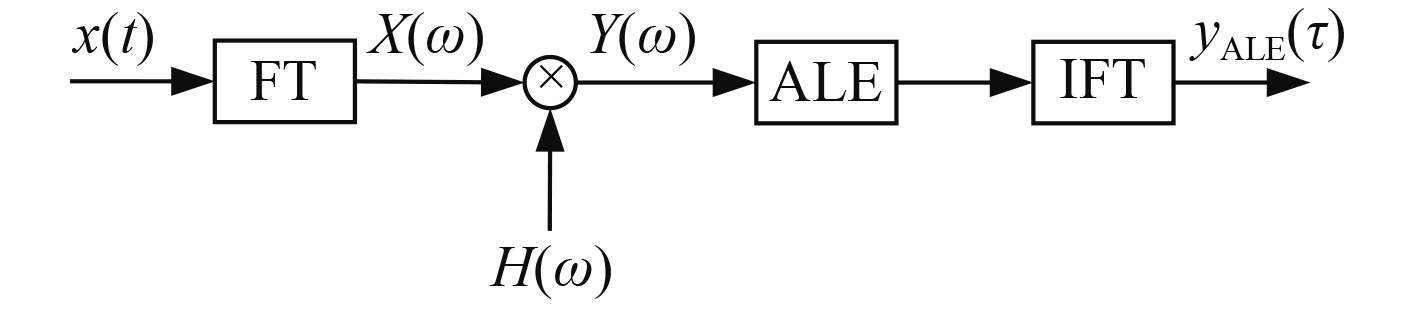
|
图 3 频域自适应匹配滤波器原理框图 Fig. 3 Block diagram of frequency domain adaptive matching filter |
将匹配滤波器的频域输出
下面通过仿真验证算法的性能。发射信号为LFM信号,中心频率为6 kHz,带宽为2 kHz,脉宽为30 ms,采样频率为60 kHz,接收信号时延值为15 ms。图4为在信噪比为−10 dB条件下传统匹配滤波器MF和本文所采用检测器FDAMF对LFM信号的检测结果。可以看出,在−10 dB的信噪比条件下,2种信号检测方法虽然都可以准确的检测到目标信号,但FDAMF处理增益明显高于MF。后文将FDAMF与混响抑制技术相结合,从而完成目标检测。
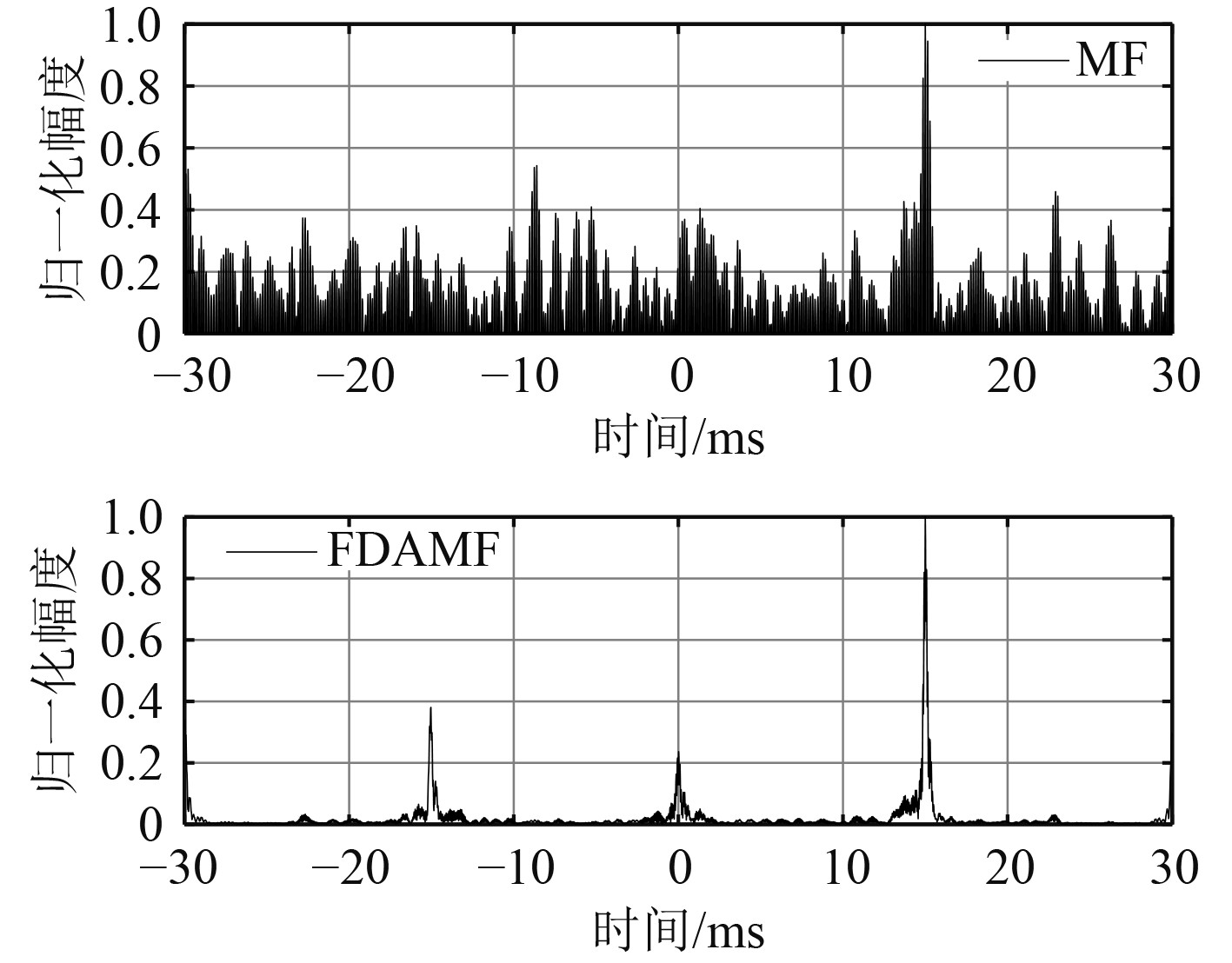
|
图 4 SNR=−10 dB时匹配滤波归一化结果 Fig. 4 When SNR=−10 dB, the result of filtering normalization is matched |
当发射信号
| $ s(t)=\left\{\begin{array}{lc}A\exp(j(2{\text{π}} f_0t+k{\text{π}} t^2)),t\in[0,T],\\ 0,其他。\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{array} \right. $ | (10) |
式中:
接收信号可表示为:
| $ y(t)=a(t)+ \omega (t) +n(t) 。$ | (11) |
式中:
本文考虑声源与目标相对静止或目标运动速度很小的情况,即忽略多普勒影响。可以认为目标回波仍保持有原有线性调频性,只是幅度和时延发生了变化。但是混响由于形成机理复杂,一般情况下不再具备较明显的线性调频性。由于LFM信号在合适的分数阶傅里叶阶数下FRFT域具有很好的能量聚集性,这样只需要对接收信号采取滑动窗截取,再进行
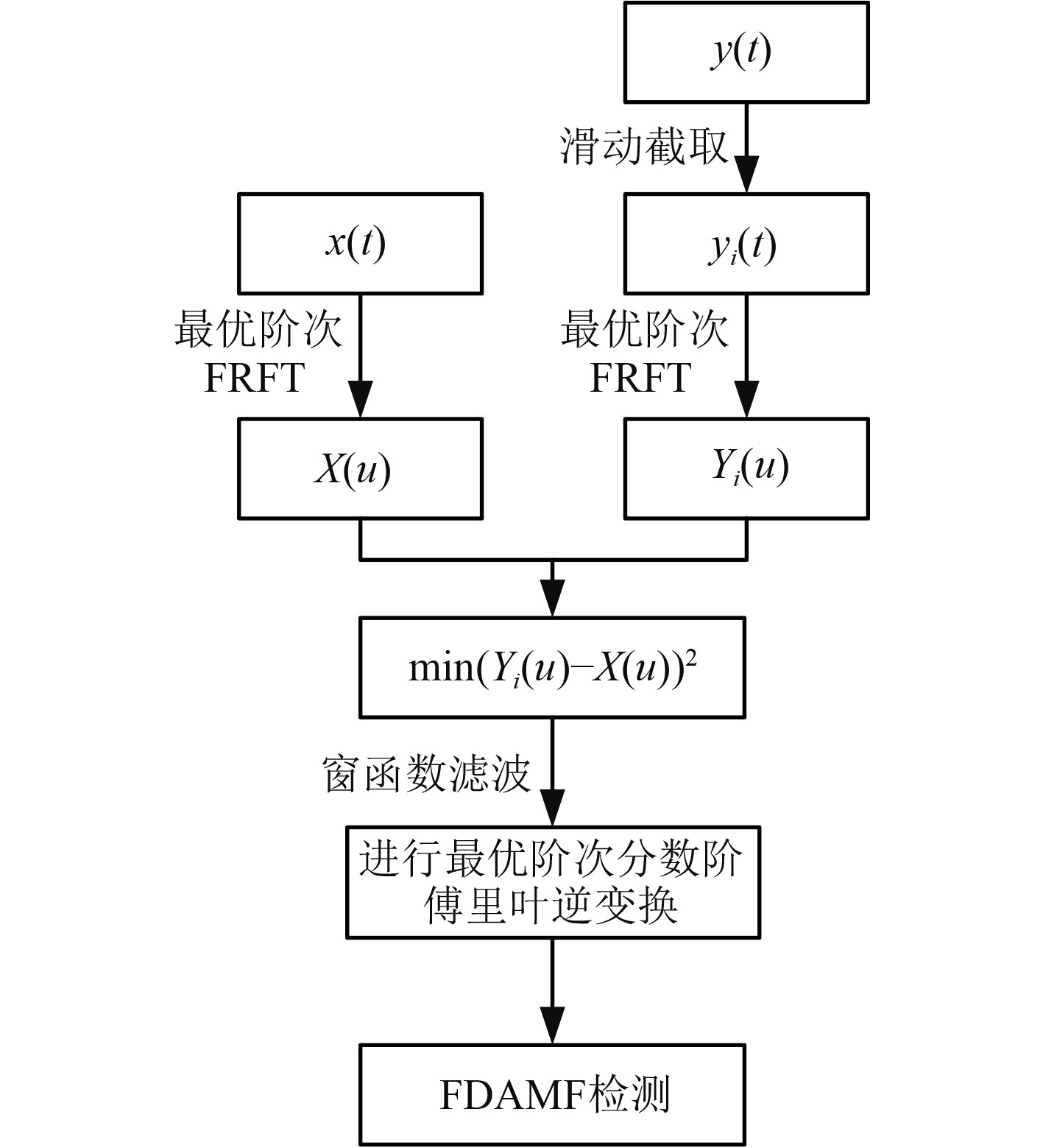
|
图 5 算法流程图 Fig. 5 Algorithm flow chart |
具体实现步骤如下:
步骤1 对接收到的总信号进行滑动窗(宽度为T,滑动步长为1)截取,截取后的信号做最优阶次的FRFT,得到u域图;
步骤2 对参考信号做最优阶次的FRFT,得到u域图;
步骤3 求取各段截取信号与参考信号u域图误差平方和;
步骤4 在误差值最小处利用窗函数进行u域的带通滤波,表达式如下:
| $ {Y'_i}(u)={Y_i}(u) M(u)。$ | (12) |
式中:
步骤5 对步骤4中得到的信号进行最优阶次的分数阶傅里叶逆变换,并对混响抑制后的信号进行频域自适应匹配滤波器处理,从而完成目标检测。
4 计算机仿真通过仿真验证算法在低信混比下的性能。发射信号为LFM信号,中心频率为6 kHz,带宽为2 kHz,脉宽30 ms,采样频率60 kHz。对该信号进行分数阶傅里叶变换,可以得到最优阶次FRFT域图,即可知最优阶次为p=1.02。
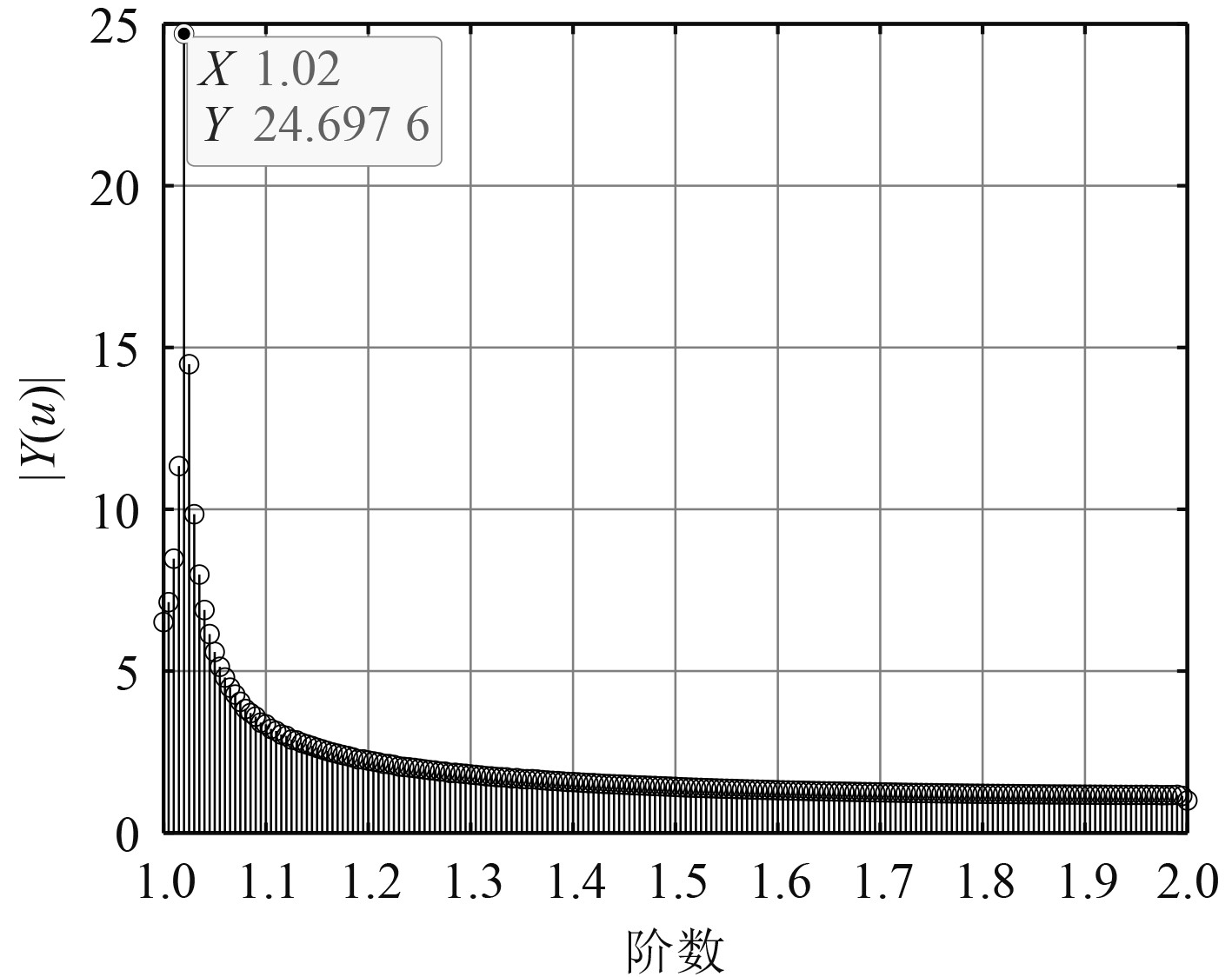
|
图 6 LFM信号的最优阶次FRFT域图 Fig. 6 The optimal order FRFT domain graph of LFM signal |
混响信号的仿真采用单元散射模型[14],仿真条件如下:忽略多普勒的影响,海深100 m,声呐到海底的距离为50 m,声速1500 m/s,单位面积的散射体数量0.9。LFM信号参数如上,混响信号采样起始时间为0.03 s,结束时间为0.3 s。混响信号的时域图和频域图如图7所示。
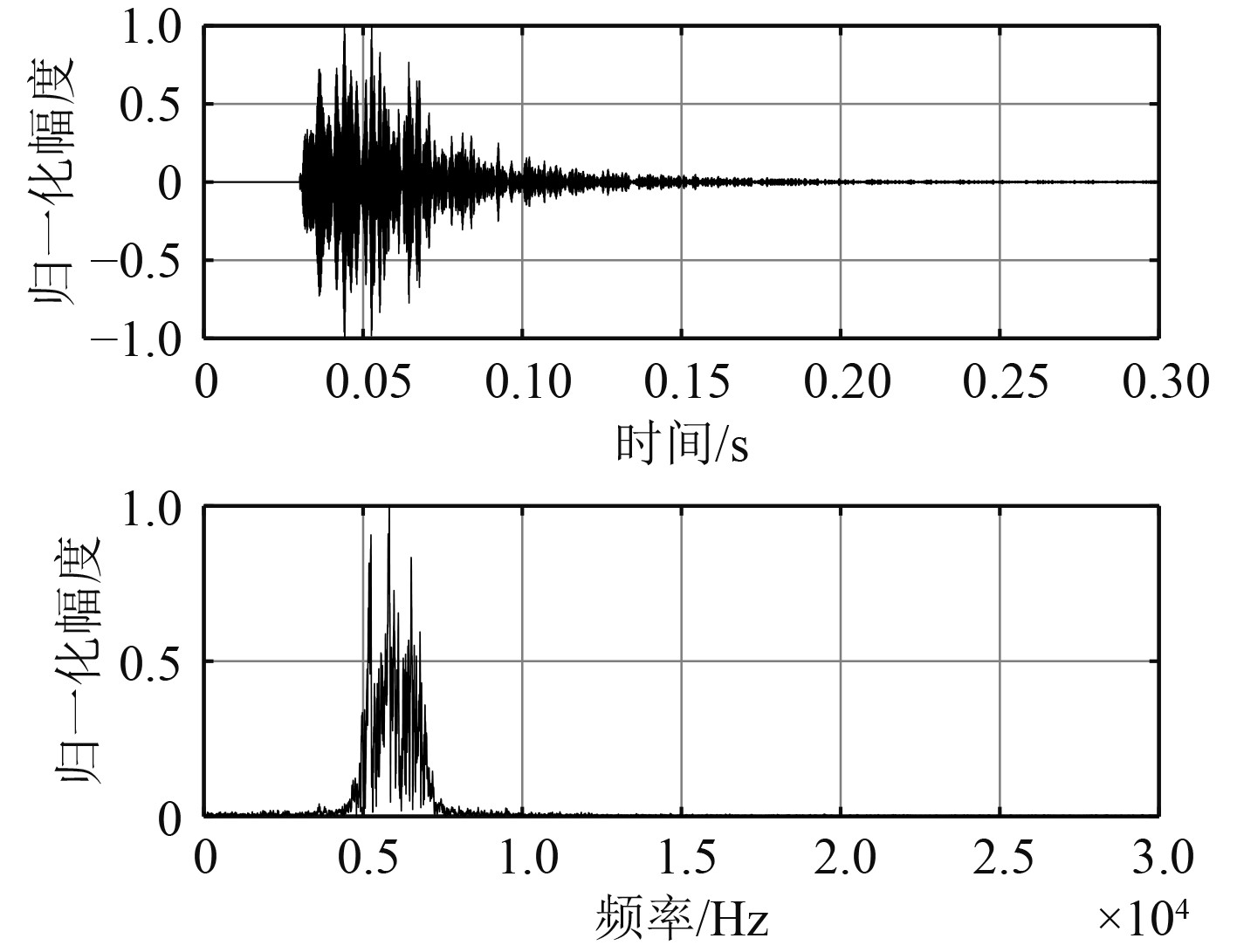
|
图 7 混响信号时域图和频域图 Fig. 7 Time domain and frequency domain of reverberation signal |
在混响信号0.1 s处加入LFM信号,信混比SSR=−15 dB,总接收信号的时域图和频域图如图8所示。
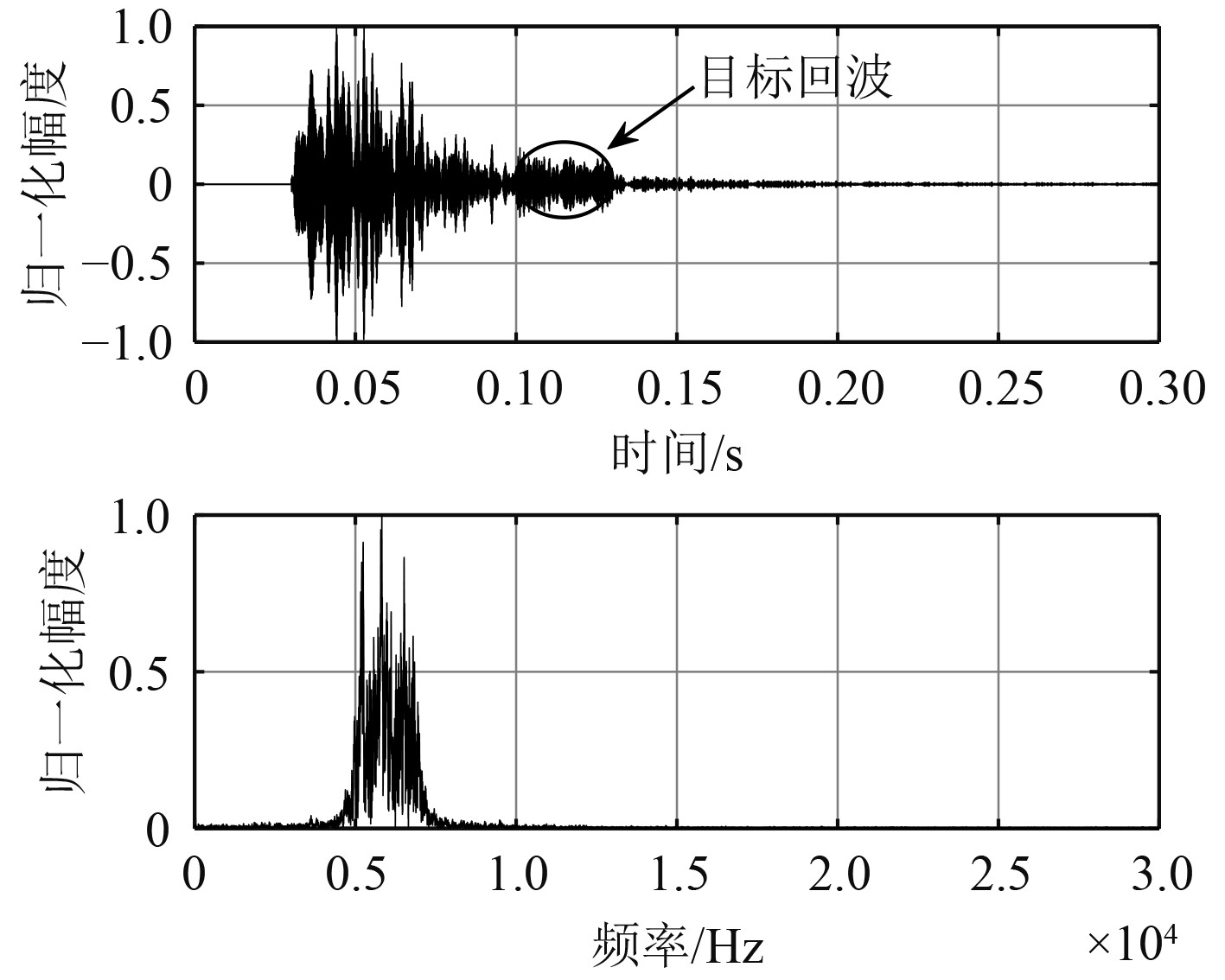
|
图 8 总接收信号时域图和频域图 Fig. 8 Time domain diagram and frequency domain diagram of total received signal |
可以看出,混响信号无论在时域还是频域都与目标回波具有较强的耦合性,即无法通过简单的时频分析进行混响信号的抑制。
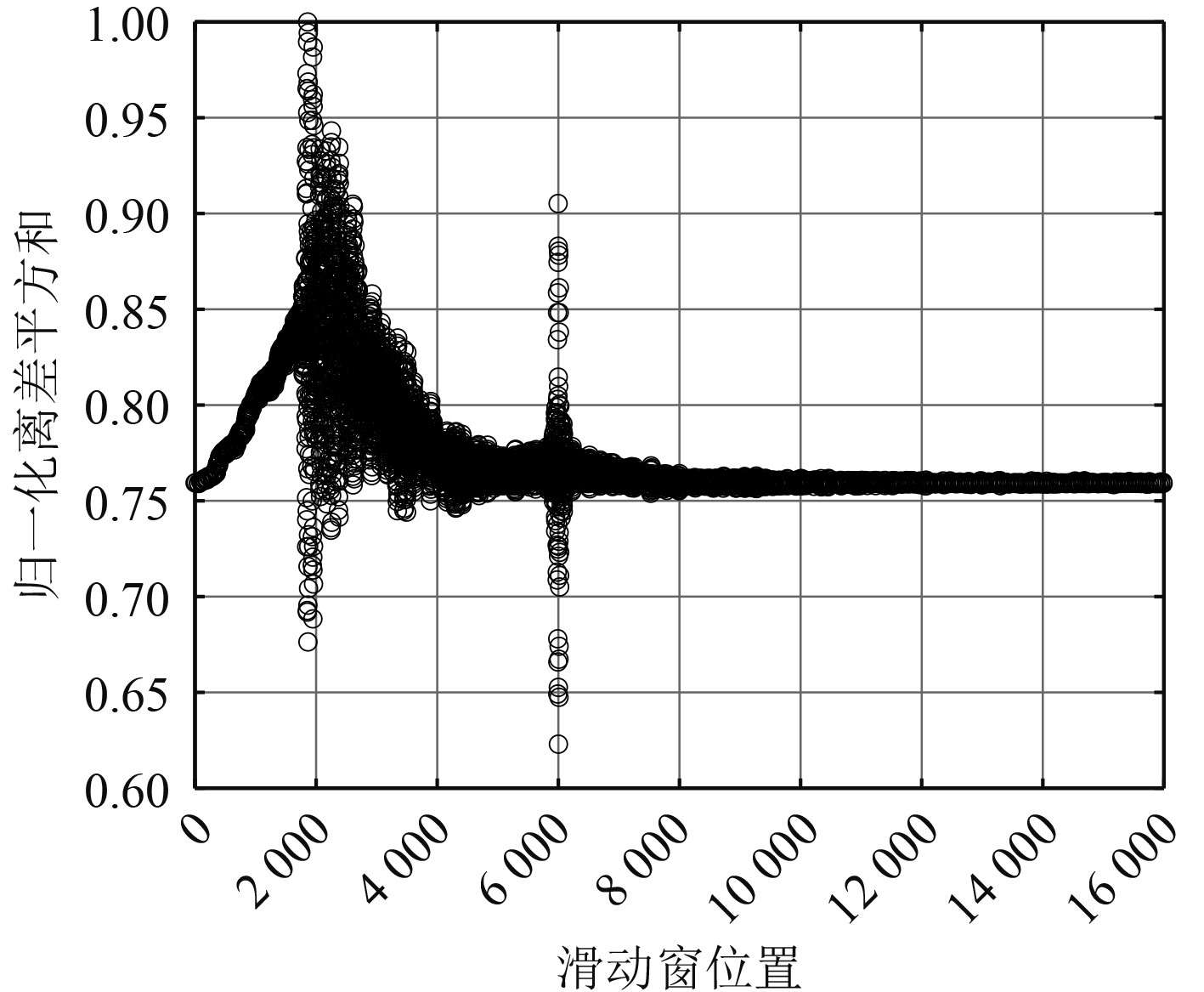
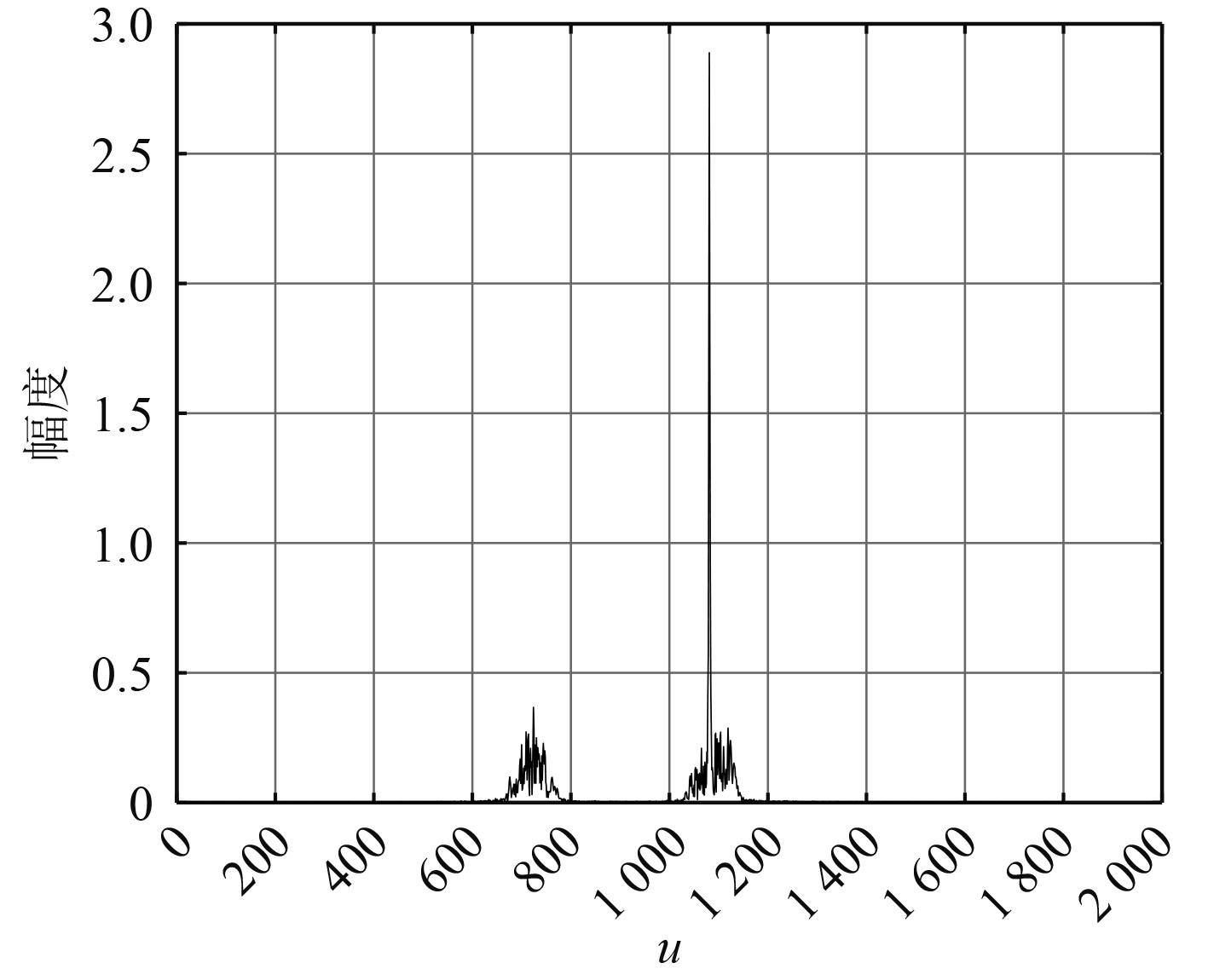
利用本文提出的基于FRFT的频域自适应匹配滤波技术进行目标检测。首先利用滑动窗对接收信号进行截取,得到滑动过程中时频离差平方和,结果如图9所示。可知,在接收信号起始端向后滑动6000个点时,与参考信号最优阶次FRFT最为接近,对该位置处的接收信号做最优阶次FRFT,结果如图10所示。
|
图 9 滑动过程中时频图误差值 Fig. 9 Time frequency graph error value during sliding |
|
图 10 混响背景下信号最优阶次时频图 Fig. 10 Optimal order time-frequency diagram of signal in reverb background |
选取带通滤波器如图11所示。
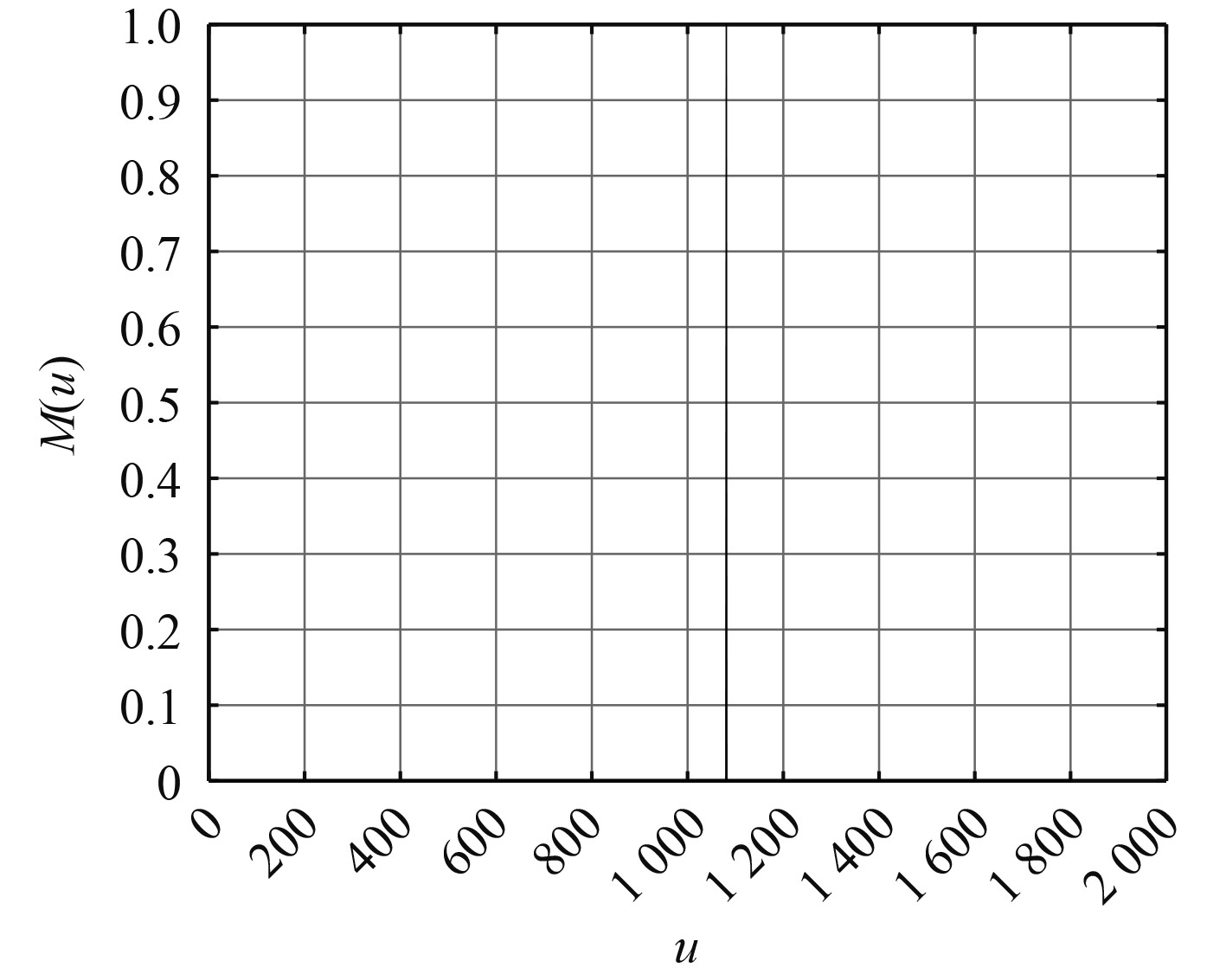
|
图 11 带通滤波器 Fig. 11 Bandpass filter |
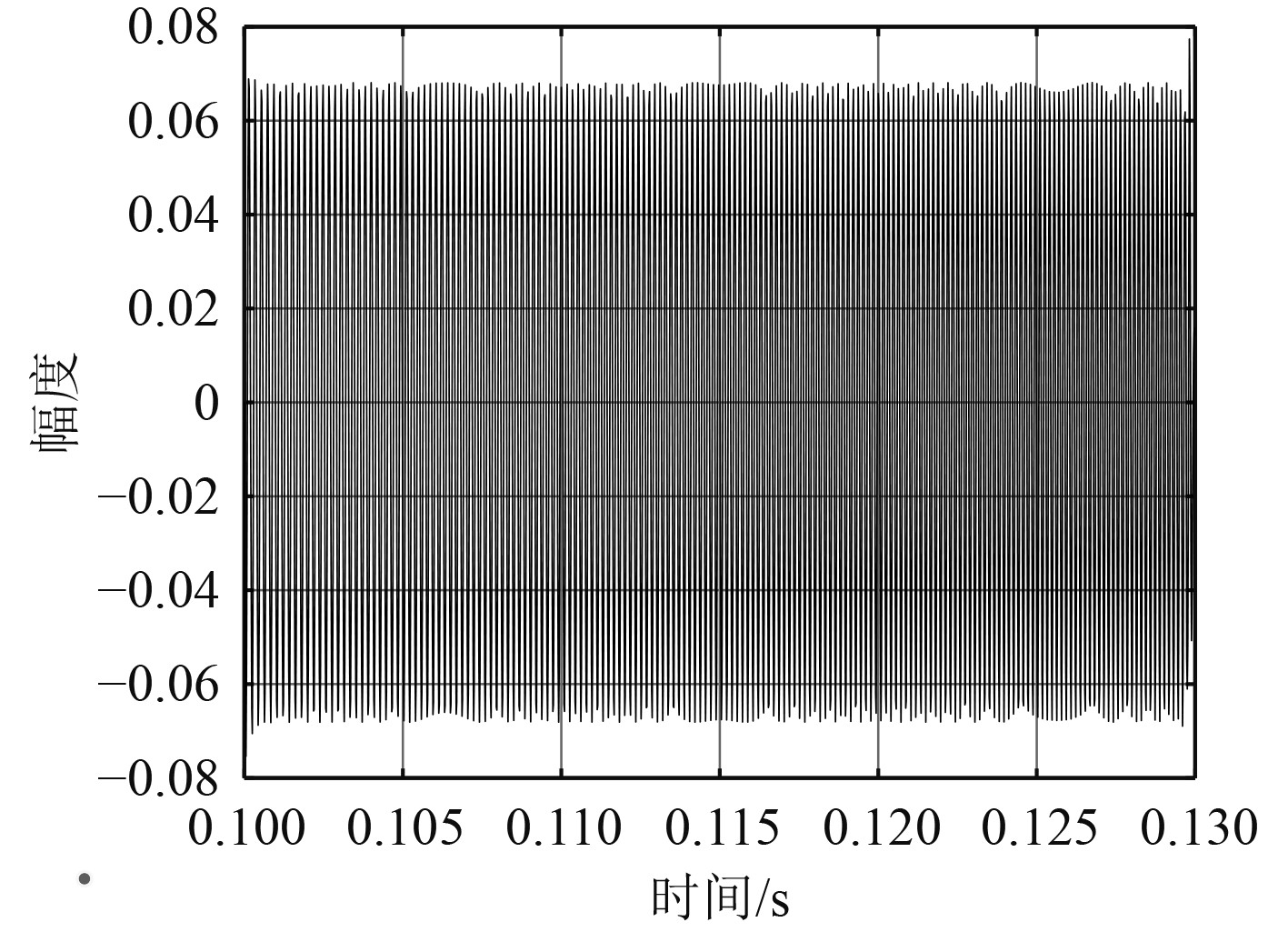
经过带通滤波器处理后,得到该部分信号的时域波形如图12所示,可见混响抑制效果较好。
|
图 12 混响抑制后LFM信号 Fig. 12 LFM signal after reverb suppression |
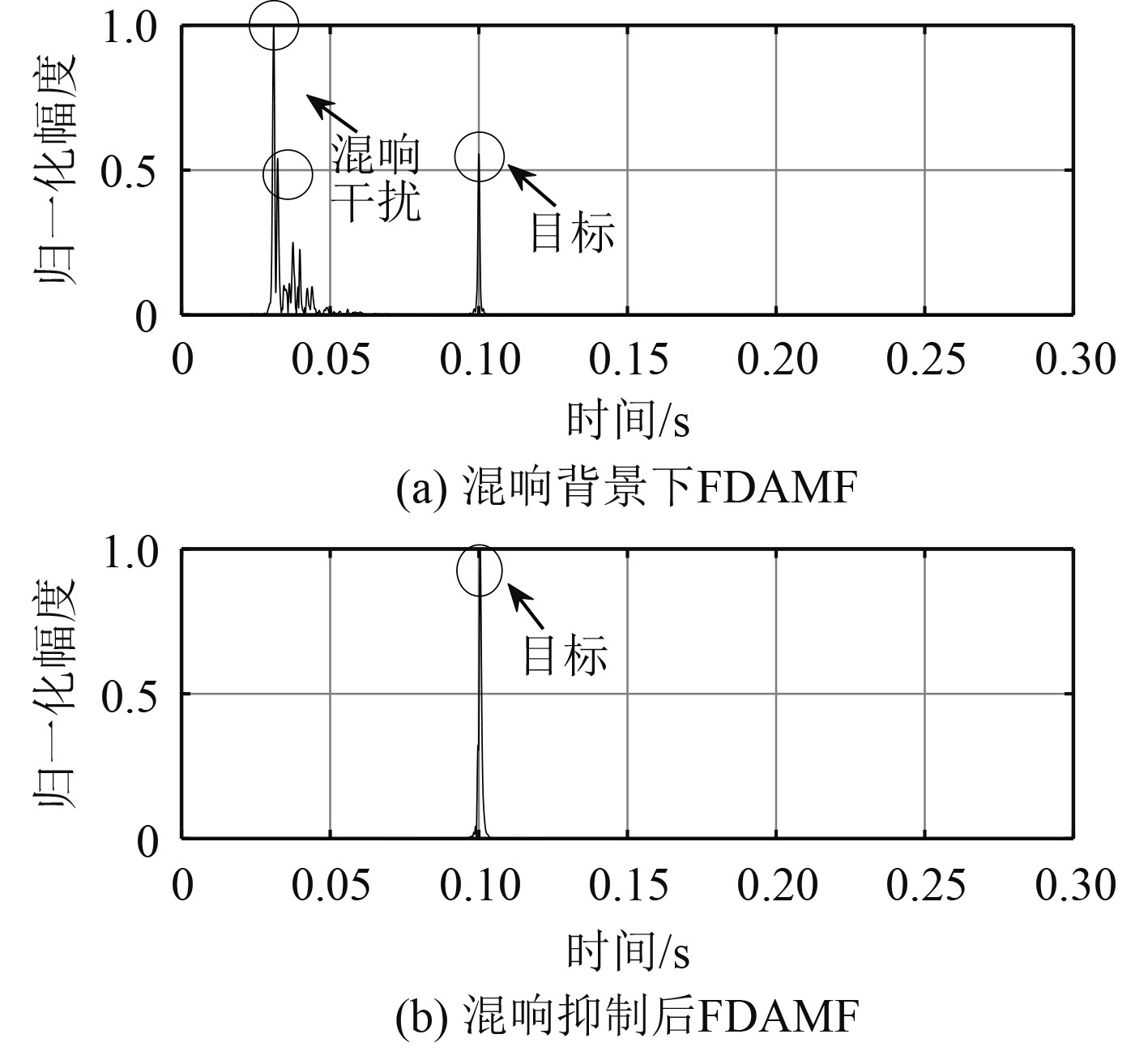
对混响抑制前后接收信号做FDAMF结果如图13所示。可以看出本文所提算法有效抑制了混响,成功检测到目标。
|
图 13 混响抑制前后FDAMF图 Fig. 13 FDAMF before and after reverberation suppression |
本文研究了一种基于FRFT的频域自适应匹配滤波检测方法,并通过仿真验证了该方法的性能。相对于传统的匹配滤波检测,该方法能够在强混响背景下完成目标回波的检测,大幅度降低了混响对于主动声呐检测的影响。且分数阶傅里叶变换和其他时频分析算法相比,计算量和复杂度更低,在需要低信混比目标检测的情况下,该算法的实时处理性能更好。由于分数阶傅里叶变换理论本身的局限性,该方法在声呐发射信号为线性调频信号情况下效果最好。
| [1] |
郝程鹏, 施博, 闫晟, 等. 主动声呐混响抑制技术与目标检测技术[J]. 科技导报, 2017, 35(20): 102-108. |
| [2] |
兰同宇, 周胜增. 一种级联型自适应滤波器的混响抑制技术[J]. 舰船科学技术, 2021, 43(3): 130-133. |
| [3] |
COX H, LAI H. Geometric comb waveforms for reverberation suppression[C]//Proceeding of IEEE, 1995, 154(6): 347-352.
|
| [4] |
姚东明, 蔡志明. 主动声呐梳状谱信号研究[J]. 信号处理, 2006(2): 256-259. |
| [5] |
KAY S, SALISBURY J. Improved active sonar detection using autoregressive prewhiteners[J]. Journal of the Acoustical Society of America. 1900, 87(4): 1603−1611.
|
| [6] |
舒象兰, 孙荣光, 马鑫. 强混响背景下LFM信号回波检测[J]. 电讯技术, 2016, 56(1): 82-87. DOI:10.3969/j.issn.1001-893x.2016.01.015 |
| [7] |
张宗堂, 杨锡铅, 戴卫国. 混响背景下回波信号起始位置提取[J]. 舰船电子工程, 2014, 11: 73-76. |
| [8] |
石亚莉. 多基地混响模拟及抑制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [9] |
赵智姗. 基于匹配滤波器的频域自适应线谱增强技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [10] |
HUANG Xiang, ZHANG Linrang, ZHANG Juan, et al. Efficient angular chirp-Fourier transform and its application to high-speed target detection[J]. Signal Processing, 2019, 164: 234-248. DOI:10.1016/j.sigpro.2019.06.011 |
| [11] |
MIAO Hongxia, ZHANG Feng, TAO Ran. Fractional Fourier analysis using the Möbius inversion formula[J]. IEEE Transactions on Signal Processing, 2019, 67(12): 3181-3196. DOI:10.1109/TSP.2019.2912878 |
| [12] |
徐伟, 许传, 马艳秋, 等. 一种基于分数阶傅里叶变换的主动声自导回波检测方法[J]. 舰船科学技术, 2022, 44(2): 161-165. |
| [13] |
刘利民, 李豪欣, 李琦, 等. 基于分数阶傅里叶变换的低信噪比线性调频信号参数快速估计算法[J]. 电子与信息学, 2021, 43(10): 2798-2804. |
| [14] |
董仲臣, 李亚安, 金彦丰. 鱼雷浅海海底混响建模及仿真[J]. 鱼雷技术, 2013, 21(2): 100-104. |
 2024, Vol. 46
2024, Vol. 46
