2. 大连理工大学 船舶工程学院,辽宁 大连 116024
2. School of Naval Architecture and Ocean Engineering, Dalian University of Technology, Dalian 116024, China
近年来,随着全球气候不断变暖,北极海冰逐渐融化,夏季出现可常规通航水域,北冰洋极有可能在2050年夏季出现无冰状态[1 − 2],这一改变将对全球经济的发展带来一定影响。北极地区自然资源丰富,其中探明的油储量占世界储量13%,天然气储量占世界储量30%,夏季无冰期的出现,将大大减小北极地区自然资源的开采难度。然而,对极地自然资源进行开发,电力供应问题亟待解决。北极地区生态环境脆弱[3],对工程装备环保要求较高,海上核电平台能够提供充足、稳定、环保的电力[4],是极区发展电力供应装备的首选,具有广阔的应用前景。
海上核电平台概念于20世纪50年代由美国最先提出[5],1963年,美军通过将MH-A核电装置设在自由号船舶上,实现了对巴拿马运河地区的电力供应,这是核电平台的首次尝试[6]。1971年4月,美国西屋电力公司(Westinghouse)进行海上核电平台技术经济研究[7]。2007年,俄罗斯进行了浮动核电站“罗蒙诺索夫”号的建造,该核电站可为俄罗斯远东地区进行功率75~300 MWe的电力供应[8],该核电平台已于2019年正式运行。2011年,法国企业DCNS提出Flexblue下沉式海上核电站概念[9],2014年,美国麻省理工学院(MIT)的Jacopo Buongiorno团队[10]与威斯康星大学和芝加哥桥铁公司研究人员共同提出了SPAR-TYPE核电平台。2021年,李红霞等[11]提出一种分离式冰区浮式核电平台概念并针对浮式核电平台的定位问题进行了研究。2022年,法国船级社与美国核电技术开发商ThorCon达成协议,对ThorCon的500 MW熔盐核电驳船进行技术认证和后续开发。2023年,韩国三星重工宣布,已完成海上浮式核电船“CMSR Power Barge”的概念设计,并获得美国船级社(ABS)的原则性认可(AIP)。
分离式核电平台有效降低了核心结构的运动响应,提高了核电平台的安全性[11],但由于增加了月池结构,月池内水体受到船体运动或外部载荷的激励,可能产生“活塞”运动和“晃荡”运动,对平台拖航阻力产生影响。Fukuda[12]在实验的基础上与理论相结合,提出一个计算月池水体“活塞”运动频率的经验公式。Faltinsen[13]通过将月池内流体简化为质量-弹簧系统,提出计算月池活塞式振荡固有周期的计算公式。Jiang等[14]从月池边缘形态及垂荡幅度两方面的变化出发,研究了月池内液体“活塞”运动特性。Yadav等[15]研究了月池位于钻井船不同位置时对钻井船阻力性能的影响,以及月池内的晃荡效应。谷家扬等[16]通过使用FINE MARINE软件研究了某钻井船“凸”字型月池内的流场特性,并分析了月池对该钻井船阻力性能的影响。Zhang等[17]通过实验及数值模拟的方法研究了流体运动模态不同时,月池对船舶阻力的影响,同时对月池内流体的运动特点进行了分析。Lee等[18]使用计算流体力学方法,研究在矩形月池不同位置增加隔板时的减阻效果。Liu等[19]通过实验及数值模拟的方法研究了在有壁面影响的情况下,环形月池对核能平台拖航阻力的影响。
传统的月池多为圆形或方形,对环形月池的研究较少。本文将对一种可在深水冰区作业的分离式海洋核能平台及一体式海洋核能平台进行介绍,采用流体动力学方法预报其拖航阻力,并分析“环形月池”对分离式极地海洋平台拖航阻力的影响。
1 极地海洋核能平台介绍分离式极地海洋核能平台由外部环境承载平台与内部核堆支撑平台两部分组成,其三维模型如图1所示,平台主要参数如表1和表2所示。

|
图 1 分离式海洋核能平台三维模型示意图 Fig. 1 Schematic diagram of the separated polar ocean nuclear energy platform |
|
|
表 1 环境载荷承载平台主要参数 Tab.1 Characteristics of the environmental load bearing platform |
|
|
表 2 核堆支撑平台主要参数 Tab.2 Characteristics of the nuclear reactor supporting platform |
外部环境载荷承载平台采用沙漏型设计,在有冰期,水线位于下椎体处,利用下椎体斜面,将冰的破坏模式从挤压破坏变为弯曲破坏,减小冰载荷对平台的影响。在无冰期,水线位于沙漏型腰线处,即上部结构和下部结构的连接面处,该处水线面面积最小,可有效减小波浪载荷,此外,上下椎体结构增加了平台垂荡阻尼,减小了平台垂荡运动幅值,使平台具有良好的水动力性能。核堆支撑平台根据麻省理工学院设计的OFNP-300[10]进行设计,核堆支撑平台为圆柱形外壳,将反应堆置于圆柱中心,可以通过多个外壳对其进行全方位的保护。中控室接近于圆柱体的三维中心,便于对核堆支撑平台进行检测与控制,并加强了对中控室的物理保护。核反应堆始终位于水线以下,海水不仅可以作为天然的散热器,对核堆进行降温,还能对辐射起到屏障作用。内外平台之间通过连接机构相连接,实现内外平台之间横摇、纵摇、垂荡三自由度运动解耦[20]。外部环境载荷承载平台使用多点系泊方式,约束平台在水平面内的运动(纵荡、横荡、首摇),内部核堆平台采用张力腿系泊方式,约束平台水平面外的运动(横摇、纵摇、垂荡),连接机构与系泊系统相配合,约束了核堆支撑平台六自由度运动,保障核堆支撑平台的安全。一体式极地海洋核能平台同样采用沙漏型设计,并使用多点系泊方式对平台进行约束,其三维模型如图2所示,主要参数如表3所示。

|
图 2 一体式海洋核能平台三维模型示意图 Fig. 2 Schematic diagram of the integrated polar ocean nuclear energy platform |
|
|
表 3 环境承载平台主要参数 Tab.3 Characteristics of the integrated polar ocean nuclear energy platform |
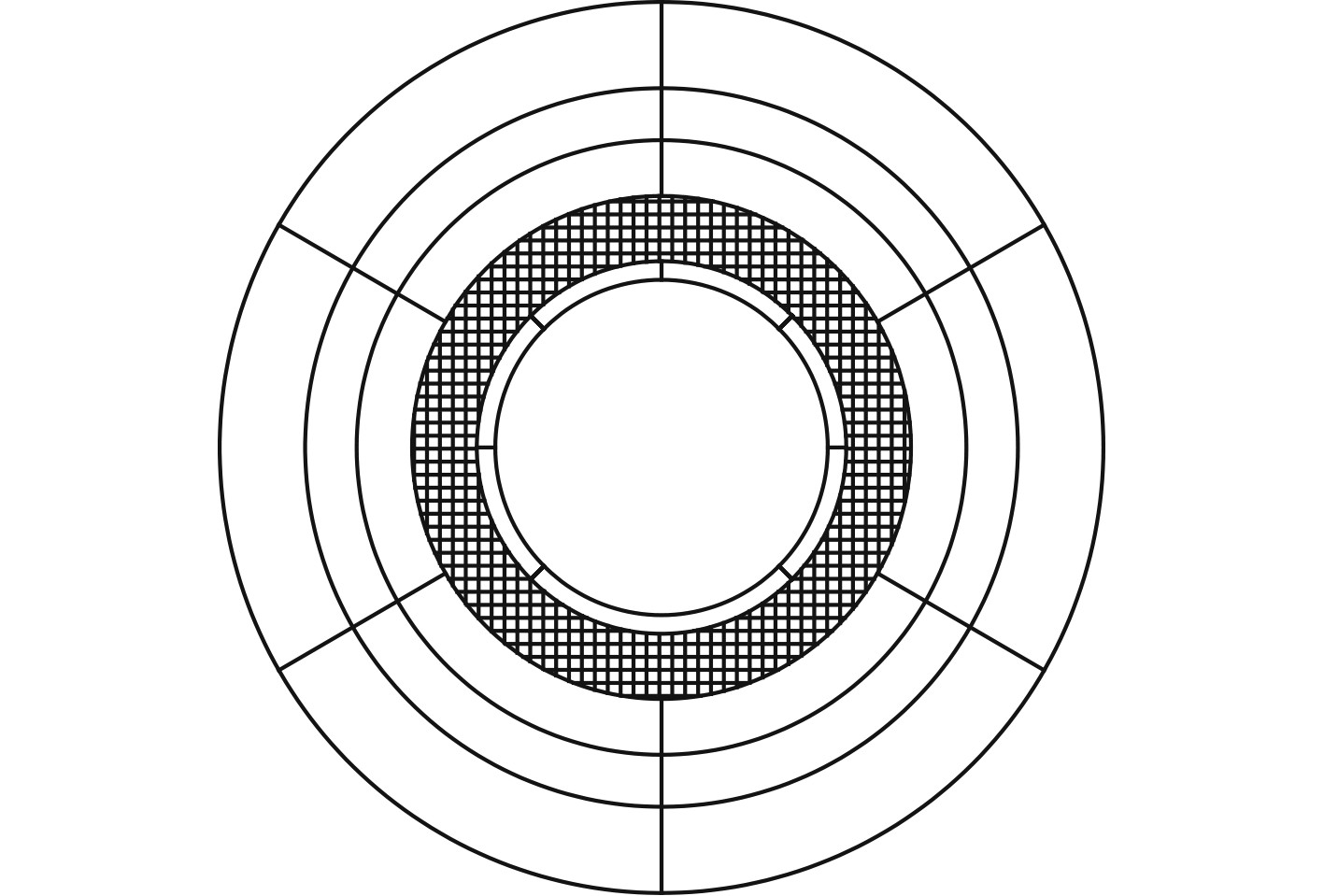
分离式极地海洋核能平台内外平台之间具有环形自由液面,称为“环形月池”,如图3中阴影部分所示,“环形月池”的存在将对平台的拖航阻力等性能造成影响。
|
图 3 环形月池示意图 Fig. 3 Schematic diagram of the annular moonpool |
对于非理想流体,流场的控制方程为连续性方程和动量方程,即:
连续性方程
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla {{\cdot}}\left( {\rho \overrightarrow u } \right) = 0,$ | (1) |
动量方程
| $ \frac{{\partial \overrightarrow u }}{{\partial t}} + \overrightarrow u {{\cdot}}\nabla \overrightarrow u = - \frac{1}{\rho }\left[ {\nabla P + \nabla {{\cdot}}\left[ \tau \right]} \right] + \overrightarrow G 。$ | (2) |
式中:t为时间;
在本文中,湍流模型选取SST
| $ \frac{{{\rm{d}}\rho k}}{{{\rm{d}}t}} = {P_k} - {\beta ^*}\rho \omega k + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right],$ | (3) |
| $ \begin{split} \frac{{{\rm{d}}\rho \omega }}{{{\rm{d}}t}} =\;& {P_\omega } - \beta \rho {\omega ^2} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] + \\ &2\rho \left( {1 - F{}_1} \right){\sigma _{{\omega _2}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}},\end{split} $ | (4) |
| $ {\mu _t} = \frac{{\rho {\alpha _1}k}}{{\max \left( {{\alpha _1}\omega ,S{F_2}} \right)}} ,$ | (5) |
| $ S = \sqrt {2{S_{{{ij}}}}{S_{{{ij}}}}},$ | (6) |
| $ {S_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right),$ | (7) |
| $ {F_2} = \tan h \left[ {\max {{\left( {\frac{{2\sqrt k }}{{{\beta ^*}\omega y}},\frac{{500\upsilon }}{{{y^2}\omega }}} \right)}^2}} \right],$ | (8) |
| $ {P_k} = {\tau _{ij}}\frac{{\partial {u_k}}}{{\partial {x_k}}},$ | (9) |
| $ {P_\omega } = {\tau _{{\text{ij}}}}\frac{{\rho \gamma {P_k}}}{{{\mu _t}}},$ | (10) |
| $ {\tau _{ij}} = 2{\mu _t}\left( {{S_{ij}} - \frac{1}{3}\frac{{\partial {u_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right) - \frac{2}{3}\rho k{\delta _{ij}} 。$ | (11) |
式中:
| $ {F_1} = \tan h \left\{ {\left\{ {\min \left[ {\max \left( {\frac{{\sqrt k }}{{{\beta ^*}\omega y}},\frac{{500\upsilon }}{{{y^2}\omega }}} \right),\frac{{4\rho {\sigma _{{\omega _2}}}k}}{{{D_{k\omega }}{y^2}}}} \right]} \right\}} \right\} ,$ | (12) |
| $ {D_{k\omega }} = \max \left( {2\rho {\sigma _{{\omega _2}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}},{{10}^{ - 20}}} \right)。$ | (13) |
式中:
本文选用VOF法追踪自由液面,该方法通过定义流体体积函数
| $ F=\left\{\begin{array}{lllllllllllll} 0,& 网格内无流体,\\ 0 < F < 1,& 网格内有流体\text{,}未被充满,\\ 1 ,& 网格被流体充满,\end{array} \right.$ | (14) |
| $ \frac{{\partial F}}{{\partial t}} + \left( {\overrightarrow u {{\cdot}}\nabla } \right)F = 0 。$ | (15) |
自由液面的法向方向可以通过F的梯度来决定,由此可以得到自由液面的位置和形状。
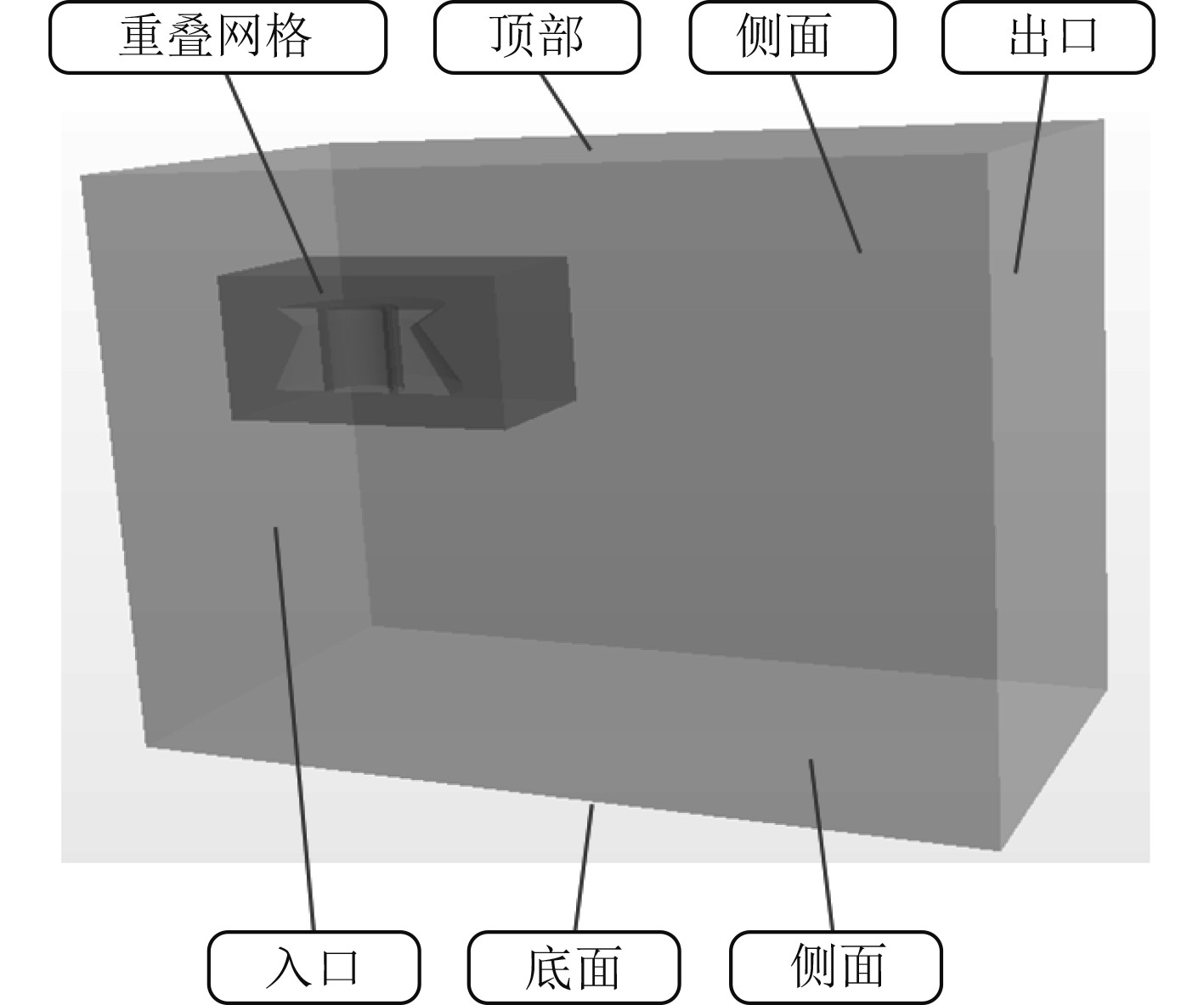
2.2 数值仿真模型本文使用STAR-CCM+建立数值模型并进行拖航阻力计算。由于平台关于x轴对称,计算中使用半个平台进行计算,本文缩尺比选为1∶20。在STAR-CCM+中的流体域如图5所示,流体域前端至平台前端距离为1倍平台直径,流体域后端至平台后端距离为3倍平台直径,流体域入口、顶部、底部均为速度入口,2个侧面为对称平面,出口为压力出口,对侧面及出口进行消波处理。由于本文使用的湍流模型为SST
|
图 4 数值水池示意图 Fig. 4 Schematic diagram of the virtual tank |
|
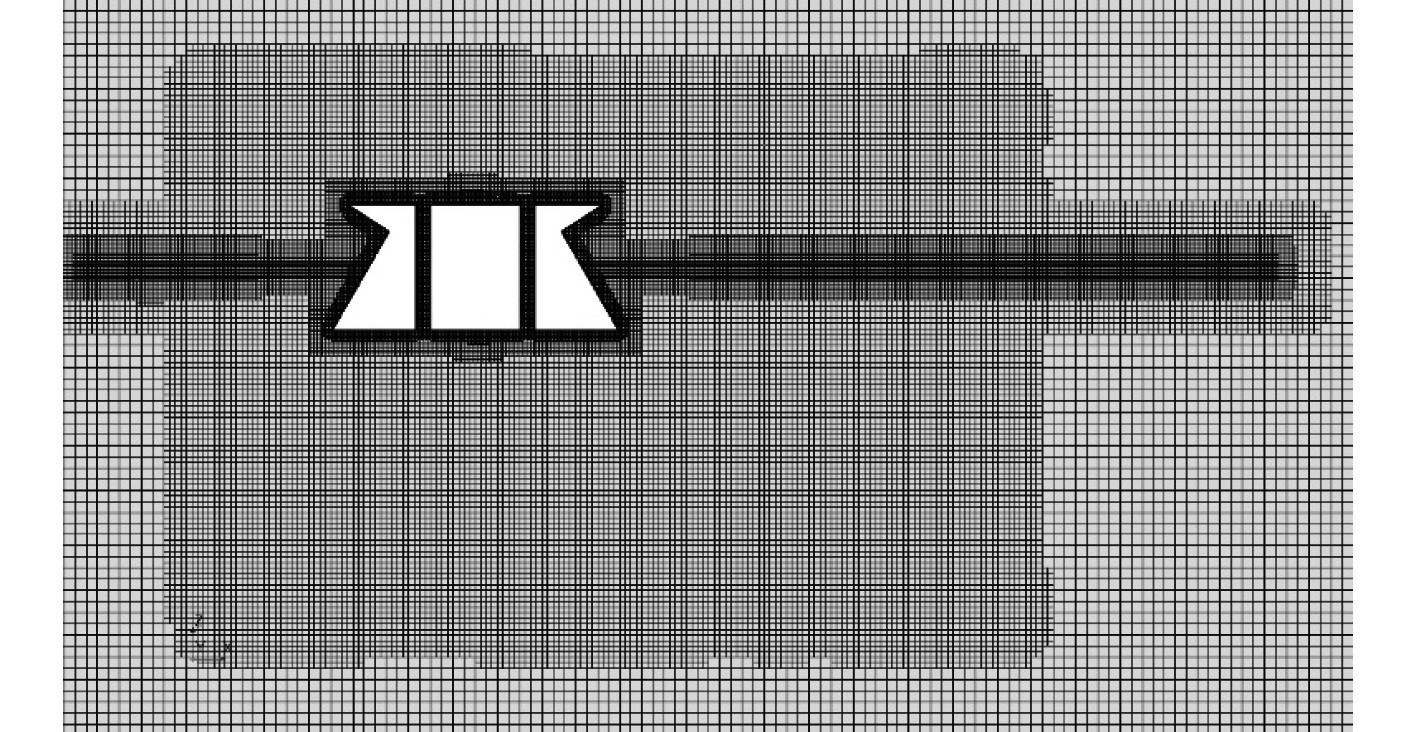
图 5 分离式海洋核能平台中纵剖面网格示意图 Fig. 5 Mesh distribution in central Longitudinal Section of the separated Polar ocean Nuclear Energy Platform |
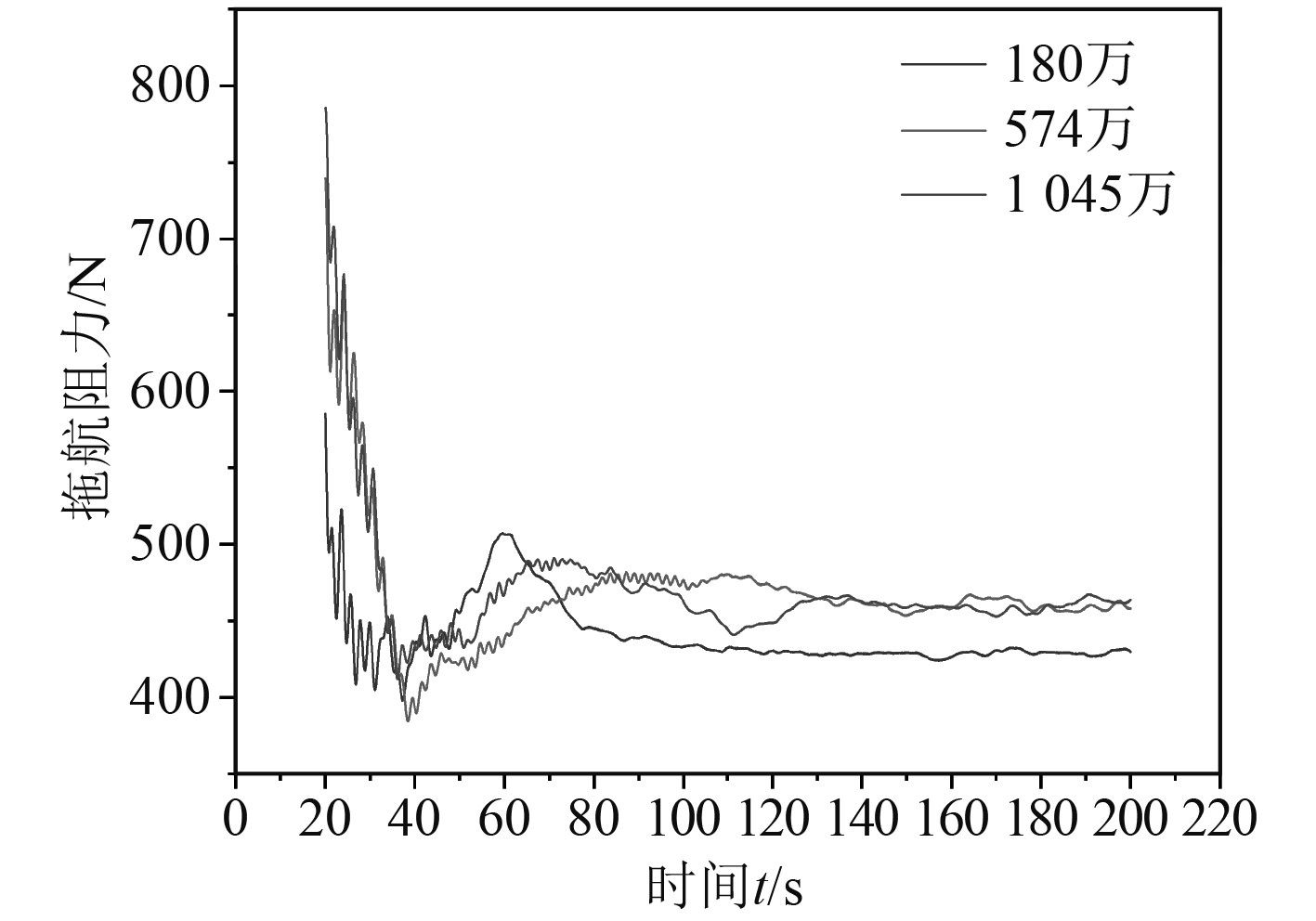
使用3种不同大小的网格进行网格无关性验证,其网格数量如表4所示。图5为分离式海洋核能平台中纵剖面网格示意图。为在保障计算精度的前提下节省计算成本,从流域外围到平台表面,网格逐渐缩小,在自由液面处采用细长网格。图6为使用3种网格计算实际平台拖航速度为5 kn时,核能平台的拖航阻力,计算其稳定阶段平台拖航阻力平均值可以得到,当网格数量为1045万时,分离式海洋核能平台拖航阻力为456.8 N,当网格数量为574万时,分离式海洋核能平台拖航阻力为458.2 N,当网格数量为187万时,分离式海洋核能平台拖航阻力为480.5 N,由此可见,574万网格及1045万网格计算所得平台拖航阻力十分接近,且满足工程要求,故为节省计算成本,以后选用574万网格进行计算。
|
|
表 4 网格无关性验证网格数量 Tab.4 Mesh resolution for convergence test |
|
图 6 分离式海洋核能平台总阻力时程曲线 Fig. 6 Time history curves of total towing resistance for the separated polar ocean nuclear energy platform |
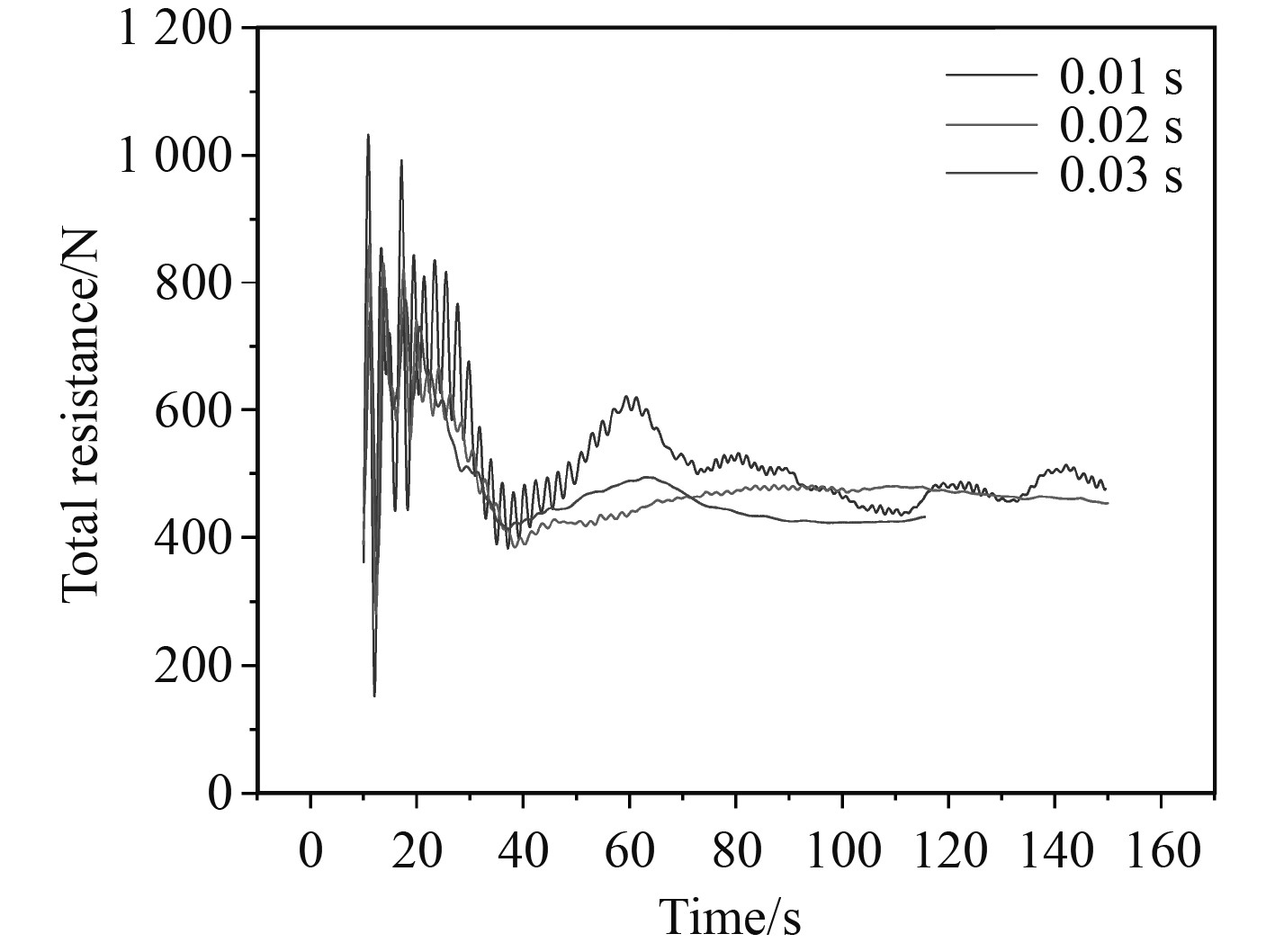
在进行时间步无关性验证时,时间步长选用0.01 s、0.02 s、0.03 s。当实际平台拖航速度为5 kn时,计算得到分离式海洋核能平台总阻力时程曲线如图7所示,计算稳定阶段平台拖航阻力平均值,可以得到:当时间步长为0.01 s时,核能平台拖航阻力为473.2 N,当时间步长为0.02 s时,核能平台拖航阻力为468.4 N,当时间步长为0.03 s时,核能平台拖航阻力为432.5 N。由此可见,时间步长为0.01 s时与时间步长为0.02 s时,总阻力较为接近,能够满足工程要求,故在以后的计算中时间步长选用0.02 s。
|
图 7 不同时间步时平台总阻力时程曲线 Fig. 7 Time history curves of total towing resistance for the separated polar ocean nuclear energy platform with different time steps |
分别对分离式海洋核能平台及一体式海洋核能平台在不同拖航速度时的拖航阻力进行计算,实际平台拖航速度范围为2 ~ 5 kn,间隔1.5 kn,在计算时固定平台六自由度运动,其计算结果如表5所示。可知,随着实际平台拖航速度逐渐增大,拖航阻力逐渐增大,月池增阻百分比也逐渐增大,当实际平台拖航速度达到5 kn时,月池增阻达到12%。
|
|
表 5 不同航速时平台拖航阻力结果 Tab.5 Towing resistance of the platforms at different towing speeds |
以拖航速度5 kn 为例,对平台周围流场进行分析。一体式平台中纵剖面流场速度矢量图如图8所示,除在平台前端有涡形成外,其余部分流体较为均匀。分离式平台中纵剖面流场速度矢量图如图9所示,与一体式平台周围流场相比,除环境承载平台前端有涡生成外,在月池前后均有涡生成,流场整体较为紊乱。在拖航过程中,平台周围产生大量的涡,涡的形成与脱落将造成能量耗散。月池中涡流的生成和脱落也会引起月池中水的振荡,对平台的阻力性能产生不利影响。与文献[9]结果相比,航速5 kn时,月池增阻百分比较大,原因包括:1)吃水不同,造成月池内水体运动方式的改变;2)文献[19]在进行实验及数值模拟时,考虑了壁面对平台拖航阻力的影响,本文模拟无限水域情况,两者存在差异。

|
图 8 一体式平台中纵剖面流场速度矢量图 Fig. 8 Velocity vector plot of flow field in the central longitudinal section of the integrated polar ocean nuclear energy platform |

|
图 9 分离式平台中纵剖面流场速度矢量图 Fig. 9 Velocity vector plot of flow field in the central longitudinal section of the separated polar ocean nuclear energy platform |
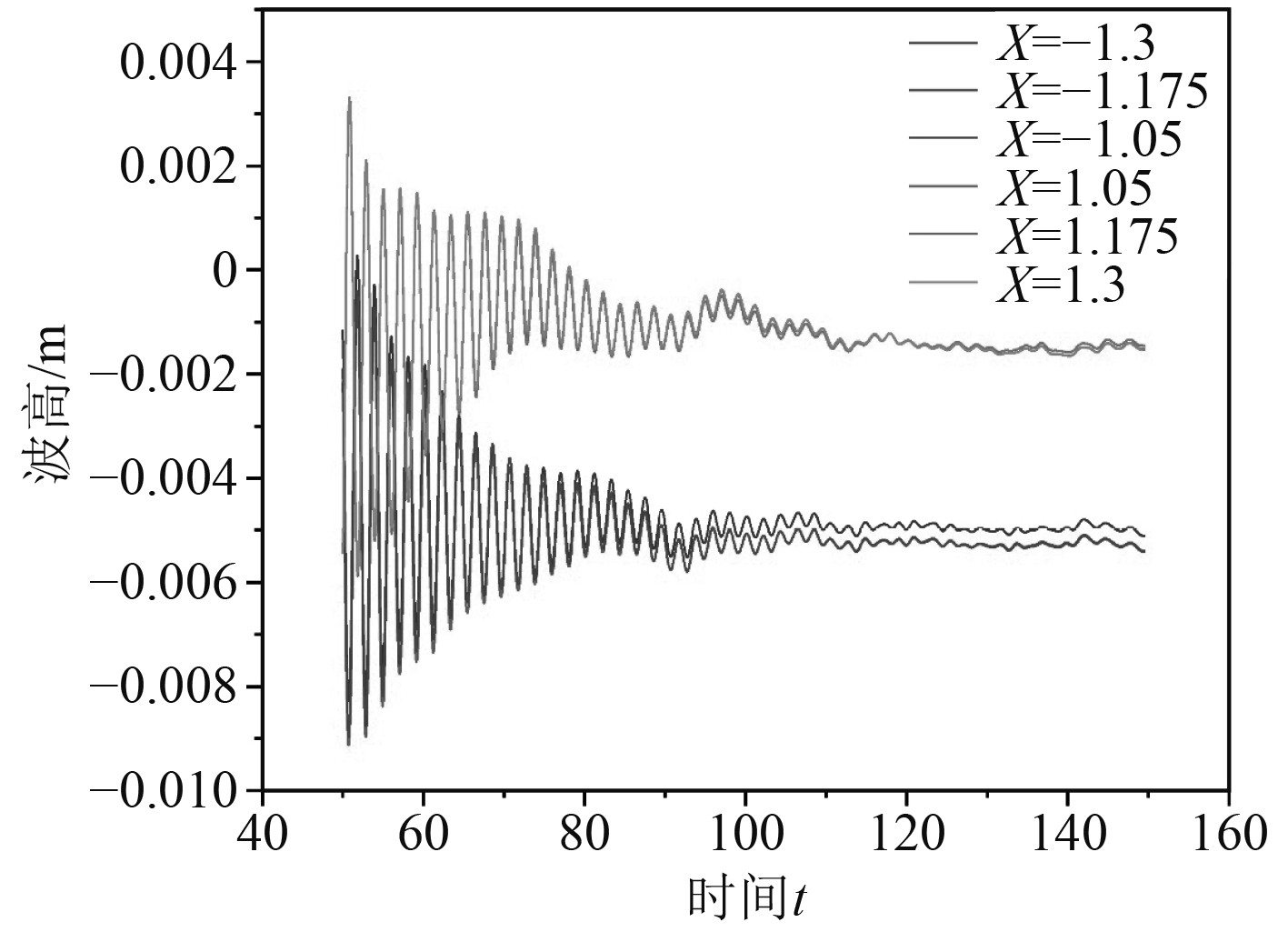
对月池内X轴上各点波高进行监测,X轴原点位于环形的圆心,以流速方向为正方向。监测点坐标分别为X=−1.3、X=−1.175、X=−1.05、X=1.05、X=1.175、X=1.3。以实际平台拖航速度5 kn 为例进行说明,图10为各点波高时程曲线(取50 s以后),可知,X=−1.3、X=−1.175、X=−1.05三点及X=1.05、X=1.175、X=1.3三点波面同时上升或同时下降,即月池前端水体与月池后端水体各自进行活塞式运动。同时,从图10可知,当月池前半部分波面达到波峰(波谷)时,月池后半部分波面恰好达到波谷(波峰),即可以认为,环形月池前后部分水体整体进行晃荡式运动。从图中还可以看到,在稳定段,6个监测点的水面始终低于水平面,月池的存在使得月池内部水面低于外界水体,且环形月池前端水体水面低于后端水体水面。
|
图 10 月池内X轴各点波高时程曲线 Fig. 10 Time history curves of wave heights at points on the X-axis in the moonpool |
本文介绍了分离式海洋核能平台及一体式海洋核能平台的概念,并采用CFD数值计算方法对2种平台拖航阻力进行计算。研究了月池中流体的流动形式、月池对平台周围流体的影响以及月池中水的运动,结论如下:
1)月池的存在会对平台的拖航阻力产生一定的影响。当月池存在时,平台的拖曳阻力会增加5%~15%。
2)月池的存在使平台周围的流场具有扰动左右,使周围流场更加紊乱。
3)月池前端和后端水体分别进行活塞式运动,而在整个月池内部,流体作为一个整体进行晃荡式运动。
4)月池水体自由面低于外界水平面,且环形月池前端水体水面低于后端水体水面。
| [1] |
李振福, 李婉莹, 蔡梅江. “冰上丝绸之路”航线开发利用系统建设研究[J]. 海岸工程, 2019, 38(2): 144-153. |
| [2] |
蔡梅江. “冰上丝绸之路”开启北半球运输物流体系新格局[J]. 中国远洋海运, 2019(7): 60-61+11. |
| [3] |
刘大辉, Ove T. G, 白勇, 等. 极地冰区海上钻井平台发展趋势研究[J]. 水利科学与寒区工程, 2019, 2(1): 66-73. |
| [4] |
李想. 分离式冰区核电平台连接机构研究[C]//中国造船工程学会船舶力学学术委员会. 2019年船舶结构力学学术会议论文集. 中国造船工程学会船舶力学学术委员会: 中国造船工程学会, 2019: 542-548.
|
| [5] |
李想, 李红霞, 李志远, 等. 分离式冰区核电平台连接机构研究[C]//2019年船舶结构力学学术会议, 2019.
|
| [6] |
ORR R S, DOTSON C. Offshore nuclear power plants.[J]. Nuclear Engineering and Design, 1973, 25(3): 334-349. DOI:10.1016/0029-5493(73)90030-7 |
| [7] |
孙雷, 罗贤成, 姜胜超, 等. 适用于渤海海域浮式核电平台水动力特性研究基础与展望[J]. 装备环境工程, 2018, 15(4): 19-27. |
| [8] |
刘怀梅. 俄建造海上浮动核电站[J]. 中国核工业. 2013(7): 9.
|
| [9] |
LEE K, KIM M, LEE J I, et al. Recent advances in ocean nuclear power plants[J]. Energies, 2015, 8(10): 11470-11492. DOI:10.3390/en81011470 |
| [10] |
ZHANG Y, BUONGIORNO J, GOLAY M, et al. Safety Analysis of a 300-MW(electric) Offshore Floating Nuclear Power Plant in Marine Environment[J]. Nuclear Technology, 2018, 203(2): 129-145. DOI:10.1080/00295450.2018.1433935 |
| [11] |
李红霞, 王莹, 黄一, 等. 冰区浮式核电平台定位系统优化设计[J]. 哈尔滨工程大学学报, 2021, 42(2): 193-199. |
| [12] |
FUKUDA K. Behavior of water in vertical well with bottom opening of ship, and its effect on ship motions[J]. Journal of the Society of Naval Architects of Japan, 1977, 141: 107-122. |
| [13] |
FALTINSEN O. M. Sea loads on ships and offshore structures [M]. Cambridge University Press, Cambridge, United Kingdom, 1990.
|
| [14] |
JIANG S C, CONG P W, SUN L, et al. Numerical investigation of edge configurations on piston-modal resonance in a moonpool induced by heaving excitations [J]. Journal of Hydrodynamics, 2019, 31(4): 682-699.
|
| [15] |
YADAV A, ANANTHA SUBRAMANIAN V, ANANTHAKRISHNAN P. Numerical and experimental investigation of the effect of moonpool positioning on the hydrodynamics of floating drilling production storage and offloading vessel [J]. Ships and Offshore Structures , 2021, 17 (5): 973-991.
|
| [16] |
谷家扬, 毛沛盛, 陶延武, 等. 航行状态下钻井船月池内流场特性[J]. 船舶工程, 2021, 43(8): 49-56+113. |
| [17] |
ZHANG X Y, SUN L, SUN C, et al. Study on the influence of the moonpool on the smooth water resistance performance of the ship [J]. Ocean Engineering, 2021, 237.
|
| [18] |
LEE S K, XU L. CFD study and model test verification of moonpool configuration modifications for minimizing drillship resistance [M]. Practical Design of Ships and Other Floating Structures. 2021: 3-27.
|
| [19] |
LIU Y, LI H, ZHOU X, et al. The influence of an annular moonpool on towing resistance of a separated polar ocean nuclear energy platform [J]. Ocean Engineering, 2022, 266.
|
| [20] |
李想. 冰区核电平台运动分析及连接机构概念设计[D]. 大连: 大连理工大学, 2020.
|
| [21] |
鲜于晨松, 吕海宁. 波浪作用下钻井船月池内流体水动力性能研究[J]. 舰船科学技术, 2018, 40(1): 62-69. DOI:10.3404/j.issn.1672-7649.2018.01.011 |
 2024, Vol. 46
2024, Vol. 46
