2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
随着弹性材料、消声瓦以及大侧斜、变距、多叶螺旋桨等技术的发展,机械噪声和螺旋桨噪声在水下航行器辐射噪声中占比逐渐减小,国内外越来越重视航行器流噪声的研究。流噪声强度随航速增加而迅速增加,辐射声功率正比于航速的5 ~ 7次方[1]。由于试验困难程度和仿真计算效率均随航速的增加而增加,高航速水下航行器流噪声仿真和试验都具有一定的困难。
不同的流噪声模型声源特性不同,李福新等[2]通过回转体流噪声相似定律实验得到其声功率谱与来流速度的7次方成正比的结论。张小锋等[3]建立了圆柱绕流流噪声总声压级与雷诺数3次方的函数关系。李玲等[4]用实验得到了吻合良好的归一化频谱曲线,验证了三维圆柱绕流气动噪声主要为偶极子源。邢宇等[5]对声功率频谱进行归一化处理,得到声功率与马赫数6次方呈正比的结论。王春旭等[6]认为,相比于气动噪声跨音速、超音速的声学问题,流噪声问题一般属极小马赫数问题,偶极子声源更为有效,两者研究的侧重点不同。国内外对水下航行器模型的流噪声计算方法研究较多,尤其是低航速下流噪声预报及其声场特性的研究,卢元涛等[7−9]验证了不同的方法计算SUBOFF模型流噪声。YAO等[10]利用边界元法比较了全附体SUBOFF流噪声和流激噪声大小,并计算了低航速下流激噪声大小随测点距离的变化。Chen等[11]对二维裸艇SUBOFF声源和声辐射特性进行了分析,得到了SUBOFF辐射特性具备偶极子特性的结论。
以上关于SUBOFF噪声特性研究的文献几乎集中在低航速范围内,无法反映水下航行器流噪声随航速变化的具体关系。本文采用Lighthill声类比理论的流噪声混合数值模拟方法,计算缩尺比为1∶24的 SUBOFF模型流噪声,分析其在水下航行器主流航速范围内的声源特性,并得到声源强度与航速的线性关系。最后进行了预报方法的验证,实现了高航速水下航行器流噪声的预报,一定程度上能够提高预报范围和预报效率。
1 不同类型声源随航速变化关系假设不存在外质量源和力源,在湍流区域内得到如下Lighthill声类比方程[12]:
| $ {\nabla ^2}{\rho ^\prime } - \frac{1}{{{c^2}}}\frac{{{\partial ^2}{\rho ^\prime }}}{{\partial {t^2}}} = - \frac{1}{{{c^2}}}\frac{{{\partial ^2}{T_{ij}}}}{{\partial {x_i}{x_j}}}。$ | (1) |
式中:
利用数学物理方程的Kirchhoff解,Curle[13]得到有边界时方程(1)的解如下:
| $ \begin{split} {\text{4}}{\text{π}} {{c}}_{\text{0}}^{\text{2}}{\rho ^\prime } =& \frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}\iiint_{{V_0}} {\frac{1}{r}\left[ {{T_{ij}}} \right]}{\mathrm{d}}V - \frac{\partial }{{\partial {x_i}}}\iint_{{\Sigma _0}} {\frac{1}{r}[{F_i}]{\mathrm{d}}S} + \\ & \iint_{{\Sigma _0}} {\frac{1}{r}\left[\frac{{\partial Q}}{{\partial t}}\right]{\mathrm{d}}S}。\\[-5pt] \end{split} $ | (2) |
式中:
均匀来流下水下航行器表面流噪声计算没有单极子噪声的产生,因此只考虑流噪声的等效偶极子源和等效四极子源。根据不同声源的辐射特性,远场条件下(
| $ \begin{split} & {I_D}\sim{\rho _0}{U^3}M{a^3}{\left(\frac{D}{r}\right)^2}{\cos ^2}\theta, \\ & {I_Q}\sim{\rho _0}{U^3}M{a^5}{\left(\frac{D}{r}\right)^2}{R^2}(\theta ) , \end{split} $ | (3) |
式中:
根据式(3)进行推导可知,相同模型下产生的不同类型声源的总声功率级(dB)与航速的理论关系如下:
| $ {L_p} = {L_m} + n \times 10\lg \left(\frac{{{U_p}}}{{{U_m}}}\right) 。$ | (4) |
式中:
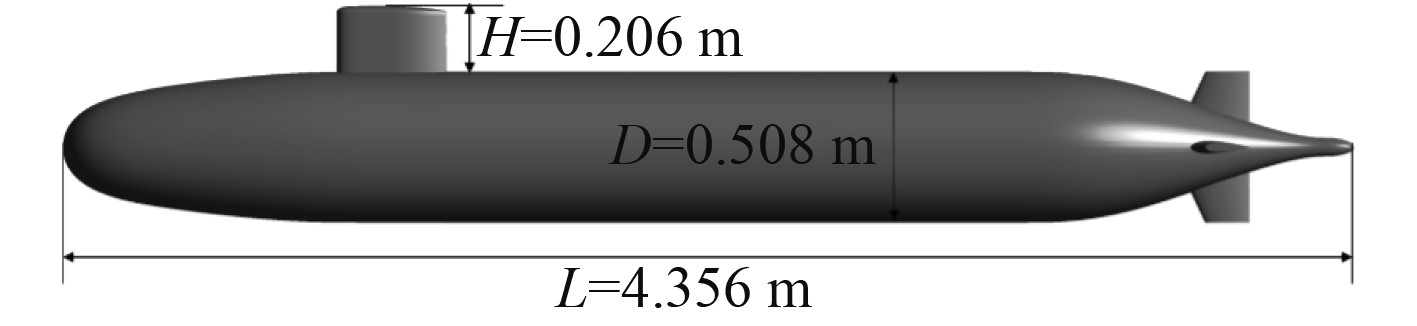
本文采用的模型是美国国防高等研究计划署(DARPA)的标准SUBOFF全附体模型[15],该模型与实际模型尺寸比例为1∶24,尺寸如图1所示。
|
图 1 1:24的全附体SUBOFF模型 Fig. 1 1:24 fully appended SUBOFF model |
数值方法验证的航速为5.93 kn,采用文献[16]关于SUBOFF验证过的LES湍流模型,数值计算方法采用文献[17]基于ACTRAN有限元/无限元的混合计算方法,即将流场和声场解耦求解。首先采用
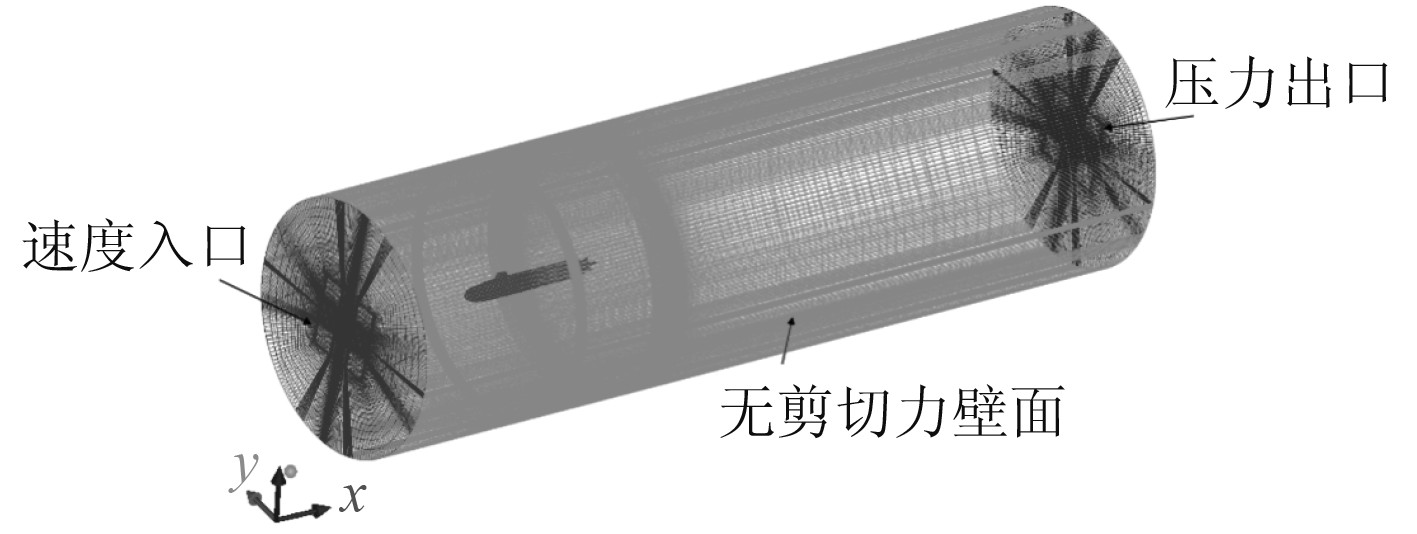
LES湍流模型需要精细的网格才能保证计算结果可靠,如图2所示为该模型计算域网格模型,坐标原点位于SUBOFF头部,圆柱计算域直径为13.8D,长为5.5L,入口边界距离SUBOFF模型前端0.92L。第一层壁面高度为0.05 mm,增长率为1.1,共15层网格,整个模型采用结构化网格划分,网格数量为620万。
|
图 2 流场模型 Fig. 2 Flow field model |
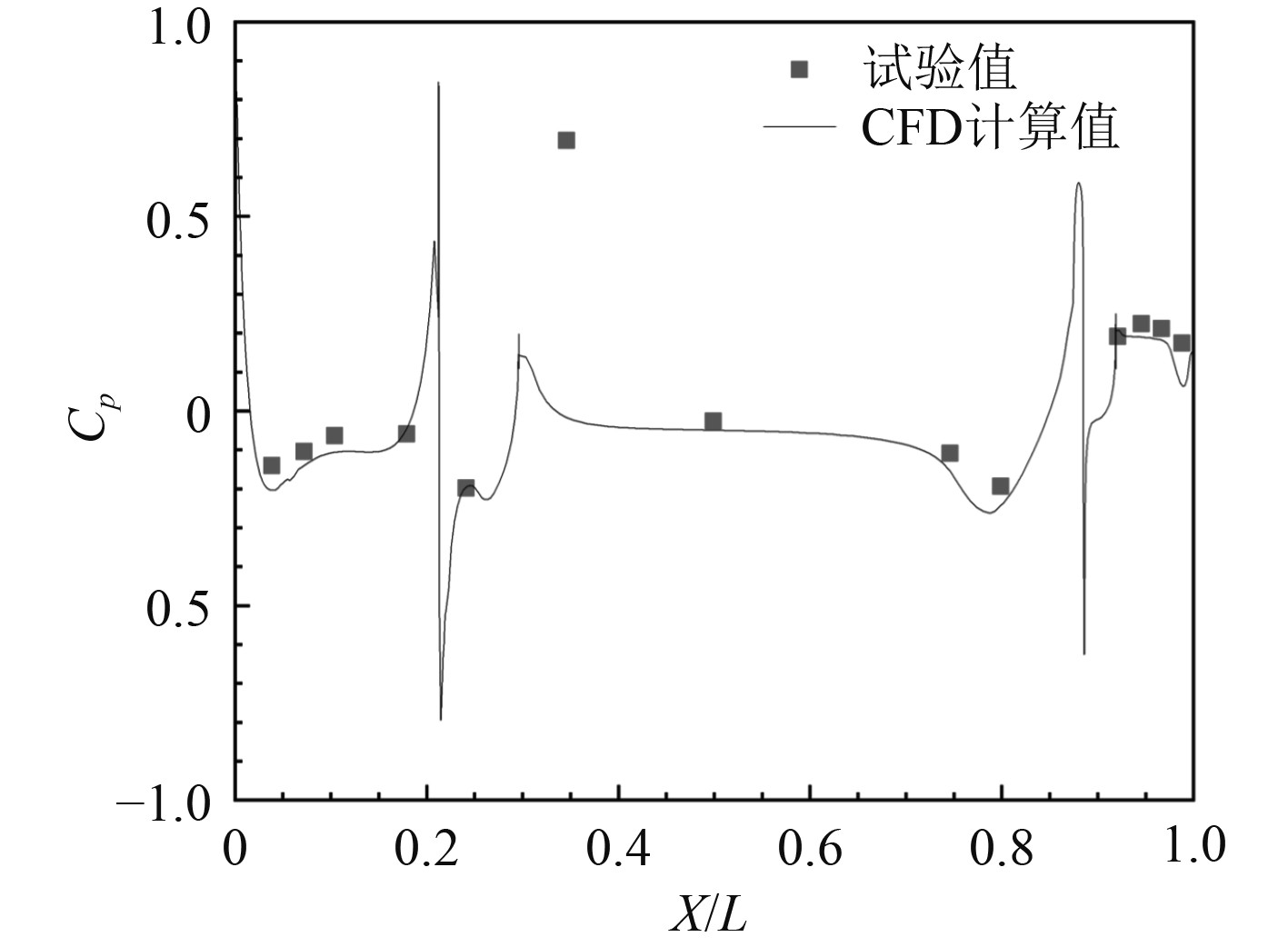
选择SSTk-ω定常计算结果与该文献试验值比较,本文计算阻力值102.8 N,文献[15]试验阻力值102.3 N,误差为0.5%。通过
|
图 3 SUBOFF中剖脊线压力系数对比结果 Fig. 3 Comparison results of pressure coefficient of ridge line in SUBOFF |
根据Lighthill声类比理论,选择SUBOFF声源较大的区域作为声场计算域。图4为SUBOFF稳定流场下的速度涡量云图,可以看出整个模型涡脱落主要集中在围壳和尾部操纵面附近,也是该航速下主要的流噪声声源区域。

|
图 4 速度涡量云图 Fig. 4 Velocity vorticity nephogram |
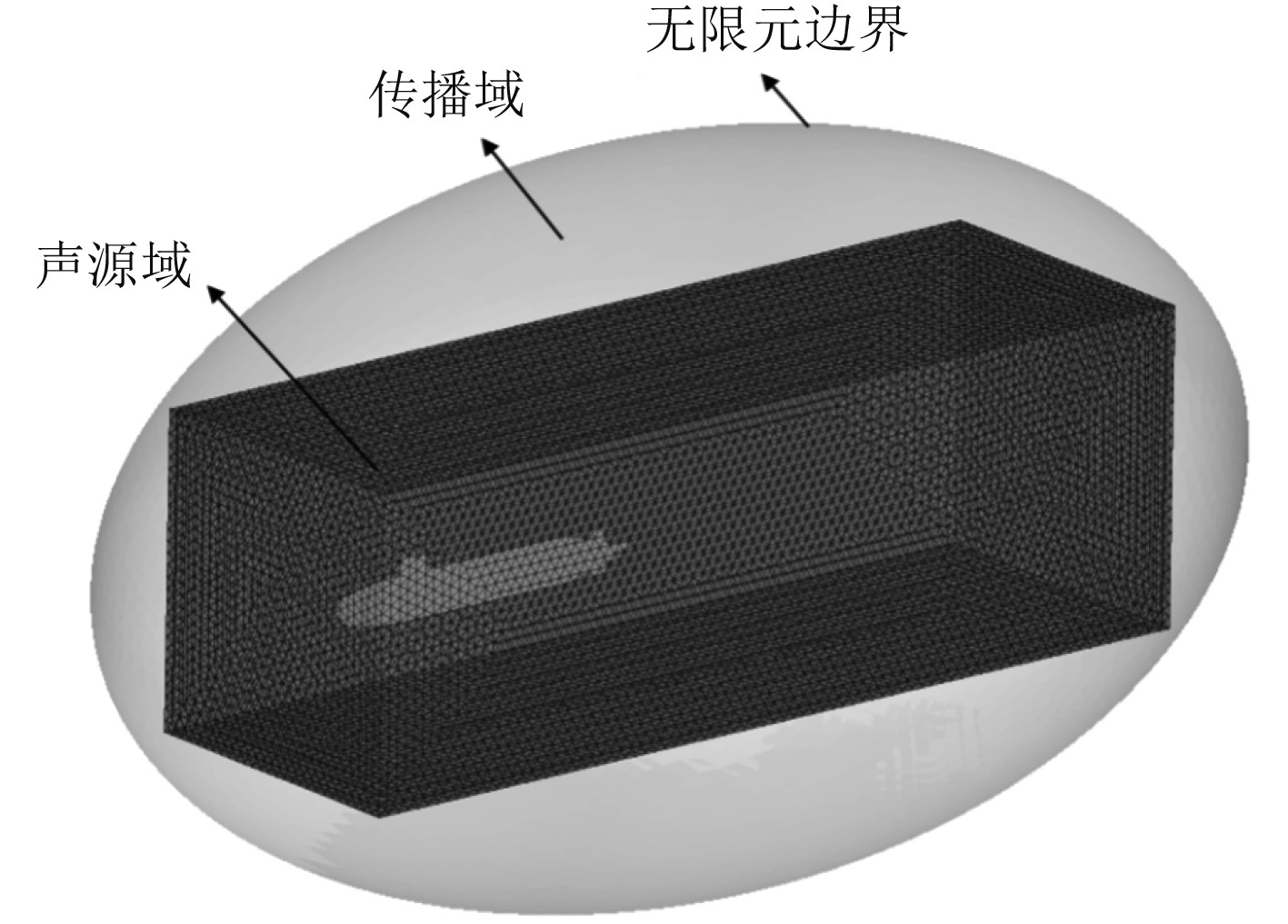
文献[19]的研究表明声源域边界要远离张量较大的区域,否者会产生非物理解,导致计算结果偏大。本文声学模型区域如图5所示,该模型分为声源域、传播域、无限元边界3部分。声源域是整个流场数据转化为声场的区域,传播域是连接声源域和无限元边界之间的区域,无限元边界是为了模拟无穷远处的无反射边界条件。声学网格尺寸小于波长的1/6即可保证计算精度,本文计算的最大频率为1 000 Hz,因此声学网格尺寸取0.25 m。
|
图 5 声学模型 Fig. 5 Acoustic model |
参照文献[7]的设置,选择SUBOFF模型正下方测点坐标(2.178 m,−2 m,0)为声学监测点。由于缺乏试验数据,国内对SUBOFF噪声的验证都是基于文献[20]关于尺度相当的“大青花鱼”模型试验结果,将与其有关SUBOFF数值模拟计算的文献总声压级结果汇总,本文总声压级计算频率范围为4 ~ 1 000 Hz,分辨率为4 Hz。如表1所示,可以看出本文计算结果与各文献差别较小,该方法可以作为水下航行器声场计算的数值模拟方法。
|
|
表 1 测点声压级与相关文献结果对比 Tab.1 Comparison between the OSPL at the measuring point and the results of relevant literatures |
根据式(2)可知,
采用第2节的数值模拟方法,计算不同航速下SUBOFF模型的声辐射云图、声指向性图、总声功率,研究水下航行器模型的声辐射特性。计算的航速工况采用的是标准SUBOFF试验航速[15],该试验航速范围与目前的主流水下航行器航速范围一致,表2为各工况计算参数和流场阻力计算结果对比,可以看出各工况阻力误差较小,表明建立的流场模型能够满足该航速范围内的所有工况条件的计算。
|
|
表 2 不同航速下阻力结果与试验数据对比 Tab.2 Comparison of the resistance results and test data at different speeds |
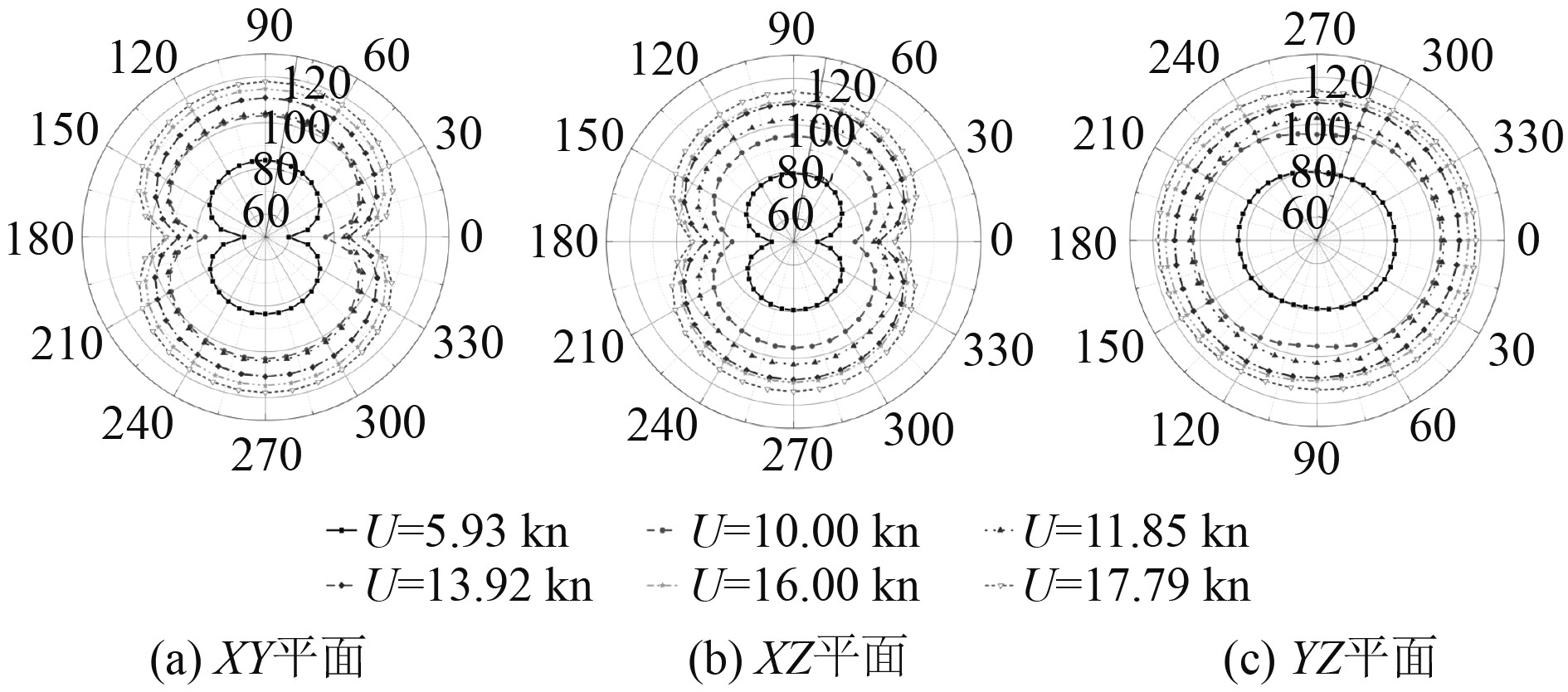
远场测点以模型中心坐标(2.178 m,0,0)为圆心,半径取50 m,在XY、XZ、YZ三个平面上每隔10°取1个测点,共36个测点。计算远场测点20 ~ 1 000 Hz内的总声压级,换算到距离中心1 m处的总声源级,得到不同工况下SUBOFF模型的声指向性图。图6为3个平面内不同航速下总声源级指向性比较。可以看出,在同一平面内,随着航速的增加,所有测点的总声源级增大,且不同航速下的声指向性一致。说明在该航速范围内,SUBOFF模型的流噪声指向性基本没有发生改变,XY和XZ平面指向性均为“
|
图 6 不同航速下SUBOFF辐射噪声指向性 Fig. 6 Acoustic directivity of SUBOFF radiated noise at different speeds |
声辐射云图可以反映不同频率下SUBOFF模型声源大小和声传播特性,由式(2)表明,同一SUBOFF流场且相同频率下,偶极子源和四极子源占比只与来流速度有关,来流速度越大,四极子声源强度占比越大。因此,本文对最大航速U=17.79 kn(工况6)下声辐射结果进行分析,该工况下XY平面内不同频率声辐射云图如图7所示。可以看出,SUBOFF流噪声的声源主要集中在围壳和尾部操纵面上,与涡量场声源位置和大小一致。在48 Hz和244 Hz下声辐射云图呈现偶极子辐射特性,当频率升高到820 Hz时,声辐射云图出现更为复杂的“瓣状”分布,表明更高阶的声源影响辐射声场。由于最大航速U=17.79 kn(工况6)时的噪声结果在低频范围内主要为偶极子声辐射特性,可以认为低于该航速范围内(工况1 ~ 工况5)的SUBOFF流噪声在相应频率范围内均以偶极子辐射特性为主。

|
图 7 XY平面声辐射云图 Fig. 7 Acoustic radiation nephogram on XY plane |
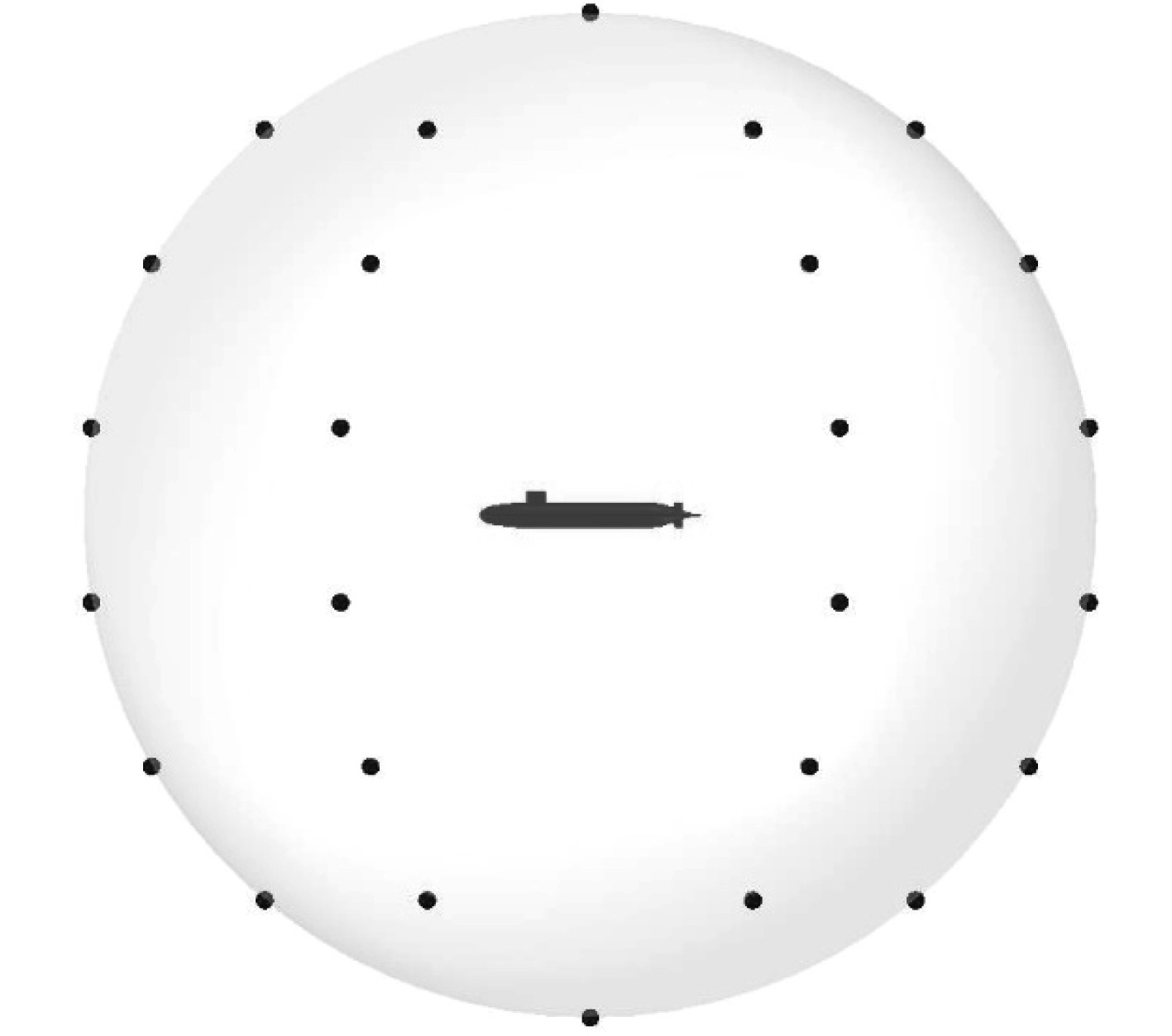
文献[14]表明,由于无法确定源,声指向性和声辐射云图只表明辐射具有偶极子辐射特性,为了更进一步确定SUBOFF声源类型,需要从辐射能量的角度进行比较。总声功率级可以反映流噪声在一定频率范围内的辐射功率大小,采用国标ISO3744测点布置方法,测点位置如图8所示,中心为SUBOFF艇体几何中心(2.178 m,0,0),测点距离R=10 m。
|
图 8 ISO3744测点布置示意图 Fig. 8 ISO3744 measuring point layout diagram |
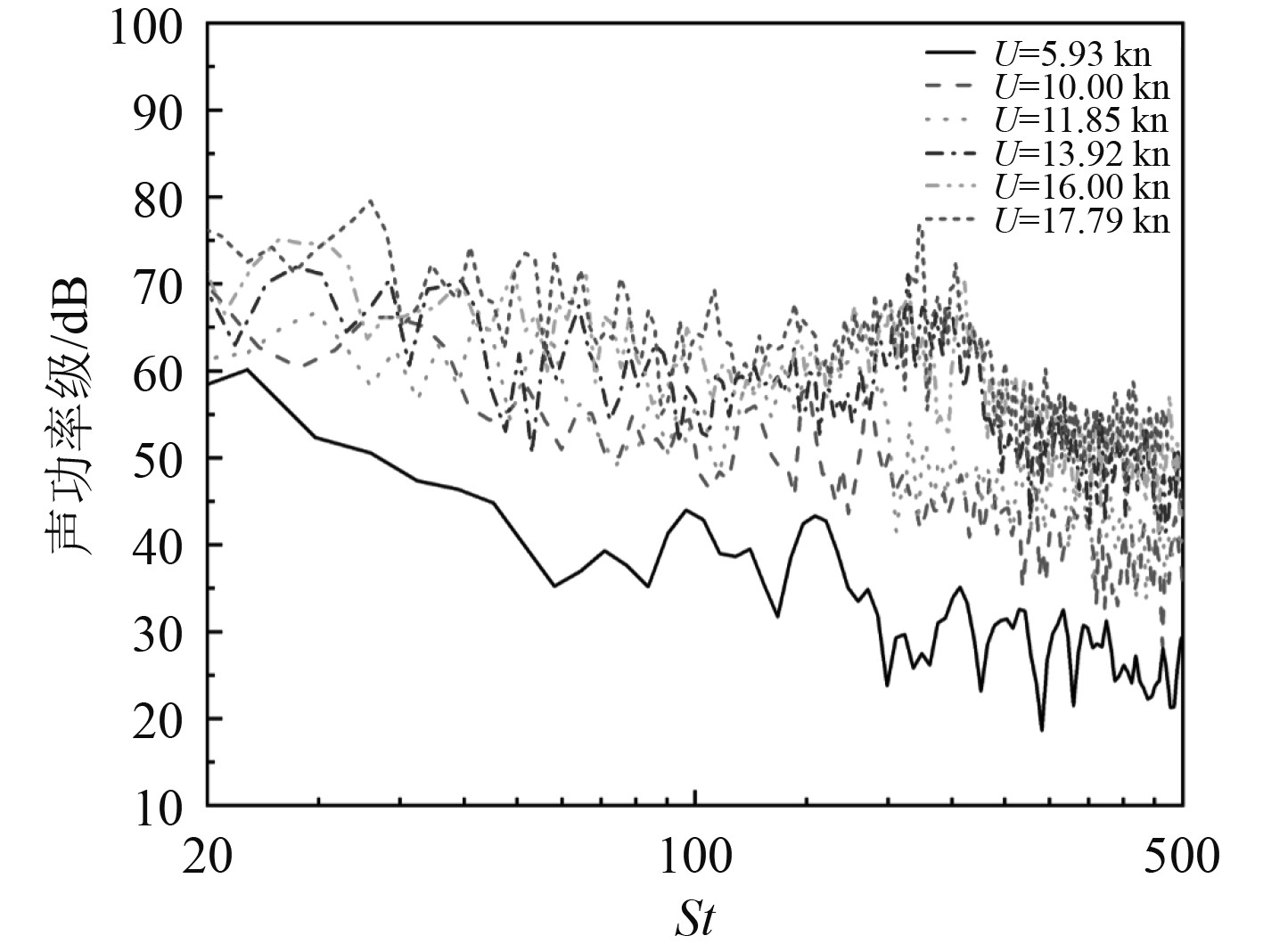
受目前计算方法和计算机运算能力的限制,无法得到全频段内的总声压级大小。文献[23]的研究表明高雷诺数下绕流物体涡脱落频率的归一化结果基本相等,本文对所有工况声功率频率按斯特劳哈尔数(
|
图 9 不同航速工况下频率归一化声功率谱 Fig. 9 Frequency normalized sound power spectrum under different speed conditions |
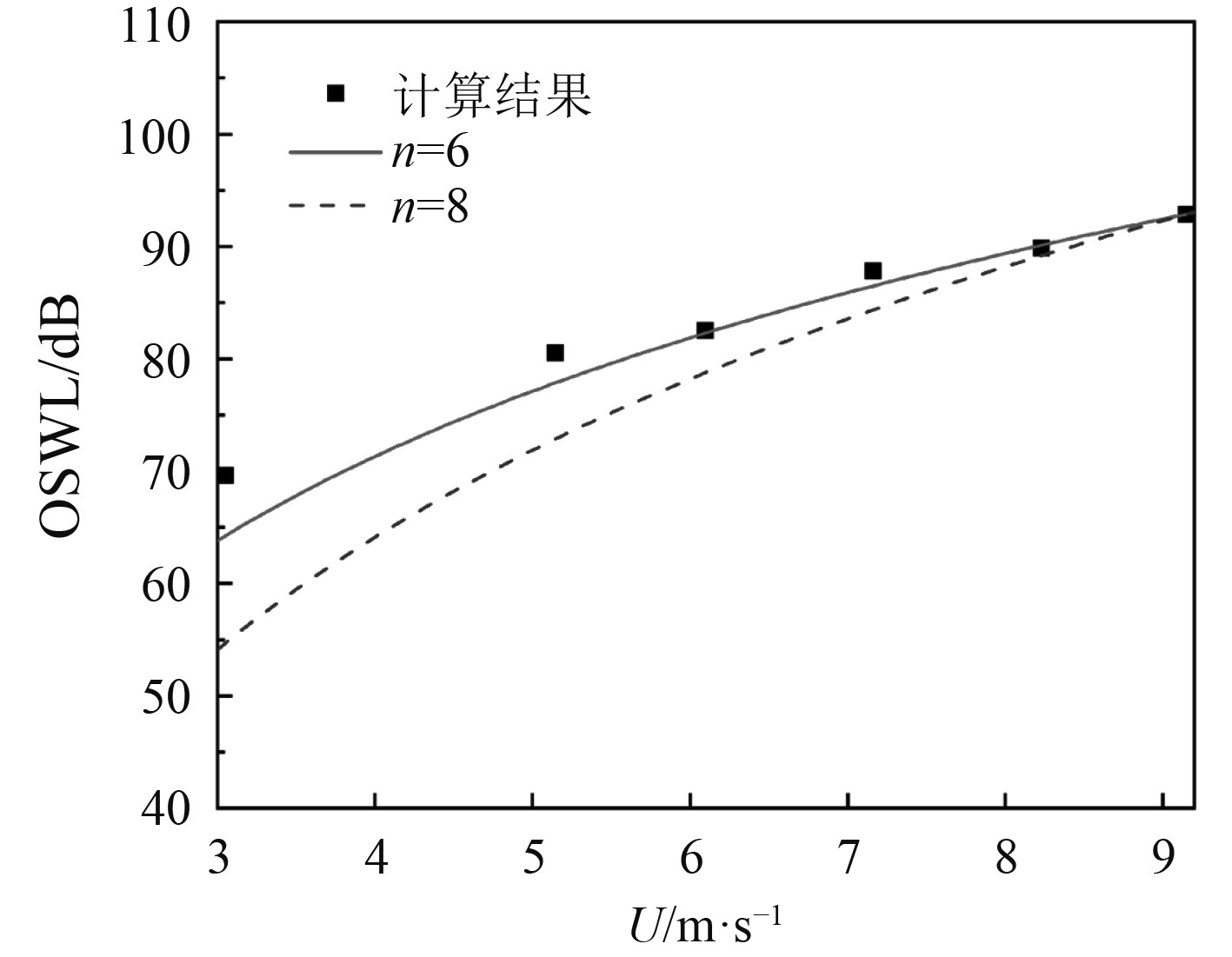
为了研究SUBOFF声辐射功率与航速的关系,计算图9中无量纲频率20~500 Hz内的总声功率级,并与式(3)中偶极子和四极子的理论值进行比较。由于计算的总声功率级精度受低频分辨率影响较大,为了保证参考工况结果的准确,选择分辨率较高的工况6作为参考工况的总声压级,通过插值得到不同航速下偶极子声源和四极子声源下的理论换算结果,并与图9中各工况总声功率级计算值进行比较。比较结果如图10所示,可以看出计算的总声功率级结果与偶极子n=6下理论曲线吻合,表明SUBOFF流噪声辐射声功率与航速的6次方呈正比。
|
图 10 总声功率级随航速变化关系 Fig. 10 Relationship between total sound power level and speed |
基于SUBOFF在主流航速范围内的偶极子声源特性,建立高航速下同尺度SUBOFF流噪声预报方法。首先建立合理的SUBOFF数值仿真流场模型和声场模型,然后基于有限元/无限元的混合数值模拟方法计算低航速SUBOFF流噪声结果,利用其偶极子声源特性下的相似换算关系得到高航速流噪声结果。本节将对该方法进行验证,由于缺乏试验数据,选择高航速模型下的流噪声计算结果作为验证对比结果。采用缩尺比为1∶24下的SUBOFF模型进行验证,验证流程如图11所示。
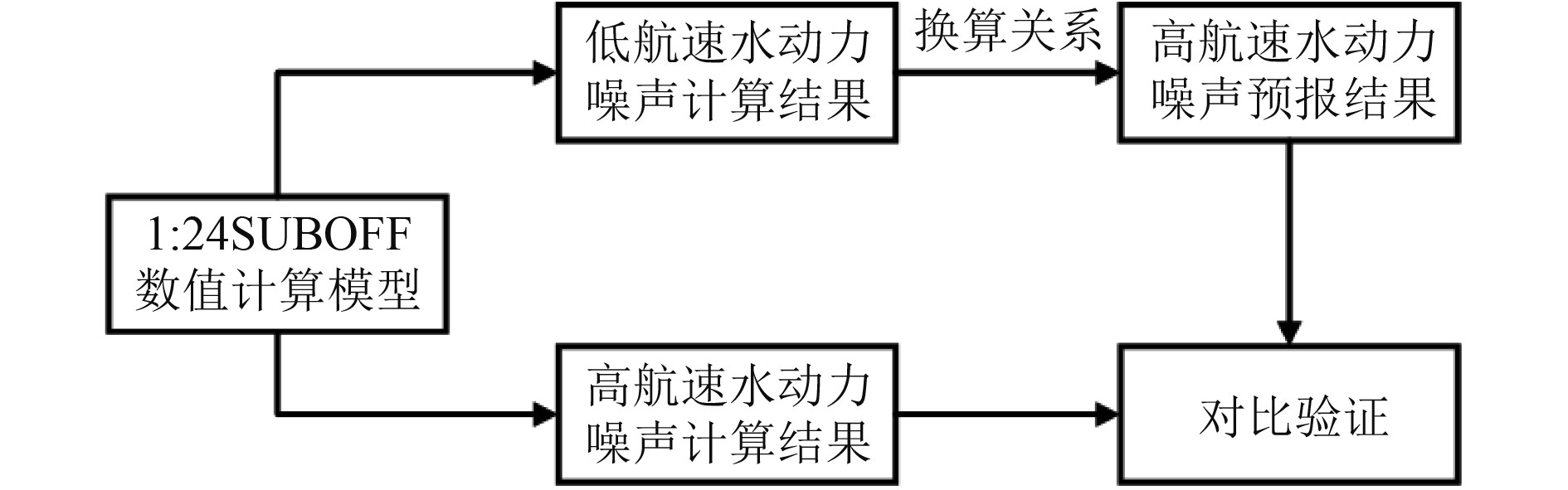
|
图 11 高航速水动力噪声预报方法验证流程图 Fig. 11 Verification flow chart of high speed hydrodynamic noise prediction method |
由于不同频率下声波的传播特性不同,水下航行器辐射噪声通常更关心声学频谱结果。频谱结果主要与幅值、频率、频率分辨率有关,因此从低航速SUBOFF模型流噪声结果预报高航速下噪声结果需要对三者进行换算。利用式(4)对幅值进行换算,其中n取为6。文献[23]研究结论表明高雷诺数下的通用斯特劳哈尔数只与阻力系数有关,结合文献[24]关于SUBOFF临界雷诺数以上阻力系数基本不发生改变的结论可以认为高雷诺数下斯特劳哈尔数近似相等,利用斯特劳哈尔数相等可以得到同尺度、不同航速下频率和频率分辨率的换算公式,即:
| $ \frac{{{f_p}D}}{{{U_p}}} = \frac{{{f_m}D}}{{{U_m}}} \Rightarrow {f_p} = \frac{{{U_p}}}{{{U_m}}}{f_m},\; \Delta {f_p} = \frac{{{U_m}}}{{{U_p}}}\Delta {f_m} ,$ | (5) |
式中:f为频率;
选择最大航速U=17.79 kn(工况6)的声场结果作为高航速原型的对比结果,最小航速U=5.93 kn(工况1)作为换算模型。为了便于数据处理和分析,将换算模型的频率范围和频率分辨率取整,表3为原型和模型的频谱相关参数。
|
|
表 3 原型(高航速1∶24 SUBOFF)和模型(低航速1∶24 SUBOFF)频率参数 Tab.3 Frequency parameters of prototype (1∶24 SUBOFF at high speed) and model (1∶24 SUBOFF at low speed) |
对原型声功率谱和声源级谱结果进行对比验证,声功率测量方法与第3章相同,声压级远场测点在SUBOFF中心的一侧50 m处,坐标为(2.178 m,50 m,0)。将低航速1:24SUBOFF模型计算的声功率谱和声源级谱幅值结果按偶极子下的式(4)换算,频率按式(5)换算,得到的频谱曲线预报结果如图12所示。可以看出预报值和计算值整体吻合较好,低频预报结果偏差较小,高频预报结果偏差相对增加。通过第3节声辐射云图可以判断是因为随着频率的升高,四极子声源比重增大,但预报是基于偶极子换算公式进行预报的,导致高频预报结果小于实际计算结果。经计算,在20~1 000 Hz内的总声功率级计算值和预报值分别是97.2 dB和98.4 dB,误差为1.24 dB;总声源级计算值和预报值分别是115.6 dB和117.9 dB,误差为2.3 dB。可以看出低航速模型预报的高航速同尺度原型噪声结果偏大。
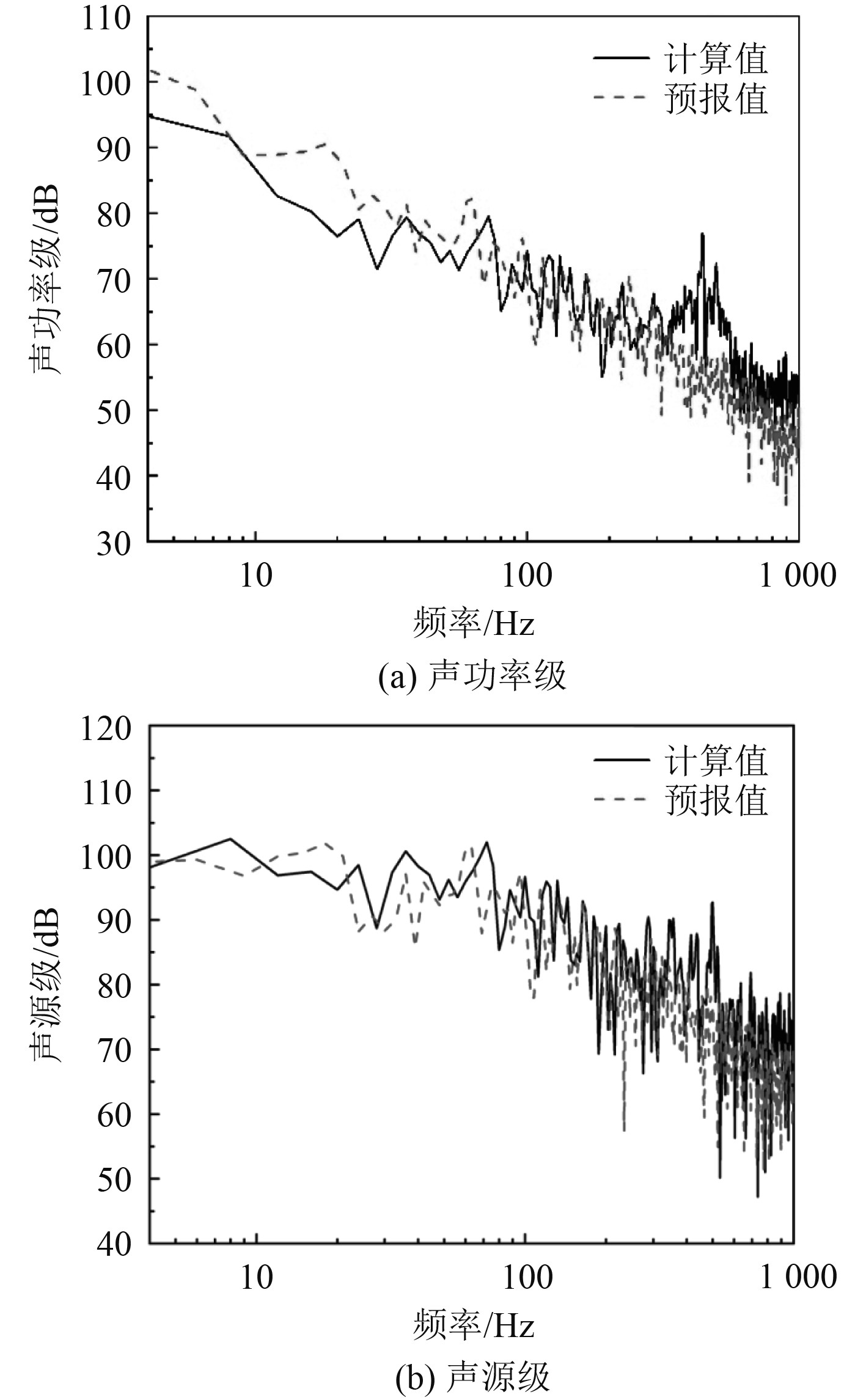
|
图 12 频谱预报结果(计算值:17.79 kn噪声数值计算结果,预报值:通过5.93 kn噪声数值计算结果结合式(4)预报得到的17.79 kn噪声结果) Fig. 12 Spectrum prediction result (calculated value: noise numerical calculation result at 17.79 kn, predicted value: 17.79 kn noise result predicted by combining the numerical calculation results at 5.93 kn with equation (4)) |
SUBOFF模型流场阻力结果、中剖面线上的压力系数、相关测点总声压级谱与试验值误差较小,表明本文采用的计算模型与计算方法的正确性,可以作为流噪声的数值计算方法。经过对不同航速下的SUBOFF声辐射特性分析,得到如下结论:
1)在17.79 kn航速下,低频范围内声辐射方向主要垂直于来流方向,随着频率升高,声辐射云图呈“瓣状”分布,出现更高阶声源的辐射特性,且辐射能量随着频率升高而减小。
2)在航速为5.97 ~ 17.79 kn范围内,SUBOFF模型的声辐射特性基本不发生改变,其声指向性具有偶极子“
3)在20 ~ 1000 Hz的频率范围内,1∶24缩尺比下的高航速SUBOFF模型声功率级和声源级频谱曲线计算值和采用低航速相似换算后的预报值吻合较好,总声功率级和总声源级预报值比计算值分别高1.2 dB和 2.3 dB,表明可以利用SUBOFF声源特性从低航速计算结果对同尺度高航速流噪声进行预报。
| [1] |
俞孟萨, 吴有生, 庞业珍. 国外舰船水动力噪声研究进展概述[J]. 船舶力学, 2007, 11(1): 7. YU M S, WU Y S, PANG Y Z. A review of progress for hydrodynamic noise of ships[J]. Journal of Ship Mechanics, 2007, 11(1): 7. |
| [2] |
李福新, 石秀华, 张宇文, 等. 回转体流噪声相似律的实验研究[J]. 流体力学实验与测量, 1999, 13(4): 14-18. LI F X, SHI X H, ZHANG Y W, et al. Experimental study of flow noise scaling of an axisymmetric body[J]. Journal of Experiments in Fluid Mechanics, 1999, 13(4): 14-18. |
| [3] |
张小锋, 刘国庆, 赵成, 等. 声类比水下圆柱绕流声学特性研究[J]. 舰船科学技术, 2019, 41(11): 120-124+128. ZHANG X F, LIU G Q, ZHAO C, et al. Research on acoustic properties of flow around underwater cylinders based on acoustic analogue[J]. Ship Science and Technology, 2019, 41(11): 120-124+128. |
| [4] |
李玲, 刘沛清, 邢宇, 等. 亚临界雷诺数圆柱绕流远场气动噪声实验研究[J]. 北京航空航天大学学报, 2016, 42(5): 977-983. LI L, LIU P Q, XING Y, et al. Far-field aeroacoustic experimental study of flow around a circular cylinder at subcritical Reynolds number[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(5): 977-983. |
| [5] |
邢宇, 刘沛清, 郭昊, 等. 简化起落架噪声相似准则及马赫数比例律[J]. 航空学报, 2017, 38(6): 72-79. XING Y, LIU P Q, GUO H, et al. Similarity rule and Mach number scaling law for simplified landing gear noise[J]. Acta Aeronautica ET Astronautica Sinica, 2017, 38(6): 72-79. |
| [6] |
王春旭, 吴崇建, 陈乐佳, 等. 流致噪声机理及预报方法研究综述[J]. 中国舰船研究, 2016, 11(1): 57-71. WANG C X, WU C J, CHEN L J, et al. A comprehensive review on the mechanism of flow-induced noise and related prediction methods[J]. Chinese Journal of Ship Research, 2016, 11(1): 57-71. |
| [7] |
卢云涛, 张怀新, 潘徐杰. 全附体潜艇的流场和流噪声的数值模拟[J]. 振动与冲击, 2008, 27(9): 142−146+189. LU Y T, ZHAN H X, PAN X J. Numerical simulation of flow-field and flow-noise of a fully appendage submarine[J]. Journal of Vibration and Shock, 2008, 27(9): 142−146+189. |
| [8] |
王曦晖, 黄桥高, 潘光. 围壳形状对潜艇水动力噪声影响数值研究[J]. 中国造船, 2020, 61(S2): 262-272. WANG X H, HUANG Q G, PAN G. Numerical research on influence of fairwater shape on flow-induced noise of submarine[J]. Shipbuilding of China, 2020, 61(S2): 262-272. |
| [9] |
张楠, 吕世金, 沈泓萃, 等. 潜艇围壳线型优化抑制脉动压力与流激噪声的数值模拟研究[J]. 船舶力学, 2014, 18(4): 448−458. ZHANG N, LV S J, SHENG H C, et al. Numerical simulation on the effect of fairwater optimization to suppress the wall pressure fluctuations and flow induced noise[J]. Journal of Ship Mechanics, 2014, 18(4): 448−458. |
| [10] |
YAO H, ZHANG H, LIU H, et al. Numerical study of flow-excited noise of a submarine with full appendages considering fluid structure interaction using the boundary element method[J]. Engineering Analysis with Boundary Elements, 2017, 77: 1-9. DOI:10.1016/j.enganabound.2016.12.012 |
| [11] |
CHEN L, MACGILLIVRAY I. Characteristics of sound radiation by turbulent flow over a hydrofoil and a bare-hull SUBOFF[C]//Australian Acoustical Society Conference, Australia: Gold Coast, 2011: 105.
|
| [12] |
LIGHTHILL M J. On sound generated aerodynamically I: generaltheory[C]//ProcRoySoc, London: RoySoc, 1952: 211A-1107: 564-587.
|
| [13] |
CURLE N. The influence of solid boundaries upon aerodynamic sound[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1955, 231(1187): 505-514. |
| [14] |
汤渭霖, 俞孟萨, 王斌, 等. 水动力噪声理论[M]. 北京: 科学出版社, 2019.
|
| [15] |
LIU H L, HUANG T T. Summary of DARPA SUBOFF experimental program data[R]. Naval Surface Warfare Center Carderock Div Bethesda MD Hydromechanics Directorate, 1998.
|
| [16] |
高顺凯, 蒋奉兼, 张志国, 等. 基于LES的潜艇绕流特性分析研究[C]//第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集(上册), 2013: 438-443. GAO S K, JIANG F J, ZHANG Z G, et al. Analyze the flow field of a submarine using LES method[C]//The 12th China Hydrodynamics Academic Conference, 2013: 438-443. |
| [17] |
张咏鸥, 张涛, 刘继明, 等. 基于Lighthill声类比的流激噪声三维计算及验证[J]. 舰船科学技术, 2014, 36(9): 55-59+64. ZHANG Y O, ZHANG TAO, LIU J M, et al. Three dimensional simulation and validation of the flow-induced noise based on lighthill's acoustic analogy theory[J]. Ship Science and Technology, 2014, 36(9): 55-59+64. |
| [18] |
傅慧萍, 缪国平. 大涡模拟在噪声计算中的应用[J]. 上海交通大学学报, 2009, 43(8): 1307−1311+1316. FU H P, MIU G P. Application of LES Method to flow noise calculation[J]. Journal of Shanghai Jiao tong University, 2009, 43(8): 1307−1311+1316. |
| [19] |
蔡建程, 潘杰, 鄂世举, 等. 圆柱绕流气动声的偶极子及四极子源法定量研究[J]. 声学学报, 2016, 41(3): 420-427. CAI J C, PAN J, E S J, et al. Quantitative study of the aerodynamic sound induced by the flow past a cylinder based on dipole and quadrupole models[J]. Acta Acustica, 2016, 41(3): 420-427. |
| [20] |
江文成, 张怀新, 孟堃宇. 基于边界元理论求解水下潜艇流噪声的研究[J]. 水动力学研究与进展A辑, 2013, 28(4): 453-459. JIANG W C, ZHANG H X, MENG K Y. Research on the flow noise of underwater submarine based on boundary element method[J]. Chinese Journal of Hydrodynamics, 2013, 28(4): 453-459. |
| [21] |
曾文德, 王永生, 杨琼方. 全附体潜艇流噪声数值计算[J]. 兵工学报, 2010, 31(9): 1204-1208. ZENG W D, WANG Y S, YANG Q F. Numerical calculation of flow noise of submarine with full appendages[J]. Acta Armamentarii, 2010, 31(9): 1204-1208. |
| [22] |
王超, 郑小龙, 张立新, 等. 用LES和无限元耦合方法预报潜艇流噪声[J]. 噪声与振动控制, 2015, 35(1): 1-6. WANG C, ZHENG X L, ZHANG L X, et al. Prediction of submarine noise based on les and infinite element method[J]. Noise and Vibration Control, 2015, 35(1): 1-6. |
| [23] |
AHLBORN B, SETO M L, NOACK B R. On drag, Strouhal number and vortex-street structure[J]. Fluid Dynamics Research, 2002, 30(6): 379. DOI:10.1016/S0169-5983(02)00062-X |
| [24] |
孙睿智, 吴方良, 许建. 雷诺数对潜艇粘压阻力和尾部伴流场影响的数值计算研究[J]. 船海工程, 2008(5): 1-5. SUN R Z, WU F L, XU J. Numerical analysis of the effects of reynolds number on the resistance and wake field of the submarine[J]. Ship & Ocean Engineering, 2008(5): 1-5. |
 2024, Vol. 46
2024, Vol. 46
