2. 中国石油大学(华东)石油工程学院,山东 青岛 266580
2. School of Petroleum Engineering, China University of Petroleum, Qingdao 266580, China
为了应对全球气候变化,响应各国对能源开发和环境保护的多重需求,开发利用环保可再生能源成为瞩目热点,其中海洋资源以其“资源丰富、可持续性开发利用”等优点受到越来越多的关注[1]。
深水油气资源的勘探与开采离不开海洋结构物的支持与保护[2],流体与结构相互作用产生交替的漩涡脱落,会在结构表面产生周期性的脉动力导致其发生自激振动。涡激振动和驰振是最常见的自激振动现象,当涡脱频率锁定在结构固有频率时会产生涡激振动[3],涡激振动在“共振区间”振动幅值较大,但具有一定区间限制性;而驰振不存在“共振区间”,随着流速的增大,振幅会持续增加,较适合于能量收集[4]。因此国内外学者对流致振动开展大量研究,在参数敏感性分析中发现雷诺数Re、约化速度Ur、结构形状等是影响流致振动类型的重要因素[5 − 6],其中研究最多的是发生涡激振动的圆形柱体[7 − 8],而具有棱角的结构形状可能会发生不同振动模式。方形截面结构常见于桥梁建筑、海上平台、系泊系统等许多海洋工程应用中,而流致振动是诱发海洋工程结构物疲劳损伤等工程问题的重要因素,但随着对流致振动现象认识的加深[9],学者们认识到流致振动所获取的能量是完全清洁的可再生能源,适用范围较广,具有显著优势和利用前景[10],因此对结构开展流致振动研究具有重要工程意义。
早期的驰振研究集中在空气动力学领域,Hartog[11]首次提出了覆冰输电导线结构驰振的起振判断依据,随后Parkinson和Smith[12]建立了准定常理论预测方柱的驰振响应,White[13]较早的利用有限元方法对结构驰振进行研究。近年来,关于方柱的驰振响应成为研究热点,邓见等[14]在低雷诺数下采用任意拉格朗日-欧拉(ALE)法对方柱流致振动进行数值研究,Su[15]对低雷诺数Re=100下的方柱自由振动进行了数值模拟,在弹性支撑情况下捕捉到多种振动模式。Barrero[16]在低质量比方柱的流致振动实验中,观察到了涡激振动与驰振共存的现象,Manzoor[17]发现质量比会影响方柱的涡激振动向驰振的转变方式,Li等[18]通过线性稳定性分析和直接数值模拟方法得出,在低雷诺数下方柱横向驰振的本质为一种单自由度振动,练继建[19]、胡德江[20]等对方柱流致振动进行试验、数值模拟研究,以探究影响振动的因素。
综上所述,非圆截面柱体流致振动比圆柱涡激振动复杂得多,对于非圆截面柱体的流致振动研究有待进一步深入。在此背景下,本文利用用户自定义函数(UDF)对Fluent软件进行二次开发,通过数值模拟研究不同来流角度下的方柱流致振动,通过分析振动响应以及尾流结构等特性,探究截面几何特征、来流角度、流速等参数对方柱流致振动特性的影响规律,以期为相关海洋领域设计提供参考。
1 数值方法 1.1 控制方程为了解释流体动力学中的流致振动,采用无量纲的N-S方程和粘性不可压缩流动的连续性方程:
| $ \frac{{\partial {u_i}}}{{\partial t}} + \left( {{u_j} - {\omega _i}} \right)\frac{{\partial {u_i}}}{{\partial {x_j}}} - \frac{1}{{{Re} }}\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}} + \frac{{\partial p}}{{\partial {x_i}}} = 0,$ |
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0。$ | (1) |
式中:ui为流体速度;ωj为第j个方向网格速度张量;p为压力;xi为笛卡尔坐标分量;雷诺数Re=DU∞/v,v为流体运动粘度;U∞为自由流速度。
本文采用剪切压力传输SST k-ω湍流模型,考虑湍流剪应力的输运效应,能对由压力梯度引起的分离现象模拟更加精准,表达式为:
| $ \begin{gathered} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}({\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}) + {G_k} - {Y_k} + {S_k},\\ \frac{{\partial (\rho \omega )}}{{\partial t}} + \frac{{\partial (\rho \omega {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}({\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega } 。\end{gathered} $ | (2) |
式中:Gk为层流速度梯度产生的湍流动能;Gω均为比耗散率;Γk、Γω均为方程扩散率;Yk、Yω均为扩散产生的湍流项;Dω、Sk、Sω均为正交发散项。
斯特劳哈尔数St为一个表征漩涡脱落的无量纲数,其与涡泄频率、结构直径和雷诺数有关,表达式为:
| $ {S_t} = \frac{{{f_s}D}}{U}。$ | (3) |
式中:fs为漩涡脱落频率,Hz;D为柱体特征长度,m;U为流速,m/s。
阻力系数
| $ C_{_{\text{l}}}^{'} = \frac{{2{F_{{L}}}}}{{\rho {U^2}D}},$ |
| $ {\overline C _{{d}}} = \frac{{2{F_{{D}}}}}{{\rho {U^2}D}}。$ | (4) |
式中:FL、FD分别为结构单位长度上的升力、阻力,N;ρ为流体密度,kg/m3。
1.2 控制方程方柱的横流向动力响应由二阶常微分方程无量纲形式控制:
| $ {\ddot y_{\left( t \right)}} + 4\pi {F_n}\zeta {\dot y_{\left( t \right)}} + {\left( {2{\text{π}} {F_n}} \right)^2}{y_{\left( t \right)}} = {{C_l^{'}} \mathord{\left/ {\vphantom {{C_l^{'}} {2{m^*}}}} \right. } {2{m^*}}} 。$ | (5) |
式中:
采用四阶Runge-Kutta法对控制方程进行求解,计算出每个时间步下结构对应的运动状态,基于此控制柱体运动和网格的更新。
| $ \left\{\begin{split} & {\ddot y_{\left( t \right)}} = \frac{{{F_{{\text{L}}\left( t \right)}}}}{m} - 2\zeta {\omega _n}{\dot y_{\left( t \right)}} - \omega _n^2{y_{\left( t \right)}},\\ & {\dot y_{\left( {t + \Delta t} \right)}} = {\dot y_{\left( t \right)}} + \frac{{\Delta t}}{6}\left( {{\beta _{\text{1}}} + 2{\beta _2} + 2{\beta _3} + {\beta _{\text{4}}}} \right),\\ & {y_{\left( {t + \Delta t} \right)}} = {y_{\left( t \right)}} + {\dot y_{\left( t \right)}}\Delta t + \frac{{{{\left( {\Delta t} \right)}^2}}}{6}\left( {{\beta _1} + {\beta _2} + {\beta _3}} \right)。\end{split} \right.$ | (6) |
式中,Δt为计算时间步长,中间函数的表达式为:
| $ {\left\{\begin{split} & {\beta _1} = \frac{{{F_{y\left( t \right)}}}}{m} - 2\zeta {\omega _n}{\dot y_{\left( t \right)}} - \omega _n^2{y_{\left( t \right)}} ,\\ & {\beta _2}=\frac{{{F_{y\left( t \right)}}}}{m} - 2\zeta {\omega _n}\left( {{{\dot y}_{\left( t \right)}} + \frac{{\Delta t}}{2}{K_1}} \right) - \omega _n^2\left( {{y_{\left( t \right)}} + \frac{{\Delta t}}{2}{{\dot y}_{\left( t \right)}}} \right),\\ & {\beta _3} =\frac{{{F_{y\left( t \right)}}}}{m} -2\zeta {\omega _n}\left( {{{\dot y}_{\left( t \right)}}+ \frac{{\Delta t}}{2}{K_2}}\right) - \omega _n^2\left( {{y_{\left( t \right)}} +\frac{{\Delta t}}{2}{{\dot y}_{\left( t \right)}} +\frac{{{{\left( {\Delta t}\right)}^2}}}{4}{K_1}} \right),\\ & {\beta _4} =\frac{{{F_{y\left( t \right)}}}}{m} -2\zeta {\omega _n}\left( {{{\dot y}_{\left( t \right)}} + \Delta t{K_3}} \right) -\omega _n^2\left( {{y_{\left( t \right)}}+\Delta t{{\dot y}_{\left( t \right)}} + \frac{{{{\left( {\Delta t} \right)}^2}}}{2}{K_2}} \right)。\end{split}\right.} $ | (7) |
为避免结构在振动过程中出现漩涡碰壁现象从而影响计算的准确性,本文的整体计算域大小设置为50D×40D。其中,D为结构的特征长度,计算域入口距离振动结构20D,出口距离振动结构30D,上下边界对称距离结构20D,本文流体域的阻塞比为2.5%,可忽略计算流体域选取对计算结果的影响。为了避免负网格造成的计算发散,选择了嵌套网格和动网格相结合的研究方法。计算域入口采用均匀流,侧向边界施加对称性条件,出口设置为完全出流条件;求解器采用基于压力的压力耦合求解器,算法为Couple算法;考虑计算结果的精度,采用二阶迎风格式进行空间离散、一阶隐式格式进行时间离散,柱体运动方程的求解用四阶Runge-Kutta并通过UDF实现。
考虑参数y+≈1的影响,在柱面附近的第一级网格间距设置为离柱面0.006D,在法线方向上,网格间距以1.05的扩展速率增加,本文计算域网格质量均可保证在0.9以上,图1为本文验证网格独立性所采用的4套网格。本文整体网格分为2种类型,即可以定义为背景网格(灰色网格)和黑色网格(前置网格),嵌套网格可避免传统动网格技术面临的网格动态更新时易出现的负体积问题,始终保持较高网格质量。

|
图 1 不同疏密程度网格示意图 Fig. 1 Schematic diagram of different density grid |
以Re=2.2×104下的方柱绕流为例,对4种疏密程度不同的网格进行网格收敛性分析。表1给出4套网格密度计算得到的平均阻力系数、均方根升力系数和无量纲涡脱频率斯特劳哈尔数及各结果的相对误差情况。由表可知,当网格数量达到13万以上后计算误差较小,结果趋于稳定。综合计算成本和效率,该计算工况选取178115网格密度进行模拟。
|
|
表 1 网格收敛性分析 Tab.1 Basic parameters of square cylindrical model |
为验证本文选取计算方法、网格划分方式的正确性,选取方柱在Re = 2.2×104工况的数值模拟结果与相关参考文献的研究结果进行对比,观察表2可知,数值结果与各参考文献中的参考数值较为接近,证明本文后续开展的数值模拟具有可靠性。
|
|
表 2 Re = 2.2×104时方柱绕流计算结果比较 Tab.2 Comparison of flow results of a sinlge square cylinder at Re = 2.2×104 |
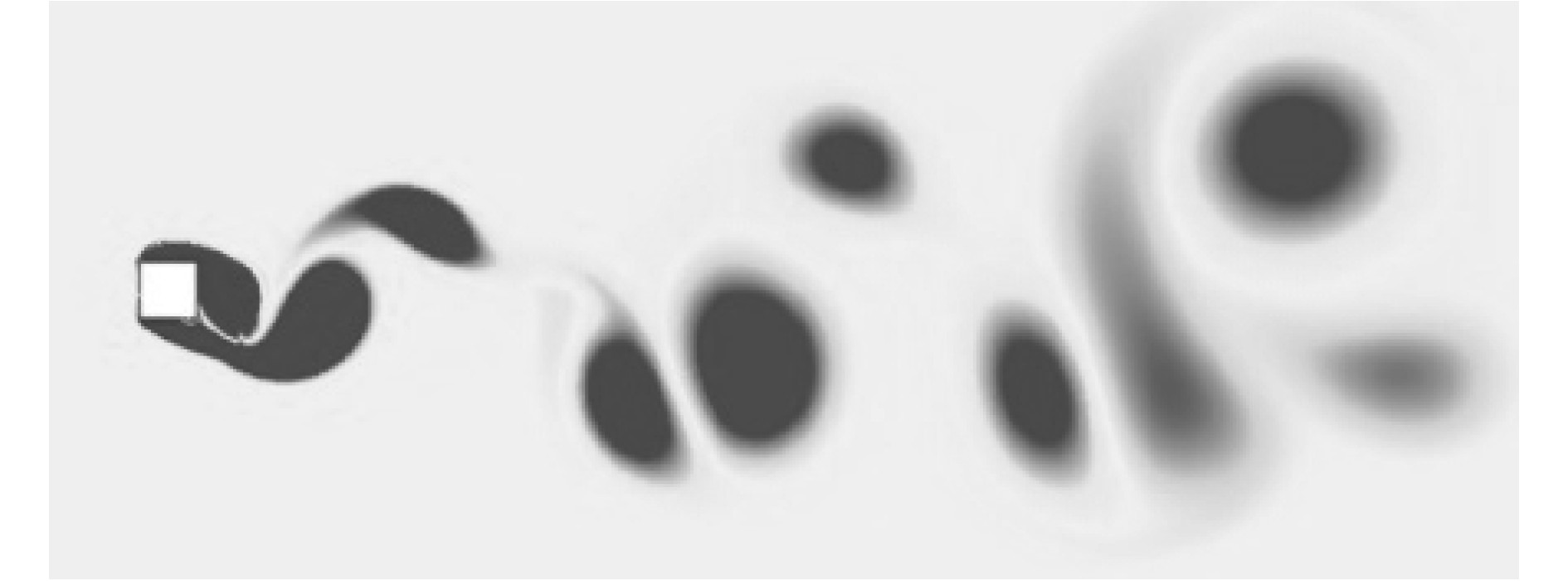
图2给出了Re = 2.2×104时,方柱固定绕流下的尾流结构图,在方柱中观察到P+S漩涡脱落模式,即一个振动周期内有一对漩涡和一个单涡脱落。
|
图 2 Re = 2.2×104时方柱的尾流结构 Fig. 2 Vortex patterns of square cylinder at Re = 2.2×104 |
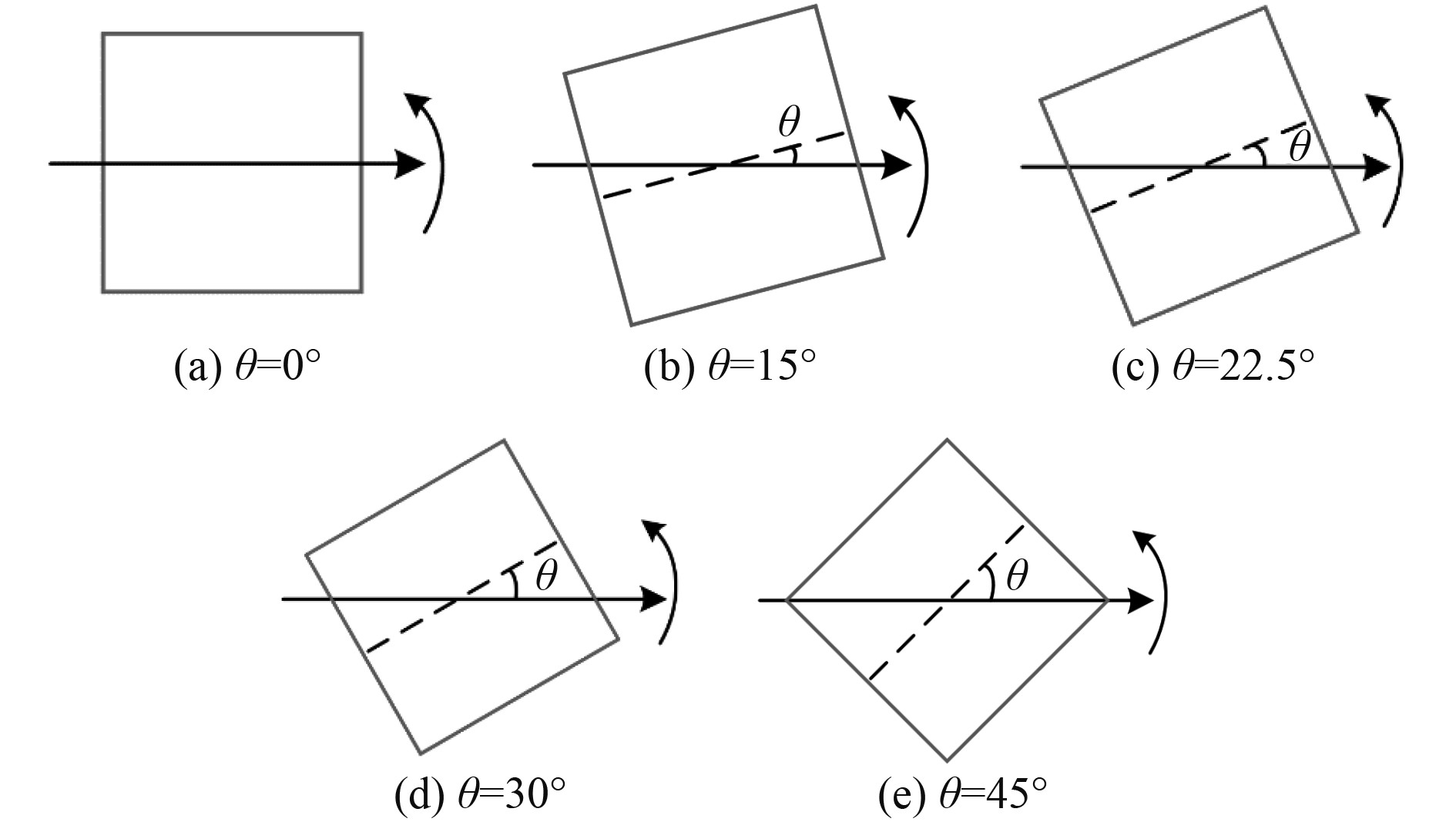
方形截面为目前研究和实现驰振响应的理想模型,为了探究方柱的流致振动特性,本文主要对5种不同来流角度(0°、15°、22.5°、30°、45°)下的方柱流致振动进行数值模拟,如图3所示。
|
图 3 方柱不同来流角度示意图 Fig. 3 Diagram of square cylinder with different incoming flow angles |
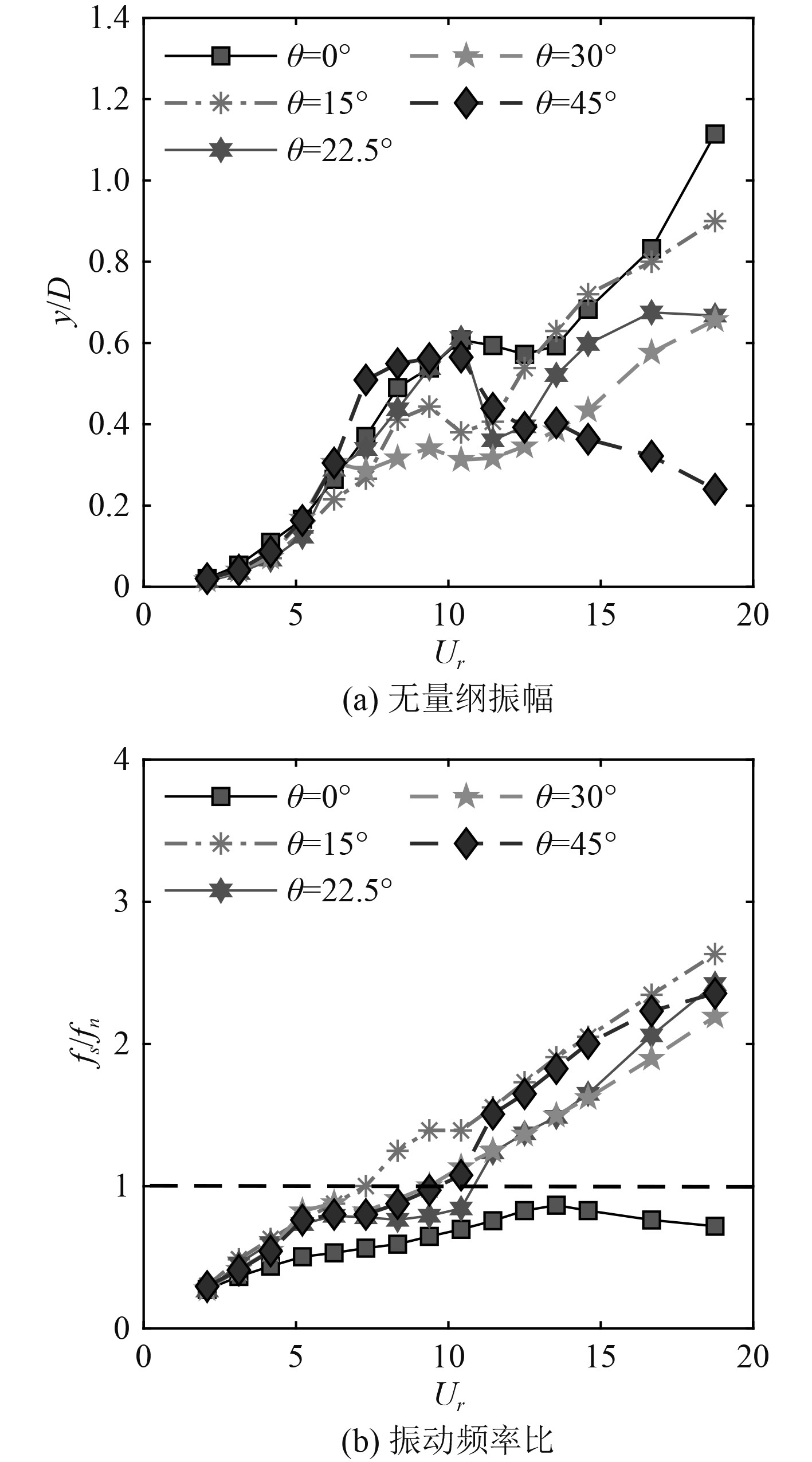
图4为不同来流角度θ下方柱的振动振幅、频率比随约化速度的变化趋势,明显观察到不同来流角度下的方柱振动响应存在区别,具体表现为:
|
图 4 方柱在不同来流角度θ下振动响应 Fig. 4 Response of square cylinder at different incident angle θ |
1)θ=0°时,方柱的振动响应规律与其他工况下的存在明显区别。方柱振动响应分为:涡激振动初始分支(2.08 ≤Ur ≤5.21)、涡激振动上分支(5.21<Ur ≤12.5)和驰振分支(Ur >12.5)这3个阶段,振动过程中振幅随约化速度的增加而呈现增大的趋势,频率比随约化速度的增加而呈现出先增加后减小的趋势,但频率比数值始终小于1。该工况下,方柱振动并未出现圆柱涡激振动的“锁定区间”以及“自限性”振动特性,而更多表现出低频高幅的驰振基本特性。
2)θ≠0°时(15°、22.5°、30°),方柱在这3种来流角度下,振动响应特性呈现出相似的变化规律,仅在数值上存在差异。振动分支为涡激振动初始分支(2.08 ≤ Ur ≤ 5.21)、涡激振动上分支(5.21 < Ur ≤ 11.46)以及高频高幅分支(Ur >11.46)。其中,频率比随约化速度的增加而呈现持续升高的趋势,Names等[23]认为高频高振幅响应分支是由涡激振动与驰振共同作用形成的共振分支,上述3种工况下方柱振动受涡激振动与驰振相互影响,振动较为复杂。
3)θ = 45°时,方柱的振动响应规律与圆柱振动响应类似,方柱振动响应主要分为:涡激振动初始分支(2.08 ≤Ur ≤5.21)、涡激振动上分支(5.21 <Ur ≤11.46)和涡激振动下分支(Ur >11.46)这3个阶段。其中,频率比随约化速度的增加而呈现上升趋势,振幅随约化速度的增加而呈现先增大保持稳定再下降的趋势。在θ=45°下,方柱振幅出现类似圆柱涡激振动的“锁定区间”,体现出圆柱涡激振动“自限性”的振动特性。由此表明,θ=45°工况下的方柱流致振动响应为涡激振动响应。
3.2 相位分析相位图能直观的描述结构振动与流场能量交换之间的关系。若升力与振动位移同步变化,则流体力做正功,流场促进柱体振动,反之则抑制振动。按照笛卡尔坐标系将相位图分为4个象限,定义当相位图位于一、三象限时,此时能量由流体流向结构,促进振动;而当相位图位于二、四象限时,相位图呈反相分布,抑制振动。
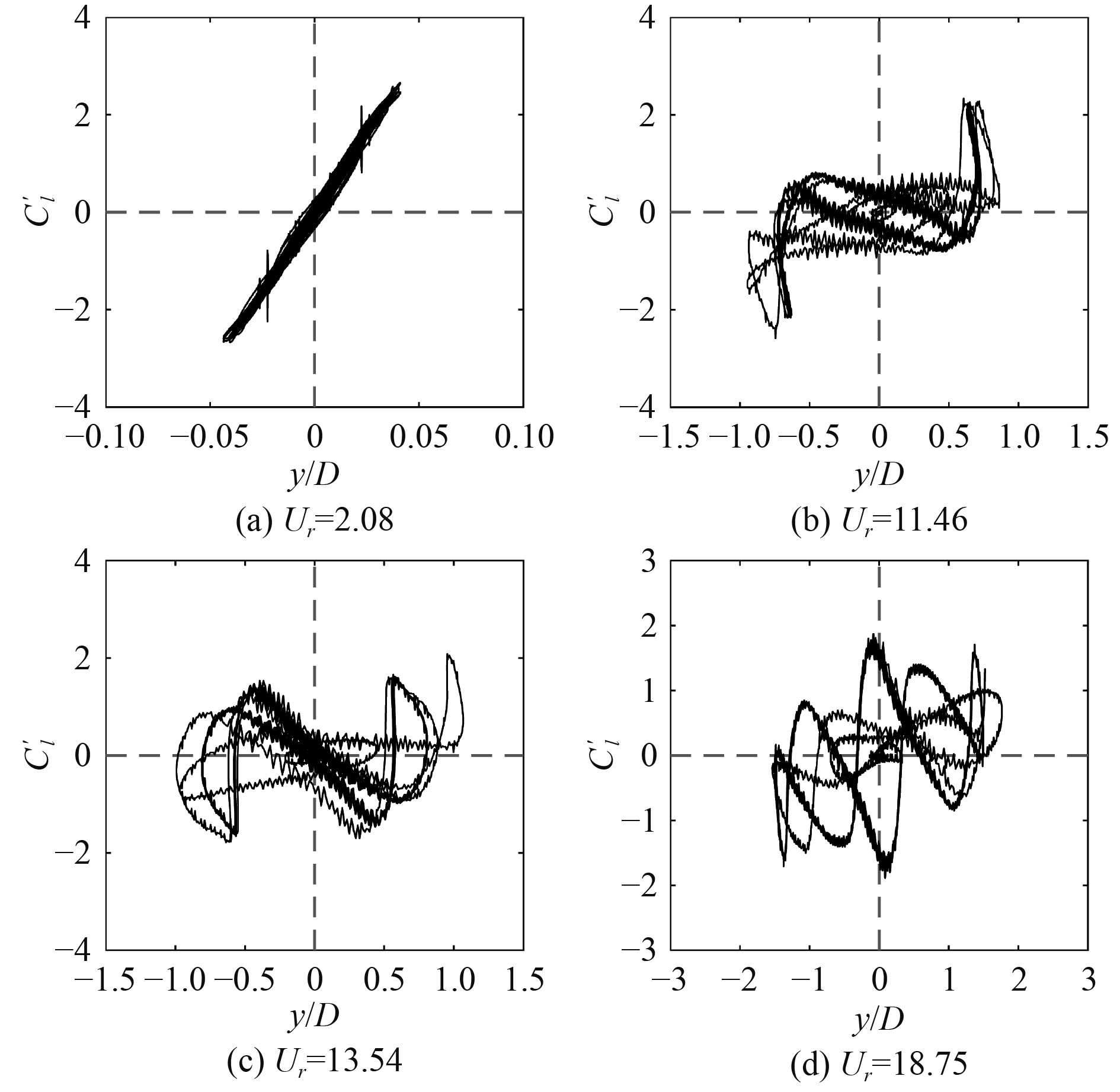
图5为方柱在来流角度θ =0°时,横流向位移和升力系数之间的相位关系图。在涡激振动分支时,如图5(a),相位图位于一、三象限,此阶段下柱体所受流体力与振动位移呈现出同相的状态,随着约化速度的增加,相位开始发生转变,如图5(b);当响应转换为驰振时,图5(c)中相位图位于二、四象限的占比增大,此时由于能量交换不稳定,但未完全“反相”;进入驰振分支后,图5(d)中相位图出现“回归”一、三象限的趋势,此阶段振幅持续增大,能量从流场流向结构。
|
图 5 0°下方柱振动振幅与升力系数的相位关系 Fig. 5 Phase relationship between vibration amplitude and lift coefficient of square cylinder at 0° |
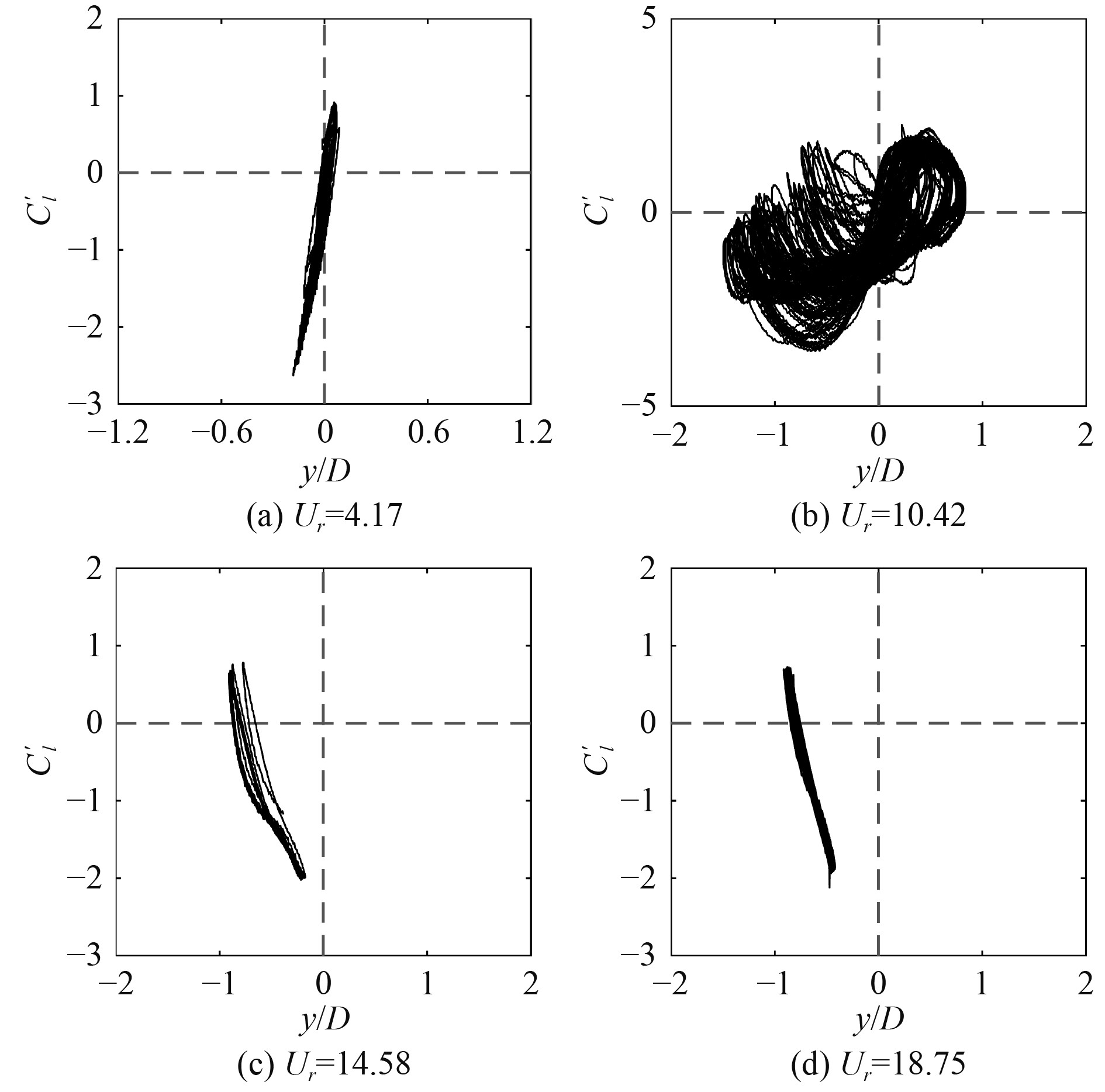
图6为方柱在来流角度θ=22.5°下的相位关系图,相位图整体向下偏移。在涡激振动初始分支,如图6(a)所示相位图主要分布在一、三现象;当进入高频高幅分支后,如图6(c)和图6(d)所示,相位图位于二、三象限,且随着流速的增大,第三象限占比较大,这也导致振动幅值没有出现大幅下降的现象。
|
图 6 22.5°下方柱振动振幅与升力系数的相位关系 Fig. 6 Phase relationship between vibration amplitude and lift coefficient of square cylinder at 22.5° |
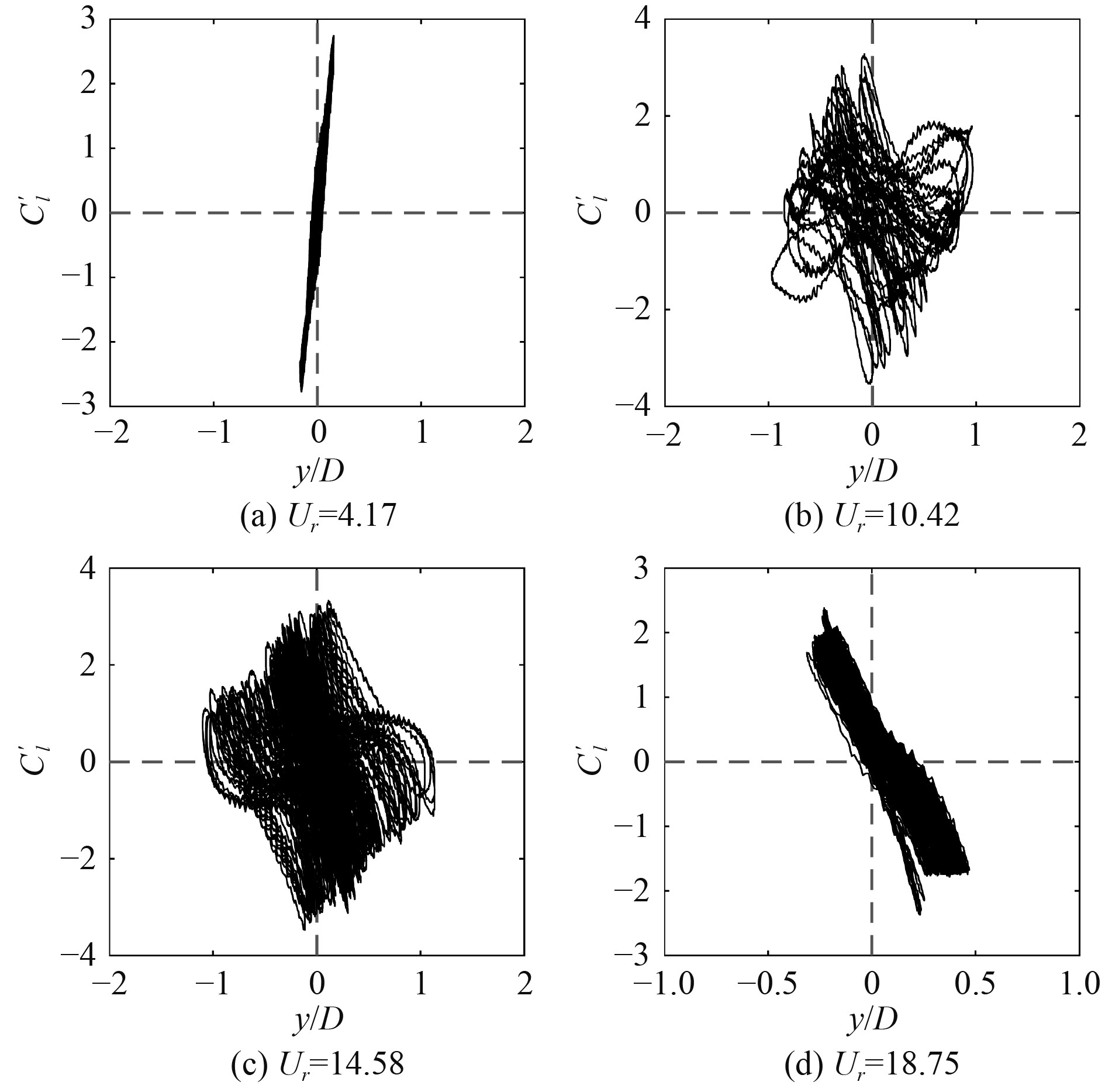
图7给出了方柱在来流角度θ = 45°时的相位关系图,整体呈现从“同相”到“反相”的变化过程,在涡激振动上分支时,如图7(a)所示,此时流场能量流向结构;进入上分支后,此时能量交换较为平衡,见图7(b)和图7(c);当进入下分支后,如图7(d)所示,此阶段处于“反相”过程,能量由结构流向流场,导致振幅减小。
|
图 7 45°下方柱振动振幅与升力系数的相位关系 Fig. 7 Phase relationship between vibration amplitude and lift coefficient of square cylinder at 45° |
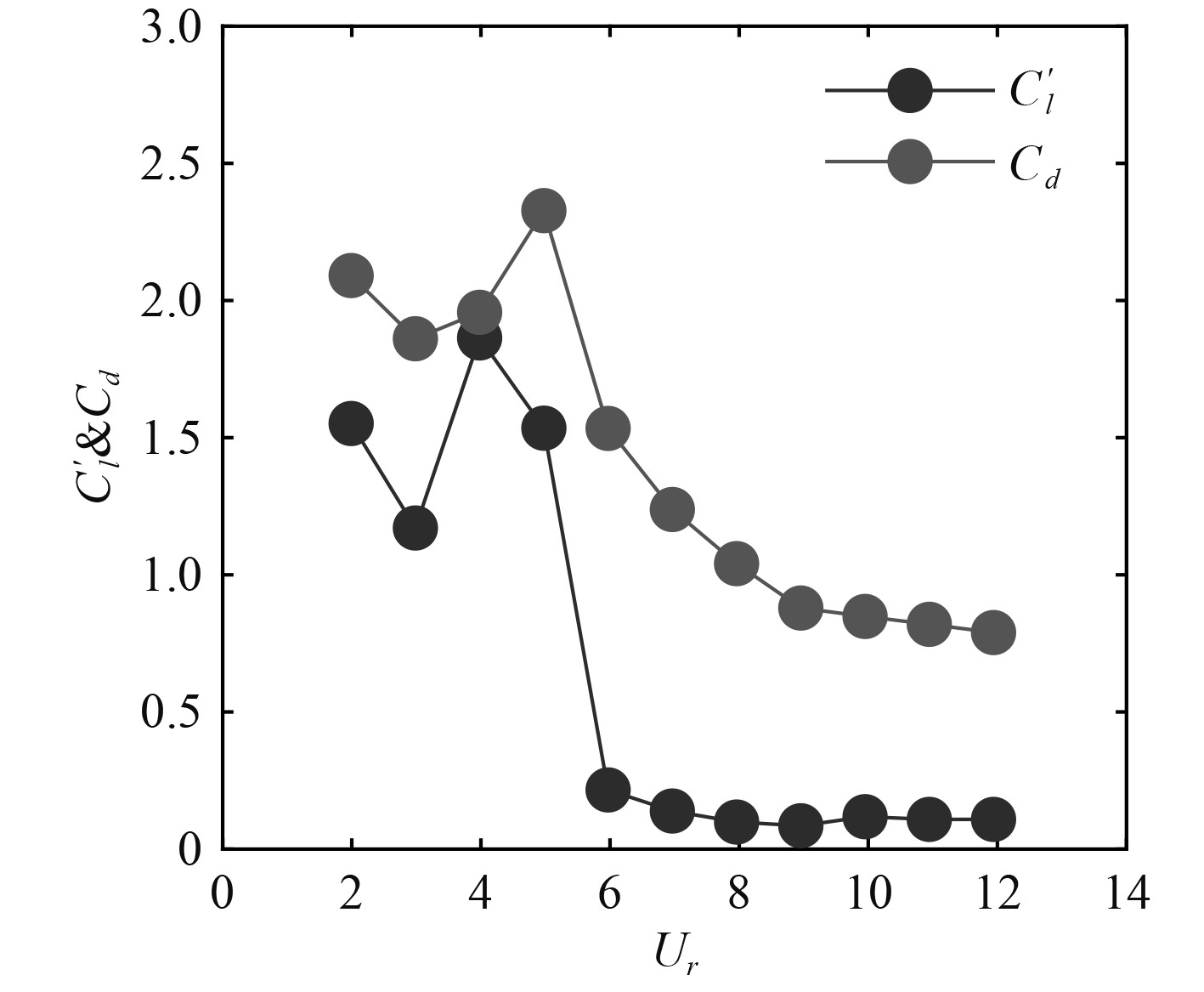
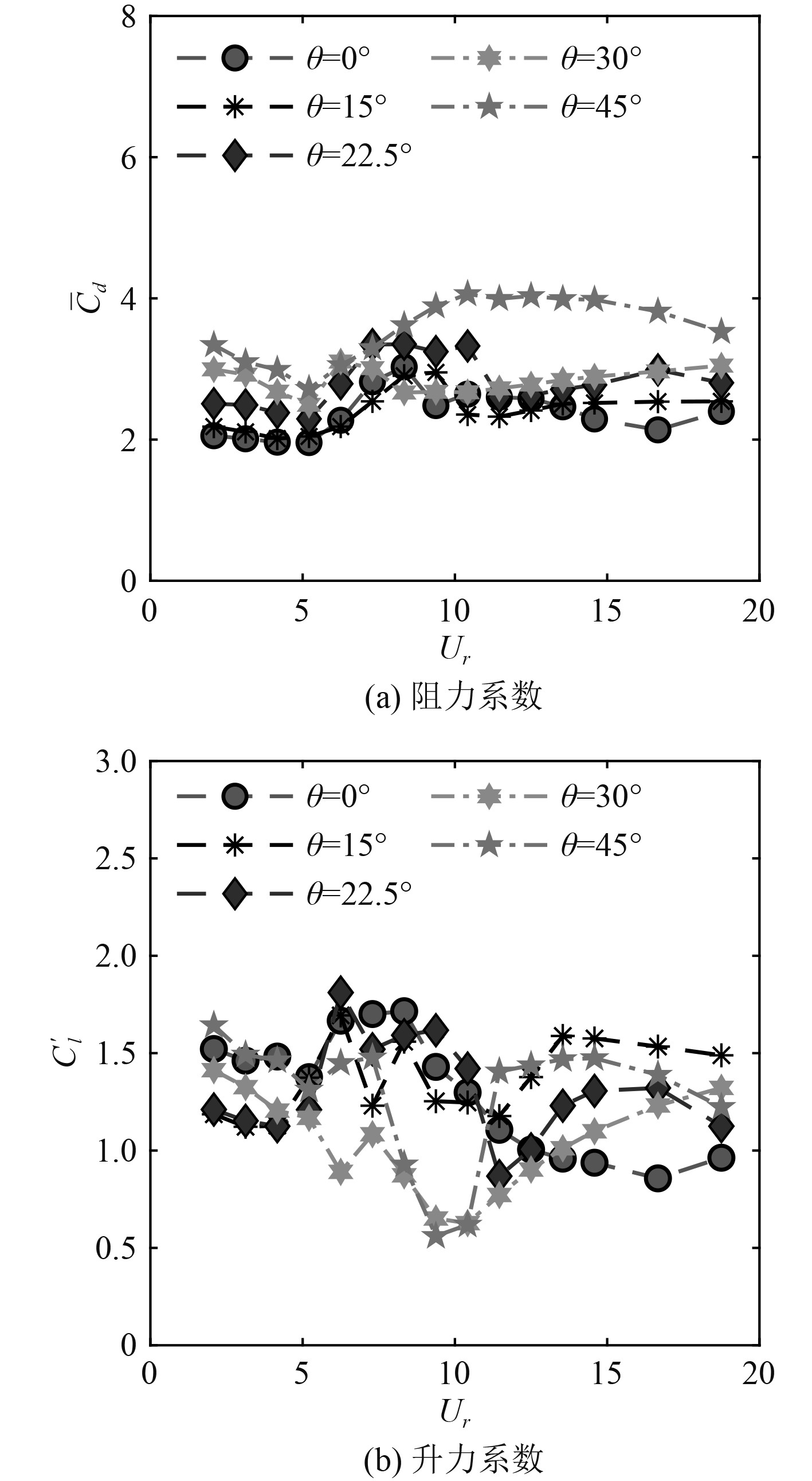
为探究方柱的升阻力变化趋势,图8为相同数值模拟条件下的孤立圆柱的受力特性进行对比,其阻力系数与升力系数随约化速度的变化过程总体相似,表现为先增后减的两段式进程。图9为不同来流角度下方柱的升阻力系数变化趋势,观察可发现,所有工况下的阻力系数变化趋势相似,整个振动过程中来流角度为45°时阻力系数最大,30°、22.5°、15°依次减小,是因为不同来流角度下的方柱流向投影长度存在差异,结构的压差阻力随投影长度的增加而增大,与孤立圆柱相比,方柱阻力系数没有出现大幅下降的现象。
|
图 8 孤立圆柱升阻力系数 Fig. 8 Lift and drag coefficient of isolated cylinder |
|
图 9 不同来流角度下方柱升阻力系数 Fig. 9 Lift and drag coefficient of square cylinder under different flow Angle |
方柱的升力系数变化趋势也相似,其中来流角度0°时方柱在Ur>8.33后,升力系数持续下降后有增加的趋势,但与孤立圆柱相比下降趋势减缓,是由于方柱进入驰振分支后,此时振动具有“自激性”,不受漩涡脱落和固有频率的影响;在来流角度45°下,7.29≤Ur≤11.46范围内,升力系数出现剧烈波动,是由于此时方柱处于“共振”区间,结构振动受到漩涡脱落的影响,此时结构升力波动性较大,振动不稳定。
本文对来流角度0°、15°下的方柱尾流结构图进行分析,根据不同的分支来观察漩涡类型,进一步分析柱体的振动响应与尾涡类型的关系。
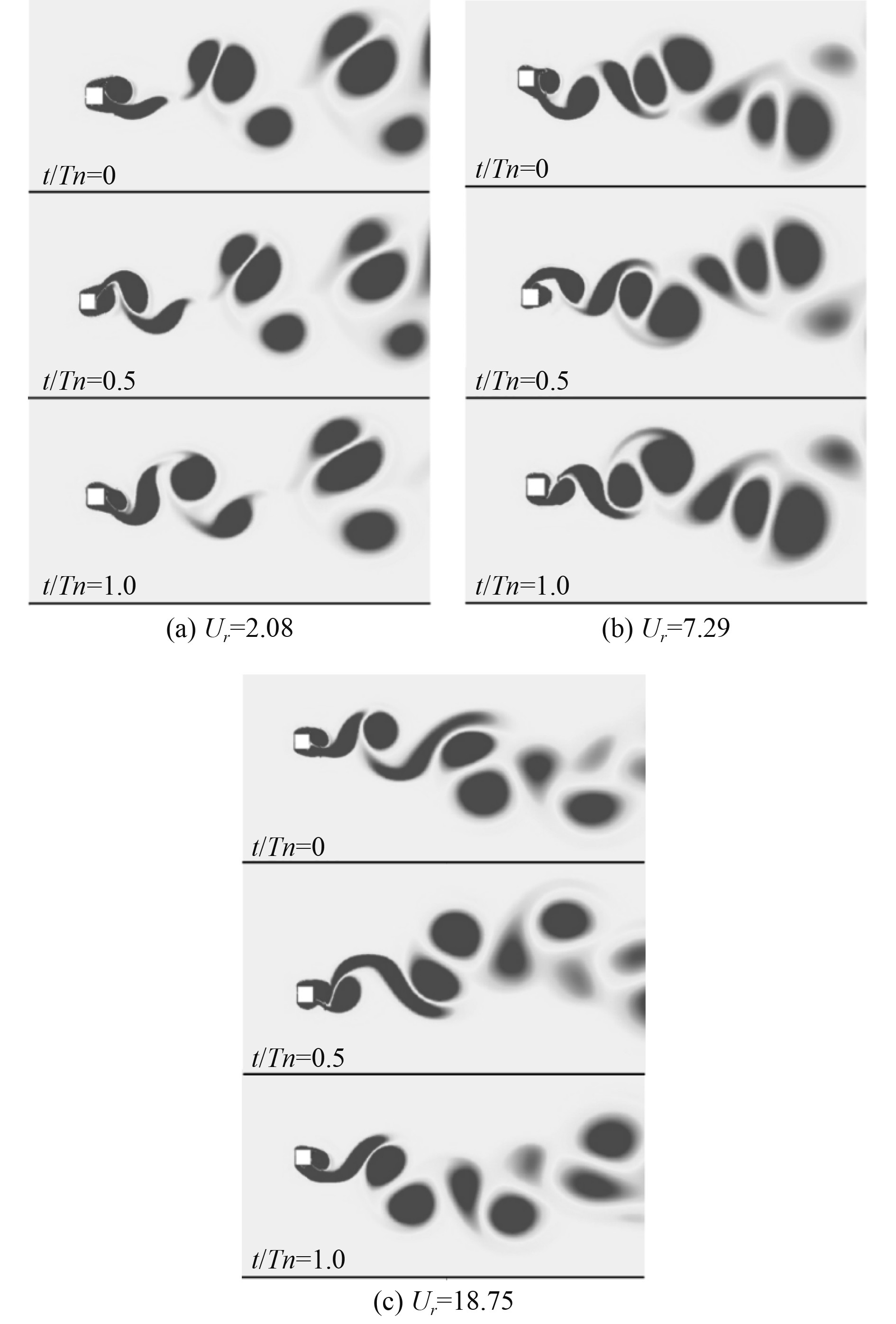
来流角度0°下方柱发生驰振响应。如图10(a)为初始分支时的方柱尾涡结构,在一个完整的振动周期内观察到“P+S”的漩涡脱落模式。图10(b)为上分支时的方柱尾涡结构,此时表现为“2P+2S”的漩涡脱落模式,在一个周期内,方柱上脱落6个漩涡;图10(c)为发生驰振的方柱尾涡结构,此时漩涡脱落模式为“4P+2S”,一个周期内有10个漩涡脱落,此阶段尾流涡街较宽且整体出现偏移,这也导致了方柱呈低频振动。
|
图 10 0°下方柱尾流涡结构 Fig. 10 Wake vortex structure of square cylinder under 0° |
来流角度15°下方柱在涡激振动与驰振共同作用发生振动响应。图11(a)所示为初始分支时的方柱尾涡结构,观察到“2S”的漩涡脱落模式,图11(b)所示为上分支时的方柱尾涡结构,此时表现为“P+S”的漩涡脱落模式,尾涡密度较小;图11(c)为涡激振动与驰振共同作用下的方柱尾涡结构,此时涡脱模式为“2S”,呈现出明显的卡门涡街规律性,但涡街较宽且尾涡强度较强,这也导致了方柱的大幅振动。

|
图 11 15°下方柱尾流涡结构 Fig. 11 Wake vortex structure of square cylinder under 15° |
1)来流角度是影响方柱流致振动响应和振动分支模式的重要因素。当来流角度0°时,方柱振动分支为初始分支、上分支和驰振分支,发生驰振响应;当来流角度为15°、22.5°、30°时,振动分支为初始分支、上分支和高频高幅分支,方柱产生涡激振动与驰振相互作用的振动响应;当来流角度为45°时,振动分支为初始分支、上分支和下分支,方柱发生涡激振动响应。
2)结构振动位移与升力之间的相位关系影响结构的振动。当处于“同相”时,能量由流场流向柱体结构,促进振动的发生,当处于“反相”时,能量由柱体结构流向流场,抑制柱体的振动。
3)尾流结构对振动的影响显著。尾流涡街发生偏移且周期内漩涡脱落丰富导致柱体发生低频高幅的驰振,在涡激振动与驰振共同作用下,较强的尾涡强度也能维持结构的大幅振动。
4)从能量俘获角度,可通过控制非圆柱体的来流角度实现大范围流速下的能量汲取。控制来流角度使方柱发生驰振响应,从而实现能量的汲取。
| [1] |
王项南, 麻常雷. “双碳”目标下海洋可再生能源资源开发利用[J]. 华电技术, 2021, 43(11): 91-96. |
| [2] |
王颖, 韩光, 张英香. 深海海洋工程装备技术发展现状及趋势[J]. 舰船科学技术, 2010, 32(10): 108-113+124. |
| [3] |
刘振雷, 娄敏, 王晓凯, 等. 不同间距比下串联圆柱涡激振动数值模拟研究[J]. 舰船科学技术, 2022, 44(22): 76-82. |
| [4] |
ZHU Hongjun, ZHAO Ying, ZHOU Tongming. CFD analysis of energy harvesting from flow induced vibration of a circular cylinder with an attached free-to-rotate pentagram impeller[J]. Applied Energy, 2018, 212: 304-321. DOI:10.1016/j.apenergy.2017.12.059 |
| [5] |
WANG Jiasong, FAN Dixia, LIN Ke. A review on flow-induced vibration of offshore circular cylinders[J]. Journal of Hydrodynamics, 2020, 32: 415-440. DOI:10.1007/s42241-020-0032-2 |
| [6] |
韩鹏, 潘光, 黄桥高, 等. 雷诺数对于方柱流致振动能量收集系统的影响[J]. 西北工业大学学报, 2020, 38(5): 928-936. |
| [7] |
邵禄宇, 白旭, 牛建杰, 等. 不同流速下磁悬浮支撑单圆柱振子流致振动响应分析[J]. 舰船科学技术, 2023, 45(4): 14-17. |
| [8] |
LOU Min, WANG Yu, QIAN Gang, et al. Investigation on the vortex-induced vibration active control of the riser in the "lock-in" region based on adaptive fuzzy sliding mode theory[J]. Ocean Engineering, 2021, 238: 1-17. |
| [9] |
张乾坤, 王博涵, 陈海龙, 等. 加强形式对翼型结构流致振动的影响[J]. 舰船科学技术, 2021, 43(1): 43-47. |
| [10] |
BERNITSAS M M, RAGHAVAN K, et al. VIVACE(Vortex Induced Vibration Aquatic Clean Energy): A new concept in generation of clean and renewable energy from fluid flow[C]//25th International Conference on Offshore Mechanics and Arctic Engineering, 2008.
|
| [11] |
HARTOG J P D. Transmission line vibration due to sleet[J]. Electrical Engineering, 1932, 51: 1-3. DOI:10.1109/EE.1932.6430091 |
| [12] |
PARKINSON G V, SMITH J D. The square prism as an aeroelastic nonlinear oscillator[J]. Journal of Mechanics and Applied Mathematics, 1964, 17: 225-239. DOI:10.1093/qjmam/17.2.225 |
| [13] |
WHITE W N. An analysis of the influence of support stiffness on transmission line galloping amplitudes[D]. New Orleans: Tulane University, 1985.
|
| [14] |
邓见, 任安禄, 邹建锋. 方柱绕流横向驰振及涡致振动数值模拟[J]. 浙江大学学报:工学版, 2005, 39(4): 595-599. |
| [15] |
SU Z, LIU Y, ZHANG H. Numerical simulation of vortex-induced vibration of a square cylinder[J]. Journal of Mechanical Science and Technology, 2007, 21(9): 1415-1424. DOI:10.1007/BF03177428 |
| [16] |
BARRERO G A, FERNANDEZ A P. Maximum vortex-induced vibrations of a square prism[J]. Wind & Structures an International Journal, 2013, 17(1): 107-121. |
| [17] |
MANZOOR S, KHAWAR J, SHEIKH N A. Vortex-induced vibrations of a square cylinder with damped free-end conditions[J]. Advances in Mechanical Engineering, 2013, 5: 1-12. |
| [18] |
LI Xintao, ZHEN Lyu, KOU Jiaqing, et al. Mode competition in galloping of a square cylinder at low Reynolds number[J]. Journal of Fluid Mechanics, 2019, 867: 516-555. DOI:10.1017/jfm.2019.160 |
| [19] |
练继建, 燕翔, 刘昉, 等. 正方形截面振子在不同来流方向的单自由度流致振动特性研究[J]. 振动与冲击, 2017, 36(15): 29-35. |
| [20] |
胡德江. 不同截面形状柱体流致振动特性实验研究[D]. 重庆: 重庆大学, 2016.
|
| [21] |
TRIAS F X, GOROBETS A, OLIVA A. Turbulent flow around a square cylinder at Reynolds number 22000: A DNS study[J]. Computers & Fluids, 2015, 123: 87-98. |
| [22] |
LYN D A, EINAV S, RODI W. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Fluid Mechanics, 1995, 304: 285-319. DOI:10.1017/S0022112095004435 |
| [23] |
NEMES A, ZHAO J, LO JACONO D, et al. The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack[J]. Fluid Mechanics, 2012, 710: 102-30. DOI:10.1017/jfm.2012.353 |
 2024, Vol. 46
2024, Vol. 46
