2. 中国船舶及海洋工程设计研究院,上海 200011;
3. 中国船舶工业系统工程研究院,北京 100036
2. Marine Design and Research Institute of China, Shanghai 200011, China;
3. Systems Engineering Research Institute, Beijing 100036, China
爆炸冲击波载荷的大小及分布特征是判定结构毁伤模式和定量分析结构毁伤效果的基础,准确获得板架结构的爆炸冲击载荷具有重要意义。现有学者对爆炸冲击波的传播规律、冲击波与不同结构物的相互作用过程以及结构物表面的爆炸载荷进行研究,如Henrych等[1]根据实验结果给出了爆炸冲击波超压和正反射压力峰值的计算方法,在工程上获得了较高的精度和便利性。美国在技术手册TM5-1300[2,3]中,根据一系列的试验和数值研究结果,建立了适用于工程计算的公式和图表来计算作用在结构上的反射超压时程曲线的各个参数。Geretto等[4]通过试验研究了不同约束条件下不同厚度靶板的变形与爆炸载荷的关系。Held等[5]利用加速度装置得到了爆炸作用下装甲钢板的形变量,为爆炸载荷获取的试验方法提供了思路。Anderson等[6]通过一系列的爆炸试验讨论了板结构对爆炸载荷的影响。在国内,候俊亮等[7]对球形及不同长径比圆柱形装药冲击波场及其传播过程进行数值模拟,得到了爆炸载荷下的挠度时间曲线。Shi等[8]对地面爆炸时爆距为10 m条件下墙柱表面的爆炸载荷进行了数值计算,并基于数值计算结果给出了柱表面爆炸压力时程曲线经验公式。李臻等[9]使用PBM方法对接触爆炸和近爆的载荷特性进行研究,并基于量纲分析推导出了比冲量的经验公式。汪维等[10,11]对近爆作用下结构表面的爆炸载荷确定方法进行研究,建立了外爆作用下结构表面爆炸载荷分布函数。陈鹏宇等[12]将舱室壁面在空间分布上分为中间非角隅区两面角隅区和三面角隅区,建立了舱内爆炸下目标壁面所受载荷的简化计算模型,提出了目标壁面所受总冲量的简化计算方法。姚熊亮等[13]对舰船舱内爆炸载荷特征进行研究,为舱内爆载荷的特征与结构毁伤提供较为合理的预报方法。
然而,目前用于计算结构物表面爆炸载荷的经验公式多为基于结构刚体假定,对于远离爆炸源且变形较小的结构物可以进行合理的预测,但对于近爆或变形较大的结构物,用该方法计算的爆炸载荷与实际作用的有一定区别。因此,为明确大变形结构迎爆面上载荷的具体形式与特征,本文对爆炸冲击波与固支圆板的相互作用过程进行数值模拟,获取变形圆板表面爆炸载荷的分布规律,并结合量纲分析,推导变形圆板表面任意一点处爆炸载荷的计算公式。
1 数值仿真 1.1 有限元模型由于研究问题具有中心对称性,采用Autodyn软件建立二维轴对称模型进行模拟计算。其中空气域采用Euler单元,尺寸为1 200 mm×800 mm,网格大小为5 mm×5 mm,除对称轴外的边界设为流出边界条件,以模拟无限空气域。圆板材料为Q235钢,采用Lagrange单元,半径为300 mm,厚度为8 mm,网格大小为10 mm×8 mm,边缘设置固支边界条件。爆源采用TNT球形裸装药,当量为10 kg,起爆方式为中心起爆,在圆板正前方500 mm处起爆。在圆板迎爆面上距圆心0、60 mm、120 mm、180 mm、240 mm处设置监测点,以研究冲击波分布规律,在冲击波传播阶段,利用映射技术将一维计算结果映射到二维模型中,以提高计算精度,有限元计算模型如图1所示。

|
图 1 2D有限元计算模型 Fig. 1 2D Finite element calculation model |
采用理想气体状态方程来描述空气域,即
| $ P = \left( {\gamma - 1} \right)\rho {e_0}。$ | (1) |
式中:
采用JWL状态方程来描述炸药爆轰过程中所产生气体的急剧扩张过程,即
| $ P = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \frac{{\omega e}}{V} 。$ | (2) |
式中:
|
|
表 1 装药JWL状态方程参数[14] Tab.1 JWL state equation parameters of charge |
圆板材料为Q235钢,采用Johnson-Cook强度模型,不设置失效模型,即
| $ \sigma {\text{ = }}\left( {A + B{\varepsilon ^n}} \right)\left( {1 + C\ln {{\dot \varepsilon }^*}} \right)\left( {1 - {T^{*m}}} \right)。$ | (3) |
式中:
|
|
表 2 Q235钢Johnson-Cook强度模型参数[15] Tab.2 Johnson-Cook strength model parameters of Q235 steel |
在冲击波到达圆板之前,其传播可以看作是在空气自由场中传播,Henrych[1]提出了装药在无限空气中爆炸的超压峰值经验公式,即
| $ \begin{split} \left\{\begin{array}{l} \Delta {P}_{m}=\frac{1.4072}{\overline{R}} + \frac{0.554}{{\overline{R}}^{2}}-\frac{0.0357}{{\overline{R}}^{3}}\text{ + }\frac{0.000625}{{\overline{R}}^{4}},\text{0}\text{.05}\leqslant \overline{R}\leqslant 0.3 ,\\ \Delta {P}_{m}=\frac{0.6194}{\overline{R}} + \frac{0.0326}{{\overline{R}}^{2}} + \frac{0.2132}{{\overline{R}}^{3}},\,\qquad\quad \text{0}\text{.3}<\overline{R}\leqslant 1 ,\\ \Delta {P}_{m}=\frac{0.066}{\overline{R}} + \frac{0.405}{{\overline{R}}^{2}} + \frac{0.3288}{{\overline{R}}^{3}},\qquad\quad\;\;\;\;\text{1}<\overline{R}\leqslant \text{10}。\end{array}\right.\\[-1pt] \end{split} $ | (4) |
式中:
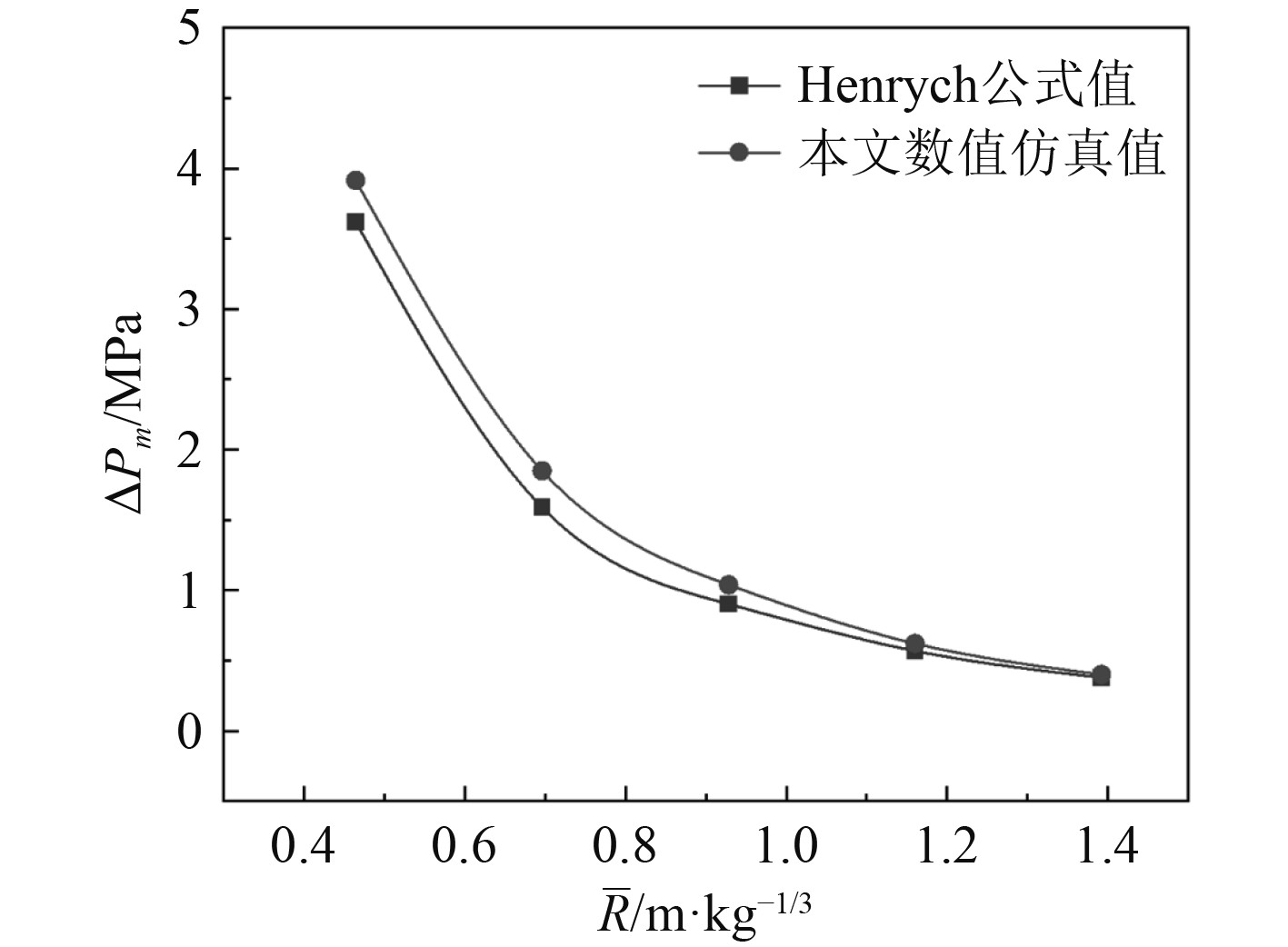
将不同监测点处的冲击波超压峰值和经验公式值进行对比,如图2所示,两者超压曲线变化趋势基本一致,且在误差允许范围之内。
|
图 2 各监测点的超压峰值曲线 Fig. 2 Overpressure peak curves of each monitoring point |
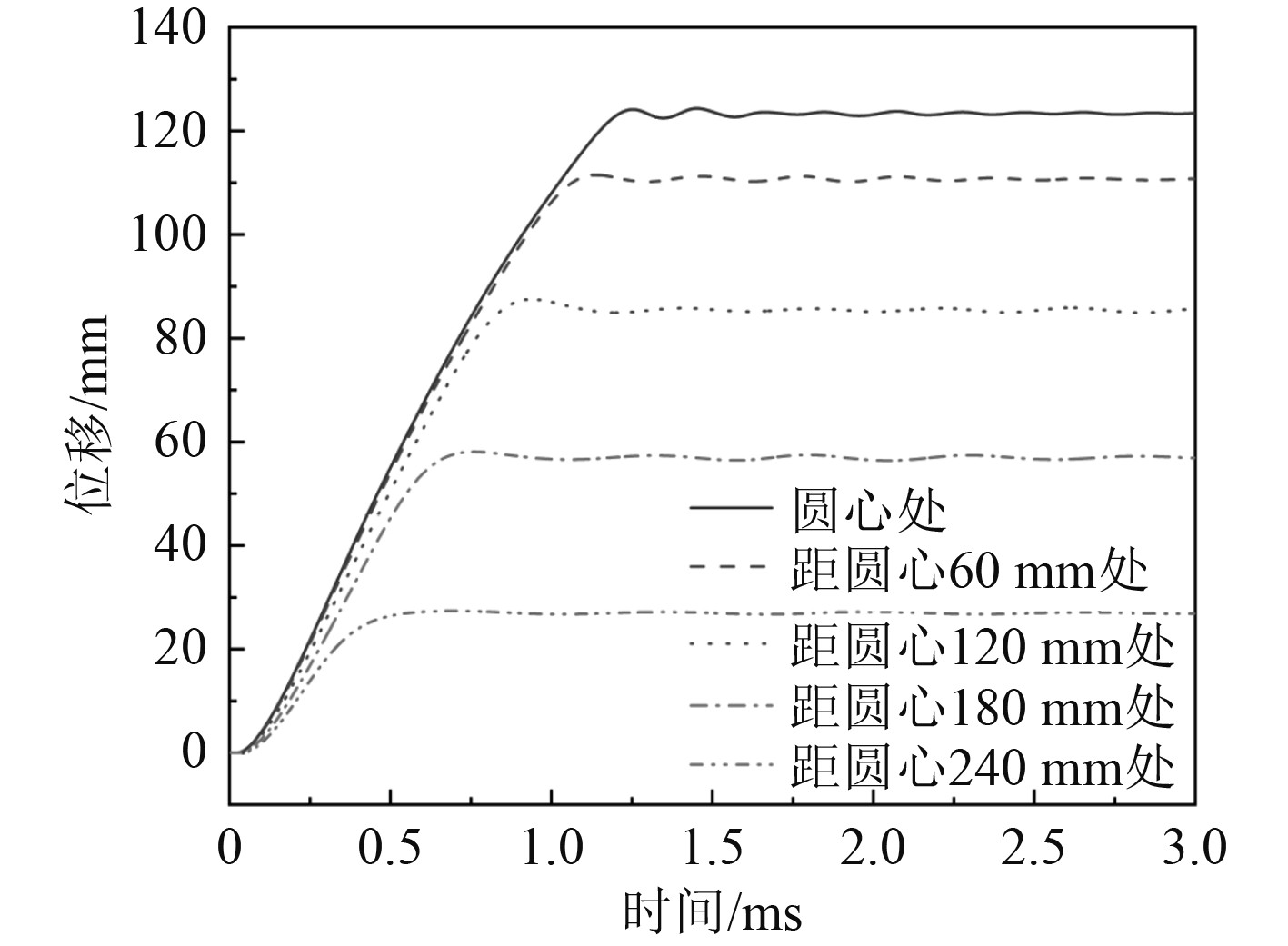
图3为爆炸冲击波的传播及其与固支圆板的相互作用过程,在0.1 ms时,冲击波以球面波的形式向外传播;在0.12 ms时,冲击波传播至圆板迎爆面并发生反射;在0.19 ms时,冲击波绕过圆板,产生绕射现象;在0.29 ms时,圆板发生了明显的塑性变形。圆板上各点位移曲线如图4所示,圆板发生大挠度塑性变形,约1.25 ms后各点位移稳定在某一数值附近。

|
图 3 爆炸波传播与板相互作用过程 Fig. 3 Blast wave propagation and its interaction with the plate |
|
图 4 圆板不同位置处位移曲线 Fig. 4 Displacement curves of circular plate at different positions |
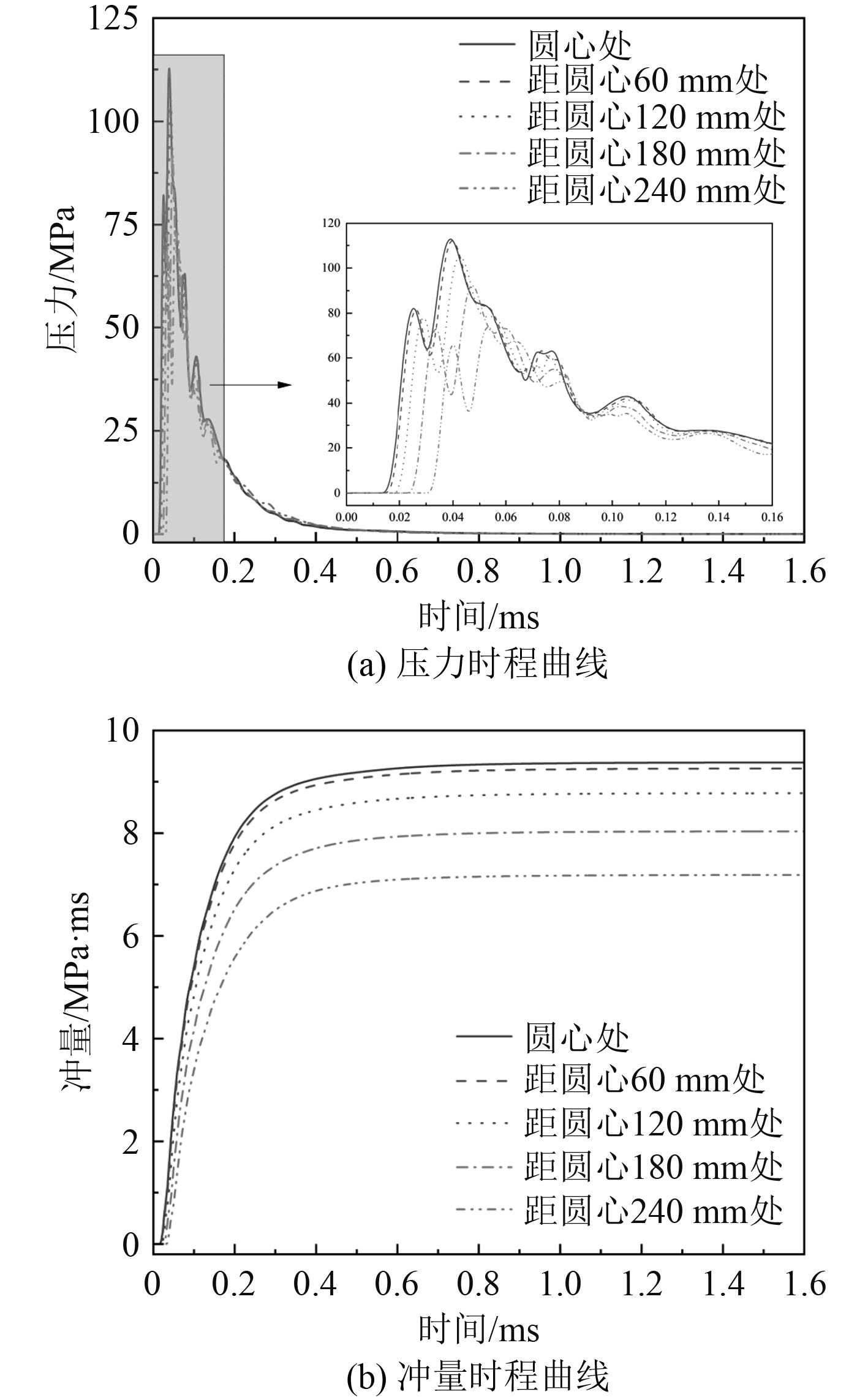
图5为在爆炸冲击波与板相互作用过程中,5个监测点的爆炸压力与冲量时程曲线。可知:在圆板的迎爆面爆炸载荷的分布非均匀,各监测点的压力和冲量时程曲线变化趋势基本一致,但随着监测点距圆心距离的增加,压力峰值和冲量逐渐减小,压力峰值到达的时间逐渐增加,距圆心240 mm处的压力峰值和最大冲量相对圆心处分别减小了34.8%和23.4%。
|
图 5 圆板迎爆面各监测点的压力及冲量时程曲线 Fig. 5 Pressure and impulse time history curves of each monitoring point |
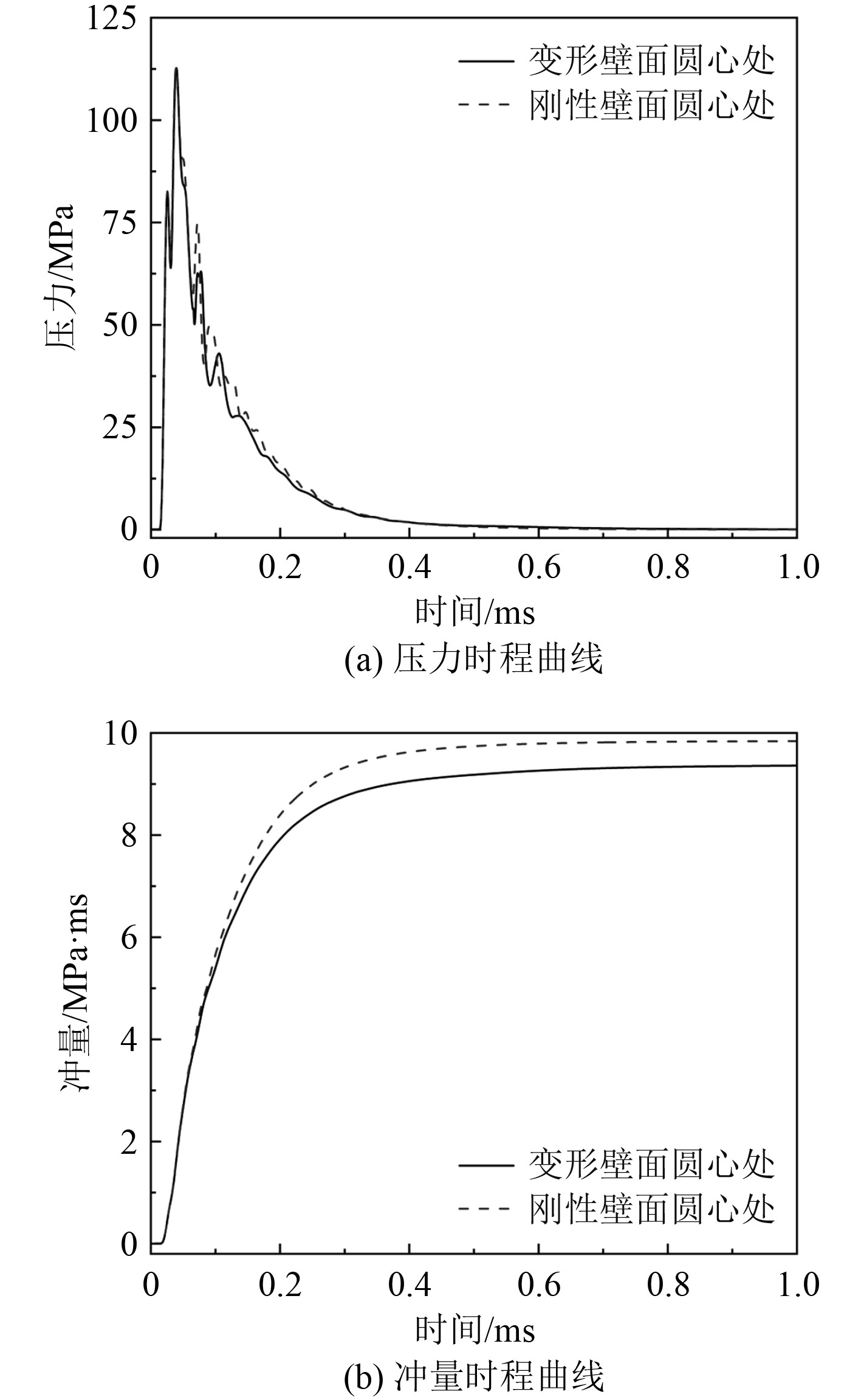
为对比变形圆板表面与刚性圆板表面载荷的差异,将圆板采用刚性边界进行模拟,其余参数保持不变进行仿真分析。图6为不同表面圆心处压力与冲量时程曲线的对比图,由图6(a)可以发现:在压力上升阶段,变形圆板表面上与刚性表面上的压力变化趋势相差不大,前2个波峰峰值基本一致;但在压力衰减阶段,刚性表面压力曲线有多个波峰,而变形圆板表面的压力曲线更为平滑。图6(b)中,两者冲量曲线变化趋势基本相同,但刚性表面冲量载荷较大,体现了圆板因变形吸收了部分能量。
|
图 6 刚性圆板表面与变形圆板表面中心处载荷对比 Fig. 6 Comparison of loads at the center of rigid round plate surface and deformed surface |
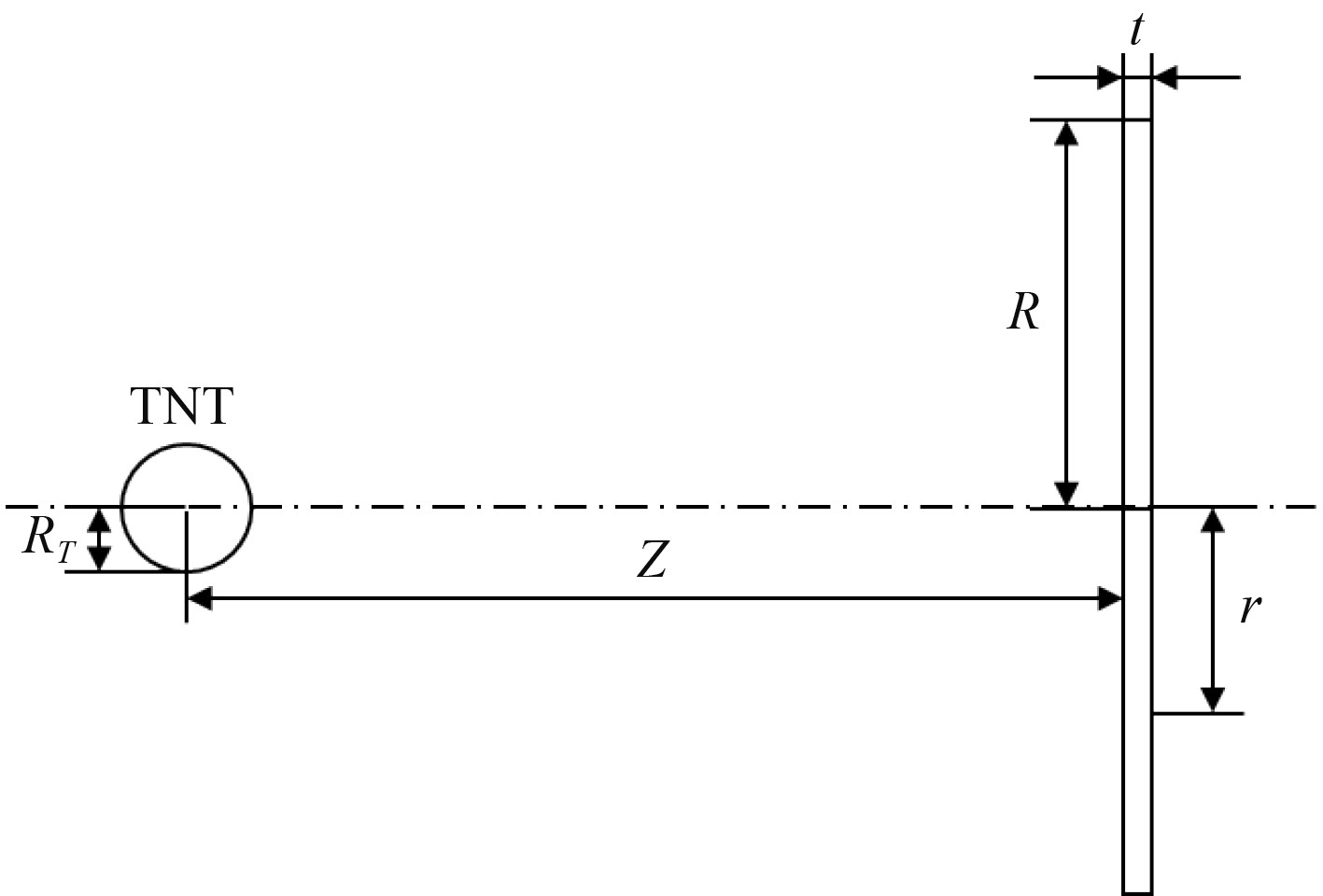
对冲量载荷分布规律进行分析,理论模型如图7所示,TNT为球形装药,圆板周围固支固定,TNT装药中心与圆板中心在同一轴线上。对于球型装药,爆炸后产生向外扩展的球型冲击波,冲击波与固支圆板相互作用,决定变形圆板表面最大冲量值及分布参数如表3所示。
|
图 7 模型示意图 Fig. 7 Schematic diagram of model |
|
|
表 3 参数分析 Tab.3 Parameter analysis |
则变形圆板迎爆面上某点最大冲量值I是表3中12个参数的函数,即
| $ I = f(R,t,Z,r,\rho ,\sigma ,c,m,e,{R_T},{\rho _0},{c_0}) 。$ | (5) |
选择圆板厚度
| $ \frac{{Ic}}{{\sigma t}} = f \left(\frac{R}{t},\frac{Z}{t},\frac{r}{t},\frac{{\rho {c^2}}}{\sigma },\frac{{m{c^2}}}{{\sigma {t^3}}},\frac{e}{{{c^2}}},\frac{{{R_T}}}{t},\frac{{{\rho _0}{c^2}}}{\sigma },\frac{{{c_0}}}{c}\right)。$ | (6) |
记圆板迎爆面上某点距圆心的距离与圆板半径的比值为α,该点与爆心的连线和圆板轴线的夹角为θ,则
| $ \alpha = \frac{r}{R},$ | (7) |
| $ \sec \theta = \frac{{\sqrt {{Z^2} + {{\left( {\alpha R} \right)}^2}} }}{Z} = \sqrt {1 + {{\left( {\frac{{\alpha R}}{Z}} \right)}^2}}。$ | (8) |
考虑采用相同的炸药和圆板材料,并且在标准大气压下,则
| $ \rho ,\sigma ,c,e,{\rho _0},{c_0} = {\text{const}}。$ | (9) |
模型中采用的TNT为球形装药,研究对象为TNT充分爆炸且在距离爆心一定距离外区域内的物理量演化问题,故TNT的形状(半径
| $ \frac{{Ic}}{{\sigma t}} = f \left(\frac{Z}{t},\sec \theta ,\frac{{m{c^2}}}{{\sigma {t^3}}}\right)。$ | (10) |
由量纲分析可知,在炸药和圆板材料相同的情况下,变形圆板迎爆面上某点的冲量与圆板半径R、厚度t、目标点距圆心距离与圆板半径比值α、爆心距圆板距离Z以及TNT当量m有关。通过控制变量法进行仿真计算,来分析各因素对变形圆板表面爆炸载荷的影响。
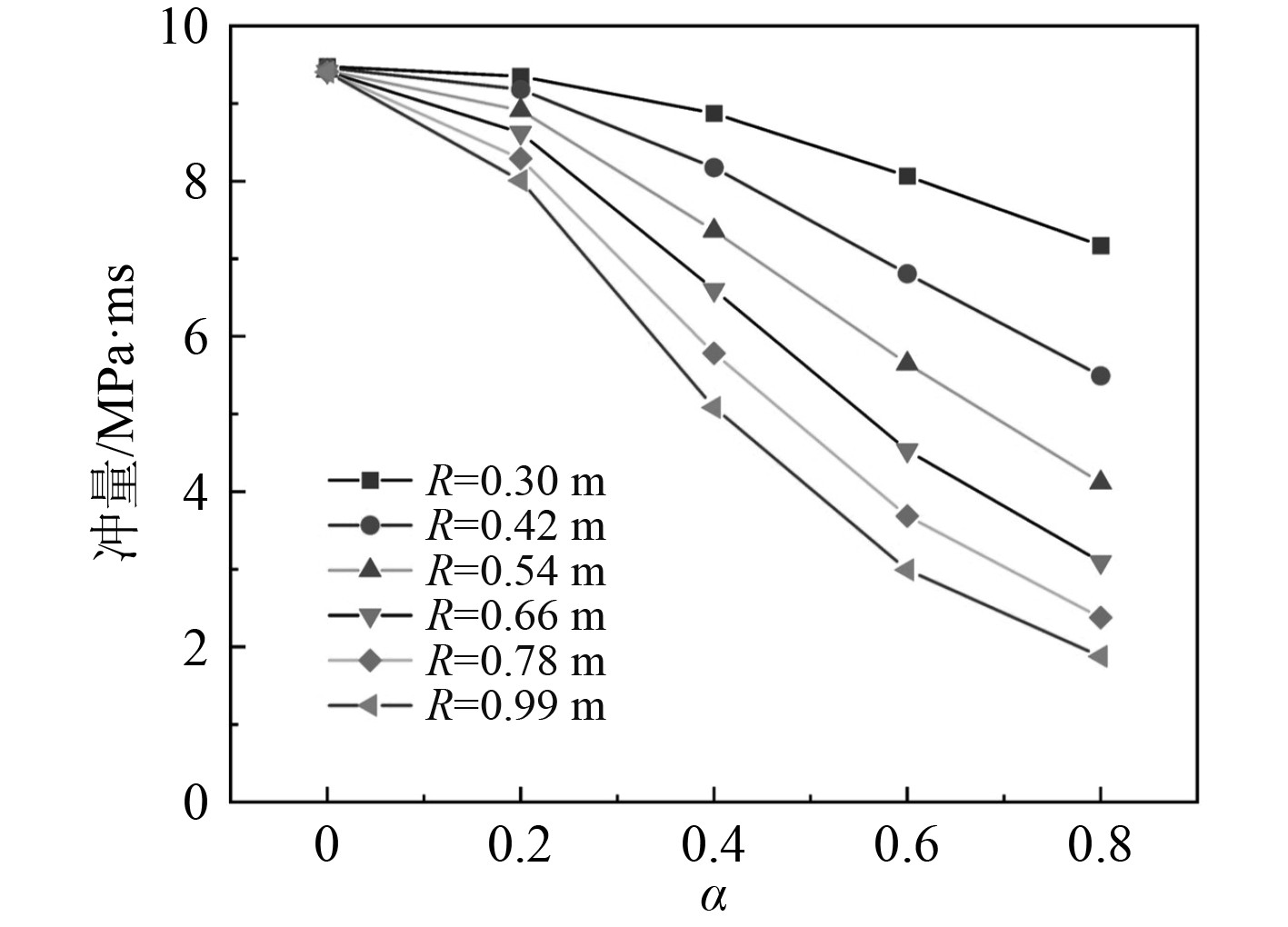
图8为t=0.010 m、Z=0.500 m、m=10 kg,R不同时变形圆板不同位置处受到的最大冲量。随着R的增加,作用在圆板中心处的冲量几乎没有变化,但在圆板迎爆面径向方向上,爆炸载荷的分布非均匀,随着点距圆心距离的增加,作用在点上的冲量逐渐减小,R越大,爆炸载荷的非均匀程度就越大。这是由于点距圆心越远,距爆心的距离就越大,压力峰值越小,冲量就越小。
|
图 8 圆板半径不同对变形圆板表面载荷影响 Fig. 8 Effect of different circular plate radii on deformed surface load |
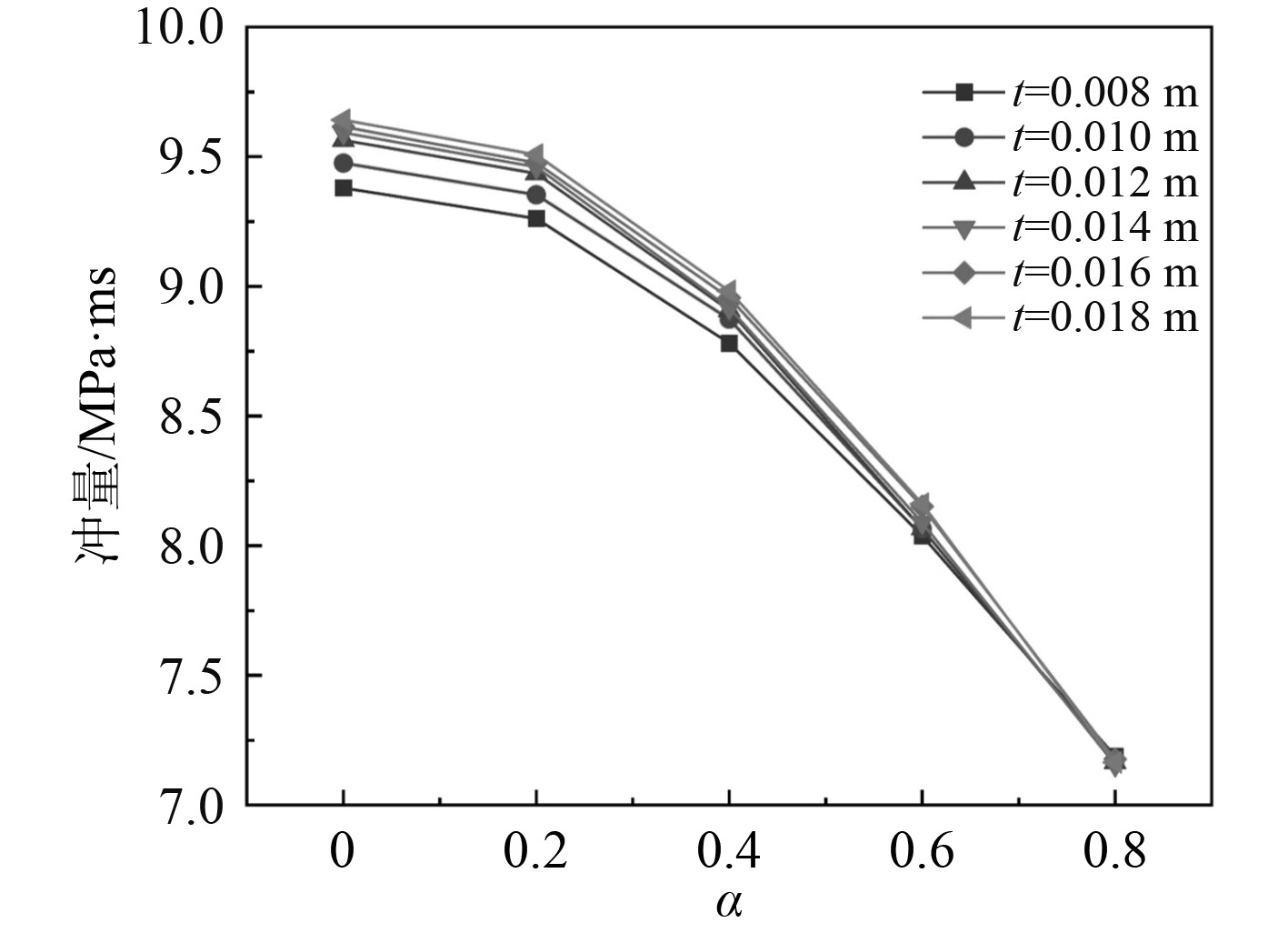
图9为R=0.300 m、Z=0.500 m、m=10 kg,t不同时变形圆板不同位置处受到的最大冲量。随着t的减小,作用在圆板上的冲量逐渐减小,但在圆板径向方向上,随着点距圆心距离的增加,冲量减小的幅度越来越小,在圆板中心处t由0.018 m减小到0.008 m时,冲量减小了2.7%,而在距圆心0.8R处,t减小,冲量几乎没有变化。这是因为t越小,圆板的刚度越小,靠近圆心的位置变形越大,冲量减小的幅度越大,圆板变形吸收的能量越多;而越靠近圆板边缘的位置,因受到固支边界的影响,变形不会因t的变化而有明显的差异,所以冲量几乎没有变化。整体来看,t的变化对变形圆板表面载荷的大小及分布影响较小。
|
图 9 圆板厚度不同对变形圆板表面载荷影响 Fig. 9 Effect of different circular plate thickness on deformed surface load |
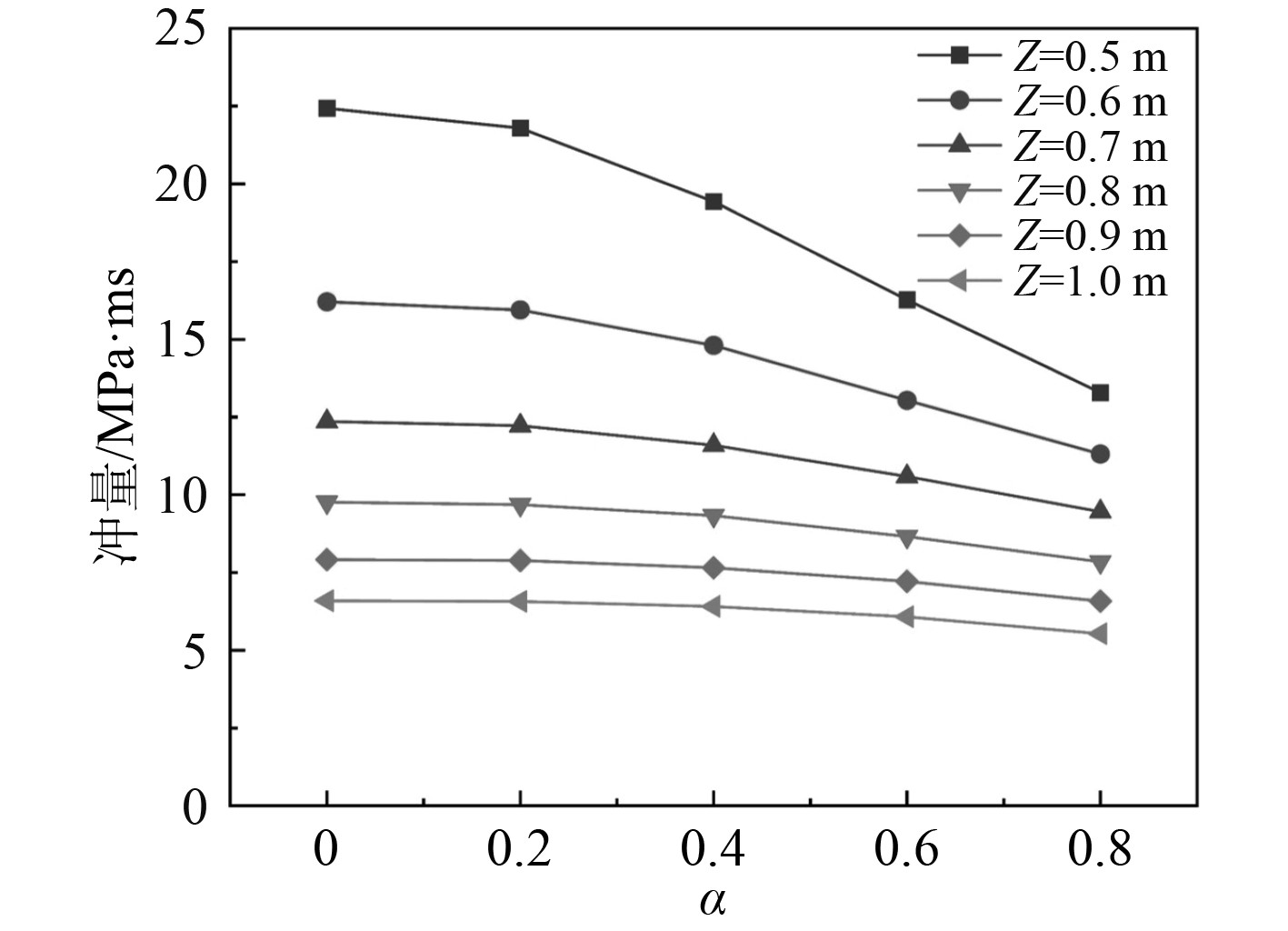
图10为R=0.420 m、t=0.014 m、m=27.4 kg,Z不同时变形圆板不同位置处受到的最大冲量。随着Z的变化,圆板各位置受到的最大冲量也大幅变化,在圆板中心位置处,Z=0.500 m时与Z=1.000 m时的冲量相差70.6%;同时随着Z的变化,冲量沿着圆板径向的非均匀程度也有较大的变化,在Z=0.500 m时,圆板中心处与距圆心0.8R处的冲量相差40.8%,而Z=1.000 m时,冲量相差仅有16.0%,出现这一现象的原因主要是爆炸冲击波是球形波,但随着Z的增大,这种影响的程度会越来越小,圆板表面受到的爆炸载荷越均匀。
|
图 10 爆心距圆板距离不同对变形圆板表面载荷影响 Fig. 10 Effect of different distance between explosion center and circular plate on deformed surface load |
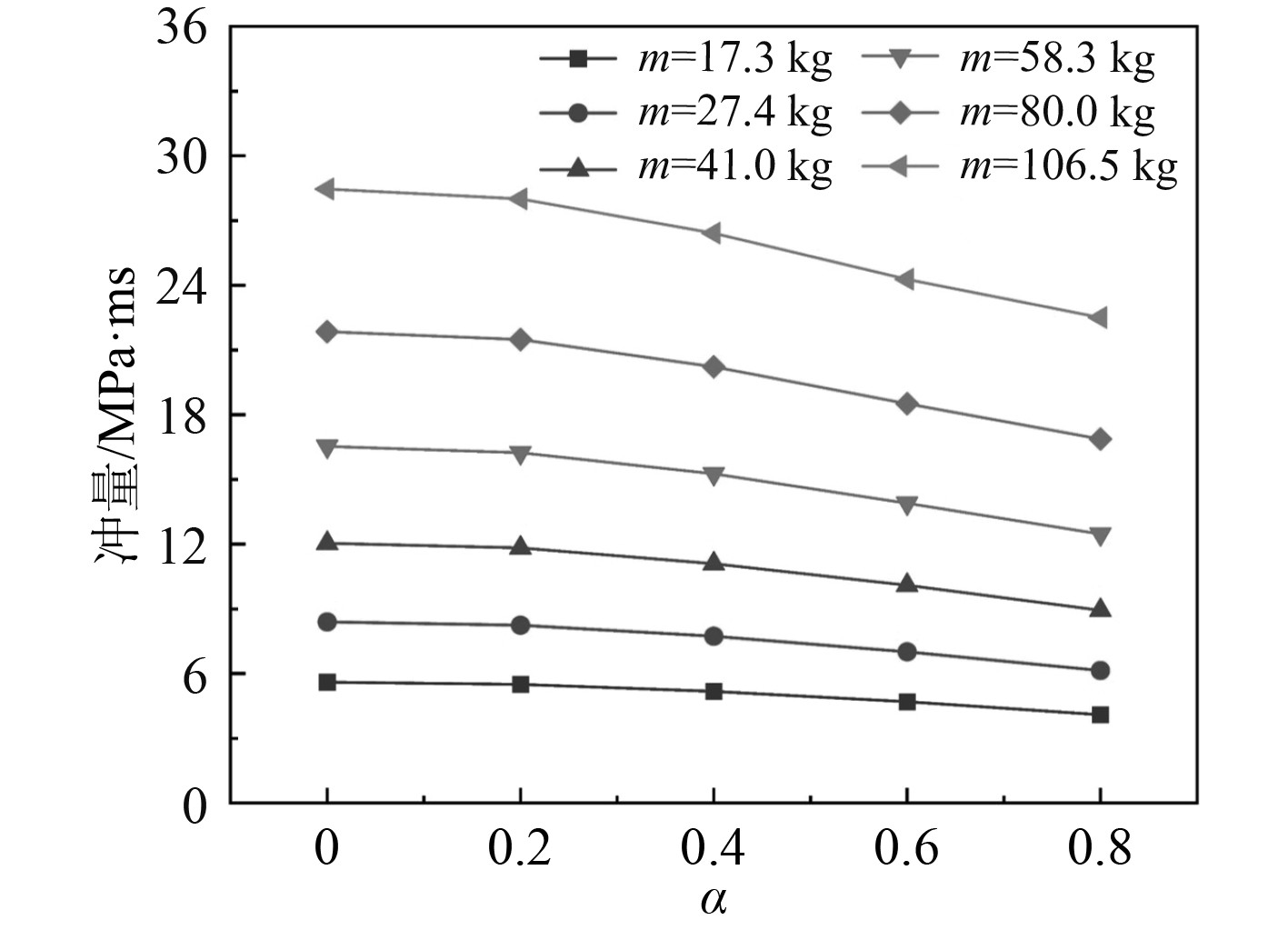
图11为R=0.540 m,t=0.018 m,Z=0.900 m,m不同时变形圆板不同位置处受到的最大冲量。TNT当量对圆板各位置受到的最大冲量影响较大,对冲量沿着圆板径向的分布规律影响较小,m=106.5 kg时圆板中心位置处的冲量约是m=17.3 kg时的5倍,而在这2种TNT当量下圆板中心处与距圆心0.8R处的冲量差值分别为20.9%和26.9%。所以m的变化对圆板表面载荷的大小影响较大,对载荷的分布影响较小。
|
图 11 TNT当量不同对变形圆板表面载荷影响 Fig. 11 Effect of different TNT equivalents on deformed palte surface load |
式(10)采用幂函数进行拟合,拟合结果如下:
| $ \frac{{Ic}}{{\sigma t}} = 0.0786{\left( {\frac{Z}{t}} \right)^{ - 1.7673}}{\left( {\cos \theta } \right)^{2.9548}}{\left( {\frac{{m{c^2}}}{{\sigma {t^3}}}} \right)^{0.8934}} ,$ | (11) |
将式(11)进行转换可得到固支变形圆板表面冲量计算公式为:
| $ I = 514.7\frac{{{m^{0.8934}}{t^{0.0871}}{{\left( {\cos \theta } \right)}^{2.9548}}}}{{{Z^{1.7673}}}} 。$ | (12) |
为了验证计算公式的准确性,以R=0.300、t=0.010、m=10 kg为基础参数,通过式(12)计算得到Z=0.400 m、0.500 m、0.600 m距离下仿真所用变形圆板表面不同位置处的最大冲量,并与仿真结果进行对比,结果如表4所示。可以看出,采用计算公式得到的表面不同位置处的冲量值,与数值仿真值之间的误差均小于6%,误差平均值为3.7%,表明计算公式能够较好计算出变形圆板表面载荷。
|
|
表 4 公式计算结果与仿真计算结果对比 Tab.4 Comparison between formula calculation results and simulation calculation results |
本文通过数值模拟,研究了爆炸冲击波与固支圆板的相互作用以及变形圆板表面载荷分布规律,在此基础上开展量纲分析,结合仿真结果得到了变形圆板表面爆炸载荷计算公式。主要结论如下:
1)对比相同条件下变形圆板表面与刚性圆板表面载荷的差异,发现了圆板因表面变形缓冲了部分能量,体现为相对于刚性表面,变形圆板表面上压力在下降阶段小型波峰数量少,下降更为平滑,最大冲量低。
2)分析了圆板半径、圆板厚度、爆心距圆板的距离、目标点距圆心的距离以及TNT当量等因素对固支变形圆板表面爆炸载荷的影响,结合仿真结果得到圆板表面任意一点最大冲量的计算公式。推导的公式能够较好快速计算出变形圆板表面载荷,该公式可为相关防护结构设计和安全评估提供快速简单的参数输入。
| [1] |
HENRYCH J. The dynamics of explosion and its use [M]. Amsterdam: Elsevier, 1979: 265-266.
|
| [2] |
TM5-1300. Structures to resist the effects of accidental explosions [M]. US Department of the Army, Navy and Air Force Technical Manual, 1990.
|
| [3] |
UFC-3-340-02. Unified facilities criteria UFC DOD structures to resist the effects of accidental explosions [M]. US Department of Defense, 2008.
|
| [4] |
GERETTO C, CHUNG KIM YUEN S, NURICK G N. An experimental study of the effects of degrees of confinement on the response of square mild steel plates subjected to blast loading[J]. International Journal of Impact Engineering, 2015, 79: 32-44. DOI:10.1016/j.ijimpeng.2014.08.002 |
| [5] |
HELD M, HEEGER P, KIERMEIR J. Displacement device to measure the acceleration of the bulge of RHA plates under anti-tank mine blast [C]// Proceedings of 22nd International Symposium on Ballistics. Vancouver: International Ballistics Committee, 2005: 995 1000.
|
| [6] |
ANDERSON C E, BEHNER T, WEISS C E. Mine blast loading experiments[J]. International Journal of Impact Engineering, 2011, 38(8): 697-706. |
| [7] |
侯俊亮, 蒋建伟, 门建兵, 等. 不同形状装药爆炸冲击波场及对靶板作用效应的数值模拟[J]. 北京理工大学学报, 2013, 33(6): 556-561. DOI:10.3969/j.issn.1001-0645.2013.06.002 |
| [8] |
SHI Y, HAO H, LI Z X. Numerical simulation of blast wave interaction with structure columns[J]. Shock Waves, 2007, 17(1): 113-133. |
| [9] |
李臻, 刘彦, 黄风雷, 等. 接触爆炸和近距离爆炸比冲量数值仿真研究[J]. 北京理工大学学报, 2020, 40(2): 143-149. |
| [10] |
汪维, 张舵, 卢芳云, 等. 近爆作用下结构表面上爆炸载荷确定方法研究[J]. 兵工学报, 2013, 34: 234-242. |
| [11] |
汪维, 刘光昆, 赵强, 等. 近爆作用下方形板表面爆炸载荷分布函数研究[J]. 中国科学:物理学 力学 天文学, 2020, 50(2): 144-152. |
| [12] |
陈鹏宇, 侯海量, 金键, 等. 舰船舱内爆炸载荷简化载荷计算模型[J]. 舰船科学技术, 2020, 42(9): 22-29. CHEN P Y, HOU H L, JIN J, et al. Simplified calculation model for explosion loading in ship cabin[J]. Ship Science and Technology, 2020, 42(9): 22-29. DOI:10.3404/j.issn.1672-7649.2020.09.005 |
| [13] |
姚熊亮, 屈子悦, 姜子飞, 等. 舰船舱内爆炸载荷特征与板架毁伤规律分析[J]. 中国舰船研究, 2018, 13(3): 140-148. |
| [14] |
焦晓龙. 多舱室结构内爆载荷下毁伤效果评估方法研究[D]. 太原: 中北大学, 2020
|
| [15] |
郭子涛, 高斌, 郭钊, 等. 基于J-C模型的Q235钢的动态本构关系[J]. 爆炸与冲击, 2018, 38(4): 804-810.
|
 2024, Vol. 46
2024, Vol. 46
