随着舰船工业的快速发展,对舰船船体的强度设计标准越来越高[1]。目前对钢板侵彻问题的研究主要基于弹体形状破片研究,船体结构中的钢板多属于薄板范畴,而立方体碎片对薄壁结构的破坏能力极强,会造成船体外壳及内部结构的严重损坏,因此研究立方体破片对船用钢的贯穿损伤的相关响应和失效模式就尤为重要[2]。
传统有限元方法在求解结构损伤、裂纹扩展和贯穿等不连续问题时,即便使用自适应网格的方法,也不能解决位移场的偏微分方程在不连续位置存在奇异性的问题,因此也难以模拟贯穿失效的过程。为了更有效地解决材料的复杂损伤等不连续问题,Silling[3 − 4]提出一种基于非局部作用的粒子理论——基于状态的近场动力学理论。近场动力学采用空间积分形式的本构方程代替传统连续介质力学中的微分方程,有效避免了传统力学在解决破坏问题时的对位移场的微分,在解决不连续问题时具有独特的优势,已经被广泛应用于分析损伤破坏等不连续问题。基于状态 PD 理论与应力张量的相似性,能够很好地观察到金属收到剪切作用时的塑性行为,而经典理论中的本构模型大多能直接套用 PD 状态理论,因此对钢材料等弹塑性材料研究主要采用基于常规态的PD理论。但目前PD数值模拟中独有的损伤数指标主要根据近场域中键的断裂进行损伤分析,对断裂的损伤情况能很好的模拟,但难以体现其他如压缩、拉伸等损伤变形情况,无法完整地展现弹塑性材料受破片冲击时的损伤变形。
基于上述船用钢侵彻问题的研究现状,本文拟对船用钢受立方体破片冲击情况进行研究。首先,结合近场动力学理论改进损伤数指标,建立符合船用钢材料规范的船用钢受立方体破片冲击模型;其次,使用高压气枪对船用钢进行破片物理冲击试验,同时采用PDLammps软件内置的eps弹塑性材料模型,并结合Python软件编写代码进行近场动力学数值模拟,针对冲击模拟中不同角度和速度下立方体冲击物对钢板冲击后产生的结果进行分析,研究破片对船用钢的贯穿损伤的相关响应模式;最后,从研究破片极限贯穿速度的影响因素入手,建立立方体破片以面、棱边、尖角3种方向冲击钢板的极限贯穿速度经验公式,从而更好为舰船用钢的设计研究提供帮助。
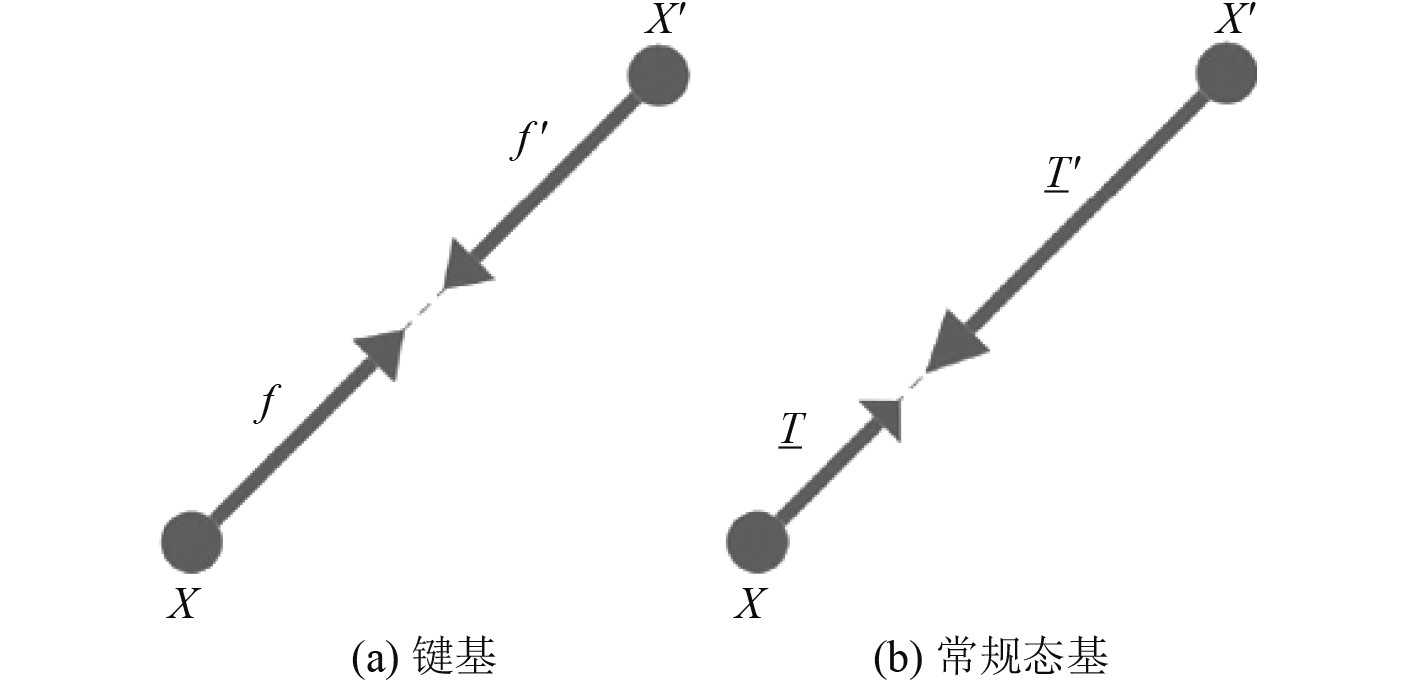
1 基于常规态的近场动力学理论如图1所示,常规态基的近场动力学与键基相比,两者之间在根本上的不同点是键基近场动力学物质点之间的内力大小相等,内力方向沿着物质点的连线且相反,而常规态基在保持内力方向不变的基础上,其物质点之间的内力大小不再相等,而是由于受到各自“状态”的影响而不同。
|
图 1 2种近场动力学方法内力之间的区别 Fig. 1 Internal force difference between two Peridynamic methods |
这里“状态”的作用是把向量映射到标量,向量或者张量,如图1以
| $ \begin{split}\rho (\boldsymbol{x})\cdot \ddot{\boldsymbol{u}}(\boldsymbol{x},t)=&{\int }_{{H}_{\boldsymbol{x}}}^{}\{\underset{\_}{\boldsymbol{T}}[\boldsymbol{x},t] < {\boldsymbol{x}}^{'}-\boldsymbol{x} > -\\ &\underset{\_}{\boldsymbol{T}}\left[{\boldsymbol{x}}^{'},t\right] < \boldsymbol{x}-{\boldsymbol{x}}^{'} > \}d{V}_{{x}^{'}}+\boldsymbol{b}(\boldsymbol{x},t)。\end{split} $ | (1) |
式中:
Siling将任意物质点
| $ \underset{\_}{\boldsymbol{T}}\left(\boldsymbol{x}\right)=t\cdot \boldsymbol{M}\left(\boldsymbol{x}\right)。$ | (2) |
式中:
在局部损伤方面,由于近场域内的键不断断裂并累计,这将会导致宏观层面上的损伤,从而观察裂纹的萌发和演变过程,而传统损伤数则是能突出显现这一变化过程的重要指标。但在研究弹塑性材料的冲击模拟过程中,除了裂纹处的损伤变形,其他区域也发生如压缩、拉伸等损伤变形情况,并最终保留塑性变形。传统损伤数通过分析近场域中键的断裂程度来说明材料的局部损伤程度,如图2所示,在使用传统近场动力学损伤数对船用钢受立方体破片以尖角冲击的损伤程度进行研究分析时,对于裂纹发生区域外的塑性变形情况无法有效说明。

|
图 2 传统损伤数下船用钢受立方体破片以尖角冲击损伤图 Fig. 2 Damage diagram of marine steel impacted by cube fragments at sharp angle under the original damage number |
因此,本文基于键的伸长量在冲击模拟中的变化情况,提出变形损伤数这个新的分析指标进行研究。键的伸长率
| $ s=\frac{\left|\boldsymbol{\eta }+\boldsymbol{\xi }\right|-\left|\boldsymbol{\xi }\right|}{\left|\boldsymbol{\xi }\right|} 。$ | (3) |
式中:
传统的损伤数中,为了定义近场域中键的损伤情况,采用一个与变形历史有关的函数
| $ {\mu }_{s}\left(t,\boldsymbol{\xi }\right)=\left\{\begin{array}{ll}1 ,& 0 < \left|s\right| < {s}_{0},\\ 0 ,& \left|s\right|\geqslant {s}_{0}。\end{array}\right.$ | (4) |
通过该函数,能够对如裂纹发生处近场域中键断裂情况进行判断,从而直接的展现裂纹扩展路径,但对裂纹发生处以外区域的损伤程度无法有效展示,难以准确且完整地说明材料的整体损伤程度。
为了能定量的分析各近场域中粒子间键的变形情况,创建一个与变形历史有关的函数
| $ {\mu }_{s}\left(t,\boldsymbol{\xi }\right)=\left\{\begin{array}{ll}1-\dfrac{\left|s\right|}{{s}_{0}},& 0 < \left|s\right| < {s}_{0},\\ 0 ,& \left|s\right|\geqslant {s}_{0}。\end{array}\right. $ | (5) |
式中:
| $ \phi \left(\boldsymbol{x},t\right)=1-\underset{{H}_{\boldsymbol{x}}}{\int }{\mu }_{s}\left(t,\boldsymbol{\xi }\right){\mathrm{d}}{V}_{\boldsymbol{x}}\left/\underset{{H}_{\boldsymbol{x}}}{\int }{\mathrm{d}}{V}_{\boldsymbol{x}}\right. 。$ | (6) |
式中:
对船体受破片冲击的损伤研究是建立在对船侧钢板被破片冲击后的板自身损伤情况和应力变化进行分析。因此为了对船用钢受破片冲击后的失效模式进行分析,本文针对船用钢受到高速立方体破片冲击的损伤工况,建立不同工况的冲击实验模型和近场动力学研究模型,使用物理冲击实验和数值模拟2种方法对船身受立方体破片冲击的工况进行冲击模拟,通过分析数值模拟结果中的损伤图和应力图结合物理冲击实验下钢板的失效图,来研究不同冲击速度和冲击角度下立方体破片冲击船用钢后钢板的最终失效情况。
3.1 材料参数的选取及冲击模型的建立根据《我国船身结构用钢力学性能规范》要求船体用钢的屈服强度不小于235 MPa,抗拉强度在400~520 MPa之间,本文结合最新船舶及海洋工程中结构钢GB5312和船身结构用钢力学性能规范,采用AH32高强度钢材,其参数如表1所示。
|
|
表 1 所选钢材材料参数 Tab.1 Selected steel material parameters |
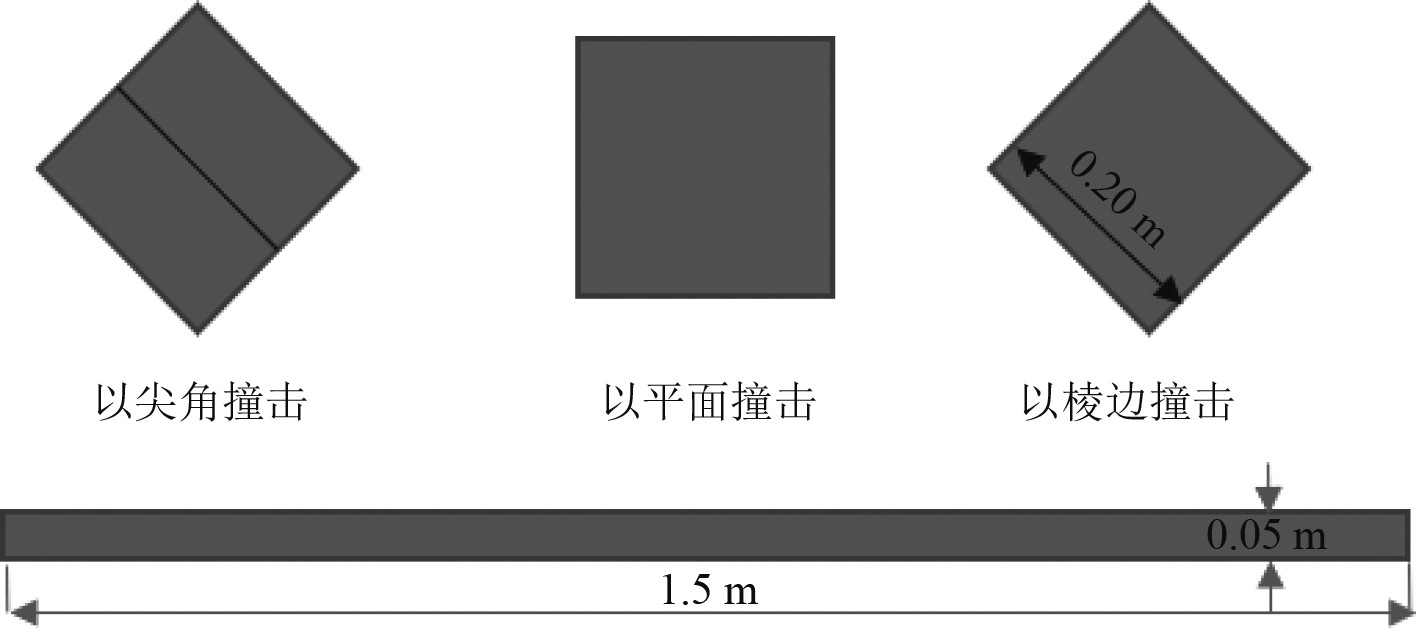
在船钢板尺寸方面,综合《船用钢板尺寸》和南钢―船板等级A、B、A32、A36认证的船级规格厚钢板尺寸选用厚度为0.05 mm,长度和宽度为1.5 m尺寸的钢板。依据钢板的材料参数和尺寸,建立冲击模型如图3所示。
|
图 3 3种冲击情况下的冲击模型 Fig. 3 Impact model under three impact conditions |
将板的四周进行固定。由于立方体碎片对薄壁结构的破坏能力最大,本文将选用立方体破片作为冲击物来模拟对钢板的冲击,立方体破片边长为0.20 m,密度为7850 kg/m3。受限于冲击实验材料,本文选用边长为0.15 m、厚度为0.005 m的AH32钢板进行物理冲击实验,冲击物为边长0.02 m的同材料立方体,基于此建立物理冲击模型。
本文基于图3冲击模型,联系弹塑性材料近场动力学本构方程使用Python软件编写代码,采用PDLammps内置的eps弹塑性模型作为物质点间联系的参考来建立近场动力学数值分析模型。因为穿甲过程中破片的刚度远大于靶板,因此假设此模型中整个破片为刚体,在冲击过程中不发生变形,冲击位置为板面中心,冲击方向为板厚度方向。把板离散为600×600×20个物质点,时间步数
基于建立的物理冲击模型和近场动力学数值分析模型,本文使用物理冲击实验和数值模拟2种方法进行船用钢受立方体破片不同角度冲击的冲击实验,并对最终的损伤失效结果进行分析。
3.2.1 物理冲击实验在模拟立方体破片撞击船用钢时,由于不同的冲击方式,立方体破片会对钢板造成不同的贯穿失效模式。实验采用单级压力气枪,所用的枪管长度为2 m和内径为0.031 m。在最大的压力下,使用高压氮气加速弹丸,这使得弹丸可以被加速到600 m/s左右,将钢板四周固定,安放在距离气枪枪口0.5 m处(经过测试0.5 m处速度达到最大且立方体破片方向不发生过大变化)。具体设备如图4所示。

|
图 4 冲击试验设备图 Fig. 4 Diagram of impact test equipment |
冲击试验共测试了以面、棱和角3种不同方向的立方体破片冲击钢板。每个实验都由高速摄像机进行记录,高速气枪将立方体破片打出并以临界速度贯穿钢板后钢板的失效图如图5所示(由于较为密封的实验环境,光线和设备的限制,尽量选取其中最为明显的失效图)。

|
图 5 钢板受到立方体破片冲击后的贯穿失效图 Fig. 5 Penetration failure mode of steel plate impacted by cube fragments |
依据上述物理实验得到的立方体破片冲击船用钢后的贯穿失效图和各工况下破片贯穿船用钢所需临界贯穿速度,本文将基于近场动力学方法进行数值模拟实验,将实验结果与物理实验结果进行对比,验证数值模拟方法的准确性和可行性。
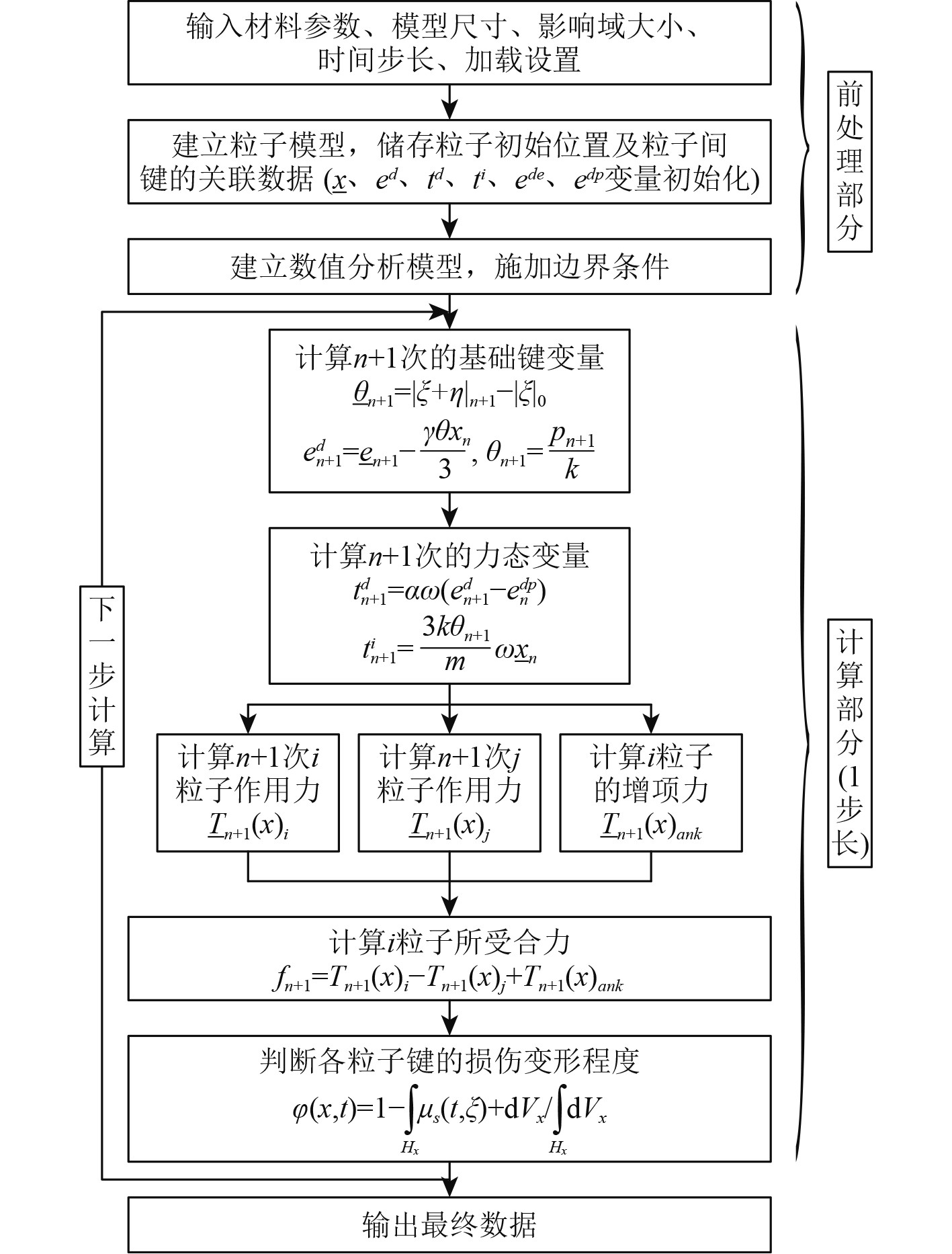
3.2.2 近场动力学数值模拟实验由于近场动力学采用逐步迭代的方式对物质点的运动状态求解,因此需要进行大量的运算,本文通过Python编程软件结合lammps分子动力学软件中PDlammps近场动力学模块进行数值模拟,其中程序的算法流程如图6所示,算法分为前处理、计算过程和后处理3部分。前处理主要是计算数据的输入以及模型的离散化;计算过程部分计算每个物质点的位移场随时间的迭代过程;后处理部分是根据输出数据绘出试件的损伤图。
|
图 6 数值分析流程图 Fig. 6 Flow chart of numerical analysis |
依据已经建立的近场动力学分析模型,对立方体以平面、棱边、尖角撞击船用钢这3个不同工况基于上述流程进行冲击模拟,通过计算站计算后得到损伤图。当一个近场域的变形损伤数达到0.5以上时,表示该区域已经发生断裂严重损伤,为了使损伤图之间对比更加突出,本文将损伤图中变形损伤数限制在0.2~0.6,在此区间损伤图上各损伤区域最为明显。本文在此基础上进行以下分析:
1)根据最终得到的损伤图与实际失效情况相比较,观察使用此近场动力学方法进行冲击模拟的准确性,其中图中损伤区域越趋于红色,表示区域损伤越严重。
2)通过对模拟后的钢板均匀选取近场域,并统筹各近场域的变形损伤数(范围从0~1),求得平均损伤数,来分析各工况在不同冲击速度下变形损伤数之间的量化差距(已脱离的部分变形损伤数取1)。
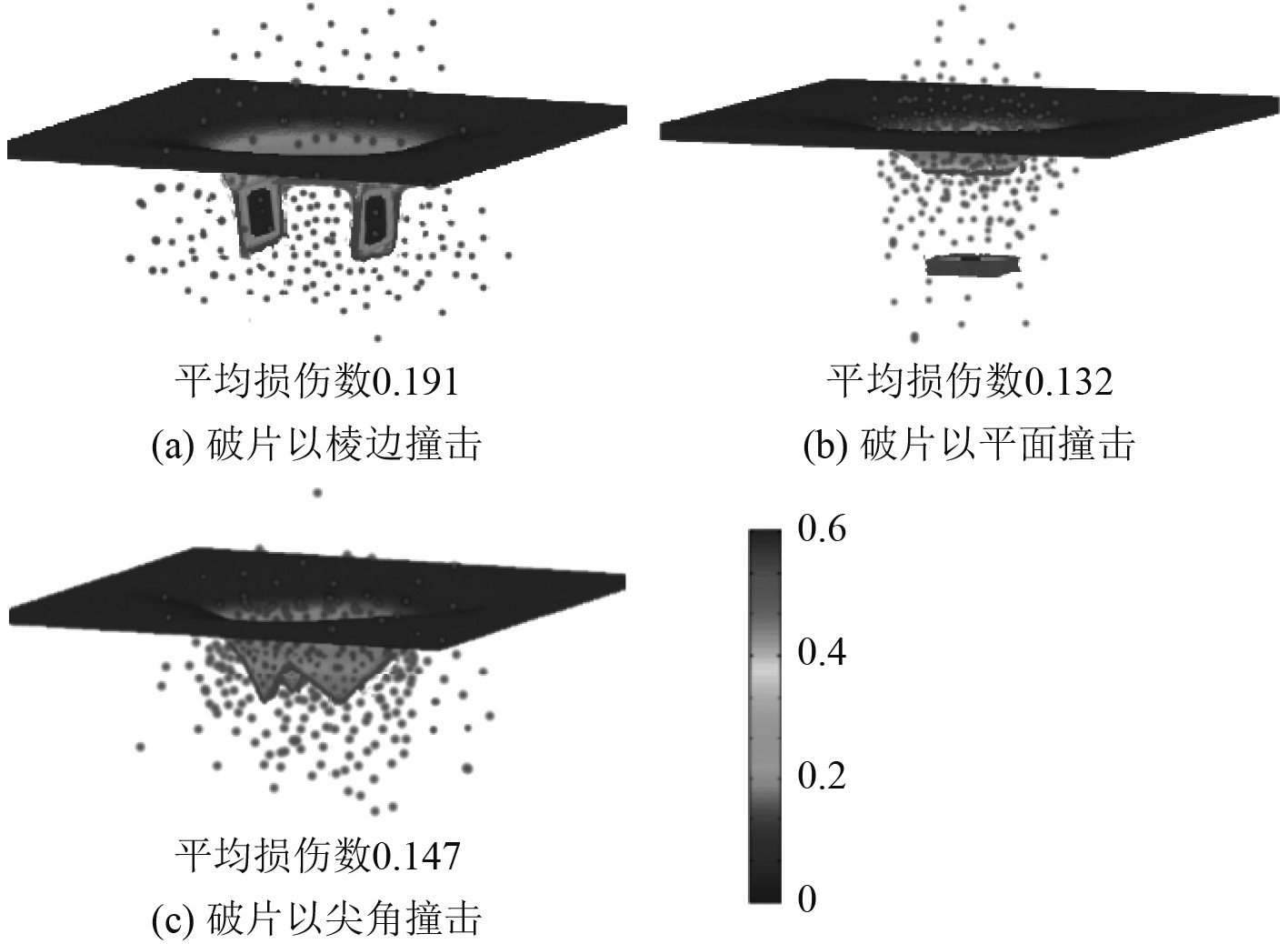
在冲击速度为320 m/s下,3种工况的钢板都被完全贯穿失效,立方体破片以棱边和尖角冲击板的工况相对而言损伤面积和程度有所增大,“花瓣”区域的物质点几乎完全损伤,形成了类似图7(a)和图7(c)钢板冲击实验的“瓣裂”失效模式。而以平面冲击的工况下,立方体破片在速度为320 m/s时完全贯穿船用钢,钢板受冲击点附近区域已经完全损伤脱离,冲击边缘也形成了剪切带,形成如图7 (b)剪切冲塞的失效模式。从平均损失程度来看,当立方体破片以上述情况完全贯穿钢板时,立方体破片以棱边冲击钢板时平均损伤数比以平面撞击的工况高44.6%,比以尖角冲击的工况高29.9%。因此对比3种不同工况下立方体破片对板的冲击模拟,可以发现立方体破片不同角度下对钢板冲击造成的损失有很大的差别,从同一速度下的平均损伤数来看钢板对以平面冲击的立方体破片具有很好的抵抗能力,而以棱边冲击的立方体破片对板的贯穿损伤最为严重。
|
图 7 破片320 m/s时钢板损伤图 Fig. 7 Damage diagram of steel plate at fragment 320 m/s |
破片冲击钢板的冲击过程可大致分为初始接触阶段、破片侵入阶段、延性扩孔阶段和贯穿破坏阶段[3],本文将选取这4个阶段对应时刻下各个工况的应力图进行分析。
图8为速度为340 m/s的立方体破片以尖角撞击板后板上表面在不同时刻下的Von Mises应力图。
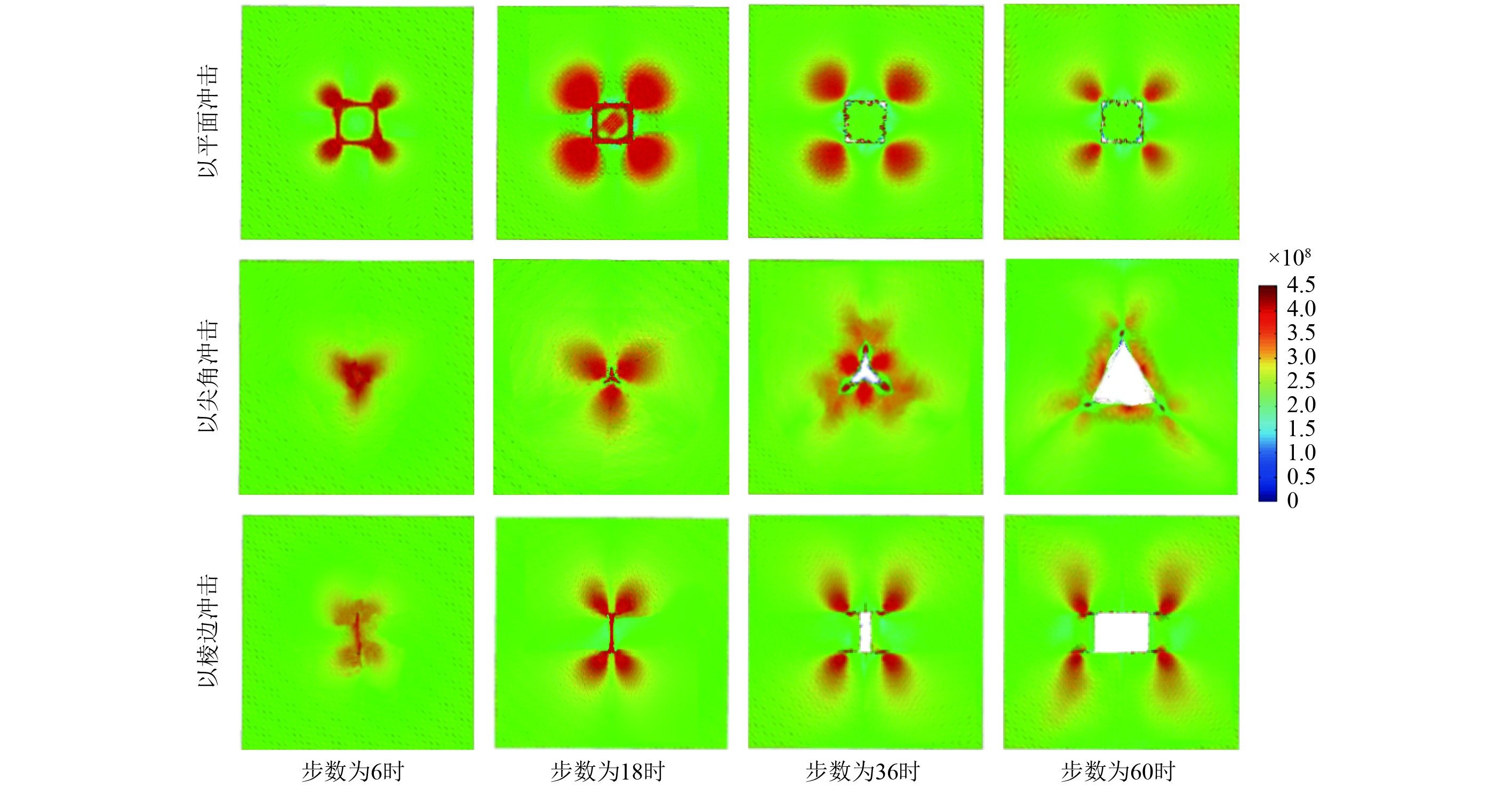
|
图 8 破片以各角度冲击钢板时Von Mises应力图 Fig. 8 Stress diagram of fragment strikes the steel plate at all angles |
综合上述3个工况下板的应力变化可知,板的各方向应力围绕着冲击点堆成分布,同时从Von Mises应力图可以看出板所受总应力呈现先增大后减少的趋势,同时总应力围绕着冲击点平均向外递减,在形成的裂纹尖端呈现明显的应力集中现象,这些都符合实际钢板受到破片侵彻作用时的应力变化[7],因此使用该数值方法对船用钢受立方体破片以平面、棱边、尖角冲击过程进行模拟时,其冲击过程中的力学变化评估准确。
3.4 钢板极限贯穿速度的影响因素从侵彻模型的极限贯穿速度公式[8 − 9]可知,在研究钢板极限贯穿速度时,破片密度、靶板厚度和屈服应力以及破片边长都是重要影响因素。为了使分析得到的规律更准确更贴近实际,本文针对以棱边冲击靶板这一最严重的工况,选用了厚度符合船用钢尺寸要求的0.025~0.075 m,破片密度选取7000~9000 kg/m3,AH32钢板屈服应力选取315~365 MPa[10],并均匀选取各参数中5个梯度作为变化参数进行冲击模拟。并对实验数据用无量纲法进行分析,结合线性回归方法建立可用于实际应用的立方体破片以棱边冲击钢板的经验公式。
通过计算得到,基于数值模拟结果的破片以棱边冲击钢板的极限速度经验公式为:
| $\begin{split}{V}_{pl}=&{V}_{pl}\left(\frac{h}{d},{\rho }_{p},{\rho }_{t},{\sigma }_{t}\right)={{e}^{1.099}\cdot \left(\frac{h}{d}\right)}^{0.655}\cdot\\ &{{\rho }_{p}}^{-0.639}\cdot {{\rho }_{t}}^{0.139}\cdot {{\sigma }_{t}}^{0.5}。\end{split}$ | (7) |
为了验证经验公式的准确性和实用性,本文取不在拟合的其他数据点对计算后的公式进行检验,如表2所示。
|
|
表 2 公式验证的参数及结果 Tab.2 Parameters and results of formula validation |
可知,通过数值模拟、物理实验结果和经验公式计算结果进行比对,6组实验的误差率都小于4%,误差在工程允许的范围之内,因此该经验公式具有工程实用价值。
本文根据上述计算方法,本文分别得到立方体破片以平面和尖角冲击钢板的经验公式。
以平面冲击钢板经验公式:
| $\begin{split} {V}_{pl}=&{V}_{pl}\left(\frac{h}{d},{\rho }_{p},{\rho }_{t},{\sigma }_{t}\right)={{e}^{1.609}\cdot \left(\frac{h}{d}\right)}^{0.832}\cdot \\ &{{\rho }_{p}}^{-0.711}\cdot {{\rho }_{t}}^{0.210}\cdot {{\sigma }_{t}}^{0.5},\end{split} $ | (8) |
以尖角冲击钢板经验公式:
| $ \begin{split}{V}_{pl}=&{V}_{pl}\left(\frac{h}{d},{\rho }_{p},{\rho }_{t},{\sigma }_{t}\right)={{e}^{1.267}\cdot \left(\frac{h}{d}\right)}^{0.713}\cdot \\ &{{\rho }_{p}}^{-0.649}\cdot {{\rho }_{t}}^{0.149}\cdot {{\sigma }_{t}}^{0.5}。\end{split}$ | (9) |
经物模和数模验证,式(8)、式(9)误差率皆小于4%,都具有工程实用价值。
基于已经得到的经验公式,本文在冲击物材料与钢板材料皆为AH32钢前提下,选取径厚比从0.1~0.5梯度研究径厚比对破片临界贯穿速度的影响,结果如图9所示。
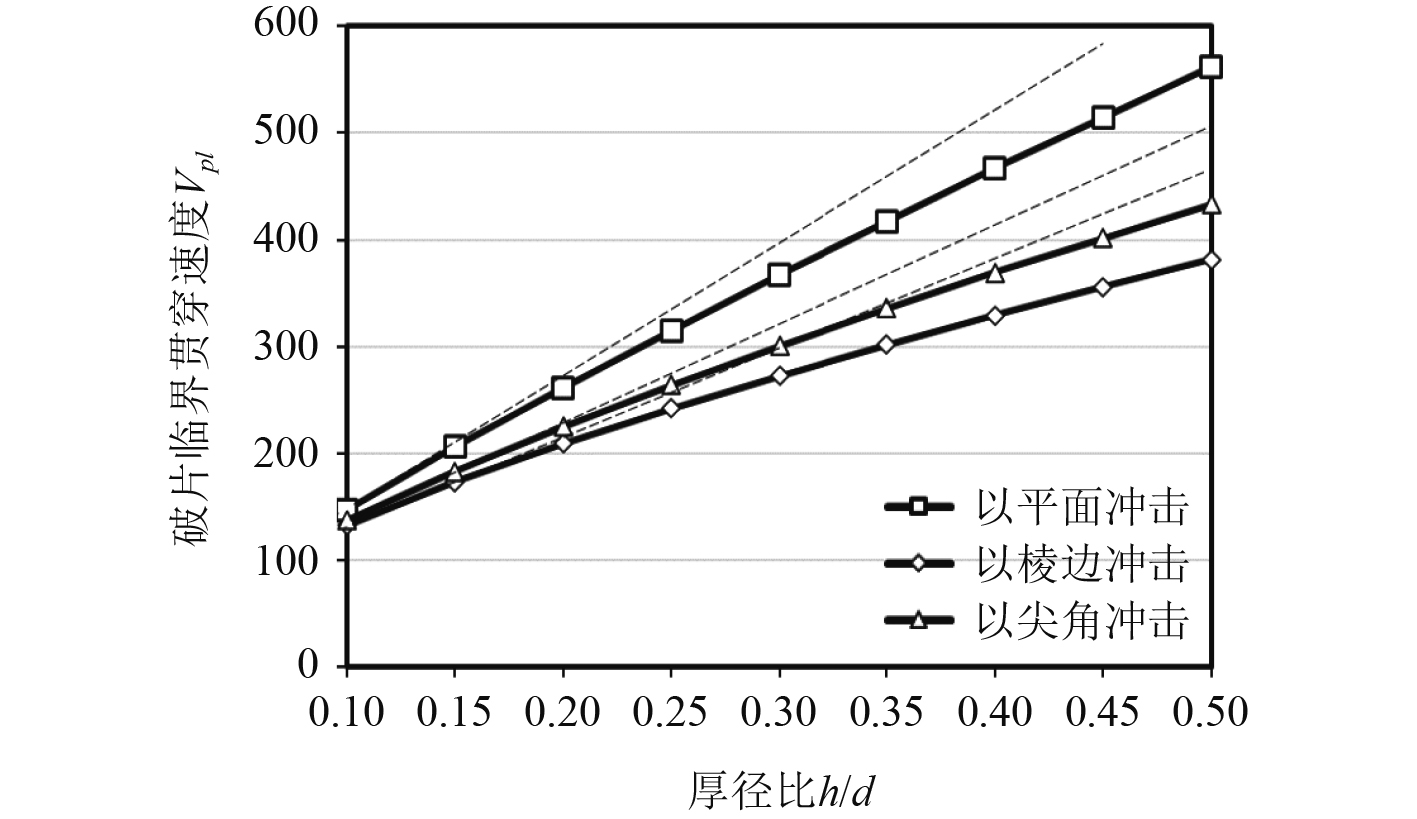
|
图 9 不同径厚比下立方体破片贯穿钢板所需临界速度 Fig. 9 Critical speed of cube fragment penetrating steel plate under different diameter-thickness ratio |
可知,随着径厚比的增加,破片所需的临界贯穿速度也随之增加,但临界贯穿速度的增长速率逐渐变缓。在同样厚度下,立方体破片以棱边撞击钢板所需临界贯穿速度最小,立方体破片以平面撞击钢板所需临界贯穿速度最大,这也符合本文通过损伤图进行分析后得到的结论。
4 结 语本文针对船用钢受高速立方体破片冲击的工况,建立了符合船用钢规范的冲击模型,采用优化后的基于常规态的弹塑性材料近场动力学理论进行数值模拟,并结合高压气枪对船用钢进行破片物理冲击试验进行说明验证。最终得出以下结论:
1)高速立方体破片冲击作用下,使用近场动力学方法进行数值模拟能够模拟出与物理冲击实验结果基本一致的失效模式,同时从数模结果中应力图的力学变化来看力学评估准确,采用该方法进行数值模拟的准确性高。
2)在相同的立方体冲击速度下,立方体破片以棱边撞击船用钢时所造成的船身损伤程度最大;在完全贯穿失效情况下,从总体损伤程度来看,当立方体破片以不同冲击方式完全贯穿钢板时,立方体破片以棱边冲击钢板时平均损伤数比以平面撞击的工况高44.6%,比以尖角冲击的工况高29.9%;而在同样厚度下,立方体破片以棱边撞击钢板所需临界贯穿速度最小,立方体破片以平面撞击钢板所需临界贯穿速度最大。因此,在船用钢防范立方体破片冲击的相关研究中,应以立方体破片以棱边对钢板冲击这个工况作为极限贯穿速度以及材料强度判断的重要工况。
3)针对立方体破片冲击钢板所需极限贯穿速度的影响因素进行分析,采用无量纲法结合多元线性回归法得出了可用于实际的立方体以面、棱边、尖角撞击钢板的极限贯穿速度经验公式,经验证发现公式计算误差小于4%,在工程许可范围内,因此具有一定的实际意义,可以对一些工程设计提供参考。
| [1] |
李彦. 船身在水下冲击作用下的动态响应仿真[J]. 舰船科学技术, 2019, 41(14): 4-6. LI Y. Simulation and research on dynamic response of ship hull under underwater impact[J]. Ship Science and Technology, 2019, 41(14): 4-6. |
| [2] |
王晓强, 朱锡, 梅志远. 陶瓷/船用钢抗破片模拟弹侵彻的实验研究[J]. 哈尔滨工程大学学报. 2011, 32(5): 555−559+588. WANG X Q, ZHU X, MEI Z Y. Experimental study on the penetration resistance of ceramic/marine steel fragments to simulated projectiles [J]. Journal of Harbin Engineering University, 2011, 32(5): 555−559+588. |
| [3] |
彭军, 袁宝慧, 程淑杰, 等. 立方形破片对钢靶的穿甲威力研究[J]. 科学技术与工程, 2011, 11(29): 7092-7096. PONG J, YUAN B H, CHENG S J, et al. Study on the armor piercing power of cubic fragments against steel targets[J]. Science Technology and Engineering, 2011, 11(29): 7092-7096. DOI:10.3969/j.issn.1671-1815.2011.29.011 |
| [4] |
SILLING S. A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175−209.
|
| [5] |
SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers and Structures, 2005, 83(17): 1526−1535.
|
| [6] |
SILLING S. A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2): 151.
|
| [7] |
侯海量, 朱锡, 谷美邦, 等. 破片模拟弹体侵彻钢板的有限元分析[J]. 海军工程大学学报, 2014(3): 78-83+88. HOU H L, ZHU X, GU M B, et al. Investigation on penetration of steel plate by fragment simulated projectile using finite element method[J]. Journal of Naval Engineering University, 2014(3): 78-83+88. |
| [8] |
WEN H M . Low velocity perforation of punch-impact-loaded metal plates[J]. Journal of Pressure Vessel Technology, 1996, 118(2): 181−187.
|
| [9] |
SUN W H, WEN H M. Transition of plugging failure modes for ductile metal plates under impact by flat-nosed projectiles[J]. Mechanics Based Design of Structures and Machines, 2010, 38: 86-104. DOI:10.1080/15397730903415892 |
| [10] |
欧阳雪娟. 水下接触爆炸载荷作用下舰船防护结构模型仿真[J]. 舰船科学技术, 2021, 43(14): 4-6. OUYANG Xue-juan. Simulation of ship protective structure model under underwater contact explosion load[J]. Ship Science and Technology, 2021, 43(14): 4-6. DOI:10.3404/j.issn.16727649.2021.7A.002 |
 2024, Vol. 46
2024, Vol. 46
