天然气(Natural Gas, NG)是一种高质量的清洁能源,占世界一次能源使用总量的24%。在液化天然气(Liquefied Natural Gas, LNG)动力船中,天然气以液体形式储存,LNG在使用前需要气化[1]。在气化过程中,可靠高效的汽化器是气化系统不可或缺的关键部件。印刷板式换热器(Printed Circuit Heat Exchanger, PCHE)是由英国Heatric公司发明的一种高效微槽道紧凑式换热器[2]。它的通道直径一般为0.5~3.0 mm[3],传热比表面积高达2 500 m2/m3[4],能承受60 MPa的高压以及−200℃的低温,是高压低温系统中很好的气化器候选者[5]。
此外,LNG在工程应用中一般处于超临界状态。Ma等[6]通过数值模拟研究PCHE中超临界LNG的局部流动和传热特性,研究发现,当冷热侧温差最小时,传热最差。值得注意的是,在实际应用中,超临界LNG在气化过程中会受到重力作用,因此浮力效应会导致复杂的传热现象[7 − 9]。在这方面,传热劣化(HTD)和传热增强(HTE)是研究热点。然而,关于浮力对超临界流体传热影响的研究大多集中在超临界CO2上[10 − 12],关于浮力对超临界LNG局部传热特性影响的研究很少。由于超临界CO2的相关关联式由于传热特性不同,不能完全适用于超临界LNG。同时,上述研究中对超临界流体的研究仅限于拟临界区,无法分析传热增强、传热恶化和恢复的全过程。在超临界LNG气化过程中,温度从−163 °C上升到8 °C,流体将经历类液区、拟临界区和类气区。浮力对传热性能的影响在不同的区域不同。此外,上述研究是在圆形或半圆形通道中进行的。在工程应用中,通道的常见横截面形状包括半圆形、矩形、三角形、梯形等。Lee等[13]研究了半圆形、矩形、梯形和圆形通道形状的锯齿状PCHE的热水力性能。经过对比结,发现矩形通道传热性能最好,但水力性能最差,而圆形通道热性能最差。超临界LNG在不同横截面通道中的流动和传热性能不同,浮力的作用会使传热性能更加复杂。因此,从理论和实践角度来看,研究浮力对不同截面形状通道中超临界LNG局部流动和传热性能的影响具有重要意义。
本文对超临界LNG气化过程中的局部流动和局部传热进行数值研究。研究了在不同形状通道内浮力对超临界LNG在类液区、拟临界区和类气区对传热性能的影响。其次考虑物性变化与流动结构变化的相互作用,表征并评价了浮力在传热性能变化中的作用。最后,分析二次流的演变和湍流动能的分布,突出了整个过程中传热增强和传热劣化的原因。
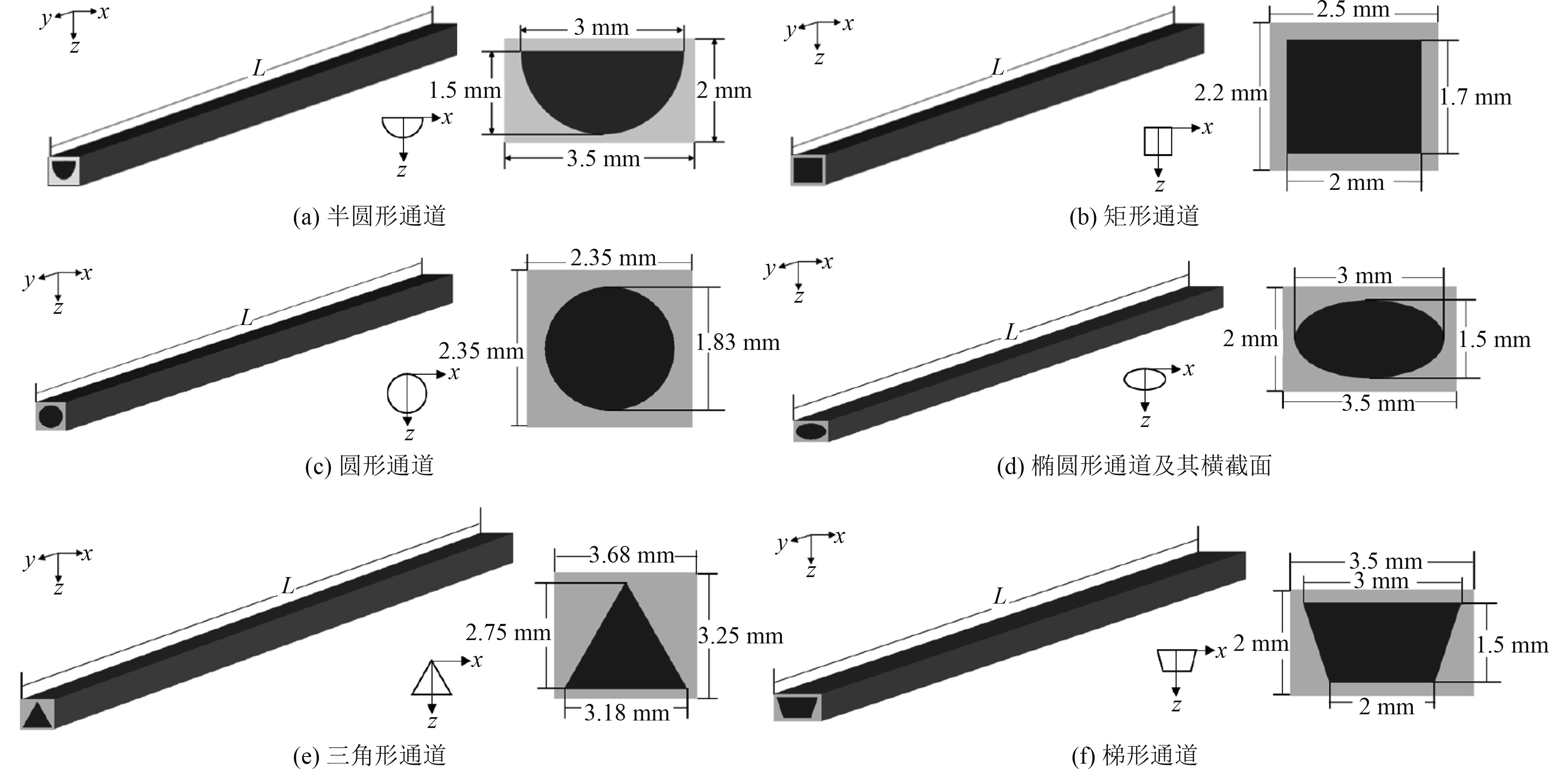
1 物理模型和控制方程 1.1 物理模型建立截面形状为半圆、椭圆、圆形、矩形、梯形和三角形的通道模型。每根管总长度为520 mm,为了保证计算结果的可对比性,6种形状的通道水力直径一致。流道三维物理模型及横截面如图1所示。
|
图 1 通道模型和通道横截面 Fig. 1 The model and the cross-section of channel |
本文假设流体为稳态且没有内热源的湍流流动。在流体流动过程中与环境的热交换忽略不计,考虑重力在流动过程中的影响。流体域的连续性方程、动量方程和能量方程表示如下:
连续性方程
| $ \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0。$ | (1) |
式中:ρ为密度;μi为速度矢量。
动量方程
| $ \begin{split} \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) =& \frac{\partial }{{\partial {x_j}}}\left[(u + {u_t})(\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}) - \frac{2}{3}(u + {u_t})\frac{{\partial {u_k}}}{{\partial {x_k}}}\right] - \\ & \frac{{\partial {P_i}}}{{\partial {x_i}}} + \rho {g_i}。\\[-1pt] \end{split} $ | (2) |
式中:p为静压;μ为动态粘度;μt为湍流粘度,湍流粘度取决于湍流模型。
能量方程
| $ \frac{\partial \left({\rho }{{u}}_{{i}}{{c}}_{{p}{T}}\right)}{\partial {{x}}_{{i}}}=\frac{\partial }{\partial {{x}}_{{i}}}\left({\lambda }\frac{\partial {T}}{{\partial {x}}_{{i}}}\right)+{\varnothing } 。$ | (3) |
式中:λ为导热系数;cp为恒压下的比热;
SST κ-ω模型在近壁面和远壁面处都能给出很好的预测。湍流动能k和比耗散率ω的输运方程表达为:
| $ \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}({\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}) + {G_k} - {Y_k} + {S_k},$ | (4) |
| $ \frac{\partial }{{\partial t}}(\rho \omega ) + \frac{\partial }{{\partial {x_i}}}(\rho \omega {u_i}) = \frac{\partial }{{\partial {x_j}}}({\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}) + {G_\omega } - {Y_\omega } + {S_\omega } + {D_\omega } 。$ | (5) |
式中:Γk和Γω分别为k和ω的有效扩散速;Gk为k的产生项;Gω为ω的产生项;Yk和Yω均为湍流引起的耗散项;Sk和Sω均为自定义源项;Dω为交叉扩散项。
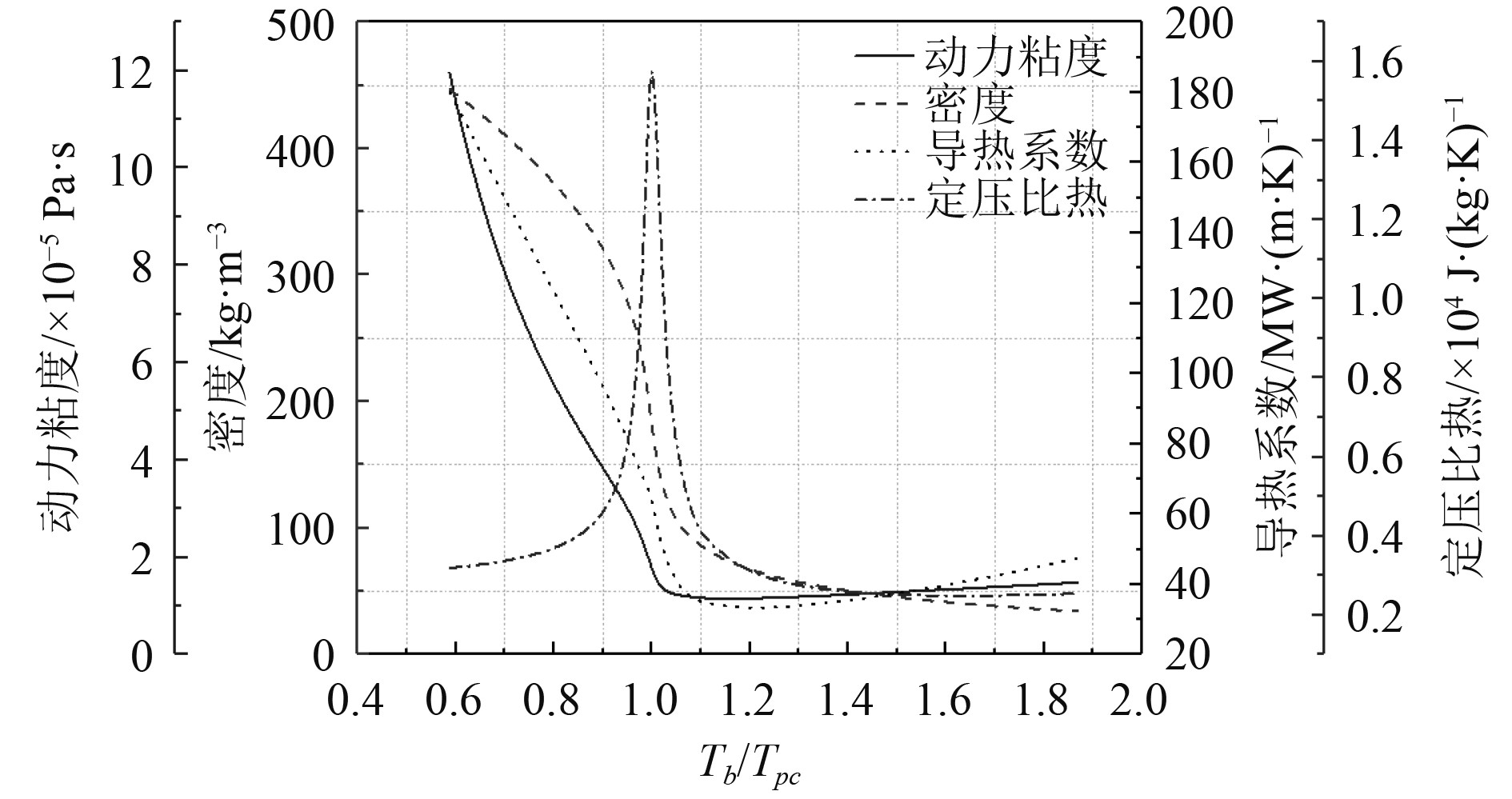
2 数值方法和边界条件本研究使用Ansys Fluent进行数值计算。图2为超临界LNG在6 MPa压力下的比热、密度、动态粘度和导热系数的变化。当Tb/Tpc≤0.9时,流体处于类液区。当0.9<Tb/Tpc<1.1时,流体处于拟临界区。当Tb/Tpc≥1.1时,流体处于类气态区。其中,Tb为流体温度,Tpc为拟临界温度。超临界LNG的热物理性质从NIST标准参考数据库(REFPROP)获得,并用分段多项式函数表示。
|
图 2 6 MPa压力下超临界LNG的热物理性质 Fig. 2 Thermo-physical properties of supercritical LNG at the pressure of 6 MPa |
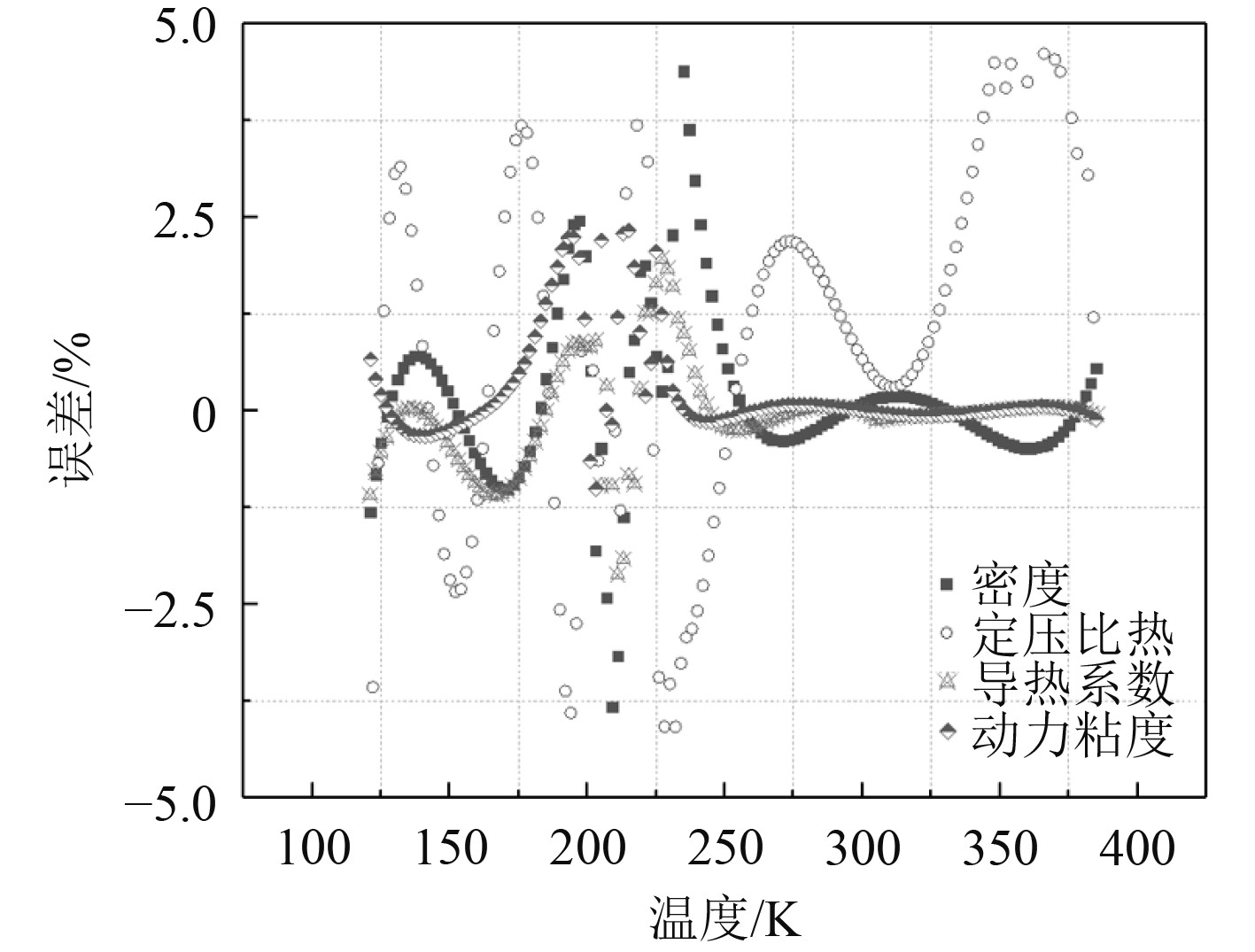
由于超临界LNG物性变化剧烈,因此拟合值和软件中查到的实际值存在一定误差,图3为6 MPa下拟合结果与的实际值的误差对比图,由图看出最大误差为4.8%,平均误差为2%,可以认为所拟合的多项式函数是合适的。选择SST k-ω模型进行数值计算。在求解方法方面,采用有限体积法求解控制方程组。此外,速度和压力的耦合计算采用SIMPLE算法。连续性方程、动量方程、能量方程等采用QUICK格式进行离散,压力项采用二阶迎风格式离散。残差值是初始值代入方程迭代计算,前后2次计算结果的差值是用于描述计算精度的一项参数。当连续性方程、动量方程和能量方程的最小残差小于1.0 × 10−6,且进出口质量流量达到平衡和出口温度不变时认为数值计算收敛。
|
图 3 压力为6 MPa下超临界LNG物性参数误差 Fig. 3 The physical parameter error of supercritical LNG at the pressure of 6 MPa |
通道入口边界条件为质量流量入口,超临界LNG入口温度为121 K,通道出口边界条件为压力出口。上下壁面施加恒定热密度,左右壁面设置为绝热边界条件。
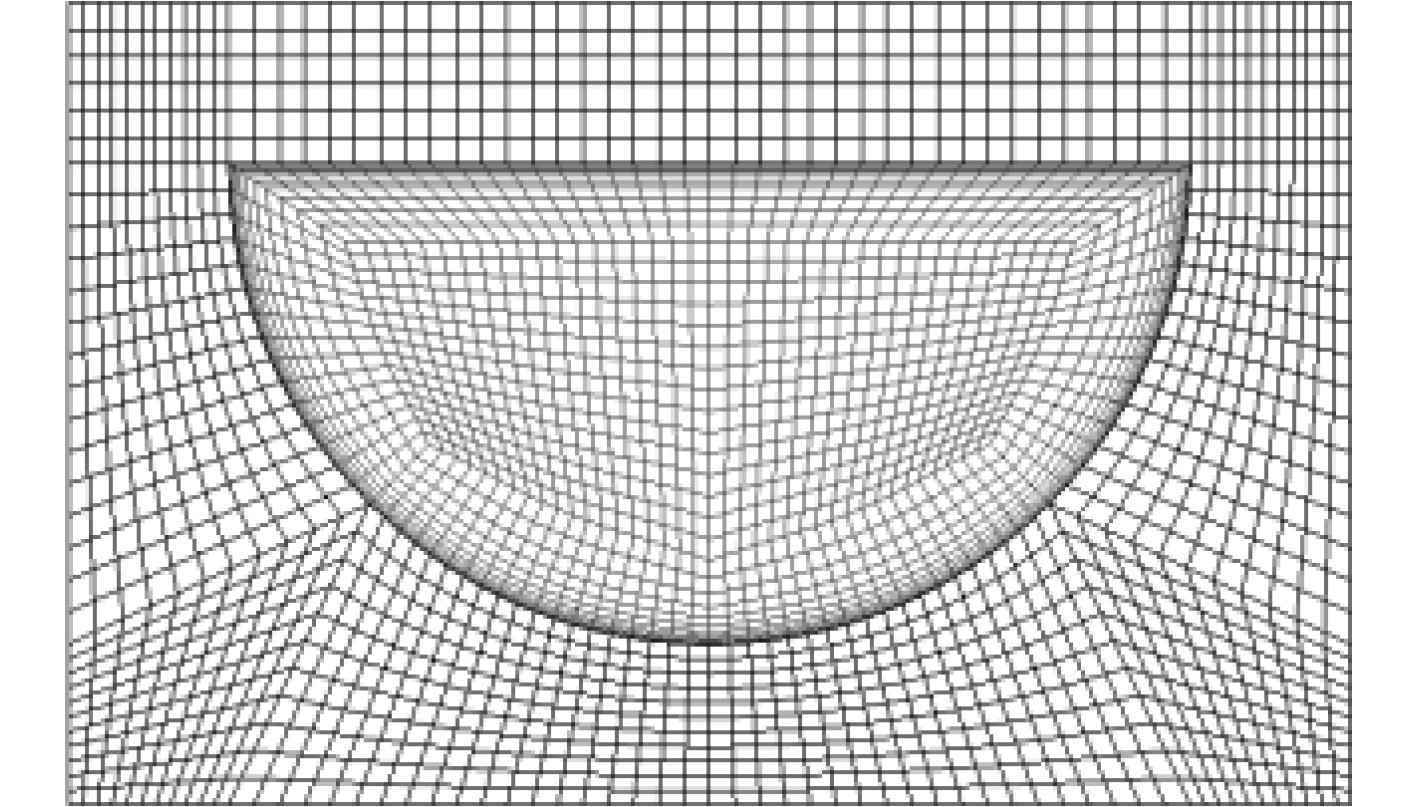
3 网格独立性验证和模型验证 3.1 网格独立性验证采用Ansys ICEM软件生成结构化六面体网格,固体和流体区域的网格如图4所示。为满足SST k-ω湍流模型要求,网格质量应大于0.6。为了保证无量纲壁面距离y+<1,对流体区域近壁面区域进行网格细化。为保证网格的可靠性及数值数据的准确性和效率,需要对网格进行独立性验证。本文比较了6种情况计算的出口温度。详细的网格节点数和计算结果如表1所示。Case5和case6之间的出口温度的相对误差只有0.03%。因此,考虑到计算精度和计算时间本文选择case5。
|
图 4 横截面网格 Fig. 4 The cross-section mesh |
|
|
表 1 网格独立性验证 Tab.1 The test of mesh independence analysis |
为了验证所实现的数值模拟方法以及所建立模型的有效性和正确性,将得到的CFD结果与之前相关工作中报道的实验结果进行对比[14]。由于LNG被认为易燃易爆,因此在实验中使用超临界氮气作为工作流体[14]。因此,数值模拟模型也采用了类似的条件,以超临界氮气为工质,验证和确认模型的正确性。实验结果与本工作得到的仿真结果之间的相对误差如表2所示。
|
|
表 2 模拟和实验结果之间的相对误差 Tab.2 Relative error between simulation and experiment results |
可以看出,温差和压降的相对误差分别为0.33%和3.16 %。由此可见,相对误差在可接受范围内,模拟结果与实验结果吻合较好。因此,本研究中的物理和数值模型可靠。
4 计算方法水力直径Dh的计算公式如下:
| $ {D_h} = \frac{{4{A_c}}}{S} 。$ | (6) |
式中:Ac为通道的横截面积;S为通道的横截面周长。
局部对流传热系数hx的计算公式如下:
| $ {h_x} = \frac{q}{{{T_{w,x}} - {T_{b,x}}}} 。$ | (7) |
式中:下标x表示局部参数;q为热流密度;Tw为相应截面的壁温;Tb为换热器通道中流体的温度。
PCHE的对流换热特性由无量纲参数柯尔朋传热因子j进行描述,j因子的计算公式如下:
| $ j = \frac{{Nu}}{{{Re} {{Pr }^{\frac{1}{3}}}}} 。$ | (8) |
对PCHE进行评价时不仅要考虑对流换热特性,还需要考虑压降。因此流体沿程摩擦压降的大小由范宁摩擦因子f来进行描述,公式如下:
| $ f = \frac{{\Delta P}}{{2\rho {u^2}}}\frac{{{d_h}}}{l} 。$ | (9) |
式中,
半经验浮力参数通常用于量化浮力的影响,特别是对水平超临界流体传热的影响。本文半经验浮力参数的计算公式为:
| $ Ri = \frac{{G{r_x}}}{{{Re} _x^2}} 。$ | (10) |
通常,当Ri大于0.01时,浮力对传热的影响可以忽略不计。
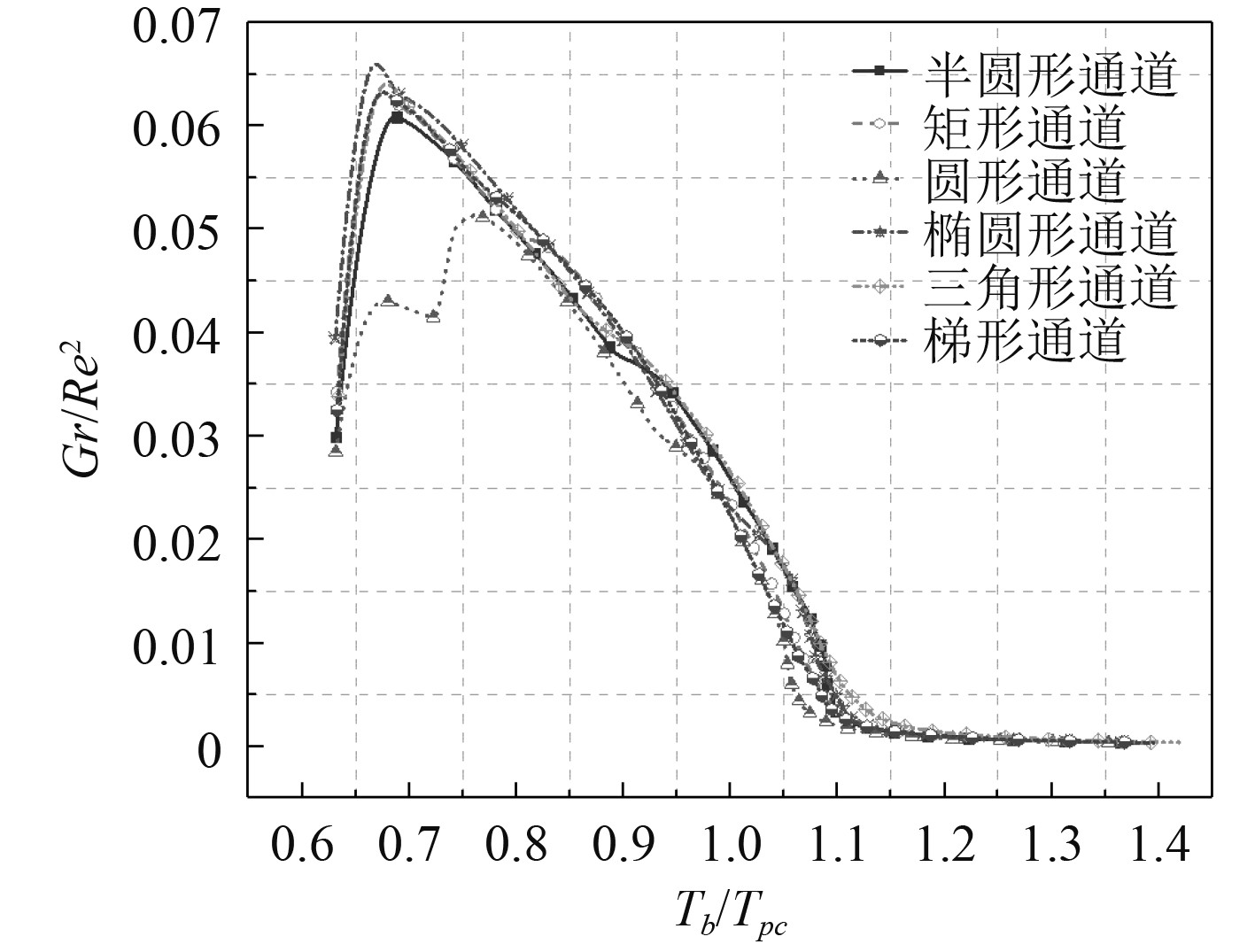
5 结果分析对横截面为半圆形、圆形、椭圆形、矩形、三角形和梯形的通道进行数值模拟。图5为压力是6 MPa时不同截面形状通道内流体沿流动方向的浮力因子。可知,在类气区,所有通道中的浮力因子均小于阈值,这意味着浮力对传热的影响可以忽略不计。在拟临界区,所有通道中的浮力因子相似。但是,在类液体区域,圆形通道中的浮力因子与其他通道不同。当Tb/Tpc=0.67时,半圆形、椭圆形、梯形、矩形和三角形通道的浮力因子达到峰值,而在圆形通道中,浮力因子在Tb/Tpc=0.75时达到峰值,圆形通道中的浮力因子明显小于类液体区域的其他通道。
|
图 5 6 MPa时的半经验浮力参数 Fig. 5 The semi-empirical buoyancy parameter at the pressure of 6 MPa |
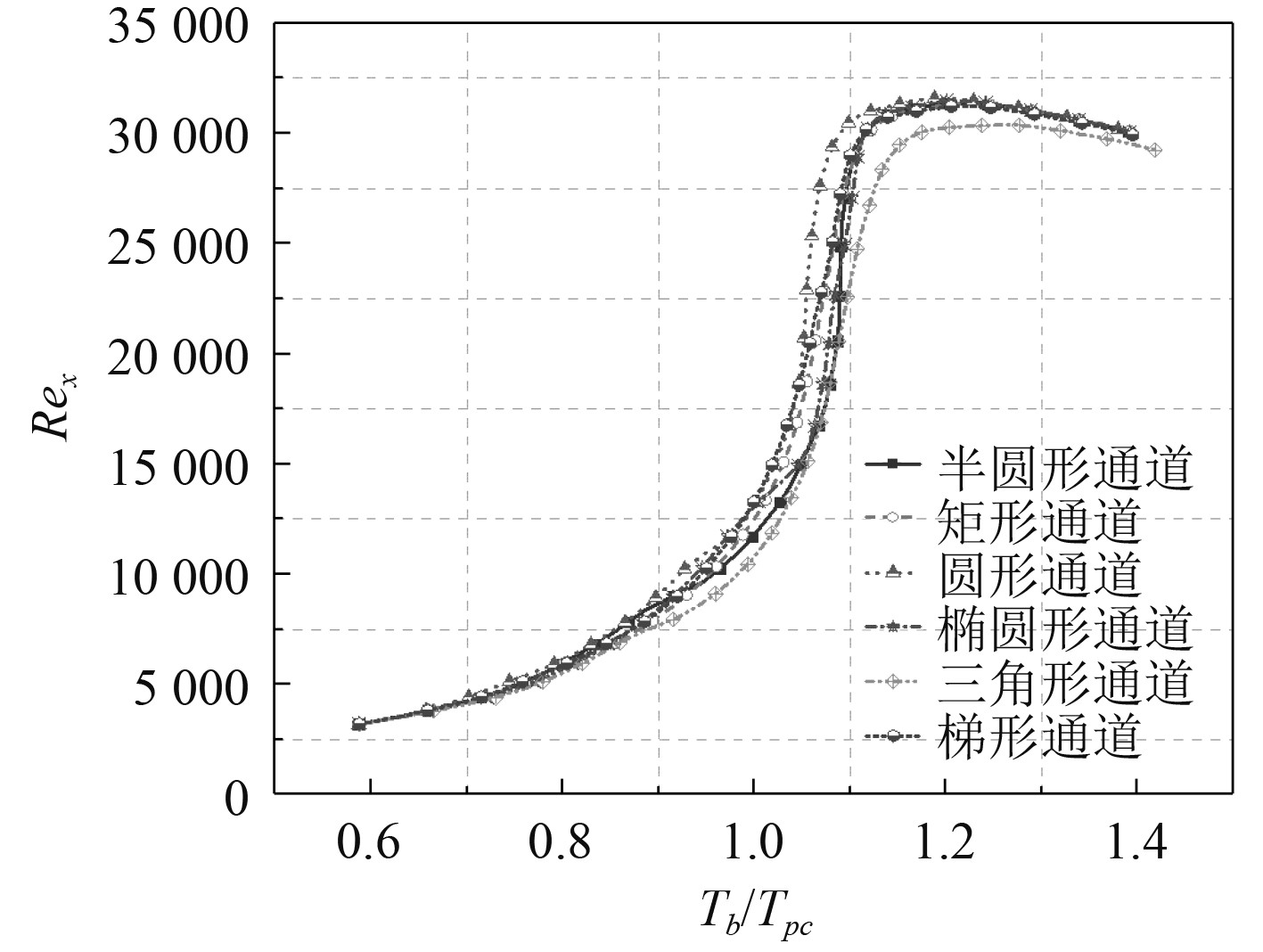
此外,图6为压力是6 MPa时各种不同截面形状通道内流体沿流动方向的局部雷诺数。可知,不同截面形状通道内局部雷诺数变化趋势是一致。通道形状对于局部雷诺数没有造成太大影响。由图2可知,超临界LNG的动力粘度随着温度的升高先减小后增大。因此,随着温度的升高,局部雷诺数先增大后减小。
|
图 6 6 MPa时沿通道的雷诺数 Fig. 6 Reynolds number along the channel at the pressure of 6 MPa |
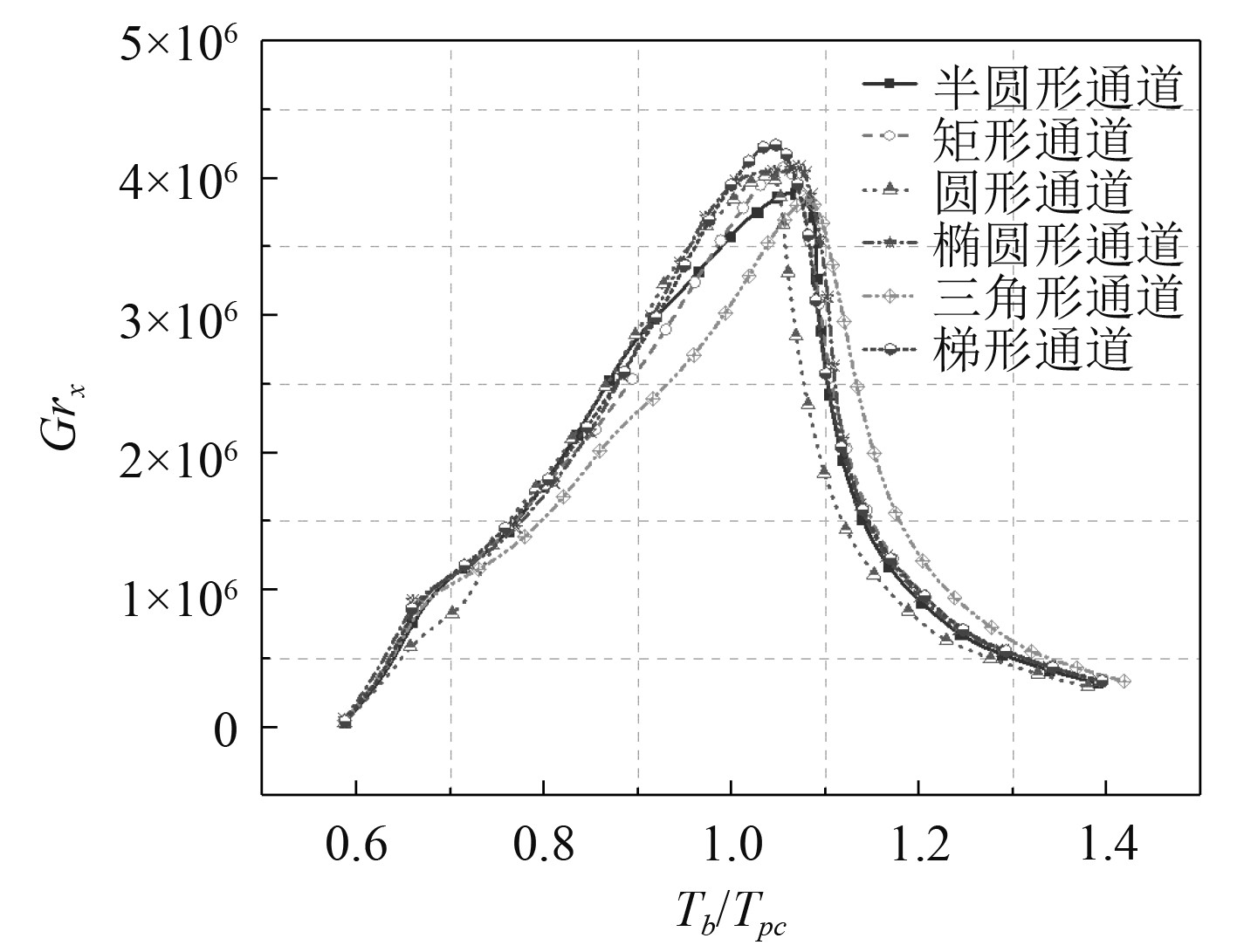
图7为压力是6 MPa时不同截面形状通道内流体沿流动方向的局部格拉晓夫数。结果表明,局域格拉晓夫数变化剧烈。在拟临界区时格拉晓夫数最大。这是因为超临界LNG在拟临界区的动力粘度相对较低,导致格拉晓夫数增大。
|
图 7 6 MPa时沿通道的格拉晓夫数 Fig. 7 Grashof number along the channel at the pressure of 6 MPa |
从局部雷诺数和局部格拉晓夫数的变化可以清楚地得出浮力因子在类气区域小于阈值的原因是类气区域格拉晓夫数相对较小而雷诺数相对较大。局部格拉晓夫数的峰值在拟临界区,但浮力因子的峰值在类液区。这表明局部雷诺数对浮力因子的变化起主导作用。
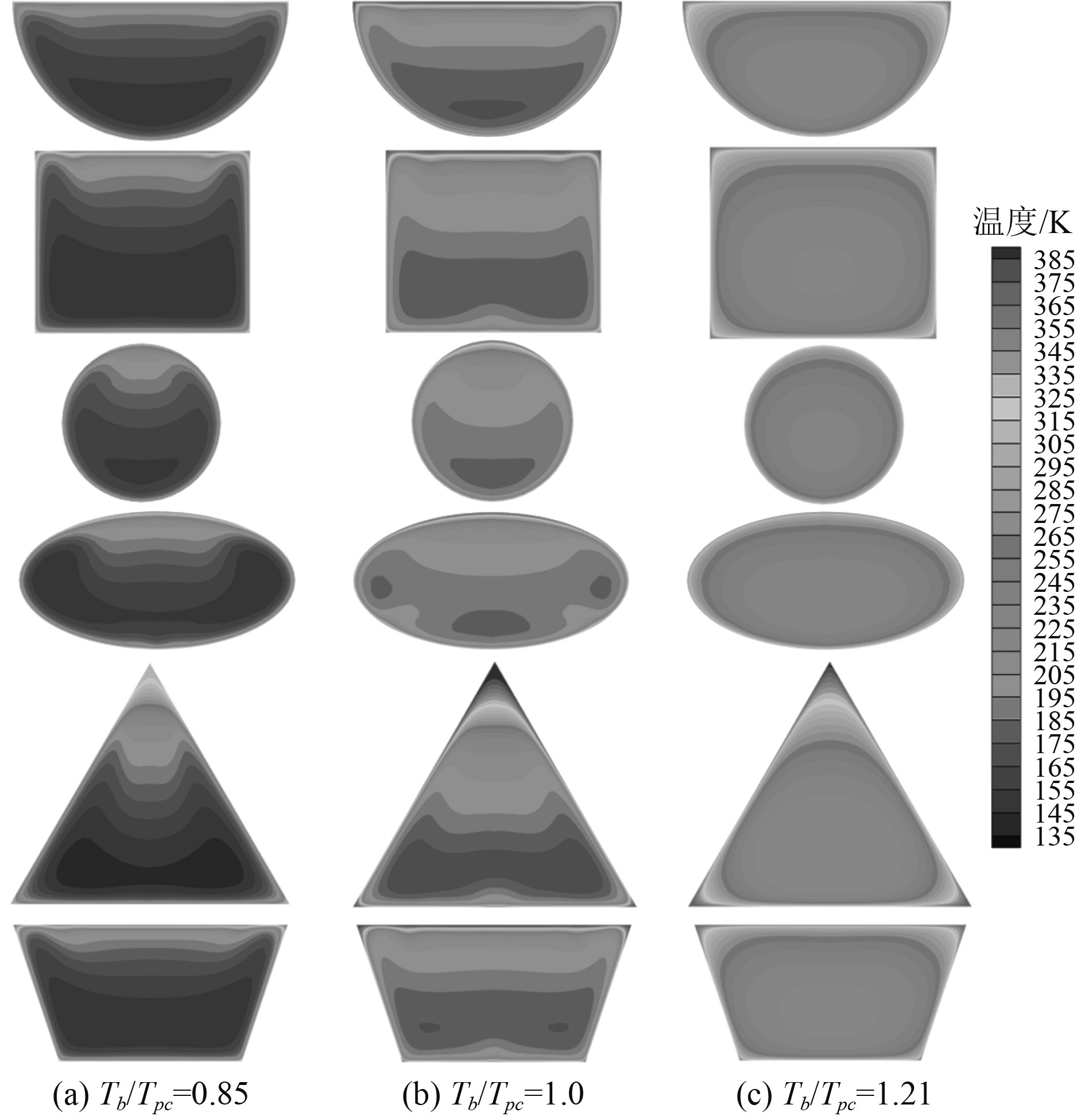
图8为通道内不同截面的温度场。可知在浮力因子大于阈值的类液区和拟临界区,低温流体向截面底部收缩。在类液区,6种形状通道内的温度场分布相类似。在拟临界区时,浮力引起的温度不均匀性变得更加明显,通道顶部附近的流体温度远高于拟临界温度。特别是在三角形通道的顶角,积聚了大量的高温流体。同时,梯形通道、矩形通道和半圆形通道的拐角处也存在高温流体聚集。结合图2可以得出结论,高温流体恒压比热低,会导致传热性能下降。此外,椭圆形和梯形通道形成其他通道所没有的低温中心,三角形和矩形通道中的低温流体呈现不规则形状。在类气体区域,由于浮力因子小于阈值,温度不均匀性减弱,高温流体的聚集也得到缓解。
|
图 8 6 MPa时沿通道不同横截面的温度场 Fig. 8 Temperature fields for different cross-sections along the channel at the pressure of 6 MPa |
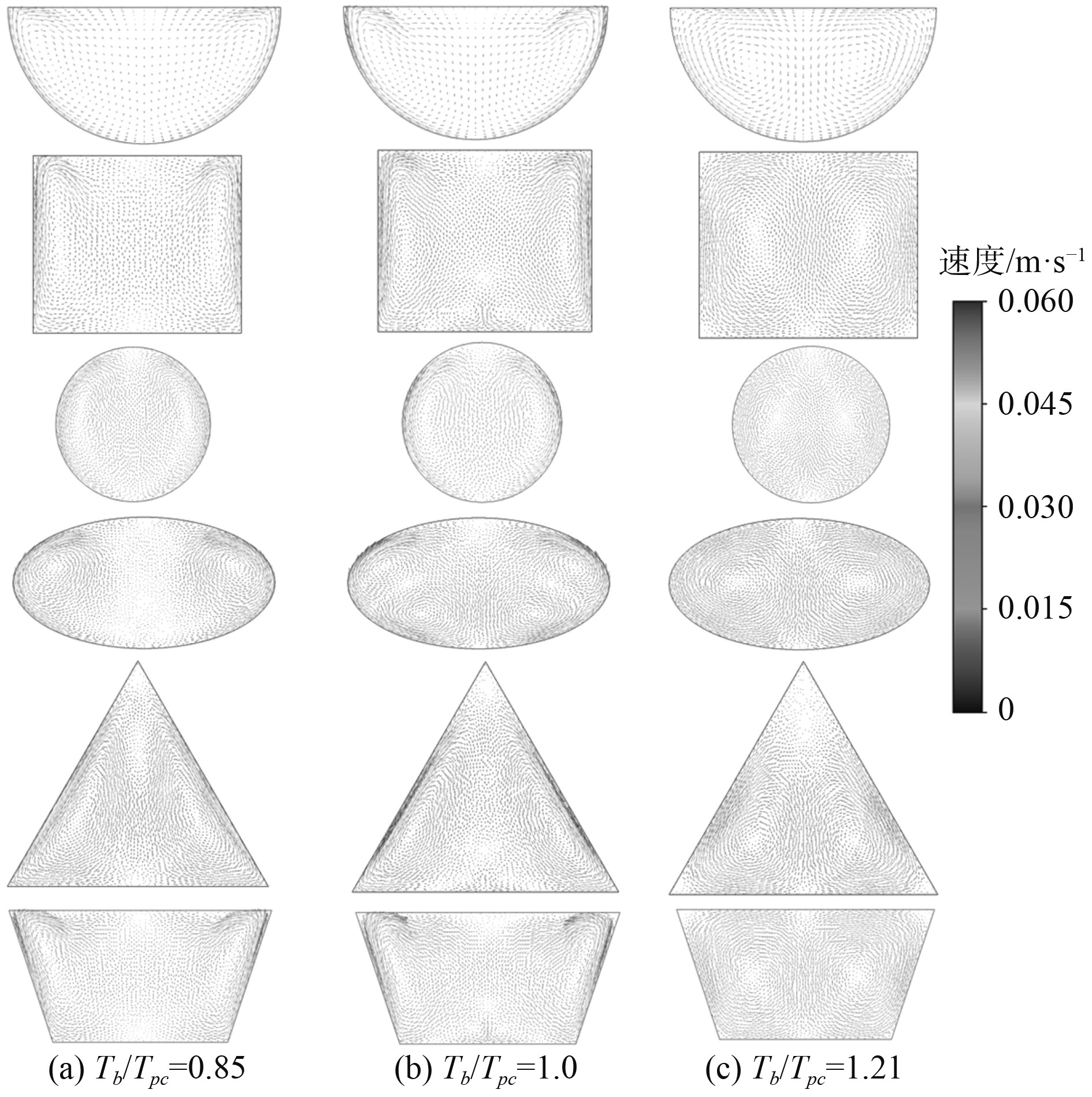
图9为通道内不同截面的径向速度场。可以看出,在类液区,流体在截面中间区域向下流动,沿通道两侧壁面向上流动,从而产生了对称旋涡,进而增大了两侧壁面附近的湍动能。值得注意的是,在三角形通道顶端,流体向下流动的速度很小,这很好地解释了图8中三角通道顶角积聚了大量高温流体,这样会使得顶端传热性能下降。在拟临界区,圆形通道和半圆形通道的截面有2个旋涡,而梯形、矩形、三角形和椭圆形通道截面上存在4个旋涡,较小的2个旋涡出现在通道底部壁面附近。造成这种复杂的二次流结构的原因是横截面上密度差的增加和通道形状的差异。在任意通道的截面上,通道左右壁附近的二次流速最大。二次流动的存在增强了传热能力。在梯形、矩形、三角形和椭圆形通道底壁附近产生的2个涡流使得换热得到加强,很好地解释了图8中低温流体的不规则形状现象。可以看出,不同的截面形状导致涡的数量和分布不同,从而导致不同的传热现象。因此,二次流在通道中的传热性能中起着重要作用。在类气区,主流速度远大于二次流速度。二次流对传热的影响减小,由图8也可以看出低温流体的向下聚集得到了缓解。
|
图 9 6 MPa时沿通道不同截面的径向速度场 Fig. 9 Radial velocity fields for different cross-sections along the channel at the pressure of 6 MPa |
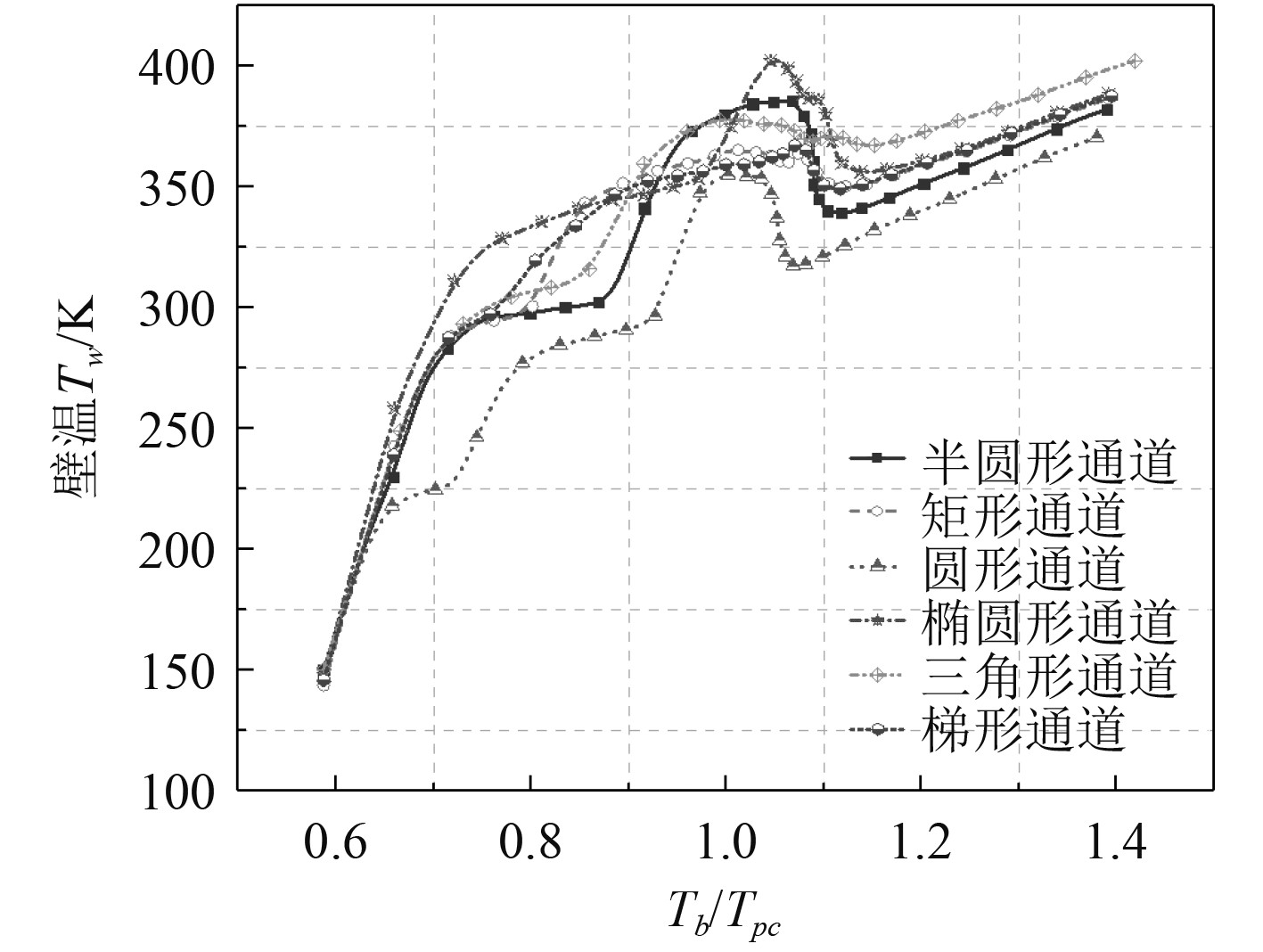
此外,图10为通道局部壁面温度沿通道的变化情况。在类液区,壁面温度最高为椭圆形通道,最低的为圆形通道。在拟临界区时,所有通道的壁温迅速升高,一般来说壁面温度的快速升高是传热恶化的结果。其中,圆形通道、半圆形通道和椭圆通道的快速上升尤为明显。此时,壁温最高的是椭圆形通道,最低的是圆形通道。在类气区,壁温最高的是三角形通道,最低的是圆形通道。
|
图 10 6 MPa时沿通道的局部壁温 Fig. 10 The local wall temperature along the channel at the pressure of 6 MPa |
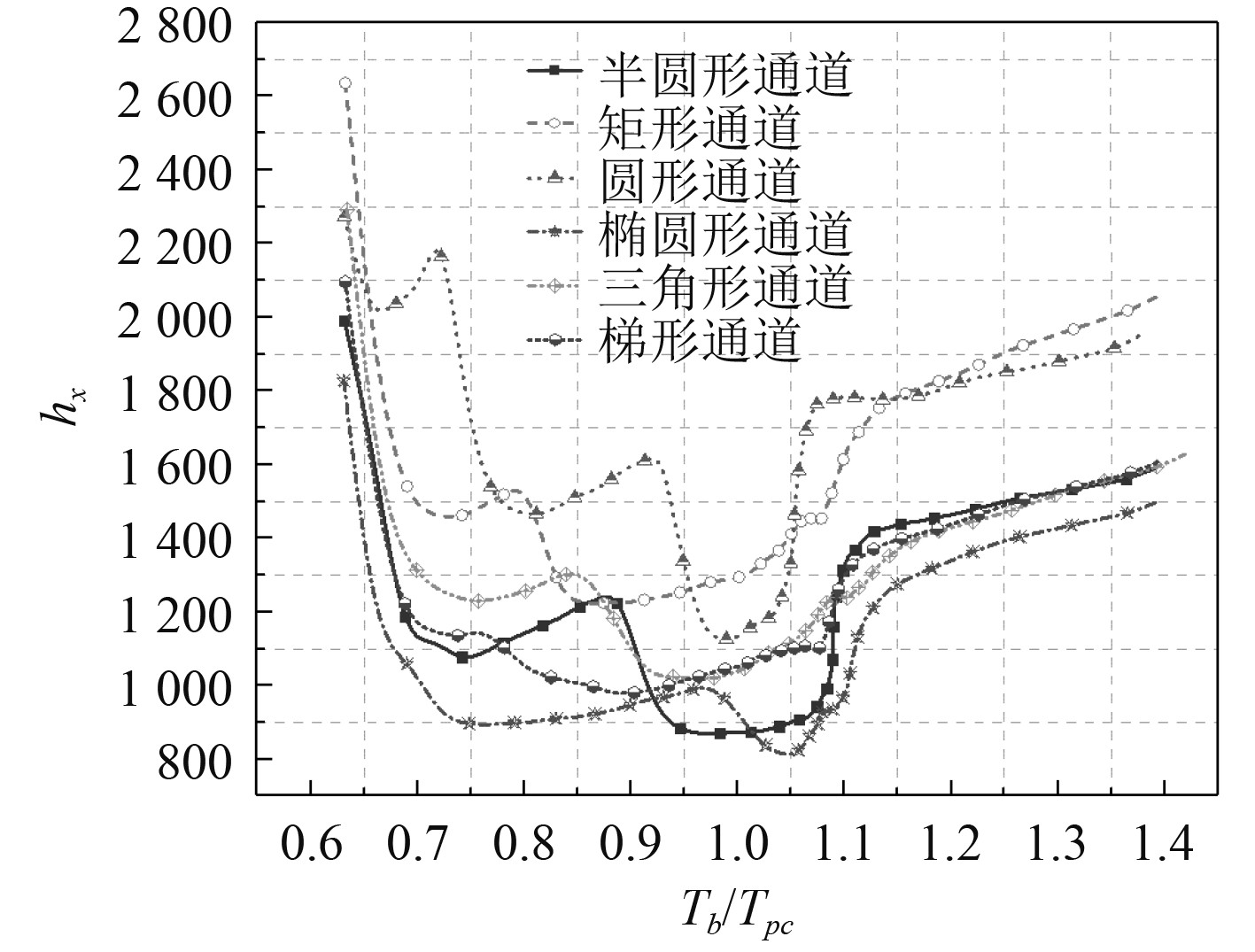
图11为通道沿流动方向的局部对流换热系数。在类液区,传热性能最好的为圆形通道,最差的为椭圆形通道。该结果与图10给出壁面温度最高的为椭圆形通道,最低的为圆形通道这一结论一致。在拟临界区时,圆形通道和半圆形通道的对流换热系数变化较大,矩形通道、三角形通道和梯形通道的变化平稳。结合图9,这种现象是由于截面形状不同,导致二次流的分布不同。二次流的分布会影响传热。在类气区传热性能最好的是矩形通道,最差的为椭圆形通道。结合图5和图10可以看出对局部对流换热系数的变化与浮力因子和壁温是相对应的,即受浮力影响越小,传热性能越好。当浮力因子增大,壁温也随之增大,而对流换热系数随之减小,并存在一定的滞后性。
|
图 11 6 MPa时沿通道的局部传热系数 Fig. 11 The local heat transfer coefficient along the channel at the pressure of 6 MPa |
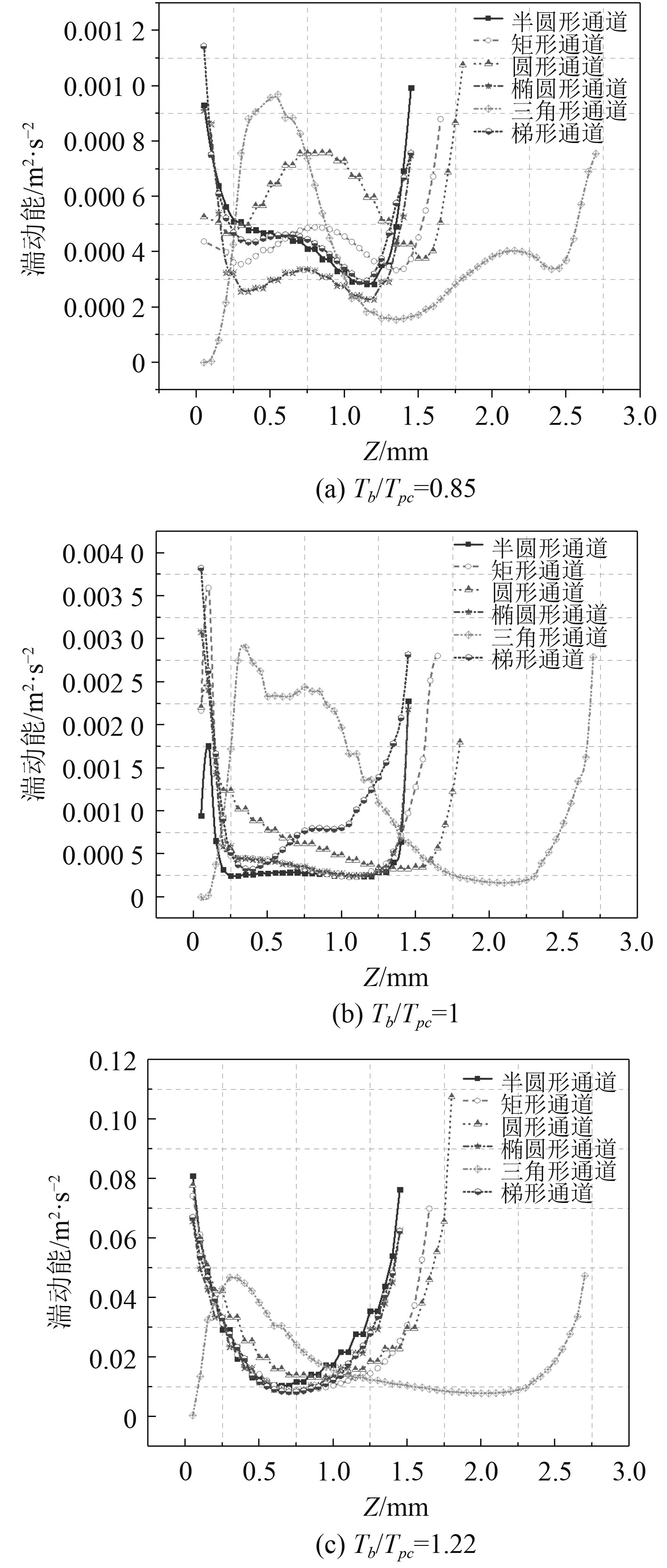
为了详细分析流动情况和传热性能,图12和图13分别为通道内湍动能及定压比热沿Z方向的分布。
|
图 12 6 MPa时Z方向上的湍动能 Fig. 12 The turbulent kinetic energy in the Z direction at the pressure of 6 MPa |
|
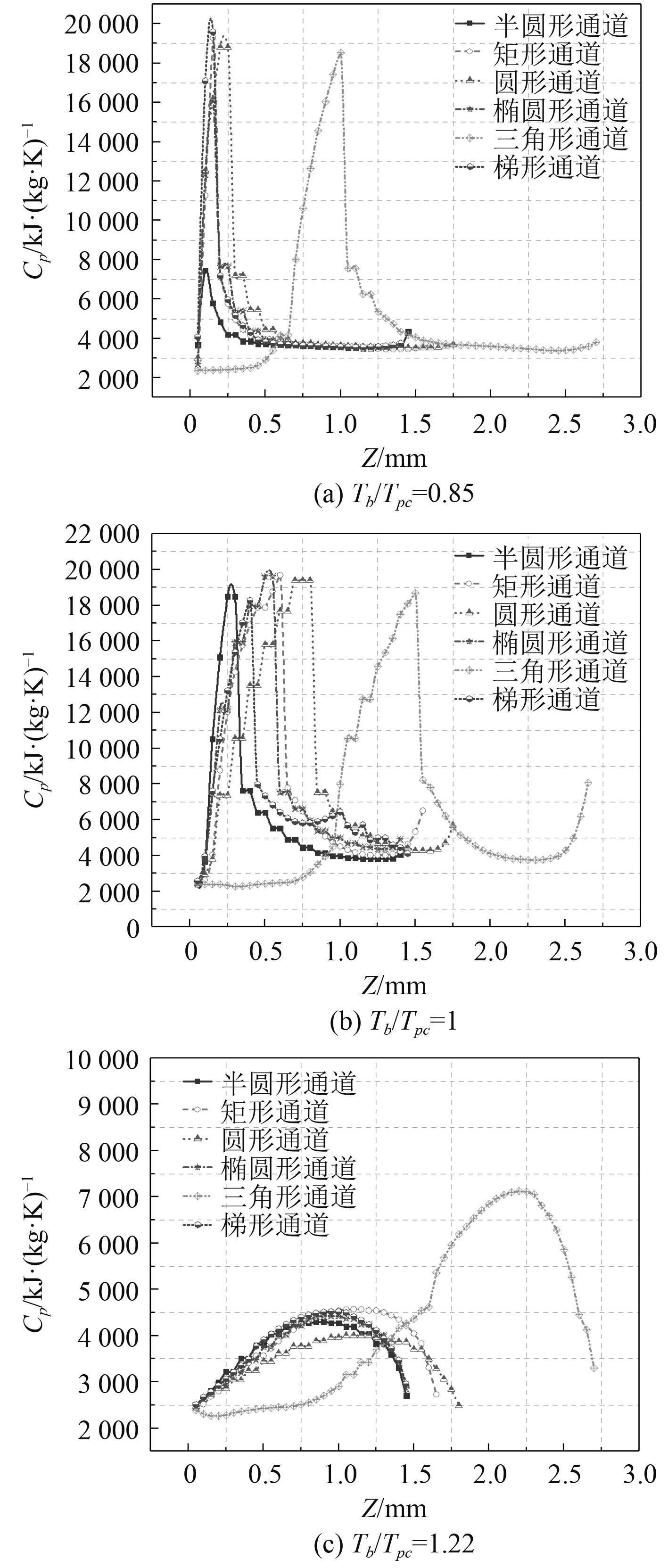
图 13 6 MPa时Z方向上的定压比热 Fig. 13 The specific heat at constant pressure in the Z direction at the pressure of 6 MPa |
由图13(a)可知,在类液区,三角形通道中流体的定压比热容的最大值远离通道顶部,而顶部附近流体定压比热容最小。结合图12(a)可知在三角形通道中,通道顶端附近流体的湍动能接近0 m2/s2,顶角处发生传热劣化,传热性能降低。通道中心部分流体湍动能最大,同时通道底部附近流体湍动能也较大,因而传热能力提高。而在其他通道中,靠近通道顶部和底部的流体的湍流动能较大,呈现W形分布。因此,通道顶部和底部的传热性能较好。随着壁与流体温差的增大,局部对流换热系数减小,这是局部对流换热系数减小的主要原因。对流换热系数减小的区域与局部壁面温度迅速升高的区域一致。但由于湍动能的分布及大小不同造成不同形状通道传热性能的不同。
在拟临界区,在三角形通道中,湍动能和定压比热的分布与在类液区时相似。在其他通道中。顶部和底部附近流体湍动能较大,呈U形分布。由图12(b)可以看出通道顶部和底部流体湍动能最大的为梯形通道,其次为矩形通道、椭圆通道、圆形通道和半圆通道。湍动能越大,流体的扰动也就越大,换热性能越强。从湍动能来看,换热能力的强弱应与上述一致,但从图11可知实际情况并非如此。
圆形通道和矩形通道具有更好的传热能力。二次流是由于浮力而产生的,二次流减少了壁面附近热边界层的厚度,提高了传热性能。但同时,由于浮力作用,高温流体聚集到通道顶部,导致通道顶部附近流体温度远高于拟临界温度,由图13(b)看出,通道顶部附近流体的定压比热仅为其最大值的1/9。因此,当Tb/Tpc=1.05时,对流换热系数最小,这也表明此时定压比热对换热性能起主导作用。从图13(b)可知通道底部附近流体的定压比热是通道顶部附近流体的2~3倍,因此在通道底部附近有更好的传热性能。同时,靠近通道底部的流体的最大比热是三角通道,其次是矩形通道和圆形通道。与湍流动能相比,底部流体定压比热的不同是造成各种截面形状通道传热性能差异的主要原因。
在类气区,浮力效应减弱,浮力因子小于阈值。通道内的径向速度趋于一致。同时,由图12(c)可以看出,在类气区湍动能远大于类液区和拟临界区。在这种情况下,通道的换热性能得进一步得到改善。因此,局部对流换热系数沿流动方向逐渐增大。
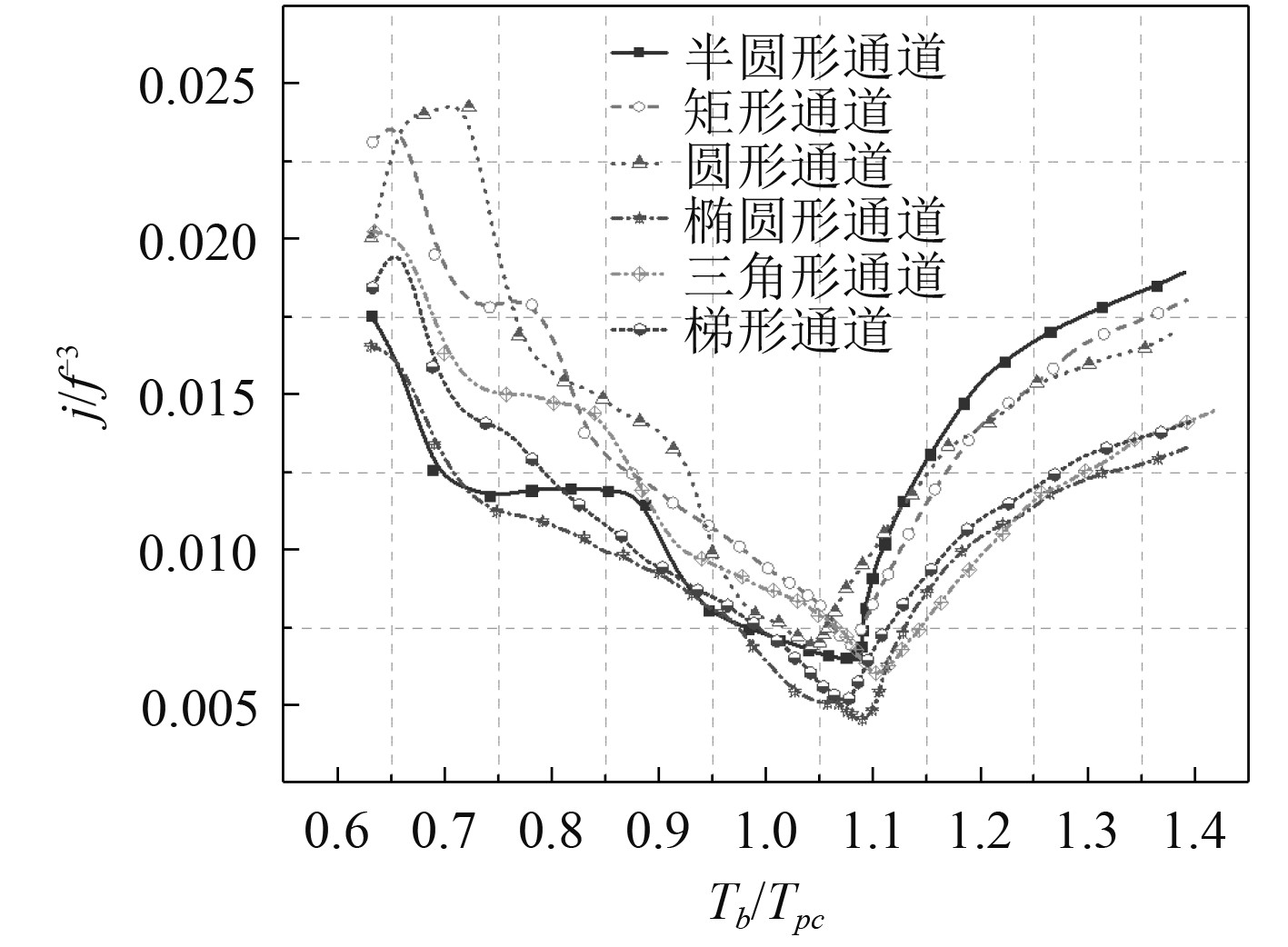
图14为通道沿流动方向的综合评价因子j/f−3。j/f−3因子在Tb/Tpc=1.1附近出现最小值,是很明显的传热恶化。通道形状的改变对于远离最小值点的j/f−3有着较大的影响,但是对于Tb/Tpc= 1.1附近的j/f−3因子影响较小。在类液区,半圆通道、梯形通道和椭圆通道的综合性能较差;在拟临界区,梯形通道和椭圆形通道综合性能较差;在类气区,三角形通道、梯形通道和椭圆通道的综合性能较差。
|
图 14 6 MPa时沿通道的局部j/f−3因子 Fig. 14 The local j/f−3 factor along the channel at the pressure of 6 MPa |
本研究通过数值模拟,对浮力对超临界LNG传热特性的影响进行了研究与分析。研究了浮力在类液区、拟临界区和类气区对换热性能的影响,得出以下结论:
1)截面形状对浮力因子的影响不大。浮力对换热性能的影响主要在类液区和拟临界区。
2)浮力和密度差引起的二次流提升了壁面与相邻流体的换热性能,但浮力使低密度、高温流体聚集在通道顶部,导致局部换热性能恶化,局部对流换热系数降低,这表明定压比热对传热性能起主导作用。
3)由于通道截面形状不同,在不同区域形成涡流的位置和数量不同。湍流动能分布和通道底部恒压比热的差异是造成各截面通道传热性能差异的主要原因。
4)通过j/f −3因子进行综合性能评价,得出综合性能最好的通道在不同区域是不同的。
| [1] |
PU L, QU Z, BAI Y, et al. Thermal performance analysis of intermediate fluid vaporizer for liquefied natural gas[J]. Applied Thermal Engineering, 2014, 65(1−2): 564−574.
|
| [2] |
KIM J H, BAEK S, JEONG S, et al. Hydraulic performance of a microchannel PCHE[J]. Applied Thermal Engineering, 2010, 30(14−15): 2157−2162.
|
| [3] |
MYLAVARAPU S K, SUN X, CHRISTENSEN R N, et al. Fabrication and design aspects of high-temperature compact diffusion bonded heat exchangers[J]. Nuclear Engineering and Design, 2012, 249: 49−56.
|
| [4] |
C. H. O. E. S. Kim. Design option of heat exchanger for the next generation nuclear plant[C]//4th International Topical Meeting on High Temperature Reactor Technology (HTR2008), ASME, Washington, DC, USA, 2008.
|
| [5] |
BOWDERY T, LNG applications of diffusions bonded heat exchangers[C]//WCPT5, Vol. 1: All Topical Conference Sessions and Non-Topical Conference Sessions, Orlando, FL, USA, 2006.
|
| [6] |
MA T, ZHANG P, LIAN J, et al. Numerical study on flow and heat transfer performance of natural gas in a printed circuit heat exchanger during transcritical liquefaction[J]. Journal of Fluids Engineering, 2021, 143(4).
|
| [7] |
TIAN R, WANG D, ZHANG Y, et al. Experimental study of the heat transfer characteristics of supercritical pressure R134a in a horizontal tube[J]. Experimental Thermal and Fluid Science, 2019, 100: 49−61.
|
| [8] |
YU S, LI H, LEI X, et al. Experimental investigation on heat transfer characteristics of supercritical pressure water in a horizontal tube[J]. Experimental Thermal and Fluid Science, 2013, 50: 213−221.
|
| [9] |
BAZARGAN M, FRASER D, CHATOORGAN V, Effect of Buoyancy on Heat Transfer in Supercritical Water Flow in a Horizontal Round Tube[J]. Journal of Heat Transfer, 2015, 127(8): 897–902.
|
| [10] |
张海燕, 超临界压力CO2通道内流动换热特性研究[D]. 北京: 中国科学院大学(中国科学院工程热物理研究所), 2021.
|
| [11] |
相梦如. 超临界压力CO2对流传热数值研究[D]. 北京: 中国科学院大学(中国科学院工程热物理研究所), 2018.
|
| [12] |
吕海财, 赵金乐, 潘辉, 等. 超临界CO2水平管内浮升力和热加速效应评判准则[J]. 西安交通大学学报, 2018, 52(9): 140−147.
|
| [13] |
LEE S M, KIM K Y, Comparative study on performance of a zigzag printed circuit heat exchanger with various channel shapes and configurations[J]. Heat and Mass Transfer, 2013, 49(7): 1021−1028.
|
| [14] |
张霄. 印刷板式汽化器汽化性能分析与研究[D]. 镇江: 江苏科技大学, 2017.
|
 2024, Vol. 46
2024, Vol. 46
