船舰目标识别分类是海上安全、渔业管理、军事防御以及海洋科学研究等多个领域中的关键技术之一[1]。为了实现有效的海上监管和响应,快速准确地识别并分类各种船舰目标尤为重要[2]。对船舰进行准确快速的识别和分类,可及时发现潜在的安全隐患,如非法捕捞、海盗行为或走私活动。这对于维护海上安全、保障航道畅通具有重要意义[3]。例如,顾鹏等[4]通过预处理雷达接收到的信号,提取脉间参数,并将提取的参数作为特征输入到KNN算法中,与已知样本进行比较,根据距离最近的K个邻居的类别进行目标识别分类。实验结果表明,该方法能够有效识别不同类型舰船目标,具有较高的识别准确率和鲁棒性。但该方法中雷达信号会受不同因素干扰,如其他舰船、气象条件等,导致该方法缺乏对复杂环境的适应性。张云等[5]结合实数域和复数域的优点,利用复数域的特性处理雷达信号,通过卷积神经网络提取特征,并识别分类舰船目标。实验证明,该方法在舰船目标识别分类任务中表现优异。但该方法主要针对特定的雷达信号和舰船类型进行了训练和验证,对于不同雷达系统和不同海域的舰船,其泛化能力较差。遗传算法(GA)作为一种优化搜索方法,能根据适应度函数对解空间进行高效搜索,从而找到最优解或近似最优解。将其应用于支持向量机(SVM)参数优化,可克服传统参数选择方法的局限性和主观性,提高分类器的精度与自适应性等性能[6]。为此,研究遗传算法优化支持向量机的船舰目标识别分类方法,期望为相关领域的研究人员和实践者提供一个全面视角,以推动船舰目标识别分类技术的进一步发展和应用。
1 船舰目标识别分类 1.1 基于HU矩的舰船目标特征提取对于实际舰船目标图像来说,其主轴方向经常变化,舰船类型大小各不相同,分布位置无规律可循[7]。因此,以HU矩为舰船目标的特征描述子,可解决旋转、平移与尺度等问题。
| $ {\mu _{pq}} = \sum\limits_{y = 1}^N {\sum\limits_{x = 1}^M {{{\left( {x - \frac{{{\varpi _{10}}}}{{{\varpi _{00}}}}} \right)}^p}{{\left( {y - \frac{{{\varpi _{01}}}}{{{\varpi _{00}}}}} \right)}^q}f\left( {x,y} \right)} }。$ | (1) |
式中:
但若
| $ {v_{pq}} = \frac{{{\mu _{pq}}}}{{{{\left( {{\mu _{00}}} \right)}^{\frac{{p + q}}{2} + 1}}}}。$ | (2) |
其中,
按照代数不变思想,通过归一化的二阶、三阶中心距
| $ {s_1} = {v_{20}} + {v_{02}},$ | (3) |
| $ {s_2} = {\left( {{v_{20}} - {v_{02}}} \right)^2} + 4v_{11}^2 ,$ | (4) |
| $ {s_3} = {\left( {{v_{30}} - 3{v_{12}}} \right)^2} + {\left( {3{v_{21}} - {v_{03}}} \right)^2} ,$ | (5) |
| $ {s_4} = {\left( {{v_{30}} + {v_{12}}} \right)^2} + {\left( {{v_{21}} + {v_{03}}} \right)^2} ,$ | (6) |
| $ \begin{split} {s_5} = \,&\left( {{v_{30}} - 3{v_{12}}} \right)\left( {{v_{30}} + {v_{12}}} \right) \left[ {{{\left( {{v_{30}} + {v_{12}}} \right)}^2} - 3{{\left( {{v_{21}} + {v_{03}}} \right)}^2}} \right] + \\ \,& \left( {3{v_{21}} - {v_{03}}} \right)\left( {{v_{21}} + {v_{03}}} \right) \left[ {3{{\left( {{v_{30}} + {v_{12}}} \right)}^2} - {{\left( {{v_{21}} + {v_{03}}} \right)}^2}} \right] ,\end{split} $ | (7) |
| $ \begin{split} {s_6} =\,& \left( {{v_{20}} - {v_{02}}} \right)\left[ {{{\left( {{v_{30}} + {v_{12}}} \right)}^2} - {{\left( {{v_{21}} + {v_{03}}} \right)}^2}} \right]+ \\ & 4{v_{11}}\left( {{v_{30}} + {v_{12}}} \right)\left( {{v_{21}} + {v_{03}}} \right),\end{split} $ | (8) |
| $ \begin{split} {s_7} =\,& \left( {3{v_{21}} - {v_{03}}} \right)\left( {{v_{30}} + {v_{12}}} \right)\left[ {{{\left( {{v_{30}} + {v_{12}}} \right)}^2} - 3{{\left( {{v_{21}} + {v_{03}}} \right)}^2}} \right] - \\ \,& \left( {{v_{30}} - 3{v_{12}}} \right)\left( {{v_{21}} + {v_{03}}} \right)\left[ {3{{\left( {{v_{30}} + {v_{12}}} \right)}^2} - {{\left( {{v_{21}} + {v_{03}}} \right)}^2}} \right] \\[-1pt] \end{split} $ | (9) |
式中:
以1.1小节构建的舰船目标特征矩
| $ h\left( s \right) = w \times \psi \left( s \right) + b。$ | (10) |
式中:
| $ J\left( h \right) = R\left[ h \right] + \lambda {\left\| w \right\|^2} = \sum\limits_{i = 1}^A {C\left( {{s_i}} \right)} + \lambda {\left\| w \right\|^2}。$ | (11) |
式中:
| $ h\left( s \right) = \frac{{\sum\limits_{i = 1}^A {{{\left| {{y_i} - h\left( {{s_i}} \right)} \right|}_\varepsilon }} }}{A}。$ | (12) |
其中,
按照统计学理论,通过最小化
| $ \min \left\{ {\frac{{{{\left\| w \right\|}^2}}}{2} + C\sum\limits_{i = 1}^A {\left( {\xi _i^* + {\xi _i}} \right)} } \right\} 。$ | (13) |
式中:
式(13)需符合的条件为:
| $ h\left( \phi \right) = \sum\limits_{i = 1}^A {\sum\limits_{j = 1}^A {\left( {\alpha _i^* - {\alpha _i}} \right)K\left( {{\phi _i},{\phi _j}} \right) + b} }。$ | (14) |
将式(13)变更成对偶问题,得到:
| $ \begin{split} & \max \Biggr[ - \frac{{\sum\limits_{i = 1}^A {\sum\limits_{j = 1}^A {\left( {\alpha _i^* - {\alpha _i}} \right)\left( {\alpha _j^* - {\alpha _j}} \right)K\left( {{s_i},{s_j}} \right)} } }}{2}+ \\ & \sum\limits_{i = 1}^A {\alpha _i^*\left( {{y_i} - \varepsilon } \right)} - \sum\limits_{i = 1}^A {{\alpha _i}\left( {{y_i} - \varepsilon } \right)} \Biggr] \end{split} $ | (15) |
式(15)需符合的条件为:
| $ \left\{ \begin{gathered} \sum\limits_{i = 1}^A {\alpha _i^*} = \sum\limits_{i = 1}^A {\alpha _i^{}},\\ 0 \leqslant \alpha _i^* \leqslant C,\\ 0 \leqslant \alpha _i^{} \leqslant C。\\ \end{gathered} \right. $ | (16) |
式中:
| $ K\left( {{s_i},{s_j}} \right) = {e^{ - \frac{{{{\left( {{s_i},{s_j}} \right)}^2}}}{{{\delta ^2}}}}} 。$ | (17) |
其中,
通过求解式(15)可获取SVM的舰船目标识别分类的决策函数,公式如下:
| $ h\left( s \right) = \sum\limits_{i = 1}^A {\sum\limits_{j = 1}^A {\left( {\alpha _i^* - {\alpha _i}} \right)K\left( {{s_i},{s_j}} \right) + b} }。$ | (18) |
通过
SVM中
GA算法内每个个体
利用GA算法寻找最佳舰船目标识别分类的SVM最佳参数组合时,通过适应度
| $ \hat f = \frac{U}{A}。$ | (19) |
式中:
GA算法内的复制过程为:
如果第
| $ \hat p\left( {{z_l}} \right) = D \times \frac{{\hat f\left( {{z_l}} \right)}}{{\sum\limits_{\gamma = 1}^D {\hat f\left( {{z_\gamma }} \right)} }}。$ | (20) |
其中,
GA算法内的交叉过程为:在复制得到的种群内,任意选取一对个体,利用交叉概率
GA算法的变异概率为:
| $ {\hat p_m} = {e^{ - \frac{{1.5 \times \frac{t}{2}}}{{D \times \sqrt A }}}}。$ | (21) |
式中:
利用GA算法优化舰船目标识别分类的SVM参数的具体步骤如下:
步骤1 实数编码个体,得到初始种群,即舰船目标识别分类的SVM参数可行解集合。
步骤2 通过式(20)计算
步骤3 复制。依据
步骤4 交叉。设置随机数
步骤5 变异。设置随机数
步骤6 分析GA算法是否达到
在3D MAX软件上建立三维舰船模型,并投影成二维图像,作为实验对象,其分辨率为200像素×200像素,舰船三维模型的几何方位如图1所示。图1中,横滚轴为
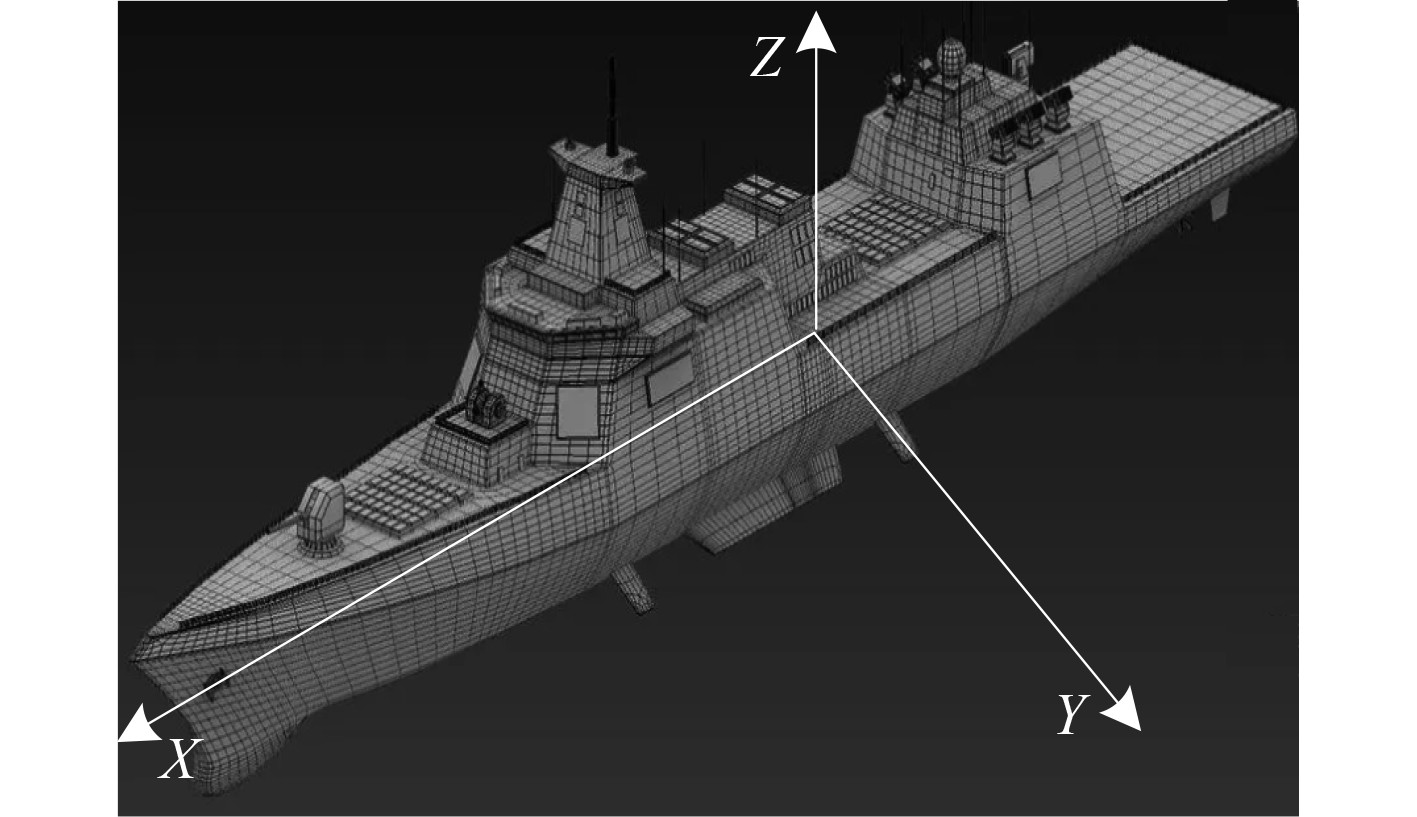
|
图 1 舰船三维几何方位图 Fig. 1 Three-dimensional geometric azimuth diagram of ship |
分别在3个轴上实施旋转,
|
|
表 1 舰船类型描述及对应的目标识别分类数值 Tab.1 Description of ship types and corresponding target recognition classification values |
在投影获取的舰船二维图像内,随机选择一幅舰船二维图像,利用本文方法对该幅图像进行特征矩提取,特征矩提取结果如图2所示。分析可知,本文方法可有效提取二维图像内的舰船目标特征矩,该舰船目标的7个特征矩分别处于不同数值。

|
图 2 舰船目标特征矩提取结果 Fig. 2 Extraction results of ship target feature moments |
为验证本文方法的支持向量机参数优化效果,分析本文方法优化前后,舰船目标识别分类效果,优化效果如图3所示。分析图3(a)可知,本文方法参数未优化前,虽然决策边界能很好地围住全部舰船目标特征矩训练点,但全部训练点均为支持向量,这样会提升决策函数的计算复杂度,影响舰船目标识别分类效率。分析图3(b)可知,本文方法经过参数优化后,仅选取部分舰船目标特征矩训练点为支持向量,可有效降低决策函数的计算复杂度,加快检测目标识别分类效率,且决策边界也能很好地围住训练点。

|
图 3 参数优化前后的舰船目标识别分类效果 Fig. 3 Ship target recognition and classification effect before and after parameter optimization |
在投影获取的舰船二维图像内,随机选择8幅舰船二维图像,共包含8种舰船类别,利用本文方法对这8幅舰船二维图像,进行舰船目标识别分类,识别分类结果如表2所示。可知,本文方法可有效识别分类舰船目标。其中,仅有编号3的识别分类结果为错误的,00001000对应的舰船目标类型为驱逐舰,而实际舰船二维图像内的舰船目标类型为巡洋舰,其余二维图像的舰船目标识别分类结果均为正确的,说明本文方法在识别分类舰船目标方面,具备较高的识别分类精度。
|
|
表 2 舰船目标识别分类结果 Tab.2 Results of ship target recognition and classification |
研究船舰目标识别分类方法对于维护海上安全、推动科研进步、增强国家安全等方面都具有重要意义,针对当前舰船目标识别分类存在的一些难题,本文设计了基于遗传算法优化支持向量机的船舰目标识别分类方法,该方法利用支持向量机优异的分类性能,同时利用遗传算法高精度参数寻优能力,通过结合遗传算法和支持向量机,对船舰目标进行识别分类是一种有效的方法遗传算法,能根据适应度函数在整个解空间中进行高效搜索,从而找到最优解或近似最优解,有助于提高支持向量机分类器的性能和鲁棒性。
| [1] |
简涛, 王哲昊, 王海鹏, 等. 基于损失加权修正的舰船目标HRRP小样本元学习识别方法[J]. 信号处理, 2022, 38(12): 2460-2468. |
| [2] |
关欣, 国佳恩, 衣晓. 基于低秩双线性池化注意力网络的舰船目标识别[J]. 系统工程与电子技术, 2023, 45(5): 1305-1314. |
| [3] |
薛安克, 毛克成, 张乐. 多分类器联合虚警可控的海上小目标检测方法[J]. 电子与信息学报, 2023, 45(7): 2528-2536. |
| [4] |
顾鹏, 王碧垚, 黄黔川, 等. 基于KNN和雷达辐射源脉间参数的舰船目标个体识别方法[J]. 中国电子科学研究院学报, 2022, 17(2): 186-192. |
| [5] |
张云, 化青龙, 姜义成, 等. 基于混合型复数域卷积神经网络的三维转动舰船目标识别[J]. 电子学报, 2022, 50(5): 1042-1049.
|
| [6] |
蔡一杰, 陈俊杰, 王君, 等. 基于遗传算法优化支持向量机的船用柴油机气门漏气故障智能诊断方法[J]. 内燃机工程, 2022, 43(2): 71-76,84. |
| [7] |
张拯宁, 张林, 王钺, 等. 基于层间分类一致性准则的舰船目标细粒度识别方法[J]. 中国空间科学技术, 2023, 43(3): 93-104. |
| [8] |
柳碧辉, 王培元. 基于改进Faster R-CNN的舰船目标三维识别算法[J]. 火力与指挥控制, 2022, 47(5): 42-52. |
 2024, Vol. 46
2024, Vol. 46








