2. 唐山工业职业技术学院,河北 唐山 063299
2. Tangshan Polytechnic College, Tangshan 063299, China
在船舶工程中,船舶零件加工的精密性、不同材料的加工参数等在很大程度上影响着船舶制造的成败。有很多的船舶零件采用数控系统加工,如三轴数控、五轴数控系统等,这些系统采用PID算法对步进或伺服电机进行控制,传统PID算法通过反馈误差调整P、I、D参数来消除误差,在零件加工过程中由于存在惯性,因而最终的输出不可能跳变,这就使整个系统会存在超调或震荡的问题,这些问题都使得加工的零件误差过大,无法满足船舶工业的使用要求。
目前,在零件加工中普遍采用改进PID算法,将遗传算法、粒子群算法、蜂群算法等和PID算法进行有效结合,从而改变PID算法在零件加工中存在的一些缺陷。许云兰[1]设计了一种改进的粒子群算法PID控制器,并将其用于数控机床的油温控制,有效减少了稳态误差,且达到系统稳定的时间较短。谭志银[2]设计了一种结合BP神经网络和PID的改进PID算法,并使用Matlab对其进行了仿真,实现了对机床滑台位置的误差跟踪。陈胤寅等[3]提出了一种改进的模糊PID算法,并将改进的模糊PID算法和传统PID算法进行了比较,发现改进后的算法能够有效减少电机在加工过程中的振动,具有良好的静态和动态性能。本文提出了一种改进的PID算法,并且设计了船舶零件加工的数控系统整体方案,对船舶复杂零件加工的轮廓控制方法进行研究。
1 改进PID算法 1.1 改进PID算法原理在船舶零件加工过程中对位置的控制尤为重要,这决定了零件的加工精度和加工速度。传统的PID算法在实现电机控制时,一般通过调节P、I、D参数来控制位置误差,从而实现对加工零件精度的控制。但传统PID在控制电机过程中存在一些问题,特别是系统超调问题得不到很好的解决,且对于加工不同零件都需重新调整PID参数,无法适应不同材料、不同零件的加工需求。在这种情况下,对传统PID算法进行改进就显得非常有必要[4 − 5]。
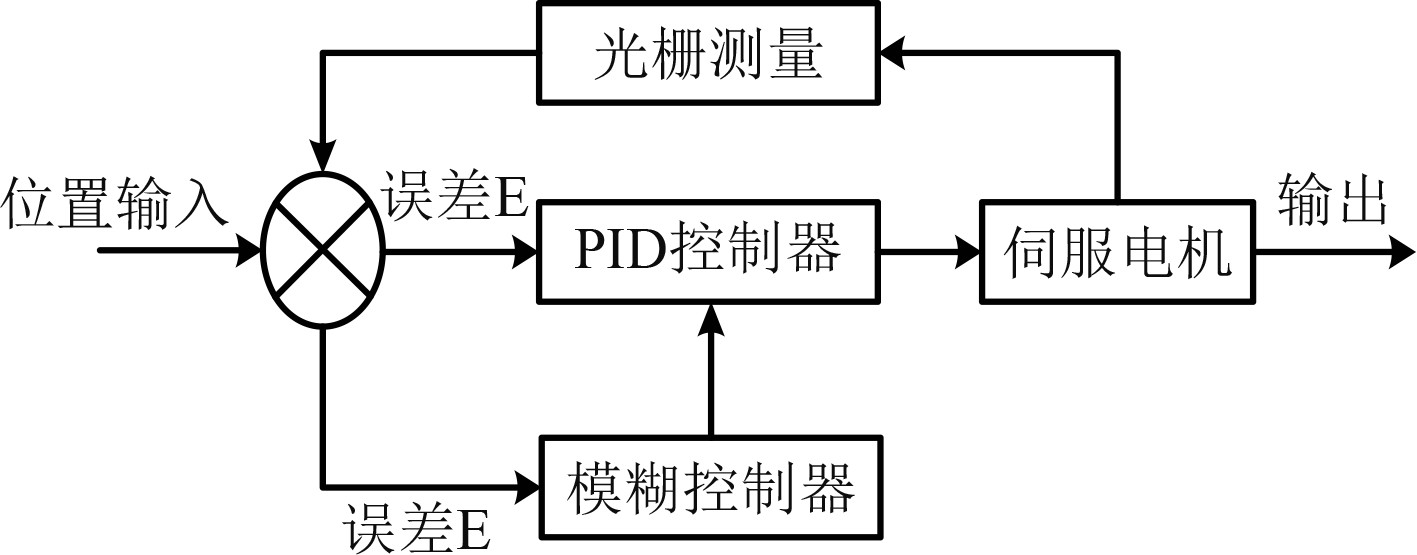
传统PID的控制参数是在特定条件下,经过不断实验而得到的一组特定参数,改进的PID算法是将模糊算法或规则应用到PID控制中,从而实现对PID算法的进一步更新。图1为模糊PID算法的控制原理,可发现在传统PID控制的基础上加入了模糊控制器,使得PID控制可在本身控制的基础上不断接收模糊控制器的输出结果,从而不断调整参数来实现更加精准的输出,保证数控机床中伺服电机的精确和快速定位。
|
图 1 模糊PID算法控制原理 Fig. 1 Fuzzy PID algorithm control principle |
模糊控制器包括模糊化、知识库、模糊推理以及模糊解释器等模块,其中模糊化是将伺服电机位置输入的控制目标进行模糊化处理,确定隶属度函数和论域范围;知识库包括数据库和规则库,数据库存储模糊PID控制中所有隶属度函数、模糊空间的分级数等,规则库则包含了所有变量的控制规则,控制规则是实现模糊PID控制的关键,一般在控制过程中会经历多次改进才能达到预定效果[6];模糊推理是根据制定的模糊规则以及关系对结果进行推导,是整个模糊控制器的核心部分;模糊解释器将模糊推理所获得的结果转换为PID控制器能够识别的参数,当伺服电机控制出现偏差时,能够快速地根据误差变化情况来确定P、I、D参数[7]。
1.2 改进PID算法建模及仿真在将改进PID算法应用于船舶零件数控机床加工前,首先在Matlab中建模并进行仿真,其具体流程为:
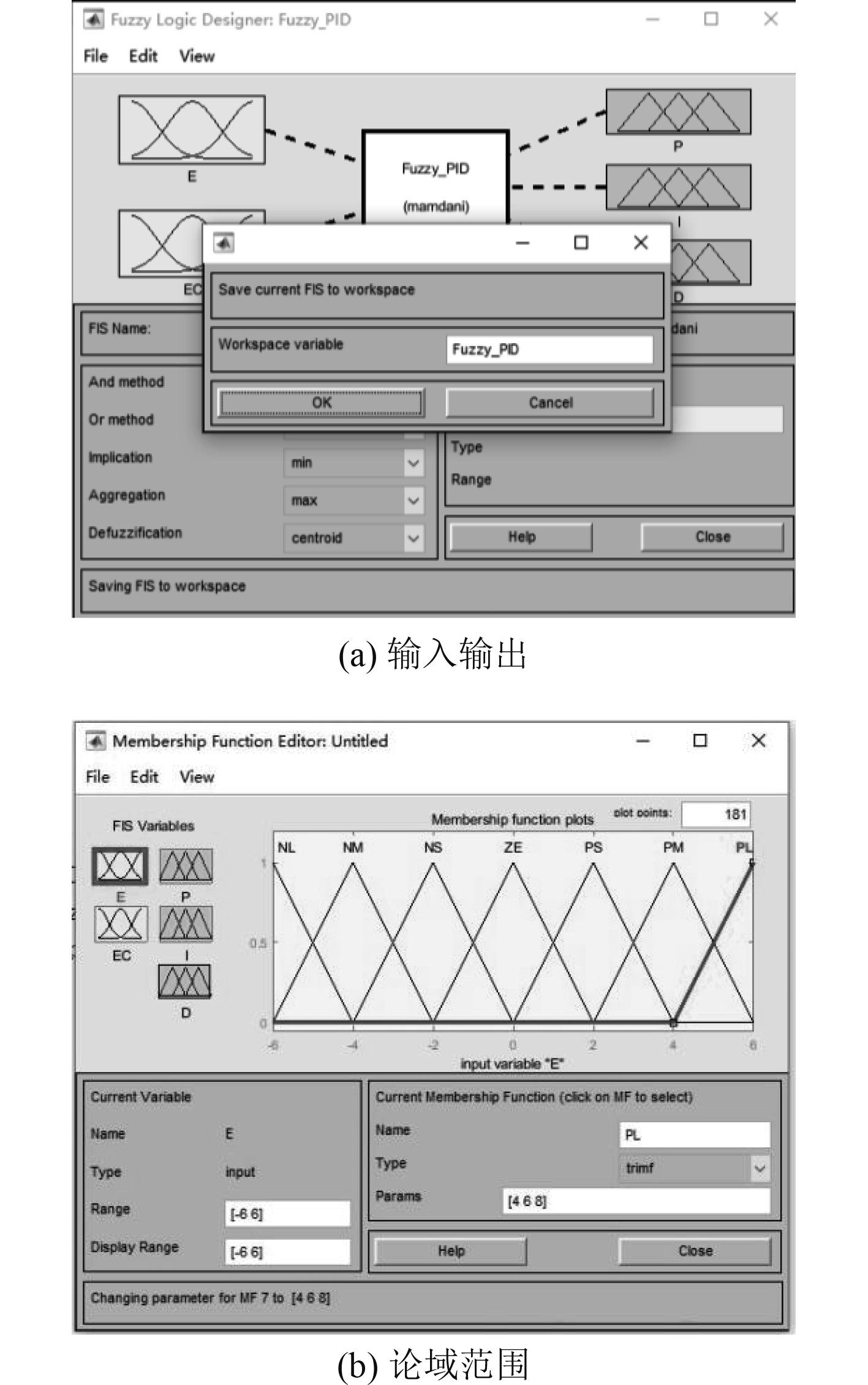
步骤1 确定输入为E和Ec,输出为电机控制参数P、I、D,同时确定输入和输出的论域范围,如图2所示。
|
图 2 模糊PID建模过程 Fig. 2 Process of fuzzy PID modeling |
步骤2 确定E、Ec、KP、KI、KD的规则表,以KP、KI、KD为例进行说明,表1为输出规则表。
|
|
表 1 输出规则表 Tab.1 Rule table of output |
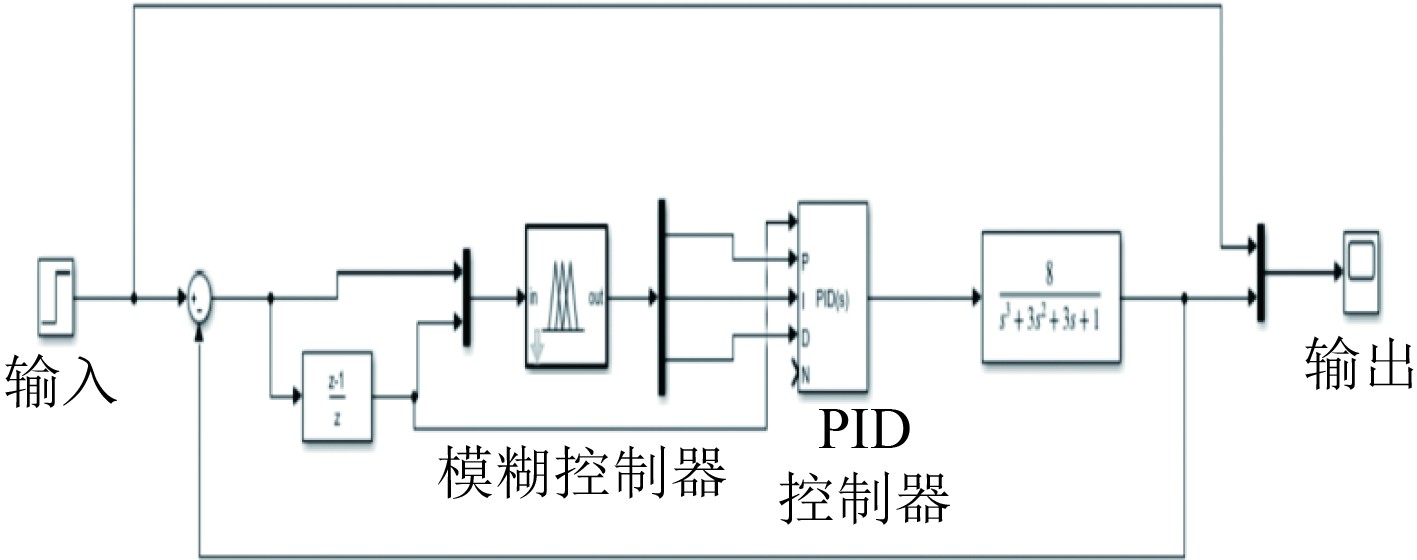
步骤3 建立的模糊PID仿真模型如图3所示。
|
图 3 模糊PID仿真模型 Fig. 3 Fuzzy PID simulation model |
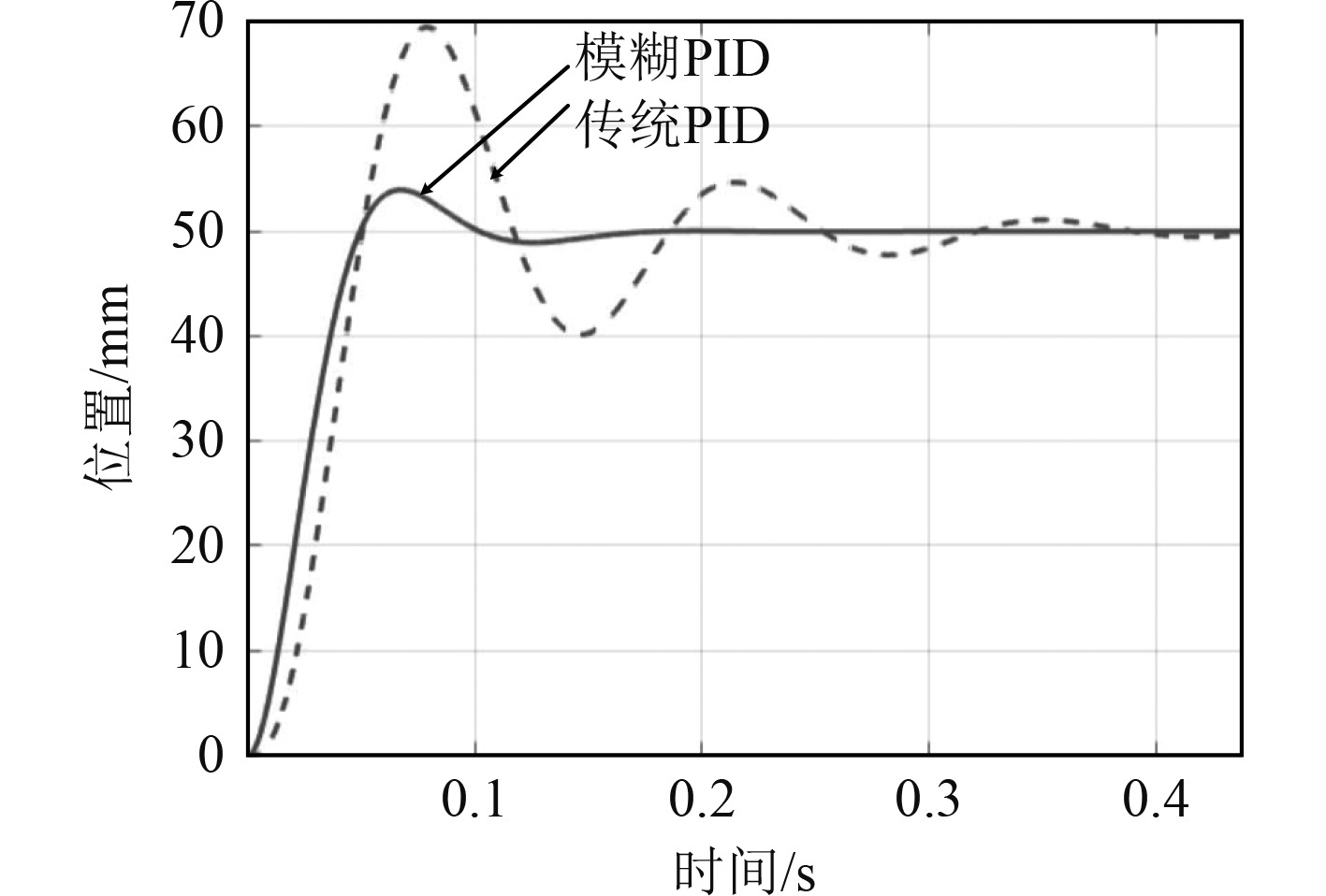
设定好目标位置为50 mm,使用模糊PID和传统PID进行仿真对比,得到的结果如图4所示,可发现传统PID出现了较大超调,且收敛较慢,这也就意味着在对零件进行加工时会花费较长时间进行定位,降低了船舶零件加工的速度,且在长时间震荡之后和目标位置之间始终存在一个误差,难以满足船舶零件加工的要求。模糊PID控制能够快速收敛,收敛时间约为0.13s,且在达到稳定之后和目标位置之间的误差值很小,能够有效提升船舶零件加工精度。
|
图 4 仿真结果对比 Fig. 4 Comparison of simulation results |
本文设计的船舶零件数控加工系统的设计目标是能够实现五轴的零件加工,设计目标包括以下方面:
1)能够实现对5个轴的控制,五轴直线加工精度能够达到3 μm,曲线加工精度为10 μm,最小分辨率能够达到0.2 μm;
2)能够识别常见G代码指令,直接导入CAD图形文件,并且实现在线预编程和船舶零件自动加工;
3)硬件具有较好的可靠性和稳定性;
4)零件加工具有高度的重复性;
5)加工零件轮廓度能够达到0.05 mm,平面度能够达到0.02 mm。
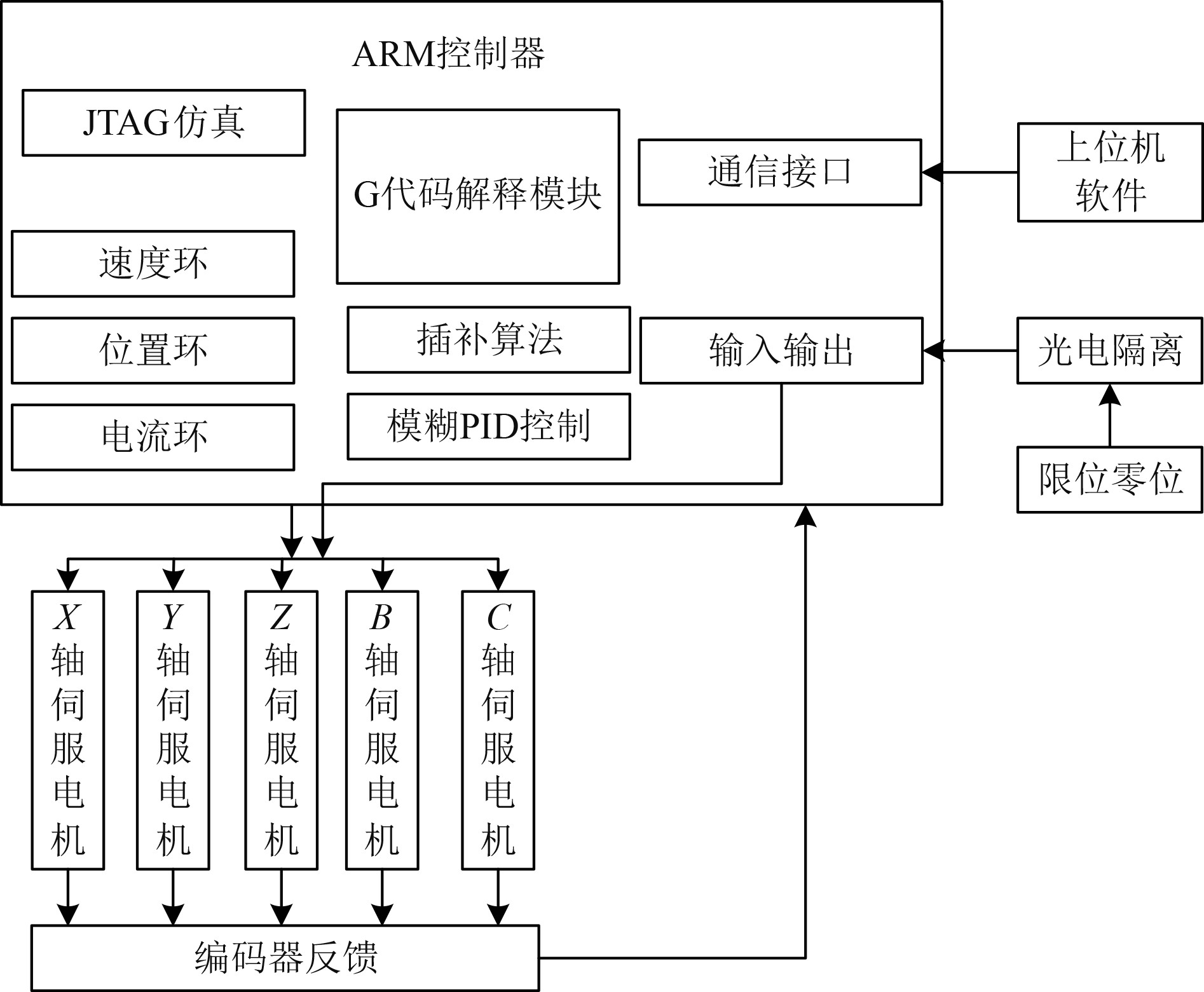
2.2 硬件设计为了实现对五轴的高精度控制,设计了如图5所示的数控系统硬件结构框图。系统以ARM控制器为核心,ARM控制器包括了JTAG仿真接口、通信接口、G代码解释模块、插补算法、模糊PID控制算法、速度环、位置环、电流环以及输入输出等。JTAG仿真主要用于设计阶段的程序下载及调试,通信接口主要实现电脑端和船舶零件加工数控机床之间的通信,可实现电脑端程序的编写及下载,在电脑端支持G代码,提升数控机床程序编写的灵活性。
|
图 5 数控系统硬件结构框图 Fig. 5 Hardware block diagram of CNC system |
在ARM控制器中无法直接执行G代码,ARM程序是由C语言或者汇编语言进行编写,因而需将G代码转换为可执行的语句,如到达一个指定位置,或者在某2个位置之间反复循环等。G代码解释模块是将G代码转化为实际位置输出,如G71指令是循环指令,那就会直接转换为一个for循环的位置控制函数,从而得以在ARM控制器中执行。插补算法分为粗插补和精插补,主要是由于在船舶零件加工中需实现特定曲线时只能通过逐次逼近的方式来完成加工位置数据的“密化”,插补精度在某种程度上也能体现数控机床的加工精度。
模糊PID算法编写好程序后,将制定的规则写入到ARM控制器中,对PID算法进行改进后可有效提升位置控制精度,和电机控制的速度环、位置环以及电流环一起实现对5个轴伺服电机的闭环控制。
船舶零件数控加工系统还具备输入输出功能,在输入端主要用于接收限位零位的信号,输出端则主要负责控制各类指示灯以及电机使能信号。
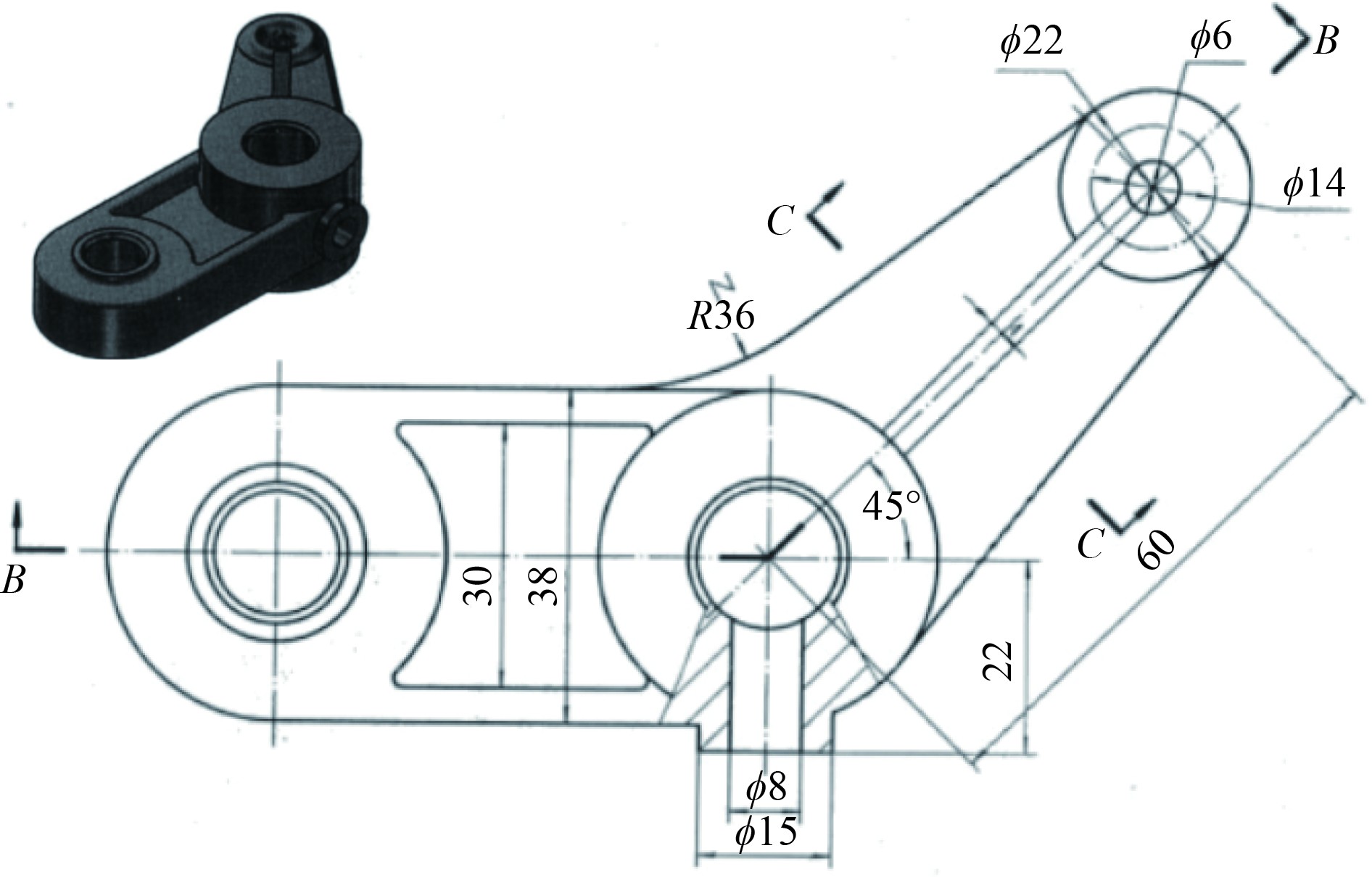
2.3 加工精度测试船舶制造中有很多零件具有复杂的轮廓,本文使用如图6所示的零件轮廓进行加工,在数控系统中设置好五轴电机的加减速时间,在加工过程中涉及直线加工、曲线加工等。以曲线加工为例来说明零件加工精度,在设定好加工程序后,通过编码器获取电机轴的实际位置,并将实际位置和理论加工曲线进行对比,得到误差结果,最终经过对比发现零件轮廓整体加工精度较高,最大加工误差为8 μm,轮廓度检测结果为0.045 mm,平面度检测结果为0.017 mm,因而满足设计要求。
|
图 6 复杂轮廓加工示意图 Fig. 6 Schematic diagram of complex contour processing |
在船舶零件加工中,数控机床的控制尤为重要。传统PID存在超调以及稳定时间过长的问题,本文提出使用模糊PID对传统PID算法进行改进,有效缩短收敛时间和控制精度。在此基础上设计了船舶零件数控五轴加工系统,使用ARM作为核心控制器,将G代码解释模块、插补算法、模糊PID算法进行有效结合,能够实现船舶复杂零件的精确加工。最后,以蜻蜓轮廓为例对零件加工精度进行了测试,发现零件平面度、轮廓度、加工误差等都能满足设计要求。
| [1] |
许云兰. 基于改进PID控制的数控机床油温控制系统研究[J]. 国外电子测量技术, 2019, 38(8): 23-27. XU Yun-lan. Research on oil temperature control system of CNC machine tool based on improved PID control[J]. Foreign Electronic Measurement Technology, 2019, 38(8): 23-27. |
| [2] |
谭志银. 基于改进PID控制的机床滑台运动位移跟踪误差研究[J]. 佳木斯大学学报(自然科学版), 2021, 39(6): 94-97. TAN Zhi-yin. Research on motion displacement tracking error of machine tool slide table based on improved PID control[J]. Journal of Jiamusi University(Natural Science Edition), 2021, 39(6): 94-97. |
| [3] |
陈胤寅, 张华彦, 钱泽禹, 等. 基于改进PID的机电一体化设备智能控制研究[J]. 机械设计与制造工程, 2023, 52(9): 50-54. CHEN Yin-yin, ZHANG Hua-yan, QIAN Ze-yu, et al. Research on intelligent control of mechatronics equipment based on improved PID[J]. Mechanical Design and Manufacturing Engineering, 2023, 52(9): 50-54. |
| [4] |
高鑫, 冯斌, 赵中刚, 等. 柔性线加工模式下航空结构件数控加工工艺设计技术研究[J]. 航空制造技术, 2022, 65(7): 96-103. GAO Xin, FENG Bin, ZHAO Zhong-gang, et al. Research on CNC machining process design technology of aeronautical structural parts under flexible line machining mode[J]. Aeronautical Manufacturing Technology, 2022, 65(7): 96-103. |
| [5] |
蒋亚坤. 数控机床进给系统融合建模及轮廓误差补偿方法研究[D]. 武汉: 华中科技大学, 2021.
|
| [6] |
高慧勤. 基于PSO-BP网络的数控系统插补控制研究[J]. 长春工程学院学报(自然科学版), 2021, 22(3): 48-51. GAO Hui-qin. Research on interpolation control of numerical control system based on PSO-BP network[J]. Journal of Changchun Institute of Technology(Natural Science Edition), 2021, 22(3): 48-51. |
| [7] |
王江涵. 薄壁难加工环形机匣壁厚的车床在机测量和加工补偿方法研究[D]. 上海: 上海交通大学, 2021.
|
 2024, Vol. 46
2024, Vol. 46
