2. 青岛海洋科技中心,山东 青岛 266237;
3. 青岛协同创新研究院,山东 青岛 266071
2. Qingdao Marine Science and Technology Center, Qingdao 266237, China;
3. Qingdao Institute of Collaborative Innovation, Qingdao 266071, China
水下无人探测技术可提升我国水下作战能力,水声目标探测跟踪是关键技术之一[1]。搭载单矢量水听器的水下缓动平台(如水下滑翔机、浮标等)能获取水声目标的方位信息[2],基于单平台探测目标纯方位信息要实现对目标的运动参数估计必须满足平台机动条件,否则系统不可观测[3 − 4],一般水下缓动平台难以满足机动条件,多平台协同探测成为重点发展方向[5 − 6]。
理想条件下,2台或多台缓动平台对目标的方位测向线的交点即为目标位置,实现基于纯方位信息的水声目标定位[7]。但复杂的海洋环境,使得测量方位受环境噪声、传感器精度及多平台协同困难等影响,增加了定位结果的不确定性[8 − 9]。探测时延在多缓动平台协同探测中影响尤为突出,由于不同平台空间布局不同,使得探测目标信息在时间上不一致,难以实现对同一目标定位和关联。时间配准是解决时延引起目标探测方位误差的较好方法,时空配准的基础就是对方位误差情况分析,现有研究多采用理想化数学近似模型或采用多约束条件进行讨论[10],误差分析结果缺乏普适性,在实际应用中依然存在误差。
为给水下纯方位定位和跟踪提供更准确的目标信息,基于双水下缓动平台建立一种基于平台空间分布的时延与方位探测误差之间的数学模型,并对多种适用条件进行分析,最后基于仿真实验和实测数据验证,掌握了方位探测误差与时延的分布规律,可提升后续目标航迹起始、目标定位、关联和跟踪精度。
1 目标运动模型在水下目标跟踪系统中,假设目标在二维平面内运动,一般水面航船等目标在短时间内很少发生机动,多以匀速直线模式运动,因此,可构建基于CV模型的目标纯方位运动离散数学模型:
状态方程
| $ {{\boldsymbol{x}}_m}(k) = {{\boldsymbol{F}}_m} \cdot {{\boldsymbol{x}}_m}(k - 1) + {{\boldsymbol{v}}_m}(k),$ | (1) |
测量方程
| $ {\theta _m}(k) = h({{\boldsymbol{x}}_m}(k)) + {w_m}(k) = \arctan \frac{{{x_m}(k) - {x_o}}}{{{y_m}(k) - {y_o}}} + {w_m}(k) 。$ | (2) |
式中:
以2台水下缓动平台作为研究对象,水下缓动平台在目标探测时间内可视为静止状态,同时假设水听器在探测过程无噪声干扰[11]。仅考虑声波在海水中的传播影响,对目标运动过程中的每一时刻节点进行测量方位误差分析。
2 时延下测角误差分析在二维平面,水面目标保持匀速直线运动,S1和S2为两台水下缓动平台,构建直角坐标系,以正北方向为0°,方位角顺时针变化,双水下缓动平台目标纯方位定位几何示意图如图1所示。

|
图 1 二维双缓动平台目标纯方位定位 Fig. 1 Bearing-only target location based on two - dimensional double quasi-stationary platform |
当目标在
| $ \Delta \theta = \left\{ \begin{gathered} \left| {{\theta _2}\left( {k + {\tau _1}} \right) - {\theta _2}\left( {k + {\tau _2}} \right)} \right|{\text{ }},{\tau _1} > {\tau _2},\\ \left| {{\theta _1}\left( {k + {\tau _2}} \right) - {\theta _1}\left( {k + {\tau _1}} \right)} \right|{\text{ ,}}{\tau _1} < {\tau _2} 。\\ \end{gathered} \right. $ | (3) |
基于目标不同运动位置,对探测平台探测方位误差大小进行讨论分析。以S1探测时间为基准讨论S2探测目标方位误差,反之适用。设S2探测平台接收目标B点辐射噪声时延为
| $ \Delta {R^2} = {(c{\tau _2})^2} + {(c\tau' _2)^2} - 2c{\tau _2}c\tau' _2 \cos \Delta {\theta _2} ,$ | (4) |
其中,c为声速,对上式进行求解可得
| $ \Delta {\theta _2} = \arccos \frac{{{c^2}\left( {\tau _2^2 + \tau _2^{'2}} \right) - {v^2}{{\left( {{\tau _1} - \tau '_2 } \right)}^2}}}{{2{c^2}{\tau _2}\tau '_2 }} 。$ | (5) |
令
| $ \tau _2^{'2} = \frac{{{c^2}\tau _2^2 - {v^2}\tau _1^2}}{{{c^2} - {v^2}}} 。$ | (6) |
对上式进行讨论:
1)因海上航船目标最大速度
| $ \tau '_2 = \sqrt {\frac{{{c^2}\tau _2^2 - {v^2}\tau _1^2}}{{{c^2} - {v^2}}}},$ | (7) |
将
2)当
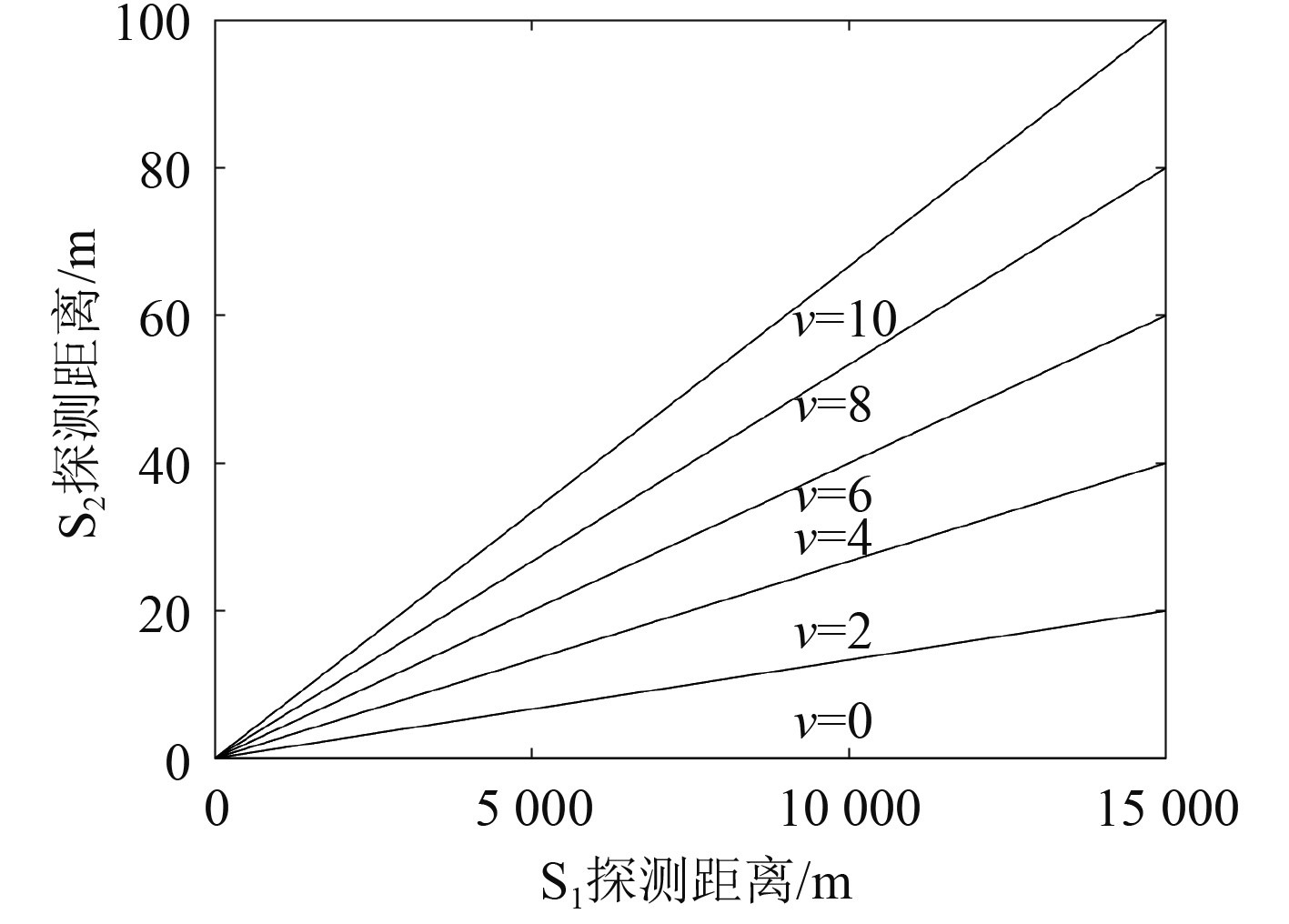
|
图 2 S2平台探测距离仿真 Fig. 2 Simulation of platform S2 detection distance |
当
| $ \max \left( {\Delta {\theta _2}} \right),s.t.\left\{ \begin{gathered} \tau '_2 > \frac{{v{\tau _1} - c{\tau _2}}}{{c + v}},\\ \tau' _2 < \frac{{v{\tau _1} + c{\tau _2}}}{{c + v}},\\ - 1 \leqslant f\left( {\tau '_2} \right) \leqslant 1 。\\ \end{gathered} \right. $ | (8) |
3)特殊情况,当两探测平台位于目标航路上时,探测方位不论怎么变化始终处于同一条航路上,无法实现对目标的有效定位跟踪。
当一个探测平台位于目标航路上,另一个探测平台不和目标航路重合时,也可实现对目标的有效定位和跟踪:当
对时延引起方位误差进行仿真分析,假设一目标以最大速度
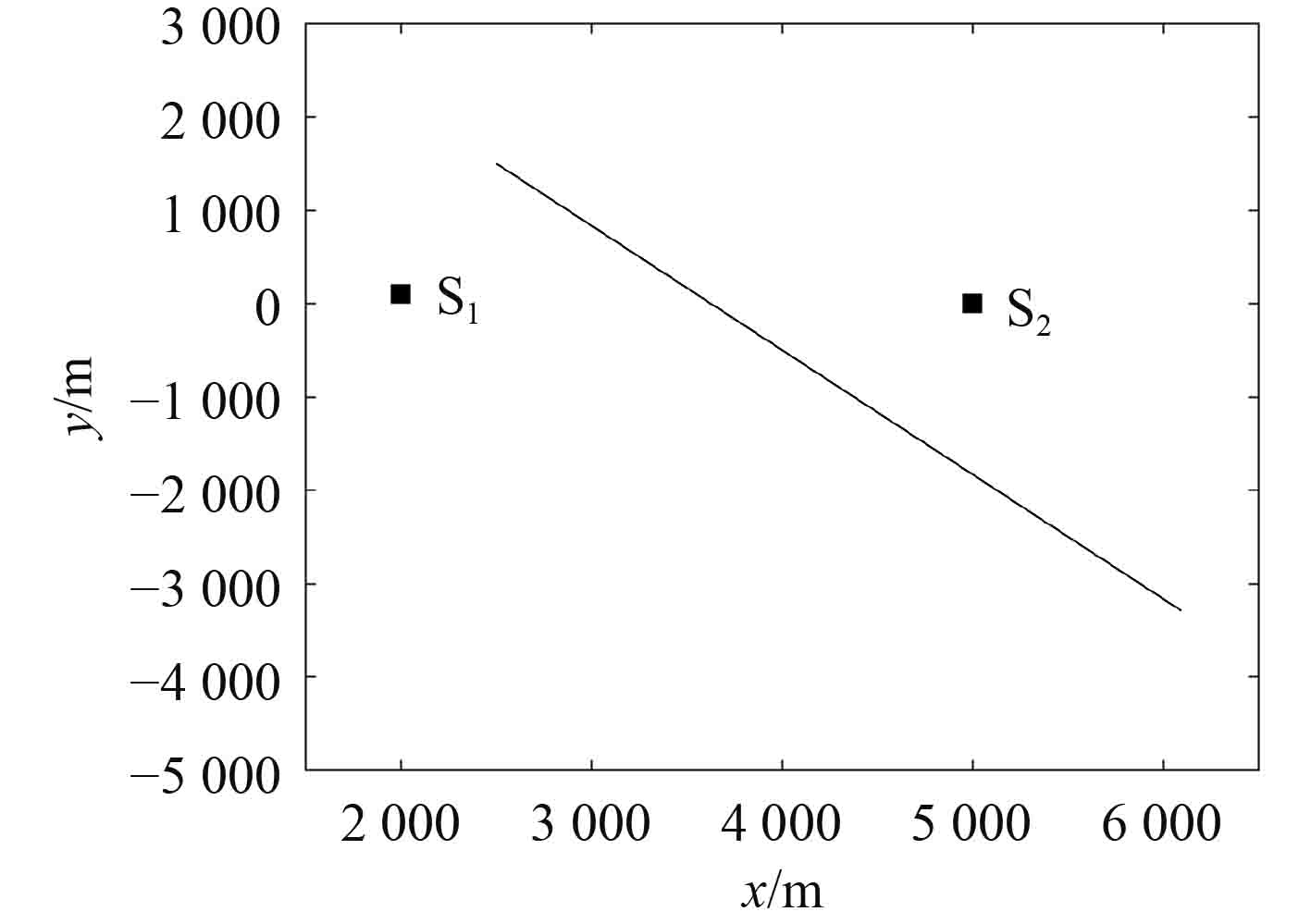
|
图 3 平台和目标空间态势 Fig. 3 Space posture of platforms and target |

|
图 4 目标方位历程图 Fig. 4 Target bearing time recording |
以S1平台探测时刻为基准,讨论S2平台探测目标方位误差,根据误差模型计算双平台不同时延影响下目标探测方位误差如图5所示。
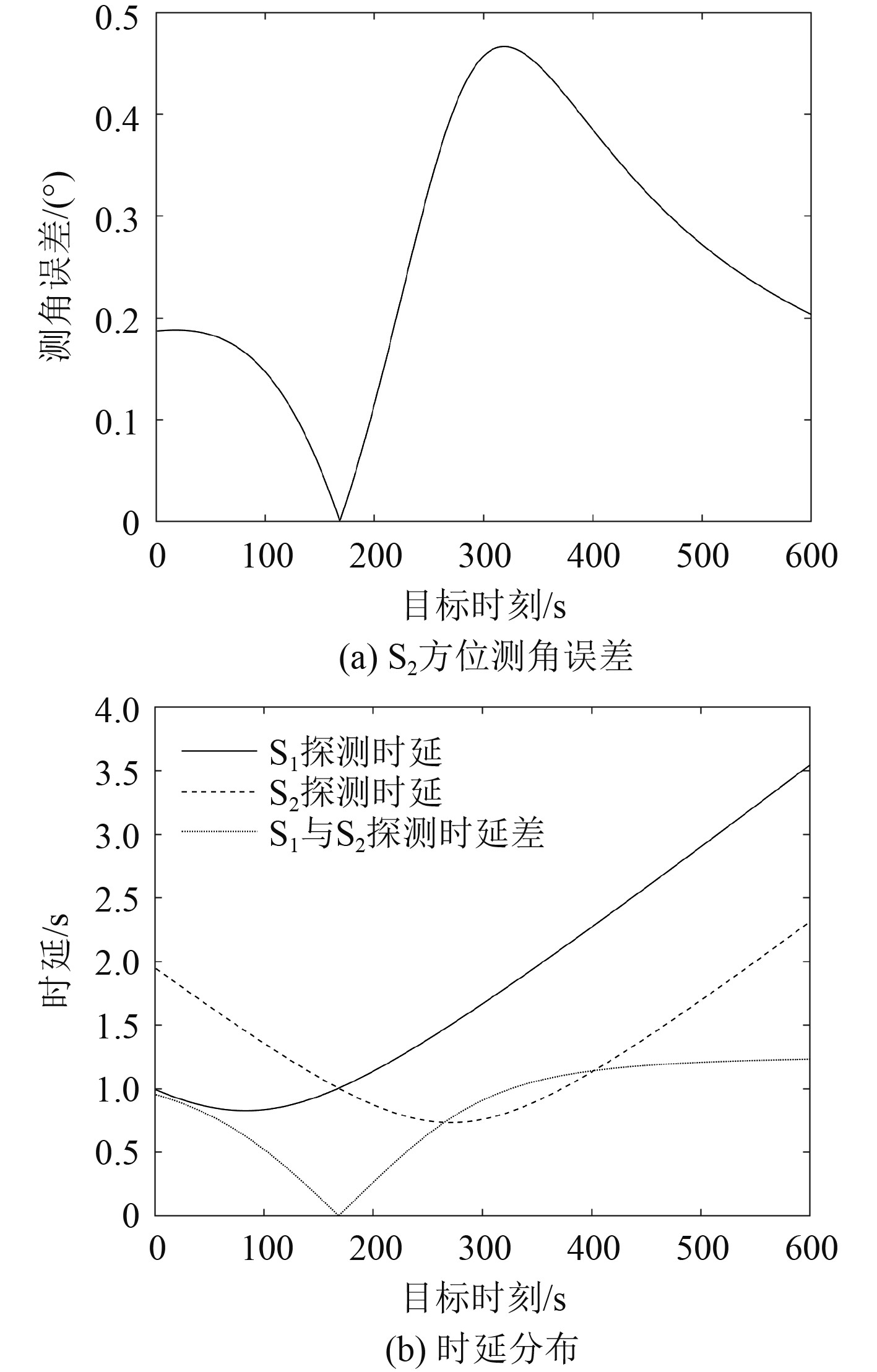
|
图 5 双站时延与方位误差关系 Fig. 5 Relation between two-station time delay and bearing error |
由图可得,目标方位测量误差与双平台时延差有着正相关关系,在双平台时延最小时测角误差也最小;在目标位于两平台正横位置时方位测量误差局部最大,在目标位于S1探测平台正横位置(S1时延为
两缓动平台位置和目标速度保持不变,设置探测空间为[−1000,8000]×[−4000,4000],假设目标位于空间的任意位置,对S2探测方位角最大误差进行仿真,结果如图6所示。
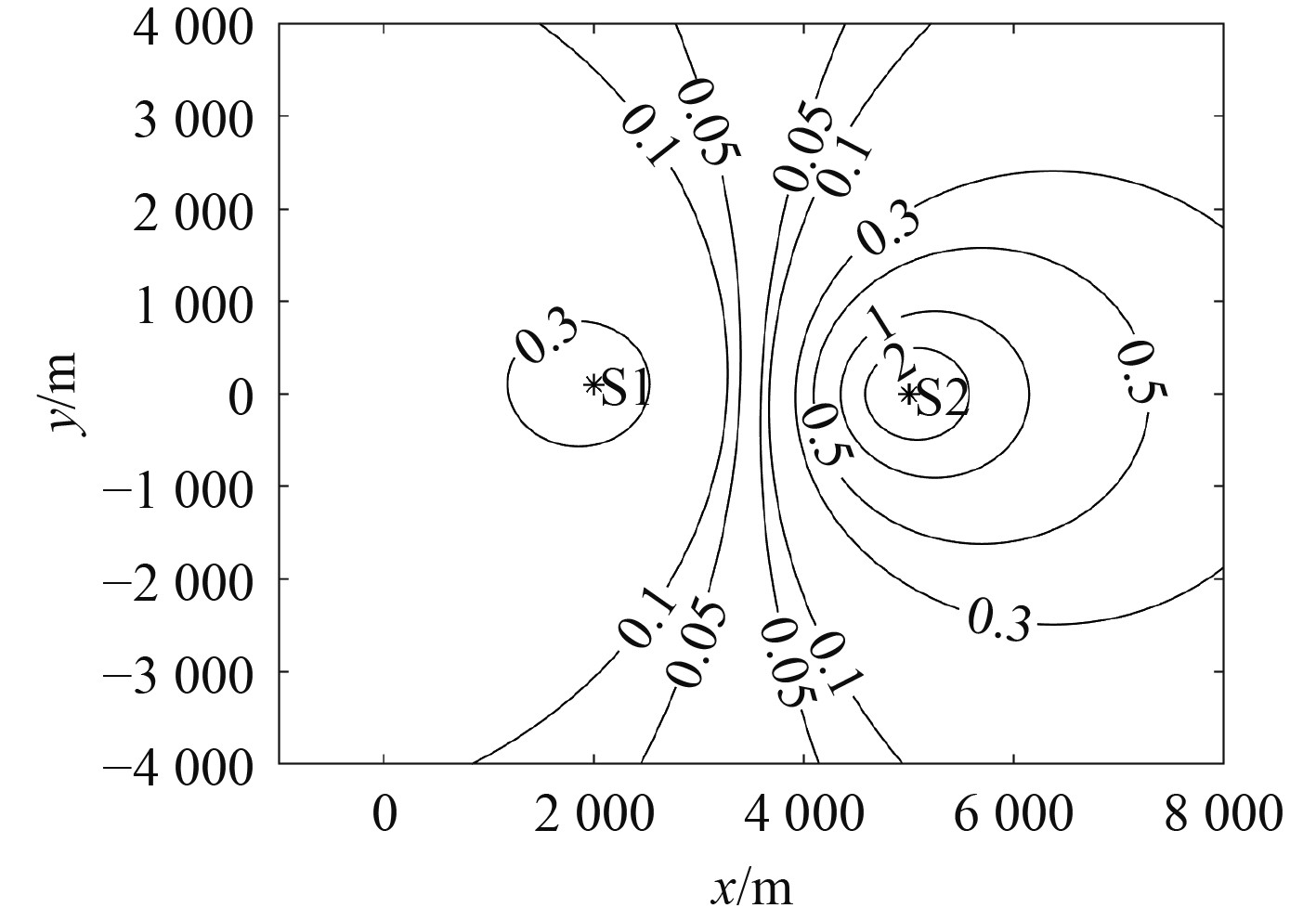
|
图 6 双站时延下测角误差分布 Fig. 6 Bearing measurement error distribution caused by bistatic time delay |
仿真结果可验证第2节误差模型分析结果,距离探测平台越近,时延引起的目标探测方位误差越大,目标距离探测平台1 km左右,方位误差可达1°,距离500 m则方位误差可达到2°,离探测平台越近误差越大且不确定性增加;方位误差分布受两平台空间布局影响,目标位于两平台之间时延较小方位误差也较小,但变化率随距离梯度变化快,方位误差变化等高线呈椭圆形分布。
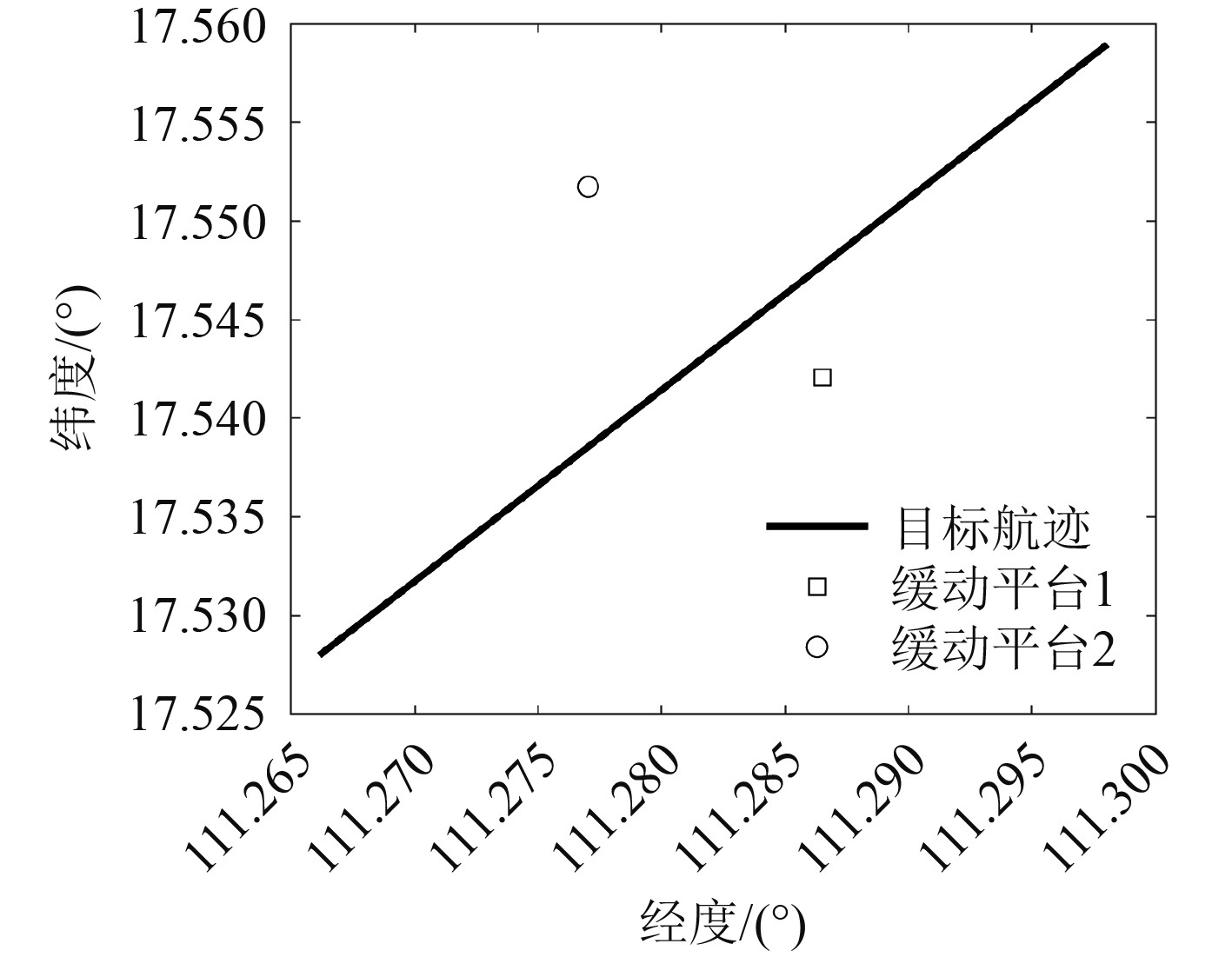
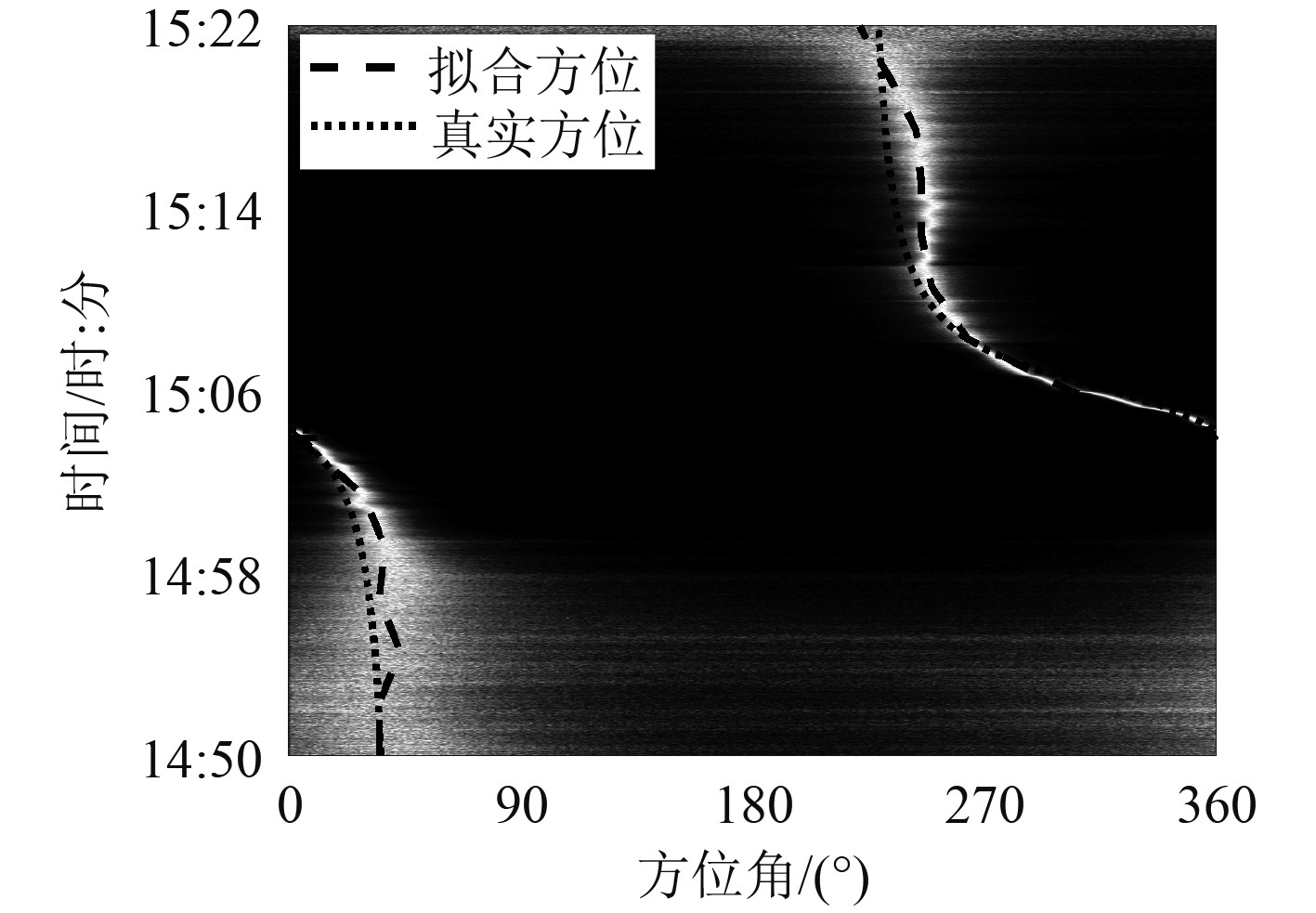
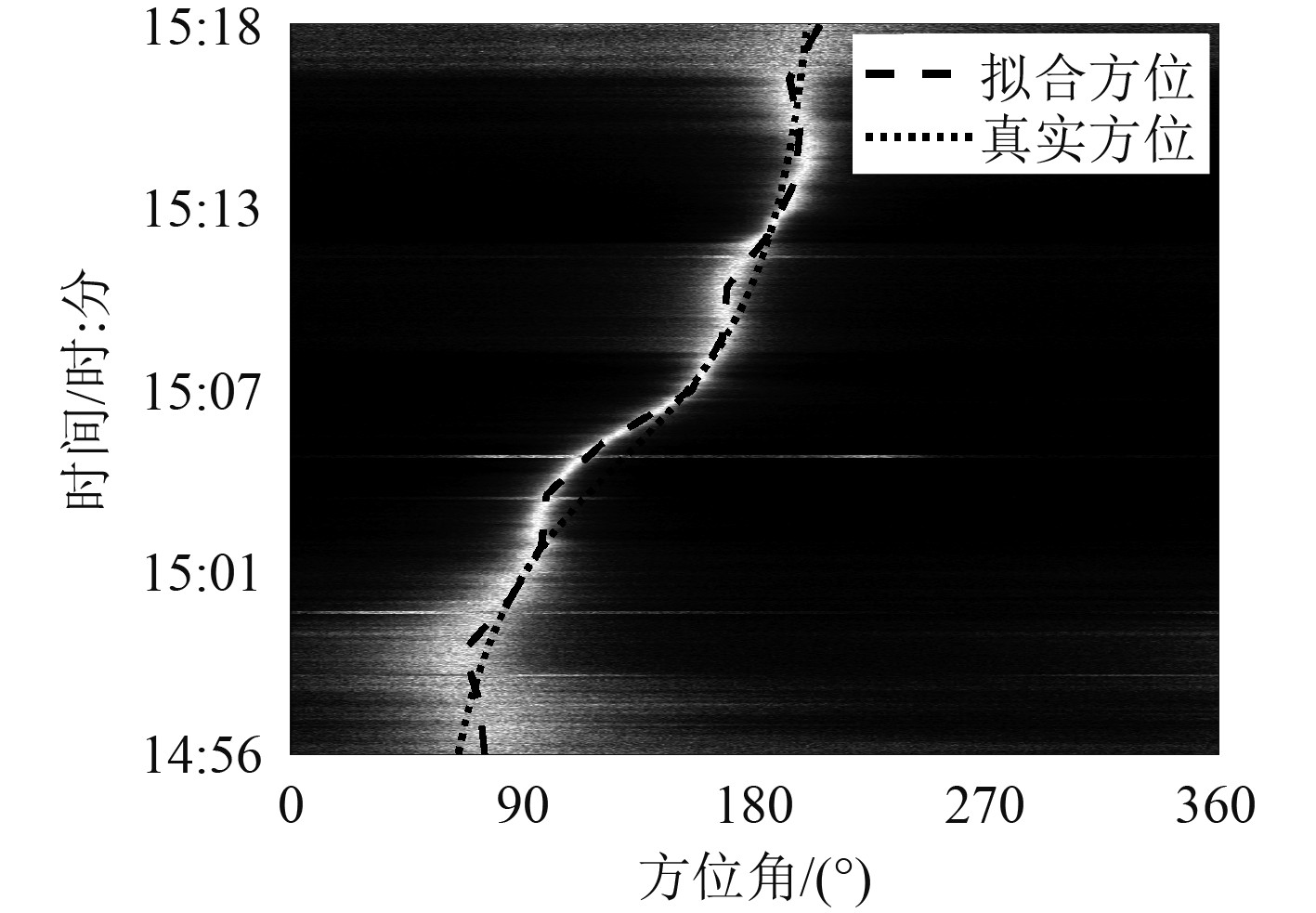
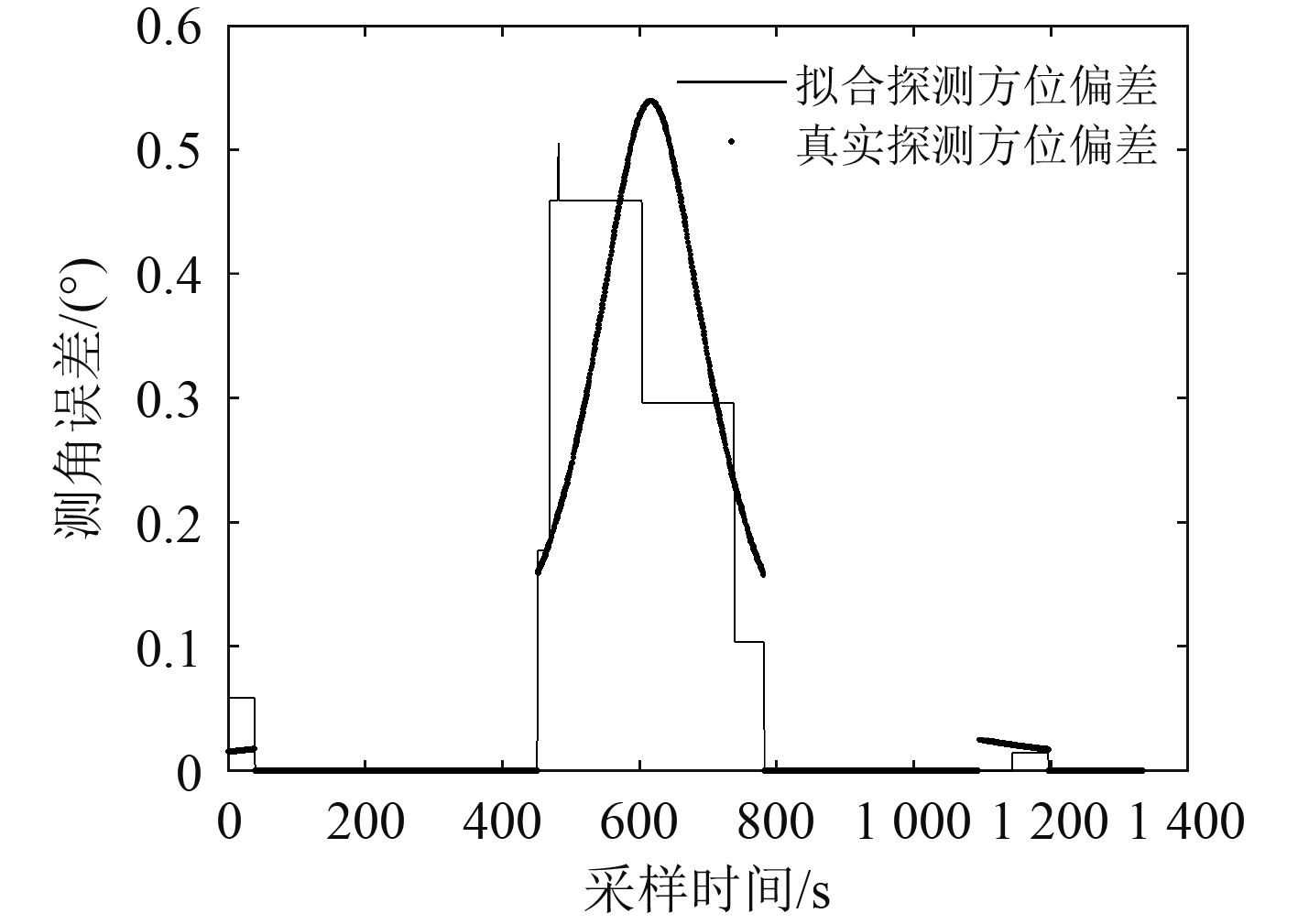
3.2 试验数据验证所示图7~图9为某次海试两台水下缓动平台协同探测的实测数据,对两缓动平台的探测时间和目标方位进行时间配准,并对环境噪声干扰和传感器精度误差进行预处理,然后进行目标探测方位误差分析,图10和图11分别为目标测量方位误差分布的模型计算和实测数据计算结果,误差分布基本一致。
|
图 7 平台和目标二维态势 Fig. 7 Situation of platforms and target |
|
图 8 缓动平台1探测目标方位历程 Fig. 8 Bearing time recording(platform 1) |
|
图 9 缓动平台2探测目标方位历程 Fig. 9 Bearing time recording(platform 2) |

|
图 10 模型计算方位测量误差 Fig. 10 Bearing error calculated by the model |
|
图 11 实测数据计算方位测量误差 Fig. 11 Bearing error calculated from measured data |
从实验结果可知,试验数据结果验证了误差模型的准确性及测角误差受双平台时延影响的分布规律。
4 结 语本文对双水下缓动平台探测时延引起目标方位偏差问题,基于实际应用场景构建目标状态方程和时延误差分析数学模型,综合考虑不同时延情况下,将目标方位测量误差规律化,并通过仿真实验和实测数据验证了模型的准确性,该模型也可推广到多平台时延误差分析。时延误差分析是目标信息关联的前提,对提高多平台协同目标定位和跟踪精度具有重要意义。
| [1] |
CHEN R, LI T, MEMON I, et al. Multi-sonar distributed fusion for target detection and tracking in marine environment[J]. Sensors, 2022, 22(9): 3335. DOI:10.3390/s22093335 |
| [2] |
WANG C, YUAN M. Application study of a new underwater glider with single vector hydrophone for target direction finding[J]. IEEE Access, 2021, 9: 34156-34164. DOI:10.1109/ACCESS.2021.3061669 |
| [3] |
杨婧, 李银伢, 戚国庆, 等. 纯方位目标运动分析可观测性研究[J]. 火力与指挥控制, 2015, 40(12): 1-8+17. YANG J, LI Y Y, QI G Q, et al. Overview of observability of bearings-only target motion analysis[J]. Fire Control & Command Control, 2015, 40(12): 1-8+17. DOI:10.3969/j.issn.1002-0640.2015.12.001 |
| [4] |
杨文生, 吴旭. 非线性约束条件下的双阵纯方位目标运动分析[J]. 舰船科学技术, 2022, 44(13): 152. YANG W S, WU X. Bearings-only target motion analysis with nonlinear inequality constraints using two arrays[J]. Ship Science and Technology, 2022, 44(13): 152. |
| [5] |
庞菲菲. 基于水声传感网络的目标被动检测和定位技术研究[D]. 西安: 西北工业大学, 2019.
|
| [6] |
谢志华, 蒋丞, 吴俊超, 等. 水下目标多平台协同定位和跟踪方法[J]. 声学学报, 2021, 46(6): 1028-1038. XIE Z H, JIANG C, WU J C, et al. Method of multi-platform cooperative localization and tracking for underwater targets[J]. Acta Acustica, 2021, 46(6): 1028-1038. DOI:10.15949/j.cnki.0371-0025.2021.06.022 |
| [7] |
王燕, 岳剑平, 冯海泓, 等. 双基阵纯方位目标运动分析研究[J]. 声学学报, 2001(5): 405-409. WANG Y, YUE J P, FENG H H, et al. Study on bearing-only target motion analysis based on association of dual arrays[J]. Acta Acustica, 2001(5): 405-409. DOI:10.3321/j.issn:0371-0025.2001.05.005 |
| [8] |
李晓花, 李亚安, 鲁晓锋, 等. 强干扰环境下水下纯方位PMHT多目标跟踪[J]. 西北工业大学学报, 2020, 38(2): 359-365. LI X H, LI Y A, LU X F, et al. Underwater bearing-only multitarget tracking in dense clutter environment based on PMHT[J]. Journal of Northwestern Polytechnical University, 2020, 38(2): 359-365. DOI:10.3969/j.issn.1000-2758.2020.02.017 |
| [9] |
KIM J. Locating an underwater target using angle-only measurements of heterogeneous sonobuoys sensors with low accuracy[J]. Sensors, 2022, 22(10): 3914. DOI:10.3390/s22103914 |
| [10] |
卢健, 陈旭, 罗毛欣, 等. 考虑通信延迟的多自治水下航行器协同定位算法[J]. 控制理论与应用, 2020, 37(9): 2061-2072. LU J, CHEN X, LUO M X, et al. Cooperative localization algorithm considering of communication delay for autonomous underwater vehicles[J]. Control Theory & Applications, 2020, 37(9): 2061-2072. |
| [11] |
袁猛, 笪良龙, 王超, 等. 缓动单站纯方位目标运动分析算法[J]. 声学学报, 2022, 47(5): 612-624. YUAN M, DA L L, WANG C, et al. Quasi-stationary single station bearing-only target motion analysis algorithm[J]. Acta Acustica, 2022, 47(5): 612-624. |
| [12] |
NUSRAT A, LI Y, CHENG C, et al. Underwater bearing only tracking using optimal observer maneuver strategies[J]. Journal of Marine Science and Engineering, 2022, 10(5): 576. DOI:10.3390/jmse10050576 |
 2024, Vol. 46
2024, Vol. 46
