2020 年,我国明确提出了实现2030年 “碳达峰”、2060年 “碳中和”的宏伟愿景,对航运业绿色化、可持续化的要求愈发严格。
目前船舶行业实现节能减排、能效优化的普遍方法是采用混合动力。混合动力系统通过协调不同能源,发挥其互补性,以此提高船舶的整体能效,实现节能减排。相较于纯柴油推进形式,柴电混合推进的主要优点在于灵活性与经济性,电力系统相对更易于调整与分配运行功率,可以提高运行效率,并使主机尽可能工作在最佳工况区间。而相较于纯电推进形式,柴电混合推进普遍拥有更长的续航和更大的输出功率,柴油机作为原动机可以弥补动力电池目前能量密度低的不足[1]。
苗东晓等[2]研究了串联式船舶柴电混合动力系统基于逻辑门限规则的能量管理策略。吴思晨等[3]针对1艘中型邮轮设计了柴电混合动力系统并研究其油耗和排放。Yu Xue等[4]分析了新能源船舶混合动力系统的结构和智能优化算法,提出未来的发展方向。但以上研究中的储能装置仅有动力电池,在面对工作船舶功率波动频率快、幅度大的工况时,动力电池难以实时响应,且对电池的寿命和能效有负面作用。
超级电容相对于动力电池拥有能量密度高,功率响应快,能量损耗小的优势,可以在负载波动剧烈的情况下对动力电池的负载实现削峰填谷,提高电池可靠性和寿命,同时使电池以效率更高的充放电功率运行。与纯电池的传统储能系统相比,引入超级电容的电池-电容复合储能系统(Hybrid Energy Storage System, HESS)拥有更好的可靠性、能效和响应速率[5]。目前复合储能系统在汽车上运用较多,而在混合动力船舶上鲜有相关研究。
本文提出一种耦合电池-电容复合储能装置的并联式船舶柴电混合动力系统,在Matlab/Simulink平台上对该系统进行模块化建模,以此为基础设计基于逻辑规则的能量管理策略。选取典型港口拖轮的工况,研究电池在不同的初始电池荷电状态(State of Charge,SOC)下,对比纯柴油机驱动、柴油机-电池混合驱动、柴油机-电池-电容复合储能驱动的柴油机油耗、等效油耗、系统总油耗以及氮氧化物(Nitrogen-Oxide, NOx)的排放量等仿真结果,分析本文提出系统的优势,为船舶混合动力复合储能系统在船舶上的应用提供指导。
1 系统组成与建模本文提出的并联式船舶柴电混合动力系统包含船用高速柴油机、永磁同步可逆电机、锂离子动力电池、超级电容、离合器、齿轮箱、螺旋桨、直流母线、直流变换器、三相整流/逆变器等部件。其中可逆电机与齿轮箱直接连接,柴油机通过离合器与齿轮箱进行连接,齿轮箱将二者功率进行耦合并传递至螺旋桨。动力电池、超级电容通过直流变换器连接至直流母线,再通过三相整流/逆变器连接至可逆电机。具体组成见图1。
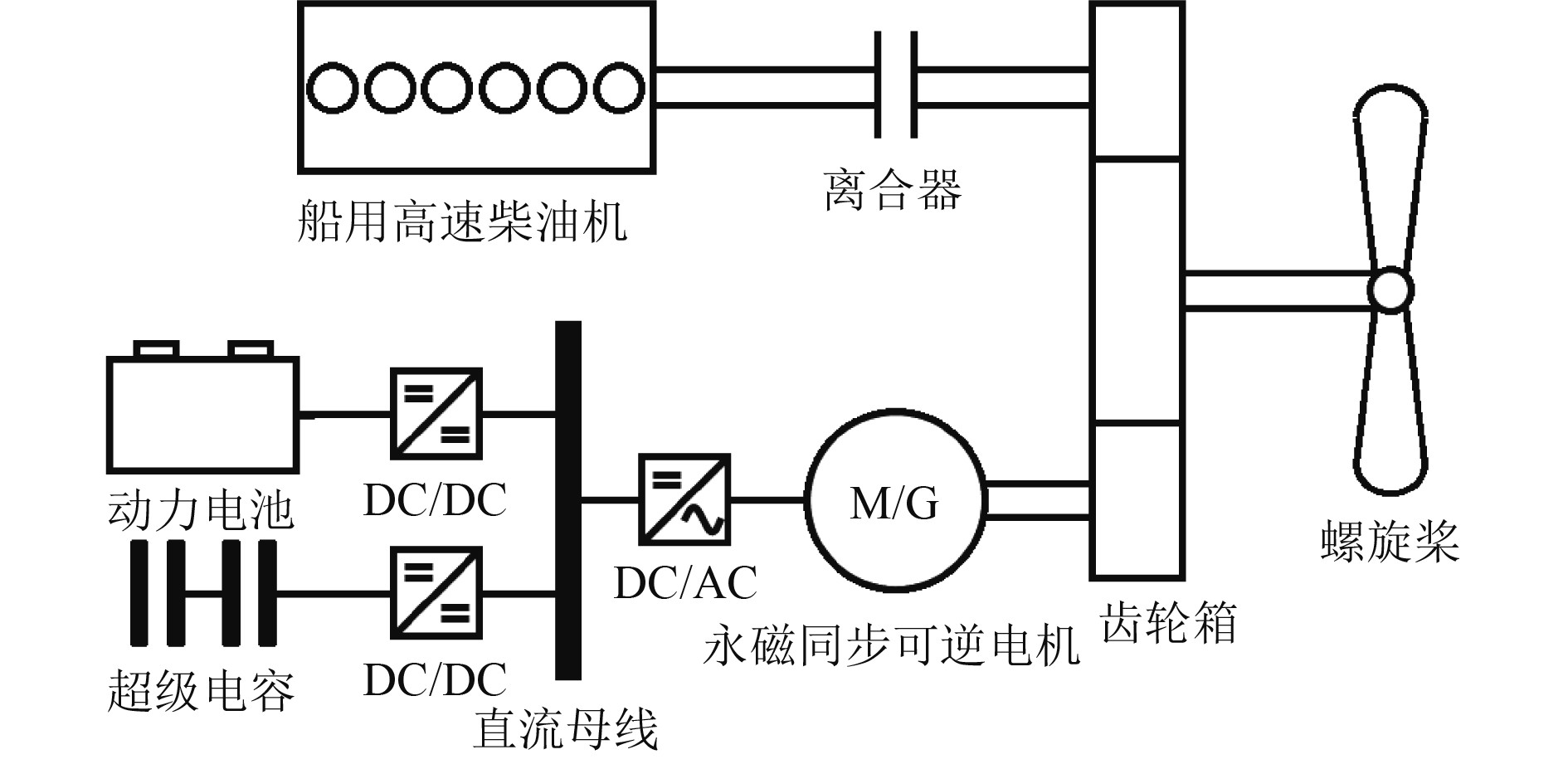
|
图 1 并联式船舶柴电混合动力系统 Fig. 1 The parallel marine hybrid power system |
本文中的柴油机为某型号的六缸四冲程高速柴油机,基础参数如表1所示。将柴油机及轴系简化为运动负载和运动轴系及柴油机转动惯量、阻尼构成的当量系统,其旋转运动方程如下式:
|
|
表 1 柴油机参数 Tab.1 Specifications of diesel engine |
| $ \begin{array}{c}\dfrac{{\text{π}} }{30}{J}_{{\rm{d}}}\dfrac{{\rm{d}}{\omega }_{d}}{{\rm{d}}t}+{F}_{d}\dfrac{{\text{π}} }{30}{\omega }_{d}={T}_{d}-{T}_{f}-{T}_{l}。\end{array} $ | (1) |
式中:Jd为柴油机内部及轴系的转动惯量,kg·m2;ωd为柴油机转速,r/min;Fd为柴油机内部的旋转阻尼系数,N·m/(rad/s);Td为柴油机输出转矩,N·m;Tf为柴油机及轴系的摩擦转矩,N·m;Tl为负载转矩,N·m。
运行中的柴油机其功率和转速的关系如下式:
| $ \begin{array}{c}{P}_{d}=\dfrac{{T}_{d}\cdot{\omega }_{d}}{9\;550}。\end{array} $ | (2) |
式中:Pd为柴油机输出功率,kW。柴油机在工作状态中一段时间的总油耗、总NOx排放量的计算如下式:
| $ \begin{array}{c}{m}_{\rm fuel}={\int }_{{t}_{0}}^{{t}_{1}}\dfrac{{P}_{d}\cdot{f}_{SFOC}({T}_{{\rm{d}}},{\omega }_{{\rm{d}}})}{3\;600}{\rm{d}}t,\end{array} $ | (3) |
| $ \begin{array}{c}{m}_{\rm NOx}={\int }_{{t}_{0}}^{{t}_{1}}\dfrac{{P}_{d}\cdot{f}_{NOx}({T}_{d},{\omega }_{d})}{3\;600}{\rm{d}}t。\end{array} $ | (4) |
式中:mfuel和mNOx分别为t0~t1时间段内柴油机消耗的燃油质量和柴油机释放的NOx的质量,g;fSFOC(Td, ωd)和fNOx(Td, ωd)分别为柴油机的燃油消耗率(Specific Fuel Oil Consumption,SFOC)和NOx释放率,二者均是柴油机转矩Td和柴油机转速ωd的函数,通过查表得到,g/kWh。
1.2 可逆电机本文中的可逆电机采用某三相永磁同步可逆电机,基础参数如表2所示。
|
|
表 2 可逆电机参数 Tab.2 3-Phase permanent magnet synchronous reversable motor |
将电动机的机械部分及轴系简化为运动负载和运动轴系及电动机转子转动惯量、阻尼构成的当量系统,其旋转运动方程如下式:
| $ \begin{array}{c}{J}_{m}\dfrac{{{\rm{d}}\omega }_{m}}{{\rm{d}}t}+{F}_{m}{\omega }_{m}={T}_{m}-{T}_{f}-{T}_{l}。\end{array} $ | (5) |
式中:Jm为电动机内部及轴系的转动惯量,kg·m2;ωm为电动机转速,rad/s;Fm为电动机内部的旋转阻尼系数,N·m/(rad/s);Tm为电动机的电磁转矩,N·m;Tf为电动机及轴系的摩擦转矩,N·m;Tl为负载转矩,N·m。
永磁同步电机在 d-q 坐标系下的数学模型可表示为:
| $\begin{split} & \dfrac{{\rm{d}}}{{\rm{d}}t}\left[\begin{array}{c}{I}_{sd}\\ {I}_{sq}\end{array}\right]=\left[\begin{array}{cc}-\dfrac{{R}_{s}}{{L}_{d}}& \dfrac{P\cdot {\omega }_{m}\cdot {L}_{q}}{{L}_{d}}\\ -\dfrac{p\cdot {\omega }_{m}\cdot {L}_{d}}{{L}_{q}}& -\dfrac{{R}_{s}}{{L}_{q}}\end{array}\right]\\ & \left[\begin{array}{c}{I}_{sd}\\ {I}_{sq}\end{array}\right]+ \left[\begin{array}{c}\dfrac{{V}_{sd}}{{L}_{d}}\\ \dfrac{{V}_{sd}-p\cdot {\omega }_{m}\cdot \phi }{{L}_{q}}\end{array}\right]。\end{split} $ | (6) |
式中:Rs为定子绕组电阻,Ω;Ld和Lq为定子d-q轴等效电感,H;Isd(t)和Isq(t)表示定子电流,A;Vsd(t)和Vsq(t)表示定子电压,V;φ为永磁电机磁链,Wb;P为极对数。
此外,电动机输出电磁转矩Tm(t)与电压的关系为:
| $ \begin{array}{c}{T}_{m}=\dfrac{3}{2}p\cdot \phi \cdot \dfrac{{V}_{sq}\cdot {R}_{s}-p\cdot {\omega }_{m}{L}_{s}{V}_{sd}-p\cdot {\omega }_{m}{R}_{s}\cdot \phi }{{R}_{s}^{2}+{L}_{s}^{2}\cdot {p}^{2}\cdot {\omega }_{m}^{2}},\end{array} $ | (7) |
d-q轴定子电压可通过(8)计算得到:
| $ \begin{array}{c}\left\{\begin{array}{c}{V}_{sd}\approx \dfrac{{V}_{bus}\cdot {I}_{red}\cdot {I}_{sd}}{{I}_{sd}^{2}+{I}_{sq}^{2}},\\ {V}_{sq}\approx \dfrac{{V}_{bus}\cdot {I}_{red}\cdot {I}_{sq}}{{I}_{sd}^{2}+{I}_{sq}^{2}}。\end{array}\right.\end{array} $ | (8) |
式中:Vbus和I red分别为直流母线电压,V;和发电机在直流侧的电流,A。
1.3 动力电池系统中动力电池总电量60.48 kWh,采用等效电路模型,不考虑温度以及电池老化对电池的影响[6]。动力电池的放电模型如式(9),充电模型如式(10)。
| $ \begin{array}{c}{V}_{bat}={E}_{0}-R\cdot i-K\dfrac{Q}{Q-it}\cdot \left(it+{i}^{*}\right)+{A}^{-B\cdot it},\end{array} $ | (9) |
| ${V}_{bat} = {E}_{0}-R\cdot i-K\dfrac{Q}{it-0.1Q}\cdot {i}^{*}-K\dfrac{Q}{Q-it}\cdot it+{A}^{-B\cdot it}。$ | (10) |
式中:Vbat为电池电压,V,E0为电池的恒定电压,V;K为极化电阻,Ω;Q为电池容量,Ah;it为
系统中的超级电容总容量198F,采用一阶RC等效电路Stern模型[7],超级电容的电压Vsc如下式:
| $\begin{aligned} & {V}_{sc}=\dfrac{{N}_{s}{Q}_{T}d}{{N}_{p}{N}_{e}\epsilon {\epsilon }_{0}{A}_{i}}+\dfrac{2{N}_{e}{N}_{s}RT}{F}\mathrm{arcsinh} \times\\ & \left(\dfrac{{Q}_{T}}{{N}_{p}{N}_{e}^{2}{A}_{i}\sqrt{8RT\epsilon {\epsilon }_{0}c}}\right)-{R}_{sc}\cdot {i}_{sc}。\end{aligned} $ | (11) |
式中:Ai为子电容电极和电解质之间的界面面积,m2;c为摩尔浓度,mol/m3,c = 1/(8NAd3);d为分子半径,m;F为法拉第常数;isc为超级电容的电流,A;Vsc为超级电容的电压,V;Rsc为超级电容的总内阻,Ω;Ne为超级电容的电极层数;NA为阿伏伽德罗常数;Np为超级电容并联子电容的个数;Ns为超级电容串联子电容的个数;QT为充电电荷量,C;R为理想气体状态常数;T为工作温度,K;ε和ε0分别为材料和真空的介电常数。
超级电容的电荷量计算式如下[8]:
| $ \begin{array}{c}{Q}_{T}={\int }_{{t}_{0}}^{{t}_{1}}{i}_{sc}{\rm{d}}t。\end{array} $ | (12) |
其中:QT为充电电荷量,C;isc为超级电容的电流,A。
1.5 电源转换器本文中电源转换器采用Ghimire等提出的效率模型[9],对于混合动力系统中的二极管整流器、逆变器、双向DC-DC变换器,其转换效率如下式:
| $ \begin{array}{c}{\eta }_{buck}=f\left(x\right)=\dfrac{114783.3833x+45255.9937}{{x}^{2}+1148.0987x+524.9216},\end{array} $ | (13) |
| $\begin{aligned} &{\eta }_{boost}=f\left(x\right)=\\ &\dfrac{129206.9856{x}^{2}-35314.5571x+2271.6225}{{{x}^{3}+1302.7838x}^{2}-314.6492x+13.2097},\end{aligned}$ | (14) |
| $ \begin{aligned} & {\eta }_{inv}=f\left(x\right)=\\ & \dfrac{5.986{x}^{2}+157624.6199x-1089.9521}{{x}^{2}+1575.4616x+760.8591} ,\end{aligned} $ | (15) |
| $ \begin{array}{c}{\eta }_{rec}=f\left(x\right)=1.5136{e}^{-18}{x}^{2}-0.0014x+99.456。\end{array} $ | (16) |
式中:ηbuck、ηboost、ηinv、ηrec分别为直流降压、升压变换器、逆变器、二极管整流器的效率;x为对应电源转换器的实际功率与额定功率的百分比值,单位%。
2 系统能量流计算方法 2.1 系统运行模式本文研究的并联式船舶柴电混合动力系统包含4种工作模式,分别为可逆电机单独推进模式(Power-Take-me-Home, PTH)、可逆电机发电模式(Power-Take-Out, PTO)、柴油机单独推进模式(Diesel-Only, DO)、可逆电机辅助推进模式(Power-Take-In, PTI)。PTH模式下由可逆电机单独驱动负载;PTO模式下可逆电机处于发电工况,主机同时驱动负载和可逆电机,可有效提升主机负荷率,改善系统能效水平;DO模式下由主机单独驱动负载;PTI模式下由主机和可逆电机共同驱动负载,此时系统具有最大输出功率。
系统4种工作模式的能量流如图2所示。
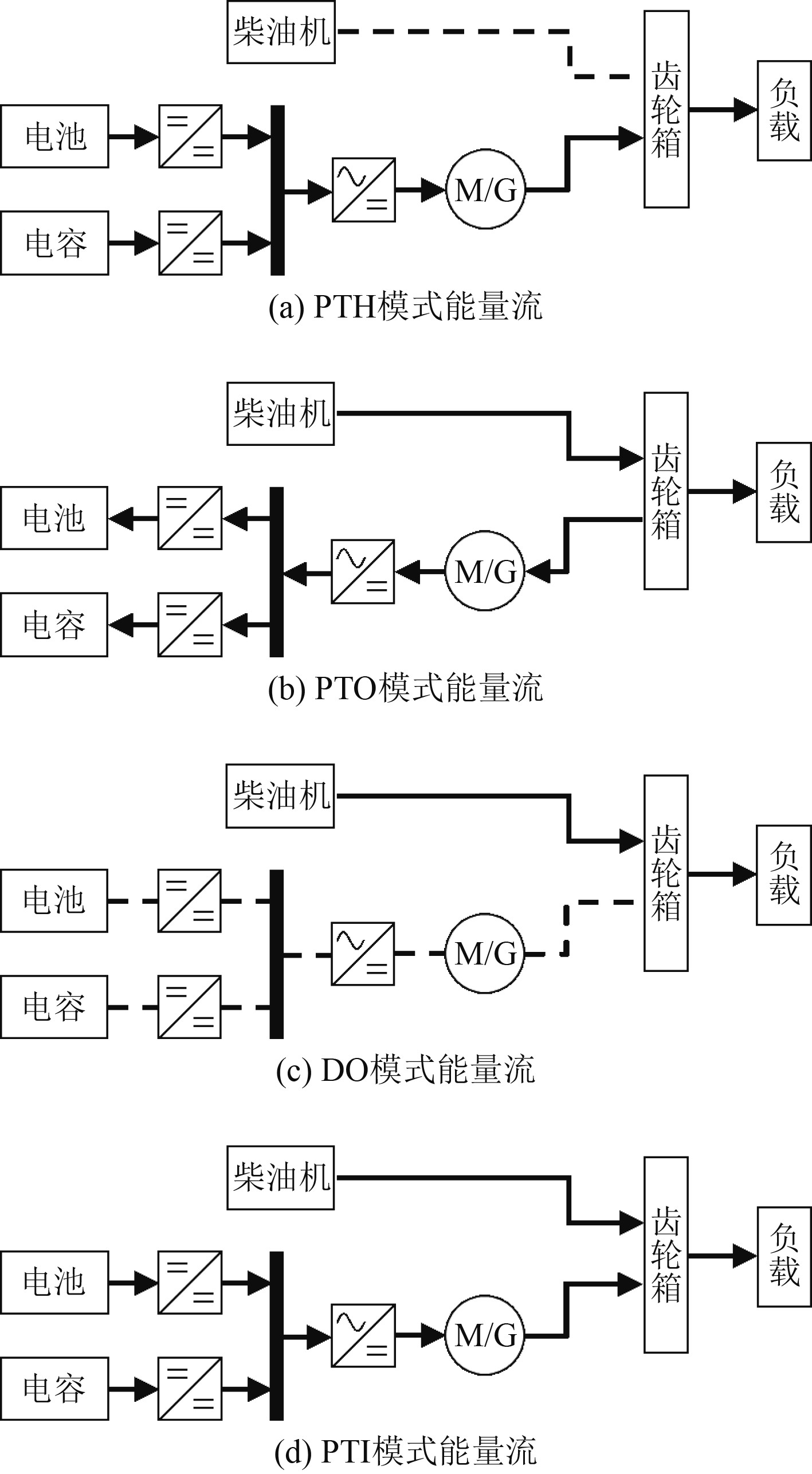
|
图 2 混合动力系统能量流图 Fig. 2 The hybrid power system energy flow |
等效油耗是衡量混合动力系统中非原动机的能耗的一个重要指标。本文计算电池系统等效油耗的公式为:
| $ \begin{array}{c}{F}_{eq,batt}=\dfrac{1000}{{\eta }_{dis,batt}{\eta }_{m}{\eta }_{e}{\eta }_{q}{\eta }_{chg,batt}H}。\end{array} $ | (17) |
式中:Feq,batt为动力电池电量的等效油耗,g/kJ;ηchg,batt和 ηdis,batt分别为电池的平均充电、放电效率;ηm为等效可逆电机的平均效率;ηd为等效柴油发动机平均效率;H为等效燃油的低热值;ηq为等效油电转换支路的机械传动效率平均值[10]。
对于超级电容的SOC,等效油耗的计算采用和动力电池类似的公式:
| $ \begin{array}{c}{F}_{eq,sc}=\dfrac{1000}{{\eta }_{dis,sc}{\eta }_{m}{\eta }_{e}{\eta }_{q}{\eta }_{chg,sc}H}。\end{array} $ | (18) |
式中:Feq,sc为超级电容电量的等效油耗,g/kJ;ηchg,sc和ηdis,sc分别为超级电容的平均充电、放电效率。
计算总油耗的时候,应考察复合储能系统初始和最终SOC的差值ΔSOC,如下式:
| $ \begin{array}{c}\Delta SOC={SOC}_{initial}-{SOC}_{final}。\end{array} $ | (19) |
ΔSOC若为负,则代表整个过程中一部分油耗被转化成电力进行储存。若为正,则代表整个过程中一部分电量被额外消耗做功。最终的总油耗质量为:
| $\begin{aligned} & {m}_{all}={m}_{fuel}+{F}_{eq,batt}\cdot {\Delta SOC}_{batt}\cdot {E}_{batt}+\\ & {F}_{eq,sc}\cdot {\Delta SOC}_{sc}\cdot {E}_{sc}。\end{aligned} $ | (20) |
式中:mall为系统总油耗质量,g;mfuel为柴油机消耗的燃油质量,g;Feq,batt和Feq,sc分别为动力电池电量和超级电容电量的等效油耗,g/kJ;ΔSOCbatt和ΔSOCsc分别为动力电池和超级电容的SOC差值;Ebatt和Esc分别是动力电池和超级电容的总能量,kJ。
3 系统仿真方法与设置 3.1 基于逻辑规则的能量管理策略本文提出基于确定逻辑规则的能量管理策略来验证系统的能效水平。通过设定的阈值和逻辑规则来确定所研究的船舶混合动力系统运行模式,同时对柴油机、可逆电机、复合储能装置的功率进行分配,使得系统各部分尽可能运行在能效水平较高的工作区间[11]。
4种运行模式之间切换的阈值由负载需求功率,柴油机、可逆电机的功率限制,动力电池、超级电容的SOC限制和实际SOC值等参数来确定。
| $ \begin{array}{l}PTH:\left\{\begin{array}{l}{P}_{load} < {P}_{m,{\rm{max}}},\\ {SOC}_{batt,{\rm{low}}}\leqslant {SOC}_{batt} < {SOC}_{batt,{\rm{max}}},\\ {SOC}_{sc,{\rm{min}}}\leqslant {SOC}_{sc} < {SOC}_{sc,{\rm{max}}}。\end{array}\right. \end{array} $ | (21) |
| $\begin{aligned} PTO: & \left\{\begin{array}{l}{P}_{m,{\rm{max}}}\leqslant {P}_{load}\leqslant {P}_{d,{\rm{high}}},\\ {SOC}_{batt,{\rm{min}}}\leqslant {SOC}_{batt} < {SOC}_{batt,{\rm{max}}}\\ {SOC}_{sc,{\rm{min}}}\leqslant {SOC}_{sc} < {SOC}_{sc,{\rm{max}}}\end{array}\right.,{\rm{or}}:\\ & \left\{\begin{array}{l}{P}_{load} < {P}_{m,{\rm{max}}},\\ {SOC}_{batt,{\rm{min}}}\leqslant {SOC}_{batt} < {SOC}_{batt,{\rm{high}}},\\ {SOC}_{sc,{\rm{min}}}\leqslant {SOC}_{sc} < {SOC}_{sc,{\rm{max}}}。\end{array}\right. \end{aligned}$ | (22) |
| $ {l}DO:\left\{\begin{array}{l}{P}_{d,{\rm{high}}}\leqslant {P}_{load} < {P}_{d,{\rm{max}}},\\ {SOC}_{batt,{\rm{min}}}\leqslant {SOC}_{batt} < {SOC}_{batt,{\rm{max}}},\\ {SOC}_{sc,{\rm{min}}}\leqslant {SOC}_{sc} < {SOC}_{sc,{\rm{max}}}。\end{array} \right. $ | (23) |
| $ \begin{array}{l}PTI:\left\{\begin{array}{l}{P}_{d,{\rm{max}}}\leqslant {P}_{load} < {P}_{all,{\rm{max}}},\\ {SOC}_{batt,{\rm{low}}}\leqslant {SOC}_{batt} < {SOC}_{batt,{\rm{max}}},\\ {SOC}_{sc,{\rm{min}}}\leqslant {SOC}_{sc} < {SOC}_{sc,{\rm{max}}}。\end{array}\right.\end{array} $ | (24) |
式中:Pload为负载功率;Pm,max为可逆电机最大功率;Pd,high为柴油机最佳工况功率;Pd,max为柴油机额定功率;Pall,max为系统最大总功率;SOCbatt,min、SOCbatt,low、SOCbatt,high、SOCbatt,max分别为动力电池的最小SOC限值,低SOC值,高SOC值,最大SOC限值,SOCsc,min、SOCsc,max分别为超级电容的最小SOC限值和最大SOC限值。
当负载功率较低时,若SOC较高,则启用PTH模式。若SOC较低,或负载功率适中,则启用PTO模式。当负载功率接近柴油机最佳功率时,则启用DO模式。当负载功率超过柴油机额定功率,则启用PTI模式。对于PTH和PTO模式中阈值范围重合的状态,系统将保持当前的运行模式,直到参数不再处于当前运行模式的阈值范围内。这是为了避免系统运行模式过于频繁的切换而造成不必要的损耗[12-13]。
3.2 功率分配每个运行模式的功率分配由柴油机在不同转速、转矩下的燃油消耗率SFOC,可逆电机在不同转速、转矩下的效率,动力电池、超级电容的额定充放电功率等参数来确定,如下式:
| $ \begin{array}{l}\left\{\begin{array}{l}{PTH:{P}_{load}+{P}_{loss}={P}_{batt,dis}+{P}_{sc,dis}},\\{PTO:{P}_{load}+{P}_{loss}+{P}_{batt,chg}+{P}_{sc,chg}={P}_{d}},\\ {DO:{P}_{load}+{P}_{loss}={P}_{d}},\\{PTI:{P}_{load}+{P}_{loss}={P}_{d}+{P}_{batt,dis}+{P}_{sc,dis}}。\end{array}\right.\end{array} $ | (25) |
式中:Pload为负载功率;Ploss为系统能量损失;Pd为柴油机功率;Pbatt,chg、Pbatt,dis分别为动力电池充放电功率;Psc,chg、Psc,dis分别为超级电容充放电功率。
在PTO以及PTI模式下,对柴油机和可逆电机的转速、转矩进行平衡,使得二者在与负载耦合时均尽可能地工作在其能效更高的工作区间。而在PTH、PTO、PTI模式下,动力电池的功率响应存在一定的滞后作用,超级电容将在此过程中削峰填谷,使动力电池的功率变化趋于平缓,以达到保护电池、提高能效的作用。
3.3 仿真模型及负载工况本文基于Matlab/Simulink建立的并联式船舶柴电混合动力复合储能系统模型主要包含柴油机模型、可逆电机模型、动力电池模型、超级电容模型、负载模型、电源变换器模型、控制策略模型等部分。系统整体模型如图3所示。

|
图 3 船舶混合动力系统模型 Fig. 3 The model of marine hybrid power system |
本文所选取的船舶工况来自Grimmelius等[14]在船舶混合动力系统控制研究中使用的工况,如图4所示。该典型工况来自于某港口拖轮,功率需求波动频率快、幅度大,是船舶混合动力复合储能系统非常理想的应用场景。
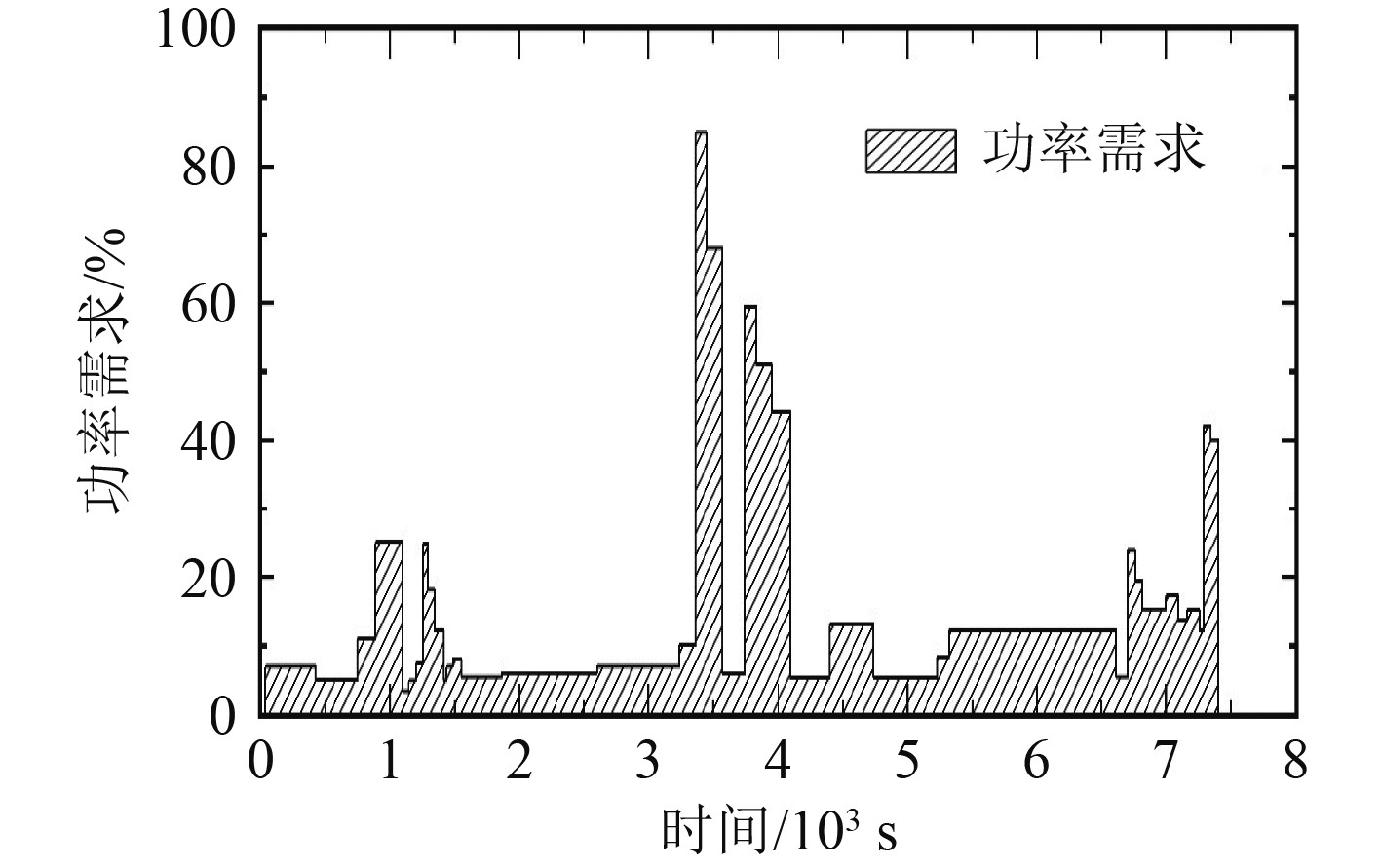
|
图 4 某港口拖轮的典型工况 Fig. 4 The typical working condition of a tugboat |
动力电池初始SOC分别为0.35、0.5、0.65、0.8,超级电容初始SOC始终为0.8,仿真时间7 500 s,仿真参数的设置见表3。通过调整模型中的能量分配规则或阈值,在纯柴油机驱动、柴油机-电池混合驱动、柴油机-电池-电容复合储能驱动3种驱动形式下以4个不同初始SOC进行仿真计算。
|
|
表 3 仿真参数设置 Tab.3 Values of simulation parameters |
图5为柴油机-电池混合驱动下电池SOC随时间变化图,图6和图7分别为柴油机-电池-电容复合储能驱动下电池、电容的SOC随时间变化图。
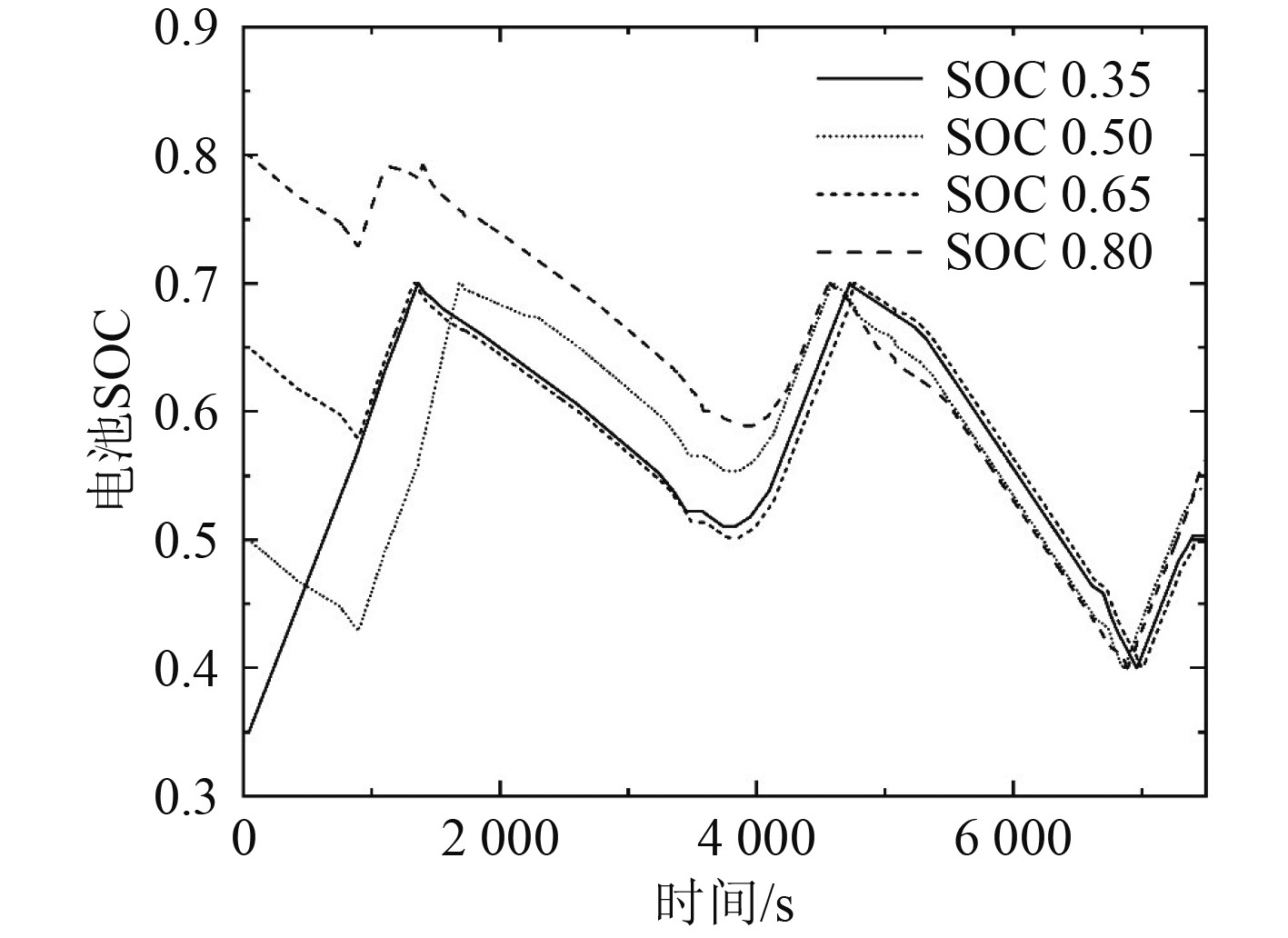
|
图 5 柴油机-电池混合驱动电池SOC变化 Fig. 5 Battery SOC of diesel-battery hybrid power system |

|
图 6 柴油机-电池-电容复合储能驱动电池SOC变化 Fig. 6 Battery SOC of diesel-battery-capacitor hybrid power system |

|
图 7 柴油机-电池-电容复合储能驱动超级电容SOC变化 Fig. 7 Capacitor SOC of diesel-battery-capacitor hybrid power system |
从图5和图6可以看出,动力电池的SOC均被稳定在了0.7~0.4之间。在这个区间内电池拥有较高的充放电效率,有助于延长电池的使用寿命[5]。在1000~2000 s、3500~4000 s、4500~5000 s、6500~7000 s时,系统工作模式切换,储能装置的功率变化幅度较大,在图5中表现为较尖锐的拐点。
在图6中,由于复合储能装置中超级电容的存在,使得原本尖锐的拐点被较为平坦的曲线所取代。这意味着电池的充放电倍率更小,此时充放电效率更高,提升了储能装置的能效[9]。
在图7中,超级电容的SOC变化在整个仿真过程中均较为剧烈,代表电容吸收了大部分高频的负载波动,在复合储能系统中起到了削峰填谷的作用,可以提高动力电池寿命。
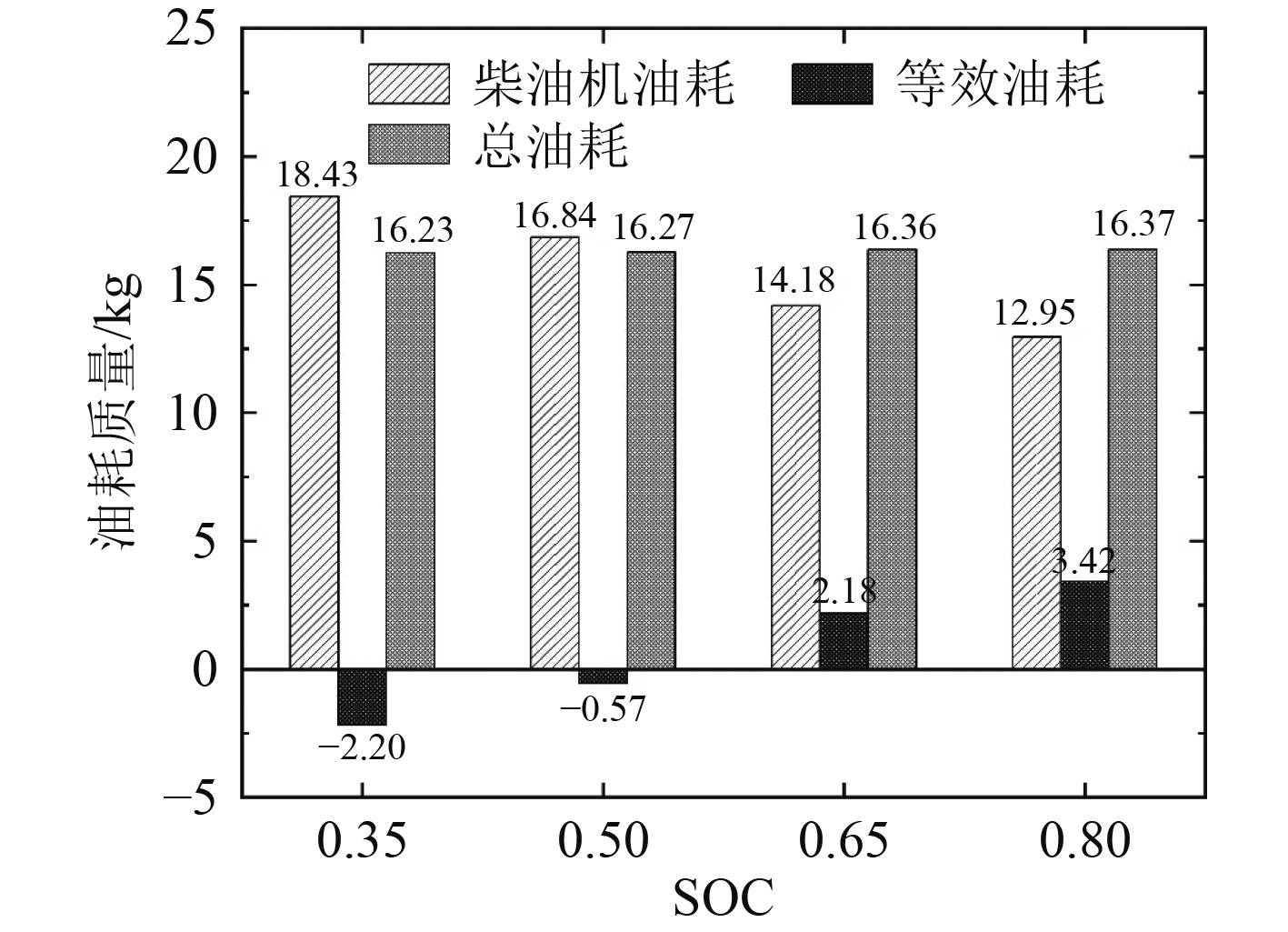
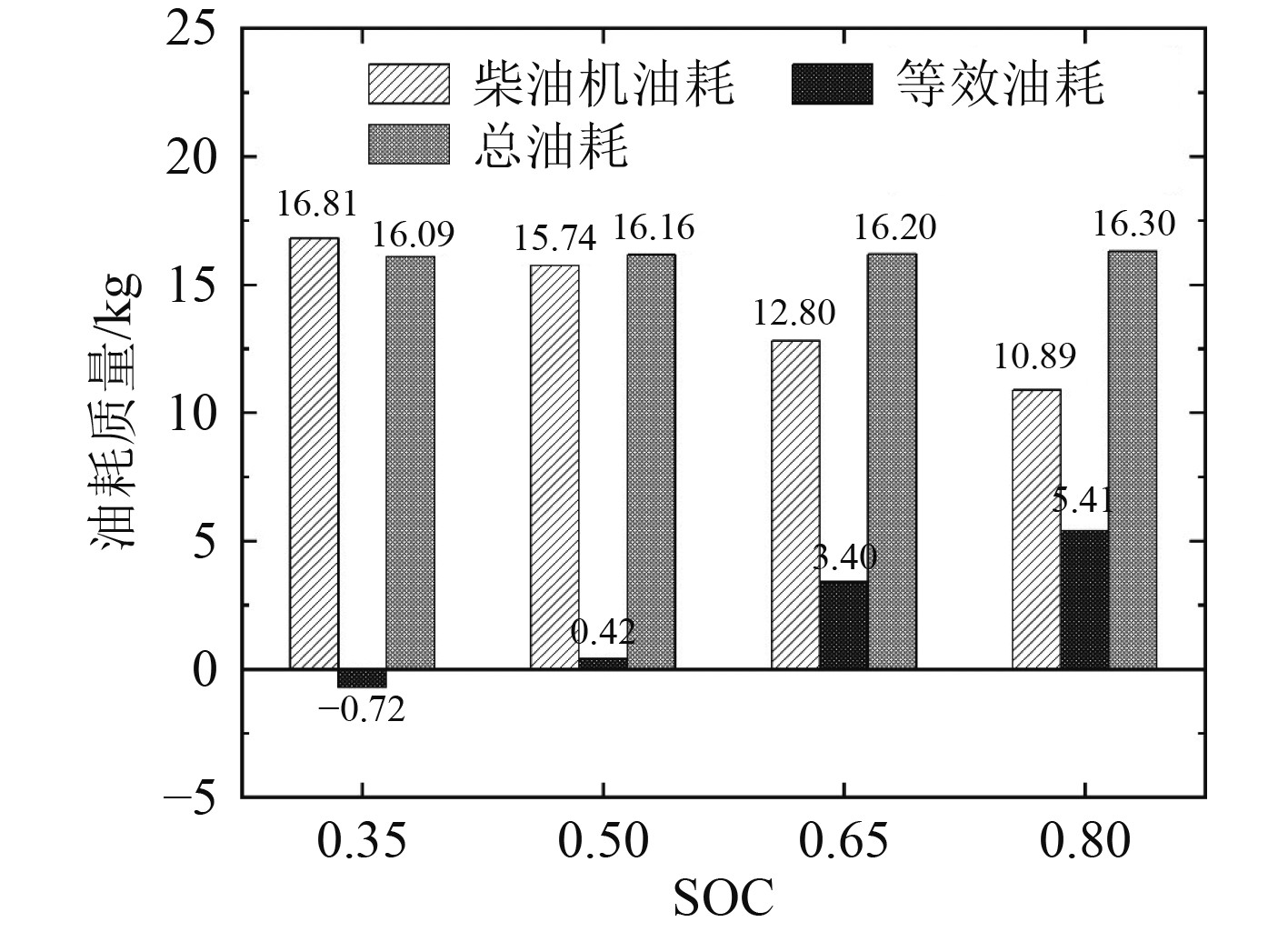
4.2 系统油耗仿真结果图8和图9分别为柴油机-电池混合驱动和柴油机-电池-电容复合储能驱动的油耗随动力电池初始SOC变化的数据。
|
图 8 柴油机-电池混合动力油耗 Fig. 8 Fuel consumption of diesel-battery hybrid power system |
|
图 9 柴油机-电池-电容复合储能驱动油耗 Fig. 9 Fuel consumption of diesel-battery-capacitor hybrid power system |
计算得纯柴油机的系统在整个仿真过程中耗油17.34 kg,NOx排放209.6 g。
由图8可知,初始SOC为0.35的情况下,柴油机耗油量高于纯柴油机驱动,这是由于柴油机更多地工作在功率相对较高的最佳工况区间。图8和图9中,初始SOC增大,柴油机油耗减少,等效油耗上升,总油耗微幅上升。因为随着初始SOC增加,系统更多运行在PTH或PTI模式,电动机运行时间上升,柴油机运行时间下降,所以柴油机油耗减少,等效油耗上升。但港口拖轮的负载工况存在较多低功率的工况,此时电动机效率无法达到最佳,造成总油耗微幅上升。
等效油耗在初始SOC等于0.35和0.5时小于0,这是由于在初始SOC、负载工况均较小时,系统会首先进入PTO模式,整个过程中PTO模式运行时间大于PTH和PTI,电池放电量少于充电量。等效油耗在初始SOC等于0.65和0.8时大于0,这是由于初始SOC较大但负载功率较小,系统会首先进入PTH模式,整个过程中PTH或PTI模式运行时间大于PTO,电池放电量大于充电量。
图9中等效油耗与图8类似,但均大于图8中的等效油耗。复合储能装置可承担的负载能量和频率均大于纯电池,PTH或PTI模式的运行时间更长,等效油耗更多。
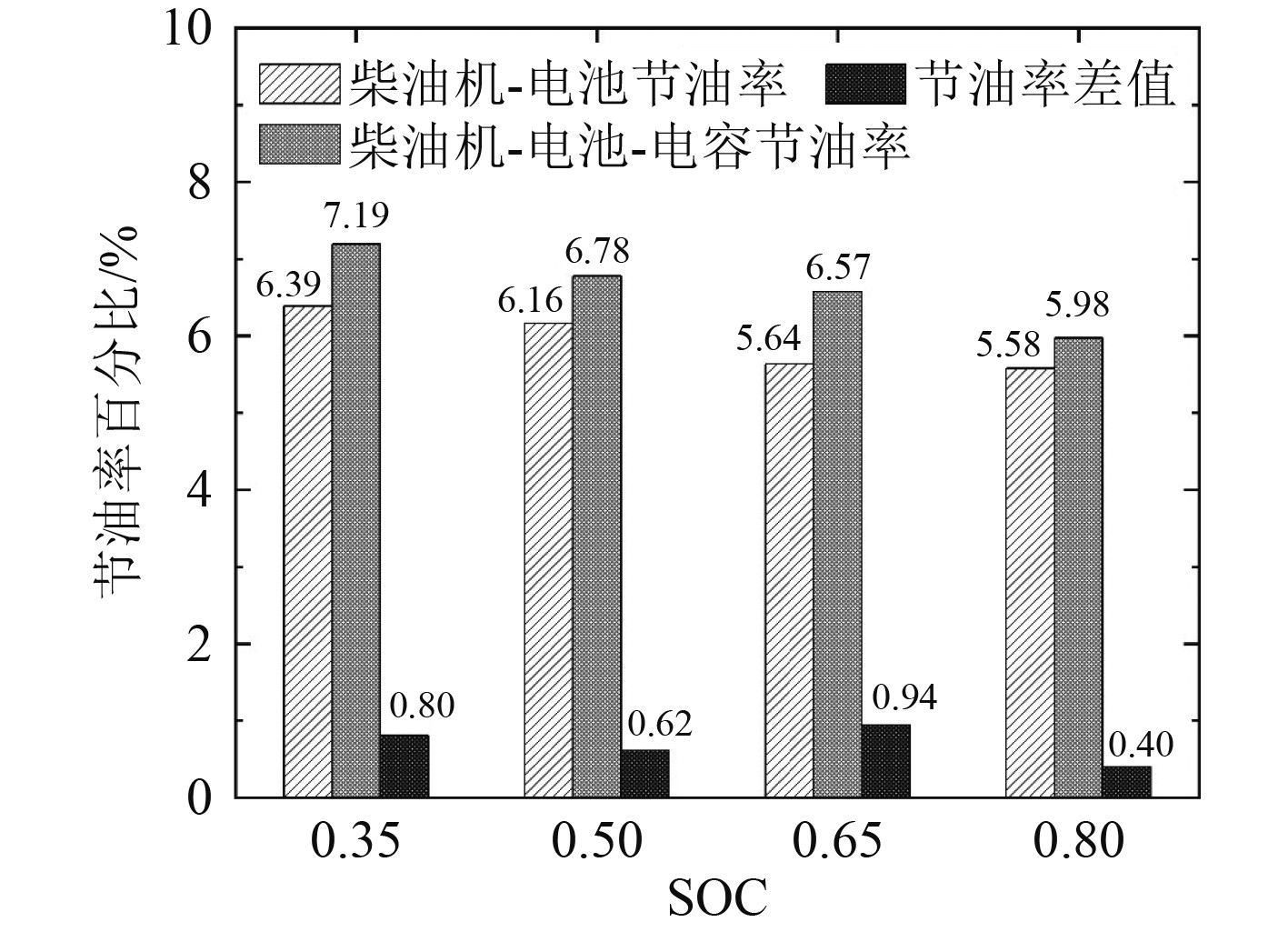
4.3 系统节油效果分析图10为不同系统形式中的节油率。可知,柴油机-电池-电容复合储能驱动的平均节油率为6.63%,柴油机-电池混合驱动平均节油率为5.94%,前者平均节油率提高了11.61%。二者的节油率随着电池初始SOC的上升而下降。由此表明,柴油机-电池-电容复合储能驱动相对于柴油机-电池的混合驱动在节油上有着较为明显的优势。
|
图 10 不同系统形式中的节油率 Fig. 10 Fuel-saving rate of different system types |
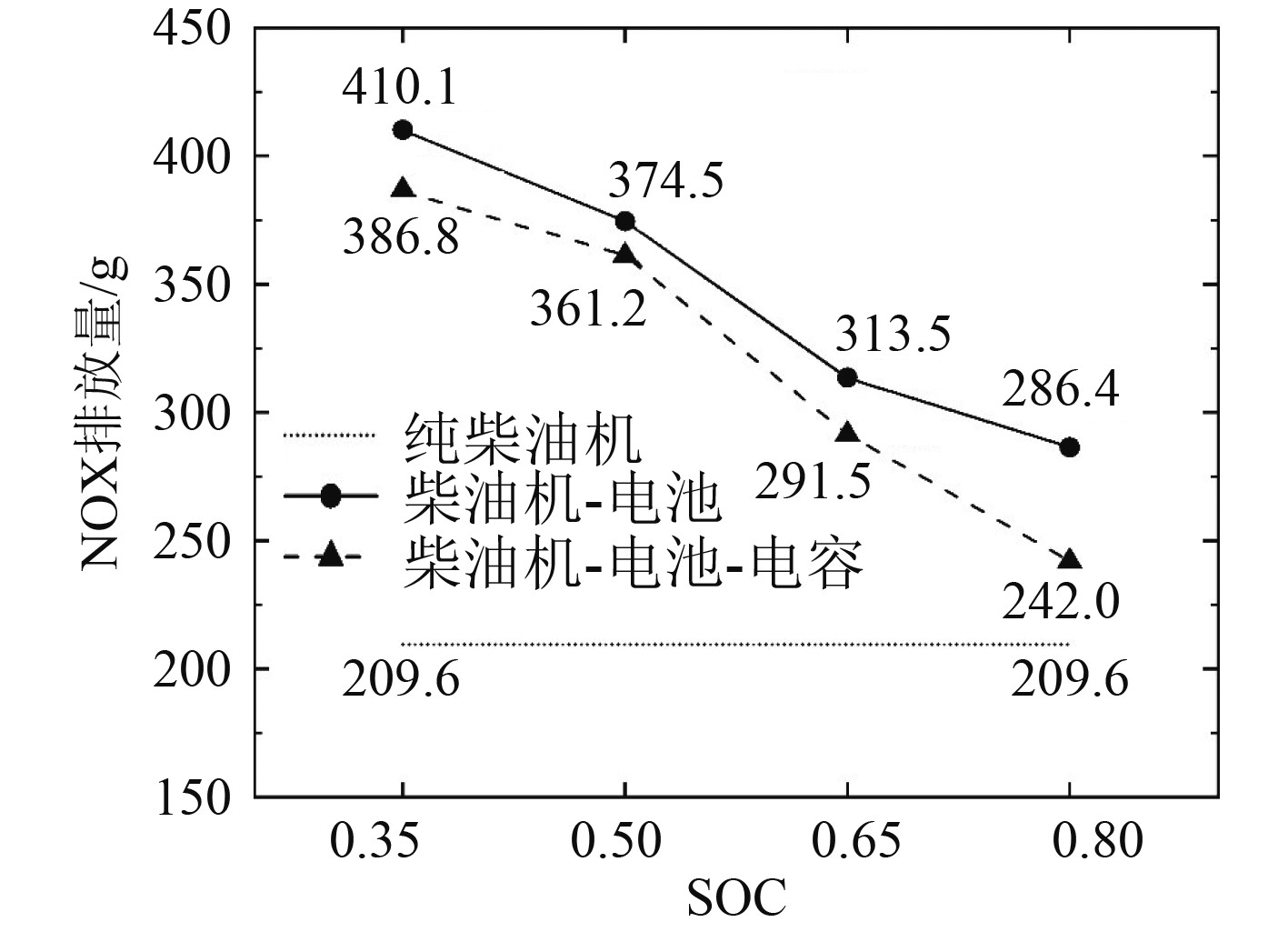
图11为不同的驱动形式中在不同电池初始SOC的条件下NOx的排放量。柴油机-电池混合驱动的NOx平均排放量346.1 g,大于柴油机-电池-电容复合储能驱动的320.4 g,后者减少了8%。随着初始SOC的增加,二者的NOx排放量均减少,但都超过纯柴油机的排放量。这是由于柴油机NOx最少排放的工况区间与油耗最佳工况区间存在偏移。以减少油耗为目标的能量管理策略会使柴油机尽可能工作在油耗最佳工况区间,而这个区间内的NOx排放量将会显著增加。因此2种混合驱动的NOx排放量都大于纯柴油机。
|
图 11 不同动力系统中的NOx排放量 Fig. 11 NOx emission of different power system |
本文提出一种并联复合储能的船舶柴电混合动力系统,对系统中柴油机、可逆电机、动力电池、超级电容、电源转换器等部件进行了模块化建模,并组合成系统仿真模型。根据系统4种不同的工作模式设计了基于逻辑规则的能量管理策略,选取了典型港口拖轮的负载工况作为仿真工况,在Matlab/Simulink平台上进行仿真计算,验证系统和能量管理策略的合理性。
计算结果表明,所提出的船舶混合动力电池-电容复合储能系统与能量管理策略相比纯柴油机的系统平均节油率为6.63%,相比柴油机-电池混合驱动平均多降低油耗约11%,且NOx排放量减少8%,在经济性和绿色性上均有较为显著的优势。且船舶混合动力电池-电容复合储能系统改善了柴油机工况,缓解了动力电池的负载波动,起到了削峰填谷的作用,对于提高动力电池的寿命和系统的可靠性有明显的效果。
| [1] |
侯慧, 甘铭, 吴细秀, 等. 混合动力船舶能量管理研究综述[J]. 中国舰船研究, 2021, 16(5): 216-229. HOU H, GAN M, WU X X, et al. Review on energy management of hybrid ships[J]. Chinese Journal of Ship Research, 2021, 16(5): 216-229. DOI:10.19693/j.issn.1673-3185.02133 |
| [2] |
苗东晓, 陈俐, 王欣然. 基于NSGA-Ⅱ优化的船舶串联式混合动力系统能量管理策略[J]. 舰船科学技术, 2022, 44(14): 113-118. DOI:10.3404/j.issn.1672-7649.2022.14.024 |
| [3] |
吴思晨, 李铁, 依平, 等. 邮船柴油发电机与电池混合电力推进系统排放研究[J]. 船舶与海洋工程, 2021, 37(4): 35-40. DOI:10.14056/j.cnki.naoe.2021.04.008 |
| [4] |
XUE Y, WANG K, HUANG L, et al, Research on the optimization and control technology of energy efficiency for new energy hybrid ships [C]//2021 6th International conference on transportation information and safety (ICTIS), 2021: 1-6.
|
| [5] |
MOHAB G, El-BANNA S H, Mahmoud El-Dabah, et al. Intelligent energy management system for an all-electric ship based on adaptive neuro-fuzzy inference system [J]. Energy Reports, 2021: 7989-7998.
|
| [6] |
NEJAD S, GLADWIN D T, STONE D A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states [J]. Journal of Power Sources. 2016, 316: 183-196.
|
| [7] |
张泽辉. 混合动力船舶复合电源能量管理策略及容量配置研究[D]. 武汉: 武汉理工大学, 2019.
|
| [8] |
OLDHAM K B. A Gouy–Chapman–Stern model of the double layer at a (metal)/(ionic liquid) interface [J]. Journal of Electroanalytical Chemistry. 2008, 613(2): 131-138.
|
| [9] |
GHIMIRE P, ZADEH M, PEDERSEN E, et al. Dynamic efficiency modeling of a marine DC hybrid power system [C]//2021 IEEE Applied Power Electronics Conference and Exposition (APEC), 2021: 855-862.
|
| [10] |
高迪驹, 张伟, 王旭阳, 等. 基于模型预测控制的混合动力船舶能量控制策略[J]. 上海海事大学学报, 2018, 39(2): 60-65. DOI:10.13340/j.jsmu.2018.02.012 |
| [11] |
张恒熙. 并联式船舶混合动力系统能量管理策略研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [12] |
KERMANI S, DELPRAT S, GUERRA T M, et al. Predictive energy management for hybrid vehicle [J]. Control Engineering Practice, 2012, 20(4): 408–420.
|
| [13] |
SUN Hui, JIANG Ji-hai, WANG Xin. Torque control strategy for a parallel hydraulic hybrid vehicle [J], Journal of Terramechanics, 2009, 12(46): 259–265.
|
| [14] |
GRIMMELIUS H, PETER V, KRIJGSMAN M, et al. Control of hybrid ship drive systems [J]. Research Gate, 2011.
|
 2024, Vol. 46
2024, Vol. 46
