2. 上海交通大学 机械与动力工程学院,上海 200240
2. Mechanical Engineering School, Shanghai Jiaotong University, Shanghai 200240, China
燃气轮机广泛应用于船舶推进、航空动力、电力能源等行业,发挥着难以替代的关键作用。燃气轮机控制系统对于确保燃机安全、可靠、高效运行意义重大。燃气轮机控制系统的性能一方面取决于燃机模型的优劣,另一方面取决于控制系统本身的性能。Yang等[1]利用LPV模型改善了航空燃气轮机的建模精度并在此基础上设计了限制保护滑模控制系统。Bonfiglio等[2]提出了基于非线性模型的燃气轮机控制系统,可有效解决燃气轮机发电机组的电网稳定性问题,设计了一种基于非线性模型的滑模控制系统,并将其在Ansaldo重型燃机上的应用结果与传统的控制方式进行对比,证明了该滑模控制的有效性和优越性。
1 三轴燃气轮机LPV模型 1.1 燃气轮机LPV模型简介燃气轮机非线性模型一般可表示为:
| $ \left\{ {\begin{array}{*{20}{c}} {\dot {\boldsymbol{x}} = f(x,{\boldsymbol{u}},\rho ,t)} ,\\ {{\boldsymbol{y}} = g(x,{\boldsymbol{u}},\rho ,t)} 。\end{array}} \right. $ | (1) |
式中:x∈Rn为状态变量,u∈Rm为控制变量,y∈Rs为输出变量,f(·)和g(·)是连续可微的。对应的燃气轮机LPV模型可表示为[3]:
| $ \left\{ {\begin{array}{*{20}{c}} {\dot {\boldsymbol{x}}(t) = {\boldsymbol{A}}(\rho (t)){\boldsymbol{x}}(t) + {\boldsymbol{B}}(\rho (t)){\boldsymbol{u}}(t)} ,\\ {{\boldsymbol{y}}(t) = {\boldsymbol{C}}(\rho (t)){\boldsymbol{x}}(t) + {\boldsymbol{D}}(\rho (t)){\boldsymbol{u}}(t)} 。\end{array}} \right. $ | (2) |
| $ \begin{gathered} {\boldsymbol{A}}(\rho (t)) = {{\boldsymbol{A}}_0} + {\rho _1}(t){{\boldsymbol{A}}_1} + \cdots + {\rho _{\text{N}}}(t){{\boldsymbol{A}}_{\text{N}}} ,\\ {\boldsymbol{B}}(\rho (t)) = {{\boldsymbol{B}}_0} + {\rho _1}(t){{\boldsymbol{B}}_1} + \cdots + {\rho _{\text{N}}}(t){{\boldsymbol{B}}_{\text{N}}} ,\\ {\boldsymbol{C}}(\rho (t)) = {{\boldsymbol{C}}_0} + {\rho _1}(t){{\boldsymbol{C}}_1} + \cdots + {\rho _{\text{N}}}(t){{\boldsymbol{C}}_{\text{N}}} ,\\ {\boldsymbol{D}}(\rho (t)) = {{\boldsymbol{D}}_0} + {\rho _1}(t){{\boldsymbol{D}}_1} + \cdots + {\rho _{\text{N}}}(t){{\boldsymbol{D}}_{\text{N}}} 。\\ \end{gathered} $ | (3) |
对式(3)做出如下说明[4]:
1)ρ=ρ(t)为具有饱和特性的时变参数,称为调度变量。饱和特性指的是当ρ超过一定范围时,其值为常数。
2)ρ一般为外部输入参数或系统状态x(t)中容易测量的参数。对于燃气轮机来说,可以是某个转子的转速或某一截面的压力。
3)ρ的选择不是唯一的,选取的原则为能否表征燃机特性的变化。
4)当ρ为某一状态参数时,系统模型又称为准LPV模型。
1.2 三轴燃气轮机LPV模型的建立以图1所示的三轴燃气轮机部件级非线性模型为研究对象,选取高压转子转速变化量为ΔNhp、低压转子转速变化量ΔNlp为状态变量,高压涡轮出口总温为T5、输出功率为Pout、燃油消耗率sfc为输出变量,燃油质量流量Wf为控制变量。由于三轴燃气轮机的动态特性随高压转子转速的变化较为连续[5],故选取高压转子转速Nhp为调度变量。考虑Nhp从80%设计转速到100%设计转速的燃机工作区间,对区间内11个平衡工作点进行雅可比(Jacobian)线性化建模[4],得到随调度变量变化的不同平衡工作点下,燃气轮机线性状态空间模型。

|
图 1 三轴燃气轮机结构示意图[6] Fig. 1 Schematic diagram of three-spool gas turbine structure |
平衡点1:ρ=Nhp=0.8Nhp,DS
| $ \begin{split} & {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{ - 5}}{{.0451{\rm{E}} - 01}}}&{{{ - 4}}{{.1816{\rm{E}} - 01}}} \\ {{\text{2}}{\text{.0164E - 01}}}&{{{ - 6}}{{.4807{\rm{E}} - 01}}} \end{array}} \right] \text{,}\\ & {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\text{2}}{{.3042{\rm{E}} + 03}}} \\ {{\text{1}}{{.5924{\rm{E}} + 04}}} \end{array}} \right],\end{split} $ |
| $ \begin{split} & {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{{ - 6}}{{.5025{\rm{E}} - 02}}}&{{{ - 4}}{{.8212{\rm{E}} - 02}}} \\ {{\text{7}}{\text{.7699E + 02}}}&{{\text{1}}{{.5364{\rm{E}} + 03}}} \\ {{{ - 1}}{{.4107{\rm{E}} - 05}}}&{{{ - 2}}{{.7510{\rm{E}} - 05}}} \end{array}} \right]\text{,}\\ & {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{\text{7}}{{.0510{\rm{E}} + 02}}} \\ {{\text{9}}{{.4769{\rm{E}} + 06}}} \\ {{\text{1}}{{.4738{\rm{E}} - 01}}} \end{array}} \right]。\end{split} $ |
平衡点2:ρ=Nhp=0.82Nhp,DS
| $ \begin{split} & {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{ - 4}}{{.9102{\rm{E}} - 01}}}&{{{ - 4}}{\text{.2465{\rm{E}} - 01}}} \\ {{\text{2}}{{.3004{\rm{E}} - 01}}}&{{{ - 6}}{\text{.5395{\rm{E}} - 01}}} \end{array}} \right] \text{,}\\ & {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\text{2}}{{.1373{\rm{E}} + 03}}} \\ {{\text{1}}{{.4686{\rm{E}} + 04}}} \end{array}} \right],\end{split} $ |
| $ \begin{split} & {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{{ - 6}}{{.4416{\rm{E}} - 02}}}&{{{ - 5}}{{.2489{\rm{E}} - 02}}} \\ {{\text{7}}{\text{.8354E + 02}}}&{{\text{1}}{{.6517{\rm{E}} + 03}}} \\ {{{ - 1}}{{.3113{\rm{E}} - 05}}}&{{{ - 2}}{{.7235{\rm{E}} - 05}}} \end{array}} \right]\text{,}\\ & {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{\text{6}}{{.6084{\rm{E}} + 02}}} \\ {{\text{9}}{{.2133{\rm{E}} + 06}}} \\ {{\text{1}}{{.3612{\rm{E}} - 01}}} \end{array}} \right]。\end{split} $ |
……
平衡点11:ρ=Nhp=1.00Nhp,DS(设计点)
| $ \begin{split} & {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{ - 8}}{{.2130{\rm{E}} - 01}}}&{{{ - 2}}{{.4261{\rm{E}} - 01}}} \\ {{\text{4}}{{.6376{\rm{E}} - 01}}}&{{{ - 6}}{{.5862{\rm{E}} - 01}}} \end{array}} \right]\text{,}\\ & {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\text{1}}{\text{.0954E + 03}}} \\ {{\text{8}}{\text{.2944E + 03}}} \end{array}} \right],\end{split} $ |
| $ \begin{split} & {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{{ - 5}}{{.4969{\rm{E}} - 02}}}&{{{ - 7}}{{.6086{\rm{E}} - 02}}} \\ {{\text{9}}{\text{.6926E + 02}}}&{{\text{2}}{\text{.1627E + 03}}} \\ {{{ - 8}}{{.0391{\rm{E}} - 06}}}&{{{ - 1}}{{.7765{\rm{E}} - 05}}} \end{array}} \right]\text{,}\\ & {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{\text{4}}{\text{.0707E + 02}}} \\ {{\text{9}}{\text{.3785E + 06}}} \\ {{\text{4}}{{.9574{\rm{E}} - 02}}} \end{array}} \right] 。\end{split} $ |
利用Matlab曲线拟合工具Curve Fitting Tool对模型系数矩阵的各个元素值进行拟合,在保证拟合精度的前提下选择三次多项式可降低拟合曲线的复杂程度。以系统矩阵A为例,各元素的拟合结果如图2所示。

|
图 2
系数矩阵A随调度变量Nhp的变化规律
Fig. 2
Changing law of coefficient matrix A with scheduling variable |
根据拟合结果插值得到三轴燃气轮机在80%设计高压转子转速(8000 r/min)到100%设计高压转子转速(10000 r/min)区间的LPV模型:
| $ \begin{split} {\boldsymbol{A}}(\bar \rho ) = & \left[ {\begin{array}{*{20}{c}} {{{ - 101}}{{.0}}}&{{{501}}{{.73}}} \\ {{{65}}{{.28}}}&{{{1}}{{.414}}} \end{array}} \right]{\bar \rho ^3} + \left[ {\begin{array}{*{20}{c}} {{{273}}{{.6}}}&{{{ - 1336}}{{.92}}} \\ {{{ - 180}}{{.06}}}&{{{ - 4}}{{.817}}} \end{array}} \right]{\bar \rho ^2} + \\ & \left[ {\begin{array}{*{20}{c}} {{{ - 247}}{{.7}}}&{{{1183}}{{.19}}} \\ {{{166}}{{.13}}}&{{{5}}{{.192}}} \end{array}} \right]\bar \rho + \left[ {\begin{array}{*{20}{c}} {{{74}}{{.31}}}&{{{ - 348}}{{.28}}} \\ {{{ - 50}}{{.91}}}&{{{ - 2}}{{.450}}} \end{array}} \right] ,\end{split} $ |
| $ \begin{split} {\boldsymbol{B}}(\bar \rho ) =& \left[ {\begin{array}{*{20}{c}} {{{ - 1}}{{.158{\rm{e}} + 06}}} \\ {{{ - 5}}{{.3214{\rm{e}} + 05}}} \end{array}} \right]{\bar \rho ^3} + \left[ {\begin{array}{*{20}{c}} {{{3}}{{.084{\rm{e}} + 06}}} \\ {{{1}}{{.5001{\rm{e}} + 06}}} \end{array}} \right]{\bar \rho ^2}+ \\ & \left[ {\begin{array}{*{20}{c}} {{{ - 2}}{{.732{\rm{e}} + 06}}} \\ {{{ - 1}}{{.4394{\rm{e}} + 06}}} \end{array}} \right]\bar \rho + \left[ {\begin{array}{*{20}{c}} {{{8}}{{.071{\rm{e}} + 05}}} \\ {{{4}}{{.7984{\rm{e}} + 05}}} \end{array}} \right]。\end{split} $ |
| $ \begin{split} {\boldsymbol{C}}(\bar \rho ) =& \left[ {\begin{array}{*{20}{c}} {{{9}}{{.8072}}}&{{{ - 7}}{{.2834}}} \\ {{{ - 4}}{{.307{\rm{e}} + 04}}}&{{{ - 5}}{{.68012{\rm{e}} + 05}}} \\ {{{8}}{{.063{\rm{e}} - 05}}}&{{{5}}{{.4428{\rm{e}} - 3}}} \end{array}} \right]{{\bar \rho }^3}+ \\ & \left[ {\begin{array}{*{20}{c}} {{{ - 24}}{{.8908}}}&{{{17}}{{.8751}}} \\ {{{9}}{{.961{\rm{e}} + 04}}}&{{{1}}{{.52755{\rm{e}} + 06}}} \\ {{{ - 8}}{{.298{\rm{e}} - 05}}}&{{{ - 1}}{{.4717{\rm{e}} - 2}}} \end{array}} \right]{{\bar \rho }^2}{{ }}+ \\ & \left[ {\begin{array}{*{20}{c}} {{{20}}{{.9263}}}&{{{ - 14}}{{.5317}}} \\ {{{ - 7}}{{.328{\rm{e}} + 04}}}&{{{ - 1}}{{.36073{\rm{e}} + 06}}} \\ {{{ - 1}}{{.725{\rm{e}} - 05}}}&{{{1}}{{.3263{\rm{e}} - 2}}} \end{array}} \right]\bar \rho+ \\ & \left[ {\begin{array}{*{20}{c}} {{{ - 5}}{{.8955}}}&{{{3}}{{.8640}}} \\ {{{1}}{{.766{\rm{e}} + 04}}}&{{{4}}{{.03401{\rm{e}} + 05}}} \\ {{{1}}{{.204{\rm{e}} - 05}}}&{{{ - 4}}{{.007{\rm{e}} - 3}}} \end{array}} \right] ,\end{split} $ |
| $ \begin{split} {\boldsymbol{D}}(\bar \rho ) = & \left[ {\begin{array}{*{20}{c}} {{{ - 9477}}} \\ {{{1}}{{.5908{\rm{e}} + 9}}} \\ {{{ - 11}}{{.88}}} \end{array}} \right]{\bar \rho ^3} + \left[ {\begin{array}{*{20}{c}} {{{3}}{{.116{\rm{e}} + 04}}} \\ {{{ - 4}}{{.1645{\rm{e}} + 09}}} \\ {{{32}}{{.07}}} \end{array}} \right]{\bar \rho ^2} + \\ & \left[ {\begin{array}{*{20}{c}} {{{ - 3}}{{.449{\rm{e}} + 04}}} \\ {{{3}}{{.6135{\rm{e}} + 09}}} \\ {{{ - 29}}{{.23}}} \end{array}} \right]\bar \rho + \left[ {\begin{array}{*{20}{c}} {{{1}}{{.321{\rm{e}} + 04}}} \\ {{{ - 1}}{{.0307{\rm{e}} + 09}}} \\ {{{9}}{{.091}}} \end{array}} \right]。\end{split} $ |
其中:
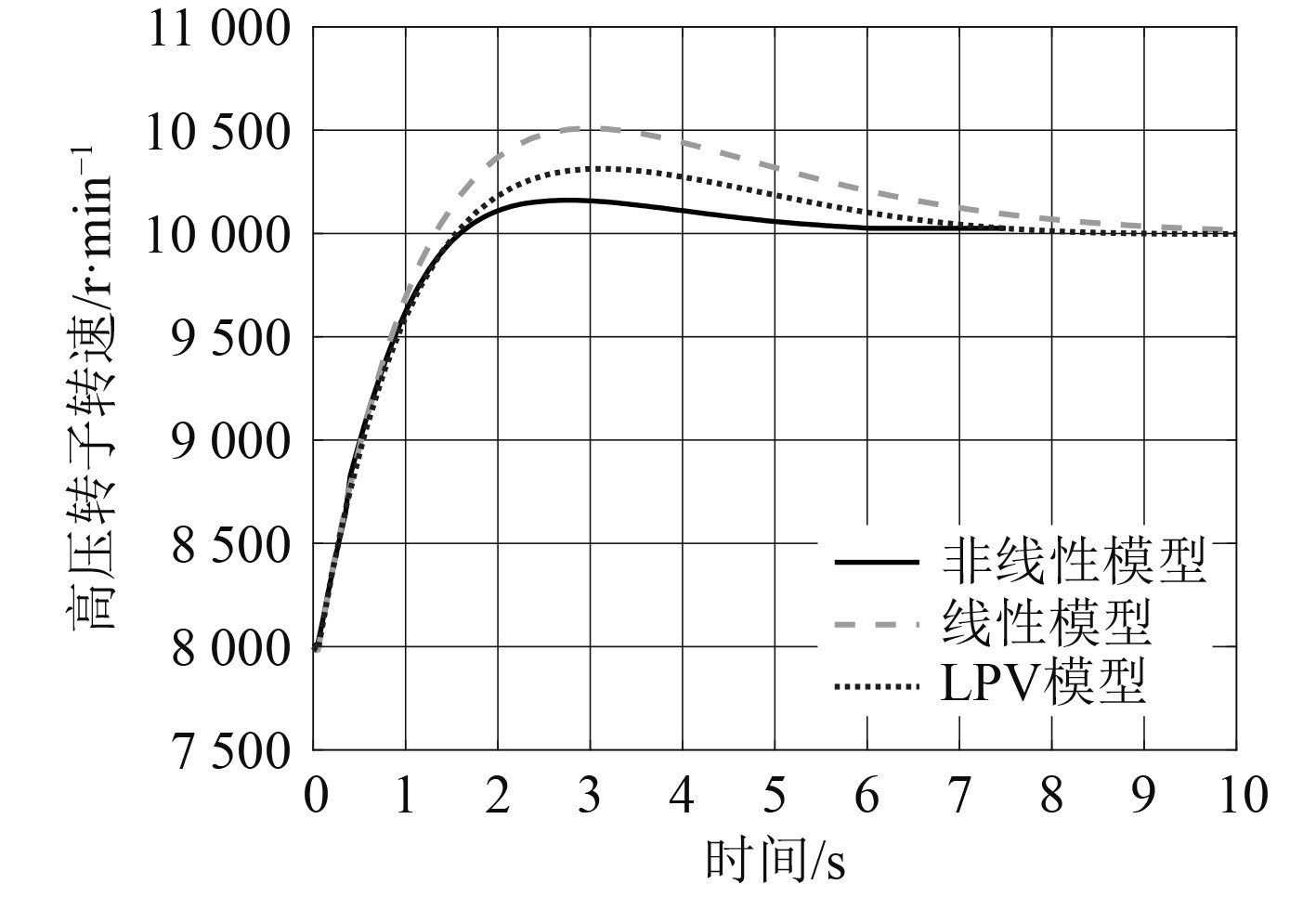
将燃机在Nhp=80%设计转速时的燃油流量Wf1=0.651 kg/s按阶跃规律变化到设计点燃油流量Wf,DS=1.858 kg/s,在Simulink仿真环境中分别计算LPV模型和线性模型下的燃气轮机响应,并将仿真结果与燃机部件级非线性模型进行对比。以高压转子转速响应为例,图3仿真结果表明LPV模型相较于线性化模型更接近非线性模型,即更能反映实际燃机的动态特性。
|
图 3 高压转子转速在不同类型模型下的燃油阶跃响应 Fig. 3 Fuel step response of high pressure rotor speed under different types of models |
LPV模型本质上是利用成熟的线性建模理论解决非线性建模问题,因而避免了非线性建模中复杂的非线性微分方程求解过程,大幅降低了建模复杂程度;同时调度变量的参与保证了LPV模型在大工况范围仍具有较高的建模精度。因而可以认为LPV模型在建模复杂度和模型精度上实现了较好的平衡,在3种模型中具有更佳的易用性和实用性。
2 自适应滑模控制器设计燃气轮机的线性状态空间模型为
| $ \dot {\boldsymbol{x}} = ({\boldsymbol{A}} + \Delta {\boldsymbol{A}}){\boldsymbol{x}} + ({\boldsymbol{B}} + \Delta {\boldsymbol{B}}){\boldsymbol{u}} + {\boldsymbol{f}} 。$ | (4) |
式中:x∈Rn为状态变量,u∈Rm为控制变量,ΔA、ΔB是由建模不确定性因素形成的系统摄动矩阵,f为外部干扰项。
若定义
| $ \dot {\boldsymbol{x}} = {\boldsymbol{Ax}} + {\boldsymbol{Bu}} + {\boldsymbol{F}} 。$ | (5) |
滑模控制律可由等效控制律ueq和切换鲁棒控制律usw构成,如下式:
| $ {\boldsymbol{u}} = {{\boldsymbol{u}}_{{{eq}}}} + {{\boldsymbol{u}}_{{{sw}}}}。$ | (6) |
对于滑模切换面s(x)=0,等效控制的作用是确保无干扰时被控系统的状态在滑模面上,切换控制则是为了保证被控系统的状态不会因为干扰而离开滑模面[7]。
在不考虑模型不确定性和外部干扰时,令滑模切换函数的导数
| $ {{\boldsymbol{u}}_{{{eq}}}} = - {({\boldsymbol{GB}})^{ - 1}}{\boldsymbol{GAx}}。$ | (7) |
式中:G为线性滑模面系数矩阵,可通过对被控燃机系统进行极点配置获得[8]。
考虑摄动矩阵的上界
| $ {{\boldsymbol{u}}_{{{sw}}}} = - {({\boldsymbol{GB}})^{ - 1}}\left[ {h(t) \cdot {\rm sgn} (s)} \right] 。$ | (8) |
其中,h(t)为待求的标量控制函数。选择Lyapunov函数为:
| $ V = \frac{1}{2}{s^{\rm{T}}}s + \frac{1}{{2{\beta _{{1}}}}}{\tilde \rho ^2}_{{a}} + \frac{1}{{2{\beta _{{2}}}}}{\tilde \rho ^2}_{{b}} + \frac{1}{{2{\beta _{{3}}}}}{\tilde \rho ^2}_{{f}} 。$ | (9) |
式中:
将s=Gx及式(5)~(8)代入式(9)中并求导,可得:
| $ \begin{split} \dot V =& {{\boldsymbol{s}}^{\rm{T}}}\dot {\boldsymbol{s}} + \frac{1}{{{\beta _1}}}{{\tilde \rho }_a}{{\dot {\tilde \rho} }_a} + \frac{1}{{{\beta _2}}}{{\tilde \rho }_b}{{\dot {\tilde \rho} }_b} + \frac{1}{{{\beta _3}}}{{\tilde \rho }_f}{{\dot {\tilde \rho} }_f} \\ = &{{\boldsymbol{s}}^{\rm{T}}}\left[ { - h(t){{\rm{sgn}}} (s) + {\boldsymbol{G}}\Delta {\boldsymbol{Ax}} + {\boldsymbol{G}}\Delta {\boldsymbol{Bu}} + {\boldsymbol{Gf}}} \right]- \\ & \frac{1}{{{\beta _1}}}{{\tilde \rho }_a}{{\dot {\hat \rho} }_a} - \frac{1}{{{\beta _2}}}{{\tilde \rho }_b}{{\dot {\hat \rho} }_b} - \frac{1}{{{\beta _3}}}{{\tilde \rho }_f}{{\dot {\hat \rho} }_f} \\ \leqslant & - h(t){\left\| s \right\|_1} + {\rho _a}{\left\| s \right\|_1}{\left\| {\boldsymbol{G}} \right\|_1}{\left\| {\boldsymbol{x}} \right\|_1} + {\rho _b}{\left\| s \right\|_1}{\left\| {\boldsymbol{G}} \right\|_1}{\left\| {\boldsymbol{u}} \right\|_1}+ \\ & {\rho _f}{\left\| {\boldsymbol{s}} \right\|_1}{\left\| {\boldsymbol{G}} \right\|_1}{\kern 1pt} - \frac{1}{{{\beta _1}}}{{\tilde \rho }_a}{{\dot {\hat \rho} }_a} - \frac{1}{{{\beta _2}}}{{\tilde \rho }_b}{{\dot {\hat \rho} }_b} - \frac{1}{{{\beta _3}}}{{\tilde \rho }_f}{{\dot {\hat \rho} }_f} 。\end{split} $ | (10) |
令控制函数为:
| $ h(t) = {\hat \rho _a}{\left\| {\boldsymbol{G}} \right\|_1}{\left\| x \right\|_1} + {\hat \rho _b}{\left\| {\boldsymbol{G}} \right\|_1}{\left\| {\boldsymbol{u}} \right\|_1} + {\hat \rho _f}{\left\| {\boldsymbol{G}} \right\|_1} + \eta。$ | (11) |
其中,η为任意小的正常数。
将式(11)代入式(10)中,有
| $ \begin{split} \dot V \leqslant & - \eta {\left\| {\boldsymbol{s}} \right\|_{\text{1}}} + {\tilde \rho _{\text{a}}}{\left\| s \right\|_{\text{1}}}{\left\| {\boldsymbol{G}} \right\|_{\text{1}}}{\left\| {\boldsymbol{x}} \right\|_{\text{1}}} + {\tilde \rho _{\text{b}}}{\left\| {\boldsymbol{s}} \right\|_{\text{1}}}{\left\| {\boldsymbol{G}} \right\|_{\text{1}}}{\left\| u \right\|_{\text{1}}} + \\ & {\tilde \rho _{{f}}}{\left\| {\boldsymbol{s}} \right\|_{\text{1}}}{\left\| {\boldsymbol{G}} \right\|_{\text{1}}} - \frac{1}{{{\beta _{\text{1}}}}}{\tilde \rho _{{a}}}{\dot {\hat \rho} _{{a}}} - \frac{1}{{{\beta _{\text{2}}}}}{\tilde \rho _{{b}}}{\dot {\hat \rho} _{{b}}} - \frac{1}{{{\beta _{\text{3}}}}}{\tilde \rho _{{f}}}{\dot {\hat \rho} _{{f}}}。\end{split} $ | (12) |
为使
| $ {\dot {\hat \rho} _{{a}}} = {\beta _{{a}}}{\left\| {\boldsymbol{s}} \right\|_{\text{1}}}{\left\| {\boldsymbol{G}} \right\|_{\text{1}}}{\left\| {\boldsymbol{x}} \right\|_{\text{1}}} ,$ | (13) |
| $ {\dot{ \hat \rho} _{{b}}} = {\beta _{{b}}}{\left\| {\boldsymbol{s}} \right\|_{\text{1}}}{\left\| {\boldsymbol{G}} \right\|_{\text{1}}}{\left\| {\boldsymbol{u}} \right\|_{\text{1}}} ,$ | (14) |
| $ {\dot {\hat \rho} _{{f}}} = {\beta _{{c}}}{\left\| {\boldsymbol{s}} \right\|_{\text{1}}}{\left\| {\boldsymbol{G}} \right\|_{\text{1}}} 。$ | (15) |
综上所述,可得基于摄动矩阵上界估计和外部干扰上界估计的自适应滑模控制律:
| $ {\boldsymbol{u}} = {{\boldsymbol{u}}_{{{eq}}}}{\text{ + }}{{\boldsymbol{u}}_{{{sw}}}} = - {({\boldsymbol{GB}})^{ - 1}}\left[ {{\boldsymbol{GAx}} + h(t) \cdot {{\rm{sgn}}} (s)} \right]。$ | (16) |
其中,
观察上述基于摄动矩阵上界估计和外部干扰上界估计的自适应滑模控制律以及对应的自适应律,可发现自适应律是对燃机建模不确定性和外部干扰的在线估计。其大小由滑模切换函数s、滑函数系数G以及控制器的状态x,输入u共同确定。在控制器的控制过程中,自适应律随着控制器、被控燃机以及各类不确定因素的动态变化而改变,因而自适应律能够使系统在满足李雅普诺夫意义下稳定性条件的同时实现对不确定项的在线估计,从而提升控制系统的适应性和鲁棒性,也就提高了整个被控系统的稳定性及性能。
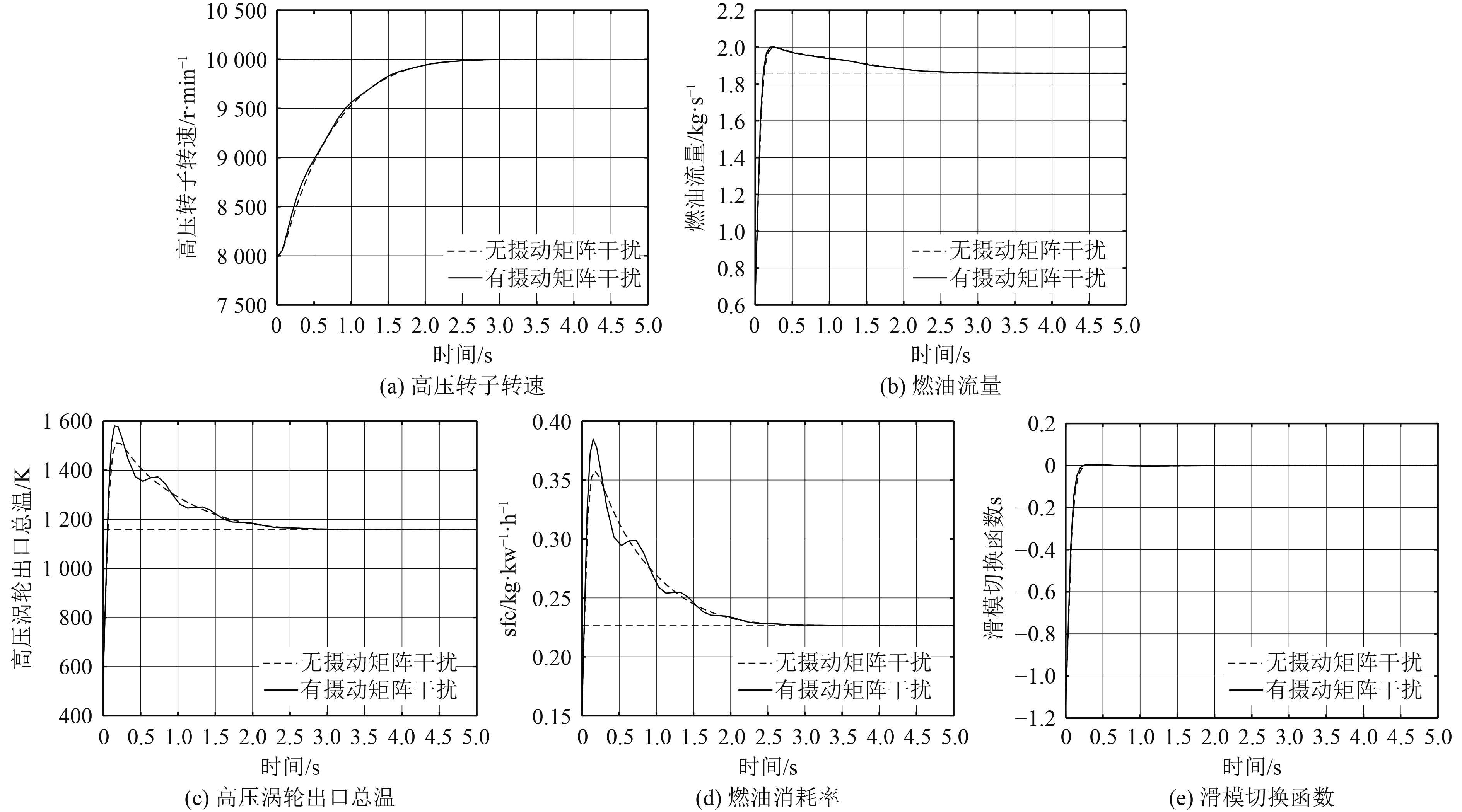
3 仿真分析 3.1 摄动矩阵干扰下的LPV滑模自适应控制仿真研究假设系统摄动矩阵ΔA、ΔB为标称值20%的正弦扰动。当自适应参数βa、βb均为0,即控制器不具备调整控制增益的能力时,仿真结果如图4所示。
|
图 4 摄动矩阵对LPV自适应滑模控制响应的影响 Fig. 4 Influence of perturbation matrix on the response of LPV adaptive sliding mode control |
可以看出,当摄动矩阵为一正弦规律变化的扰动时,其引入使得系统响应曲线在原轨迹的基础上产生了一定的振荡,但摄动矩阵干扰不会使系统状态产生稳态误差,高压转子转速Nhp对目标信号保持了较好的跟踪能力,且响应曲线的波动很小。燃油流量的响应轨线亦是如此。说明基于LPV模型的滑模控制具有较好的转速跟踪能力。高压涡轮出口总温T5产生了较大幅度的超调,总温最高点增加了约100 K,实际温度逼近1600 K。该温度已经接近甚至超过涡轮的耐受极限,因而从保证涡轮及整个燃气轮机安全稳定运行的角度来看,必须对控制系统做出改进以解决动态过程中的涡轮超温问题。另一方面,燃油消耗率sfc也出现了较大超调,其超调会增大燃机在过渡过程中的燃油消耗量,增加燃机运行成本,降低经济性。
无论从保证燃机安全稳定工作还是增强燃机过渡过程的经济性考虑,都有必要抑制摄动矩阵对燃机系统的影响。
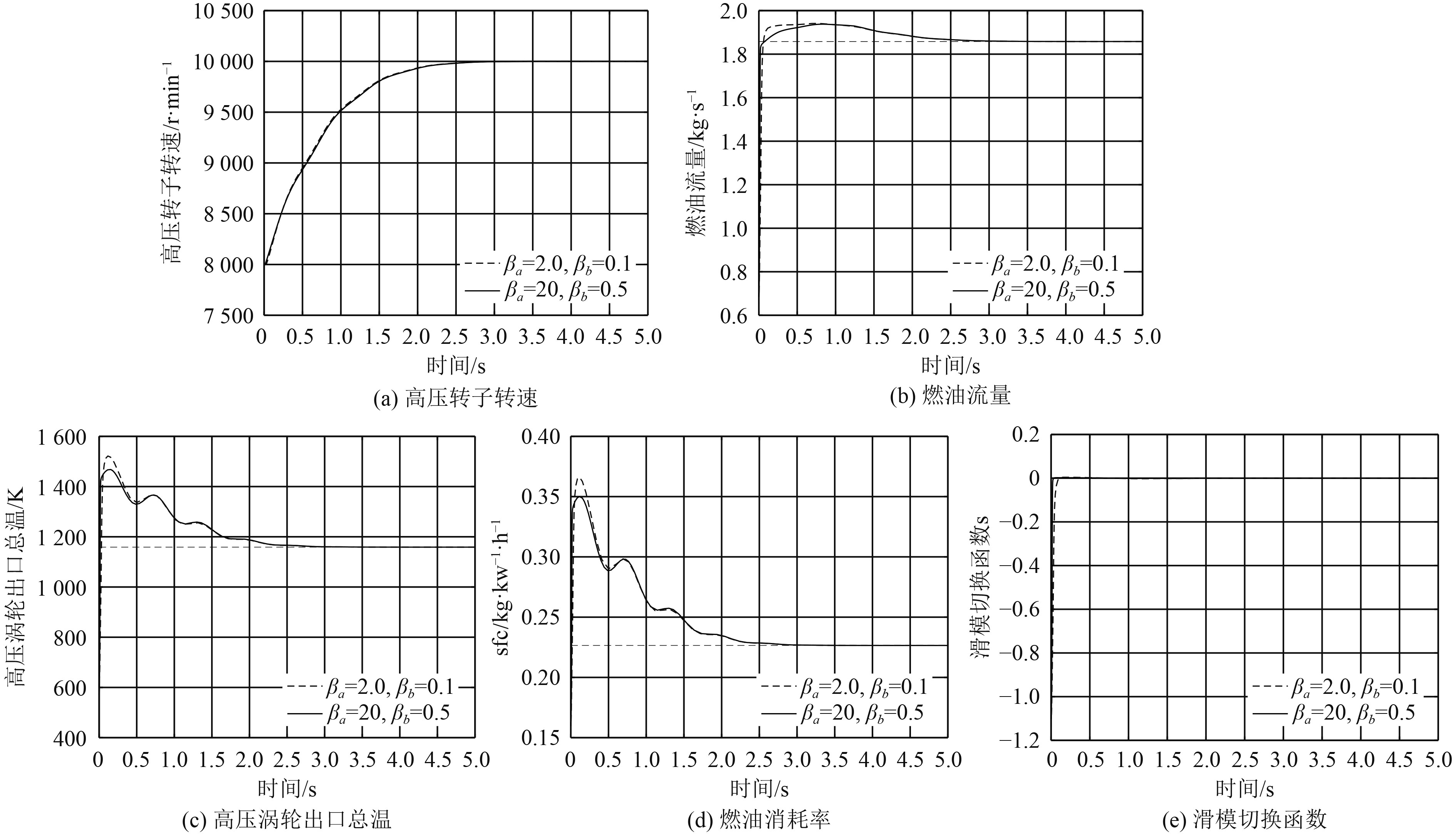
考虑具有摄动矩阵上界估计的自适应滑模控制。将自适应律中进行摄动矩阵ΔA和ΔB上界估计的参数设置为βa=2.0,βb=0.1以及βa=20,βb=0.5,记录仿真过程中摄动矩阵上界的估计值
|
图 5 不同自适应参数对摄动矩阵影响的抑制情况 Fig. 5 Suppression of the influence of different adaptive parameters on the perturbation matrix |
由图5 (c)与图5 (d)可以看出,第2组自适应律参数较好地抑制了高压涡轮出口燃气总温T5和燃油消耗率sfc的超调,且系统响应速度有所加快。
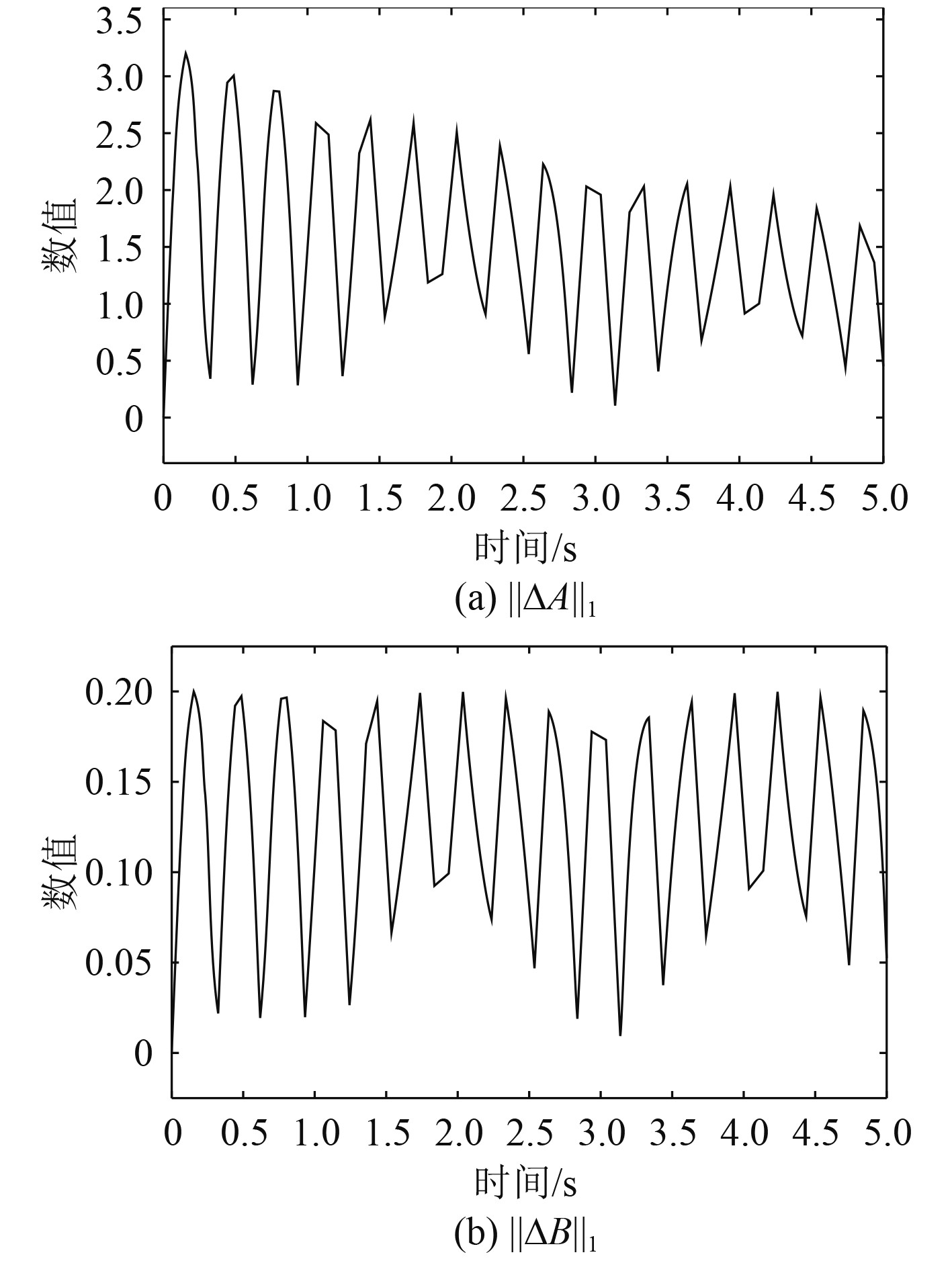
如图6所示,在系统的动态过程中摄动矩阵ΔA和ΔB均有上界,且
|
图 6 摄动矩阵ΔA和ΔB的1-范数变化 Fig. 6 Change of 1-norm of perturbation matrix ΔA, ΔB |
|
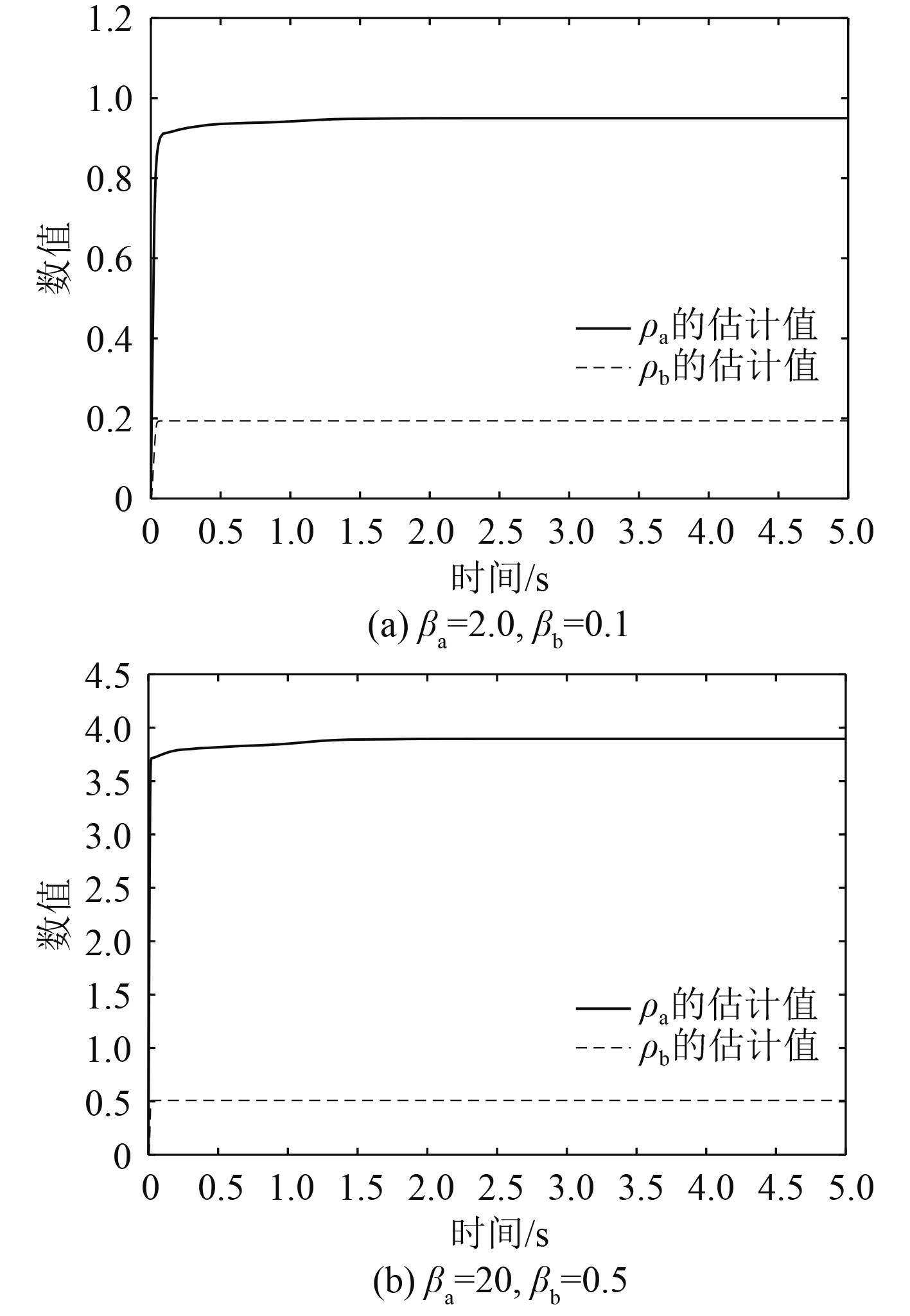
图 7
2组自适应参数下摄动矩阵ΔA、ΔB上界估计值 |
基于上述分析,可认为:自适应滑模控制对于摄动矩阵干扰的抑制作用取决于自适应参数的选择,若自适应参数能使摄动矩阵上界的估计值大于摄动矩阵的实际上界,则可有效抑制干扰,反之则不能。
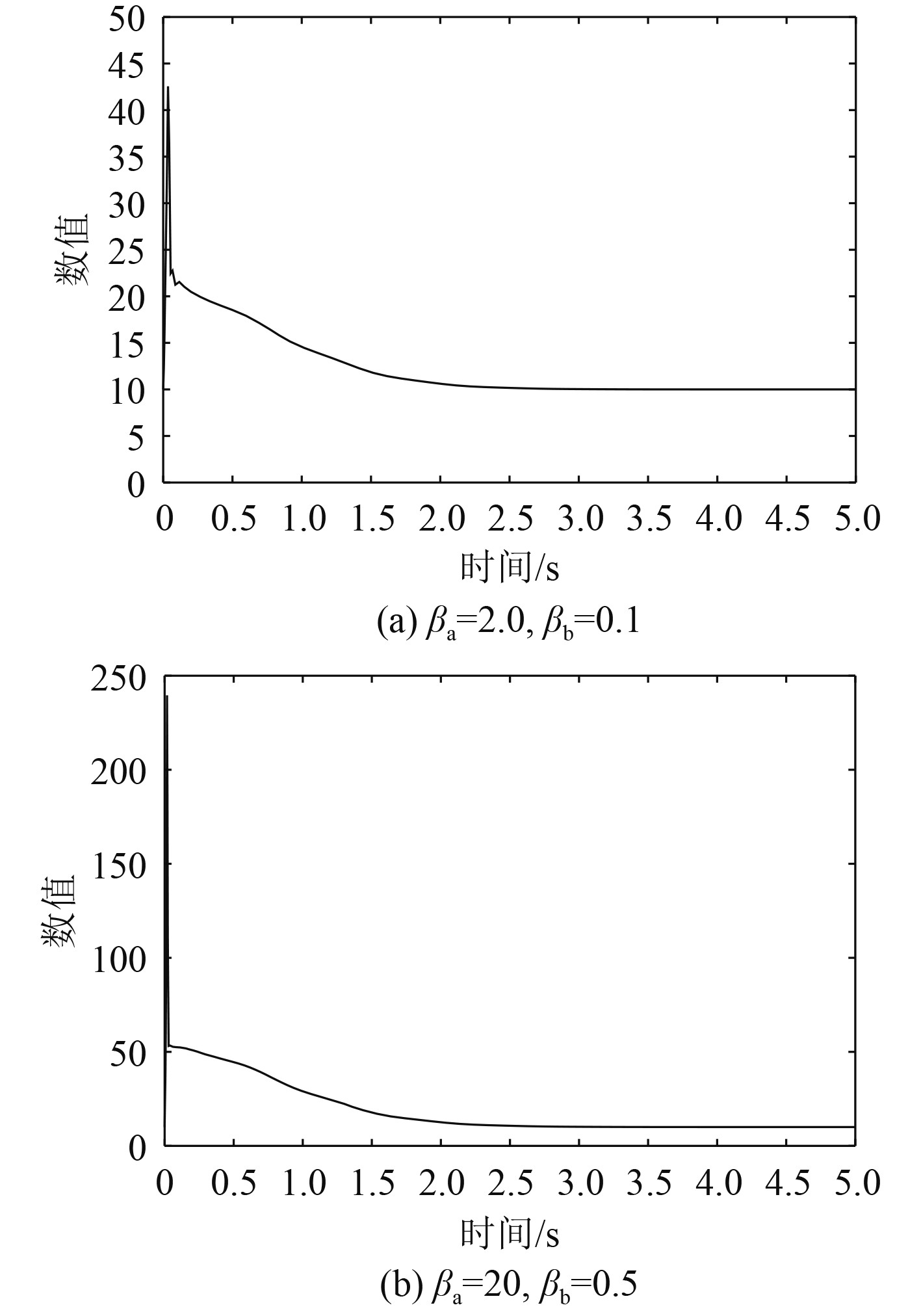
图8给出了动态过程中控制增益h(t)的变化曲线,2组自适应参数配置下的终态控制增益均为10,但配置2的初期控制增益明显高于配置1,说明自适应律在动态过程的初期对系统的响应及调节能力更强,因而出现了图8中配置2响应速度更快的现象。
|
图 8 2组不同自适应参数下LPV滑模控制器的控制增益变化 Fig. 8 Control gain variation of LPV sliding mode controller under two different sets of adaptive parameters |
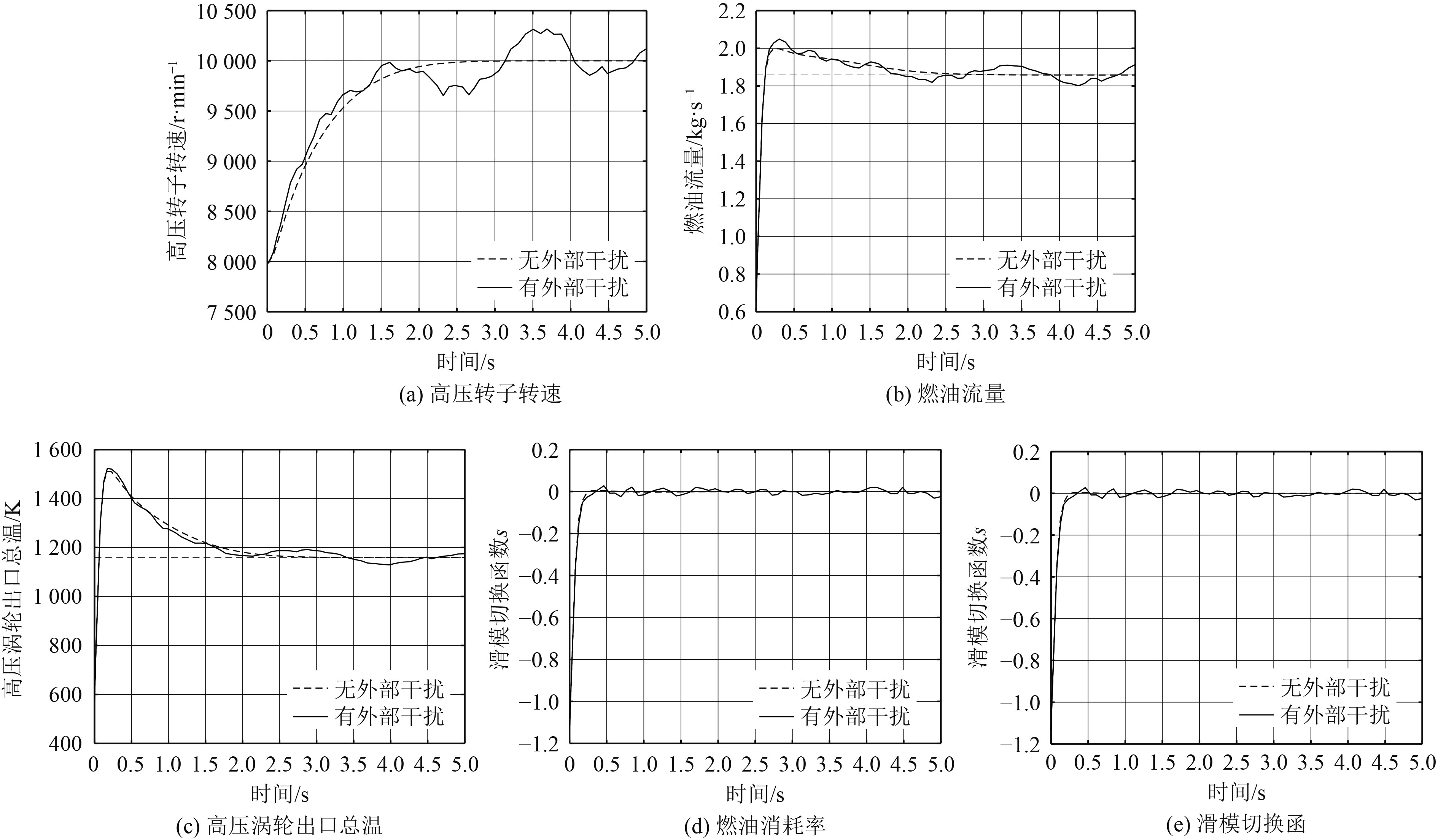
假设系统受到的外部干扰为高斯白噪声类型,即随机干扰。扰动信号均值u=0,方差s2= 0.02,当式(13)~(15)中的自适应参数βa、βb、βf均为0,即控制器不具备调整控制增益的能力时,仿真结果如图9所示。
|
图 9 外部干扰对LPV自适应滑模控制响应的影响 Fig. 9 Influence of external disturbance on the response of LPV adaptive sliding mode control |
图9说明高斯白噪声型的外部干扰会对三轴燃气轮机LPV模型的动态响应曲线造成无规则、大幅度的扰动。由图9 (e)可以看出,当系统状态到达滑模切换面s(x)=0后,由于干扰信号f的幅值较大,常规的滑模控制无法完全抑制状态量的波动,导致系统状态未能沿着滑模切换面运动,而是在滑模切换面附近上下振动。系统的控制量Wf及状态量Nhp均可能产生较大的超调量。
考虑具有外部干扰上界估计的自适应滑模控制。将自适应律中进行干扰估计的参数设置为βa=20,βb=0.5,βf=5,并记录仿真过程中,外部干扰上界的估计值

|
图 10 自适应滑模控制对外部干扰影响的抑制情况 Fig. 10 Suppression of the influence of adaptive sliding mode control on the external disturbance |
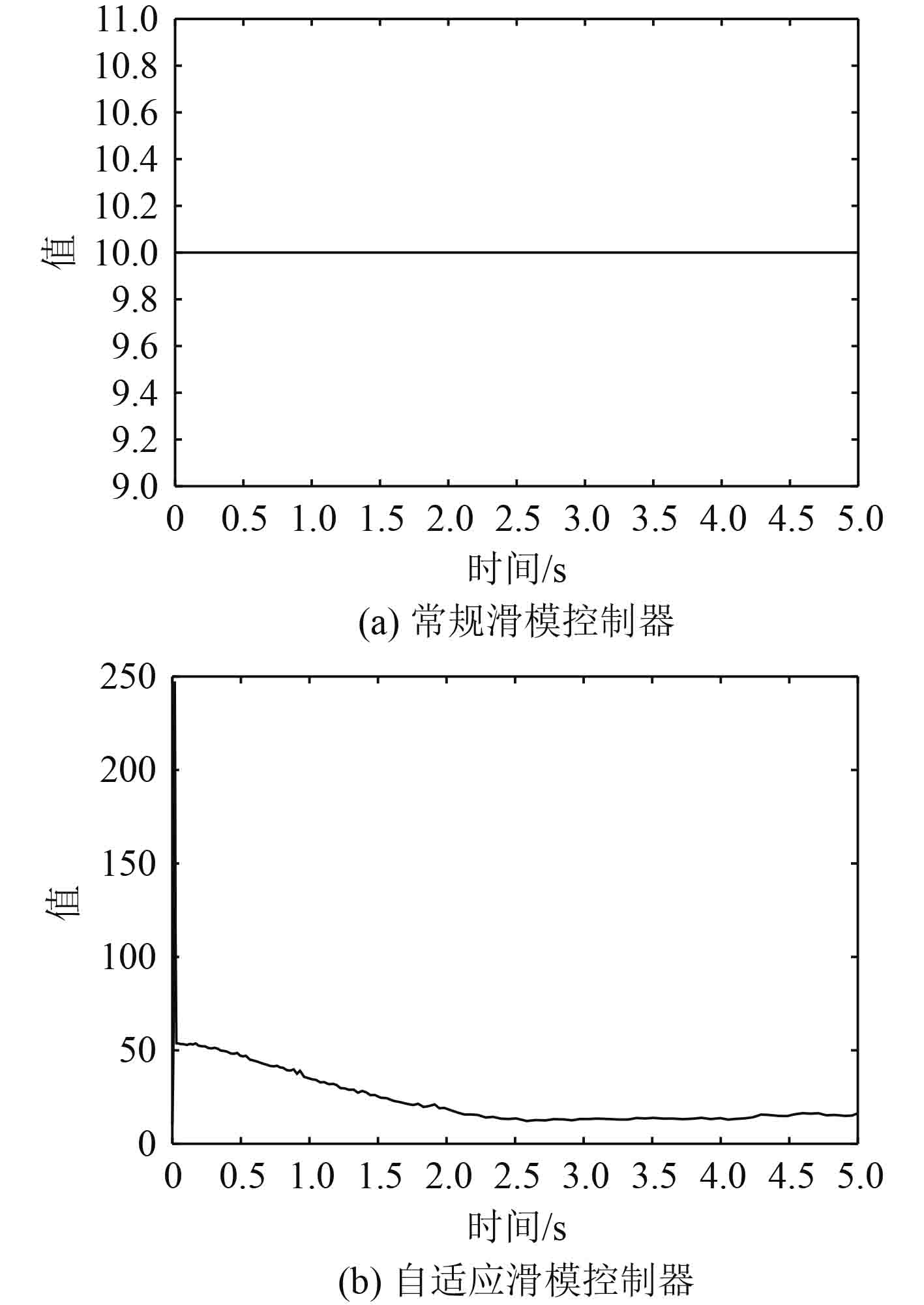
图10表明,自适应滑模控制对于外部的无规则扰动并无显著的抑制能力,但能有效降低动态过程中燃油流量Wf、高压涡轮出口总温T5及燃油消耗率sfc的最大超调量。由于自适应滑模控制相对于常规滑模控制特有的可变控制增益,因而系统的响应速度有所加快,如图11所示。
|
图 11 2种不同LPV滑模控制器的控制增益变化 Fig. 11 Control gain variation of two different LPV sliding mode controller |
本文从三轴燃气轮机大工况范围的建模和控制需求出发,建立了三轴燃气轮机LPV模型,并在此基础上设计了基于摄动矩阵上界估计和外部干扰上界估计的自适应滑模控制器。通过仿真试验和分析得出如下结论:
1)LPV模型能在较大工况范围内与实际燃机保持较高的相似程度,以LPV模型为基础的滑模控制器能够实现对系统更加精准的控制。
2)基于LPV模型的自适应滑模控制由于具备对摄动矩阵上界和外部干扰上界的估计能力,因而能够对上述不确定因素实现不同程度的抑制。此外,由于自适应滑模控制的时变控制增益,因而其具有加快系统响应速度的能力。
摄动矩阵干扰不会使系统状态产生稳态误差,当自适应律中的摄动矩阵上界估计参数使得上界估计值大于摄动矩阵的实际上界时,自适应滑模控制能较好地抑制摄动矩阵对高压涡轮出口总温和燃油消耗率的超调。
外部干扰的存在使得系统状态产生稳态误差,自适应滑模控制无法消除这一稳态误差,但具有一定的抑制能力,且自适应滑模控制能降低扰动造成的高压涡轮出口总温、燃油质量流量和燃油消耗率的最大超调量。
| [1] |
YANG S, WANG X, ASME. LPV based sliding mode control for limit protection of aircraft engines [M]. 2018.
|
| [2] |
BONFIGLIO A, CACCIACARNE S, INVERNIZZI M, et al. A sliding mode control approach for gas turbine power generators [J]. IEEE Transactions on Energy Conversion, 2018: 921−932.
|
| [3] |
孙晖. 航空发动机的多变量滑模控制方法研究 [D]. 北京: 清华大学, 2015.
|
| [4] |
樊思齐. 航空发动机控制(下册) [M]. 西安: 西北工业大学出版社, 2008.
|
| [5] |
孙昊博, 潘慕绚, 黄金泉. 基于双层LPV模型的涡扇发动机切换控制[J]. 推进技术, 2018, 39(12): 2828-2838. SUN H B, PAN M X, HUANG j Q. Switching control of turbofan engine based on double-layer LPV model[J]. Journal of Propulsion Technology, 2018, 39(12): 2828-2838. DOI:10.13675/j.cnki.tjjs.2018.12.023 |
| [6] |
ZHU P, ZHU. Simulation of an advanced twin-spool industrial gas turbine. (includes related article)[J]. Journal of Engineering for Gas Turbines and Power, 1992, 114(2): 180-186. DOI:10.1115/1.2906568 |
| [7] |
刘金琨. 滑模变结构控制Matlab仿真 [M]. 北京: 清华大学出版社, 2015.
|
| [8] |
肖玲斐. 航空动力系统滑模控制 [M]. 杭州: 浙江大学出版社, 2018.
|
| [9] |
肖红亮, 李华聪, 李嘉, 等. 变循环发动机模型参考自适应滑模控制方法研究[J]. 西北工业大学学报, 2018, 36(5): 824-830. XIAO H L, LI H C, LI J, et al. Research on variable cycle engine control based on model reference adaptive sliding mode control method[J]. Journal of Northwestern Polytechnical University, 2018, 36(5): 824-830. DOI:10.3969/j.issn.1000-2758.2018.05.003 |
 2024, Vol. 46
2024, Vol. 46
