2. 江苏科技大学 海洋学院,江苏 镇江 212100
2. Ocean College, Jiangsu University of Science and Technology, Zhenjiang 212100, China
随着船舶向大型化、智能化的不断发展,船舶动力系统结构更加复杂,对其故障诊断、识别和预测提出了更高要求[1]。在设备故障预测过程中,需要对反映设备运行状态的信息进行提取和分析,但由于船舶动力设备自身结构的复杂性,使得获取的有用信息很有限。此外,一般船舶动力设备使用寿命较长,而较短的工作时间内反映其工作状态信息的数据变化较为微弱以及短时间内的数据变化不明显,使得能够获取的有效状态信息有限[2],如果早期潜在的故障没有得到及时预测和准确识别,设备功能将持续退化直至发生故障。因此,如何通过历史数据和实时状态数据预测设备的潜在故障,提高其预测效率、故障识别准确率成为了关键。
近些年来故障预测在船舶领域的应用广受关注,包括数据驱动、物理模型、BP神经网络、支持向量机等方法。杨奕飞等[2]提出一种基于HMM-SVR的船舶动力设备故障模式识别与状态预测的方法;Yang等[3]提出一种基于改进的CS-LSSVM算法,用于船舶动力设备故障模式识别;王文波等[4]提出一种基于深度学习与增量更新的故障预测方法;CHOI等[5]提出一种结合RNN和LSTM的剩余使用寿命预测算法;石彪等[6]提出一种利用灰狼优化算法(GWO)对LSTM优化的船舶主机性能的预测;于飞等[7]提出一种基于蝗虫优化Bi-LSTM网络的电机轴承故障预测方法。顾吉峰等[8]提出一种基于改进粒子群算法的孪生支持向量机的方法。上述方法中,对船舶发动机故障预测的研究主要面向柴油发动机,而针对LNG双燃料发动机的研究很少,故障预测的实时性、效率和准确度均需进一步提升。此外,在采用SVM的识别算法时,如果根据人为经验确定SVM参数,将影响故障识别的有效性和准确性。因此,对SVM的参数进行优化非常关键,PSO优化算法在参数优化上被认为是调整少、速度快的函数优化器[9]。PSO虽然能够提高SVM的故障识别精度,减少函数的迭代次数,但传统的PSO算法在进化后期所有粒子进化会停留不前,速度快速下降并且易于早熟收敛。
针对上述问题,本文提出一种基于长短期记忆网络(Long Short-Term Memory,LSTM)模型、改进的粒子群优化算法(Particle Swarm Optimization,PSO)优化支持向量机(Support Vector Machine,SVM)模型融合的方法,用于LNG双燃料发动机故障预测。利用LSTM时间序列变化的能力预测未来的运行状态,提高其预测的准确性和实时性;利用改进PSO优化SVM模型参数,保障其寻优能力强,收敛速度快,避免陷入局部最优;利用改进PSO优化后的SVM模型对LSTM预测数据进行故障识别,从而实现对LNG双燃料发动机的故障预测,该方法可为船舶LNG双燃料发动机实现视情维修提供重要的技术支撑。
1 LSTM故障预测模型的建立 1.1 LSTM模型长短期记忆网络(LSTM)是一种具有选择记忆功能的特殊神经网路模型,有利于读取信号序列的非线性特征,解决长序列数据的长期依赖问题,并且在梯度消失和梯度爆炸上有很好的拟合能力[10]。LSTM主要包括、输入门、输出门和忘记门,通过引入“门”控制,用来调节和保护网络的状态[11]。t时刻单元状态更新由下式完成:
| $ {f_t} = \sigma ({w_f}[{h_{t - 1}},{X_t}] + {b_f}),$ | (1) |
| $ {i_t} = \sigma ({w_i}[{h_{t - 1}},{X_t}] + {b_i}) ,$ | (2) |
| $ {C_t} = {f_t} \odot {C_{t - 1}} + {i_t} \odot C_t^* ,$ | (3) |
| $ {O_{\text{t}}} = \sigma ({w_o}[{h_{t - 1}},{X_t}] + {b_o}),$ | (4) |
| $ {h_t} = {O_t} \odot \tan h ({C_t})。$ | (5) |
式中:
以某船用大型LNG/柴油双燃料发动机为例,具体针对与柴油发动机不同的气体系统开展故障预测研究。双燃料发动机气体系统的运行状态数据变化包含着丰富的信息。气体系统的运行状态主要受活塞底面气体浓度、供气压力、发动机怠速、燃料的转换、进气流量和电磁阀损坏等因素的影响,常见的潜在故障因素如活塞下侧气体浓度过低/高、气体过滤器堵塞、节气门污染严重、高频电磁阀未关闭、减压器上电磁阀接触不良、储气系统无LNG和手动截止阀损坏等。实验数据主要采集上述影响双燃料发动机气体系统运行状态的关键参数。基于LSTM的故障预测步骤如下:
步骤1 模型构建
对状态监测数据进行主成分分析,得出各因素的特征权重,进一步得到特征向量序列[12]。由相关参数特征分析可知双燃料发动机功率、活塞底面气体浓度、供气压力、发动机怠速、燃料的转换、进气流量和电磁阀损坏7个特征参数权重较大,故选取以上7个特征参数作为预测模型的输入参数。特征权重序列如表1所示。
|
|
表 1 相关因素特征权重重要性排序 Tab.1 Ranking of the weight of relevant factors |
该双燃料发动机的排气系统包含7种特征参数,每个特征参数对应有m条数据,则模型的输入矩阵
| $ {{\boldsymbol{X}}_{\text{t}}} = \left( {\begin{array}{*{20}{c}} {a_{t1}^1}& \ldots &{a_{tm}^1} \\ \vdots & \ddots & \vdots \\ {a_{(t + n - 1)1}^7}& \cdots &{a_{(t + n - 1)m}^7} \end{array}} \right) 。$ | (6) |
式中,n为时间窗口的大小
步骤2 数据处理
为了避免状态特征参数中的随机因素对LSTM模型的预测准确度产生影响,需对数据进行预处理。本文利用滑动平均窗口的方法进行预处理,可以消除随机因素对预测结果变化的影响[13]。选取时间窗口n=24,步长为1。
步骤3 模型训练
通过发动机监控系统中的DCE单元收集LNG/柴油双燃料发动机的45 d历史运行数据,数据采集间隔为15 min,利用步骤2获得一个时间序列集,其中前80%作为训练集数据,后20%作为测试集数据。隐藏层设为2,训练次数设为200。选择均方根误差(RMSE)、平均绝对百分比误差(MAPE)、决定系数R2和损失函数值(LOSS)作为模型训练的指标。RMSE值越低,说明模型的稳定性越好;MAPE越趋于0,说明模型的准确性越好;R2取值在0~1范围内,值越大,模型的拟合效果越好。
1) 记忆单元数目选择
如表2所示,记忆单元数分别为50、80、150所对应的RMSE、LOSS、MAPE和R2 指标值。可以看出,随着记忆单元数目的增加,各项指标变化并不明显,但模型的训练时间会有所增加,综合考虑,本文模型中的记忆单元数目设为50。
|
|
表 2 不同记忆单元数目对应评价指标 Tab.2 The number of different memory units corresponds to the evaluation index |
2) 隐藏层的选择
隐藏层设为2,用来进行模型的训练,通过评估不同隐藏层对该模型的影响,可以进一步确定隐藏层的最佳层数。记忆单元数目设为50,分别对不同层隐藏层进行模型训练,结果如表3所示,当隐藏层为1时,RMSE、MAPE值最小,R2值最大,可见其准确度最高,模型拟合效果好,而且训练时间也最短。
|
|
表 3 不同隐藏层数目对应评价指标 Tab.3 The number of different hidden layers corresponds to the evaluation index |
步骤4 仿真结果
将上述数据中1~44 d的数据作为样本输入,2~45 d的数据作为模型输出的真实值,对LSTM模型的有效性进行验证。图1为真实值和预测值的拟合效果图,均方根误差RMSE为0.78396,均方误差MSE为0.6146,决定系数R2为0.99847;相对误差如图2为0.0253。可见LSTM模型拟合效果好,适应度佳,预测误差小,预测精度高,说明该参数设置下的模型预测性能好。
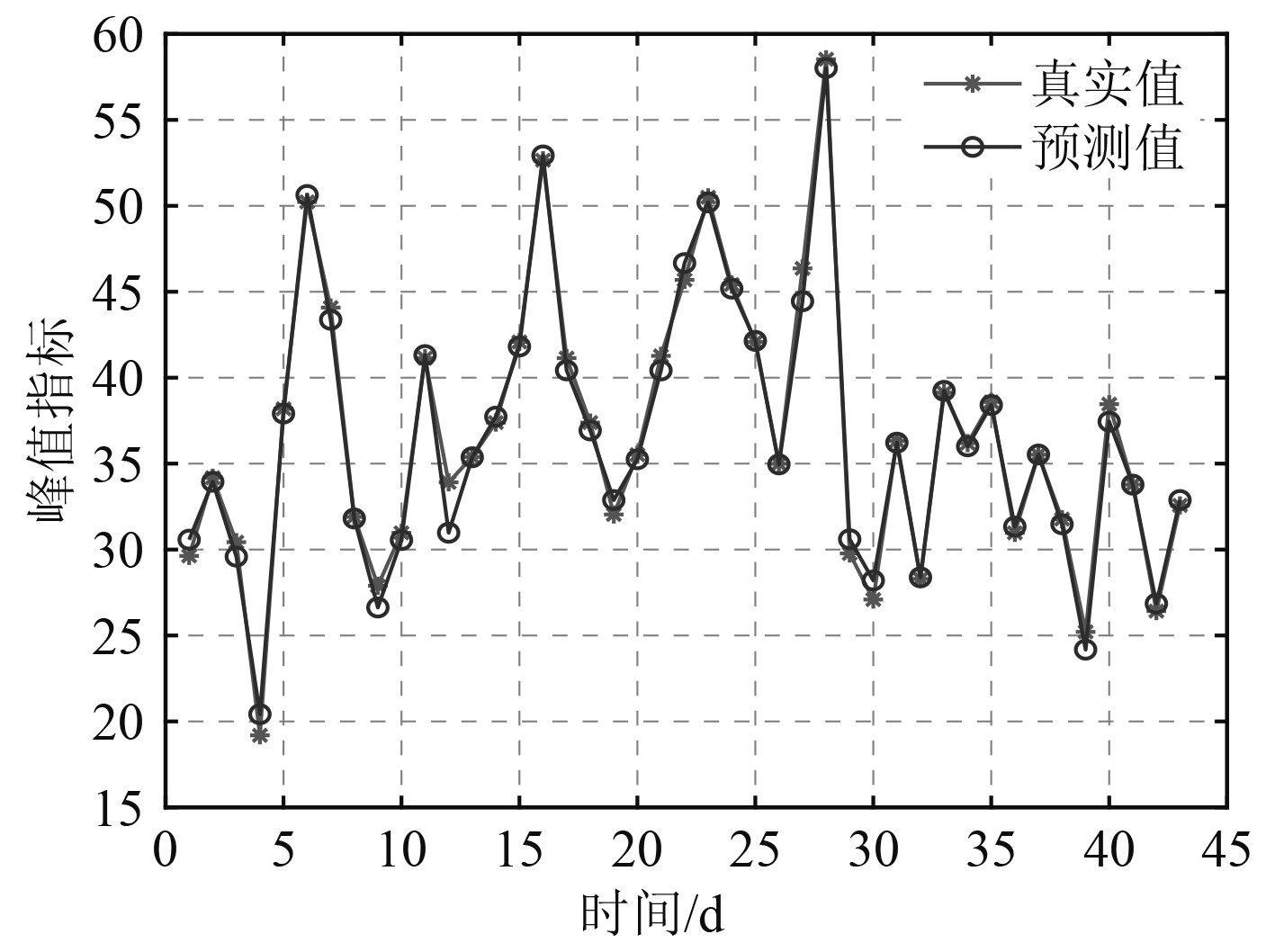
|
图 1 LSTM预测效果图 Fig. 1 Effect of LSTM prediction |

|
图 2 LSTM预测相对误差图 Fig. 2 LSTM prediction relative error chart |
利用LSTM可以对设备关键状态参数进行预测,但却不能对设备是否故障进行识别,而支持向量机(SVM)在解决小样本和多分类的问题中具有优异的性能[14]。SVM与LSTM模型相结合,可实现故障的预测和识别,精确识别设备的潜在故障。
2.1 发动机故障识别SVM模型将影响发动机气体系统7个关键参数作为SVM模型的输入,每一个参量作为一个输入量
约束SVM的式为:
| $ {y}_{i}=(w\cdot{X}_{i}+b)\geqslant 1-{\zeta }_{\text{i}},\text{i}=1,2\cdots l 。$ | (7) |
式中:
利用径向基函数对内核函数K进行数据空间映射为:
| $ K(X,{X}_{i})=(\phi (X)·\phi ({X}_{i}))={e}^{-\gamma |X-{X}_{i}{|}^{2}} 。$ | (8) |
式中,
船舶发动机气体系统的某一时刻运行状态
| $ \begin{gathered} [({X_1},{Y_1}),({X_2},{Y_2}) \cdots ({X_i},{Y_i})] = \\ [(\varphi ({X_1}),{Y_1}),(\varphi ({X_2}),{Y_2}) \cdots (\varphi ({X_i}),{Y_i})] ,\\ \end{gathered} $ | (9) |
由
| $ \mathop {\min }\limits_{w \in H,b \in R,\zeta \in R} \frac{1}{2}||w|{|^2}c\sum\limits_{i = 1}^l {{\zeta _i}} ,$ | (10) |
| $ {Y}_{i}=[(w\cdot{X}_{i})+b]\geqslant 1-{\zeta }_{i}。$ | (11) |
式中:
确定超平面
则对于每一个关键参数的输入量,SVM预测判别输出的结果为:
| $ Y = {{\mathrm{sign}}} \left(\sum\limits_{i = 1}^{{N_s}} {{Y_i}{\alpha _i}K({X_N},X) + b} \right) 。$ | (12) |
式中:N为支持向量
为保证SVM模型的识别准确度,需对其核函数参数进行寻优。PSO优化算法在参数优化上被认为是调整少、速度快的函数优化器。PSO能够提高SVM的故障识别的精度,减少函数的迭代次数,但传统的PSO算法在进化后期所有粒子进化会停留不前,速度快速下降,并且在寻优过程中易于早熟收敛,需对其进行改进。
2.2.1 改进PSO算法在LNG双燃料发动机故障识别中,对识别模型的精度要求高,不仅数据量庞大,而且故障类型复杂多样且呈非线性。PSO算法的搜索性能直接影响到识别模型的识别速度、精度。传统的PSO算法中一般将惯性权重设置为一固定值,或者是线性递减、指数递减、余弦递减的惯性权重,其收敛速度慢,而且极易产生早熟的现象[15]。为了提高PSO算法在识别模型关键参数寻优的速度和精度,引入非线性的自适应惯性权重对传统PSO进行改进,如下式:
| $ w = {w}_{\mathrm{max}} - ({w}_{\mathrm{max}} - {w}_{\mathrm{min}})\frac{1}{1+\mathrm{exp}[-10b(\frac{2t}{k(t)\cdot{T}_{\mathrm{max}}}-1)]}。$ | (13) |
式中:
为获得最佳的SVM模型参数,采用上述改进的PSO算法对SVM模型核函数参数和惩罚系数进行寻优,改进PSO算法优化SVM参数的流程如图3所示。
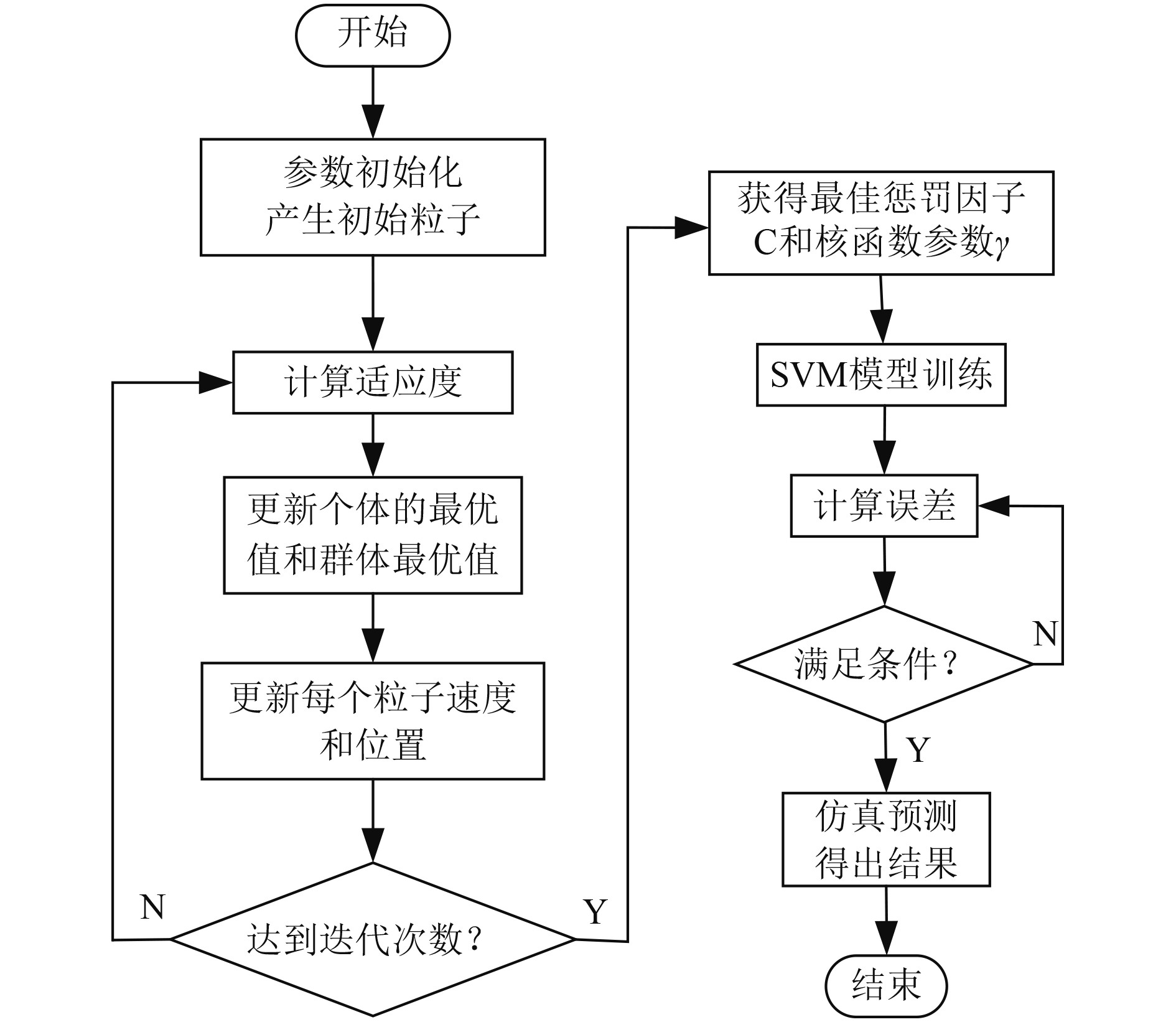
|
图 3 改进PSO优化SVM模型流程图 Fig. 3 Flow chart of SVM model optimization with improved PSO |
仿真实验对LNG/柴油双燃料发动机进气系统的8种典型状态进行预测识别,正常状态编码为1,7种典型故障编码为2~8,分别为活塞下侧气体浓度过低、气体过滤器堵塞、节气门污染严重、高频电磁阀未关闭、减压器上电磁阀接触不良、储气系统无LNG和手动截止阀损坏。在收集到的数据中选取200个故障数据,其中105个数据作为训练样本,95个数据作为测试样本。采用PSO-SVM模型的故障识别结果如图4所示。可以看出,不管是训练样本还是测试样本,效果都不理想,识别准确率分别为82.32%和84.56%。

|
图 4 PSO-SVM故障识别效果 Fig. 4 Effect of SPSO-VM fault identification |
改进PSO-SVM方法的故障识别结果如图5所示,对训练样本和测试样本的识别准确度均达到98%以上,此时SVM模型的核函数参数

|
图 5 改进PSO-SVM故障识别效果 Fig. 5 Effect of improved PSO-SVM fault recognition |
分别用传统PSO算法和改进PSO算法对SVM模型的核函数参数
|
|
表 4 PSO-SVM和改进PSO-SVM对应识别率 Tab.4 Corresponding recognition rate of PSO-SVM and improved PSO-SVM |
将本文的改进PSO-SVM模型与其他文献中提出的故障识别模型进行比较,通过仿真得到识别准确率如表5所示。可以看出,本文提出的改进PSO-SVM模型比RBM-SVM和CNN模型的故障识别准确率高,说明了改进PSO-SVM模型的可行性。
|
|
表 5 模型识别准确率对比 Tab.5 Comparison of model recognition accuracy |
将LSTM与上述改进的PSO-SVM模型融合,得到改进LSTM-PSO-SVM的故障预测模型,主要步骤如下:
步骤1 采集设备某一时间段内的实时数据,将处理过的数据利用1.2节训练好的LSTM模型进行预测,获得一个预测序列
步骤2 利用2.2节改进的PSO-SVM模型对当前设备运行状态进行判别,为
步骤3 利用改进的PSO-SVM模型对(1)获得的预测序列进行状态的判别,为
步骤4 将步骤3中得到的预测状态与当前状态作比较,得到预测结果,用偏离度表示预测状态与正常状态之间的偏差程度来反映设备的健康水平,偏离度计算公式为:
| $ {P}_{预测}=\left|\frac{{Y}_{预测}\left\{O\right|X\}-{Y}_{正常}(X)}{{Y}_{预测}\left\{O\right|X\}}\right| 。$ | (14) |
将偏离度阈值
按照上述步骤,利用基于改进LSTM-PSO-SVM模型对4台双燃料发动机未来一段时间内的运行状态进行预测仿真,结果如图6所示。可以看出,4台发动机在故障发生前偏离度均有明显上升趋势。
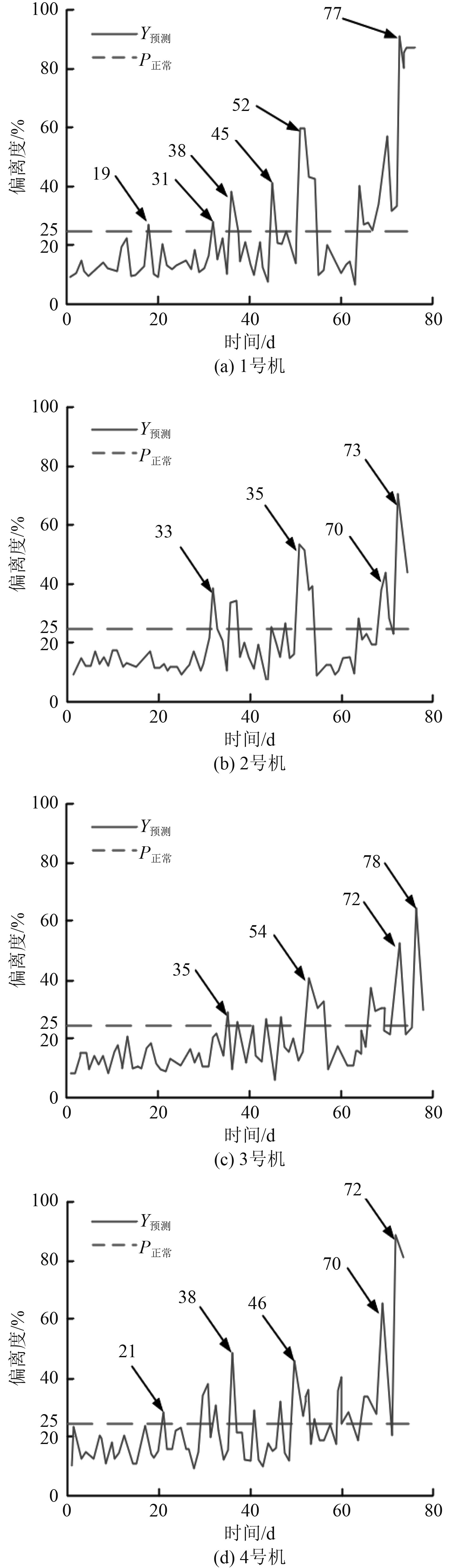
|
图 6 LSTM-PSO-SVM故障预测 Fig. 6 LSTM-PSO-SVM fault prediction |
1号机在第19天第一次略超出偏离度阈值,随后设备恢复到正常值范围,表明设备出现故障的概率不高;随后1号机在第31天、第38天和第45天频繁超出阈值范围,偏离度达到40%,起到故障预警的作用,虽然还能继续工作,但要时刻注意设备的状态;在第52天设备的状态预测值与正常值偏离度到达60%,说明设备处于持续的状态退化状态,需要进行维护检修;在第77天,偏离度超过了85%,表明设备处于故障状态,不能继续工作,需立即维修。2号机在除了第73天偏离度超出60%,其余均在50%以下。3号机在第35天略微超出阈值,随后第54天、第72天处于故障预警状态,在第78天上升为恶化状态,在第78天前需要进行维护检修。4号机在第38天、第46天处于故障预警,随后在第70天偏离度达60%,需要提前进行维护。可以看出,本文提出的融合LSTM和改进PSO优化SVM的模型对设备短时间的异常信号较敏感,能够准确地对双燃料发动机的故障进行预测,可以达到故障预警的效果。
4 结 语本文将LSTM与改进PSO优化SVM模型进行融合,对LNG/柴油双燃料发动机的潜在故障进行预测研究。通过LSTM对双燃料发动机的实时数据进行预测,进一步通过改进的PSO算法对SVM模型参数进行优化,提高了模型的故障预测精度。通过对船用双燃料发动机进行实例分析和仿真研究,验证了LSTM-PSO-SVM模型的有效性,可为船舶发动机实现视情维修提供参考。
| [1] |
雷伟, 甘少炜, 周国强. 船用双燃料发动机关键技术分析[J]. 船海工程, 2016, 45(3): 86-89+98. LEI W, GAN S W, ZHOU G Q. Analysis of key technologies of marine dual-fuel engine[J]. Ship and Sea Engineering, 2016, 45(3): 86-89+98. DOI:10.3963/j.issn.1671-7953.2016.03.021 |
| [2] |
杨奕飞, 冯静. 基于HMM-SVR的船舶动力设备故障模式识别与状态预测研究[J]. 船舶工程, 2018, 40(3): 68-72+97. YANG Y F, FENG J. Study on fault pattern recognition and state prediction of marine power equipment based on HMM-SVR[J]. Marine Engineering, 2018, 40(3): 68-72+97. DOI:10.13788/j.cnki.cbgc.2018.03.068 |
| [3] |
YANG Y, TAN M, DAI Y. An improved CS-LSSVM algorithm-based fault pattern recognition of ship power equipments[J]. Plos One, 2017, 12(2): e0171246. DOI:10.1371/journal.pone.0171246 |
| [4] |
王文波, 彭伟, 顾寄南, 等. 基于深度学习与增量更新的滚动轴承故障预测方法研究[J]. 江苏科技大学学报(自然科学版), 2022, 36(5): 54-59. WANG W B, PENG W, GU J N, et al. Research on rolling bearing fault prediction method based on deep learning and incremental updating[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2022, 36(5): 54-59. |
| [5] |
CHUI KT, GUPTA BB, VASANT P. A genetic algorithm optimized RNN-LSTM model for remaining useful life prediction of turbofan engine[J]. Electronics, 2021, 10(3): 285. DOI:10.3390/electronics10030285 |
| [6] |
石彪, 王海燕, 焦品博. 基于改进GWO-LSTM的船舶主机性能预测模型[J]. 上海海事大学学报, 2022, lancet(2): 96-102. SHI B, WANG H Y, JIAO P B. Based on improved GWO comes-LSTM ship host performance prediction model[J]. Journal of Shanghai maritime university, 2022, lancet(2): 96-102. |
| [7] |
于飞, 樊清川, 宣敏. 基于蝗虫优化Bi-LSTM网络的电机轴承故障预测[J]. 电机与控制学报, 2022, 26(6): 9-17. YU F, FAN Q C, XUAN M. Based on locust optimization Bi-LSTM network of motor bearing fault prediction[J]. Journal of motor and control, 2022, 26(6): 9-17. |
| [8] |
顾吉峰, 王蓓. 基于改进粒子群算法的孪生支持向量机[J]. 计算机工程与设计, 2020, 9(11): 3078-3082. GU J F WANG B. Based on improved particle swarm optimization twin support vector machine[J]. Computer engineering and design, 2020, 9(11): 3078-3082. DOI:10.16208/j.issn1000-7024.2020.11.012 |
| [9] |
WANG Y, WANG D, TANG Y. Clustered hybrid wind power prediction model based on ARMA, PSO-SVM, and clustering methods[J]. IEEE Access, 2020, 8: 17071-17079. DOI:10.1109/ACCESS.2020.2968390 |
| [10] |
PENG W, WANG J, YING S. Short-term load forecasting model based on attention-LSTM in electricity market[J]. Power System Technology, 2019, 43(5): 1745-1751. |
| [11] |
LIU J, PAN C, LEI F, et al. Fault prediction of bearings based on LSTM and statistical process analysis[J]. Reliability Engineering & System Safety, 2021, 214: 107646. |
| [12] |
李元, 张昊展, 唐晓初. 基于多模态数据全信息的概率主成分分析故障检测研究[J]. 仪器仪表学报, 2021, 42(2): 75−85. LI Y, ZHANG H Z, TANG X C. Modal data based on probabilistic principal component analysis of comprehensive information fault detection study [J]. Journal of Instruments and Meters, 2021 (2): 75−85. |
| [13] |
王超, 李大中. 基于LSTM网络的风机齿轮箱轴承故障预警[J]. 电力科学与工程, 2020, 36(9): 40-45. WANG C, LI D Z. Fault warning of fan gearbox bearing based on LSTM network[J]. Electric Power Science and Engineering, 2020, 36(9): 40-45. DOI:10.3969/j.ISSN.1672-0792.2020.09.006 |
| [14] |
YANG Y, ZHANG M, DAI Y. A fuzzy comprehensive CS-SVR model-based health status evaluation of radar[J]. Plos one, 2019, 14(3): e0213833. DOI:10.1371/journal.pone.0213833 |
| [15] |
高金武, 贾志桓, 王向阳, 等. 基于PSO-LSTM的PEMFC退化趋势预测[J/OL]. 吉林大学学报(工学版), 1-10[2022-12-01]. GAO J W, JIA Z H, WANG X Y, et al. Based on PSO-LSTM PEMFC degradation trend prediction [J/OL]. Journal of Jilin University (Engineering Science), 1-10[2022-12-01]. |
| [16] |
张鑫, 徐遵义, 何慧茹, 等. 基于RBM和SVM的风电机组叶片开裂故障预测[J]. 电力系统保护与控制, 2020, 13(15): 134-140. ZANG X, XU Z Y, HE H R, et al. Matter and the SVM based wind turbine blade crack fault prediction[J]. Power System Protection and Control, 2020, 13(15): 134-140. DOI:10.19783/j.cnki.pspc.191093 |
| [17] |
梁川. 基于一维卷积神经网络的风机故障预测[J]. 科技创新与应用, 2020(32): 132-135. LIANG C. Fan fault prediction based on one-dimensional convolutional neural network[J]. Science and Technology Innovation and Application, 2020(32): 132-135. |
 2024, Vol. 46
2024, Vol. 46

