永磁同步电机(Permannet Magnet Synchronous Motor,PMSM)效率高、功率因数高、结构简单灵活,是舰船电力推进的最优选择[1 − 3]。船舶推进电机工作环境较为恶劣,会大大降低传感器的可靠性。无位置传感器技术可以降低运行环境需求,简化系统结构,解决在航维护困难,具有重要研究意义。
由于PMSM在启动时,反电动势小,信噪比差,会给如滑膜观测器法[4 − 5]、磁链观测器法[6]、扩展卡尔曼滤波法[7 − 8]等高精度算法带来很大的误差。一些学者提出了V/f控制从零起动电机,传统的开环V/f控制虽然具有控制结构简单、在线计算时间短等优点,但由于没有闭环控制,且船舶推进电机直连螺旋桨,始终会有一个较大负载[9],这种方法很容易失去同步或者根本无法起动。而传统的I/f控制则可以在起动的瞬间输出最大的电磁转矩,适用于螺旋桨负载场景。刘计龙等[10]和Wang等[11]就在电机起动阶段运用传统的I/f控制方法。在参数设定得当的情况下,能够有一个良好的过渡周期,但由于给定电流不可调整,运行效率低,且电机转速是开环控制,无负载转矩补偿手段,存在转速波动大、负载突然易失步等问题。YANG等[12]针对传统I/f控制效率低的问题,对转矩角采取闭环控制,通过实际转矩角与设定转矩角差值来调节定子电流幅值,使转矩角收敛于给定值,显著提升系统的效率。尹泉等[13]针对速度波动大,收敛较慢的问题,建立负载转矩观测器,实时观测负载变化,根据负载大小在线调节给定电流幅值,实现电机转速波动的有效抑制。SHEN等[14]和王萌等[ 15]分析PMSM转速变化量与电磁转矩的负相关关系,在电机转速达到给定值后,通过补偿给定转速来给控制系统增加阻尼转矩,实验验证了该方法的转速收敛性能和抗干扰性。
目前对I/f控制相关研究中,大多针对小型PMSM,对于类似船舶推进电机这种大负载、大惯量的电机鲜有研究。针对上述文献中体现出的问题,本文研究了一种适用于表贴式永磁同步推进电机的优化I/f控制方案。该方案针对I/f控制固有的低效率问题,建立转矩角观测器,通过调节给定电流幅值,使电机运行状态逼近最大转矩/电流比状态,提高系统运行效率。针对转矩和速度波动问题,通过有功功率的反馈,闭环调节定子电流转速以增加系统阻尼转矩,加快电机转速转矩收敛,提高抗负载扰动能力。
1 开环I/f控制方法 1.1 开环I/f控制的PMSM数学模型传统I/f控制是一种电流闭环但位置开环的控制方法,位置角
以转子磁链定向的表贴式永磁同步电机(Surface Permanent Synchronous Motor, SPMSM)定子电压方程为
| $ \left\{\begin{aligned} & {U}_{d}=R{i}_{d}+{L}_{d}\frac{\text{d}{i}_{d}}{\text{d}t}-{\omega }_{\text{re}}{L}_{q}{i}_{q} ,\\ & {U}_{q}=R{i}_{q}+{L}_{q}\frac{\text{d}{i}_{q}}{\text{d}t}+{\omega }_{\text{re}}{L}_{d}{i}_{d}+{\omega }_{\text{re}}\psi 。\end{aligned}\right. $ | (1) |
式中:
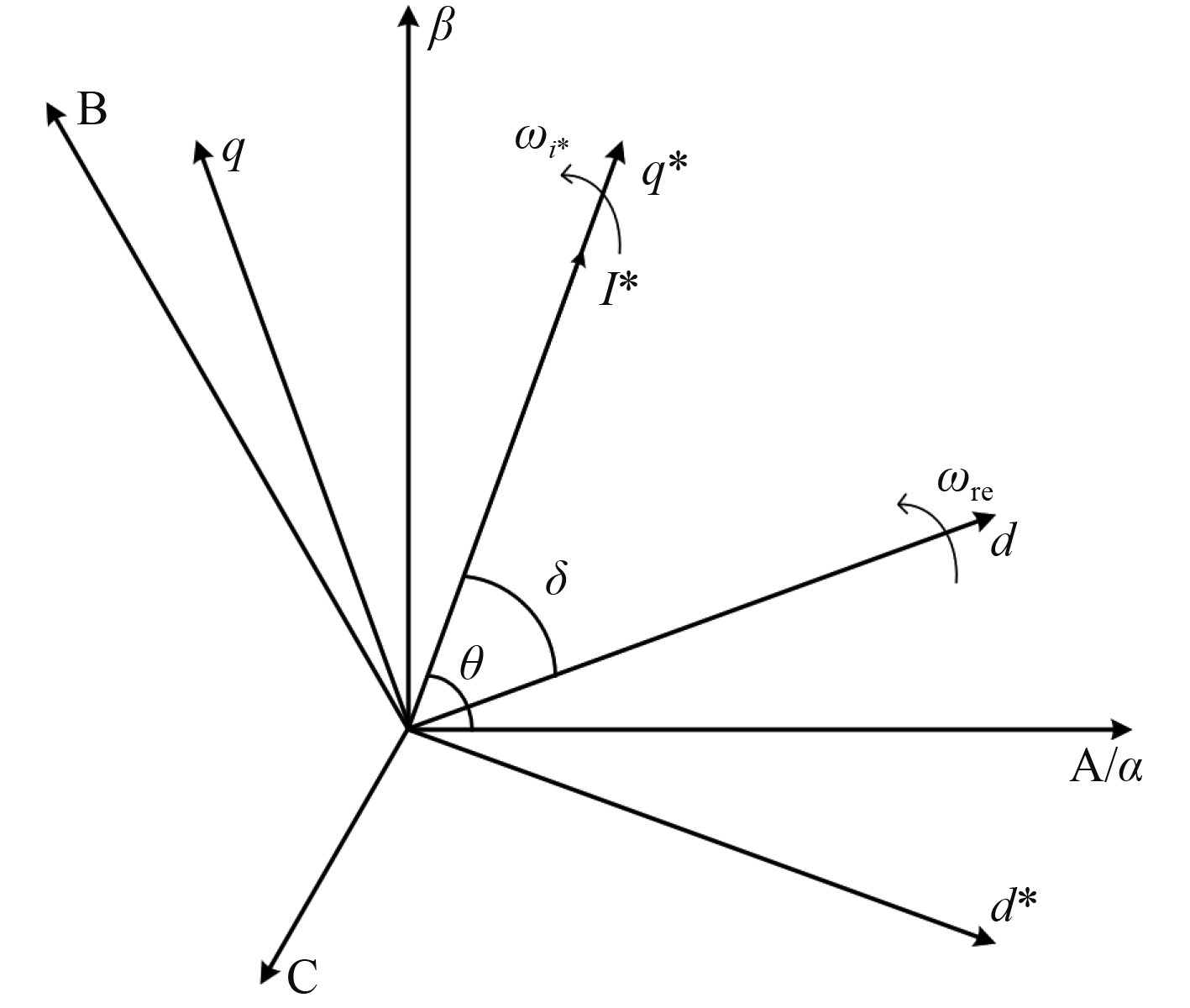
|
图 1 PMSM空间矢量图 Fig. 1 Space vector diagram of PMSM |
| $ \left\{ \begin{aligned} & {{U_{{d^*}}} = R{i_{{d^*}}} + L\frac{{{\text{d}}{i_{{d^*}}}}}{{{\text{d}}t}} - {\omega _{{i^*}}}L{i_{{q^*}}} - {\omega _{{\text{re}}}}\psi {\text{cos}}\delta } ,\\ & {{U_{{q^*}}} = R{i_{{q^*}}} + L\frac{{{\text{d}}{i_{{q^*}}}}}{{{\text{d}}t}} + {\omega _{{i^*}}}L{i_{{d^*}}} + {\omega _{{\text{re}}}}\psi {\text{sin}}\delta } 。\end{aligned} \right. $ | (2) |
| $ {T_{\text{e}}} = \frac{3}{2}n\psi \left( {{i_{{q^*}}}{\text{sin}}\delta - {i_{{d^*}}}{\text{cos}}\delta } \right) 。$ | (3) |
式中:
对SPMSM的控制多采用
| $ \left\{\begin{aligned} & {U}_{{d}^{*}}=-{\omega }_{{i}^{*}}L{i}_{{q}^{*}}-{\omega }_{\text{re}}\psi \text{cos}\delta ,\\ & {U}_{{q}^{*}}=R{i}_{{q}^{*}}+L\frac{\text{d}{i}_{{q}^{*}}}{\text{d}t}+{\omega }_{\text{re}}\psi \text{sin}\delta 。\end{aligned} \right. $ | (4) |
| $ {T_{\text{e}}} = \frac{3}{2}n\psi {i_{{q^*}}}{\text{sin}}\delta。$ | (5) |
图2为开环I/f控制下的PMSM控制框图。电流矢量
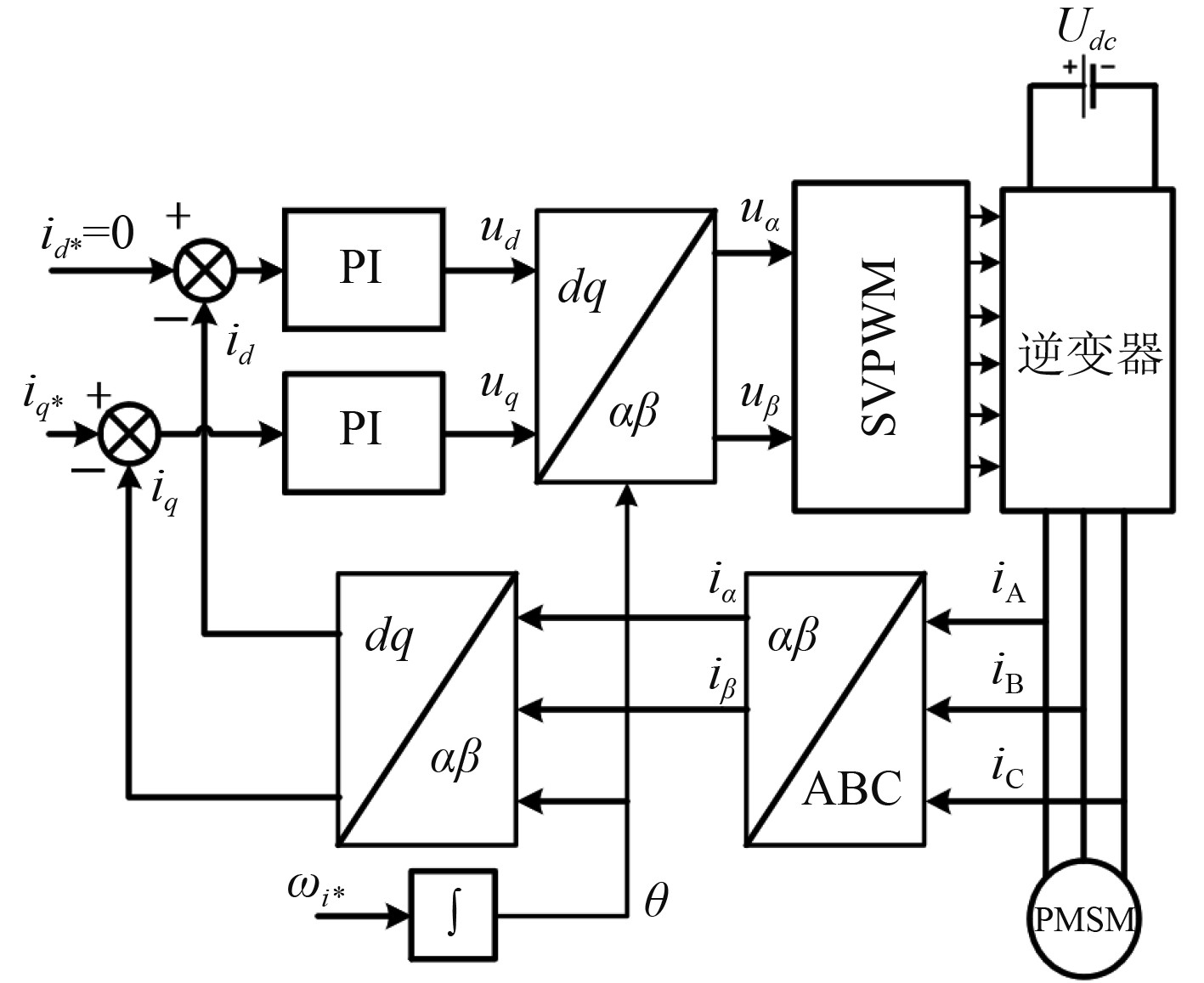
|
图 2 开环I/f控制框图 Fig. 2 Control block diagram of open-loop I/f |
电机运动平衡方程:
| $ J\frac{{{\text{d}}{\omega _{{\text{rm}}}}}}{{{\text{d}}t}} = {T_{\text{e}}} - {T_{\text{L}}} - B{\omega _{{\text{rm}}}} 。$ | (6) |
式中:
由上式可知,转动惯量
对于船舶推进电机而言,电机阻尼转矩可忽略不计,电机达到稳定状态的条件:
| $ {T_{\text{e}}} = {T_{\text{L}}} = \frac{3}{2}n\psi {i_{{q^*}}}{\text{sin}}\delta 。$ | (7) |
由于I/f开环控制,
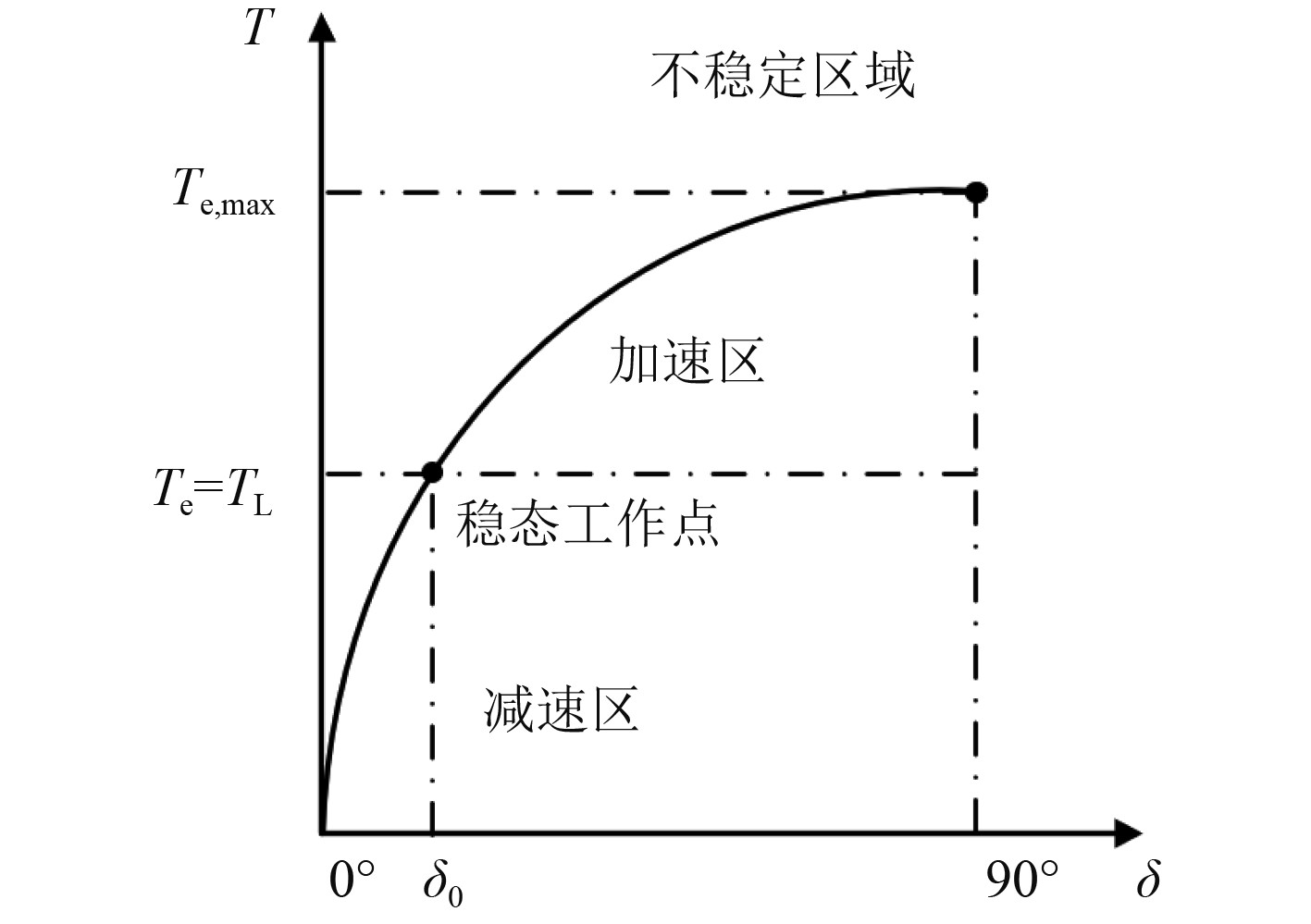
|
图 3 转矩平衡关系图 Fig. 3 Diagram of torque balance |
所以为了保证电机稳定运行,转矩角
| $ 0^\circ < \delta < 90^\circ。$ | (8) |
可知,开环的I/f控制方法特点是没有转子位置信息,电流矢量转动速度恒定,转速依靠SPMSM的转矩-功角自平衡特性振荡至稳态工作点,转矩角不可调,系统效率低。在负载变化过大过快时,转矩角
因此,需要针对船舶推进电机优化I/f控制方法,提高其收敛特性,同时又能兼顾稳定性和经济性,使其具有实际应用价值。
2 I/f控制的优化方案在开环I/f的基础上,引入2个反馈环节,分别对电流矢量的转速和幅值进行调节,控制框图如图4所示,
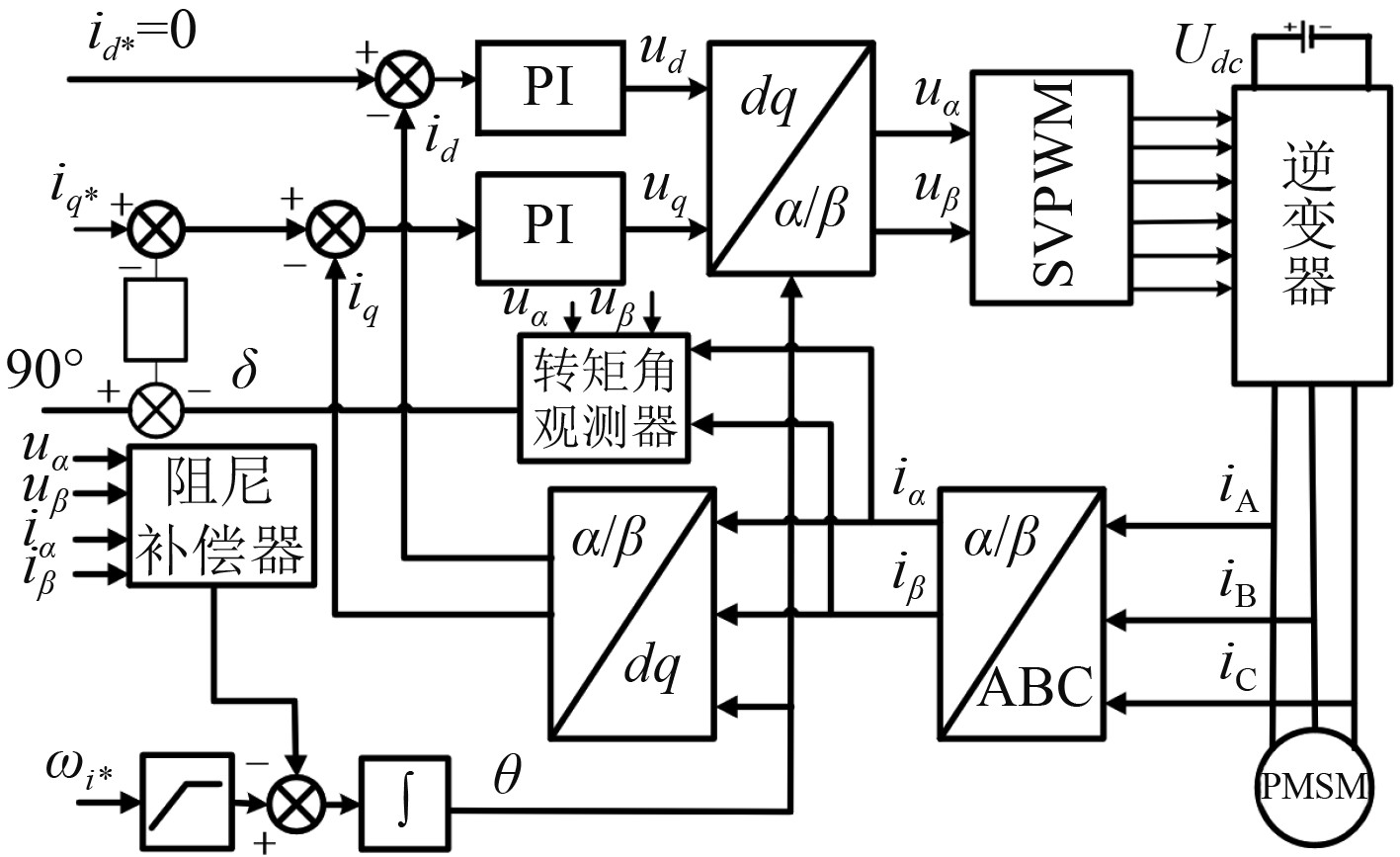
|
图 4 优化后的I/f控制框图 Fig. 4 I/f control block diagram after optimization |
I/f控制优化方案主要分为2个方面:建立转矩角观测器,在线调节给定电流矢量的幅值;通过有功功率的扰动分量调节电流矢量的旋转速度,增加系统的阻尼转矩。
2.1 电流矢量补偿控制策略由式(7)可知,电磁转矩大小只与电流矢量的幅值和转矩角
实际上,将式(4)左右两边同乘
| $ \left\{\begin{aligned} & {U}_{{d}^{*}}{i}_{{q}^{*}}=-Q=-{\omega }_{{i}^{*}}L{i}_{{q}^{*}}^{2}-{\omega }_{\text{re}}\psi {i}_{{q}^{*}}\text{cos}\delta,\\ & {U}_{{q}^{*}}{i}_{{q}^{*}}=P=R{i}_{{q}^{*}}^{2}+L\frac{\text{d}{i}_{{q}^{*}}^{2}}{\text{d}t}+{\omega }_{\text{re}}\psi {i}_{{q}^{*}}\text{sin}\delta。\end{aligned} \right.$ | (9) |
式中:
进而可得转矩角
| $ {\text{tan}}\delta = \frac{{P - Ri_{{q^*}}^2 - L\frac{{{\text{d}}i_{{q^*}}^2}}{{{\text{d}}t}}}}{{Q - {\omega _{{i^*}}}Li_{{q^*}}^2}} 。$ | (10) |
忽略逆变器的损耗,瞬时有功功率
| $ \left\{ \begin{aligned} & {P = {u_\alpha }{i_\alpha } + {u_\beta }{i_\beta }},\\ & {Q = {u_\beta }{i_\alpha } - {u_\alpha }{i_\beta }} 。\end{aligned} \right. $ | (11) |
由式(10)可获得转矩角
船舶永磁同步推进电机大多为无阻尼转矩电机,或者阻尼转矩对于负载转矩和电磁转矩来说可忽略不计。这种无阻尼特性,会导致系统转速波动大,负载突变易失步。为了解决上述问题,需要通过对电流矢量旋转频率进行反馈调节,以增加系统阻尼转矩。
由式(5)和式(6)可知,若负载转矩突然增大,则转子速度
| $ \vartriangle {\omega _{{\text{rm}}}} = - k\vartriangle {T_{\text{e}}}。$ | (12) |
由电机学理论可知,电磁转矩与电机的瞬时有功功率有如下关系:
| $ \vartriangle {T_{\text{e}}} = k\frac{{\vartriangle P}}{{{\omega _{{\text{rm}}}}}} 。$ | (13) |
式(12)和式(13)中的
| $ \left\{ \begin{aligned} & {{\omega _{{\text{rm}}}} \approx {\omega _{{i^*}}}},\\ & {\vartriangle P \approx HPF\left( P \right)} 。\end{aligned} \right. $ | (14) |
将式(12)和式(13)代入式(14)可得:
| $ \vartriangle {\omega _{{\text{rm}}}} = - \frac{k}{{{\omega _{{i^*}}}}}{{HPF}}\left( P \right) = - k{{HPF}}\left( P \right)。$ | (15) |
可知,可通过电机瞬时有功功率的变化量来调节电流矢量的转速,达到增加系统阻尼转矩的作用,降低系统转速振荡幅值,加快电机转速收敛特性。
2.3 参数设计系统中有2个参数需要离线给定,分别是电流矢量幅值和电流矢量旋转速度,2个参数的选择直接决定了电机起动时的性能。
2.3.1 电流矢量幅值的参数设计由式(5)可知,电机所能输出的最大电磁转矩直接由
| $ {i_{{q^*}}} \geqslant \frac{{2{T_{\text{L}}}}}{{3n\psi }} 。$ | (16) |
电机的起动过程分为加速阶段和稳定阶段,
由式(6),忽略粘滞摩擦系数,可得电机机械角加速度
| $ {a_{\text{r}}} = \frac{{{T_{\text{e}}} - {T_{\text{L}}}}}{J}。$ | (17) |
电机启动初始时刻,
| $ \left\{ \begin{aligned} & {{a_{\text{r}}}T \geqslant {\omega ^*}} ,\\ & {{a^*}{T^*} = {\omega ^*}} 。\end{aligned} \right. $ | (18) |
假定已知给定电流幅值
| $ {\theta _0} = \arcsin \left( {\frac{{2{T_{\text{L}}}}}{{3n\psi {i_{{q^*}}}}}} \right) ,$ | (19) |
电流矢量转动至
| $ t = {T^*} - T ,$ | (20) |
由于电流矢量是匀加速运动,所以
| $ {\theta _0} = \frac{1}{2}n{a^*}{t^2} ,$ | (21) |
联立式(18)、式(20)和式(21)可得:
| $ T = \frac{{{\omega ^*}}}{{{a^*}}} - \sqrt {\frac{{2{\theta _0}}}{{n{a^*}}}},$ | (22) |
将上式代入式(18)中的不等式,可得:
| $ {\omega ^*}{a^*} + {a_{\text{r}}}\sqrt {\frac{{2{\theta _0}}}{n}\sqrt {{a^*}} } - {\omega ^*}{a_{\text{r}}} \leqslant 0 ,$ | (23) |
若要上式有解,需要
| $ \left\{\begin{aligned} & {a}^{*} > 0 ,\\ & {a}^{*}\le \left( \frac{\sqrt{\dfrac{2{a}_{\text{r}}^{2}{\theta }_{0}}{n}+4{\omega }^{{*}^{2}}{a}_{\text{r}}}-{a}_{\text{r}}\sqrt{\dfrac{2{\theta }_{0}}{n}}}2{\omega }^{*} \right)^{2}。\end{aligned}\right. $ | (24) |
为了验证上述控制策略的性能,在Matlab/Simulink环境下进行仿真验证。将I/f控制优化方法与开环I/f控制方法在电机起动和负载突变时的性能进行对比,验证优化后控制策略的经济性、转速收敛性能和变负载工况下系统的稳定性。仿真中的电机模型采用中铁渤海铁路轮渡的永磁同步推进电机,参数如表1所示。
|
|
表 1 电机参数 Tab.1 Parameters of permanent magnet synchronous motors |
初始时刻,给定电流矢量幅值为1 000 A,负载转矩
转矩角
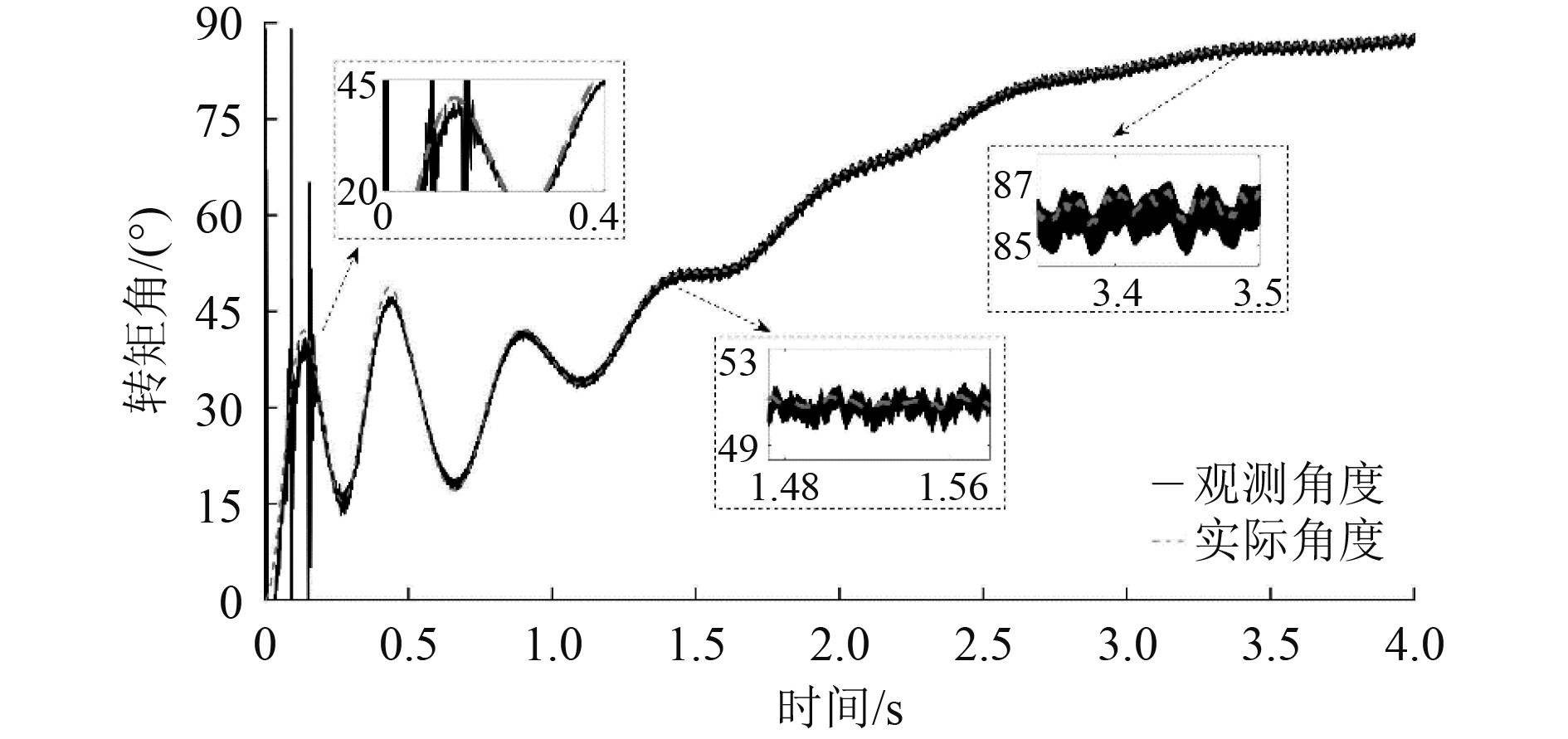
|
图 5 转矩角观测值与真实值关系 Fig. 5 Relationship between observed and true values of torque angle |
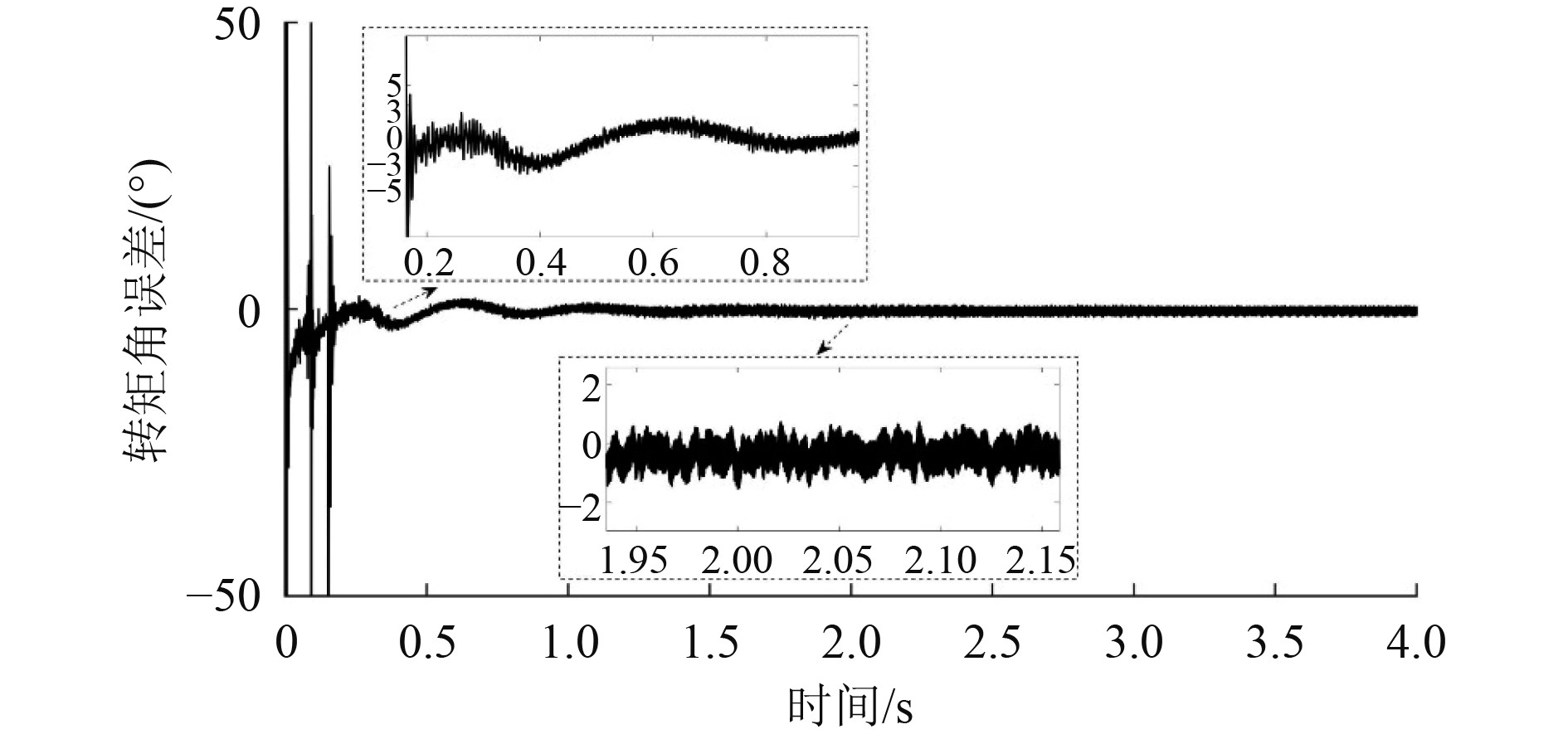
|
图 6 转矩角观测值与真实值的差值 Fig. 6 Difference between observed and true values of torque angle |
由图可知,转矩角观测器观测在启动初始阶段有一定的高频扰动,随着转子速度加速,观测角度与真实角度基本重合,观测误差在
图7为开环I/f启动的曲线图,图8为优化后的I/f控制系统仿真波形,对比可以看出,2种方法都可以将速度提升至设定速度,但开环I/f控制电机转速转矩震荡持续至仿真结束,而优化后的I/f控制方法在1 s后,转速转矩就收敛至给定值,收敛速度快。开环I/f控制的转矩角无法进行调节,电机效率低,而优化后的I/f控制由于转矩角的反馈闭环对电流矢量幅值的调节,转矩角最终收敛至90°,达到MTPA运行状态,运行效率非常高。
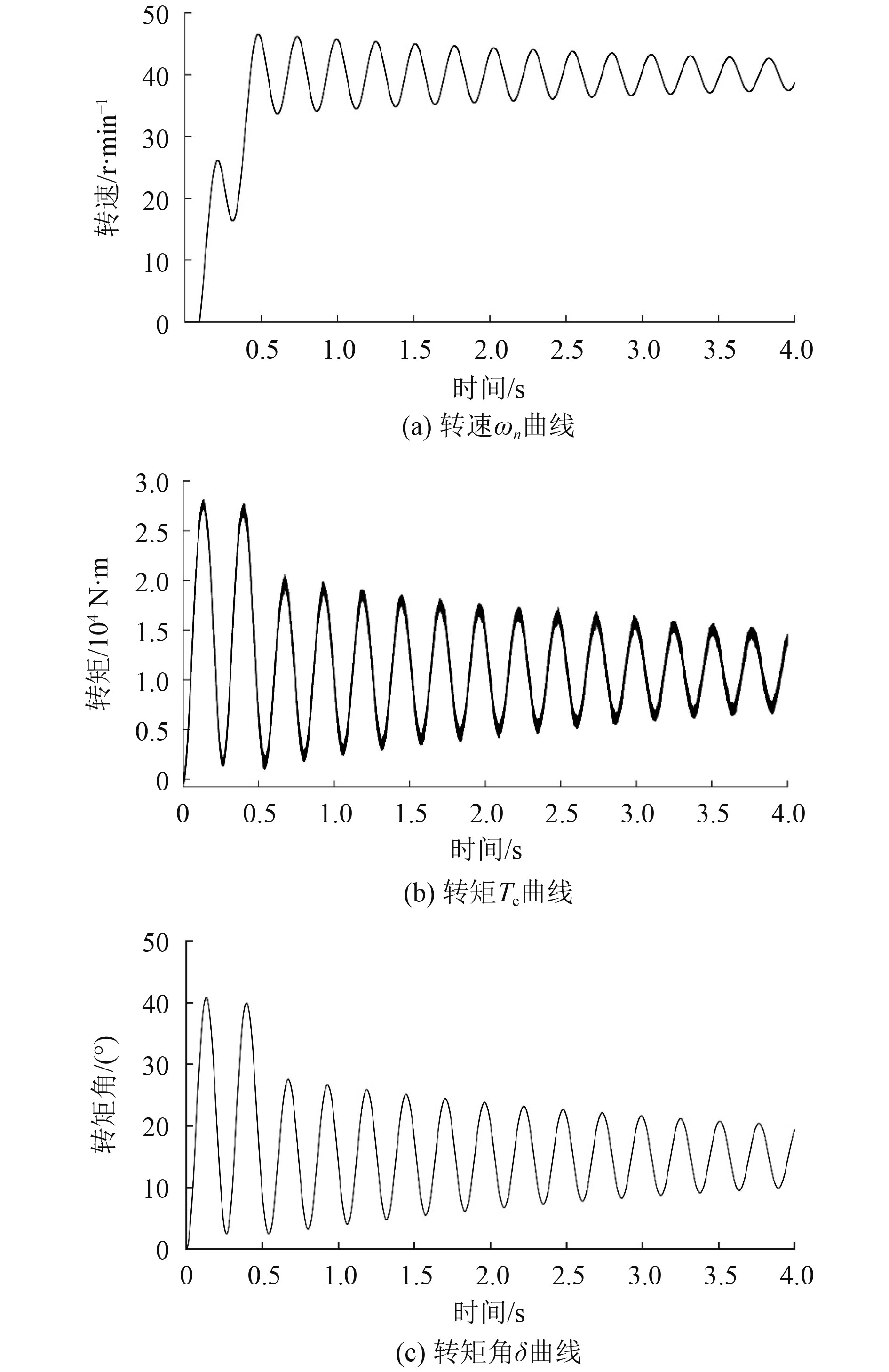
|
图 7 开环I/f控制仿真结果 Fig. 7 Simulation results of open-loop I/f control |
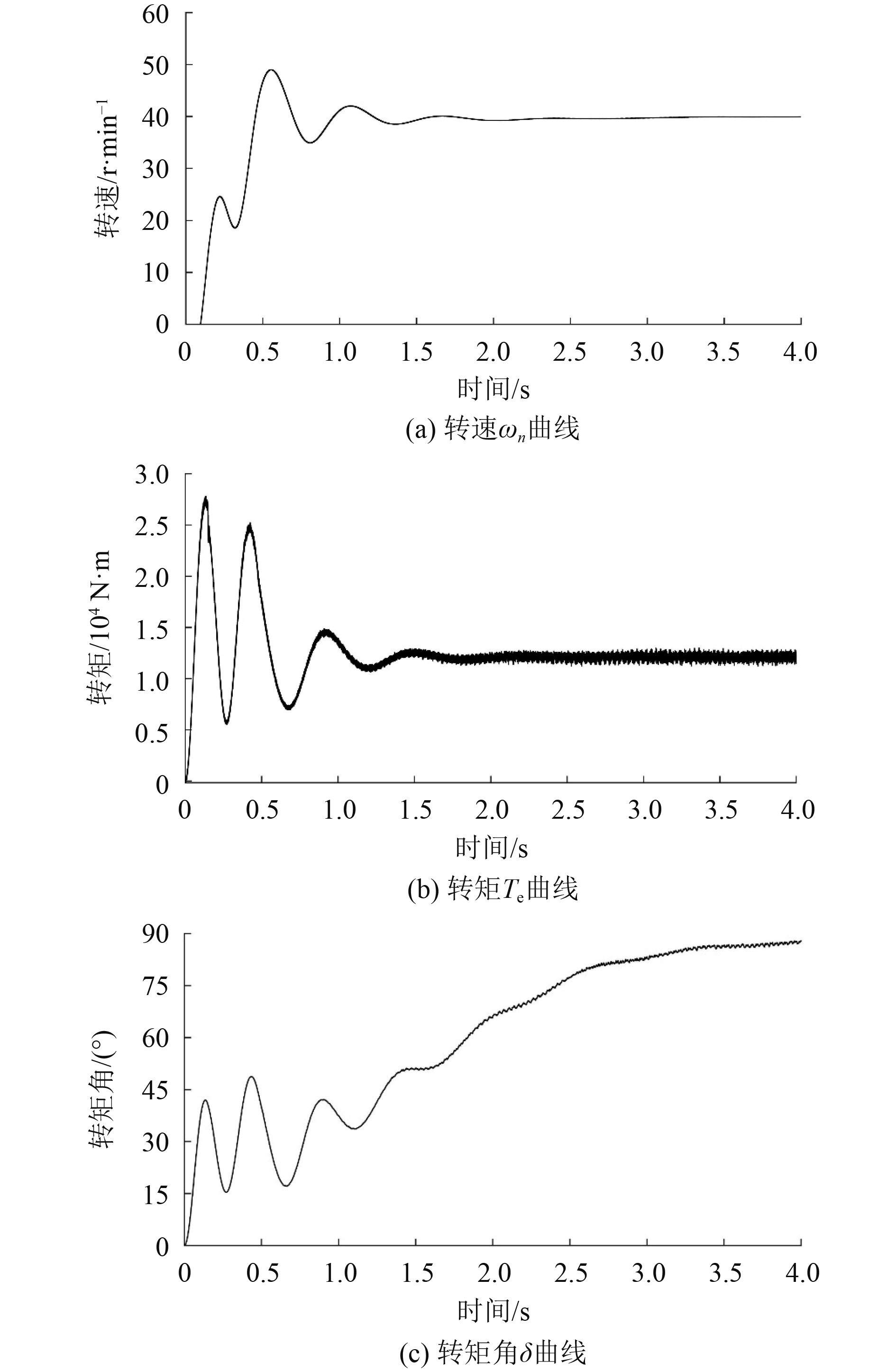
|
图 8 优化后I/f控制仿真结果 Fig. 8 Simulation results of the optimized I/f control |
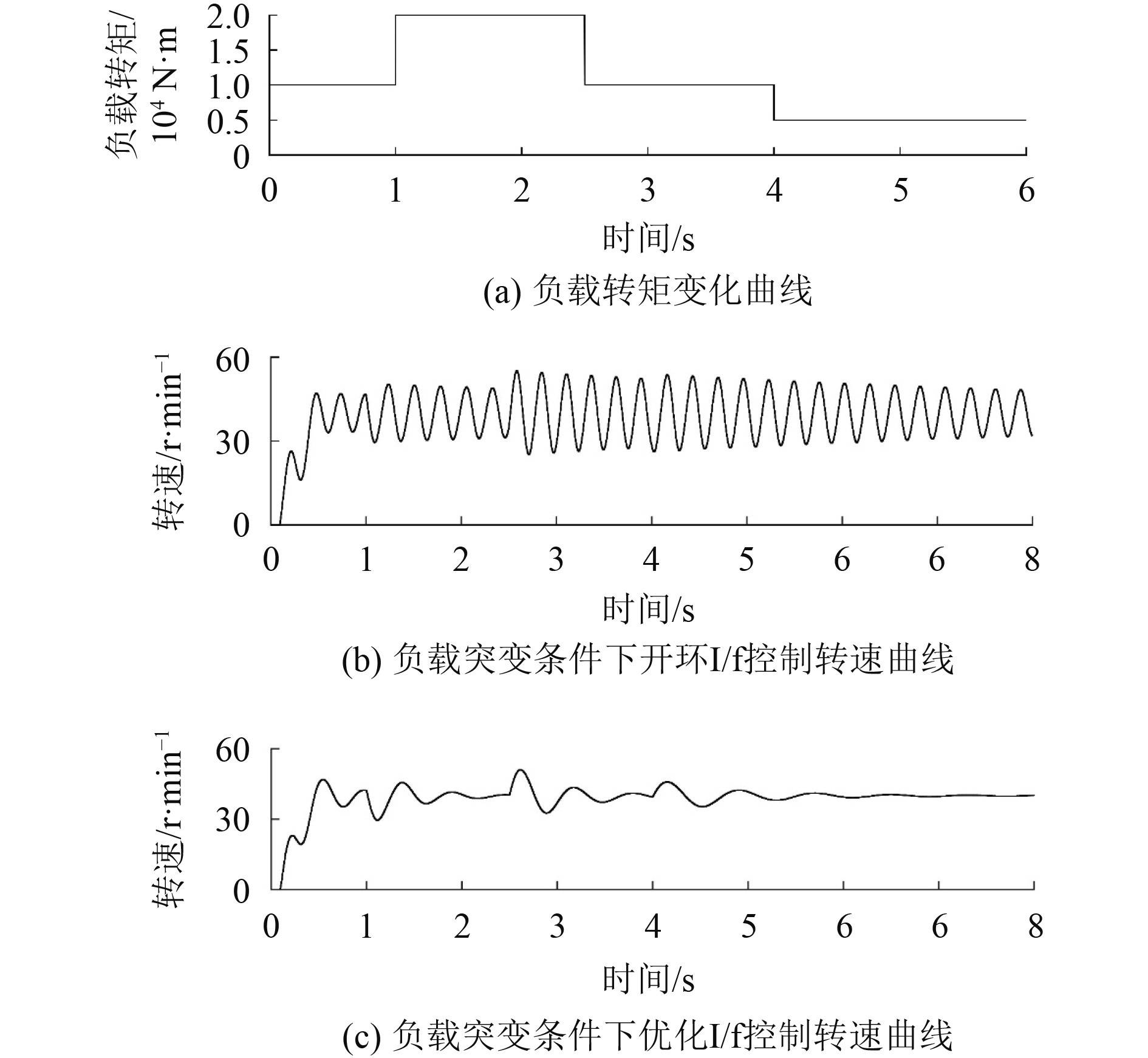
该实验主要验证该方法在应对负载突加突减时,电机快速响应性能。给定变负载曲线如图9(a)所示。为保证负载突变时,电机能够兼顾抗扰动性与经济性,将给定转矩角设定为
|
图 9 负载突变时的仿真结果 Fig. 9 Simulation results of load torque sudden changes |
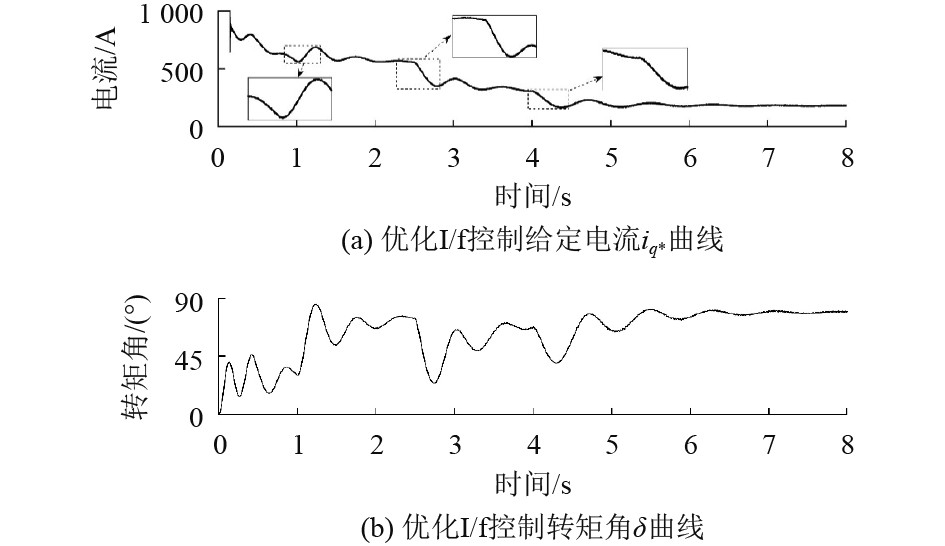
图10为优化I/f控制的转矩角及给定电流矢量的变化图。由图可知,在每个负载突变点,由于反馈环节的存在,给定电流
|
图 10 负载突变时优化I/f控制方法的仿真结果 Fig. 10 Simulation results of the optimized I/f control method when load torque sudden changes |
仿真结果表明,由于2个反馈环节的加入,本文优化的I/f控制方法改善了转速与转矩收敛性能,并且在负载突变的工况下,转速与转矩角都具有良好的动态响应过程,改善了电机的稳定性,且系统能工作在高效区间,提升了电机效率。
4 结 语本文以船舶永磁同步推进电机为研究对象,提出了一种优化的I/f控制方法,得出结论如下:
1)针对I/f控制中转速波动大、收敛慢的的问题,通过瞬时有功功率调节电流矢量的角速度,给系统加入阻尼转矩,加速了电机转速收敛。
2)针对电机运行效率低的问题,设计转矩角观测器,通过转矩角来动态的调节电流矢量的幅值,使转矩角收敛至接近
仿真实验结果表明优化的I/f控制方法在稳定运行和负载突变时相比开环I/f控制,稳定性与经济性都得到了较大提升,可作为一种简单实用的起动方式用于船舶永磁同步电机。
| [1] |
邓智浩, 李争光, 祝后权, 等. 永磁同步电机无传感器控制在电力推进中的应用综述[J]. 船电技术, 2021, 41(7): 49-55. DOI:10.13632/j.meee.2021.07.012 |
| [2] |
计青山. 胡即明. 一种船用永磁同步电动机的起动方法[J]. 船舶工程, 2012, 34(S2): 94-96. |
| [3] |
范爱龙, 贺亚鹏, 严新平, 等. 智能新能源船舶的概念及关键技术[J]. 船舶工程, 2020, 42(3): 9-14. DOI:10.13788/j.cnki.cbgc.2020.03.02 |
| [4] |
SAADAOUI O, KHLAIEF A, ABASSI M, et al. Position sensorless vector control of PMSM drives based on SMO[C]//2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), 2015: 545−550.
|
| [5] |
高键, 吴祥瑞. 基于滑模控制的船舶电力推进调速系统仿真[J]. 舰船科学技术, 2018, 40(1): 104-107. DOI:10.3404/j.issn.1672-7649.2018.01.018 |
| [6] |
JIANG Y, XU W and MU C. Improved SOIFO-based rotor flux observer for PMSM sensorless control[C]//IECON 2017 - 43rd Annual Conference of the IEEE Industrial Electronics Society, 2017: 8219−8224.
|
| [7] |
薛树功, 魏利胜, 凌有铸. 基于扩展卡尔曼滤波的永磁同步电机无传感器矢量控制[J]. 电机与控制应用, 2011, 38(8): 15-18. DOI:10.3969/j.issn.1673-6540.2011.08.004 |
| [8] |
BOLOGNANI S, OBOE R, ZIGLIOTTO M. Sensorless full-digital PMSM drive with EKF estimation of speed and rotor position[J]. IEEE Transactions on Industrial Electronics, 1999, 46(1): 184-191.
|
| [9] |
ZHANG Z, GUO H, LIU H, et al. An improved sensorless control strategy of Ship IPMSM at full speed range[J]. IEEE Access, 2019, 7: 178652−178661.
|
| [10] |
刘计龙, 肖飞, 麦志勤, 等. IF控制结合滑模观测器的永磁同步电机无位置传感器复合控制策略[J]. 电工技术学报, 2018, 33(04): 919-929. DOI:10.19595/j.cnki.1000-6753.tces.161597 |
| [11] |
WANG Z, LU K and BLAABJERG F. A simple startup strategy based on current regulation for back-emf-based sensorless control of PMSM[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3817−3825.
|
| [12] |
YANG J, HUANG W, CAO Ret al. A closed-loop I/f sensorless control based on current vector orientation for permanent magnet synchronous motors[C]//2015 18th International Conference on Electrical Machines and Systems (ICEMS), 2015: 1609−1614.
|
| [13] |
尹泉, 张馨月, 罗慧, 等. PMSM抑制I/f启动策略稳态速度波动的新型方法[J]. 电气传动, 2020, 50(6): 3-9. DOI:10.19457/j.1001-2095.dqcd19199 |
| [14] |
SHEN H, ZHANG C. A new efficient sensorless I/f control method for IPMSM drives[C]//2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), 2017: 209−213.
|
| [15] |
王萌, 杨家强, 张翔, 等. 一种表贴式永磁同步电机电流矢量闭环I/f控制方法[J]. 中国电机工程学报, 2015, 35(10): 2513-2521. DOI:10.13334/j.0258-8013.pcsee.2015.10.018 |
 2024, Vol. 46
2024, Vol. 46

