0 引　言

船用低速机具有较大冲程比，由于良好的可靠性、动力性能和燃油经济性，已广泛应用于各类船舶^[1-2]。低速机具有复杂的振动特性，各类环境诱发的振动变化可能会影响其可靠性以及船舶的正常运行。过去，基于状态监测的故障诊断是一项重要问题，需大量的健康运行数据监测基础，但目前对低速机的状态监测以及其振动特性的有关研究仍然缺失。因此，揭示低速机健康状态下的振动特性并合理构建其振动特征具有重要意义。

目前，基于振动信号的特征处理算法已得到了进一步发展，常见包括快速傅里叶变换、短时傅里叶变换、小波变换和经验模态分解（Empirical Mode Decomposition，EMD）等。快速傅里叶变换虽然降低了离散傅里叶变换的计算量，但并不适合处理非稳态信号；短时傅里叶变换可用于处理非稳态信号，但其窗口大小不能进行自适应调整^[3]。小波分析弥补了上述缺点，通过一个大小可变的“时间-频率”窗口提供时频分析。EMD是一种自适应的信号分解方法，可将信号分解为有限个固有模态分量与残余分量之和^[4]，但存在模态混叠和伪分量的缺陷，故需在此基础上进行改进。相继发展的有集总平均经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）、补充的集总平均经验模态分解（Complementary Ensemble Empirical Mode Decomposition，CEEMD）和改进的集总平均经验模态分解（Modified Ensemble Empirical Mode Decomposition，MEEMD）等方法。特别是MEEMD方法能更好地抑制模态混叠问题，减少伪分量的出现^[5]，该方法也已广泛应用于轴承、地震等分析中^[6-7]。目前，小波包分析与EMD类算法结合的方法，在振动信号特征提取中取得了较好效果。孙抗等^[8]采用了小波包和EMD结合的方法，对断路器振动信号进行了特征提取，具有较好的实用性。郑国刚等^[9]计算了滚动轴承振动信号的小波包能量熵，对熵值较大的节点进行EEMD分解，实现了轴承故障特征提取。

基于上述分析，本文采用小波包能量谱和MEEMD结合的方法，评估了长冲程船用低速机稳定运行状态下典型推进工况的振动特性，结合时域和气缸燃烧压力分析，澄清了低速机健康状态下的振动特征，为低速机的健康状态监测和故障诊断提供方法和依据。

1 试验装置与信号采集 1.1 试验装置

本试验以MAN B&W 6S35ME-B9型长冲程船用低速机为研究对象，其结构和技术参数见表1。

1.2 信号采集

由于低速机2号缸缸盖的振动信号易于测试，同时也便于今后对此缸进行状态监测，故本试验对2号缸缸盖的振动信号进行了测量。测量时选用Coinv(INV9832-50)三向振动传感器，其灵敏度为100 mV/g。使用该振动传感器可同时获得x、y和z轴的数据，本试验仅对z轴振动信号进行分析处理。低速机转速及扭矩参数由水力测功器测得。气缸压力信号由KISTLER(6613CG2)压力传感器测试而得。本试验分别在25%、40%和50%这3种典型推进工况下进行，各工况对应的转速和扭矩如表2所示。

曲柄转角脉冲信号、振动信号和气缸压力信号同时传递给数据采集系统（INV3062-C2(L)），再经传输电缆将数据一并传送于1台便携式电脑，通过其内置的信号处理软件进行离线数据处理。信号采集是待低速机在各工况下状态稳定6 h后进行的，以保证信号分析结果的准确性。信号的采样时间均为30 s，采样频率为5 kHz。

1.3 试验方法 1.3.1 小波包分析

柴油机振动信号属于非稳态时变信号，其中，通常含有低频和高频成分。为了获得较好的时频分辨率，处理低频成分时应采用大时间窗，而在处理高频成分时采用小时间窗。小波分析弥补了短时傅里叶变换窗口大小固定不变的缺点，提供了一个可随频率改变其大小的“时间-频率”窗口，在信号分析中，获得了较好分辨率，实现了更高应用价值。

然而，小波分析只对信号的低频部分进行逐层分解，忽略了高频部分，以致高频部分的频率分辨率较差。图1为3层小波分解示意图。

不同于小波分析，在原始信号$X(t)$分解之后，小波包分析仍继续对每一层的高频部分进行分解。在每层分解中，各节点均被分解为高频和低频2个部分，该方法从而较小波分析具有更好的时频分辨率。图2为3层小波包分解示意图，经$n$次小波包分解之后，原始信号将被分解为${2^n}$个节点，即3层小波包分解将生成8个节点频带。

小波包分解的计算公式为：

$ \left\{ \begin{gathered} {d_{i,j,2m = }}\sum {h(k - 2i){d_{k,j + 1,m}}}，\\ {d_{i,j,2m + 1 = }}\sum {g(k - 2i){d_{k,j + 1,m}}}。\\ \end{gathered} \right. $

(1)

小波包重构的计算公式为：

$ {d_{i,j + 1,m}} = \sum\limits_k {h(i - 2k){d_{i,j,2m}} + \sum\limits_k {g(i - 2k){d_{i,j,2m + 1}}} }，$

(2)

式中：${d_{i,j,m}}$为第$j$层中第$m$个节点的第$i$个小波包系数（$m$=0，1，…，${2^j}$-1）；$h(k)$和$g(k)$分别为展开系数。

1.3.2 小波包能量谱（WPES）

低速机缸盖振动信号经小波包j次分解后各重构节点的能量为：

$ {E_{j,m}} = {\sum\limits_i {\left| {{d_{i,j,m}}} \right|} ^2}，$

(3)

小波包分解第j层总能量的计算公式：

$ {E_j} = \sum\limits_{m = 0}^{{2^j} - 1} {{E_{j,m}}} ，$

(4)

$ {P_{j,m}} = \frac{{{E_{j,m}}}}{{{E_j}}} \times 100\% 。$

(5)

式中：${E_{j,m}}$和${P_{j,m}}$分别为第$j$层的第$m$个节点重构信号的能量和在总能量${E_j}$中的百分比（$m$=0，1，…，${2^j}$-1）。

1.3.3 改进的总体平均经验模态分解（MEEMD）

长度为$N$的柴油机原始信号$X(t)$中，添加$i$对均值为零的正、负白噪声信号$\varepsilon _i^ + $和$\varepsilon _i^ - $，得到：

$ X_i^ + (t) = X(t) + {a_i}\varepsilon _i^ + (t) ，$

(6)

$ X_i^ - (t) = X(t) + {a_i}\varepsilon _i^ - (t)。$

(7)

式中：$X_i^ + (t)$和$X_i^ - (t)$分别为添加正、负白噪声的信号；${a_i}$为白噪声幅值（$i$=1，2，…，$Ne$），本文取0.2；$Ne$为白噪声对数，本文取为50。

分别对$X_i^ + (t)$和$X_i^ - (t)$进行EMD分解，获得一阶IMF（Intrinsic Mode Functions）分量$\left\{ {I_{i1}^ + (t)} \right\}$和$\left\{ {I_{i1}^ - (t)} \right\}$（$i$=1，2，…，Ne），对上述分量进行集总平均计算：

$ {I_1}(t) = \frac{1}{{2Ne}}\sum\limits_{i = 1}^{Ne} {\left[ {I_{i1}^ + (t) + I_{i1}^ - (t)} \right]}。$

(8)

采用排列熵算法判断I₁(t)是否为异常分量。首先对I₁(t)进行相空间重构：

$ \left\{ \begin{gathered} J(1) = \left\{ {{I_1}(1),{I_1}(1 + \lambda ), \cdots ,{I_1}(1 + (m - 1)\lambda )} \right\}，\\ \vdots \\ J(k) = \left\{ {{I_1}(k),{I_1}(k + \lambda ), \cdots ,{I_1}(k + (m - 1)\lambda )} \right\}，\\ \vdots \\ J(N - (m - 1)\lambda ) = \\ \left\{ {{I_1}(N - (m - 1)\lambda ), {I_1}(N - (m - 2)\lambda ), \cdots ,{I_1}(N)} \right\} 。\\ \end{gathered} \right. $

(9)

式中：$m$为嵌入维数，本文取6；$\lambda $为时间延迟，本文取1。

$J(k) = \left\{ {{I_1}(k),{I_1}(k + \lambda ), \cdots ,{I_1}(k + (m - 1)\lambda } \right\}$中的$m$个向量按大小升序排列，可得：

$ J(k) = \left\{ {{I_1} (k + ({j_1} - 1)\lambda ,{I_1} (k + ({j_2} - 1)\lambda , \cdots ,{I_1} (k + ({j_m} - 1)\lambda } \right\}，$

(10)

式中，${j_1},{j_2}, \cdots ,{j_m}$互异，若${I_1}(k + ({j_{i1}} - 1)\lambda ) = {I_1}(k + ({j_{i2}} - 1)\lambda )$，则依据j值的大小升序排列。

提取重构向量$J(k)$内部向量的符号序列：

$ S(g) = \left[ {{j_1},{j_2}, \cdots ,{j_m}} \right] ，$

(11)

式中：$g$=1，2，…，$k \leqslant m!$，$m!$为$S(g)$的所有序列排列总数。计算各个符号序列$S(g)$出现的频次${N_g}$，及其在总数中出现的概率${P_g}$，${P_g} = \dfrac{{{N_g}}}{{\sum\nolimits_{g = 1}^k {{N_g}} }}$，且$\sum\nolimits_{g = 1}^k {{P_g} = 1} $。

根据香农（Shannon）熵的公式形式，可将排列熵定义为：

$ {H_p}(m) = - \sum\limits_{g = 1}^k {({P_g}In{P_g})}。$

(12)

当${P_g} = 1/(m!)$时，${H_p}(m)$有最大值$\ln (m!)$，并可借此将排列熵进行归一化处理：

$ 0 \leqslant {H_p} = \frac{{{H_p}(m!)}}{{\ln (m!)}} \leqslant 1。$

(13)

${H_p}$可表征低速机振动信号序列的随机性程度。${H_p}$值越大，表明${I_1}(t)$分量越随机、不规则，当大于阈值时，将被认定为异常分量。本文设定排列熵阈值${\theta _0}$=0.6，当${I_1}(t)$分量的${H_p}$≥0.6时，该分量将被视为异常分量并从原始信号中剔除。循环上述步骤，计算其余各阶IMF分量${I_2}(t)$，…，${I_{p - 1}}(t)$，并判断是否为异常分量，直到第$p$个分量${I_p}(t)$为平稳分量，结束循环。将$p - 1$异常分量从原始振动信号中剔除后，得到信号序列$r(t)$：

$ r(t) = {X_t} - \sum\limits_{j = 1}^{p - 1} {{I_j}(t)}。$

(14)

最后对$r(t)$进行EMD分解，得到各阶的IMF分量。MEEMD的公式则可表示为：

$ X(t)\xrightarrow{{MEEMD}}\sum\limits_{i = 1}^n {IM{F_i}(t) + res(t)} 。$

(15)

式中：为$IM{F_i}(t)$各分量; $n$为分解结果中$IM{F_i}(t)$的个数；$res(t)$为最后余量。关于MEEMD方法更详细的说明，可参阅文献[10-11]。

2 结果与讨论 2.1 时域分析

图3为典型工况下，测得的缸盖表面振动信号时域波形图。可看出，在较低发动机负荷时，25%和40%负荷下的振动幅值基本一致，最大振动幅值约100 m/s²。振动幅值开始增强的负荷出现在50%发动机工况，部分周期内幅值增加程度较大，周期间出现较大的振动波动，最大振动幅值约150 m/s²。

为了进一步研究时域信号特征，采用了特征参数对信号进行了特征提取。均方根和峭度分别为表征低速机振动的强度和锐度，可表示为：

$ {x_{RMS}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {x_i^2} }，$

(16)

$ {x_{Kurtosis}} = \frac{\dfrac{1}{N}\displaystyle\sum\nolimits_{i = 1}^N {{{({x_i} - \overline x )}^4}} }{{\left(\dfrac{1}{N}\displaystyle\sum\nolimits_{i = 1}^N {{({x_i} - \overline x )}^2}\right)^2 }}。$

(17)

式中：${x_{RMS}}$为振动加速度均方根值，m/s²；${x_{Kurtosis}}$为振动加速度峭度值；$N$为振动信号离散序列的总点数；${x_i}$为第$i$个振动加速度点的振动幅值，m/s²；$\overline x $为振动加速度离散序列的平均幅值，m/s²。

对每个典型工况下，提取15次单个燃烧循环的振动加速度信号，进行均方根和峭度计算，统计结果如图4所示。可看出，25%和40%负荷下，均方根和峭度基本一致，均方根分布在3～6 m/s²范围内。而在50%负荷时，均方根稍有增加，且呈更离散的分布，分布范围在4.3～8.2 m/s²，表明振动波动增强。这一结果进一步印证了2.1节的时域振幅研究结果，即在40%以下的较低发动机负荷运行时，振动幅值基本一致，运行较为稳定。

峭度结果表明，25%负荷下，峭度分布范围为19～105；40%负荷下，峭度分布范围减小至23～95；50%负荷下，峭度分布范围进一步减小至50～93。可看出，随着负荷的增加，低速机峭度的统计结果趋于集中，表明振动信号的锐度随负荷的增加而趋于稳定和集中。

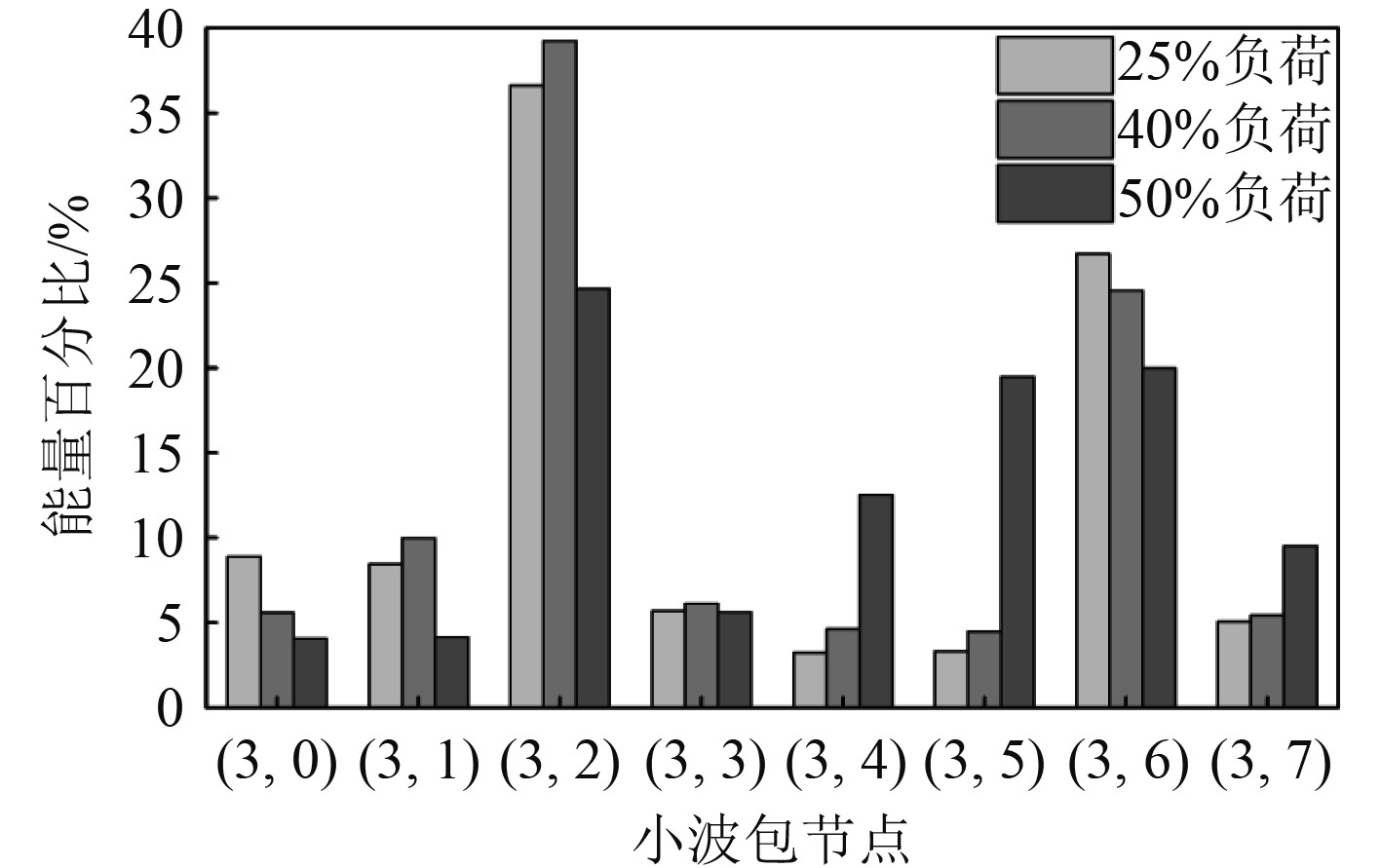
2.2 WPES与MEEMD分析

为进一步揭示低速机的能量分布情况，采用小波包分解将振动信号分解到各频带内，并通过能量谱，为舰船管理人员直观呈现发动机运行状态。通过试验采集到的振动信号数据，利用db3小波函数对其进行３层小波包分解，计算得到了各节点能量占比分布，如图5所示。

由图可知，典型负荷下，能量主要集中在中低频节点（3，2）和高频节点（3，6）这2个节点，其余节点能量占比相对较小。当负荷增加时，节点（3，2）和（3，6）所含的能量百分比均出现了持续下降。在25%和40%负荷下，各节点能量占比分布均较为相近，振动能量占比状况较为相似。而提升至50%负荷时，节点（3，2）和（3，6）处的能量占比开始发生下降，这是由于该2个节点的能量向其他节点频带发生了转移造成的。能量占比统计表明，中高频节点（3，4）、（3，5）和（3，7）的能量为低速机的主要振动能量，能量之和占总能量的41.51%，表明低速机的振动以中高频为主。

进一步对能量占比较大的中低频节点（3，2）和高频节点（3，6）的小波包重构信号进行MEEMD分析，获得IMF1分量进行频谱，结果如图6和图7所示。研究结果表明，健康状态下，2个主要节点的IMF1分量频谱范围均为0～0.8 kHz。随负荷增加，节点（3，2）IMF1分量的频谱峰值有所降低，从7.66×10³ m/s²下降为6.20×10³ m/s²，下降了19.1%。在任意负荷下，中低频节点（3，2）的能量始终高于高频节点（3，6），可见，节点（3，2）的中低频对优化低速机振动十分重要，包括旋转频率数十倍频以内的低频振动。

2.3 燃烧压力

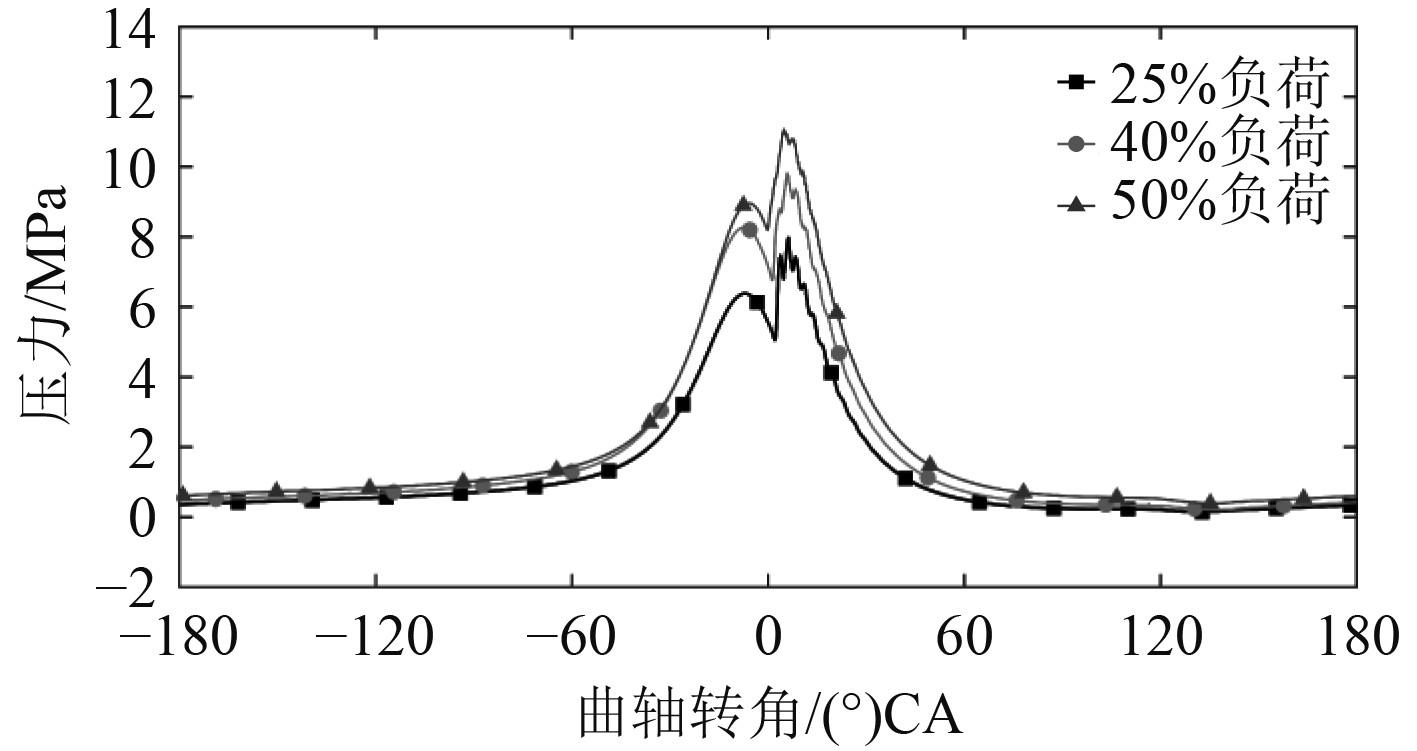
由上可见，中高频能量在低速机振动和噪声优化中具有重要性。振动的强度与燃烧初期的压力梯度密切相关，还与预混燃烧量、点火延迟时间等燃烧过程有关。图8为所测得的气缸内燃烧压力随曲轴转角的变化曲线。可看出，燃烧压力随负荷增强而明显提升。从上止点后开始，3种典型工况下，低速机的燃烧压力均存在一定范围的压力振荡。这一发现也在其他压燃发动机中得到证实^[12]。由于此刻排气阀与扫气口均未开启，因此这一振荡应与缸内湍流以及局部燃烧有关^[13-14]。进一步统计表明，25%负荷下的压力振荡持续了约27°CA，40%负荷下的压力振荡持续了约23.2°CA，而50%负荷下的压力振荡持续了约17.1°CA。可见，压力振荡的持续时间随发动机负荷的增加而明显缩短。由于喷射参数的影响以及减少的换气时间，负荷和转速的提升引起了低速机压力振荡的减小。

3 结　语

1）船用长冲程低速柴油机健康状态下，低负荷工况点运行的振动特征趋于一致。25%与40%负荷下，各单次燃烧循环的加速度均方根值基本相同，约为3～6 m/s²，波动较小。

2）50%负荷以上时，燃烧循环引起振动的不稳定性增强，加速度均方根值开始出现波动，范围为4.3～8.2 m/s²。峭度统计结果与均方根值统计结果均可作为健康状态诊断的特征指标。

3）提出的WPES-MEEMD方法可有效提取低速机的振动特征。在50%的常用推进工况下，发现中高频能量占总能量的41.51%，为低速机的主要振动源。

4）低速机存在燃烧压力振荡，且持续时间随负荷的增加而下降，产生的中高频能量对低速机的振动和噪声优化具有重要作用。