2. 中国船舶集团有限公司第七一三研究所,河南 郑州 450052
2. The 713 Research Institute of CSSC, Zhengzhou 450052, China
半潜式平台具有稳性好、抗风浪能力强、甲板面积大、可变载荷大、适用水深范围广等优点,是世界上应用广泛、最具有发展前途的一种平台[1]。半潜式平台在油气开发和浮式风机开发方面具有不少的应用。
半潜式平台主要由浮体、立柱、横撑、甲板等结构组成,油气开发式的多采用四立柱式。在水动力方面,张剑锋等[2]利用Ansys AQWA对四立柱式半潜式平台进行了水动力性能及时域耦合分析,发现平台性能满足设计要求。陈鹏等[3]应用AQWA对第6代深水半潜式钻井平台水动力性能及极端工况的系泊性能进行数值计算。周红杰等[4]利用AQWA对浮式风机三浮筒式平台考虑风、浪、流载荷的联合作用,对平台的动态响应进行数值模拟分析,得到了F-K力(波浪力)和绕射力对平台6个自由度运动的影响以及各波浪力随波浪频率的变化趋势。
在平台结构方面,史俊奇等[5]研究了立柱纵向增加附体以及改变附体形状对半潜式平台水动力性能的影响,通过数值计算和模型试验,发现纵向立柱附体可以减小平台纵向平均波浪力以及平台的纵摇运动 RAO,可显著改善平台在极端海况下的垂向运动响应,立柱附体的截面形状变化则几乎没有影响。张文旭等[6]分别对立柱、连接横撑以及下浮筒进行多方案设计,共组合得到8个平台设计方案。应用数值方法首先对A1方案完成性能计算,并与该平台的模型试验结果对比,研究表明,浮体构型对于半潜式平台的运动性能有较大影响,且尖角型浮筒、变截面立柱及圆管型横撑的构型具有更优的综合运动性能。Coulling 等[7]利用 FAST 软件对 DeepCwind 半潜式基础浮式风机的动力响应问题进行了研究,对风机性能、塔柱的形状及振动频率、粘性阻尼以及系泊回复力进行验证分析。Masciola等[8]专门研究了系泊动力效应对 DeepCwind 半潜式基础浮式风机动力响应的影响。在当前海上浮式风机半潜式平台中,美国可再生能源实验室(NREL)开发的DeepCwind型号半潜式平台为较为广泛流行的设计。探究DeepCwind型号半潜式平台结构变化对其水动力性能影响具有一定的意义,为未来海上浮式风机的平台基础开发提供一些参考,有利于我国未来新能源开发。
1 平台计算理论 1.1 运动方程在半潜式平台水动力计算中,假设流体无黏、无旋、不可压缩,基于势流理论计算分析。速度势函数满足拉普拉斯方程,考虑自由水面和不可穿透的物面边界条件,采用满足自由水面条件的频域计算格林函数,采用边界元法计算速度势函数。按照Bernoulli公式计算物体湿表面上的压力分布。
引入在简谐波作用下平台运动的系统线性假定,进一步确定平台的运动响应。在单位波幅的规则简谐波作用下,浮体的响应函数为:
| $ R(\omega,t)=ARe\left\{\left|H\left(\omega\right)\right|\exp[i(\omega t+\varphi)]\right\}。$ | (1) |
式中:A为入射波波幅;ω为谐波圆频率;t为时间参量;j为谐振初始相位;H(ω)为传递函数RAO。
结构物的运动响应谱计算公式为:
| $ {S_r}\left( \omega \right) = {S_\omega }\left( \omega \right){\left| {H\left( \omega \right)} \right|^2} 。$ | (2) |
式中:Sω(ω)为波谱密度函数;Sr(ω)为平台运动响应谱函数。基于以上理论,用谱分析方法可以预报平台在某工况下的运动响应。
1.2 波浪谱常用的不规则波波浪谱有PM谱、JONSWAP谱,其介绍如下:
1)PM谱(Pierson-Moskowiz),其表达式为:
| $ {S_{PM}}\left( \omega \right) = \frac{5}{{16}}H_S^2\omega _P^4{\omega ^{ - 5}}\exp \left\{ { - \frac{5}{4}{{\left( { - \frac{\omega }{{{\omega _P}}}} \right)}^{ - 4}}} \right\} 。$ | (3) |
式中:ωP=2π/Tp,Tp为谱峰周期;PM谱为单参数谱,由Tp决定谱形状。
2)JONSWAP谱,本质上为PM谱的变形,如下:
| $ {S_{JON}}\left( \omega \right) = A{S_{PM}}\left( \omega \right){\gamma ^{\exp \left( { - 0.5{{\left( {\frac{{\omega - {\omega _p}}}{{\sigma {\omega _p}}}} \right)}^2}} \right)}}。$ | (4) |
式中:γ为谱峰升高因子;σ为谱型参数,当波浪频率ω>ωp时,σ=0.09;反之,σ=0.07。A=1-0.287ln(γ)为无因次参数。
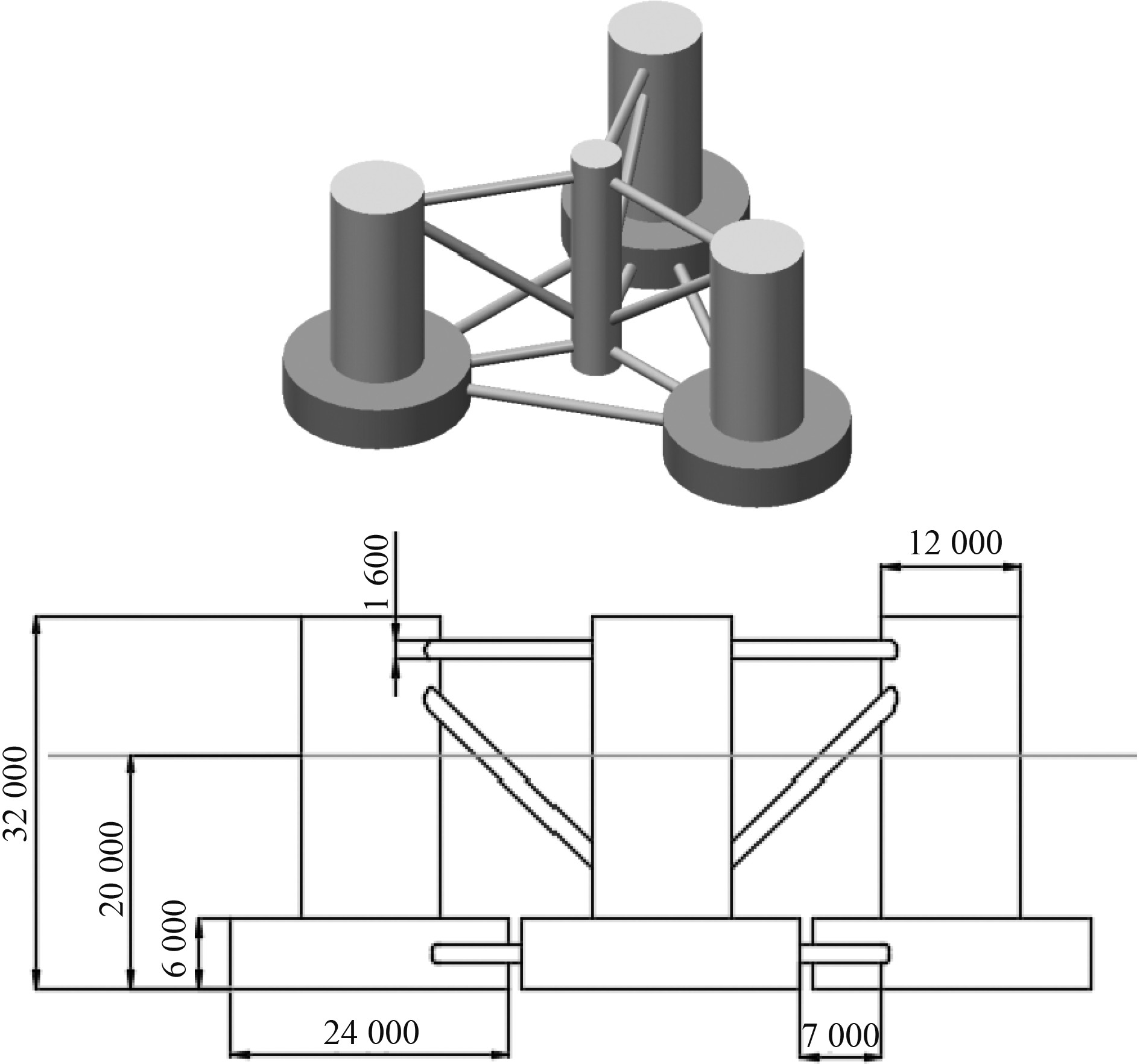
2 平台参数及仿真模型 2.1 平台主要参数研究对象为NREL开发的DeepCwind型号半潜式平台,如图1所示,主要由侧立柱、斜撑、支撑柱等多部分组成。显然,立柱又同时分为底部浮筒与上部浮筒,底部浮筒直径较大于上部浮筒。由于浮筒尺寸会对半潜式平台的水动力性能具有较大影响,因此,考虑将浮筒直径增大,探究其水动力性能变化情况。为便于分析,改造后的平台模型被称为DeepCwind-G。其中,DeepCwind半潜式平台与增大立柱之后的DeepCwind-G半潜式平台模型的主要设计参数如表1所示。
|
图 1 DeepCwind半潜式平台模型(单位:mm) Fig. 1 DeepCwind platform model(unit:mm) |
|
|
表 1 DeepCwind平台和DeepCwind-G平台主要设计参数 Tab.1 The major design parameter of DeepCwind platform and DeepCwind-G platform |
DeepCwind-G半潜式平台仅增大其底部浮筒直径与上部浮筒直径,吃水深度等保持不变。
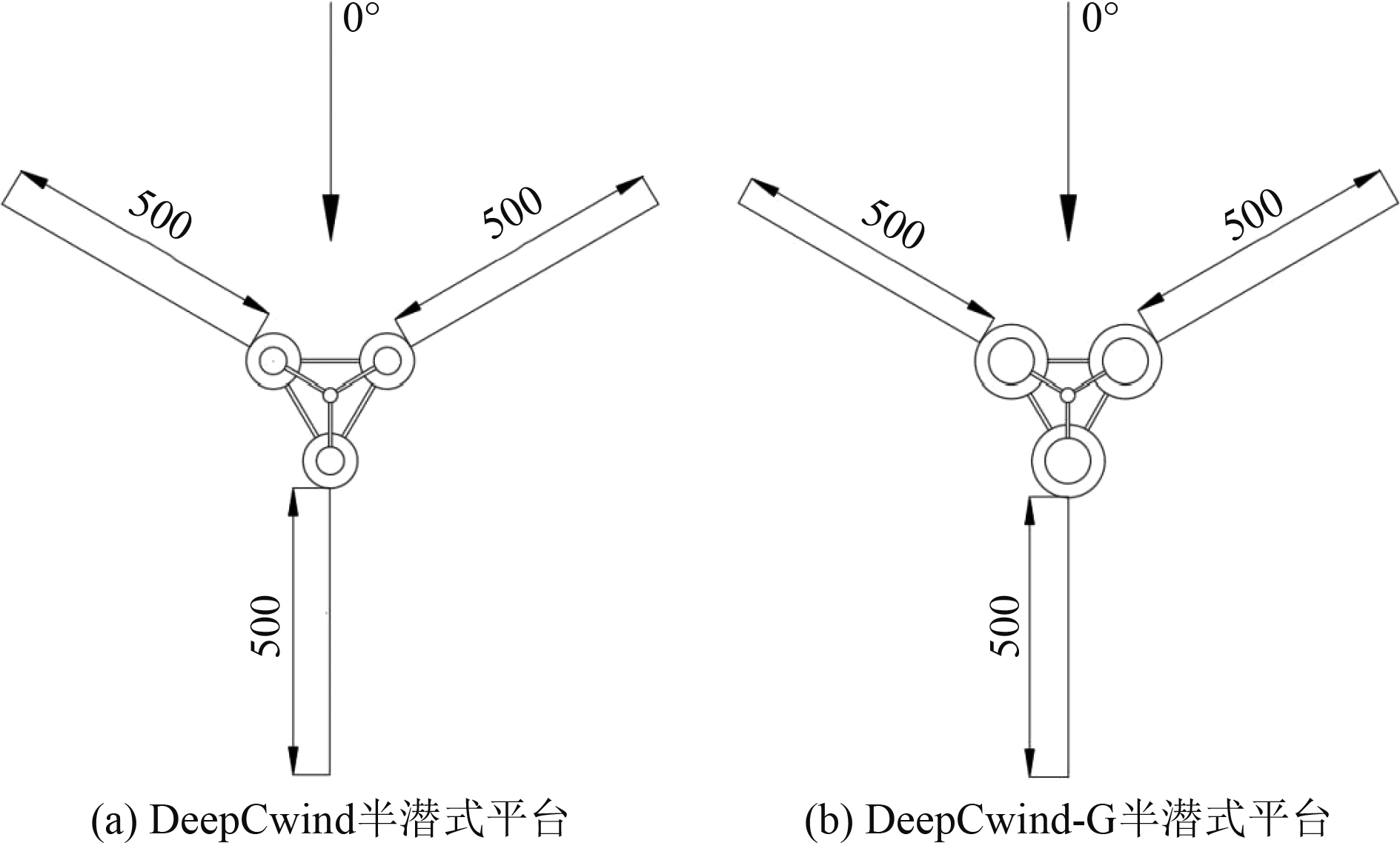
2.3 系泊系统系泊系统采用3根系泊缆绳于半潜式平台周围均匀布置,两两之间呈120°分布,于z轴反方向俯视而看,3根系泊缆绳的分布长度均为500 m,如图2所示。DeepCwind半潜式平台与DeepCwind-G半潜式平台的系泊系统布置相同。
|
图 2 系泊系统(单位:m) Fig. 2 Mooring system (unit: m) |
系泊系统缆绳根据相关规范,选用系泊单缆参数如表2所示[9],而与图2中所示的总缆绳,每根总缆绳由8根系泊单缆组成。
|
|
表 2 系泊系统系泊单缆设计参数 Tab.2 Mooring system mooring single line design parameters |
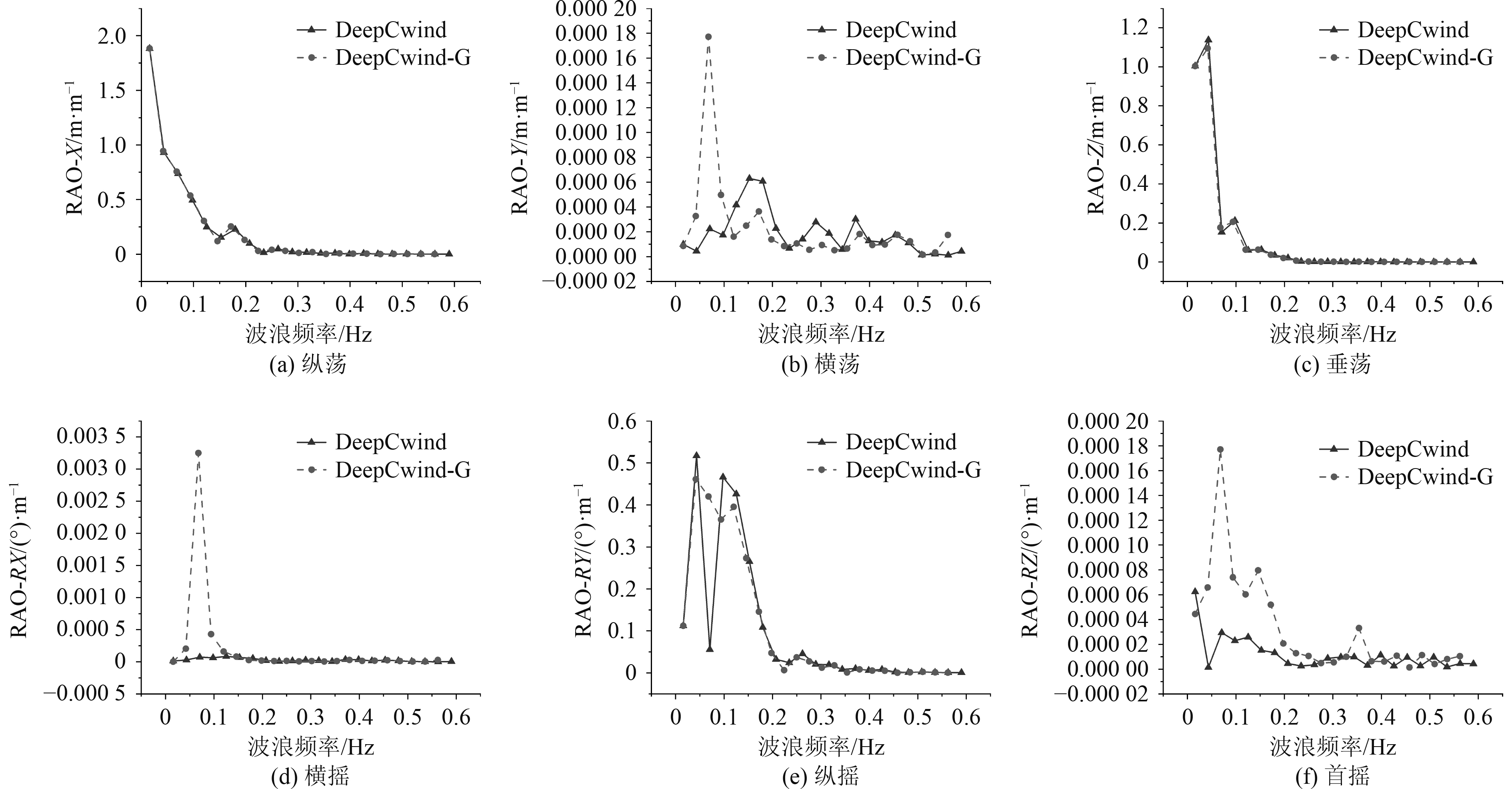
取波频范围在0.016~1.695之间的20个规则波频作为设计波,波浪方向−180°~180°每隔30°作为一波浪方向,利用AQWA-line模块进行规则波频域分析,其中0°方向如图2所示,为沿x轴正方向,各角度逆时针逐渐增加。关注于0°入射方向处DeepCwind半潜式平台和DeepCwind-G半潜式平台的各自由度的RAO(运动幅值响应算子),如图3所示。
|
图 3 两平台0°浪向下的各自由度RAO响应 Fig. 3 Motion responses of RAOs with different degrees of freedom in the 0-degree wave down of the two platforms |
可观察到,在该入射角规则波影响下,两平台的纵荡和垂荡方向自由度差别不大,几乎重合。其他各自由度下,DeepCwind和DeepCwind-G两半潜式平台均表现出对低频波浪响应较为敏感。其中在横荡和横摇自由度下,DeepCwind-G半潜式平台的峰值提前,并比DeepCwind大,横摇自由度尤为明显。纵摇自由度下,低频段波浪作用下的DeepCwind-G半潜式平台运动RAO响应略低于DeepCwind,而高频段两者几乎重合。DeepCwind-G半潜式平台于首摇自由度下RAO响应整体高于DeepCwind半潜式平台。
4 时域耦合分析 4.1 环境条件据国内相关研究表明,南海海况一年一遇的最大波高为2.7 m[10],因此对一年一遇的JONSWAP不规则波对各平台影响进行研究。考虑OC4浮式风机额定风速为11.4 m/s,故采用该平均风速的NPD风谱,并结合0.9 m/s的流荷载,作为环境条件。因此定义风浪流联合作用下的各工况如表3所示。
|
|
表 3 环境条件 Tab.3 Environmental conditions |
系泊系统采用2.3节所示布置,分别对DeepCwind半潜式平台和DeepCwind-G半潜式平台进行表3中各环境工况下的时域分析,进行7 200 s的模拟。由于横荡、横摇和首摇自由度下的运动响应较小,故只关注其余自由度。DeepCwind半潜式平台和DeepCwind-G半潜式平台其他自由度运动响应统计值如表4所示,其中最大值为响应绝对值的最大值。
|
|
表 4 2种平台于纵荡、垂荡、纵摇三自由度运动响应统计值 Tab.4 Statistical values of motion responses of two platforms in surge,heave,pitch,and three degrees of freedom |
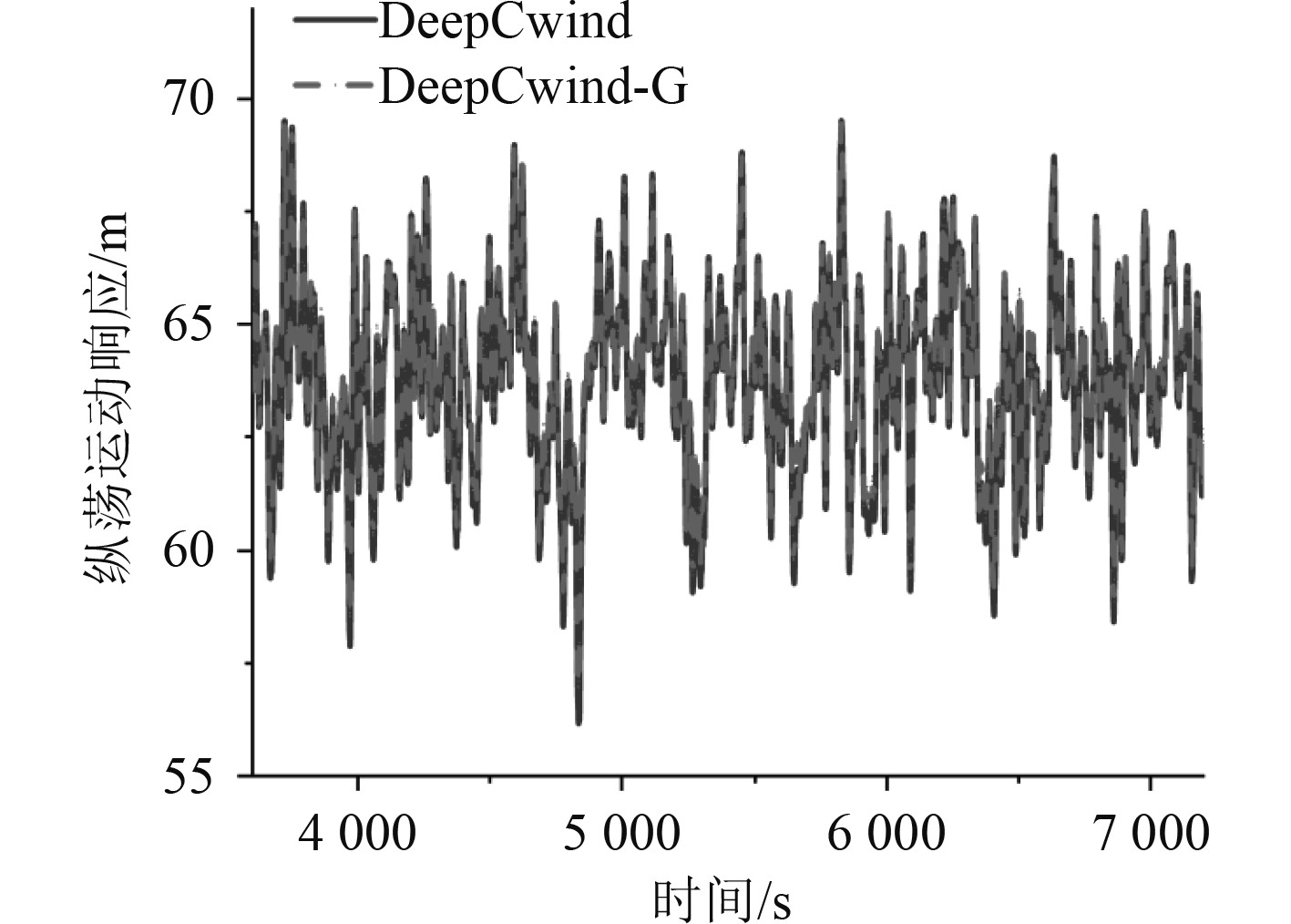
随着不规则波浪谱峰周期的增大,两平台的运动响应变化趋势基本一致,其中平均值方面,纵荡、垂荡自由度运动响应逐渐减小,纵摇则相反。最大值方面,纵荡、垂荡和纵摇自由度运动响应均随不规则波浪谱峰周期的增大而增大。在纵荡自由度下,各工况下,DeepCwind半潜式平台运动响应平均值均低于DeepCwind-G半潜式平台,最大值方面两者运动响应大小与周期相关,低周期情况下DeepCwind半潜式平台运动响应高于DeepCwind-G半潜式平台,高周期与之相反。而在垂荡、纵摇自由度方面,DeepCwind半潜式平台运动响应平均值低于DeepCwind-G半潜式平台,而最大值绝对值则与之相反。如图4~图6所示,分别为DeepCwind半潜式平台和DeepCwind-G半潜式平台之间在1工况下的纵荡、垂荡、纵摇运动响应的时域分析响应时历曲线。
|
图 4 纵荡运动响应时历曲线 Fig. 4 Time-history curve of the surge motion response |
|
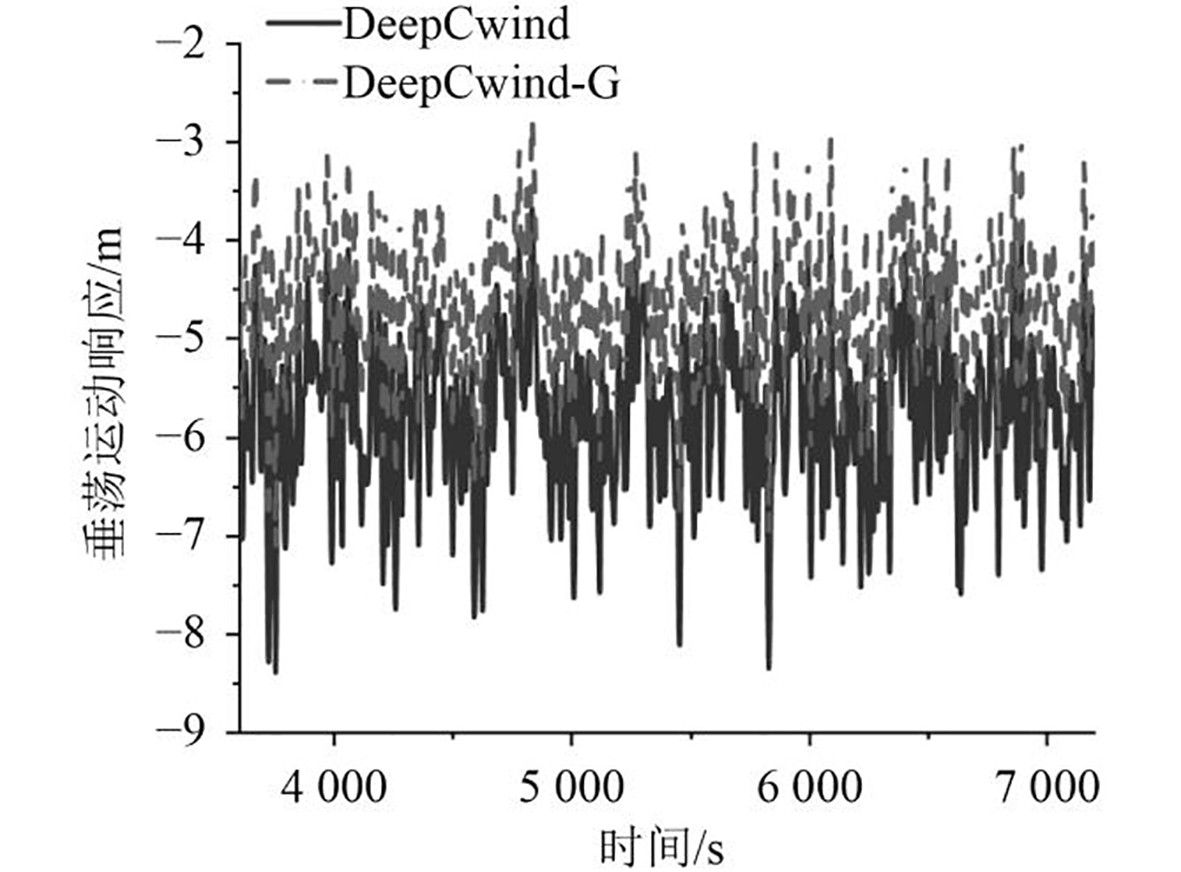
图 5 垂荡运动响应时历曲线 Fig. 5 Time-history curve of the heave motion response |
|
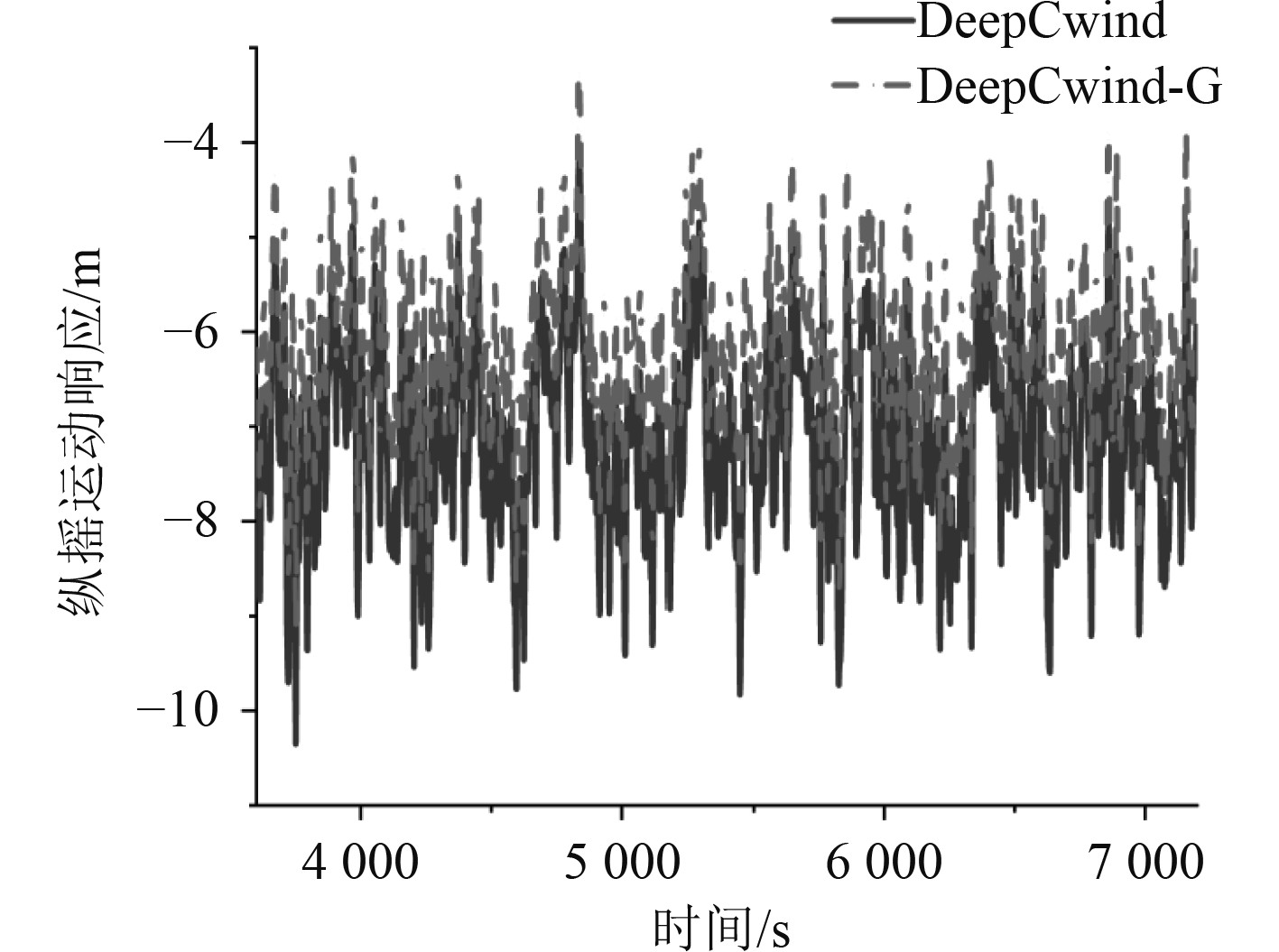
图 6 纵摇运动响应时历曲线 Fig. 6 Time-history curve of the pitch motion response |
为便于分析与展示,图4~图6仅表示出3 600 ~7 200 s时间段之间,DeepCwind半潜式平台和DeepCwind-G半潜式平台在纵荡、横荡和纵摇自由度下的运动响应时历曲线。显然,相比DeepCwind半潜式平台,立柱增大后的DeepCwind-G半潜式平台的纵荡、垂荡和纵摇整体向上偏移,即在平均值方面,增大立柱使得主要运动响应平均值增大。而平均值绝对值方面,增大立柱使得垂荡和纵摇运动响应值减小。
4.3 系泊系统校核表5和表6,分别反映DeepCwind半潜式平台和DeepCwind-G半潜式平台各工况下系泊缆绳最大张力的情况。在上述环境条件下,缆1受力较小,而由于对称布置且荷载处于对称轴上,因此缆2和缆3的顶端张力大小接近。2种平台之间缆绳顶端张力对比发现,DeepCwind-G半潜式平台的缆1顶端张力低于DeepCwind半潜式平台,而缆2和缆3则均高于DeepCwind半潜式平台。显然,两半潜式平台的各工况下的系泊单缆的最大张力均低于单缆断裂张力,满足强度要求,系泊系统设计布置较为合理。
|
|
表 5 DeepCwind半潜式平台各工况下系泊单缆绳最大张力 Tab.5 Maximum tension of single mooring rope under each working condition of DeepCwind platform |
|
|
表 6 DeepCwind-G半潜式平台各工况下系泊单缆绳最大张力 Tab.6 Maximum tension of single mooring rope under each working condition of DeepCwind-G platform |
1)DeepCwind和DeepCwind-G两半潜式平台均表现出对低频波浪响应较为敏感,在低频波浪设计波作用下运动值较大;
2)频域分析发现,两者在纵荡和垂荡方向差别不大,增大立柱后,横荡和横摇、首摇自由度峰值提前且增大,高频段趋于一致,纵摇自由度在低频略低于原DeepCwind半潜式平台。
3)在风浪流联合作用下,荷载方向一致为0°时,两者纵荡、垂荡和纵摇主要自由度运动响应最大值均随不规则波浪谱峰周期的增大而增大,平均值方面,纵荡、垂荡自由度运动响应逐渐减小,纵摇则相反。
4)一定环境条件下,增大立柱使得平台的垂荡、纵摇方向的运动响应平均值绝对值和最大值绝对值均减小,有利于抑制该两方向的运动,而纵荡自由度,增大立柱使得平均值增大,最大值情况与不规则波频谱周期相关,周期越大,对其最大值增大效果越明显。
| [1] |
王天英, 王树青. 一种新型半潜式平台概念设计研究[J]. 海洋工程, 2020, 38(5): 134−141.
|
| [2] |
张剑锋, 陈海泉, 孙玉清, 等. 基于 AQWA 的半潜式平台动力特性分析[J]. 船舶工程. 2016(S2): 174−176+240.
|
| [3] |
陈鹏, 马骏, 黄进浩, 等. 基于 AQWA 的半潜式平台水动力分析及系泊性能计算分析[J]. 船海工程, 2013, 42(3): 44. |
| [4] |
周红杰, 李春, 郝文星, 等. 半潜式平台浮式风力机的动态响应[J]. 热能动力工程, 2017, 32(2): 113. |
| [5] |
史俊奇, 肖龙飞, 杨立军, 等. 立柱附体对半潜式平台水动力性能的影响[J]. 船舶力学, 2018, 22(10): 1205−1212.
|
| [6] |
张文旭, 陆超, 李亚军, 等. 深海半潜式平台不同构型的运动性能[J]. 中国舰船研究, 2015, 10(5): 27. |
| [7] |
COULLING A J, GOUPEE A J, ROBERTSON A N, et al. Validation of a FAST semi-submersible floating wind turbine numerical model with DeepCwind test data[J]. Journal of Renewable and Sustainable Energy, 2013, 5(2): 023116. DOI:10.1063/1.4796197 |
| [8] |
MASCIOLA M, ROBERTSON A, JONKMAN J, et al. Assessment of the importance of mooring dynamics on the global response of the DeepCWind floating semisubmersible offshore wind turbine[C]//Proceedings of Twenty-third International Offshore and Polar Engineering, June 30-July 5, 2013, Anchorage, Alaska, USA.
|
| [9] |
孙丽萍, 牛之友, 刘子健, 等. 半潜式平台耦合动力响应分析[J]. 舰船科学技术, 2016(5): 5+. |
| [10] |
郑崇伟, 周林. 近10年南海波候特征分析及波浪能研究[J]. 太阳能学报, 2012, 33(8): 1349-1356. |
 2024, Vol. 46
2024, Vol. 46
