由于海洋环境的复杂性以及水下作业的危险性,在开发利用各种海洋资源的过程中,许多危险的水下作业如环境参数的测量获取、海底地貌地形的勘探等等,都已逐渐由水下机器人替代。水下机器人是一种具有操作灵活、续航时间长等优点的较为有效的深海探测装置,已成为执行耗时的监测任务、军事应用等方面的重要工具[1]。此外,螺旋桨作为一种简单且实用的推进装置,也越来越多应用于水下机器人系统中,通过多个螺旋桨进行差动配合还能实现运动轨迹与航行姿态的控制,其研究也呈现出不断发展的趋势。
近年来,螺旋桨在非设计情况下,水动力性能日益受到关注。在改变航行方向、洋流的不规则流动等因素的影响下,会加剧螺旋桨附近流场的随机性与不均匀性,从而影响螺旋桨推力的稳定性及其推进效率。因此,对螺旋桨在斜向来流下的情况下,水动力性能研究在水下机器人系统、水下拖曳体系统、船舶等领域具有重大意义。在流体力学的研究方面,数值模拟实验近年来逐渐成为主流之一,数值模拟实验既克服了理论分析不能解决复杂流场问题的缺陷,又避免了物理模型实验的高成本与严苛条件要求,具有适应性强、应用面广的特点。目前,流体力学中各类问题已广泛运用计算流体力学(CFD)方法进行数值模拟分析[2]。李想等[3]对DTMB4679螺旋桨进行了非定常数值计算,并与敞水工况下的计算结果进行对比,分析了斜流中船后,螺旋桨的伴流场和压力分布规律。张文照等[4]对不同进速和攻角下的潜艇螺旋桨进行水动力计算,进而对螺旋桨水动力预报问题进行研究,但缺乏对于桨盘面流场结果的分析。VARTDAL等[5]对比分析了不同来流角度下,螺旋桨所受的横向流体力及螺旋桨绕轴心扭矩的变化规律。张嶔等[6]采用延迟分离涡模拟和滑移网格相结合的方法,对小角度斜流下导管桨和螺旋桨尾流场进行模拟分析,发现导管具有对不稳定流动的屏蔽效果,从而使得导管螺旋桨的尾流倾斜角度较普通螺旋桨小,但文中并没有考虑船桨一体时伴流场的影响。
已有研究通常只单独模拟计算了斜流中螺旋桨自身的水动力性能,忽略了水下运动主体运动产生的伴流场影响。本文采用滑移网格技术,对某水下机器人整体在斜流中航行进行数值模拟,对斜流中水下机器人的导管桨水动力性能和流场特性进行分析研究。
1 水下机器人CFD仿真的基本原理 1.1 控制方程本文所研究的螺旋桨运动速度较低,周围的流体可近似为不可压缩粘性流体,只考虑流场的连续性方程和动量方程,不计入能量方程,控制方程形式如下[7]:
连续性方程
| $ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0,$ | (1) |
动量方程
| $ \begin{split} \rho \left(\frac{\partial {u}_{i}}{\partial t}+\frac{\partial \left({u}_{i}{u}_{j}\right)}{\partial t}\right)=\,& \rho \frac{\partial }{\partial {x}_{j}}\left[\mu \left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right)-{u}_{i}^{{'}}{u}_{j}^{{'}}\right]+\\ & \rho {g}_{i}-\frac{\partial p}{\partial {x}_{i}}。\end{split} $ | (2) |
式中:
目前,关于螺旋桨粘性绕流场数值计算一般采用
| $ \frac{\partial \left(\rho k\right)}{\partial t} + \frac{\partial \left(\rho k{u}_{i}\right)}{\partial {x}_{i}} + \frac{\partial \left(\rho k\right)}{\partial t}=\frac{\partial }{\partial {x}_{j}}\left[{\mathrm{\Gamma }}_{k}\frac{\partial k}{\partial {x}_{j}}\right] + {G}_{k}-{Y}_{k} + {S}_{k},$ | (3) |
| $ \frac{\partial \left(\rho \varepsilon \right)}{\partial t} + \frac{\partial \left(\rho \varepsilon {u}_{i}\right)}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left\lfloor {{\mathrm{\Gamma }}_{\omega }\frac{\partial \omega }{\partial {x}_{j}}} \right\rfloor + {G}_{\omega } + {D}_{\omega }-{Y}_{\omega } + {S}_{\omega }。$ | (4) |
| $ {{\varGamma }}_{k}=\mu +\frac{{\mu }_{t}}{{\sigma }_{k}},$ | (5) |
| $ {{\varGamma }}_{\omega }=\mu +\frac{{\mu }_{t}}{{\sigma }_{\omega }}。$ | (6) |
式中:
滑移网格法也称刚体运动法(Rigid Body Motion),该方法通过计算区域内网格的旋转来模拟研究对象结构的真实刚体旋转运动,旋转区域与背景静止区域之间的交界面通过相互滑动线性插值来交换传递流场各种物化参数,从而实现2个计算区域之间信息的传通。此外,为了保证数值模拟计算的精度,滑移网格交界面两侧区域的网格尺寸差距不宜过大。
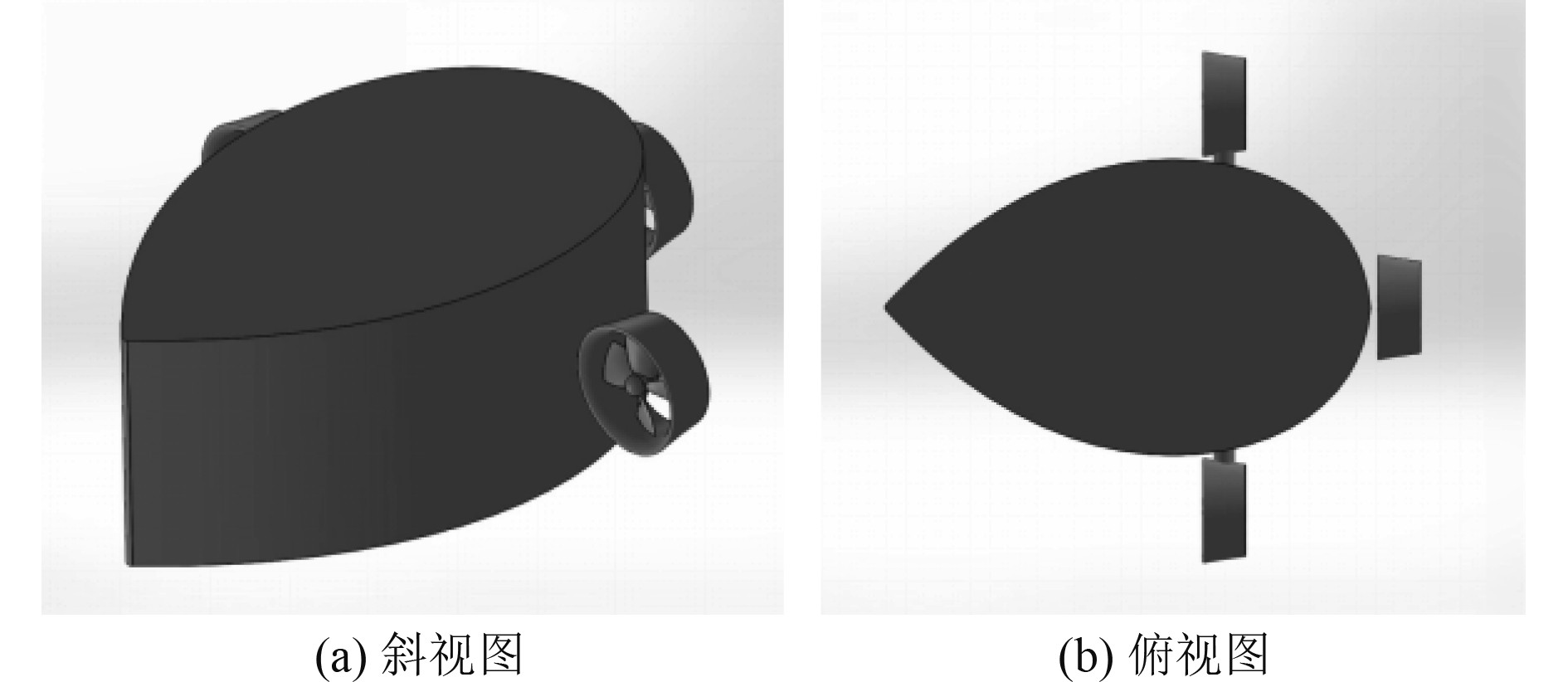
2 计算模型及试验验证 2.1 水下机器人模型分析对象为某自主研发的水滴流线型柱体结构水下机器人,如图1所示。机器人主体部分总长为0.5 m,在离最前端约0.3处达最大宽度0.3 m,机器人的高度为0.2 m。2个导管螺旋桨对称地安装在机器人左右舷侧,用于控制水下机器人的转向运动;第3个导管螺旋桨设置在机器人尾部,主要作用则是为主体产生前进或后退的推力。机器人系统中,导管螺旋桨采用No. 19A导管配以Ka 4-70的标准螺旋桨,参数如表1所示。
|
图 1 水滴流线型柱体结构水下机器人 Fig. 1 Water droplet streamlined column structure underwater robot |
|
|
表 1 Ka 4-70/19A标准导管螺旋桨尺寸数据 Tab.1 Size data for Ka 4-70/19A standard ducted propeller |
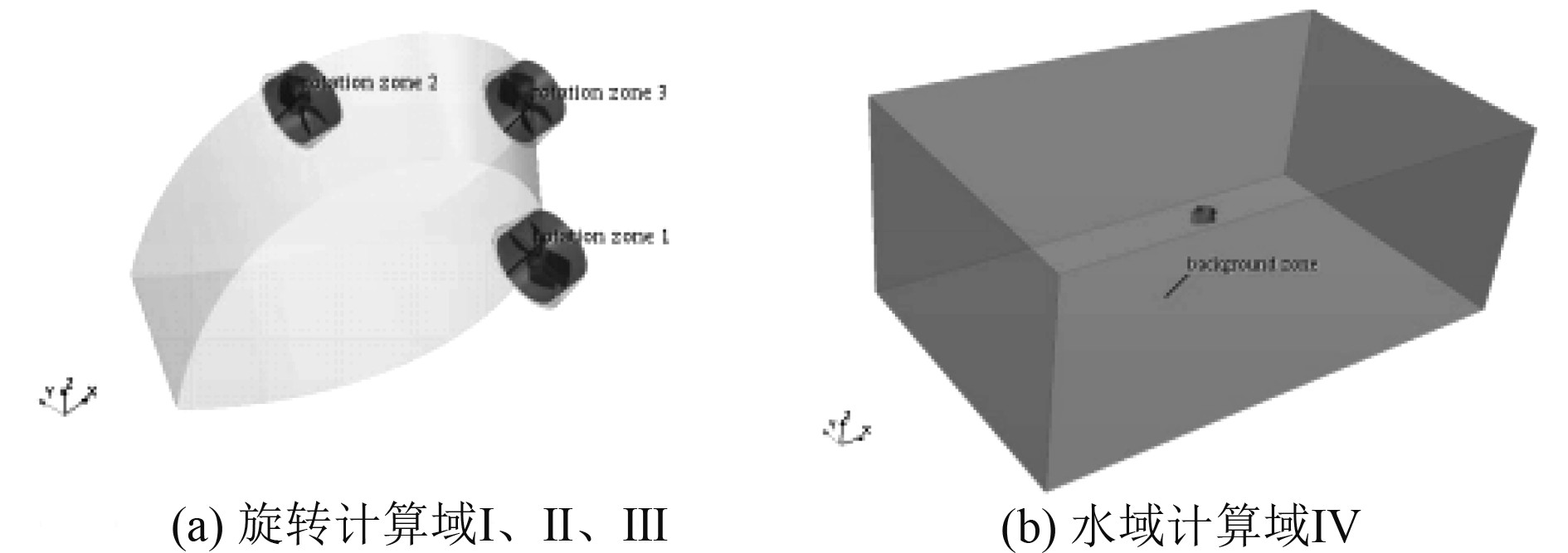
本文采用STAR CCM+软件对水下机器人在斜流环境下航行所表现出来的水动力特性,为此设置如图2所示的计算域。计算中采用相对运动原理,将机器人置于计算域中间,来流参数通过边界条件来规定。当流域中的水以一定的流速从进口流向出口时,根据相对运动原理,水下机器人可视为在水中向前运动,从而模拟其运动状态。整个计算域划分为分别包含3个螺旋桨的旋转计算域Ⅰ、Ⅱ、Ⅲ,以及包含整个数值试验水池的开放水域计算域Ⅳ。其中,旋转计算域Ⅰ、Ⅱ、Ⅲ均是长度为48 mm,直径为102%螺旋桨直径的圆柱体,开放水域计算域Ⅳ是长为10 m、宽为6 m、高为4m的长方体。计算域Ⅳ尺度是从足够避免机器人周围与边界流场之间的干扰,同时减少计算工作量这2个因素综合考虑而确定的。图2为整体计算域划分示意图。
|
图 2 计算域划分示意图 Fig. 2 Calculation domain division diagram |
1)边界条件的设置
对于数值计算模型,组合计算区域及其各子区域的边界条件恰当设置是保证计算精度的重要一环。本文数值模型中各计算区域的边界条件设置,如表2所示。
|
|
表 2 边界条件的设置 Tab.2 Setting of boundary conditions |
2)时间步长的选择
时间步长的合理选择对水下机器人模拟,尤其是螺旋桨水动力特性模拟的计算效率和计算质量有极大影响,时间步长过大容易出现数值计算难以收敛、网格负体积、导致计算发散等现象;反之,时间步长过小将需要更多的数值计算迭代时间,严重降低计算效率。因此,在时间步长的设置上需在效率与精度上平衡取舍,避免因步长过大而导致出现负体积网格。
对于一些简单的运动,时间步长可依照下式进行估算:
| $ \Delta t=\frac{\Delta x}{u} 。$ | (7) |
式中:
根据过往经验,对于处于螺旋桨旋转运动的数值模拟,时间步长选择为转速倒数的1/10时可得较好的模拟结果,其中,ω为转速,rad/s。
| $ \Delta t=\frac{1}{10\omega }。$ | (8) |
本文模拟中,导管螺旋桨转速为1 000 r/min,参照对比上面2个公式计算结果后,故在后续的数值模拟中时间步长取值为0.001 s。
2.4 网格无关性验证本文采用切割体网格类型。根据所需的运动状态不同,创建了2种不同尺寸大小的网格连续体。由于旋转流场计算域涉及到旋转运动,网格的精度对模拟结果关系极大,因此旋转流场计算域采用的网格连续体更加细致;而开放水域计算域中的流体流动较简单,适当增加网格尺寸以减少网格数量,从而提高计算效率。除划分体网格外,还需对导管螺旋桨叶片、水下机器人模型各交界面等局部网格进行加密。通过网格的局部体积控制,以减少因网格带来的误差。
此外,本文对导管螺旋桨的数值模拟还进行了网格无关性检验,进行验证时,导管桨的转速设置为1 000 r/min,来流速度设置为0.5 kn,结果如表3所示。通过数据对比分析可观察出,在不同网格生成策略下,随着网格尺寸的精细与网格值增加,各数值计算结果相对于网格生成策略1的相对偏差值逐渐减小。可发现,螺旋桨表面网格尺寸小于0.06 mm时,网格尺寸对结果的影响已小于2%,可认为此时的网格已达到无关性的要求。为了提高效率与节约计算成本,本文的后续水下机器人系统的数值模型中,采用策略3的网格生成策略。水下机器人系统数值计算模型的网格总数约为477万,具体流场与水下机器人系统的网格划分情况,如图3所示。
|
|
表 3 网格无关性验证 Tab.3 Grid independence verification |

|
图 3 网格划分示意图 Fig. 3 Diagram of grid division |
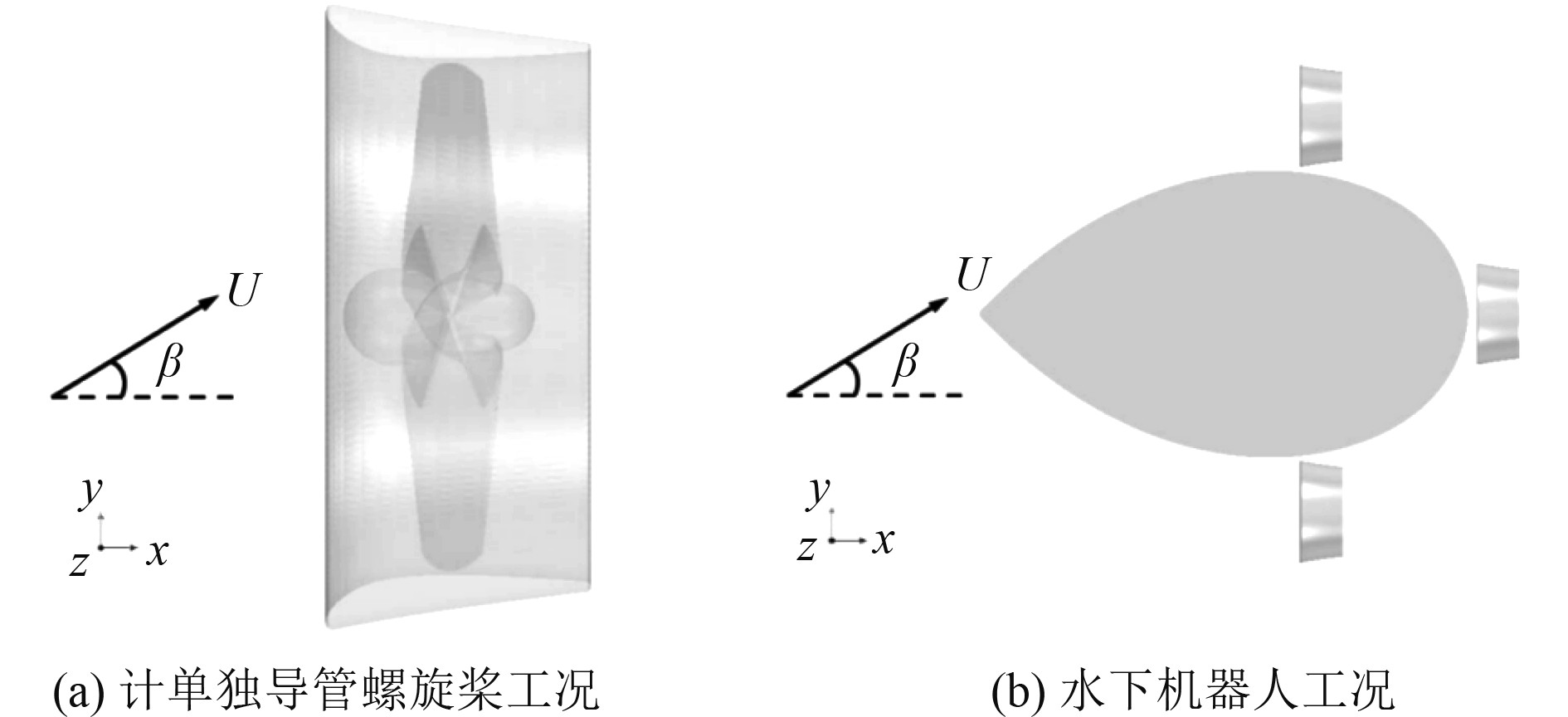
本节对水下机器人系统在不同的斜流环境条件下,以左、右、后3个导管螺旋桨为观察对象,对在水下机器人主体流场影响下,导管螺旋桨所发出的推力进行分析,观察在不同斜流工况下,旋桨旋转一周时间段内所发出的推力时间历程、推力峰谷值的变化规律、不同导管螺旋桨所发出的平均推力变化特征,研究机器人主体对螺旋桨推力要素的影响规律。作为对比,本节还给出了没有考虑机器人主体时,单独导管螺旋桨在相同工况下随斜流角变化所产生的推力。计算中,来流速度取为0.514 m/s,各螺旋桨转速为16.67 r/s,斜流角分别取为0°、15°、30°。图4给出了斜流角的定义,表4给出的是本文计算工况的定义。
|
图 4 斜流角的定义 Fig. 4 Definition of oblique flow angle |
|
|
表 4 计算工况 Tab.4 Calculation conditions |
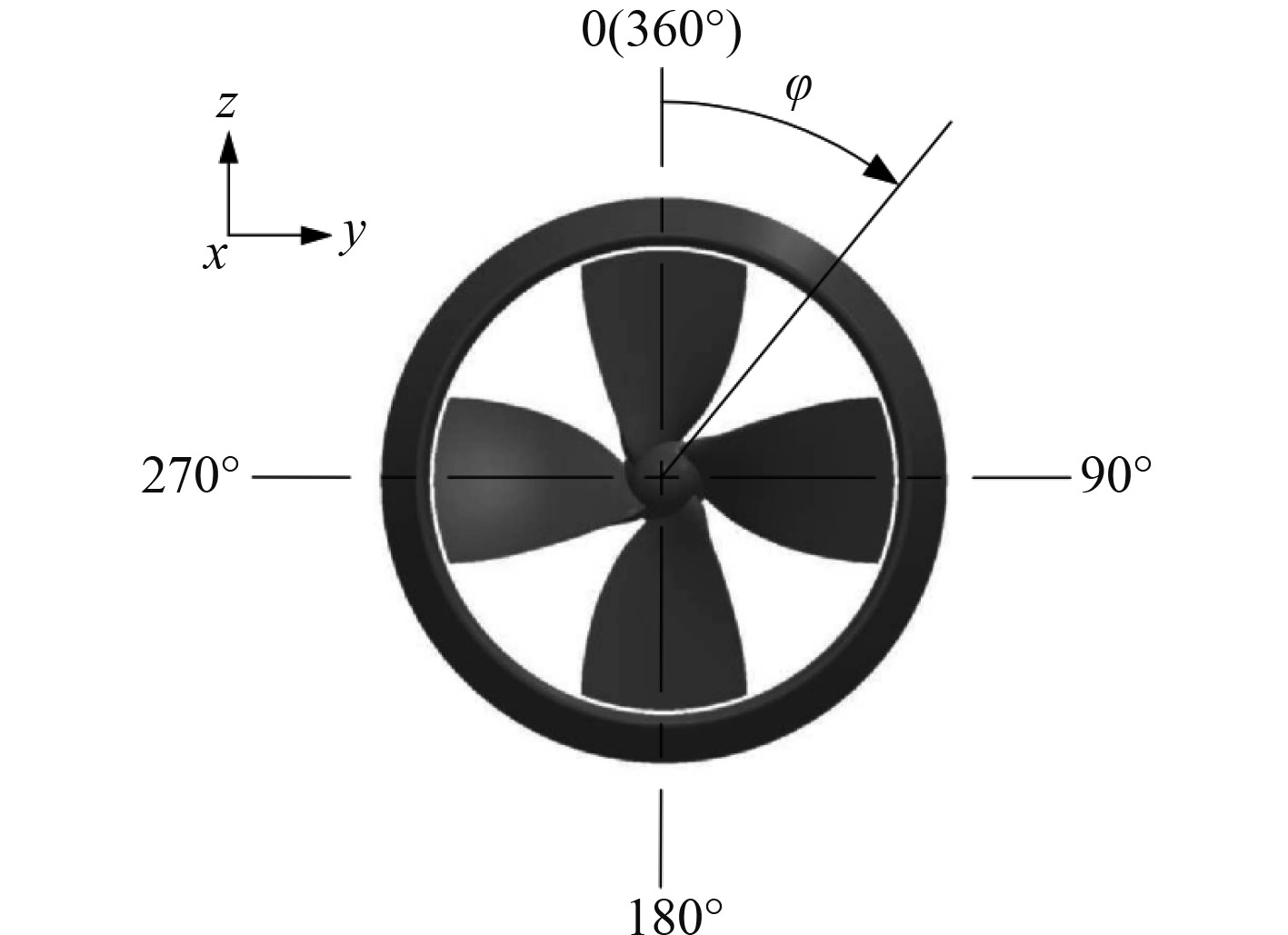
图5给出了各工况不同斜流角下,各导管螺旋桨旋转一周时间段内计算桨叶所发出的推力时间历程。图5中横坐标值为计算桨叶的相位角,其定义见图6。从图5的计算结果可发现有如下规律:

|
图 5 导管螺旋桨一个旋转周期内推力变化时间历程 Fig. 5 Time history of thrust variation of ducted propeller in one rotation cycle |
|
图 6 桨叶的相位角定义 Fig. 6 Definition of phase angle of paddle blade |
1)不论是在哪种斜流角度下,单独导管螺旋桨与水下机器人系统中的导管螺旋桨推力计算结果,都会在一个旋转周期出现4个振荡波峰与4个振荡波谷值。这是因为本文水下机器人系统所采用的导管螺旋桨为四叶桨,在每一个螺旋桨旋转周期内,4个桨叶都会相继旋转至同一相位角度,从而在推力计算结果中,表现出一个旋转周期拥有4个推力峰谷值。
2)在不同的斜流角来流工况下,3个处于机器人不同部位的螺旋桨旋转一周表现出了不同推力振荡特征。对比图5(b)~图5(c)的结果可看出,机器人尾部的导管螺旋桨(后导管螺旋桨)所发出的推力振荡平均值与峰谷差值均大于左、右导管螺旋桨。这一水动力现象表明机器人主体在斜流条件下所形成的流场对后导管螺旋桨的影响要大于左、右导管螺旋桨。实际上,由于主体的阻挡,处在机器人尾部的后导管螺旋桨所感受到的进速要小于左、右两侧的导管螺旋桨。因为后导管螺旋桨叶流体进速的降低,从而在相同的流场工况下,其桨叶切面所受到的水动力攻角要大于左、右导管螺旋桨,所发出的推力自然也大于两侧导管螺旋桨。
3)对于左、右导管螺旋桨,在不同的斜流工况下,表现出了不同的推力幅值特征,沿桨轴向来流工况(斜流角为0°)下,导管螺旋桨发出的推力要小于斜向来流(斜流角为15°、30°)工况。而对于后导管螺旋桨,其推力振荡形态与来流斜流角的大小关系不明显。就本文模型而言,导致3个导管螺旋桨在不同斜流环境条件下所表现出的这些不同推力幅值与振荡幅值特征的主要原因,也是由于机器人主体对3个处于不同位置的导管螺旋桨、不同流场干扰而造成的。对于左、右导管螺旋桨,在斜流工况下所受到的机器人主体流场干扰相对较小,它们所发出的推力变化特征主要与斜流角的大小相关。对于相同的来流速度,斜流角越大,来流在桨轴的轴向速度分量越小,导管螺旋桨所感受到的进速也越小,螺旋桨叶切面所受到的水动力攻角就越大,所发出的推力也就越大,所以斜流角度越大,螺旋桨产生的推力也就越大。而对于后导管螺旋桨,由于受到机器人主体阻挡,斜流角的改变对其所发出的推力影响就较小。
为了解机器人主体影响下,机器人系统中不同位置导管螺旋桨平均推力特性,表5给出了各斜流工况下,单独导管螺旋桨与在机器人系统中不同位置的3个导管螺旋桨所产生的平均推力。从表5的结果可以看出,对于单独导管螺旋桨(工况1 ~ 工况3),它所产生的推力是随着斜流角角度的增加而增大;对于机器人系统中的3个导管螺旋桨(工况4 ~ 工况6),左、右导管螺旋桨所产生的推力同样是随着斜流角角度的增加而增大;但位于水下机器人尾部的后导管螺旋桨在不同的斜流工况下,螺旋桨产生的推力值几乎没有变化;左、右导管螺旋桨产生的推力略小于无主体影响的单独导管螺旋桨,而后导管螺旋桨产生的推力值则远大于左、右导管螺旋桨。
|
|
表 5 各斜流工况下各导管螺旋桨产生的平均推力比较 Tab.5 Comparison of average thrust generated by ducted propellers under different oblique flow conditions |
不管是单独还是机器人系统中的左、右导管螺旋桨,它们所产生的推力随着斜流角角度的增加而增大,后导管螺旋桨推力大于左、右导管螺旋桨的原因与对图5结果讨论的水动力原理类似。左、右导管螺旋桨产生的推力略小于无主体影响的单独导管螺旋桨的原因,在于本文计算的水滴流线型柱体结构水下机器人主体两侧形成具有一定向后速度的负伴流,使得两侧螺旋桨的轴向进速增加,叶切面所受到的水动力攻角也会相应地减小,因此其推力也小于单独导管螺旋桨。
3.2 桨叶表面压力分布结果分析图7和图8分别为各工况不同斜流角度下,螺旋桨叶背和叶面表面压力分布云图。观察图7叶背表面压力分布云图可知,随着斜流角度的增加,水螺旋桨和机器人左右两侧螺旋桨的叶背表面压力比较相似,叶背中心和叶根处压力变化较为均匀平缓,在叶根叶梢处有明显的低压区,叶背导边处变化梯度较大。而位于水下机器人尾部的螺旋桨本身处于后方的非均匀伴流中,同时受到斜流与两侧螺旋桨尾流的影响,叶背的压力分布基本一致,但压力绝对值明显大于其他螺旋桨,压力梯度变化较大。而从图8的螺旋桨叶面表面压力分布云图观察到,图中各螺旋桨叶面的压力分布都比较均匀,无明显突变,叶面相对于叶背为高压面,导边处的叶面和叶背压强差最大,导边提供了最大推进力。

|
图 7 螺旋桨叶背表面压力分布云图 Fig. 7 Pressure distribution nephogram of propeller blade back surface |

|
图 8 螺旋桨叶面表面压力分布云图 Fig. 8 Pressure distribution nephogram of propeller blade surface |
总的来说,在不同斜流角度的来流情况下,螺旋桨沿横向和纵向的桨叶压力分布存在着不同程度的非对称性,从而会增加螺旋桨轴承力的不均匀性且有所损害螺旋桨的激振力稳定性。
4 结 语1)本文采用的数值计算方法对斜流中水下机器人的导管桨水动力性能有效。
2)在斜流中,随着斜流角度在一定范围内增加,螺旋桨产生的推力也会相应地有所增加。
3)随着斜流角度的增加,斜方来流那一侧的轴向速度增加,导致伴流场的不均匀性与周向速度分布不均匀,从而对螺旋桨的推进效率与空泡性能产生不利影响。
4)在不同斜流角度的来流情况下,螺旋桨沿横向和纵向的表面压力分布,存在着不同程度的非对称性,从而会增加螺旋桨轴承力的不均匀性且有所损害螺旋桨的激振力稳定性。
| [1] |
王永鼎, 王鹏, 孙鹏飞. 自主式水下机器人控制技术研究综述[J]. 世界科技研究与发展, 2021, 43(6): 636-648. DOI:10.16507/j.issn.1006-6055.2021.01.004 |
| [2] |
SIMEONI P , SARRAZIN J , NOUZE H , et al. Victor 6000: new high resolution tools for deep sea research. «Module de Mesures en Route»[M]. 2007.
|
| [3] |
李想, 万民, 吉志伟. 斜流中船后螺旋桨水动力性能及伴流场研究[J]. 舰船科学技术, 2022(2). |
| [4] |
张文照, 肖昌润. 斜流中艇后螺旋桨水动力数值计算方法[J]. 舰船科学技术, 2014. DOI:10.3404/j.issn.1672-7649.2014.02.012 |
| [5] |
VARTDAL B J, GJESTLAND T, ARVIDSEN T I. Lateral propeller forces and their effects on shaft bearings[C]// First International Symposium on Marine Propulsors. 2009.
|
| [6] |
张嶔, 何聪, 许情, 等. 小角度斜流下导管桨/螺旋桨尾流场数值分析[J]. 哈尔滨工程大学学报, 2022, 43(8). |
| [7] |
VERSTEEG M. An introduction to computational fluid dynamics: the finite volume method[M]. Wiley, New York, 1995.
|
| [8] |
A S C S , B D M E , C W C W. Design and characterization of a small-scale azimuthing thruster for a mobile offshore base module[J]. Marine Structures, 2001, 14(1–2): 215-229.
|
| [9] |
吴家鸣, 赖宇锋, 李江伟, 等. 水下潜器系统导管螺旋桨水动力特性及周围流场分布预报与分析[J]. 船舶力学, 2018, 22(5). |
| [10] |
王楠. 导管桨水动力性能的数值分析[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [11] |
胡洋, 胡健, 刘亚彬. 斜流中螺旋桨的水动力性能研究[J]. 武汉理工大学学报: 交通科学与工程版, 2019, 43(2): 262−268.
|
 2024, Vol. 46
2024, Vol. 46
