2. 深海技术科学太湖实验室,江苏 无锡 214082
2. Taihu Laboratory of Deepsea Technological Science, Wuxi 214082, China
水下无人航行器(Unmanned Underwater Vehicle,UUV)自诞生以来,在海洋资源开发、军事搜索以及水下环境监测方面发挥了重要作用[1]。随着海洋环境资源竞争的日益激烈,在未来很长的一段时间,UUV仍然会承担重要使命。然而,不管何种类型的UUV,其由于体积的限制,导致自身携带的能源有限,需在其能量即将消耗殆尽时进行回收[2]。UUV在对接回收时,受到海洋洋流以及对接装置的干扰,这就对其航行操控提出了严格要求。鉴于此,为了提高UUV对接回收的成功率,实现有效控制和回收[3],必须对UUV动态回收过程中的流体动力演化规律进行探索。
本文以二维回转体为研究对象,借助商业软件Fluent中的重叠网格技术对二维回转体垂向回收的动态过程进行数值模拟研究。通过改变二维回转体垂向运动速度以及俯仰攻角,分析不同运动姿态下二维回转体流体动力演变规律。
1 数值方法UUV作业的环境一般满足粘性不可压缩条件,其周围的流体可用N-S方程表征。粘性N-S方程表达式如下[4]:
| $ \frac{{\partial {{\overline u }_i}}}{{\partial {x_i}}} = 0,$ | (1) |
| $ \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \frac{{\partial \overline {{u_i}{u_j}} }}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{{x_j}}}\left( {\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \overline {u_i^{'}u_j^{'}} } \right) + {g_i}。$ | (2) |
式中:
考虑到UUV时刻处于运动状态,因此需采用动网格技术对其运动边界进行捕捉。由于UUV运动的幅度过大,因此本文采用网格弹性变形(Smoothing)和网格重生技术(Remeshing)相结合来进行求解[5]。对于网格重生技术,其基本思想是将网格节点视作弹簧相连的网格系统。对于二维工况,一旦网格变形的幅值S满足S>(1+ζ)St,网格则开展重构。其中,为St设定网格高度,ζ为高度因子。在本文计算时,高度因子固定为ζ=0.3。
2 数学模型如图1所示,本文计算对象均为二维模型。其中UUV计算模型为图1(a)所示,其横截面最大直径为0.092 m,长度为0.72 m。头部长轴长0.112 m,尾部长轴为0.162 m。图1(b)为Suboff模型,其总长为4.261 m,最大直径为0.462 m。考虑到Suboff为对称结构,且UUV采用垂向对接的方式进行回收,因此在后续求解时仅选择一半模型进行求解。

|
图 1 计算模型 Fig. 1 Diagram of computation model |
对于网格划分,基于提升计算精度和节省计算资源的考虑,全局采用结构化网格进行求解。如图2所示,全局网格基本尺寸为0.01 m,对于近壁面网格采用局部细化,远处流场则采用稀疏网格处理,稀疏因子设为1.212。全局网格总数为12.8万。

|
图 2 计算网格及边界条件 Fig. 2 Computation grid and boundary conditions |
在数值计算时,UUV与Suboff的垂向距离设为h,且以固定移动速度u沿着垂向进行移动。对于边界条件的设定,计算域右侧设为均匀速度入口边界条件,即来流以速度V均匀自右向左流过计算域。相应地,计算域的左侧设为压力出口边界条件。Suboff和UUV均设为无滑移壁面条件(No-Slip Wall)。计算域其他边界均按照对称边界条件处理。
对于数值计算方法的精度验证,本文选取摆动翼典型计算结果进行验证[6]。所谓摆动翼,即一个机翼绕着自身旋转中心进行往复摆动运动。摆动运动为动边界研究领域的一个典型问题。采用本文数值计算方法获得的摆动翼阻力系数和升力系数与参考文献对比结果如图3所示。可知,本文计算结果与参考文献结果吻合较好,说明本文的数值计算方法可用于开展UUV的动态对接计算。

|
图 3 数值方法验证结果 Fig. 3 Validation test results of numerical method |
开展UUV运动姿态对其对接过程中流体动力性能的影响分析。考虑到UUV运动过程中阻力系数、升力系数为操纵控制主要考虑的流体动力,因此主要对阻力系数和升力系数进行分析评估。二者的定义如下:
| $ C_{D} = D/0.5 \rho V^{2}l^{2}, C_{L} = L/0.5 \rho V^{2}l^{2} 。$ | (3) |
式中:D和L分别为UUV的阻力和升力,其正负定义为升力向上为正,阻力自右向左为正;ρ为流体密度,l为UUV的长度。
3.1 不同运动速度下UUV干扰力随距离变化规律开展UUV不同垂向运动速度下其所受到的干扰力演变规律研究。取攻角为0°,UUV重心的纵向位置距离Suboff围壳后缘0.1倍体长。分别选取3个不同垂向运动速度,即u = 0.25 m/s、0.50 m/s以及1.0 m/s进行计算。入口速度固定为4 m/s。UUV重心与Suboff甲板面的垂向距离为3.0 m。
图4给出了不同垂向运动速度下,UUV阻力系数和升力系数随着UUV与Suboff间距h之间的变化曲线。

|
图 4 不同垂向速度下UUV流体动力曲线 Fig. 4 Variation curves of UUV′s fluid dynamics under various vertical velocities |
结合图4(a)可看出,对于阻力系数,不同垂向速度下,UUV阻力系数随着垂向距离h的减小,呈现出先增大后减小的趋势。阻力系数在h = 1.5~3.0 m区间的变化较为平缓,即此时的流体干扰不是很强烈。而阻力系数在h = 0~1.0 m区间的变化很剧烈,此时应加强安全操控。另一方面,垂向下潜速度对其阻力系数影响很大。具体地,垂向速度的增加使得UUV的阻力系数显著增大,且UUV靠近Suboff时的“吸力效应”会亦会随着垂向速度的增大而有所削弱,其具体表现为UUV高速靠近Suboff时相应阻力系数减小值有所下降。
对于升力系数,如图4(b)所示,对于给定垂向运动速度,随着UUV与Suboff间距的减小,UUV的升力系数在区间[1.0,3.0]时变化较小,且基本保持零升力。当壁面距离变为[0.5,1.0]时,升力系数显著增大且为正值,意味着此时受到了向上的流动干扰;随着壁面距离的继续减小, h = [0, 0.5],UUV升力系数逐渐变为负值,即此时完成了“斥力”与“吸力”的转换。
图5为不同垂向距离下UUV附近的流场结构图,此时垂向运动速度固定为u = 0.50 m/s。可知,当垂向距离较大时,Suboff围壳后的流场对UUV的干扰较小,因此UUV在对应区间运动时阻力系数和升力系数变化较为缓慢。随着UUV进一步靠近Suboff,Suboff围壳后逆时针转向的涡漩结构对UUV产生了与流动方向相反的促进力,此时表现为UUV阻力系数的减小;另外,结合图5中UUV的压力场可看出,壁面距离的变化直接导致了UUV上下表面压力差的变化,进一步地改变了UUV升力系数值。

|
图 5 给定运动速度不同垂向距离下UUV附近流场结构图 Fig. 5 Flow structures of UUV under various vertical distances at certain motion velocity |
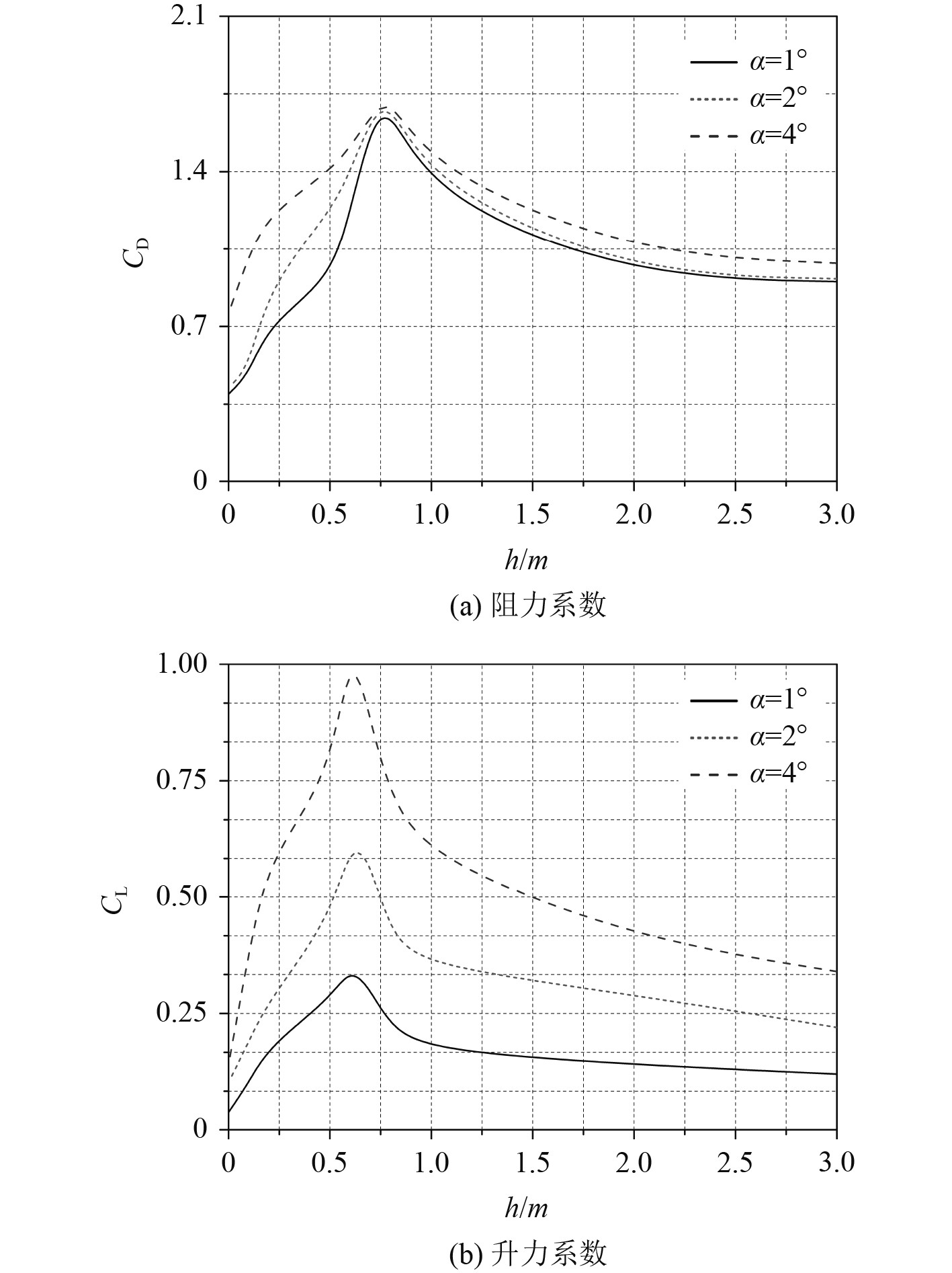
开展UUV不同攻角下其所受到的干扰力演变规律研究。垂向速度固定为u = 0.25 m/s。分别选取3个不同局部攻角进行计算,即α = 1º、2º、4º进行计算。入口速度以及UUV初始位置与前文保持一致。图6为不同局部攻角下,UUV阻力系数和升力系数随着UUV与Suboff间距h之间的变化曲线。图7为给定攻角下(α = 4°)不同垂向距离UUV附近流场结构图。
|
图 6 不同局部攻角下UUV流体动力曲线 Fig. 6 Variation curves of UUV′s fluid dynamics under various attack angles |

|
图 7 给定攻角不同垂向距离下UUV附近流场结构图 Fig. 7 Flow structures of UUV under various vertical distances at certain attack angle |
对于推力系数,结合图6(a)可知,给定攻角下UUV的阻力系数值随着壁面距离的减小,呈现出先增大后减小的趋势,与图7中UUV上下表面压力差的变化趋势相符合。此外,来流攻角的增加亦使得干扰力的影响有所增大,具体表现为给定壁面距离下,攻角越大,阻力系数值增加越多。因此,在后续试验对接时,近壁区建议采用小攻角或零攻角对接。
对于升力系数,结合图6(b)可知,不同局部攻角下UUV的升力系数在逐渐靠近Suboff时,均伴随着明显的“斥力”与“吸力”的转换。具体地,当UUV与Suboff距离较远时,此时“斥力”的影响占优,表现为升力系数的增大;反之,随着UUV逐渐贴近Suboff表面,图7中流动结构表明,UUV下表面流线增多,局部流速显著增大,此时“吸力”区出现,表现为UUV升力系数的减小。
4 结 语为了提高UUV对接回收的成功率,实现有效控制和回收,本文借助商业软件Fluent中的动网格技术采用非定常模拟方法,针对UUV不同运动姿态下(主要是不同垂向运动速度和局部攻角)的流体动力性能进行数值模拟研究。数值计算结果表明,UUV的运动姿态对其水动力性能影响很大,UUV的阻力系数随着对接速度和局部攻角的增加将会显著增大,建议在后续对接中应当选择低速零攻角对接。
| [1] |
李经. 水下无人作战系统装备现状及发展趋势[J]. 舰船科学技术, 2017, 39(1): 1-5. DOI:10.3404/j.issn.1672-7619.2017.01.001 |
| [2] |
李永成, 马峥, 王小庆. 水下滑翔机高效滑翔水动力特性研究[J]. 中国造船, 2020, 61(4): 52-59. DOI:10.3969/j.issn.1000-4882.2020.04.006 |
| [3] |
杜晓旭, 宋保维, 潘光. AUV水下回收过程中的操纵性仿真研究[J]. 船舶力学, 2011, 15(8): 837-843. DOI:10.3969/j.issn.1007-7294.2011.08.002 |
| [4] |
陈强, 孙嵘. 潜艇布放回收UUV方式[J]. 舰船科学技术, 2011, 33(7): 145-149. DOI:10.3404/j.issn.1672-7649.2011.07.036 |
| [5] |
杨壮滔, 张镇, 何文生. 水下无人平台动态布放UUV过程水动力特性[J]. 水下无人系统学报, 2022(1): 115-121. |
| [6] |
WU J, SHU C, ZHAO N, et al. Fluid dynamics of flapping insect wing in ground effect [J]. Journal of Bionic Engineering, 2014, 11: 52−60.
|
 2024, Vol. 46
2024, Vol. 46
