2. 上海电子信息职业技术学院,上海 201411
2. Shanghai Technical lnstitute of Electronics & Information, Shanghai 201411, China
船舶航行速度估计是航海领域中的一个重要问题,对于船舶的航行安全、路径规划、节能减排等方面都具有重要意义[1]。由于船舶航行环境复杂多变,航行速度的准确估计受到多种因素的影响,如风、浪、流等自然因素,以及船舶自身的结构、性能等[2]。因此,建立一个准确、可靠的船舶航行速度估计模型是航海领域的重要研究课题[3]。
针船舶航行速度估计模型问题进行深入研究,如朱晓晨等[4]利用了LightGBM的优点,建立高效的决策树模型,对船舶航行数据进行学习和预测,其中船舶航速预测模型的实现过程,包括数据预处理、特征选择、模型训练和评估等步骤。最后,通过实验验证了所提出模型的有效性和鲁棒性,能为船舶航行安全和效率优化提供有力支持。张阳等[5]采用多个预测模型进行船舶航行速度估计,包括线性回归、支持向量回归和随机森林等,通过将它们的预测结果进行融合,得到更准确的航行速度估计结果。但上述模型的灵活性与可扩展性较差,无法根据不同的需求和场景进行定制和优化。
改进神经网络具备强大的学习和预测能力、高效的特征处理能力、较优的灵活性和可扩展性[6],能提高船舶航行速度估计模型的鲁棒性和泛化能力。为此,设计基于改进神经网络的船舶航行速度估计数学模型,为提高船舶航行安全、优化路径规划、降低能耗等方面提供有力支持。
1 改进神经网络的船舶航行速度估计数学模型构建构建的船舶航行速度估计数学模型以编解码卷积神经网络为核心算法,通过自注意力机制改进神经网络。引入编解码卷积神经网络是因其够自动从图像中提取高级特征表示、具备良好的参数共享性、适用于不同的输入数据、能够处理大规模数据集、并且在数据处理和生成任务中具有出色的性能。构建基于改进神经网络的船舶航行速度估计数学模型,建模步骤如下:
步骤1 利用位置编码对船舶航向速度相关数据(风速、风向、波高、水流速度、吃水等)展开编码处理。
步骤2 在编解码卷积神经网络内,输入编码后的船舶航速相关数据,并在编解码卷积神经网络内,引入自注意力机制,对其进行改进,用于提取和船舶航行速度相关的数据序列特征,每次编码过程中,通过自注意力蒸馏剔除船舶航行速度相关数据序列特征的冗余特征。
步骤3 利用编码后的风速与风向等船舶航向速度训练数据,训练改进编解码卷积神经网络,建立船舶航行速度估计数学模型。
步骤4 在船舶航行速度估计数学模型内,输入风速与风向等船舶航向速度测试数据,利用该模型的全连接层,处理船舶航行速度相关数据序列特征,输出船舶航行速度估计结果。
1.1 船舶航行速度相关数据位置编码因编解码卷积神经网络不能处理历史船舶航行速度相关序列数据元素的序列信息,所以利用位置编码机制,编码处理历史船舶航行速度相关信息。位置编码公式如下:
| $ {U_{E\left( {{p_o},2j} \right)}} = \sin \left( {\frac{{{u_o}}}{{{{\left( {2{V_x}} \right)}^{\frac{{2j}}{d}}}}}} \right)。$ | (1) |
式中:
在传统的编解码卷积神经网络中,每个位置或通道的特征权重是固定的,无法动态地根据不同任务和输入数据进行调整。而自注意力机制通过引入注意力机制,可以根据输入数据的内容自动学习权重,并对不同位置或通道的特征进行加权处理。引入自注意力机制改进神经网络可提高模型的表征能力和建模能力,使其能更充分地利用输入数据的信息,并更精确地预测船舶航行速度。基于此,在该网络内输入编码后UE的训练数据,对其进行训练,建立船舶航行速度估计数学模型,在该模型内输入编码后UE的测试数据,输出船舶航行速度估计结果。
自注意力机制包含空间注意力与通道注意力,利用空间注意处理UE全部位置上的特征,确保类似航速序列数据特征间存在关联。通过通道注意力整合全部航速序列数据特征,在彼此关联的通道内,提取重要通道的航速序列数据特征。
令编码后的历史船舶航行速度相关数据位置
| $ {z_{il}} = \frac{{{e^{\left( {{{\boldsymbol{A}}_i},{{\boldsymbol{B}}_l}} \right)}}}}{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{l = 1}^N {{e^{\left( {{{\boldsymbol{A}}_i},{{\boldsymbol{B}}_l}} \right)}}} } }}。$ | (2) |
式中:N为历史船舶航行速度相关数据位置向量特征数量;
利用
| $ {s_l} = \alpha \sum\limits_{l = 1}^N {\left( {z_{il}^{\mathrm{T}}C_l^*} \right) + {P_l}}。$ | (3) |
其中,
通过重构P可获取P*,将P*和其转置矩阵P*T相乘,并输入Softmax层内,便可获取通道注意力矩阵
| $ {z'_{il}} = \frac{{{e^{\left( {{P_i},{P_l}} \right)}}}}{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{l = 1}^N {{e^{\left( {{P_i},{P_l}} \right)}}} } }} 。$ | (4) |
将
| $ {s{'}_l} = \beta \sum\limits_{l = 1}^N {\left( {z{'}_{il}^T P_i^*} \right) + P_l^*}。$ | (5) |
其中,
通过融合
通过对
| $ {\hat s_{i,\tau + 1}} = {\mathrm{MaxPool}}\left( {L\left( {Convld{{\left( {{{\hat s}_{i,\tau }}} \right)}_\phi }} \right)} \right)。$ | (6) |
式中:
改进编解码神经网络内,解码器通过各Maxpooling层存储的索引,上采样处理编码器输出的船舶航速数据特征
| $ {\tilde s_{i,\tau + 1}} = h \cdot G + {\hat s_{i,\tau + 1}}。$ | (7) |
其中,
在全连接层内输入
以某4 698 t的船舶为实验对象,该船舶共包含183900条风向、风速、水流速度等船舶航速相关数据。该船舶的相关参数如表1所示。
|
|
表 1 船舶相关参数 Tab.1 Ship related parameters |
1)目的:建立基于改进神经网络的船舶航行速度估计数学模型,提高船舶航行速度估计的准确性和精度。
2)数据预处理:对船舶航速相关数据进行预处理,包括数据清洗、缺失值处理、归一化等步骤,以确保数据质量和可用性。
3)模型架构设计:在编解码卷积神经网络的编码器内引入自注意力机制,以处理位置编码后的船舶航向速度相关数据。利用自注意力机制提取船舶航速数据特征,并结合自注意力蒸馏剔除冗余特征。通过全连接层处理船舶航速数据特征,输出船舶航行速度的估计结果。
4)实验实现步骤:①将船舶航速相关数据分为训练集和测试集,按照一定比例划分。②使用训练集数据对改进神经网络进行训练,优化模型参数。③使用测试集数据评估模型性能,包括计算决定系数等指标,判断船舶航行速度估计的精度和准确性。④对不同浪向下进行实验和评估,以分析模型在不同环境条件下的性能表现。
2.3 船舶航行速度序列数据特征提取结果与分析利用本文模型提取船舶航行速度序列数据特征,特征提取结果如表2所示。可知,本文模型可有效在历史船舶航行速度相关数据内,提取船舶航速序列数据特征,为后续船舶航行速度估计提供有利数据支持。本文模型具有较高的可解释性,提取的特征能清楚地揭示影响船舶航行速度的各种因素。
|
|
表 2 船舶航行速度序列数据特征提取结果 Tab.2 Feature extraction results of ship speed sequence data |
利用特征间的相似性,衡量本文模型的船舶航速序列数据特征提取效果,不同特征间的相似性低于0.4(包含0.4),则特征提取效果越佳,分析本文模型引入注意力机制和蒸馏操作后的特征提取效果,分析结果如图1所示。根据图1(a)可知,仅引入自注意力机制后,本文模型提取的不同特征间,存在个别特征间的相似性为0.6,其余不同特征间的相似性均小于等于0.4,说明大部分船舶航速序列数据特征提取效果较优。根据图1(b)可知,引入自注意力机制与蒸馏操作后,可有效剔除冗余特征,全部不同特征间的相似性均小于等于0.4,说明本文模型的船舶航速序列数据特征提取效果优。
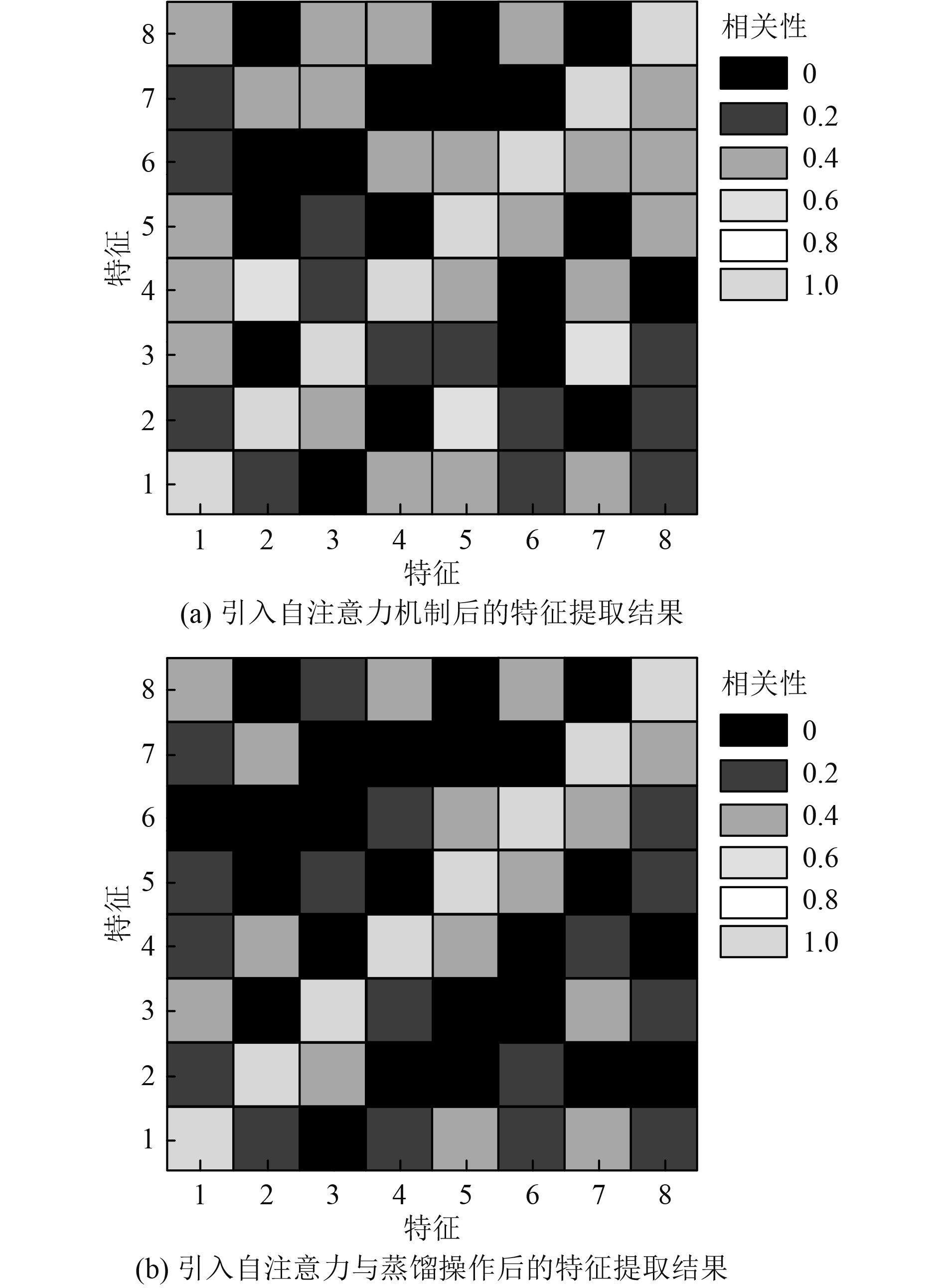
|
图 1 本文模型的特征提取效果 Fig. 1 Feature extraction effect of the model in this paper |
利用本文模型估计该船舶的航行速度,船舶航行速度估计结果如图2所示。可知,本文模型可有效估计船舶航行速度,且本文模型的船舶航行速度估计结果,与实际船舶航行速度非常接近,说明本文模型的船舶航行速度估计精度较高。
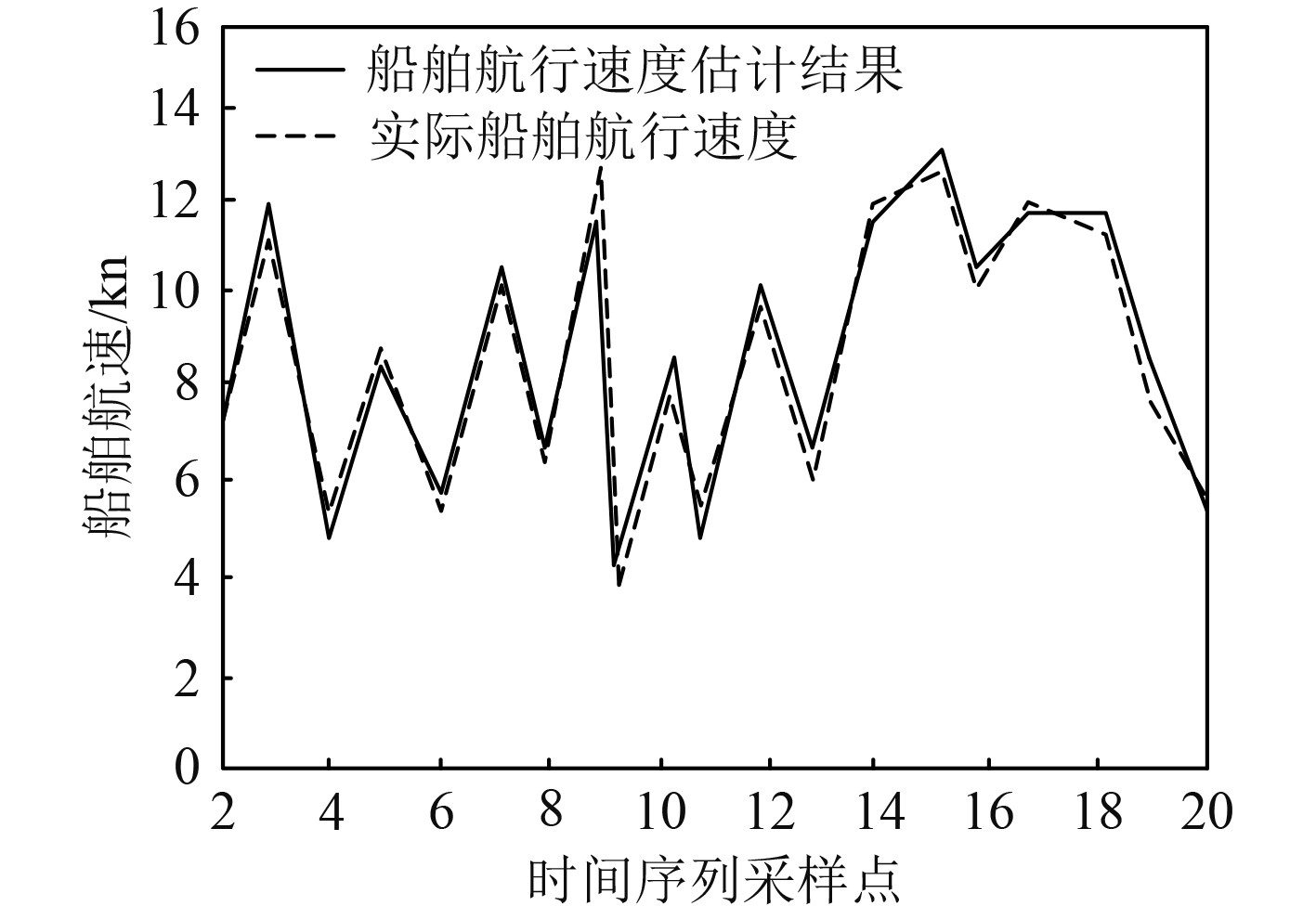
|
图 2 船舶航行速度估计结果 Fig. 2 Ship speed estimation results |
利用决定系数衡量本文模型的船舶航行速度估计精度,其值越接近1,本文模型的估计精度越高,分析不同浪向时,本文模型船舶航行速度估计的决定系数,分析结果如图3所示。可知,随着浪向的增长,本文模型估计船舶航行速度的决定系数,开始不断下降,最低决定系数在0.97左右,与1较为接近,说明不同浪向下,本文模型船舶航行速度估计的决定系数均较高,即估计精度较高。

|
图 3 决定系数分析结果 Fig. 3 Analysis results of determination coefficient |
改进神经网络在船舶航行速度估计中具有显著优势,能有效地提高估计的准确性和鲁棒性。应用改进神经网络能更好地学习和预测船舶航行速度的复杂非线性关系,适应各种复杂的航行环境和条件,为船舶航行安全和效率优化提供有力支持。同时,本文模型还具有高效的计算和训练速度,可快速地进行模型训练和推理,以应对大规模的船舶航行数据。
| [1] |
王均刚, 丁惠倩, 胡柏青. 基于滑动窗口PSO-LSSVR的船舶轨迹预测模型[J]. 武汉理工大学学报, 2022, 44(12): 35-43,59. |
| [2] |
贾雨薇, 邵忻. 基于多蚁群系统的多无人机反侦察航迹规划[J]. 舰船电子对抗, 2023, 46(3): 14-19. |
| [3] |
张青山, 陈伟民, 杜云龙, 等. 基于实尺度船舶自航数值模拟的航速预报[J]. 中国造船, 2022, 63(5): 11-21. |
| [4] |
朱晓晨, 尹奇志, 赵福芹, 等. 基于LightGBM的船舶航速预测模型[J]. 大连海事大学学报, 2023, 49(1): 56-65. |
| [5] |
张阳, 高曙, 何伟, 等. 基于多模型融合的内河船舶航行轨迹预测方法[J]. 中国机械工程, 2022, 33(10): 1142-1152. |
| [6] |
刘长德, 顾宇翔, 张进丰. 基于小波滤波和LSTM神经网络的船舶运动极短期预报研究[J]. 船舶力学, 2021, 25(3): 299-310. |
 2024, Vol. 46
2024, Vol. 46
