0 引　言

船舶触礁是一种严重的海上交通事故，可能会导致船体破损、人员伤亡和环境污染等后果^[1]。据统计，在海洋事故中，大约半数事故是因船舶触礁造成，在各种极端气象的影响下，船舶触礁事故率呈不断走高趋势发展。船舶高速航行情况下，需更加精确地掌握船舶动态以及周围环境信息，以避免碰撞和触礁等事故的发生。通过实时计算触礁距离，可更加准确地评估船舶与礁石等危险物体之间的距离，以便及时采取避碰措施，避免事故的发生^[2]。

宋全记^[3]在建立船舶模型的基础上，通过模拟船舶行驶和触礁过程，计算触礁距离数据，实现船舶安全预警分析，该方法实现需以大量时间和资源为代价；李克祥等^[4]根据船舶航行状态和周围环境，建立相应的数学模型，计算船舶的安全指数，并根据安全指数得到触礁距离的估计值。这种方法相对简单易行，但需较为准确的船舶航行状态和环境数据作为支持。

为确保船舶航行安全，避免发生船舶触礁事故，本文提出海上高速航行船舶触礁距离实时计算方法，通过对雷达探测设备、船舶自动识别系统（AIS）信息的合理利用，确定船舶触礁距离实时计算结果，为船舶驾驶员提供船舶航行决策依据。

1 海上高速航行船舶触礁距离实时计算方法具体设计 1.1 基于雷达的礁石探测及位置坐标转换

雷达是一种应用在航行船舶上，利用电磁波进行目标探测的助航设备^[5]。它的工作原理是发射电磁波信号，并接收这些电磁波在遇到目标后的反射信号，通过分析发射与接收信号的时间差实现目标距离、方向和速度的确定。雷达的远程探测能力、目标识别和跟踪能力以及提供水流信息的能力，能在海上高速航行船舶触礁监测中起到关键作用。借助雷达设备，船舶驾驶员能更好地了解周围航行环境，从而做出更准确的航行决策，避免碰撞。

1.1.1 航海雷达

雷达站主要包括雷达设备、光电摄像设备（CCTV）、船舶自动识别系统（AIS）接收天线以及雷达数据分析终端等部件，其中前3个部件部署于室外，后一部件放置于室内。本文选择AIDOS公司研发的远距离导航雷达实现船舶航行环境礁石目标的探测；选择上海翊臻电子科技有限公司生产的YAB-1000-JC型AIS接收机。

1.1.2 礁石位置坐标转换

采用雷达设备对船舶航行环境下的礁石目标进行探测时，雷达观测值是以极坐标系形式描述，雷达站址位置坐标则通过经纬度进行表示，需对探测到的礁石位置坐标作转换处理，得到地心直角坐标系下的礁石坐标，具体转换过程为：

在极坐标系下，礁石目标位置坐标通过$ \left( {\rho ,\theta ,\varphi } \right) $表示，先将其向平面直角坐标系下转换，转换后坐标通过$ \left( {o' - v,u,w} \right) $表示，转换公式描述为：

$ \left\{ \begin{gathered} u = \rho \cos \varphi \cos \theta，\\ v = \rho \cos \varphi \sin \theta，\\ w = \rho \sin \varphi 。\\ \end{gathered} \right. $

(1)

然后，再将其向地心直角坐标系下转换，即可确定用$ \left( {x,y,z} \right) $表示的礁石目标坐标，通过下式完成坐标转换：

$ \left[ \begin{gathered} x \\ y \\ z \\ \end{gathered} \right] = P\left( {{L_0},{B_0}} \right)\left[ \begin{gathered} u \\ v \\ w \\ \end{gathered} \right] + \left[ \begin{gathered} {x_s} \\ {y_s} \\ {z_s} \\ \end{gathered} \right]。$

(2)

式中，$ P\left( {{L_0},{B_0}} \right) $表示旋转矩阵，计算式描述为：

$ P\left( {{L_0},{B_0}} \right) = \left[ \begin{gathered} - \sin {B_0}\mathop {}\nolimits^{} - \sin {L_0}\cos {B_0}\mathop {}\nolimits^{} \cos {L_0}\cos {B_0} \\ \mathop {}\limits^{} \cos {B_0}\mathop {}\nolimits^{} \;\;- \sin {L_0}\cos {B_0}\mathop {}\nolimits^{} \cos {L_0}\sin {B_0} \\ \mathop {}\nolimits^{} 0\qquad\qquad\quad \cos {L_0}\qquad \quad \sin {L_0} \\ \end{gathered} \right]。$

(3)

式中：$ {L_0} $为雷达站天线所在经度，$ {B_0} $为纬度，$ \left( {{x_s},{y_s},{z_s}} \right) $为雷达站的经纬度和海拔高度。

1.2 基于PLSTM-FCN的高速航行船舶航迹预测

为提高高速航行船舶航迹预测效果，本文设计基于PLSTM-FCN的航迹预测模型。从船舶自动识别系统（AIS）中获取高速航行船舶历史位置、航速、航向等动态数据以及船舶长度、宽度以及吃水深度等静态数据，通过对其进行整理得到高速航行船舶大规模历史航迹数据，即特征向量，利用该数据训练基于PLSTM-FCN的船舶航迹预测模型，实现高速航行船舶实时航行位置的预测。对$ t $时间点前的$ k $个不间断航迹点信息进行选取，将其输入到船舶航迹预测模型中，以对$ t + 1 $时间点下的船舶实际航行位置进行预估，位置预测公式通过下式进行描述：

$ {\hat y_{t + 1}} = g\left( {{x_t},{x_{t - 1}}, \cdots ,{x_{t - k + 1}}} \right)。$

(4)

式中：$ {\hat y_{t + 1}} $表示在$ t + 1 $时间点下，船舶航行实时位置预测结果，$ \left( {la{t_{t + 1}},lo{n_{t + 1}}} \right) $为位置信息；$ {x_t} $为$ t $时间点下，船舶航行的航迹特征向量。

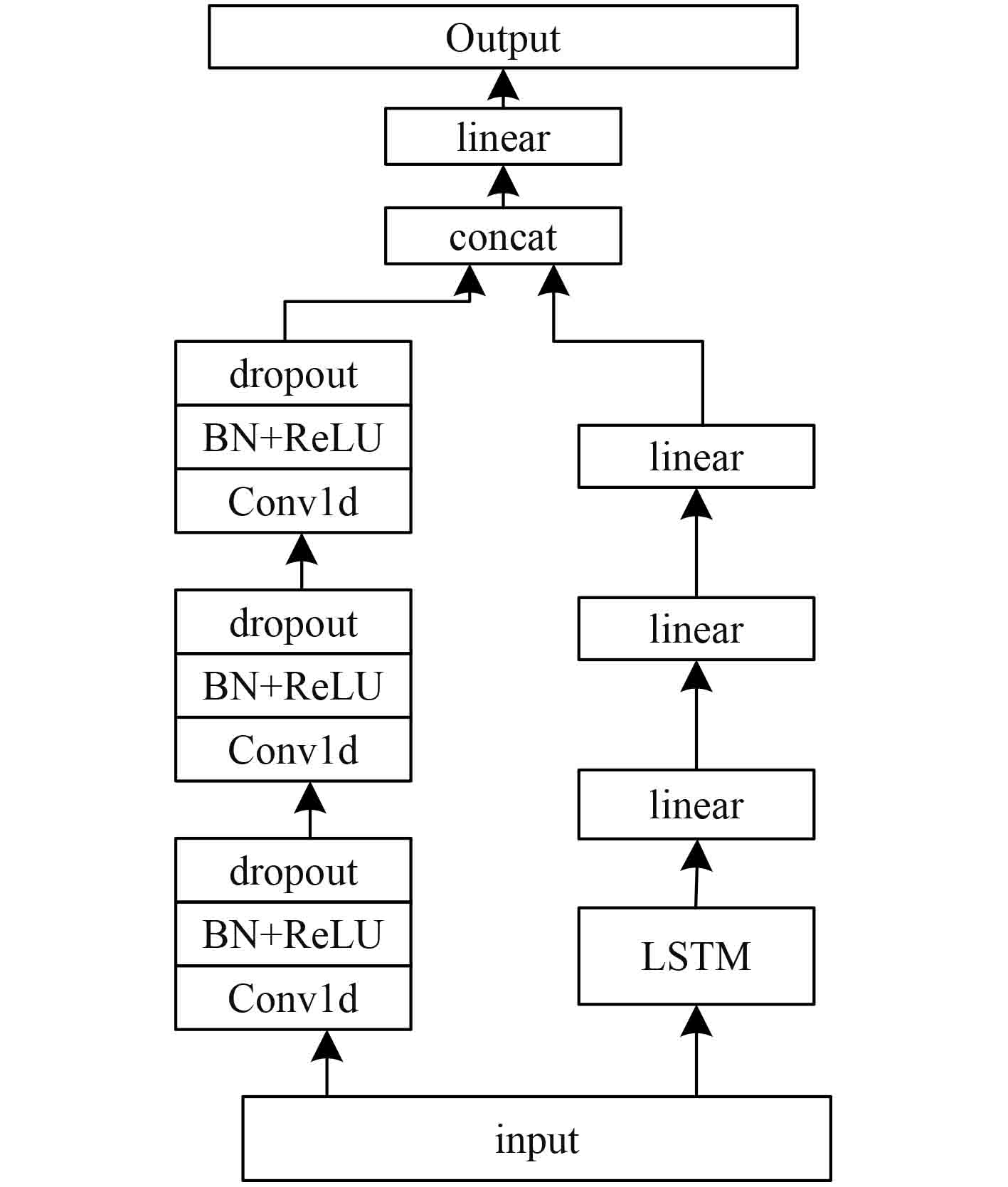
基于PLSTM-FCN的船舶航迹预测模型结构如图1所示。该模型由LSTM模块和FCN模块构成，前者用于对船舶航行航迹数据的长期变化规律进行捕捉；后者用于提取切片航迹数据特征。两模块的联合使用，在捕获船舶航行长期变化规律的同时，可完成细节特征的有效提取。FCN模块中包含3个时序卷积单元，1个一维卷积层、1个批处理规范层+ReLU函数与1个dropout层共同构成了1个时序卷积单元。为满足高速船舶航行航迹数据处理要求，本文将3个时序卷积单元的卷积核尺寸分别设定为3、3、1，输入通道数量分别为8、32、64，输出通道数量分别为32、64、32。LSTM层和全连接层为LSTM模块结构的重要内容，对应数量分别为1、3，在LSTM中，循环层、隐含层总数分别为4、100，其作用是对船舶航迹预测模型输入作映射处理，得到100维特征向量；全连接层可实现特征向量的降维，得到32维向量，利用concat层实现LSTM模块和FCN模块的融合，得到64维向量，将其输入到全连接层进行处理，可获得3维向量，即实现船舶航行实时位置坐标$ \left( {{x_{bt}},{y_{bt}},{z_{bt}}} \right) $的确定。

1.3 触礁距离实时计算

船舶实时位置坐标与礁石目标坐标之间关系如2图所示。其中，$ \left( {x,y,z} \right) $为利用雷达探测到的礁石目标位置坐标，$ \left( {{x_{bt}},{y_{bt}},{z_{bt}}} \right) $为高速航行船舶实时位置坐标预测结果，通过下式即可完成触礁距离的计算：

$ D = \sqrt {{{\left( {x - {x_{bt}}} \right)}^2} + {{\left( {y - {y_{bt}}} \right)}^2} + {{\left( {z - {z_{bt}}} \right)}^2}} 。$

(5)

礁石与高速航行船舶的相对角度通过下式进行确定：

$ \delta = {\cos ^{ - 1}}\left( {\frac{{{v_t} - {v_t} \cdot \cos \left( {{\psi _0} - {\psi _1}} \right)}}{D}} \right) 。$

(6)

式中：$ {v_t} $为此刻高速航行船舶航行速度，$ {\psi _0} $为航行方向。

2 实验结果与分析

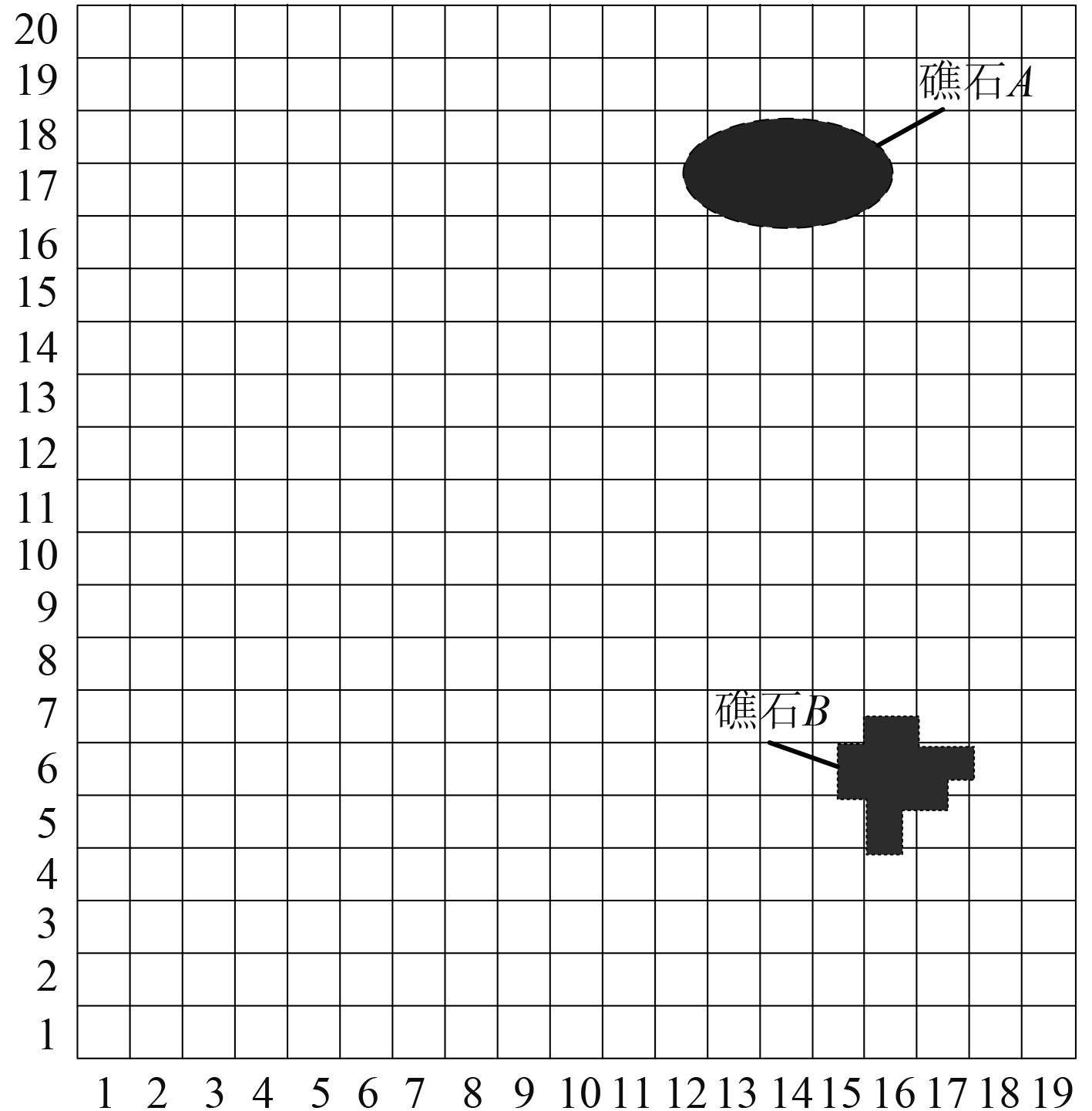
以高速航行在某海域的某船舶为实验对象，在Maltab软件工具上模拟该海域船舶航行环境，该海域礁石分布如图3所示。其中，A礁石呈椭圆形，长、宽分别为400 m、284 m，礁石周围海域平均水深120 m，礁石高度40 m；B礁石形状不规则，长、宽分别为120 m、38 m，其周围海域平均水深为88 m，高度为25 m。采用研究方法对该海域礁石进行探测，并对前一个月航行于该海域的所有船舶AIS数据进行采集，构建样本数据集，其中，包括15300条航迹数据信息，按4:1比例对航迹数据进行分组，将其中7650条航迹作为测试样本，其余为训练样本。在PyTorch框架下开展船舶触礁距离实时计算实验，分析研究方法的触礁距离计算效果。

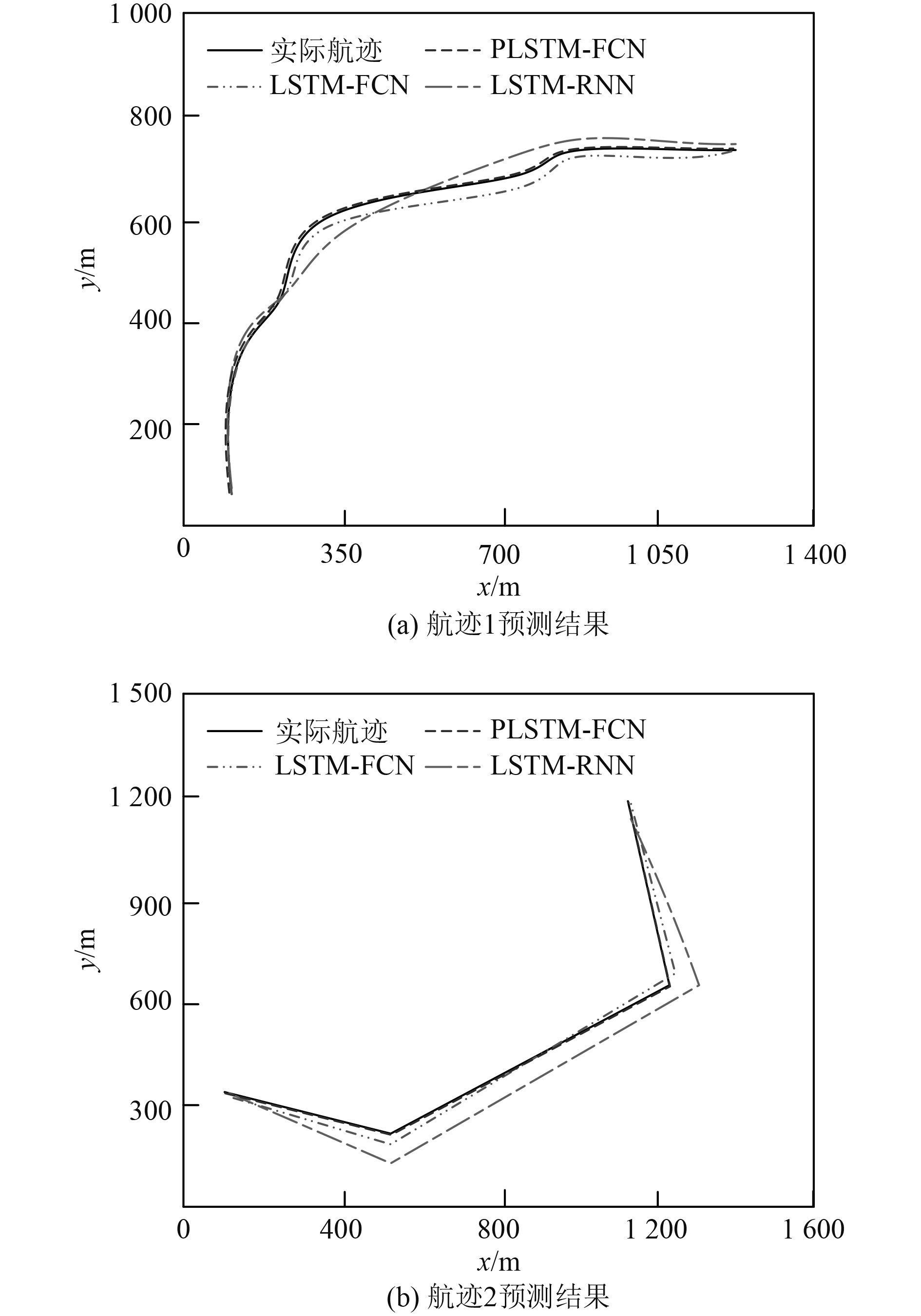
将LSTM-FCN模型、LSTM-RNN模型作为研究方法所用PLSTM-FCN模型的对比模型，将训练样本作为各个船舶航迹预测模型的输入，完成各模型的训练后，从测试样本集中任意选取2条航迹进行预测，将均方误差（MSE）作为航迹预测效果评价指标，通过对比分析3个模型的航迹预测结果以及均方误差指标差异，验证研究方法的实用性，实验结果如图4和表1所示。可知，应用LSTM-RNN模型进行航迹预测，MSE指标值高于其他2个模型，LSTM-FCN模型的航迹预测效果略优于LSTM-RNN模型，MSE指标降低幅度并不大；PLSTM-FCN模型在航迹预测上能取得更好的预测效果，MSE指标明显低于其他2模型，其值仅为0.0022。图4（a）中的船舶航行轨迹大体呈圆弧形状，图4（b）中的航行轨迹有2次转弯情况，LSTM-RNN模型能够在平直段航迹预测中取得较好效果，对转弯段航迹预测存在较大偏差，导致航迹预测结果远远偏离实际航迹曲线；LSTM-FCN模型预测的航迹曲线无法与实际航迹曲线密切贴合，仍存在一定偏差；PLSTM-FCN模型预测后的船舶航行轨迹与实际轨迹曲线保持相同的走势规律，且二者基本完全重合，这是由于研究方法所用模型既能对船舶航行航迹数据的长期变化规律进行捕捉，同时也能实现提取切片时间序列特征的高效提取，从而提升了航迹预测精度。

将研究方法应用到实验船舶触礁距离实时计算中，航迹预测结果以及部分航迹点下的触礁距离计算结果分别如图5和表2所示。可知，船舶在高速航行过程中，航行环境中存在礁石静态障碍物的同时，还包含动态障碍物，研究方法可实现船舶航迹预测，确定船舶航行实时位置，结合礁石位置探测结果，可完成船舶触礁距离的实时计算，距离计算结果与实际距离偏差介于0.77～1.55 m之间，计算误差在允许误差范围之内。实验结果表明，研究方法可实现高速航行船舶触礁距离实时计算，计算误差较小。

3 结　语

触礁距离实时计算对保障船舶航行安全具有重要意义，通过实时确定触礁距离，可及时发现船舶航行中的安全隐患，避免船舶触礁事故发生。因此，本文研究高速航行船舶触礁距离实时计算方法，通过对PLSTM-FCN模型性能、实验船舶航迹预测结果以及触礁距离计算结果进行分析，验证了研究方法的可应用性。