2. 中国人民武装警察部队海警学院 航海系,浙江 宁波 315801
2. Nautical Department, China Coast Guard Academy, Ningbo 315801, China
水下滑翔机[1 − 3]以及仿生机器人[4 − 5]技术日益成熟,本文结合水下滑翔机和仿生机器蟹,探索一款兼具仿生机器蟹灵活性和水下滑翔机长续航性的仿蟹滑翔机器人[6],具有爬行、滑翔和推进3种不同模式[7]。爬行模式具有灵活性,能够应对复杂海底环境,滑翔模式具有长续航的特点,推进模型具有机动性和抵抗恶劣环境的能力。通过变形能使仿蟹滑翔机器人在滑翔模式和爬行模式之间自由切换。通过在外壳预留接口,可根据实际情况加装螺旋桨,来应对复杂海况。
水下滑翔机[1 − 3]以及仿生机器人[4 − 5]技术日益成熟,本文结合水下滑翔机和仿生机器蟹,探索一款兼具仿生机器蟹灵活性和水下滑翔机长续航性的仿蟹滑翔机器人[6],具有3种不同模式爬行模式、滑翔模式和推进模式[7]。爬行模式具有灵活性,能够应对复杂海底环境,滑翔模式具有长续航的特点,推进模式具有机动性和抵抗恶劣环境的能力。通过变形能使仿蟹滑翔机器人在滑翔模式和爬行模式之间自由切换。通过在外壳预留接口,可根据实际情况加装螺旋桨,来应对复杂海况。
本文基于粘流理论方法,应用CFD软件Fine/Marine,选用合适的螺旋桨,对螺旋桨的敞水性能进行计算,研究加装螺旋桨后,仿蟹滑翔机器人推进模式下的推进特性,分析仿蟹滑翔机器人的自航性能。
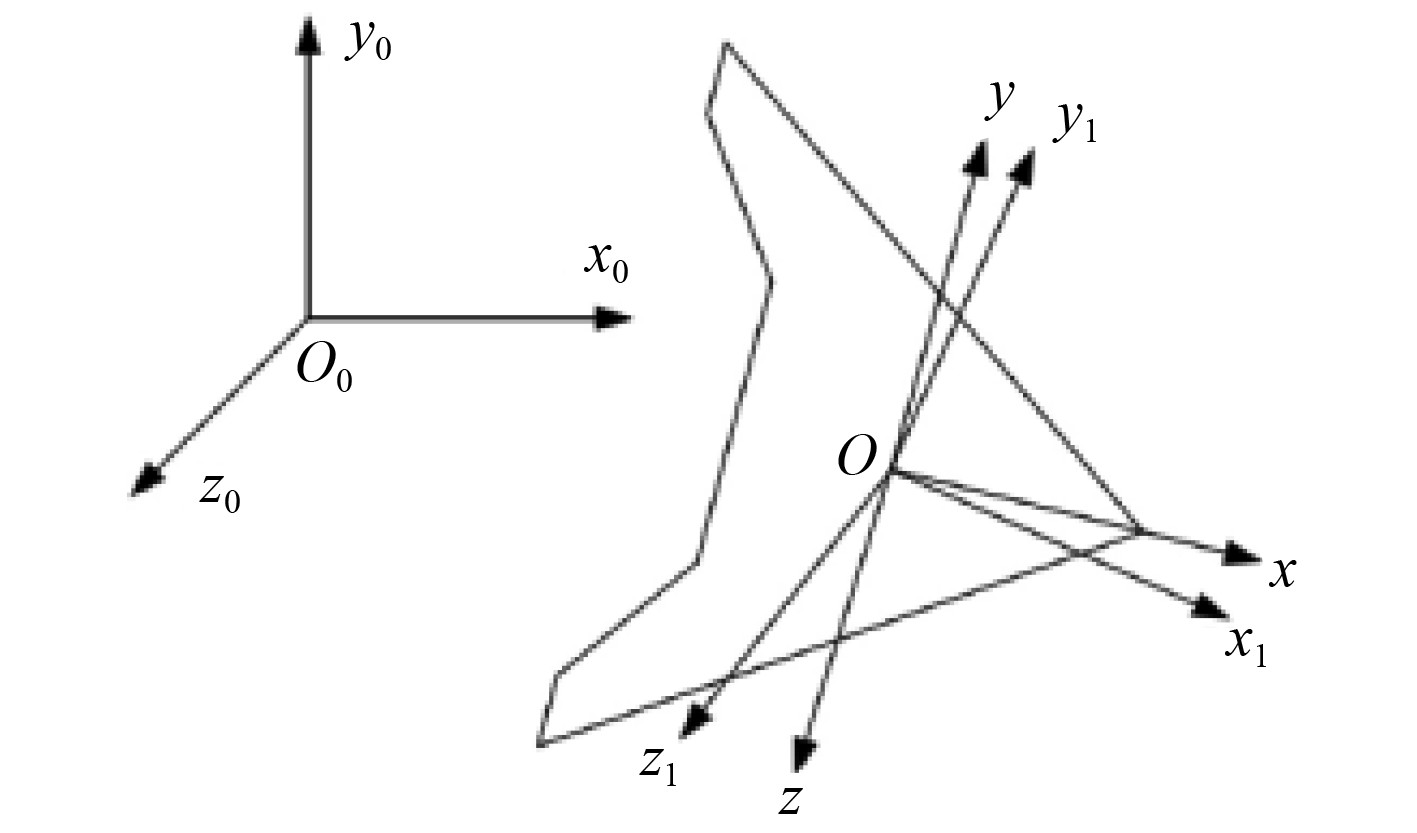
1 坐标系定义与数值方法标定 1.1 坐标系定义仿蟹滑翔机器人和螺旋桨耦合可视为刚体,在重浮力、推进器推力和流体动力等作用力综合影响下,形成自航运动。为了便于问题分析,本文建立3个坐标系,分别是惯性坐标系O0x0y0z0、载体坐标系Ox1y1z1和速度坐标系Oxyz,如图1所示。
|
图 1 仿蟹滑翔机器人坐标系定义 Fig. 1 Crab gliding robot coordinate system definition |
惯性坐标系O0x0y0z0在海平面水平面任取一点作为坐标系原点,遵循右手法则:O0x0取水平面,仿蟹滑翔机器人航向为正,O0y0右为正,O0z0垂向下为正。
载体坐标系Ox1y1z1与仿蟹滑翔机器人一起运动,其原点O位于为仿蟹滑翔机器人的浮心,遵循右手法则;Ox1轴在仿蟹滑翔机器人的中心内,向头部为正;Oy1向右翼为正;Oz1轴垂直向下为正。
载体坐标系Ox1y1z1的原点与速度坐标系Oxyz的原点重合。Ox轴与原点处仿蟹滑翔机器人的速度矢量重合,Oy轴位于仿蟹滑翔机器人的纵对称面内,与Ox轴垂直并指向上方,Oz轴垂直xOy。
1.2 数值方法标定为了确保计算结果具有参考意义,选用已有试验结果的“海鸥一号”为验证对象[8],将本文所使用的数值方法用于“海鸥一号”,求解直航运动下阻力值,计算航速为0.2~0.5 m/s,步长为0.1 m/s,网格划分采用全六面体非结构网格,数值模拟结果与“海鸥一号”拖曳试验结果,如图2所示。

|
图 2 阻力对比图 Fig. 2 Resistance comparison chart |
可以看出,对比曲线基本一致,最大偏差低于3%,证明数值方法的可行性,具有一定参考意义。
2 螺旋桨敞水性能求解T200导管桨的敞水性能,得到其推力系数、扭矩系数以及敞水效率。
2.1 模型建立螺旋桨的敞水性能主要参数为进速系数
| $ J = \frac{{{V_A}}}{{nD}} ,$ | (1) |
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}},$ | (2) |
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}} ,$ | (3) |
| $ {\eta _0} = \frac{{{K_T}}}{{{K_Q}}} \cdot \frac{J}{{2\text{π} }}。$ | (4) |
式中:
本文T200型导管螺旋桨主要参数如表1所示。
|
|
表 1 T200参数 Tab.1 T200 parameters |
网格划分将滑移网格法与多计算域法相结合[9],计算所采用的网格类型为全六面体非结构网格。外域为12D×8D×8D的长方体的静止域,长方体域入口在导管上方4D处,出口在导管下方8D处,导管至其余边界的距离均为4D。静止外域网格数约为175万,旋转内域的网格数约为130万。通常螺旋桨桨轴浸深小于0.625D,流体兴波对螺旋桨水动力性能有影响,但该计算域浸深远大于0.625D,兴波的影响可忽略不计。计算域设置如图3所示。

|
图 3 网格划分 Fig. 3 Meshing |
基于粘性流体理论,仿蟹滑翔机器人计算方法参数设置如下:流体参数设定为15℃海水,密度为1026 kg/m3,动力粘性系数取0.0009 Pa·s;计算物理模型选用非稳态时间布局模型;选用
求解敞水性能时,桨叶转速设置为63.33 r/s,求解螺旋桨的敞水性能通常调整来流速度来改变进速系数,本文计算进速系数J从0~0.8等9个计算工况。计算工况详见表2。
|
|
表 2 计算工况 Tab.2 Calculate the operating conditions |
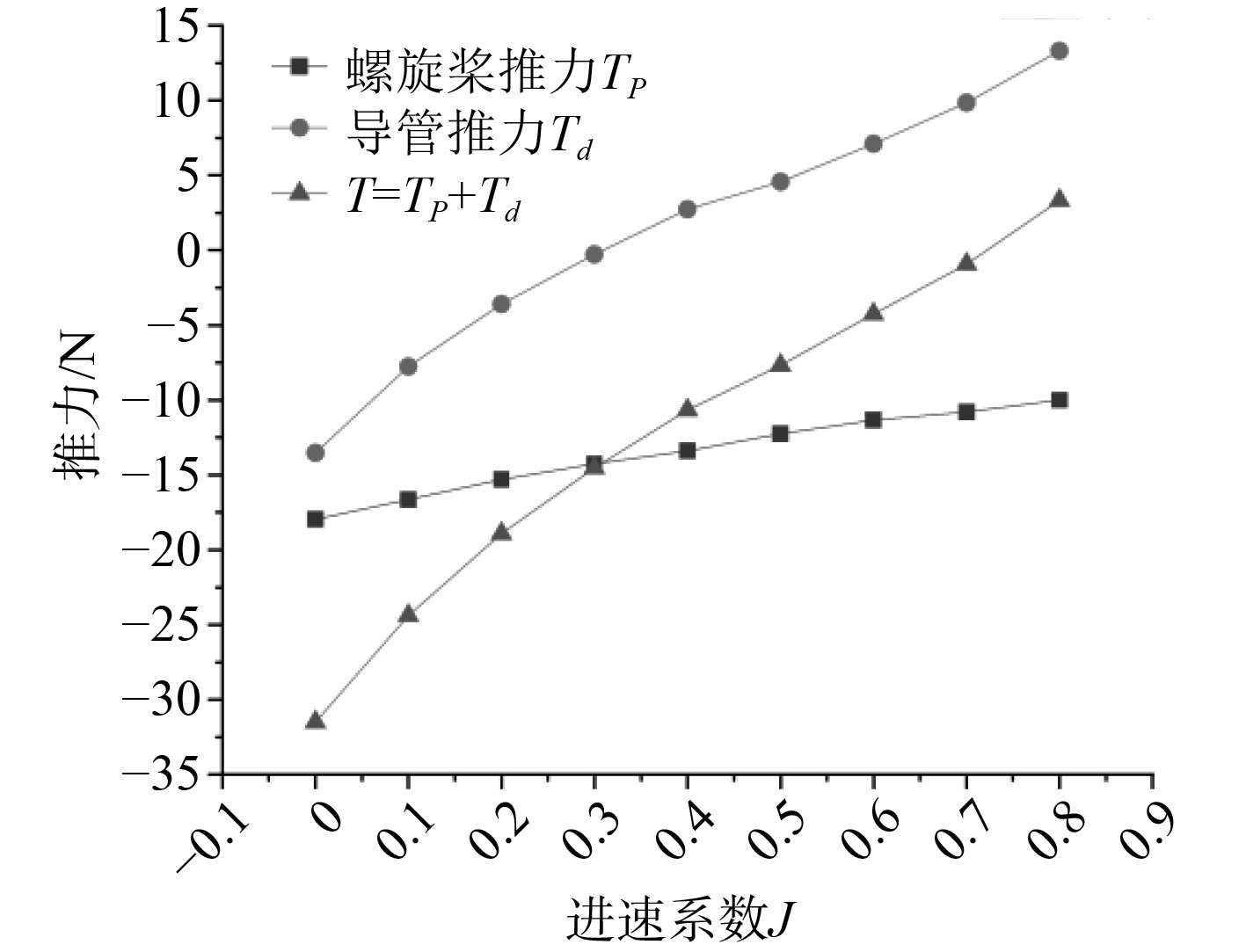
|
图 4 T200推力数值计算结果 Fig. 4 T200 thrust numerical calculation results |
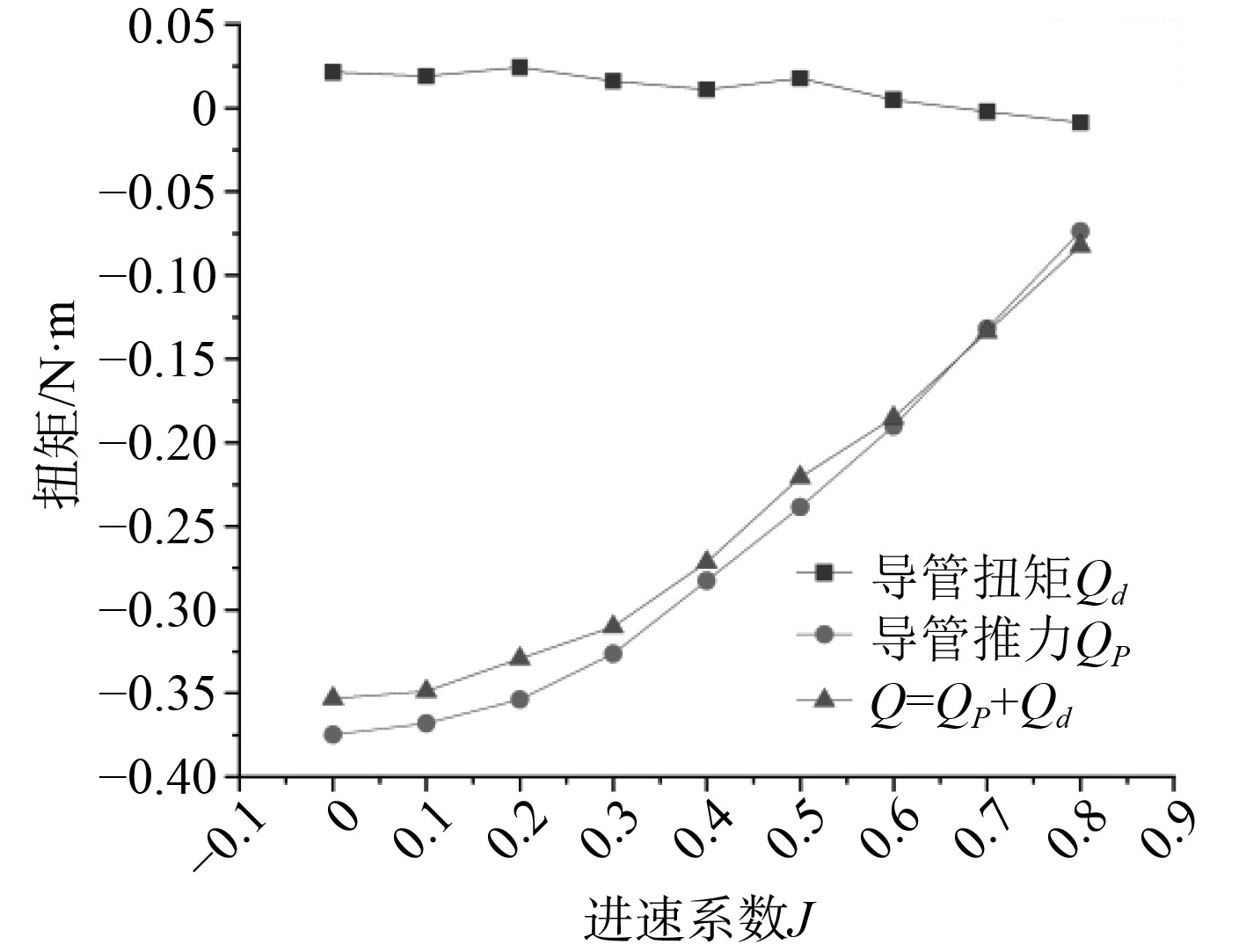
|
图 5 T200扭矩数值计算结果 Fig. 5 T200 torque numerical calculation result |
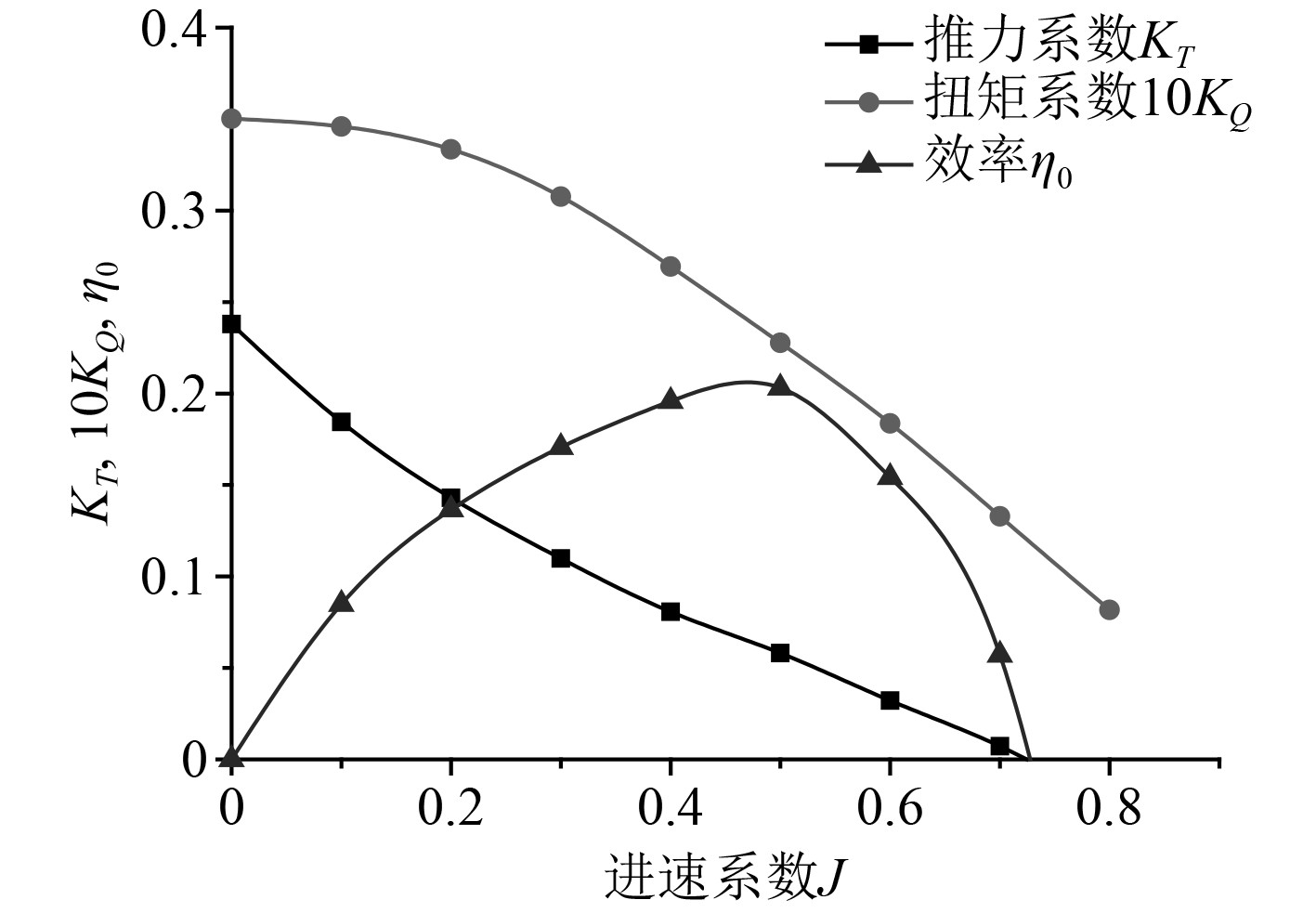
|
图 6 T200敞水性能曲线 Fig. 6 T200 open water performance curve |
本文采用的求解方法将多计算域法与滑移网格法结合,仿蟹滑翔机器人被划分为多个运动状态不同的计算域,研究推进模式下,仿蟹滑翔机器人本体-多桨耦合系统的自航性能[10 − 12]。
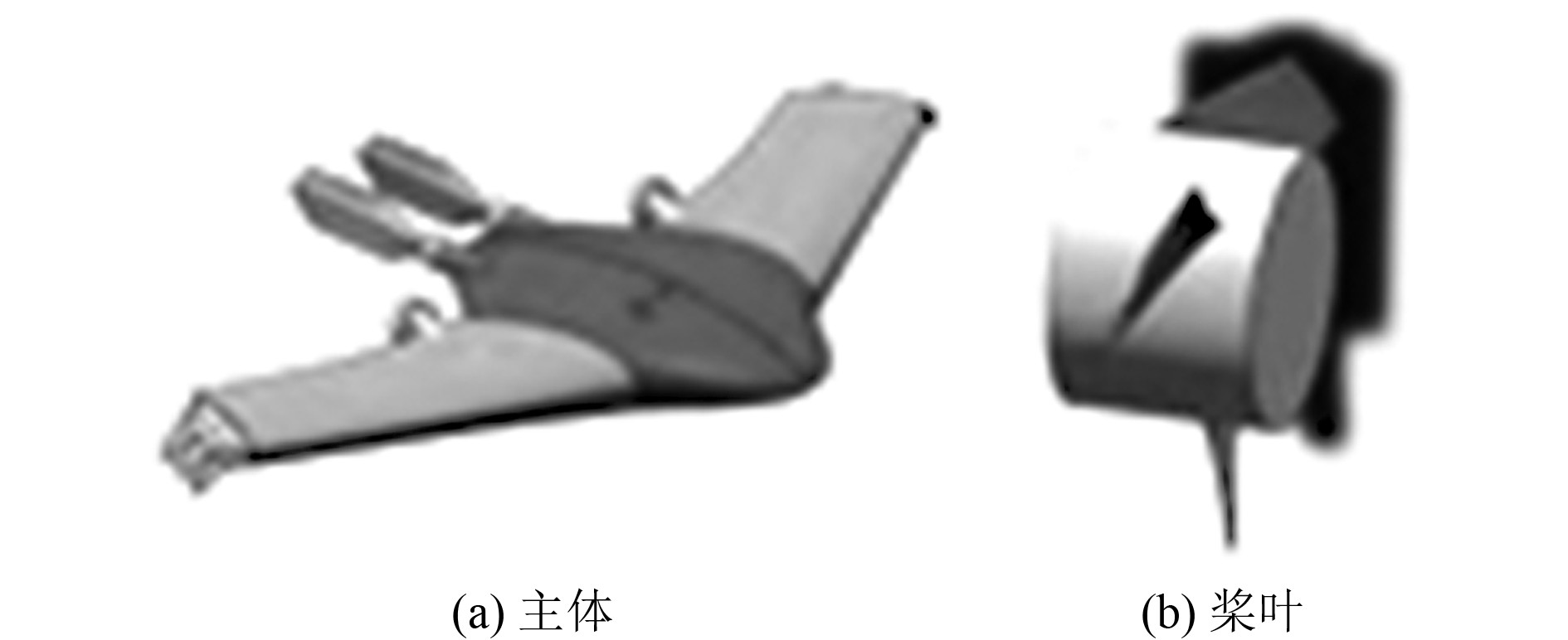
3.1 计算模型数值计算模型仿蟹滑翔机器人分为仿蟹滑翔机器人主体以及2部T200型导管螺旋桨,采用滑移网格法对计算模型进行前处理。为模拟实际运动状况,计算模型被分割为1个刚性体和2个旋转体,仿蟹滑翔机器人主体及导管可视为刚体,旋转体为导管螺旋桨的桨叶。为了计算的高效性,将仿蟹滑翔机器人进行简化。以仿蟹滑翔机器人的浮心为坐标原点建立右手坐标系并输出模型。简化后的仿蟹滑翔机器人如图7所示。
|
图 7 仿蟹滑翔机器人 Fig. 7 Crab gliding robot |
采用滑移网格法与多计算域法将计算模型划分为3个计算域,包括1个长方体外域和2个旋转内域。刚性体位于长方体域中,旋转体位于旋转域中,旋转域的边界即为滑移面。外域为7L×4L×3L的长方体域,以仿蟹滑翔机器人浮心为坐标原点,距离入口边界2L,距离出口边界5L。其中,L为仿蟹滑翔机器人长度。旋转域以桨叶轴中心线为轴的圆台体,圆台体直径略大于桨叶直径,并避开导流罩连接支柱。为了保证网格的高质量,加密航行区域、尾舵以及螺旋桨叶梢等部位网格。最终生成全六面体非结构网格。长方体域的网格数约为230万,单个旋转内域网格单元约为50万。利用HEXPRESS软件组合划分完毕的3个计算域网格,最终生成330万网格,如图8所示。

|
图 8 网格划分图 Fig. 8 Meshing diagram |
为保证本文采用的数值模拟方法能准确预报仿蟹滑翔机器人自航性能,选取仿蟹滑翔机器人的设计航速为计算时目标航速,即V=1.0 m/s。
结合计算的导管螺旋桨敞水性能,通过预估自航点处目标航速,选取33.33~43.33 r/s范围内的转速,间隔3.33 r/s。这4个转速作为研究仿蟹滑翔机器人自航性能的计算工况,具体计算工况如表3所示。
|
|
表 3 仿蟹滑翔机器人自航计算工况表 Tab.3 Self-propelled calculation working conditions of crab gliding robot |
计算域边界条件设置:长方体外域上方边界、下方边界设为指定压力梯度条件;其余边界设为速度远场;圆台体侧面为滑移面;仿蟹滑翔机器人与导管螺旋桨表面为壁面函数条件。工作环境为100~200 m水深的海洋环境;选择单相流;流体模型选择
采用非定常条件,时间步长Δt=0.01 s,总步数设置为4000步,总计算时间为40 s。
3.4 直航运动下的数值模拟与分析研究4个工况下仿蟹滑翔机器人直航运动。为提高计算效率,考虑仿蟹滑翔机器人具有姿态调节系统,可根据实际情况调整姿态,因此关闭横摇、横移和首摇三自由度,只求解直航、纵摇和升沉三自由度运动。计算完成后,通过后处理,观察各个工况下仿蟹滑翔机器人主体相应数据数值上有所差别,但各工况数据变化趋势基本一致,此时求解出仿蟹滑翔机器人的当前转速下航行速度Vx、直航状态下阻力Fx以及导管螺旋桨推力T。
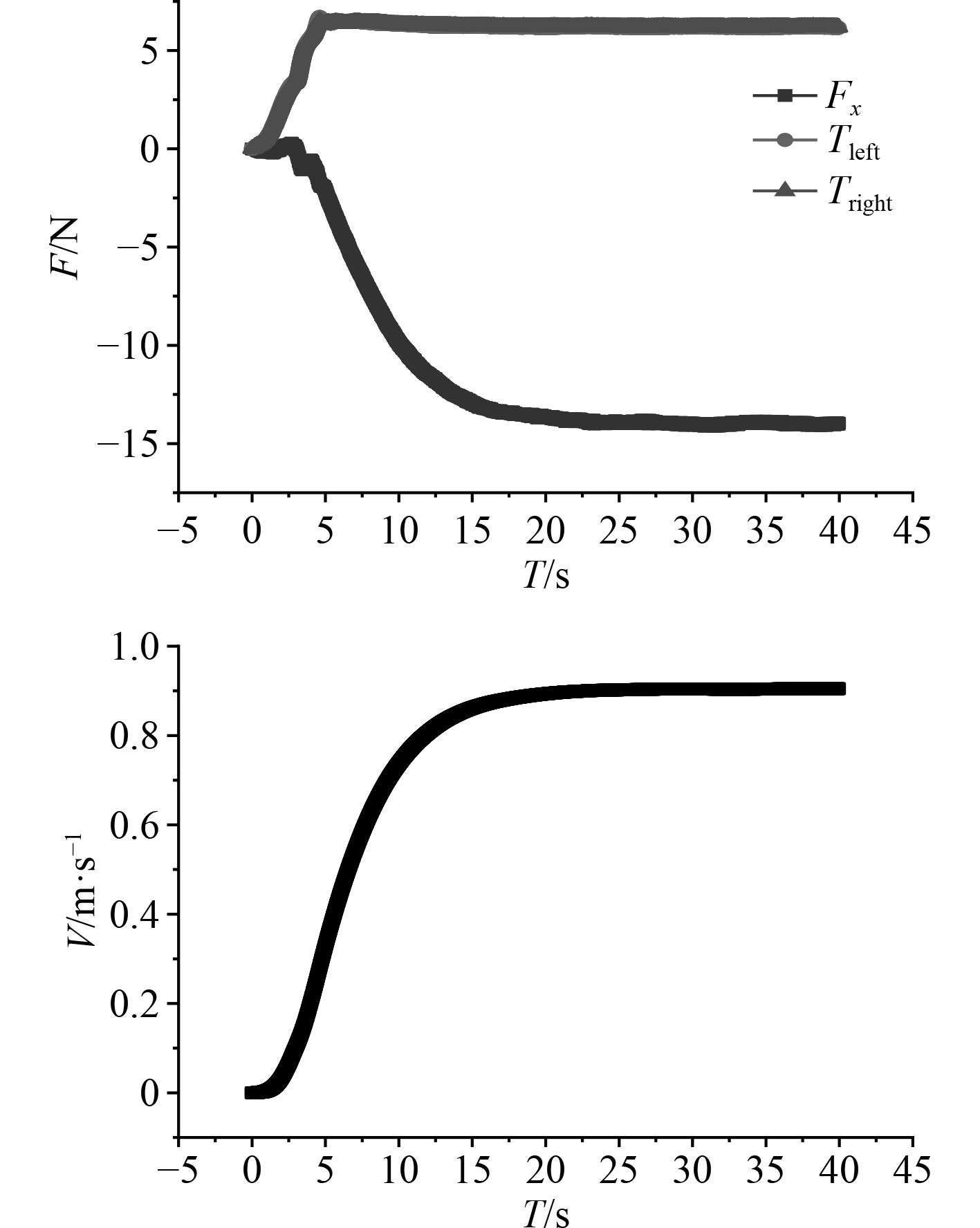
以转速 n=33.33 r/s为例,结果如图9 所示。可知:螺旋桨在5 s时间里从0逐步加速到指定转速,加速过程中,导管桨推力随着转速增大而不断增大;5 s后,导管桨转速达到指定转速,仿蟹滑翔机器人整体航速还在逐步增加,不过导管桨推力趋于稳定,由于模拟直航运动,左右导管桨桨叶旋向相反,但推力变化趋势基本一致;t=20 s后,导管桨、桨推力与阻力趋于平衡,运动状态趋于稳定,左右导管桨推力的合力与仿蟹滑翔机器人所受阻力近似相等,仿蟹滑翔机器人开始稳定自航;由于仿蟹滑翔机器人的足尖设计,导致其外形的不对称性,自航运动过程中会有微小的俯首力矩产生,导致仿蟹滑翔机器人自航运动过程中会产生姿态变化,出现主体纵摇和下降趋势,可通过姿态调节保证稳定直航。
|
图 9 n=33.33 r/s时仿蟹滑翔机器人的航速Vx、阻力Fx、桨推力Tleft和Tright Fig. 9 The speed Vx, drag Fx, propeller thrust Tleft and Tright of the crab gliding robot at n=33.33 r/s |
通过模拟,求解出各转速下仿蟹滑翔机器人的航速Vx、阻力Fx以及左右导管桨推力Tleft和Tright的数值结果,如表4所示。可以看出,不同转速下仿蟹滑翔机器人稳定自航时,仿蟹滑翔机器人所受阻力与左右导管桨推力的合力近似相等,仿蟹滑翔机器人本体自航运动状态趋于平衡;稳定自航状态下的航速Vx、阻力Fx以及螺旋桨推力T随着导管桨转速增加逐渐增加。
|
|
表 4 自航数值模拟结果 Tab.4 Results of self-propelled values |
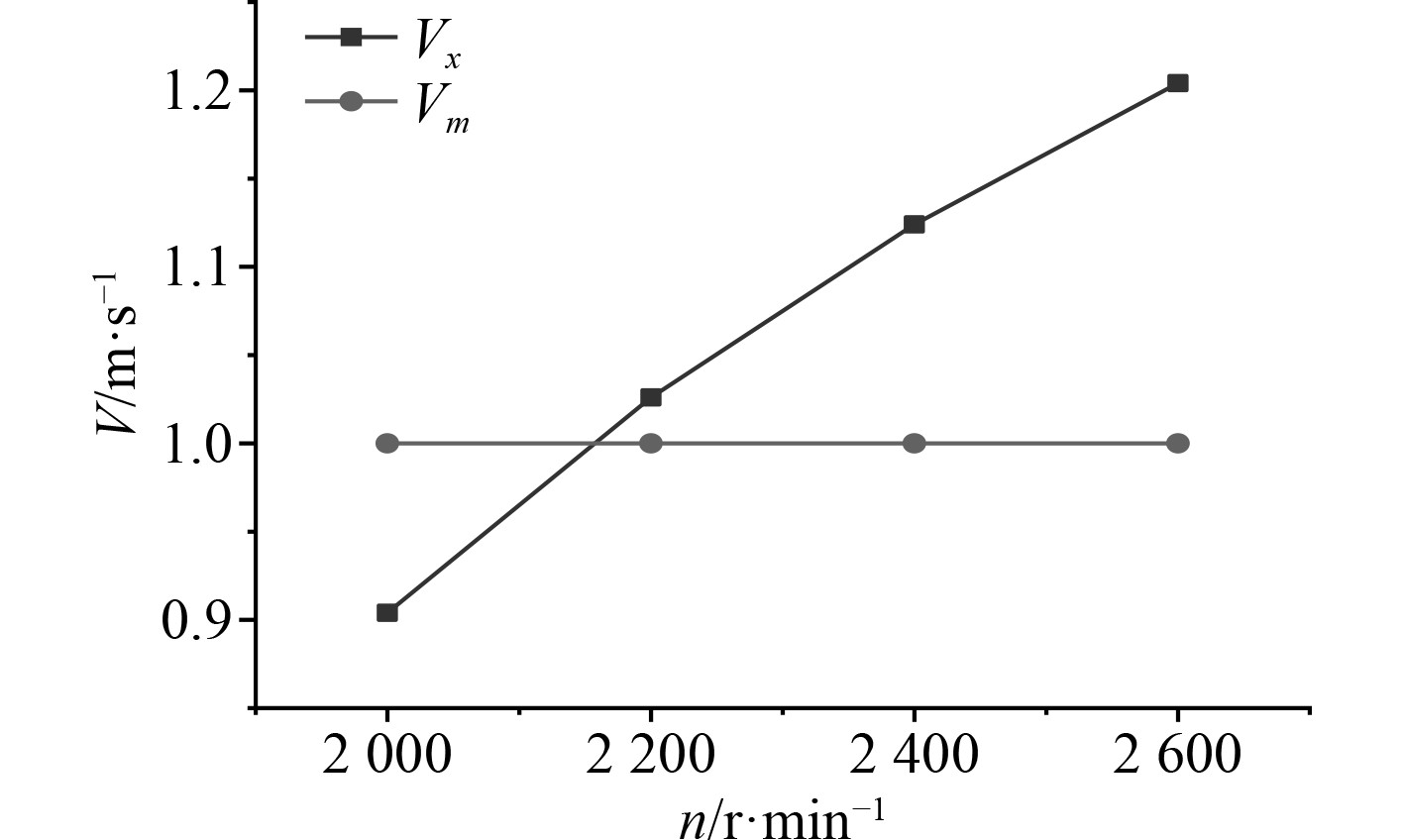
采用插值法,求得目标航速Vx=1.0 m/s 时的自航点导管桨转速n=36.2 r/s,如图10所示。数值模拟自航曲线,如图11所示。通过插值法,求得阻力Fx=–17.16 N,左桨推力Tleft=8.56 N,右桨推力Tright=8.49 N。考虑到左右桨均为型号相同的导管螺旋桨,故取左右桨推力的均值作为桨推力,Tave=8.535 N。
|
图 10 航速-导管桨转速曲线 Fig. 10 Speed-guide propeller speed curve |

|
图 11 数值模拟自航曲线 Fig. 11 Simulates the self-propelled curve numerically |
根据目标航速 Vx=1.0m/s 可得出进速系数J=0.3625,在导管螺旋桨的敞水性能曲线上采用插值法,求得推力系数KT=0.09553,扭矩系数10KQ=0.2811,效率η0=0.1853。仿蟹滑翔机器人目标航速下自航数值模拟结果如表5所示。
|
|
表 5 目标航速下自航数值模拟结果 Tab.5 Numerical simulation results of self-propelled aircraft at target speed |
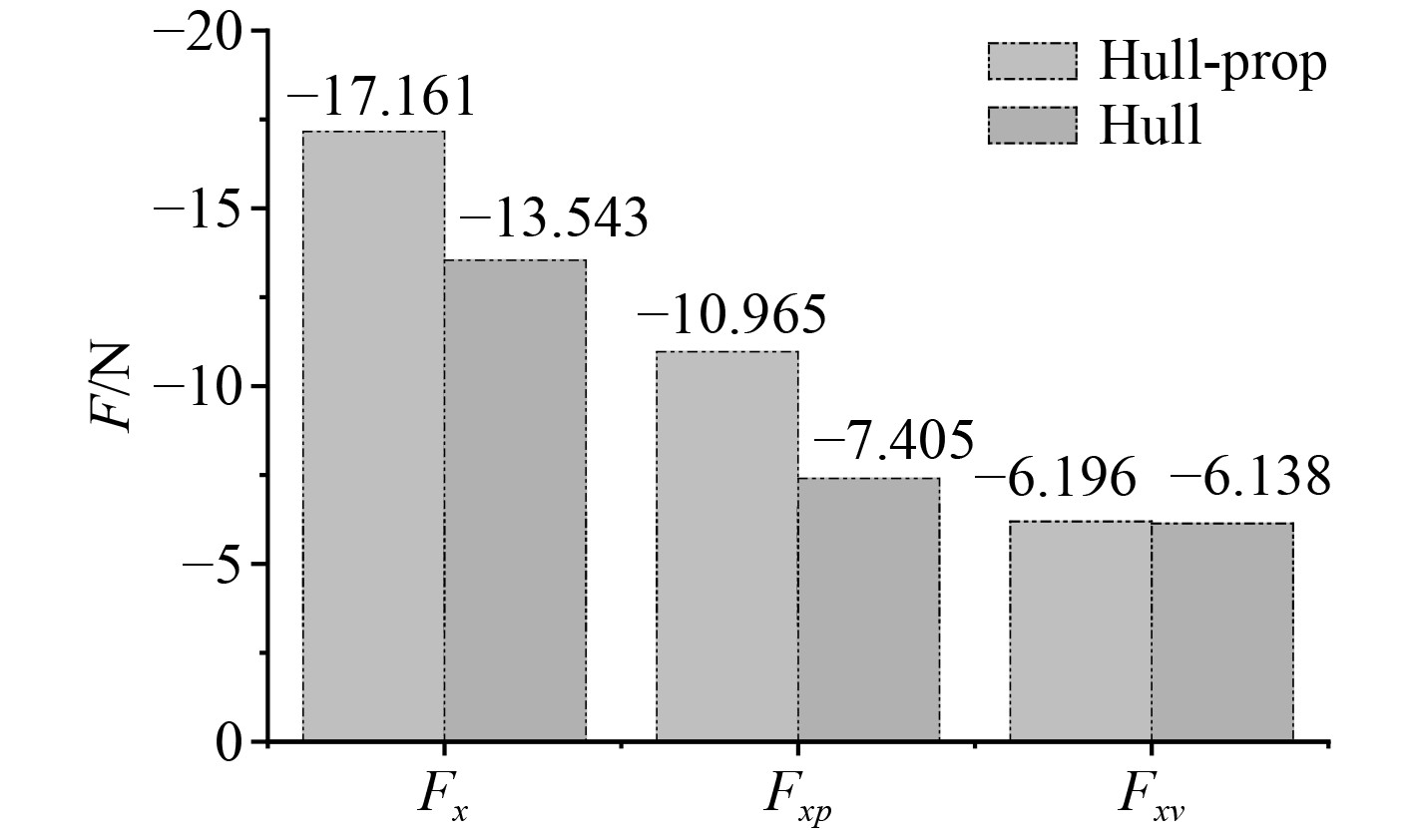
对比设计航速下带桨与不带桨的仿蟹滑翔机器人阻力,计算结果如图12所示。可知:加装导管螺旋桨,仿蟹滑翔机器人摩擦阻力增大,增加数值较小,小于1%;由于导管螺旋桨的抽吸作用,导致仿蟹滑翔机器人尾部压力大幅度增加,使得仿蟹滑翔机器人整体压差阻力大幅度增加,增加48.1%;仿蟹滑翔机器人总阻力也随之增加了26.7%。一定程度上体现了导管桨与仿生机器蟹之间的相互干扰。
|
图 12 带桨、不带桨仿蟹滑翔机器人阻力计算结果对比 Fig. 12 Comparison of resistance calculation results of imitation crab gliding robot with and without oars |
本文研究导管螺旋桨耦合作用下,仿蟹滑翔机器人自航性能。建立仿蟹滑翔机器人动力学模型;基于滑移网格法和多计算域法,对导管螺旋桨的敞水性能进行研究,并对仿蟹滑翔机器人本体-多桨耦合系统处于直航运动时转速为33.33~43.33 r/s范围内,间隔3.33 r/s的工况进行了自航运动操纵性能数值模拟,设置螺旋桨在5 s时间里从0逐步加速到指定转速,真实模拟了仿蟹滑翔机器人从缓慢加速到稳定自航全过程,求解出仿蟹滑翔机器人的航速Vx、阻力 Fx、左桨推力 Tleft 和右桨推力 Tright 随时间的变化规律。采用插值法,求得设计航速 Vx=1.0 m/s 下自航点的导管桨的转速 n=36.2 r/s,以及该转速下仿蟹滑翔机器人进速系数 J=0.3625、推力系数 KT=0.09553、扭矩系数10KQ=0.2811、效率 η0=0.1853。
对比加装螺旋桨前后仿蟹滑翔机器人阻力,得到加装螺旋桨后仿蟹滑翔机器人总阻力增加了 26.7%,但抵抗外界复杂环境能力大大增强,为仿蟹滑翔机器人样机设计提供理论依据。
| [1] |
刘雁集, 杨勇, 张桂臣. 水下滑翔机及其应用技术发展[J]. 船舶工程, 2021, 43(9): 14-21. LIU Y J, YANG Y, ZHANG G C. Underwater glider and its application technology development[J]. Ship Engineering, 2021, 43(9): 14-21. |
| [2] |
李永成, 马峥, 王小庆. 水下滑翔机高效滑翔水动力性能研究[J]. 中国造船, 2020, 61(4): 52-59. LI Y C, MA Z, WANG X Q. Research on the Hydrodynamic Performance of High Efficiency Gliding of Underwater Gliders[J]. China Shipbuilding, 2020, 61(4): 52-59. |
| [3] |
李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 16(7): 829-837. LI Z W, CUI W C. A review of research on the hydrodynamic shape of underwater gliders[J]. Ship Mechanics, 2012, 16(7): 829-837. |
| [4] |
王刚, 张立勋, 王立权. 八足仿蟹机器人步态规划方法[J]. 哈尔滨工程大学学报, 2011, 32(4): 486-491. WANG G, ZHANG L X, WANG L Q. Eight groups of crab like robot gait planning methods[J]. Journal of Harbin Engineering University, 2011, 32(4): 486-491. |
| [5] |
王立权, 王海龙, 陈曦, 等. 八足仿蟹机器人行走稳定性分析[J]. 中南大学学报(自然科学版), 2014, 45(10): 3416-3422. |
| [6] |
孔维翔, 凌宏杰, 王志东, 等. 仿蟹滑翔机器人水动力外形优化设计[J]. 船舶工程, 2021, 43(1): 131−137. SUN W X, LING H J, WANG Z D, et al. Optimization design of hydrodynamic shape for crab like gliding robot [J]. Ship Engineering, 2021, 43(1): 131−137. |
| [7] |
张士鹤. 水下滑翔机航向控制研究[D]. 天津: 天津大学, 2020.
|
| [8] |
陈晖. 温差能水下滑翔机试验系统研究与滑翔机外形设计[D]. 上海: 上海交通大学, 2012.
|
| [9] |
陈志明, 袁剑平, 严谨, 等. 基于MRF方法和滑移网格的螺旋桨水动力性能研究[J]. 船舶工程, 2020, 42(S1): 157-162311. CHEN Z M, YUAN J P, YAN J, et al. Research on hydrodynamic performance of propellers based on MRF method and sliding grid[J]. Ship Engineering, 2020, 42(S1): 157-162311. |
| [10] |
凌宏杰, 王志东, 孙玉山, 等. 混合驱动无人水下滑翔机耦合运动响应数值预报[J]. 中国海洋平台, 2021, 36(2): 17-22. LING H J, WANG Z D, SUN Y S, et al. Numerical prediction of coupled motion response of hybrid driven unmanned underwater glider[J]. China Ocean Platform, 2021, 36(2): 17-22. |
| [11] |
张学丰. 混合驱动的水下无人航行器总体设计与性能研究[D]. 镇江: 江苏科技大学, 2019.
|
| [12] |
彭冲. 自主航行模式下水下机器人(ROV)的操纵性能数值预报[D]. 镇江:江苏科技大学, 2018.
|
 2024, Vol. 46
2024, Vol. 46
