在高速大舵角下回转的舰船中,由于舵机的大幅度动作和高速旋转,横摇力矩波动成为了影响舰船稳定性和操控性能的重要因素[1]。为了提高舰船的稳定性和操控性能,需对横摇力矩波动进行自动控制[2 − 3]。因此,研究相关的横摇力矩波动控制方法具有重要的理论意义和实践价值。徐涛等[4]采用神经网络逆控制方法抑制横摇力矩波动。方琼林[5]采用分数阶微积分理论,设计了自适应滑模控制器,用于对横摇力矩波动进行抑制。但上述方法均未考虑高速大舵角下回转对横摇力矩的影响,导致横摇力矩波动控制效果并不理想。在高速大舵角下,由于水流与舵叶的相互作用,会引发舰船横摇力矩的波动。这种横摇力矩波动可能会导致舰船不稳定,甚至造成危险。为了提高舰船的安全性、航行稳定性和操作效率,研究高速大舵角下回转舰船横摇力矩波动自动控制方法,确保舰船安全稳定航行。
1 舰船横摇力矩波动自动控制 1.1 高速大舵角下回转舰船横摇力矩计算舰船在高速大舵角操作时,产生的横摇力矩对其稳定性有较为重要的影响。因此,在横摇力矩波动自动控制前,首先计算高速大舵角下回转舰船横摇力矩。令舰船与附加质量的转动惯量为
| $ M\left(\alpha,w,t\right)=I_{\phi}\ddot{\phi}+J_{\phi}\ddot{\phi}+R\left(\dot{\phi},t\right)+U\left(\phi,t\right)。$ | (1) |
式中:
舰船航行时,受高速大舵角下回转影响,会形成非期望的舰船横摇力矩波动现象,导致舰船航向出现改变,影响舰船航行的安全稳定性。当舵角较大时,在水流与舵叶的相互作用下,造成了较强的横向力矩。这种横向力矩会引起舰船发生横摇运动,即舰船绕纵轴进行左右晃动。因此,根据高速大舵角下回转形成的波浪激励力矩
| $ Z=\frac{M\left(\alpha,w,t\right)}{s\left(\omega\right)\exp\left(D_x\right)h_xA_x}-\frac{C_x}{2}\sin\alpha。$ | (2) |
式中:
考虑高速大舵角下回转形成的斜波浪,高速大舵角下回转形成的波倾角的频谱函数
| $ s\left(\omega\right)=\sum\limits_{n=1}^NE_n\cos\left[\omega_n^2\cos\alpha-t\left(\omega_n^{ }-\cos\alpha\right)+\varepsilon_n\right]。$ | (3) |
式中:
根据式(2)得到的高速大舵角下回转形成的波倾角频谱函数,考虑舵叶操纵产生的操纵力、舰船在运动中所受到的阻力对横摇力矩的影响以及动态相互作用因素后,结合舰船动力学理论,可得高速大舵角下回转形成的高频波浪作用下,舰船横摇力矩的计算式如下:
| $ \begin{split} Z'=& \frac{{M\left( {\alpha ,w,t} \right)}}{{\sum\limits_{n = 1}^N {{E_n}\cos \left[ {\omega _n^2\cos \alpha - t\left( {\omega _n^{} - \cos \alpha } \right) + {\varepsilon _n}} \right]} \exp \left( {{D_x}} \right){h_x}{A_x}}}-\\ & \frac{{{C_x}}}{2}\sin \alpha。\\[-1pt] \end{split} $ | (4) |
基于式(3)的舰船横摇力矩计算结果,可为后续基于鲁棒PID的舰船横摇力矩波动自动控制算法提供准确的数据支持,提高舰船在高速大舵角操纵时的航向稳定性,增强回转性能和操纵安全性。通过该过程,可确保舰船在各种运行条件下的稳定性和可靠性。
1.2 基于鲁棒PID的舰船横摇力矩波动自动控制在高速运动状态下,舰船受到波浪的影响会产生横摇力矩,进而影响舰船的稳定性和安全性[7]。为了减小或消除这种横摇力矩带来的不利影响,利用闭环增益成形算法,设计舰船横摇力矩波动自动控制的鲁棒PID控制器,并输入1.1节计算获取的高速大舵角下回转舰船横摇力矩与期望力矩间的误差,以及误差变化率,输出横摇力矩波动自动控制律,抑制横摇力矩波动现象,提高舰船的横摇稳定性和航行安全性。
令舰船横摇带宽频率为
| $ K\left(Z'\right)=\frac{1}{s\left(Z'\right)T_1s'}。$ | (5) |
式中:
令
| $ s\left(Z'\right)\text{ = }\frac{a_1}{b_0T_1}+\frac{a_2s'}{b_0T_1}+\frac{a_0}{b_0T_1s'}。$ | (6) |
式(6)中的标准PID控制器比例、积分、微分系数为
在舰船行进过程中[7],面临高速大舵角情况时,舰船横摇力矩波动自动控制的鲁棒PID控制器输出控制律为:
| $ \mu=-\left(K_Pe+K_D\dot{e}+K_I\frac{e}{\dot{e}}\right)。$ | (7) |
其中,
为了验证和评估所提的高速大舵角下回转舰船横摇力矩波动自动控制方法的实用价值,以具有高速性能和大舵角操纵特点的某舰船为实验对象,进行实验。该舰船的相关参数如表1所示。
|
|
表 1 舰船相关参数 Tab.1 Ship related parameters |
设置该舰船在航速为10°/s,舵角为35°时,进行回转。摄像机系统安装在舰船的中央控制台上,用于记录舰船回转过程中的横摇角度和舰船运动情况。采用高分辨率摄像机,以确保数据记录的精确性。具体测试过程如下:
步骤1 准备阶段。在陆地实验室中对舰船的操纵系统进行校准,确保其正常工作并与船体动力系统相匹配。
步骤2 舰船设置。将摄像机固定在舰船的中央控制台上,并确保其视野覆盖整个舰船回转区域。
步骤3 测试场地选择。选择一个平静的水域作为测试场地,避免外界因素对实验结果的干扰。
步骤4 数据采集。开始实验前,启动摄像机系统并确保其采集和记录舰船回转过程中的视频,包括横摇角度和船体运动。
步骤5 实验。执行高速大舵角下的回转操作,并记录相应的摄像机数据。控制系统根据横摇力矩波动自动调整舰船操纵,使其维持在目标轨迹上。
数据分析使用视频回放工具对摄像机数据进行分析,测量舰船横摇角度和横摇力矩的变化,评估自动控制系统的效果。表2为舰船运动数值。
利用本文方法对高速大舵角下回转舰船横摇力矩波动展开自动控制,横摇力矩波动自动控制结果如图1所示。
|
|
表 2 舰船相关参数 Tab.2 Ship related parameters |
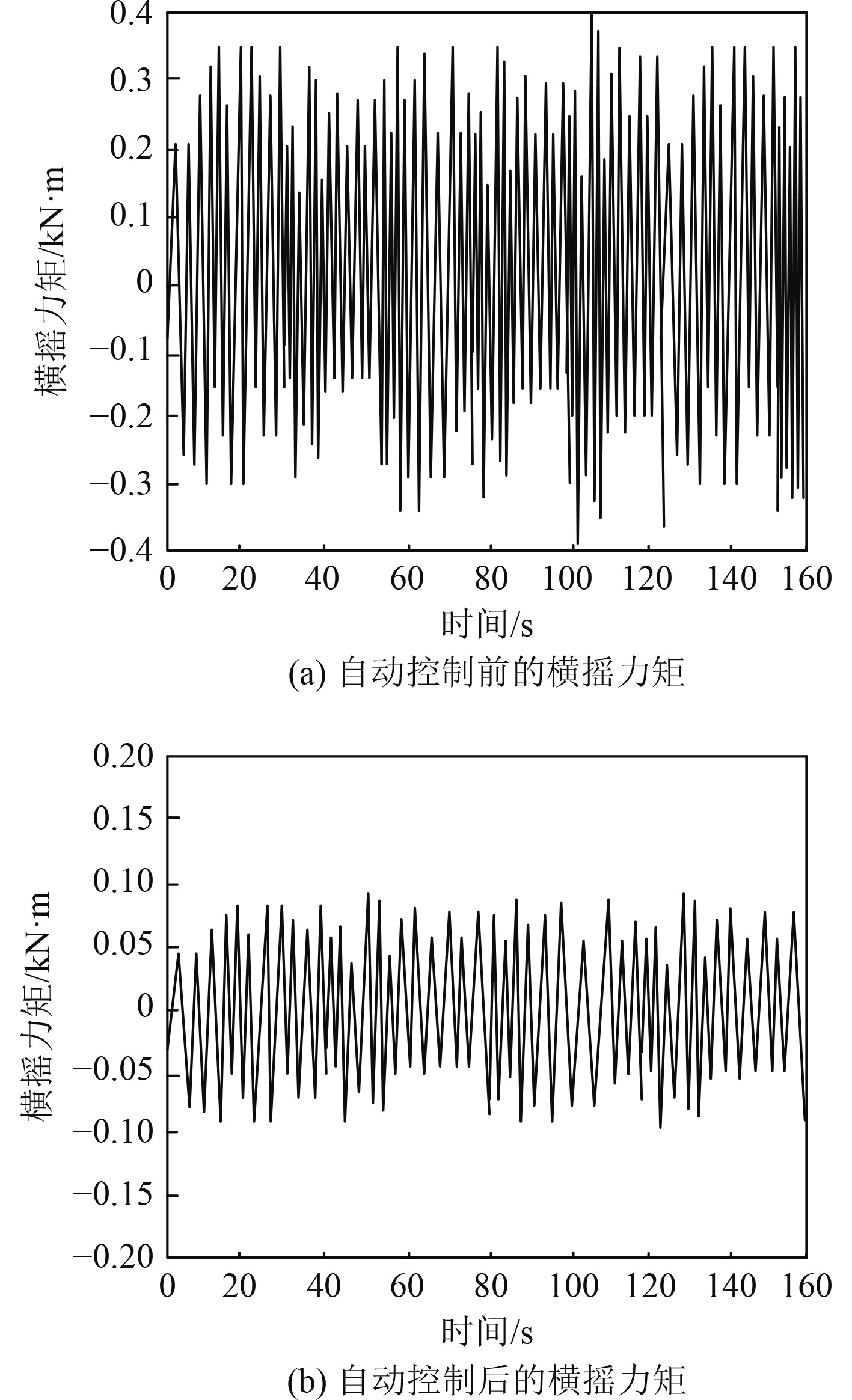
|
图 1 本文方法的横摇力矩波动自动控制结果 Fig. 1 Results of automatic control of rolling moment fluctuation of the proposed method |
对比分析可知,未经本文方法自动控制前,该舰船在高速大舵角回转时,其横摇力矩在±0.4 kn·m之间波动;经过本文方法自动控制后,该舰船的横摇力矩在±0.1 kn·m之间波动,说明在高速大舵角下回转,本文方法可有效自动控制舰船横摇力矩波动,降低横摇力矩的波动幅度。上述结果表明,本文方法不仅提升了舰船的回转稳定性和操纵性能,还减少横摇力矩的波动。
为了进一步验证本文方法在实际应用中的效果,分析在高速大舵角下回转时,利用本文方法自动控制舰船横摇力矩波动后,舰船横摇角的变化情况。如果横摇角过大,会导致舰船的航向稳定性变差,影响舰船航行的安全稳定性。如果横摇角过小,则表示舰船的横摇运动阻尼过大,导致舰船无法有效地吸收和消耗波浪能量,影响其使用性能和寿命。为此,舰船横摇角的允许变化区间为±10°。分析结果如图2所示。
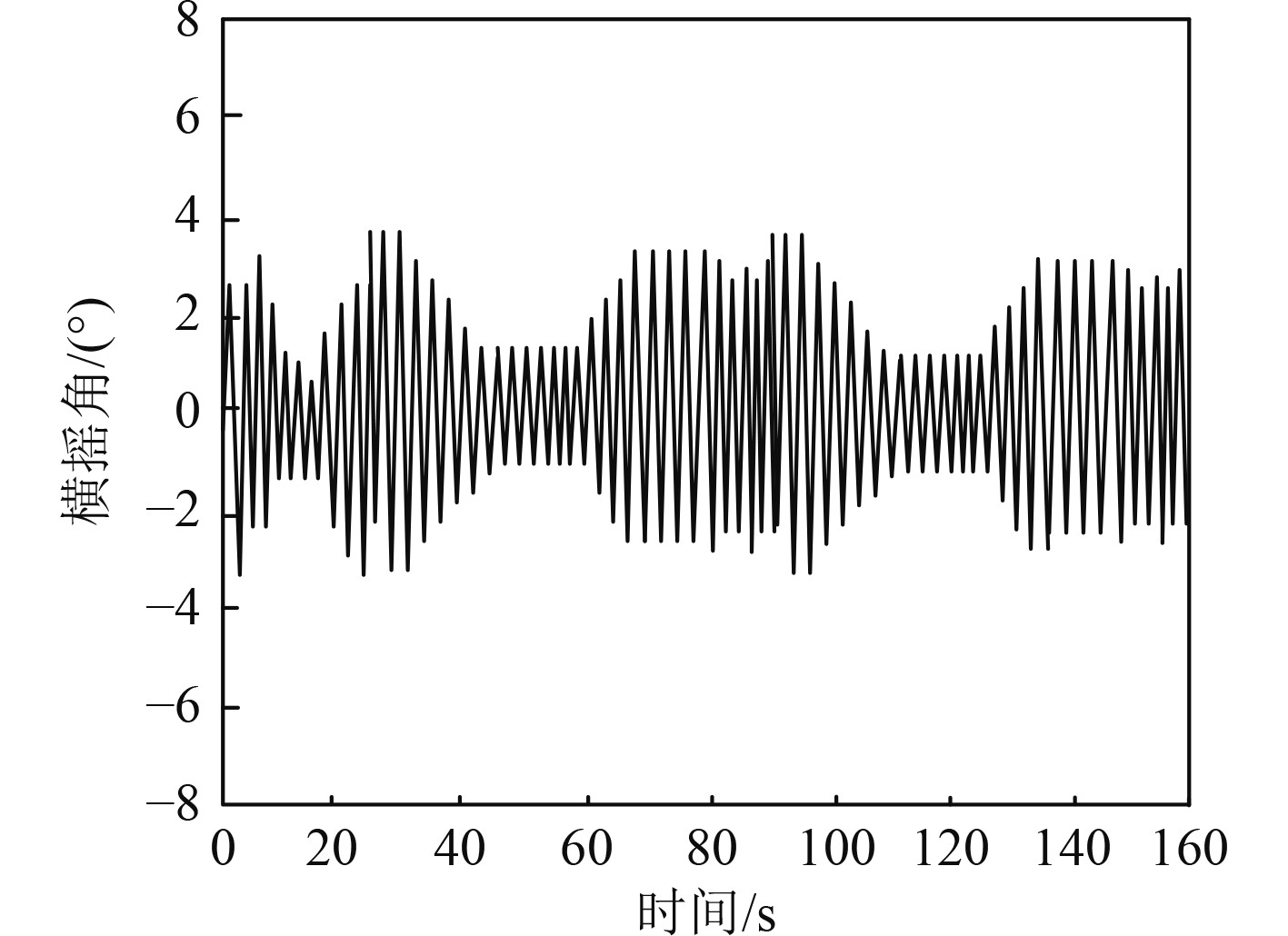
|
图 2 舰船横摇角的变化情况 Fig. 2 Changes of ship roll angle |
可知,经过本文方法自动控制后,该舰船在高速大舵角回转时,其横摇角始终在±4°之间波动,始终在舰船横摇角的允许范围内波动,说明应用本文方法自动控制后,可确保舰船回转过程中,其横摇角始终在允许范围内,保证舰船回转的安全稳定性。图2测试结果对实际舰船操纵具有重要的补充说明。在高速大舵角回转时,舰船的横摇角是一个关键参数,其超出允许范围可能导致失控、倾覆甚至事故。通过应用本文方法对其进行自动控制,舰船的横摇角能够始终保持在安全范围内,确保了舰船回转过程的可控性和稳定性。
在高速大舵角回转时,舰船的回转轨迹对于其操作和航行安全至关重要。过大的偏离会导致航向失稳、操作困难等问题,可能对舰船的安全造成影响。回转轨迹是舰船在进行回转操作时,所经过的轨迹路径,通过分析回转轨迹的特征和与期望轨迹的接近程度,可得出本文方法自动控制的实际效果。为此,分析本文方法自动控制后,该舰船的回转轨迹,分析结果如图3所示。
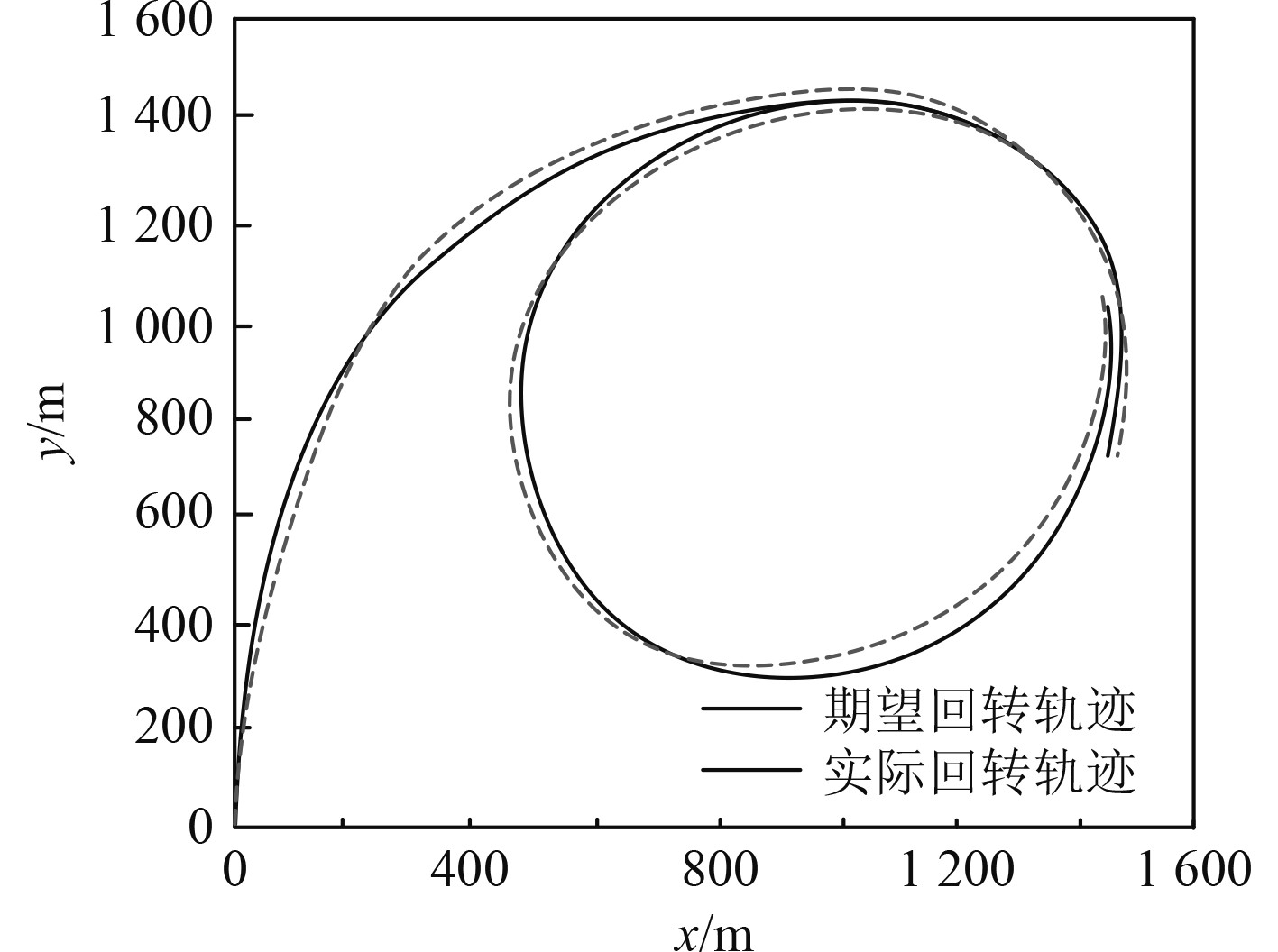
|
图 3 舰船回转轨迹变化情况 Fig. 3 Changes of ship's turning trajectory |
可知,经过本文方法自动控制后,高速大舵角回转时,舰船回转轨迹与期望回转轨迹非常接近,说明本文方法舰船横摇力矩波动自动控制效果较优,确保舰船的回转轨迹不会偏离期望轨迹,能有效保持舰船回转轨迹的稳定性,并确保舰船在高速大舵角下回转时能够保持良好稳定性。通过采用本文方法的自动控制,舰船的回转轨迹能与期望回转轨迹非常接近,避免出现航向失稳、操作困难等问题,保证了高速大舵角下回转的稳定性和操作的可控性。
3 结 语为了有效地抑制横摇力矩波动,提高舰船的回转性能和稳定性,研究高速大舵角下回转舰船横摇力矩波动自动控制方法。本文方法在对舰船横摇力矩现象的深入理解和分析的基础上,结合鲁棒PID控制方法,以计算得到的横摇力矩及其误差为输入,实现舰船横摇力矩波动的自动控制。这个控制方法的研究与之前的横摇力矩计算相辅相成,将科研成果转化为实际应用价值,解决了高速大舵角下回转舰船横摇力矩振动的问题,为舰船操纵提供了更稳定的环境。实验结果表明,应用本文方法后,能够使舰船在复杂海况下保持稳定的回转轨迹,从而确保舰船的安全性和操作性能。
| [1] |
李云波, 付峥, 龚家烨, 等. 横浪中三体船横摇运动稳定性研究[J]. 中国造船, 2021, 62(4): 89-100. DOI:10.3969/j.issn.1000-4882.2021.04.007 |
| [2] |
朱倩云, 梁玉珂, 沈林维. 目标海域中航行船舶横摇谱密度值的预报策略[J]. 船舶力学, 2023, 27(10): 1487-1495. DOI:10.3969/j.issn.1007-7294.2023.10.006 |
| [3] |
李彪, 隋芳芳, 董宇豪, 等. 船舶陀螺减摇器减摇性能的全系统数值仿真研究[J]. 江苏科技大学学报(自然科学版), 2022, 36(4): 6-12. |
| [4] |
徐涛, 李晖, 祁昱豪. 船舶参数横摇抑制的神经网络逆/内模控制[J]. 船舶工程, 2022, 44(6): 109-116. |
| [5] |
方琼林. 基于分数阶自适应滑模的船舶非线性减摇控制[J]. 中国舰船研究, 2021, 16(4): 132-139. |
| [6] |
赵文浩, 张文, 李高磊, 等. 船舶横摇系统的多稳态动力学及其控制[J]. 振动与冲击, 2022, 41(18): 192-196,204. |
| [7] |
马山, 丰思鑫, 张祖妍, 等. 迎浪随机波中C11集装箱船参数激励横摇对应波群特性分析[J]. 哈尔滨工程大学学报, 2022, 43(7): 921-927. |
| [8] |
谢嘉令, 施伟锋, 兰莹, 等. 基于幂次指数趋近律的船舶电力推进控制研究[J]. 计算机仿真, 2022, 39(6): 279-283. |
 2024, Vol. 46
2024, Vol. 46
