轮缘推进器(Rim-driven Thruster,RDT)是一款新型的船舶推进器,近年来被广泛应用。RDT由电机、轴承、螺旋桨和导管等部分基本机构组成。轮缘推进器的电机被嵌于导管内,因而可以将电机的直驱模式发挥到极致[1],不仅大大减少了船上空间的布置,也使推进器布置更加灵活[2]。
目前,RDT的水动力性能研究主要是基于CFD对螺旋桨结构设计、导管形状和尺寸、气隙厚度和其他因素进行水动力效率影响进行分析。贾文超等[3]采用CFD模拟软件计算了无轴轮缘推进器在不同桨叶数目螺旋桨的推力与扭矩值,并与经验公式的计算结果对比验证了仿真计算的准确性。左新平等[4]评估了7叶轮缘推进器的水动力性能,通过CFD仿真计算与试验结果进行对比,具有较好的契合度。熊立众等[5]采用SST k-ω湍流模型对轮缘推进器的桨叶进行了多参数分析,总结了桨叶参数变化对于推进器水动力性能的影响。杨蕾等[6]构造了叶梢厚、叶根薄的反厚度规律桨叶,通过设计3套桨叶翼型进行敞水性能分析,得到了较优的桨叶,为RDT的反厚度螺旋桨设计提供了参考。兰加芬等[7]采用CFD计算了某无轴轮缘推进器轮缘内外表面、前后端面的摩擦扭矩值,并与经验公式值进行对比,结果显示误差非常小,具有良好的预测预报能力。Liu等[8]对管道螺旋桨和RDT进行了数值比较,与导管式螺旋桨相比,RDT对螺旋桨和管道产生的推力更小,而且由于轮辋的存在,RDT的整体效率明显较低。Yakovlev等[9]对轮缘推进器有无轮毂的情况进行研究,并通过试验对数值仿真结果进行验证,数值模拟结果与试验结果吻合较好,并发现无轮毂时的推进效率要高于有轮毂时的推进效率。Dubas等[10 − 11]对B4-70螺旋桨组成的RDT的导管进行了模型优化,发现优化后模型的最大效率较原模型可提高6%。Hughes等[12]将对称型导管和标准非对称型导管的RDT的水动力性能进行对比,发现标准非对称型导管的RDT在单位功率下产生的推力要小于对称型导管的RDT。Sharkh等[13]分析各类型的导管轮廓对RDT水动力性能的影响,发现非对称导管螺旋桨虽然在系柱状态下产生的推力更大,但其消耗的功率更多。
在RDT的研究中,RDT的外形,如桨叶、导管、桨毂、轮缘对于推进器的敞水效率均会产生一定的影响。本文使用STAR-CCM+仿真软件只考虑水动力模型的情况下,使用以19A+Ka4-70导管螺旋桨为原型分析了导管、桨毂、轮缘对于RDT的水动力性能差异。
1 计算模型与物理模型 1.1 常规导管桨采用常见的Ka4-70+NO.19A导管螺旋桨进行物理模型的验证,该导管螺旋桨有大量的实验数据可供参考。根据文献[14]中的Ka系列图谱,通过二维翼型和三维翼型的坐标导出建立螺旋桨模型。螺旋桨叶片的螺距比均为1.0,桨毂比为0.2,桨叶参数如表1所示,最后得到的模型如图1所示。
|
|
表 1 Ka4-70螺旋桨特征参数 Tab.1 Characteristic parameters of the Ka4-70 propeller |

|
图 1 Ka4-70+19A导管螺旋桨 Fig. 1 The Ka4-70 + 19A duct propeller |
轮缘推进器(RDT)与导管螺旋桨的主要区别在于驱动形式和螺旋桨安装方式的不同,由于RDT的桨叶通过梢部与驱动环固定,电机的扭矩会直接通过转子传递至叶梢,使得叶梢处应力集中而产生较大的形变[6],影响桨叶强度和水动力性能,因此RDT的桨叶厚度分布通常采用叶梢厚、叶尖薄的厚度分布。
目前关于RDT桨叶的设计暂时没有统一的标准,最简单的厚度分布变化就是将原来的厚度分布直接倒置,使桨叶具有一定的抗弯强度。因此,采用该厚度分布进行RDT螺旋桨的建模。保持Ka4-70螺旋桨的其他参数分布不变,仅改变其厚度分布,以anti-Ka4-70命名。其厚度与螺旋桨直径的比值如表2所示,其模型图如图2所示。
|
|
表 2 桨叶叶切面最大厚度与直径的比值 Tab.2 Ratio of maximum thickness and diameter of blade section |

|
图 2 anti-Ka4-70轮缘推进器模型 Fig. 2 anti-Ka4-70 rim-driven propeller model |
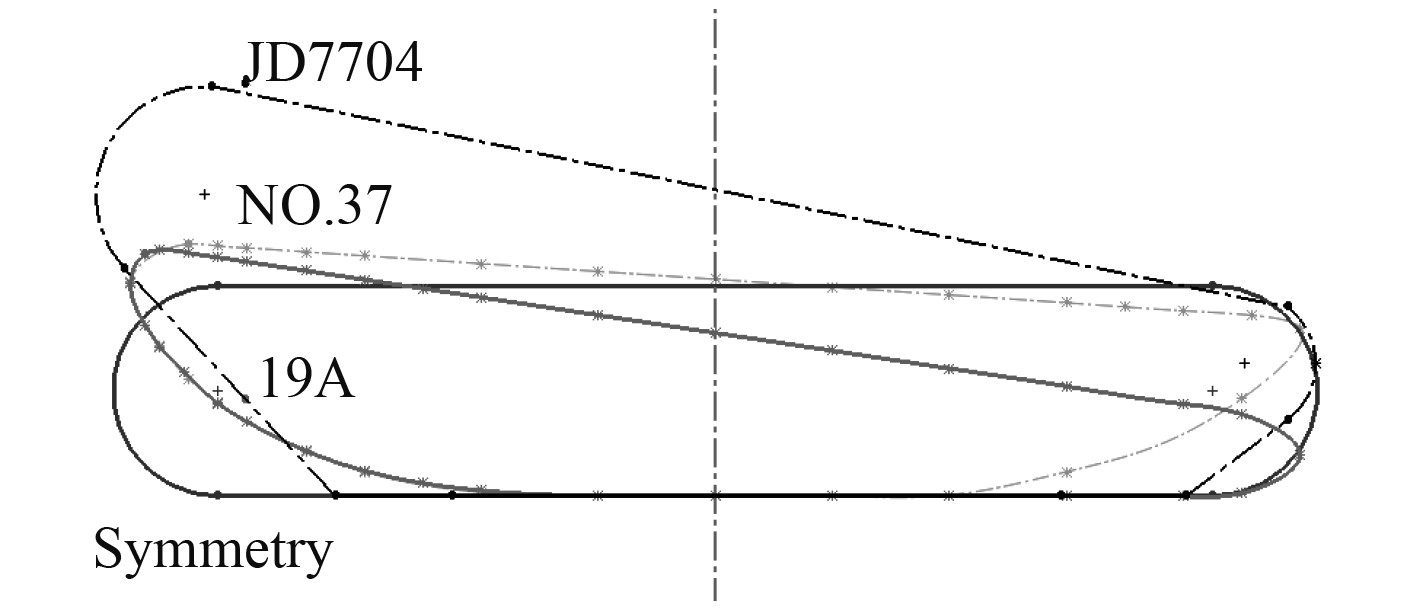
在RDT的导管设计中,以对称型导管最为常见,对称型导管更便于电机和轮缘的安装。因此,选取对称型导管和导管螺旋桨中常用的4种导罩轮廓,分别为19A型导管、NO.37型导管和JD7704导管进行水动力性能的对比计算分析。4种导罩轮廓如图3所示,导管尺寸均进行了相应修改,使其内部适合轮缘的放置,导管的长度为100 mm,轮缘的宽度为48 mm,间隙宽度为1 mm。
|
图 3 导罩轮廓曲线 Fig. 3 Duct contour curve |
采用RANS方程用于控制流的传输,其雷诺时均化后的不可压缩连续性方程和动量方程如下:
| $ \frac{{\partial \left( {\overline {{u_i}} } \right)}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{{\partial \left( {\rho \overline {{u_i}} } \right)}}{{\partial t}} + \rho \overline {{u_j}} \frac{{\partial \overline {{u_j}} }}{{\partial {x_j}}} = \rho \overline {{F_i}} - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho \overline {u'_i u'_j} } \right) 。$ | (2) |
式中:ui、uj均为略去平均符号的雷诺平均速度分量;ρ为密度;p为压强;
采用Menter[15]开发的SST
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _k}\frac{{{\partial _k}}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k} ,$ | (3) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _\omega }\frac{{{\partial _\omega }}}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {S_\omega } + {D_\omega } 。$ | (4) |
式中:
| $ {\Gamma _k} = \mu + \frac{{{\mu _t}}}{{{\partial _k}}},$ | (5) |
| $ {\Gamma _\omega } = \mu + \frac{{{\mu _t}}}{{{\partial _\omega }}}。$ | (6) |
式中:
网格生成主要依赖于STAR-CCM+的自动网格生成功能,并对局部进行加密处理。计算域由2个子域所组成,分别为轮缘、桨叶所在的旋转域和围绕旋转域的静态域。静态域为一个圆柱体的区域,长度为10D,半径为3D。旋转域的长度为D,半径为D,RDT螺旋桨盘面距离静态域的入口边界为3D,如图4所示。图中内部区域为旋转域,D为螺旋桨的直径。

|
图 4 计算域和网格 Fig. 4 Computation domain and the grid |
采用围绕实体表面建立的切割体网格,静止域的网格基础尺寸设置为0.04D,静态域的网格基础尺寸设置为0.16D。并设置棱柱层,对于旋转域内实体壁面的棱柱层总厚度设置为0.001 m,设置10层,其y+平均值大约为4.6。均对于旋转域,采用多参考系(MFR)方法。对于桨叶、轮缘和导管表面、静止域外表面采用壁面条件,在入口边界采用速度进口条件,在出口边界采用压力出口条件,采用均匀分离流进行计算。
本文采用的螺旋桨无量纲水动力参数公式如下:
| $ J{\text{ = }}\frac{{{V_a}}}{{{{n}}D}}\text{,}{K_T}{\text{ = }}\frac{T}{{\rho {{{n}}^2}{D^4}}}\text{,}{K_Q}{\text{ = }}\frac{Q}{{\rho {{{n}}^2}{D^5}}}\text{,}{\eta _0}{\text{ = }}\frac{J}{{2{\text{π}} }}\frac{{{K_T}}}{{{K_Q}}},$ |
| $ T = {T_P} + {T_D},{C_p}{\text{ = }}\frac{{p - {p_\infty }}}{{\frac{1}{2}\rho {v^2}}} 。$ | (7) |
式中:
由于RDT的相关试验数据难以找到,因此,本文采用对Ka4-70+NO.19A导罩螺旋桨的试验数据[17],对数值模拟的结果进行验证。分别生成了中等、紧密2组密度的网格进行敞水性能计算并试验值进行对比,如图5所示,并对J=0.1和0.6时的KT、10KQ、η0采用Roache[18]提出的双网格评估程序进行网格灵敏度分析,网格不确定度在1%以内为佳。

|
图 5 不同网格密度的敞水性能曲线 Fig. 5 Open water performance curves for different grid densities |
网格不确定度的计算结果如表3所示。可知,2种网格上的推力和扭矩预测几乎相同。在低进速时,网格不确定度稍大,在较高进速时,网格不确定度都在1%以内。此外,图3突出显示了计算出的RDT的推力和转矩系数与实验数据的拟合较为良好,最大误差分别为4.3%和2.6%,误差控制均在5%以内,计算结果具有一定的可靠性。考虑到计算效率,本文采用中等密度网格进行计算。
|
|
表 3 网格不确定度分析 Tab.3 Grid uncertainty analysis |
图6所示为RDT和导管螺旋桨的敞水性能曲线(J=0.1~0.8),由于导管所产生的扭矩几乎为0,因此暂不将其计入整体的扭矩系数计算中。可以看到anti-Ka4-70的整体性能要低于导管螺旋桨,其主要原因是anti-Ka4-70的扭矩要大于Ka4-70桨,两者均在J=0.6时达到最大的推进效率。

|
图 6 RDT和导管螺旋桨的敞水性能比较 Fig. 6 Comparison of open water performance between RDT and duct propeller |
图7为2组推进器在J=0.6时的螺旋桨的表面压力分布情况。图中正值表示正压,负值表示负压,颜色越深,值越大。可知,2组推进器的螺旋桨表面的压力分布较为相似,等值线的分布较为一致,桨叶的前后表面压差基本相等,说明两者螺旋桨的推力输出较为一致。但在吸力面,RDT的负压区要明显小于导管螺旋桨,这是由于轮缘的对桨叶表面和叶梢处水流具有阻挡作用,类似于端板的效果,据此推测可以减少空泡的产生。

|
图 7 螺旋桨表面的压力分布云图 Fig. 7 Cloud map of the pressure distribution on the propeller surface |
图8为不同导管轮廓的敞水性能曲线,可见看出导管轮廓的不同,对RDT的整体性能的影响也会有一定的差异。4种导管在J=0.6时均达到最大的效率,其效率在达到最大值后均下降较快,其中,NO.19A导管下的推进器效率最高,其最大效率较对称型导管、NO.37导管、JD7704导管分别高出1.5%、3.7%、4.2%。然而,随着进速系数的增大,尤其是在达到最大推进效率之后,这种差异逐渐增大,效率下降加速。对称型导管在高进速时,效率下降较慢,具有较优的水动力性能。4种导管RDT的KQ有较大的差异,与螺旋桨桨叶的KT呈正相关,其中,19A导管和NO.37导管所产生的扭矩较小,不同导管在效率上的差异,主要是通过螺旋桨的扭矩差异体现。

|
图 8 不同导管轮廓的RDT的敞水性能比较 Fig. 8 Comparison of open water performance of RDT for different duct |
图9为在J=0.6时的19A导管、NO.37导管、对称型导管、JD7704导管的轮廓截面流速度分布和压力系数分布,颜色区域表示在流域的压力系数分布,箭头的方向和长度表示流场的方向和大小。

|
图 9 不同导管廓线附近的流场(J=0.6) Fig. 9 Flow field near different catheter profiles (J=0.6) |
图中箭头较密集的区域说明流场较为紊乱,流向变化较急,主要发生在导管的前缘和后缘,以及轮缘前后的缝隙进出口处,其中对称型导管的流场变化较小,19A导管、NO.37导管、JD7704导管的流场变化较大。图中分别对1、2、3、4这4个区域进行了局部放大。由区域1可知,在水流经过导管时,与导管的前缘壁面发生了碰撞,在导管外表面发生了流体分离,尤其是19A导管的流动分离最为明显,另外3个导管只观察到轻微的分离。分离区的范围随着推进系数的增加而增大,因为更快的流速使迎角较小,并体现为较为明显的分离现象。由区域2可知,经过导管前缘后,水流在导管外表面基本贴合导管表面流动,并呈现为粘性流动,具有较为明显的梯度变化,边界层设置较好。由区域3可知,在轮缘与导管的交界处,由于存在缝隙,会有水流经过,但在此交界处的水流方向与进速方向相反,在沿着轮缘的方向形成环流。由区域4可知,但当流经导管后缘时,由于导管表面曲率的变化,其尾流产生了回流,形成一个负方向的流场区域,可以观察到19A导管的负流场区域范围最小,受到尾涡的影响较小。
为了更好地了解4种导管设计中推力产生的差异,截取了螺旋桨参考平面的纵向截面,并表示其压力系数,如图10所示。图中显示了压力系数相对于轴向的导管长度的函数,其中位置0.05和−0.05分别对应于管道的前缘和后缘的位置。可见,在所有4种导管的设计中,导管外部的压力分布几乎相同,其表面的压力系数保持不变,这一点从图9区域2的分析中得到了印证;而可以观察到的最大的压力差异是在导管内部。在导管的进流区域,4种导管内部均产生了较大的负压区,其负值由小到大排列为19A导管、NO.37导管、对称型导管、JD7704导管,而在导管出流区域,4种导管的压力系数差异不大,因此,由于前后区域的压强差,使得导管产生了较大的推力。沿着导管长度方向,压力系数的绝对值的趋势不断减小,并趋向于0,随着进速的增大,该趋势会减弱,导致导罩前后压差减小,使得导罩产生的推力减小。

|
图 10 4种导管的RDT纵向截面的压力分布(J=0.6) Fig. 10 Pressure distribution of the RDT with four ducts(J=0.6) |
在轮缘推进器的叶尖处增加桨毂,以增强桨叶的强度,本文对有无桨毂的情况进行分析。采用桨毂比为0.2的桨毂分别对NO.19A导管和对称型导管在有无桨毂的情况下进行敞水性能计算,如图11所示。

|
图 11 有无桨毂敞水性能对比 Fig. 11 Comparison of open water performance for hub |
在低进速时,当进速系数较低时,有桨毂和无桨毂的推进效率曲线几乎重合,可见在重载荷情况下,有无桨毂对于RDT的整体性能基本无影响,但随着进速的增大,其效率的差异就显现出来,桨毂降低了螺旋桨的推进效率。在进速系数J=0.6时,效率达到最大值,NO.19A导管在有无桨毂情况下最大效率相差4.5%,对称型导管在有无桨毂的情况下最大效率相差2.9%。在高进速时,有桨毂的情况效率下降更快。而对于不同导管的情况,其差异主要体现在推力输出和扭矩消耗上,但在效率变化上较为相似。
3.4 轮缘尺寸对敞水性能的影响轮缘是连接螺旋桨的部分,电机通过带动轮缘旋转来驱动螺旋桨。由于整体设计和电机转子设计要求,轮缘的宽度不宜过大也不宜过小,但轮缘宽度的尺寸会在一定程度上影响轮缘与导管接触面的水流流动。通过改变轮缘的宽度,分别生成了较窄(38 mm)、中等(48 mm)、较宽(58 mm)3种宽度的轮缘,并计算其敞水性能曲线如图12所示。

|
图 12 不同轮缘宽度的敞水性能对比 Fig. 12 Comparison of open water performance for different rim widths |
通过对比图中不同参数的曲线,3种轮缘宽度的RDT的水动力性能的变化趋势相同,但可以清晰地看到,三者的效率值在不同的进速系数下有较大的差异。在低进速时,三者的效率变化基本一致,但当J >0.3之后,三者的效率差异开始产生。3类宽度的效率在J=0.6时达到最大值,其中较窄宽度的最大效率最高,分别较中等宽度和较宽宽度高出2%、5.4%。从扭矩的变化上看,随着轮缘宽度的增加,会使得轮缘推进器整体产生的扭矩增大,对于整体的效率的提升不利。在对比中,中等宽度的轮缘推进器的效率在进速系数的变化中,有较高的敞水性能效率。
4 结 语1)通过19A+Ka4-70导管螺旋桨进行数值计算,并将结果与实验数据对比,采用网格不确定度分析,验证了本文数值计算方法的准确性和网格的收敛性。
2)在对比的4种导管中,19A导管的RDT具有较好的水动力性能,产生的尾涡区域较小,内外表面压差较小。19A导管较对称型导管,NO.37导管、JD7704导管分别高出1.5%、3.7%、4.2%。称型导管虽然推进效率要低于19A导管,但其在高进速时,效率下降较慢。
3)增加桨毂会降低推进器的敞水效率,但在低进速时,该影响较小。对于使用不同导管的情况,其差异主要体现在推力输出和扭矩消耗上,19A导管在有无桨毂情况下最大效率相差4.5%,对称型导管在有无桨毂的情况下最大效率相差2.9%
4)通过改变轮缘宽度可以提升推进器的最大效率,轮缘宽度的增大会直接影响扭矩,造成敞水效率的降低。同时在低进速下,轮缘宽度变化对敞水效率影响较小。
| [1] |
杨植, 严新平, 欧阳武, 等. 船舶轮缘推进装置驱动电机及控制方法研究进展[J]. 电工技术学报, 2022, 37(12): 2949-2960. YANG Zhi, YAN Xinping, OUYANG Wu, et al. Research progress of driving motor and control method of ship rim propulsion device[J]. Journal of Electrical Technology, 2022, 37(12): 2949-2960. |
| [2] |
REZA S, HASSAN G, DAVID M, et al. Numerical hydrodynamic evaluation of propeller (with hub taper) and podded drive in azimuthing conditions[J]. Ocean Engineering, 2014, 76.
|
| [3] |
贾文超, 樊思明, 刘正林, 等. 无轴轮缘推进器中可拆卸螺旋桨的性能分析[J]. 船舶工程, 2017, 39(8): 25-29. JIA Wenchao, FAN Siming, LIU Zhenglin, et al. Performance analysis of the removable propeller in the axeless rim thrusters[J]. Ship Engineering, 2017, 39(8): 25-29. DOI:10.13788/j.cnki.cbgc.2017.08.025 |
| [4] |
左新平, 郑少雄, 周俊雄. 某拖轮200 kW轮缘推进器水动力性能分析[J]. 广东造船, 2022, 41(4): 20-23. ZUO Xinping, ZHENG Shaoxiong, ZHOU Junxiong. Hydrodynamic performance analysis of 200 kW tupropeller[J]. Guangdong Shipbuilding, 2022, 41(4): 20-23. DOI:10.3969/j.issn.2095-6622.2022.04.007 |
| [5] |
熊立众, 孙江龙. 轮缘推进器水动力性能数值分析[J]. 舰船科学技术, 2021, 43(3): 83-88. XIONG Lizhong, SUN Jianglong. Numerical analysis of the hydrodynamic performance of the rim thrusters[J]. Ship Science and Technology, 2021, 43(3): 83-88. DOI:10.3404/j.issn.1672-7649.2021.02.018 |
| [6] |
杨蕾, 周军伟, 闫文辉, 等. 轮缘推进器反厚度规律桨叶的翼型对比分析[J]. 中国造船, 2022, 63(1): 113-125. YANG Lei, ZHOU Junwei, YAN Wenhui, et al. Comparative analysis of airfoil of reverse thickness of wheel propeller[J]. China Shipbuilding, 2022, 63(1): 113-125. DOI:10.3969/j.issn.1000-4882.2022.01.010 |
| [7] |
兰加芬, 欧阳武, 严新平. 无轴轮缘推进器水动力性能分析及桨叶强度校核[J]. 船舶工程, 2018, 40(10): 52-58. LAN Gafen, OUYANG Wu, YAN Xinping. Hydrodynamic performance analysis and blade strength check of the shaft propeller[J]. Ship Engineering, 2018, 40(10): 52-58. DOI:10.13788/j.cnki.cbgc.2018.10.052 |
| [8] |
LIU Bao, VANIERSCHOT M. Numerical study of the hydrodynamic characteristics comparison between a ducted propeller and a rim-driven thruster[J]. Applied Sciences, 2021, 11(11): 4919.
|
| [9] |
YAKOVLEV A Y, SOKOLOV M A, MARINICH N V. Numerical design and experimental verification of a rim-driven thruster[J]. Second International Symposium on Marine Propulsors smp'11, 2011, 8: 8150.
|
| [10] |
DUBAS A. Robust automated computational fluid dynamics analysis and design optimization of rim driven thrusters[J]. University of Southampton, 2014(10): 1−11.
|
| [11] |
DUBAS A J, BRESSLOFF N W, FANGOHR H, et al. Computational fluid dynamics simulation of a rim driven thruster[J]. University of Southampton, 2011(9): 3−4.
|
| [12] |
HUGHES A W, SHARKH S A, TURNOCK S R. Design and testing of a novel electromagnetic tip-driven thruster[M]. International Society of Offshore and Polar Engineers, 2000.
|
| [13] |
ABU-SHARKH S M, TURNOCK S R, DRAPER G. Performance of a tip-driven electric thrusters for unmanned underwater vehicles[C]// The Eleventh (2001) International Offshore and Polar Engineering Conference, 2001.
|
| [14] |
盛振邦, 刘应中. 船舶原理(下册)[M]. 上海: 上海交通大学出版社, 2004.
|
| [15] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32.
|
| [16] |
SONG B W, WANG Y J, TIAN W L. Open water performance comparison between hub-type and hubless rim driven thrusters based on CFD method[J]. Ocean Engineering, 2015, 103: 55-63.
|
| [17] |
OOSTERVELD M . Wake adapted ducted propellers[J]. H. Veenman & Zonen, 1970(2): 8−130.
|
| [18] |
ROACHE, PJ . Quantification of uncertainty in computational fluid dynamics[J]. Annual Review of Fliud Mechanics, 1997.
|
 2024, Vol. 46
2024, Vol. 46

