水下航行体目前应用最为广泛的是十字舵,十字舵的水动力设计方法较为成熟,且有大量的模型试验数据。近年来,随着自动操纵技术的发展及X舵的诸多优点,X舵逐渐应用于水下航行体[1-2],许多国内外学者针对X舵的水动力特性开展了研究。胡坤[3-4]、栾和春[5]、王京齐[6]等分别从X舵水下航行体数学模型、X舵和十字舵之间的等效舵角等方面开展了研究,为基于数学模型方法研究X舵水下航行体操纵特性预报奠定了基础。胡坤等[7]基于六自由度数学模型对比研究了X舵与十字舵操纵特性,研究结果表明,X舵的舵效高于十字舵,且X舵能有效控制潜艇水下高速回转时的横倾。张露等[8]采用数值仿真方法针对Suboff模型研究了潜艇直航和垂直面变攻角2种工况下,X舵和十字舵的水动力性能,结果表明,X舵的水动力性能优于十字舵。焦玉超等[9]采用数值模拟的方法针对X舵不同的分开角度对潜艇阻力特性开展研究,研究结果表明45°X舵潜艇的水动力特性更优。
但国内学者针对X舵水动力设计方法的研究较少,目前国内还没有建立X舵水下航行体的水动力设计方法。在水下航行体操纵性设计初始阶段,由于CFD数值计算和模型试验还未开展,需依靠经验或其他方法预报其线性水动力系数,从而进行水下航行体操纵面水动力尺寸的设计。十字舵水下航行体一般是依靠母型法进行估算。
由于目前国内X舵水下航行体研制基础薄弱,母型艇资料匮乏,而十字舵水下航行体母型艇资料较为丰富,因此本文拟采用数值仿真的方法[10-11],研究X舵与十字舵水下航行体之间的水动力特性,建立基于十字舵水下航行体为母型进行X舵水下航行体水动力设计的工程方法。
1 计算模型 1.1 数值计算模型以Suboff模型为研究对象,采用Ansys Fluent模拟Suboff水平面操纵性试验的线性水动力系数。几何模型如图1所示,Suboff模型的几何尺寸如表1所示。

|
图 1 计算模型 Fig. 1 Computational model |
|
|
表 1 Suboff主要参数 Tab.1 Main parameters of Suboff |
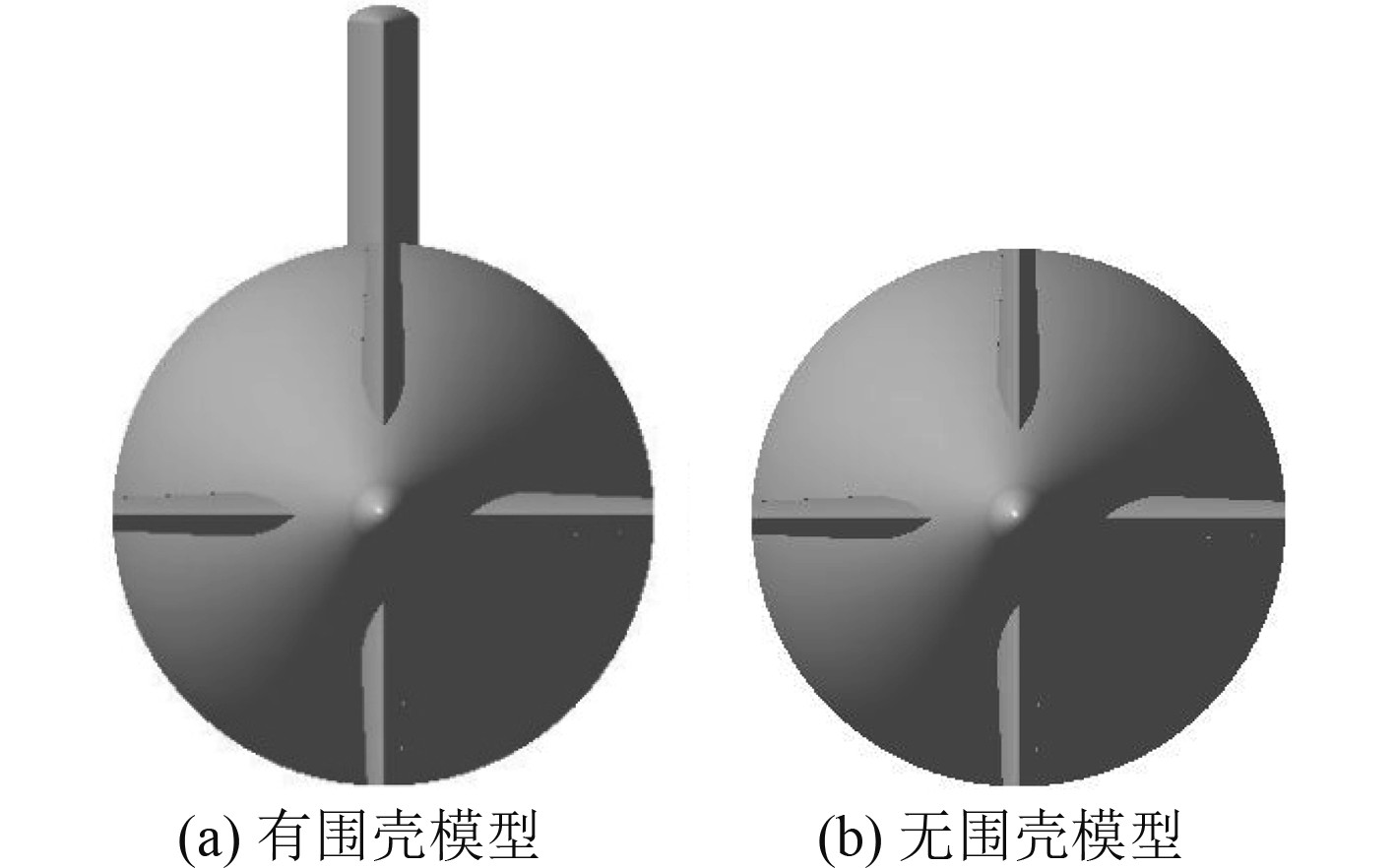
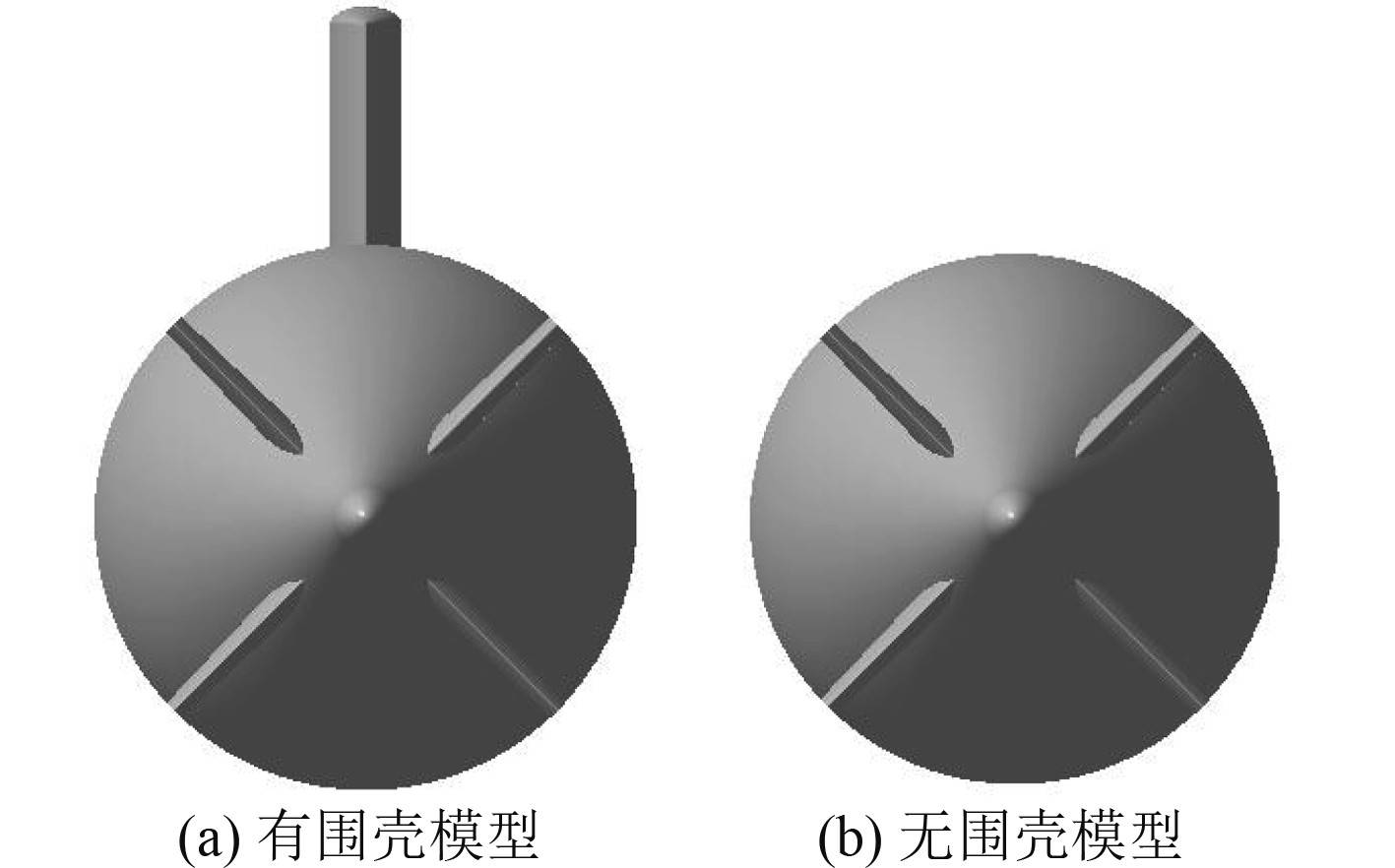
本文的模拟对象为分别配置十字舵、X舵的水下航行体在有无围壳状态的水动力性能,如图2和图3所示。X舵由十字舵旋转45°形成,因此,X舵与十字舵的尺寸完全相同。X舵的参数定义见图4。
|
图 2 十字舵模型 Fig. 2 The model with cross rudder |
|
图 3 X舵模型 Fig. 3 The model with X rudder |

|
图 4 X舵参数定义示意图 Fig. 4 Schematic diagram of parameter definition in X rudder |
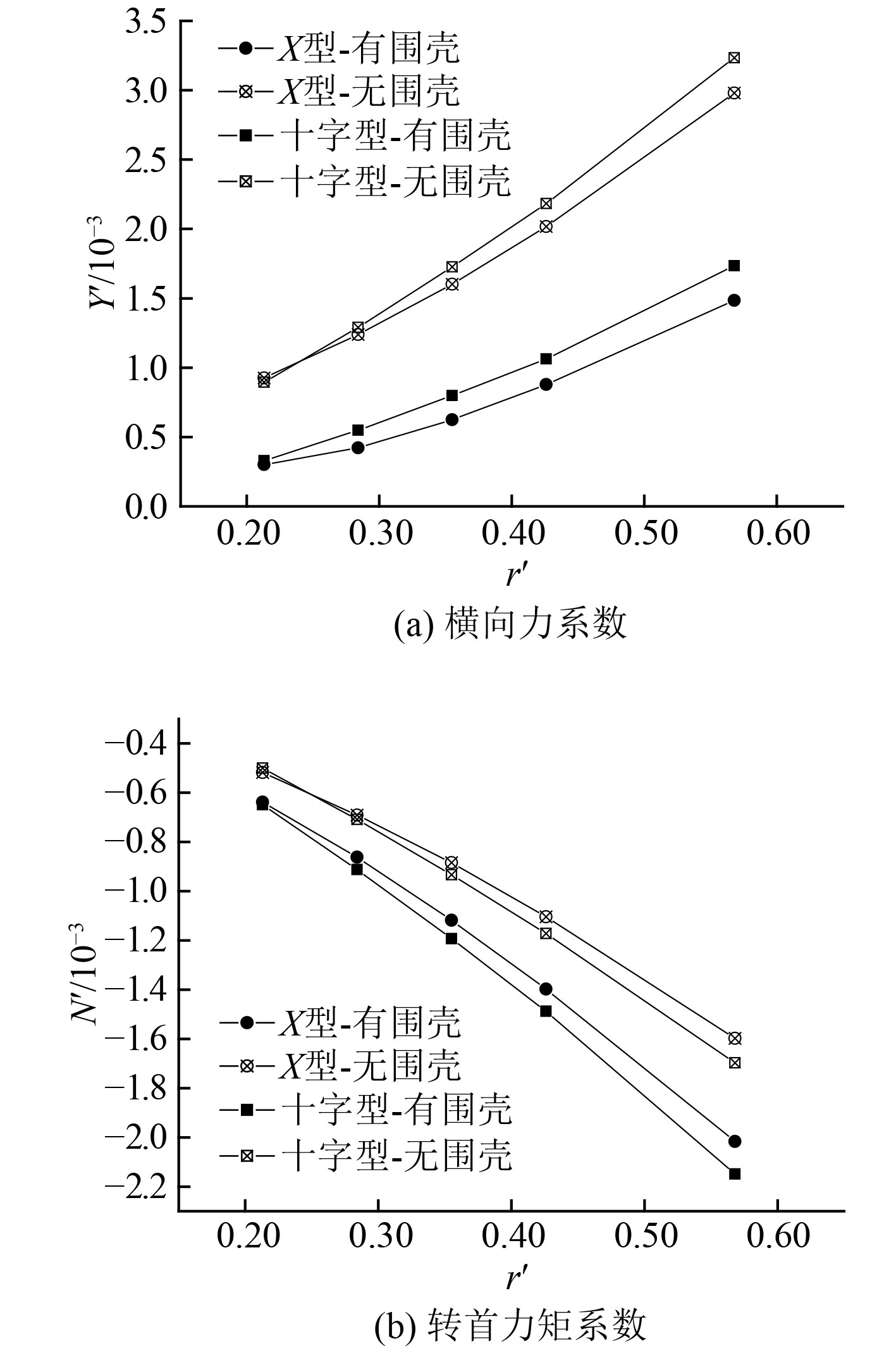
针对1.2节的十字舵与X舵开展水平面水动力系数数值仿真分析,仿真结果如图5和图6所示。经线性拟合[1]得到水动力系数如表2所示。可知,无围壳模型下,与十字舵相比,X舵水动力系数

|
图 5 横向力与转首力矩系数随漂角的变化 Fig. 5 Variation of the later force and yaw moment coefficient with drift angle |
|
图 6 横向力与转首力矩系数随角速度的变化 Fig. 6 Variation of the later force and yaw moment coefficient with rotating velocity |
|
|
表 2 十字舵与X舵水动力系数对比 Tab.2 The comparison of hydrodynamic coefficient between cross rudder and X rudder |
有围壳模型下,与十字舵相比,X舵水动力系数
可知,设计参数相同的情况下,有围壳、无围壳2种模型下X舵的动稳定性系数均低于十字舵。有围壳、无围壳2种模型下,对比X舵与十字舵水动力系数发现,
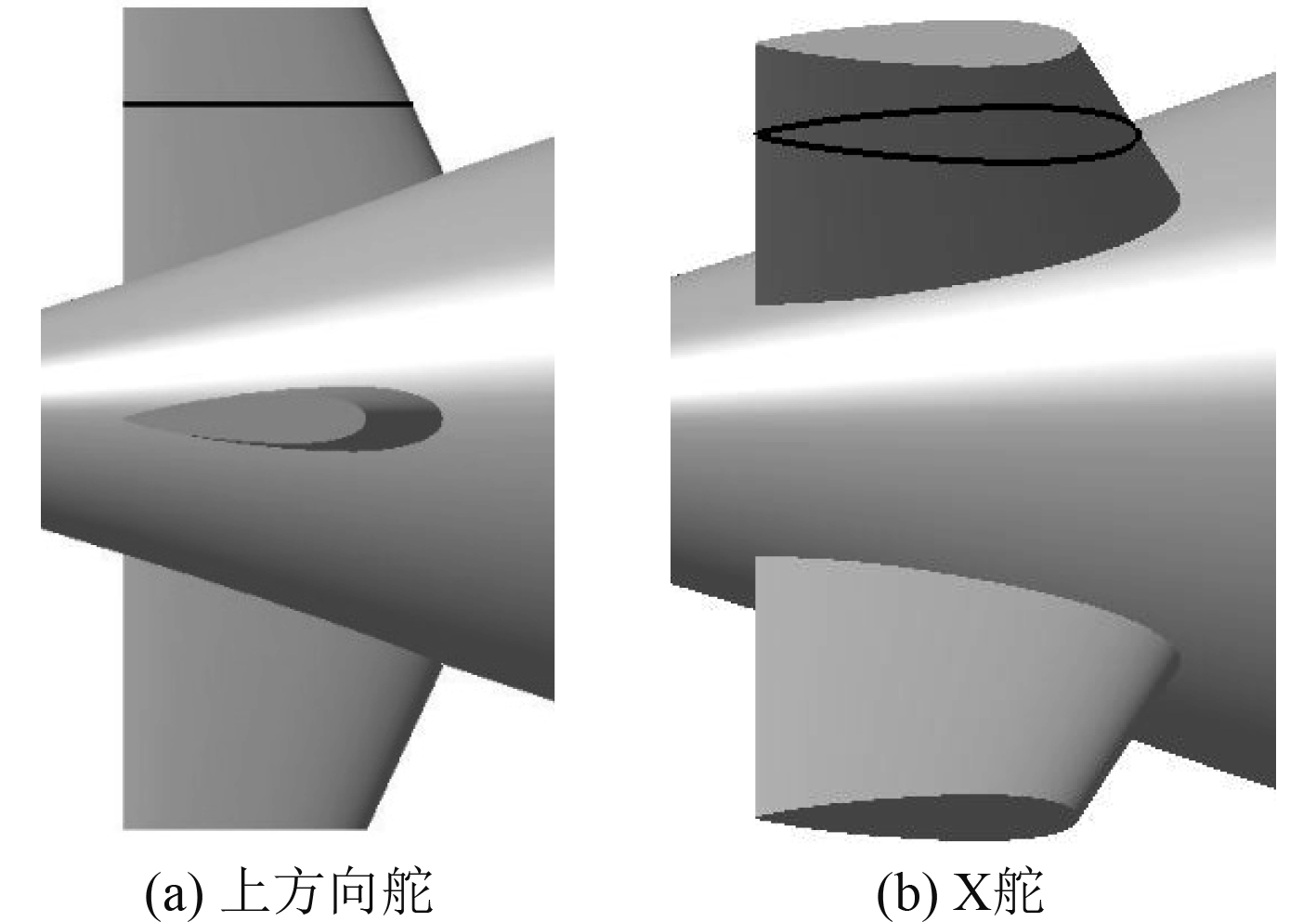
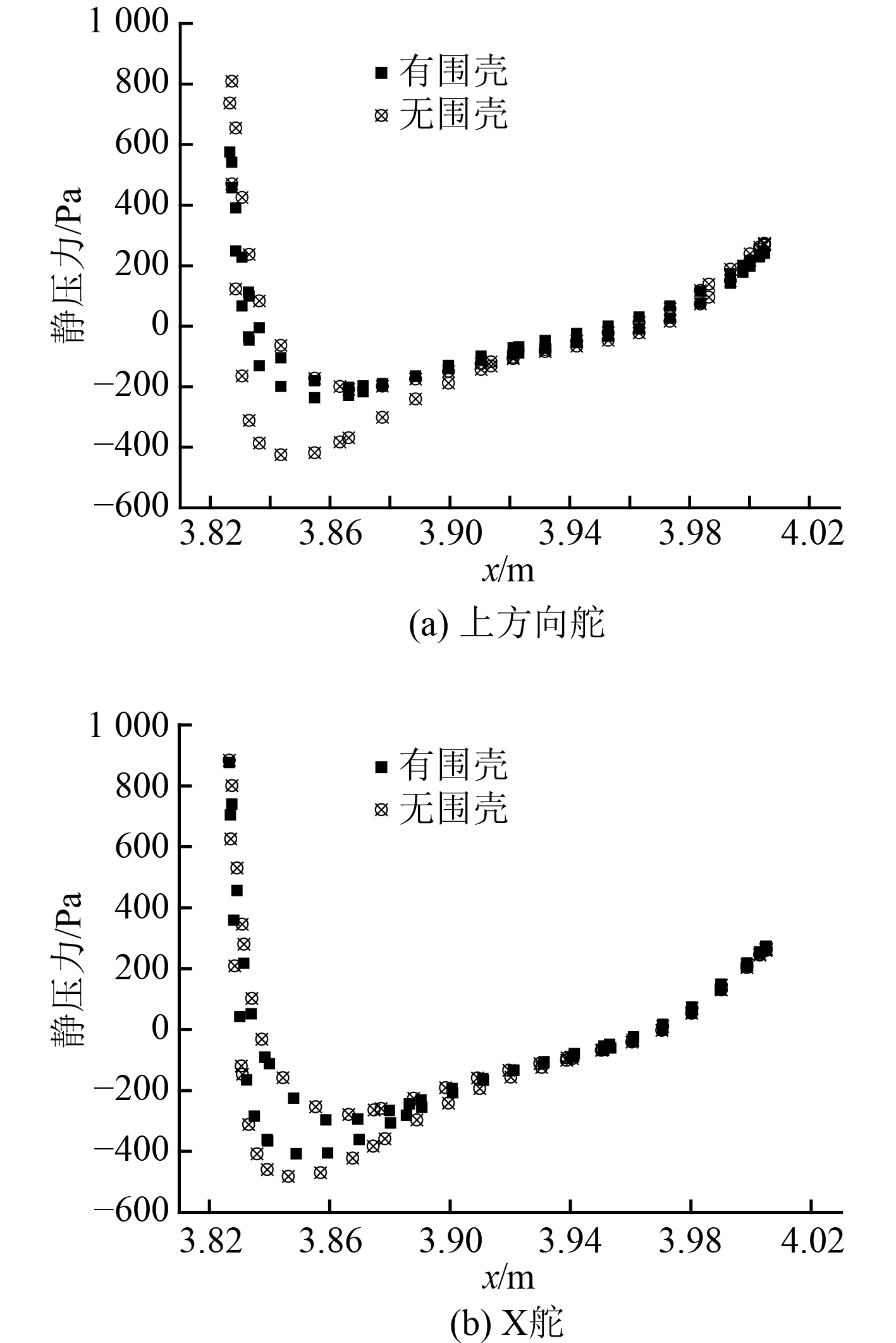
根据图4和图7所示对十字舵上方向舵、X舵右上舵展长方向194 mm截面处沿x方向的压力分布进行分析,结果分别见图8和图9。可知,拖曳水池和旋臂水池中,围壳对上方向舵和X舵的压力分布影响均在舵板前缘区域,约为舵板弦长的20%,且围壳对上方向舵的压力分布影响明显大于X舵,与2.1节水动力系数的变化规律一致。
|
图 7 十字舵与X舵截面定义 Fig. 7 Definition of the section plane in cross rudder or X rudder |
|
图 8 拖曳水池中舵板沿x方向的压力分布曲线 Fig. 8 Variation of the rudder surface pressure with x coordinate from towing tank |
|
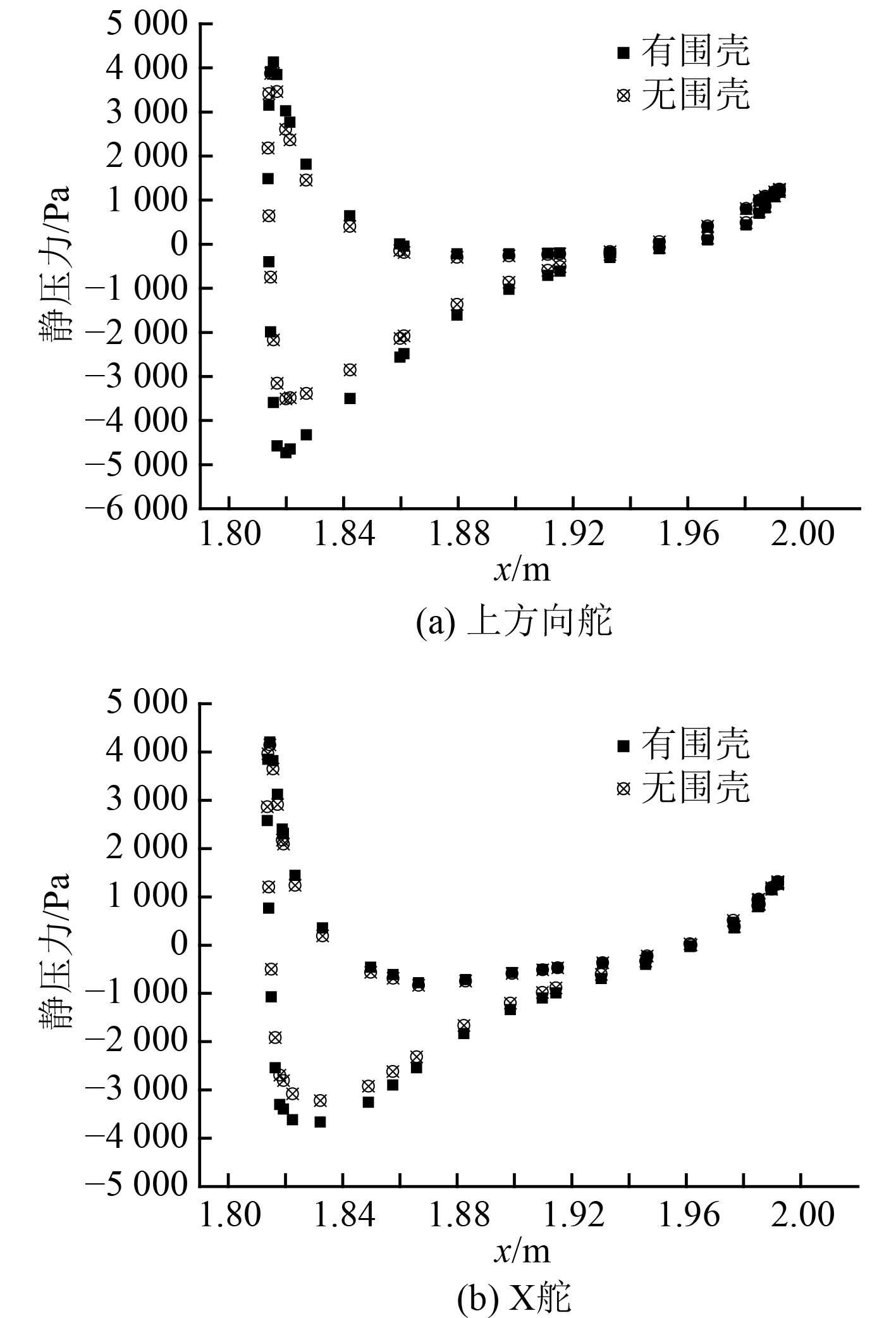
图 9 旋臂水池中舵板沿x方向的压力分布曲线 Fig. 9 Variation of the rudder surface pressure with x coordinate from rotating arm |
针对十字舵、X舵开展长为254 mm、292 mm、336 mm、380 mm方案的水动力系数研究,分别为方案1、方案2、方案3、方案4。表3和表4分别为不同展长参数下,十字舵与X舵的水动力系数数值计算结果。表中
|
|
表 3 不同展长方案十字舵水动力系数 Tab.3 The hydrodynamic coefficient of cross rudder with different span |
|
|
表 4 不同展长方案X舵水动力系数 Tab.4 The hydrodynamic coefficient of X rudder with different span |
由表可知,十字舵与X舵水动力系数均随展长增加
不同展长方案下,X舵与十字舵水动力系数的比例系数,见式(1)~式(4)。将4个展长方案下,X舵与十字舵之间水动力系数的比例系数进行算数平均,得到其平均值,见式(5)。结果如表5所示。其中,
|
|
表 5 十字舵与X舵水动力系数的比例系数 Tab.5 The ratio of hydrodynamic coefficient with X rudder to that with cross rudder |
| $ {K_{{{Y'}_v}}} = \frac{{{{Y'}_{vx}}}}{{{{Y'}_{v + }}}},$ | (1) |
| $ {K_{{{N'}_v}}} = \frac{{{{N'}_{vx}}}}{{{{N'}_{v + }}}},$ | (2) |
| $ {K_{{{Y'}_r}}} = \frac{{{{Y'}_{rx}}}}{{{{Y'}_{r + }}}},$ | (3) |
| $ {K_{{{N'}_r}}} = \frac{{{{N'}_{rx}}}}{{{{N'}_{r + }}}},$ | (4) |
| $ {\bar K_i} = \sum\limits_{i = 1}^4 {{K_i}} 。$ | (5) |
基于该比例系数平均值和十字舵水动力系数数值计算结果,进行X舵水动力系数的预报,预报结果如表6所示。将表6中的数据与表4数值仿真结果进行对比,可知该预报值与数值仿真结果的误差低于3.5%。
|
|
表 6 基于比例系数进行X舵水动力系数预报结果 Tab.6 The prediction results of hydrodynamic coefficient with X rudder using hydrodynamic coefficient ratio |
根据3.1节研究成果可知,在已有十字舵水下航行体水动力系数的基础上,可利用X舵与十字舵水动力系数的比例系数,进行X舵水动力系数的预报,实现X舵水动力的快速设计。其快速设计方法如下:
已知十字舵的水动力系数
| $ {Y'_{vx}} = {Y'_{v + }} \times {K_{{{Y'}_v}}},$ | (6) |
| $ {N'_{vx}} = {N'_{v + }} \times {K_{{{{\rm N}'}_v}}},$ | (7) |
| $ {Y'_{rx}} = {Y'_{r + }} \times K{}_{{{Y'}_r}}^{} ,$ | (8) |
| $ {N'_{rx}} = {N'_{r + }} \times {K_{{{N'}_r}}} 。$ | (9) |
根据上述计算公式,在已有十字舵水下航行体的水动力系数基础上,可快速完成X舵水下航行体水动力系数的估算,实现X舵水动力构型的工程化快速设计。
4 结 语本文针对水下航行体,对比研究了围壳、展长对十字舵和X舵水动力特性的影响,掌握了X舵与十字舵之间水动力系数的比例关系,从而建立了基于十字舵水动力系数进行X舵水动力快速设计的工程方法,主要结论如下:
1)设计参数相同的情况下,有围壳、无围壳2种模型下X舵的动稳定性系数均低于十字舵。
2) 围壳对十字舵水动力系数的影响大于X舵。围壳对上方向舵和X舵压力分布的影响均在舵板前缘区域,约为舵板弦长的20%,且围壳对上方向舵的影响明显大于X舵。
3)配置X舵与十字舵的水下航行体线性水动力系数
| [1] |
王京齐, 施生达, 等. 现代潜艇尾操纵面的发展状态[J]. 舰船科学技术, 2007, 29(1): 33-36. |
| [2] |
焦玉超, 肖昌润, 等. 潜艇X舵研究综述[C]//第十届武汉地区船舶与海洋工程研究生学术论坛, 2017.
|
| [3] |
胡坤, 徐亦凡. X舵潜艇空间运动仿真数学模型[J]. 计算机仿真, 2005, 22(4): 50-52. DOI:10.3969/j.issn.1006-9348.2005.04.014 |
| [4] |
胡坤, 徐亦凡, 王树宗. 潜艇X舵发展概况及其操纵控制特性分析[J]. 中国造船, 2007, 48(2): 130-135. DOI:10.3969/j.issn.1000-4882.2007.02.017 |
| [5] |
栾和春, 林俊兴. X型尾舵潜艇操控与运动关系研究[J]. 船海工程, 2007, 36(2): 100-103. DOI:10.3963/j.issn.1671-7953.2007.02.030 |
| [6] |
王京齐, 李亚楠. 潜艇X型尾操纵面的操纵特性[J]. 船海工程, 2006(2): 1−3.
|
| [7] |
胡坤, 徐亦凡. 舵型对潜艇操纵特性影响的仿真分析[J]. 船舶工程, 2005, 27(1): 41-45. DOI:10.3969/j.issn.1000-6982.2005.01.010 |
| [8] |
张露, 肖昌润, 焦玉超. 十字舵与X舵潜艇的水动力性能数值比较[J]. 舰船科学技术, 2017, 39(7): 24-28. DOI:10.3404/j.issn.1672-7649.2017.07.005 |
| [9] |
焦玉超, 肖昌润. 潜艇X舵的布局优化[J]. 兵器装备工程学报, 2018, 39(3): 40-44. DOI:10.11809/bqzbgcxb2018.03.009 |
| [10] |
胡芳芳, 刘继明, 何斌, 等. 支杆对水下航行体操纵性水动力系数的数值分析[J]. 舰船科学技术, 2021, 43(10): 41-45. |
| [11] |
胡芳芳, 陈静, 涂卫民, 等. 围壳对水下航行体水动力系数的影响特性研究[J]. 舰船科学技术, 2022, 44(7): 31−36.
|
 2024, Vol. 46
2024, Vol. 46
