2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;
3. 武汉第二船舶设计研究所,湖北 武汉 430064
2. School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China;
3. Wuhan Second Ship Design and Research Institude, Wuhan 430064, China
水下航行体的尾流研究具有重要研究价值,主要体现在2个方面:航行体的尾流场是影响其隐蔽特性的一个重要因素;航行体的尾流与航行体的阻力密切相关[1]。
水下航行体的艇体尾流是典型的剪切流,即其壁面边界层速度梯度方向与流动方向垂直,尾流内部存在显著的质量和动量交换;此外,航行体上的附体,如指挥台、尾舵的尾流与艇体尾流之间的干涉会使得整个航行器尾流的流体机理显得尤为复杂[2 − 5] 。
限于实际水下航行体结构特征的敏感性,国内外公开文献中主要以Suboff模型[6]为对象开展相关实验测量和数值模拟研究工作,对国内外典型研究工作的总结概述如下。
实验测量方面的典型研究包括。Huang等[7]测量在Re=1.2×107 时Suboff模型的流场,并得到了艇体上的压力、摩擦系数和速度的流动分布数据;Jimenez等[8]基于上述模型,测量了更宽Re数范围(1.1×106~6.7×107)艇体壁面压力和尾流速度场的分布特征;Ashok等[9]则通过实验研究了俯仰角为12°,Re数在106~30×106范围内艇体尾流的非对称特征;进一步地,Jimenez等[10]采用实验方法对比研究了尾舵对航行体尾流发展的影响。
相对于较少的实验测量研究,近年来,基于Reynolds时均[11 − 12]和大涡模拟[13 − 15]的数值模拟方法被更广泛应用于水下航行体伴流流场的研究。其中,Kumar等[11]研究了不带任何附件(指挥台和尾舵)的轴对称光艇体结构尾流的演化特征;Posa等[14 − 15]研究了指挥台、尾舵和艇体共同作用下的尾流演化特征,进一步地,Posa等[16]研究了拖曳和推进2种状态下,航行体的伴流流场及其尾迹演化特征;Qu等[17]基于数值模拟结果采用不同的涡识别方法研究了航行体不同部位的流动特征。
上述实验和数值工作促进了研究人员对于水下航行体尾流场特征的理解。例如,Kumar等[11]研究结果表明光艇体的尾流平均速度分布在X/D=5处达到自相似状态,但Posa等[14 − 15]研究结果表明当考虑指挥台和尾舵时,在X/D=9处尾流速度分布依然没有达到自相似状态。但引起上述变化的具体原因和机理尚缺乏深入分析。
实际航行体的尾流至少是由2种不同的尾流特征叠加形成。第1种是艇体尾流,其接近或者逐渐趋近于轴对称尾流特征;第2种是指挥台和尾舵尾流,接近或逐渐趋近于平面尾流特征。需强调,这2种尾流具有不同的演化特征,关于这2种尾流的基本特征可参考文献[18 − 19]。
本文在上述理论、数值和实验研究的基础上,开展航行体伴流及尾流场的数值模拟研究。研究目的在于澄清艇体、指挥台和尾舵尾流的各自演化规律以及它们之间的干涉作用对整个航行体尾流演化影响的重要性。
1 研究对象及数值模拟方法 1.1 计算对象本文的研究对象是DRAPA Suboff标准航行体的缩比模型[20],其主要结构特征和尺寸如图1和表1所示。该模型主要包括回转体结构的艇体、类翼型的指挥台以及沿周向均匀分布的4个对称翼型组成的十字型尾舵。在建模过程中,以船首中心为坐标原点,回转体中心线位于X正轴上。
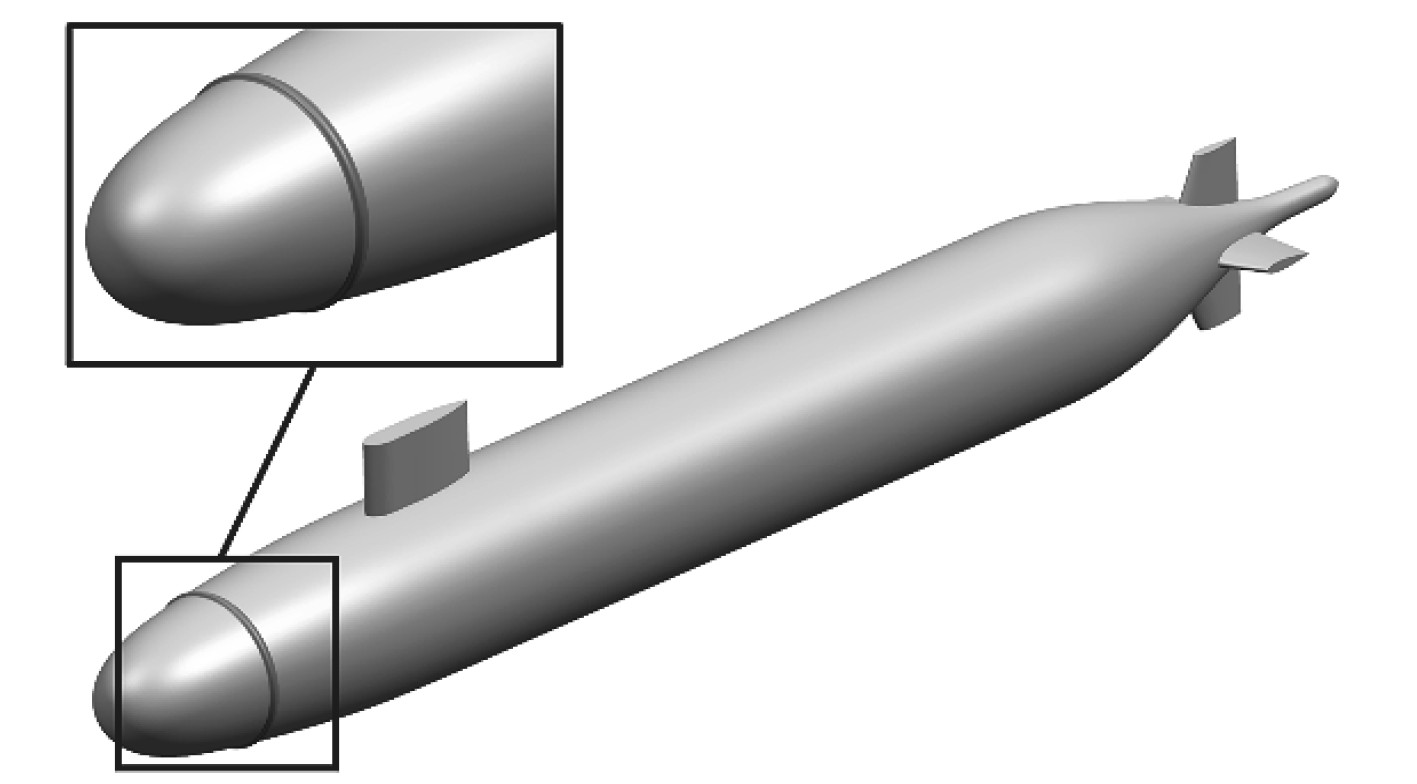
|
图 1 模型几何结构示意图 Fig. 1 Schematic diagram of geometric structure |
|
|
表 1 Suboff模型的主要结构尺寸 Tab.1 Main structural dimensions of Suboff model |
已有学者针对Suboff标模或近似模型开展了有关的实验测量[7 − 8, 20 − 21]和数值模拟[11, 17]研究,上述文献中部分数据将与本文数值模拟的计算结果进行对比验证。
需说明的是,文献[8, 21]中的实验测量均是在低湍流度风洞中进行的,此时,光滑航行体结构沿流向会存在较长的层流边界层区域,这与水下航行体的实际流动特征存在明显差异。因此,在风洞中测量时通常会在船首区域布置粗糙单元来实现层流边界层的强制转捩。为了与风洞实验测试的结果进行对比,数值模拟选取空气为流动介质,在船首X/D=0.75处沿周向布置一层高度为5 mm的环形单元,如图1所示,以实现强制转捩。
1.2 数值模拟方法采用雷诺时均方法将三维不可压缩N-S方程中的速度项分解为时均速度和扰动速度,上述处理后的控制方程中新增雷诺应力项假设满足如下特征:
| $ \overline {u_i^\prime u_j^\prime } = - {\nu _t}\left( {\frac{{\partial {U_i}}}{{\partial {x_j}}} + \frac{{\partial {U_j}}}{{\partial {x_i}}}} \right) + \frac{2}{3}{\delta _{ij}}k,$ | (1) |
其中,涡粘系数
| $ {v_t} = {C_\mu }{k^2}/\varepsilon 。$ | (2) |
式中:
此次计算中选用标准
流场计算区域为长方体,如图2所示。其中,根据文献[11]的推荐,计算域的上游边界距离船首的距离为3D,计算域的下游边界距离船尾的距离为17D,计算域四周边界距离航行体中心线的距离为6D。计算设置的运行条件和已有实验数据[8]一致,即计算域上游边界设置垂直入口边界的流速U0=3.092 m/s。取艇体长度L为特征长度,计算工况对应Re=1.1
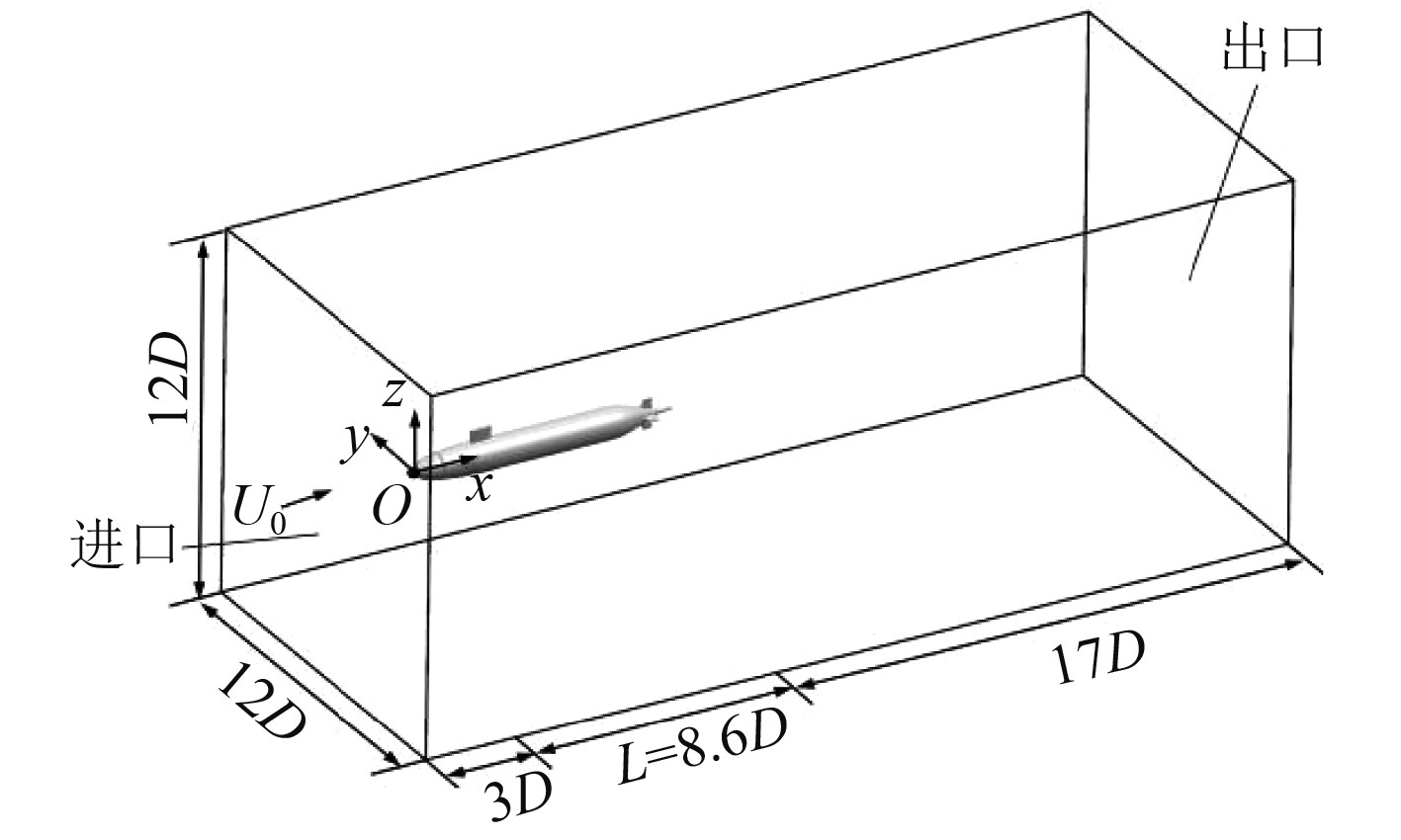
|
图 2 计算域示意图 Fig. 2 Schematic diagram of computational domain |
整个计算域采用六面体结构化网格进行离散,网格单元总数量约为619万。壁面边界层中的流动速度沿法向存在较大梯度,因此,需对近壁面的流体区域用小尺度的网格进行离散。在数值计算中,近壁面第1层网格单元的高度为0.5 mm,壁面法向的增长率为1.1。计算域的网格如图3(a)所示,壁面y+值分布如图3(b)所示,其值位于20~50范围内,满足标准壁面函数的推荐值要求[23 − 24]。
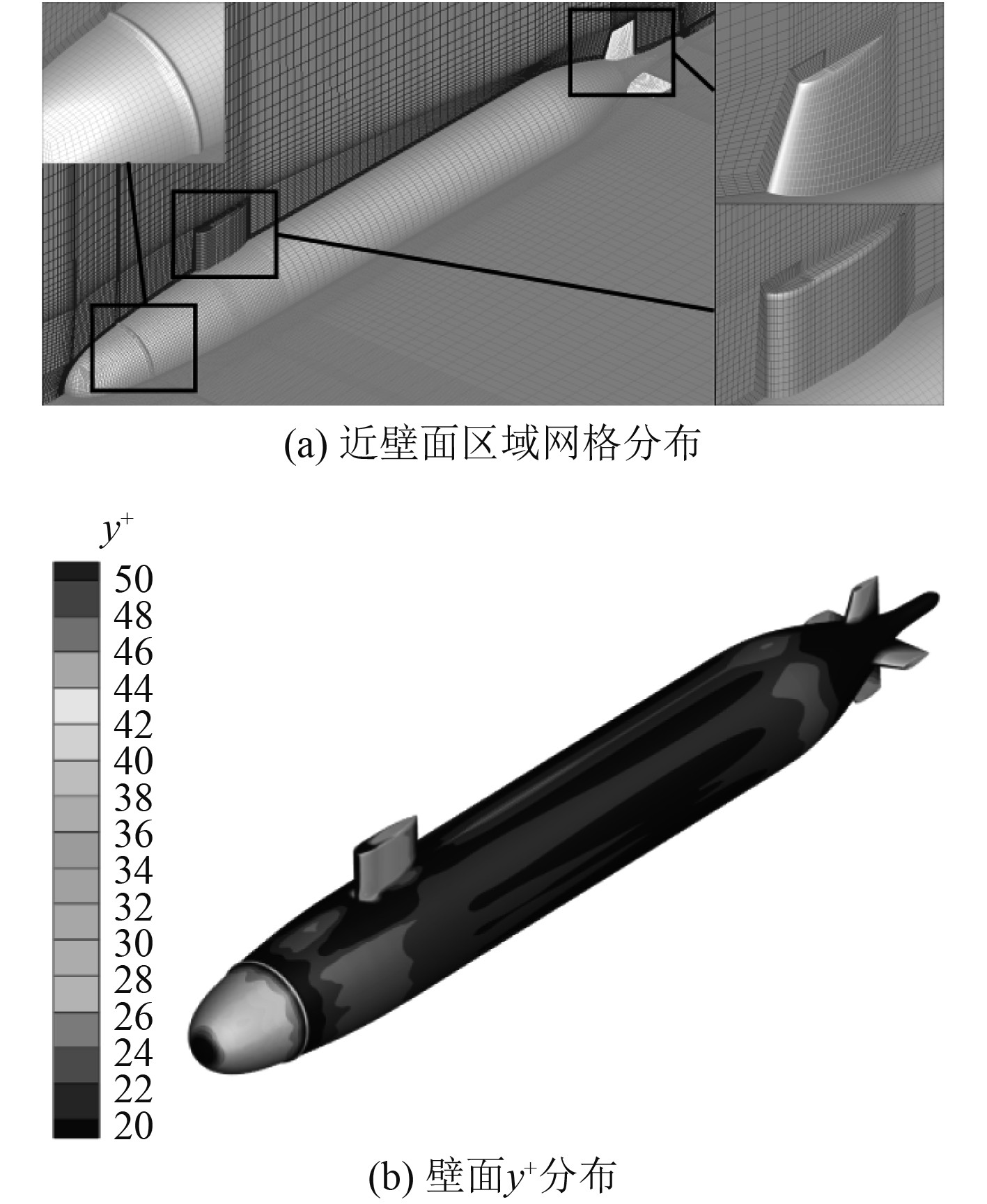
|
图 3 计算域网格示意图 Fig. 3 Schematic diagram of computational domain grid |
为了验证数值模拟结果的可靠性,本节将壁面压力系数、摩擦系数和尾流场速度的数值计算结果与已有实验测量结果[7 − 8]以及LES数值计算结果[11]进行对比分析。
2.1 壁面压力系数和摩擦系数的对比验证图4给出了本文数值计算得到的壁面压力系数和摩擦系数与已有实验测量和数值计算结果的对比。其中,Jimenez[8]的实验测量和Kumar[11]的数值数据与本文的数值计算工况具有相同的Re数,但这2项工作中均没有考虑尾舵的影响,而Huang[7]实验测量是在Re=12 ×106下进行的。此外,Jimenez[8]实验测量采用展向很长的支撑结构替代指挥台。
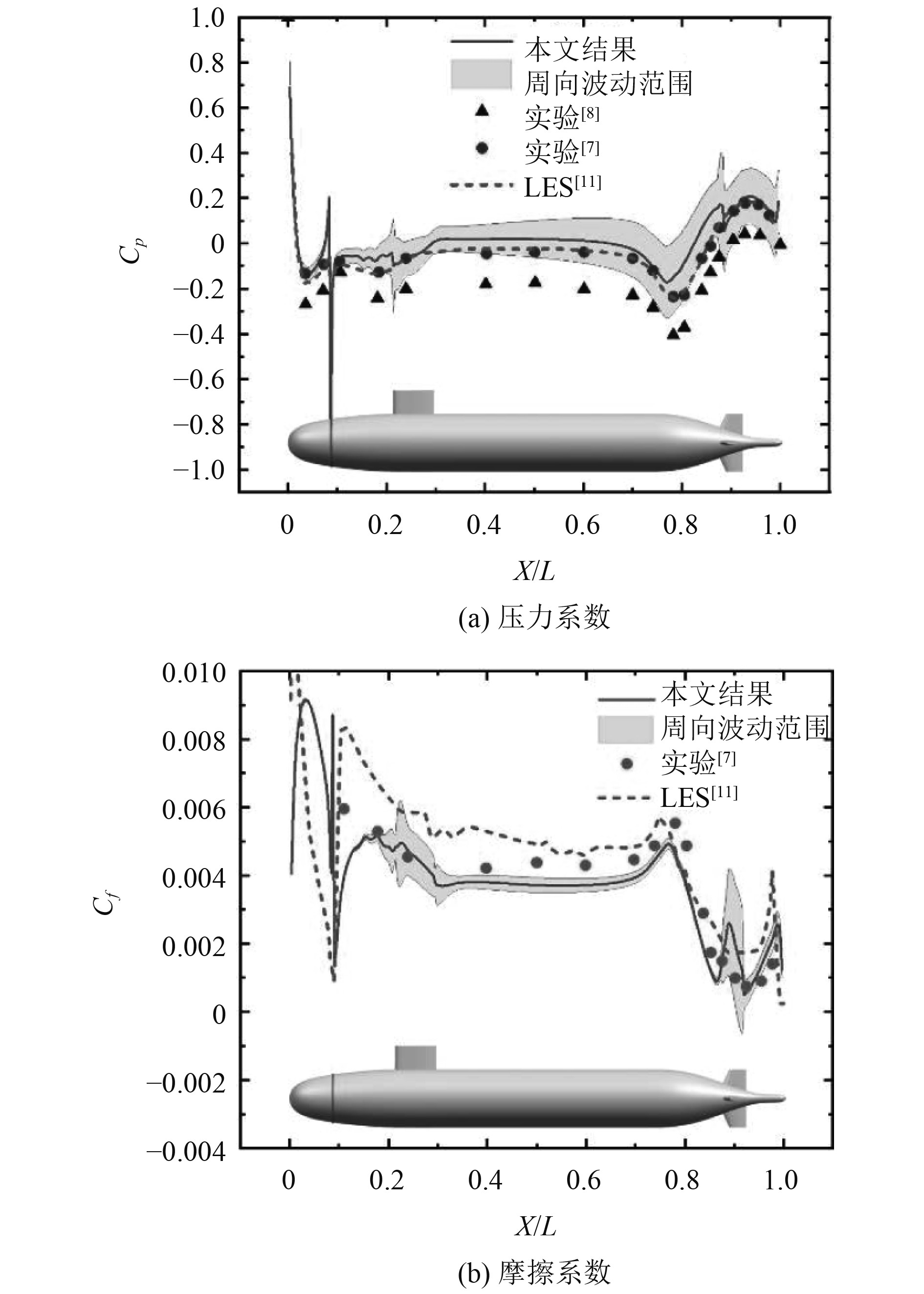
|
图 4 无量纲系数的对比 Fig. 4 Comparison of dimensionless coefficients |
壁面压力系数和摩擦系数的定义分别为:
| $ {C_p} = \frac{{{P_0} - {P_\infty }}}{{\rho \cdot U_0^2/2}} ,$ | (3) |
| $ {C_f} = \frac{{{\tau _w}}}{{\rho \cdot U_0^2/2}}。$ | (4) |
式中:
文献[7 − 8]中只测量了图2所示位于Y=0平面上的部分测点位置壁面压力系数分布特征。因此,图4中以散点形式给出实验测量的结果。本文基于数值计算结果统计了艇体表面不同周向角位置的壁面压力系数及摩擦系数分布,在图4中以误差带的形式显示,其中,实线数据为本文数值计算获得的不同周向角度数据平均值。通过壁面压力系数和摩擦系数的对比表明,无论是在中段近零压力梯度区域还是在船尾的逆压梯度区域,数值计算和实验结果之间的偏差都在合理范围之内,验证了本文计算结果的可靠性。特别的,摩擦系数和实验测试结果的对比误差较小,表明本文的数值模拟能良好地模拟近壁面区域的边界层剪切流动特征,这是准确模拟尾流演化的重要前提。
此外,图4的数值计算结果显示,在船首至强制转捩单元的层流区域,壁面压力系数和摩擦系数基本与周向角度无关;在强制转捩单元的下游区域,由于湍流边界层、指挥台以及尾舵的共同作用,壁面压力系数和摩擦系数不再沿周向均匀分布。指挥台下游区域误差带范围逐渐增大,表明壁面压力系数沿周向分布的不均匀性逐渐增强,这是指挥台的尾流与艇体边界层相互干涉造成的,关于尾流详细特征的分析见下文。
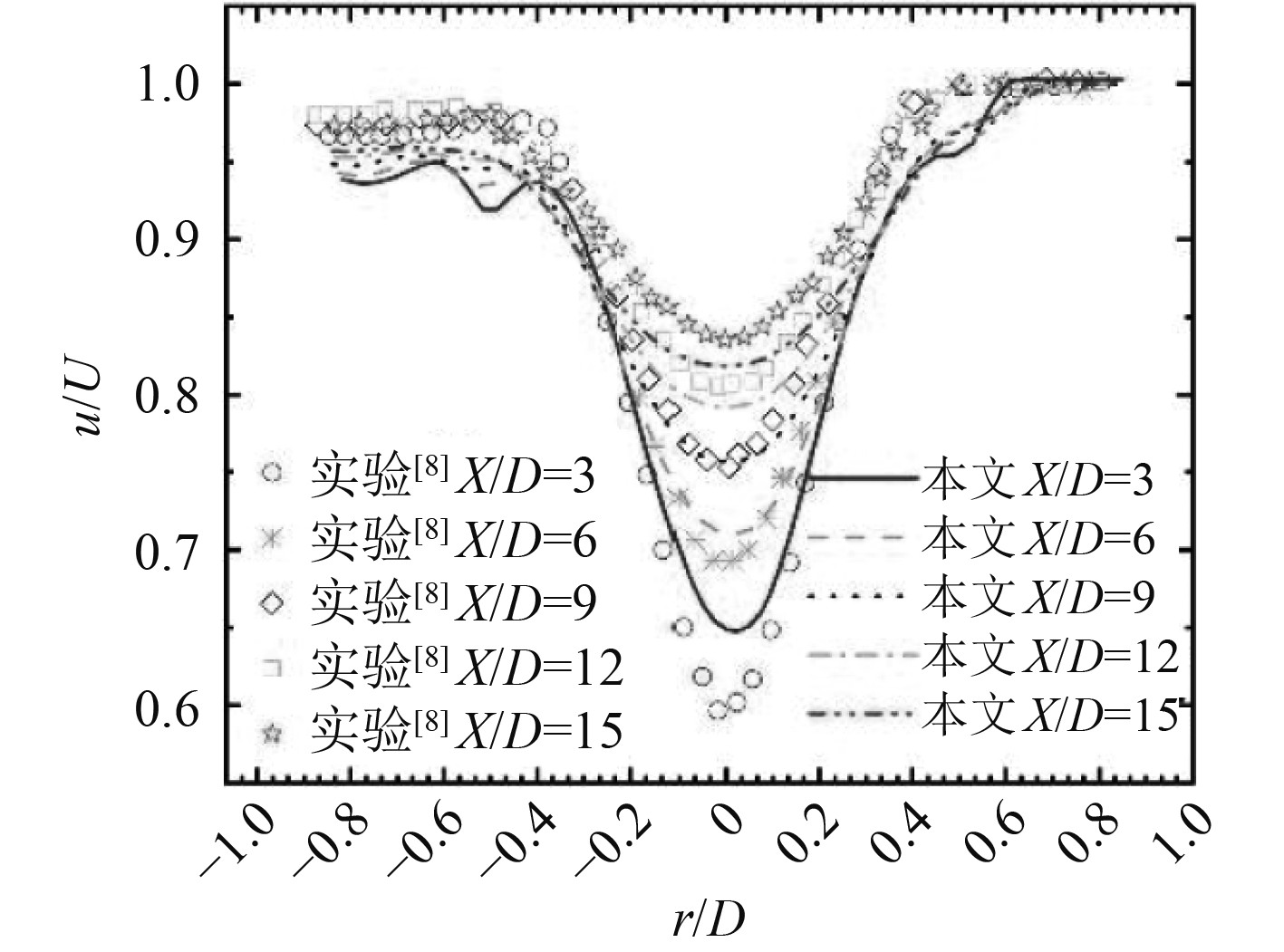
2.2 尾流时均速度特征的对比验证Jimenez[8]获取了以艇体尾部为原点的航行体下游X/D=3、6、9、12、15位置流动速度分布特征。实验结构如图5所示,实验只测量指挥台所在平面上的尾流分布特征。
图6给出了与文献[8]相同测量截面上尾流速度分布特征,该截面尾流受到艇尾、垂直尾舵以及上游指挥台尾流三者的共同影响。需说明,文献[8]的实验研究仅考虑了艇体与指挥台尾流相互干涉的影响,而没考虑垂直尾舵的影响。数值计算和实验测量在5个截面上的结果对比表明,数值计算结果能较好捕捉航行体尾流的演化特征,包括尾流最大亏损速度和尾流宽度随流向的演化特征。但数值计算和实验测试的结果存在一定偏差,这种偏差通常是由于目前的湍流模型对尾迹区域内涡黏系数的计算偏差导致,类似现象和分析可参见文献[25]。此外,数值计算和实验测量结果均表明在近场区域的尾流速度不是呈现出完全对称的特征,这是因为实验测量受到指挥台尾流的干涉影响而数值计算则同时受到指挥台以及垂直尾舵的影响。
|
图 6 尾流速度的实验测量和数值计算结果对比 Fig. 6 Comparison between experimental measurement and numerical calculation of wake velocity |
通过上述壁面压力系数、摩擦系数以及尾流速度分布特征的对比表明,数值计算和实验测量结果存在一定偏差,但数值计算能较好地模拟壁面边界层和尾流的演化特征。
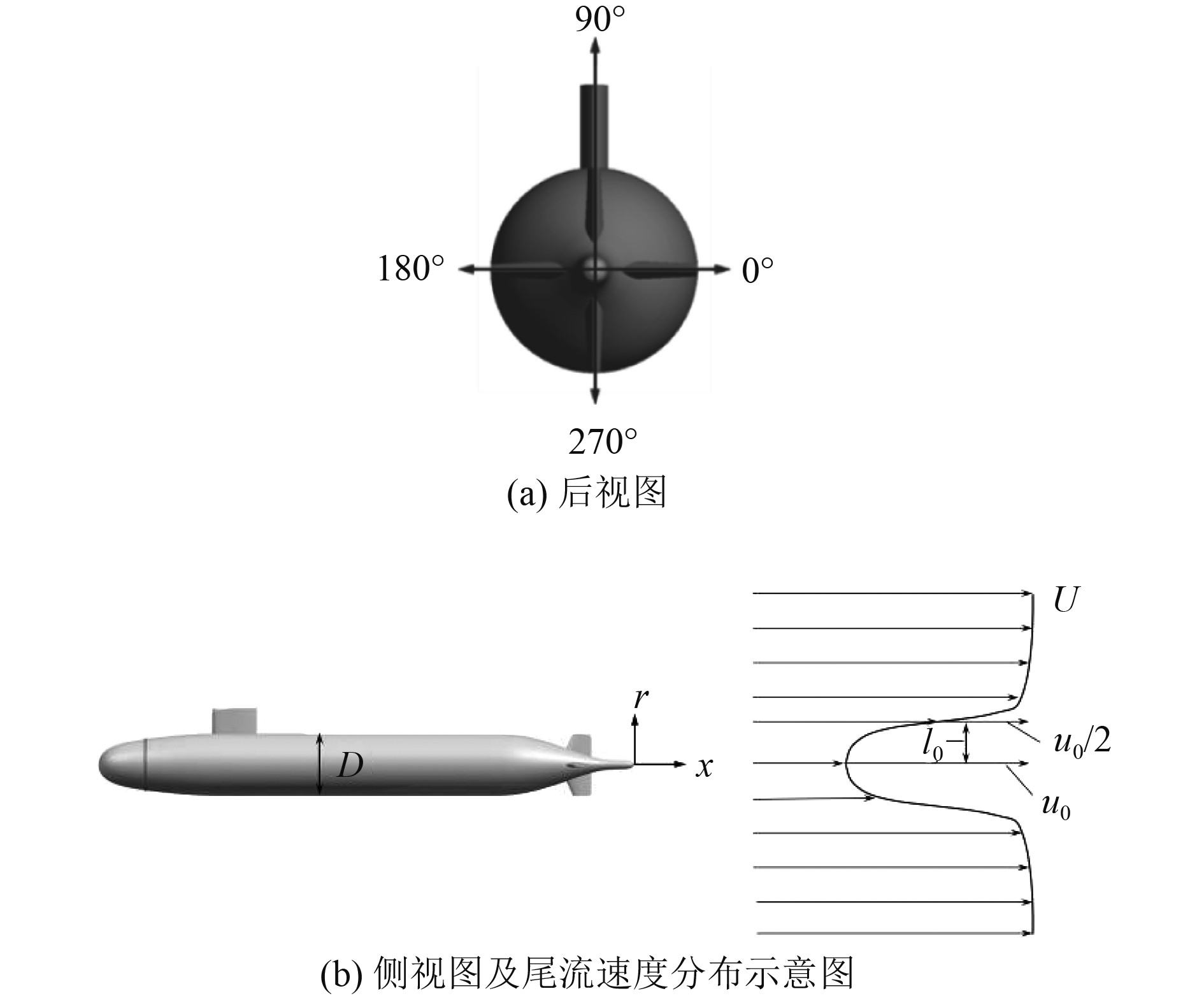
3 数值计算的分析与讨论 3.1 尾流速度场的特征为了分析指挥台、尾舵和艇体尾流之间的相互干涉作用,本文选取了3个不同周向角的二维特征截面进行分析,如图7所示。其中,45°截面仅表征艇体尾流的特征而不受到任何附体尾流的影响,0°对应的是水平截面,其流动会受到艇体和水平尾舵下游尾流的共同影响;90°对应的是垂直截面,其流动会受到艇体、指挥台和垂直尾舵下游尾流的共同影响。
|
图 7 水下航行体尾流速度分布示意图 Fig. 7 Schematic diagram of wake velocity distribution of underwater vehicle |
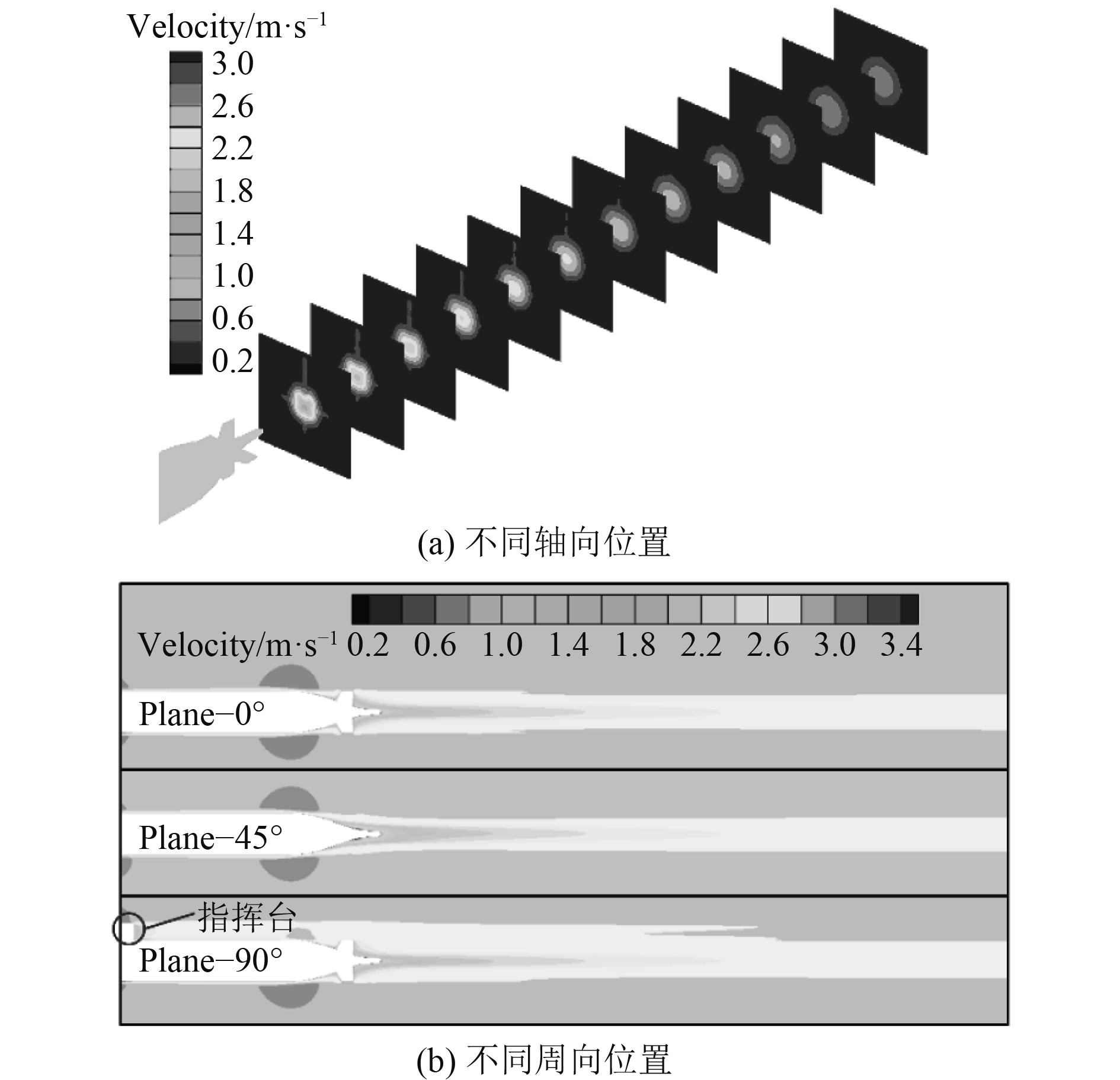
图8分别为航行体下游不同轴向位置和周向位置的速度场分布。结果表明,在航行体尾流的近场区域,速度沿周向存在明显的周向不均匀性,表明指挥台、尾舵尾流对艇体尾流在近场区域存在较为明显的干涉效应;随着尾流向下游发展,尾流速度逐渐沿周向呈均布特征,表明指挥台和尾舵尾流对艇体尾流的干涉作用逐渐弱化,航行体尾流逐渐向自相似状态演化。
|
图 8 水下航行体下游速度场分布 Fig. 8 Velocity field distribution downstream of underwater vehicle |
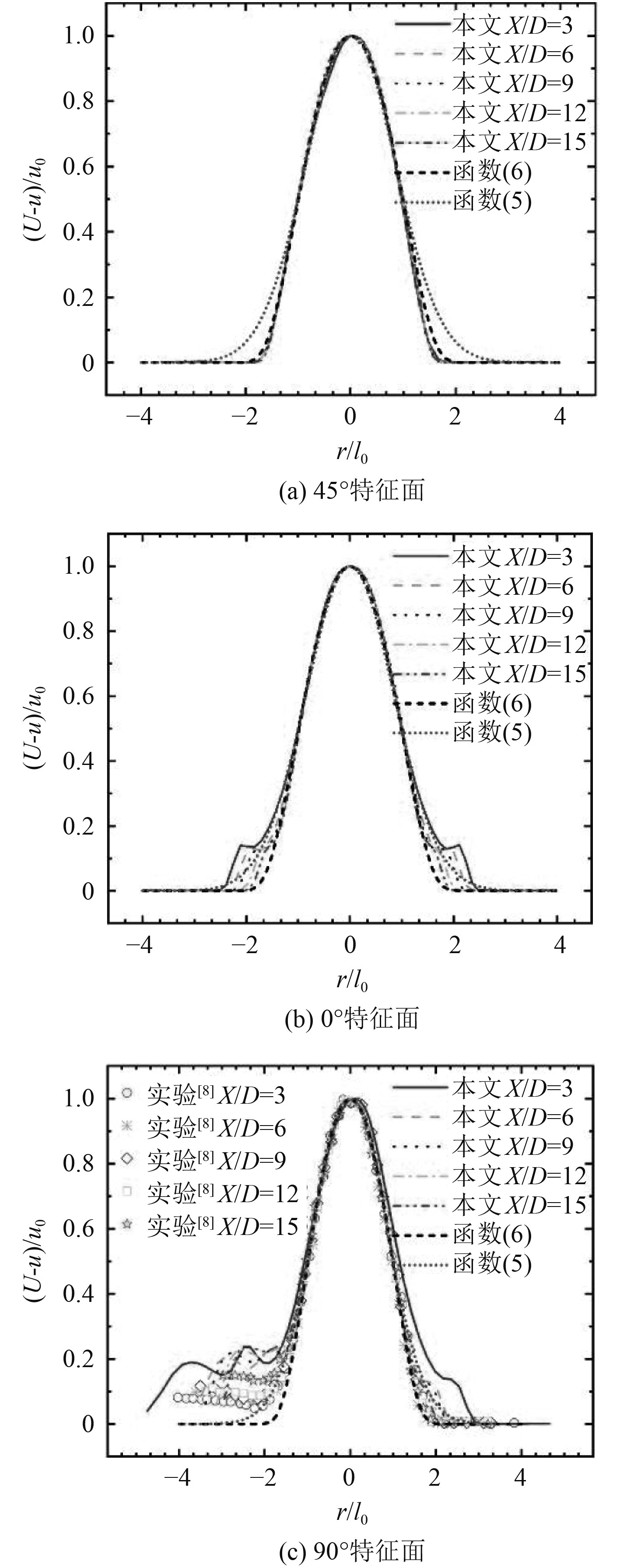
图9给出了3个周向特征截面上尾流速度在不同轴向位置的(X/D=3、6、9、12、15)分布特征。为了便于比较分析,对尾迹宽度和亏损速度进行了无量纲化处理,其中,r为径向距离,D为艇体最大直径,半尾宽度l0作为特征尺度;u为当地流体速度,U-u为亏损速度,最大亏损速度u0作为特征速度。图9(a)为45°特征平面内尾流亏损速度分布特征。结果表明,在X/D=3及下游区域,采用无量纲化处理后的艇体尾流亏损速度分布曲线几乎完全重合,可认为艇体尾流已基本满足自相似状态。文献[18 − 19]的理论研究给出了平面射流达到自相似状态时,亏损速度满足Gaussian分布特征:
|
图 9 水下航行体周向特征面速度分布 Fig. 9 Velocity distribution of circumferential feature plane of underwater vehicle |
| $ f(\eta ) = \exp ( - \ln 2 \times {\eta ^2}),$ | (5) |
其中,
文献[8]在实验测量的基础上拟合得到光艇体轴对称尾流亏损速度的分布特征如下:
| $ f(\eta ) = \exp \left( { - 0.61{\eta ^2} - 0.065{\eta ^4} - 0.03{\eta ^6} - 0.006{\eta ^8}} \right) 。$ | (6) |
图9(a)表明本文的数值计算与式(5)和式(6)的结果十分接近,因此,可证实二维平面尾流和三维轴对称尾流在达到自相似状态时,尾流亏损速度分布均满足Gaussian分布特征。
图9(b)为水平特征截面上尾流亏损速度分布特征,在该平面上存在艇体尾流与水平尾舵尾流的相互干涉。图9(a)和图9(b)的对比表明:水平尾舵导致尾流边缘区域存在附加的速度亏损;水平尾舵的对称性布置使得水平特征截面上的尾流亏损速度依然具备对称性。从尾流速度分布的自相似特征分析,水平尾舵导致尾流边缘区域在本文计算区域内接近但并没达到自相似状态;另一方面,水平尾舵对尾流核心区域的速度分布几乎不存在影响,该区域在X/D=3及下游区域已达到了自相似状态。
图9(c)为垂直特征截面上尾流亏损速度分布特征,在该平面上存在艇体尾流与指挥台、垂直尾舵尾流的相互干涉,主要体现在如下2个方面:一是尾流边缘区域的亏损速度更大;二是尾流不再满足对称性的特征。而且,在本文计算域范围内,垂直特征面上的尾流边缘位置速度分布远没有达到自相似状态。
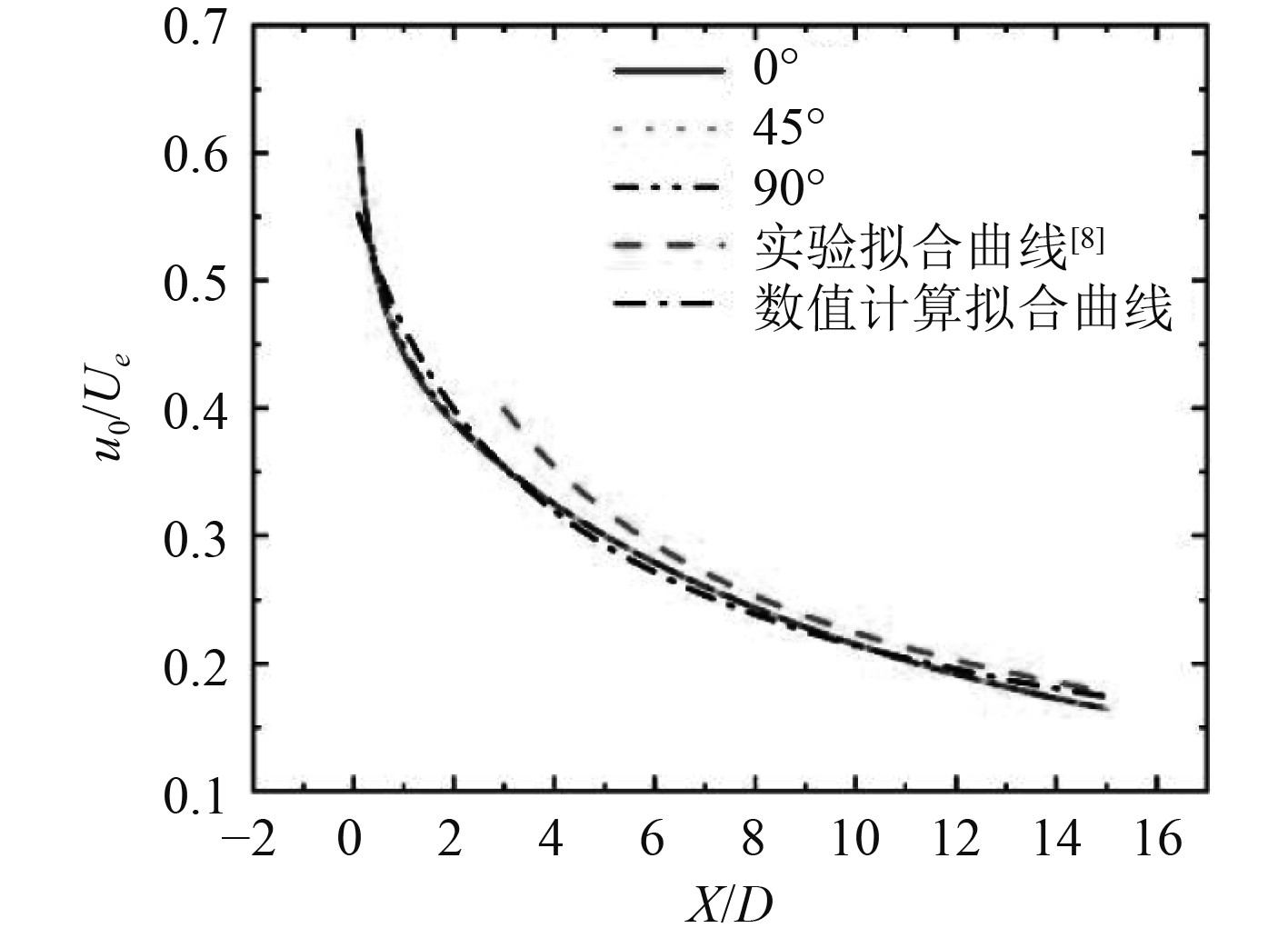
3.2 尾流的亏损动量图10进一步给出了3个周向特征截面在X/D=0到X/D=15范围内最大亏损速度的演化规律。3个周向特征截面的最大亏损速度分布曲线几乎完全重合。综合图9和图10的结果表明,指挥台和尾舵对航行体下游尾流最大亏损速度的演化几乎不存在任何影响。
|
图 10 航行体尾流沿流向最大亏损速度分布 Fig. 10 The maximum velocity deficit distribution of the wake of the underwater vehicle along the flow direction |
文献[18 − 19]的理论研究指出二维平面尾流最大亏损速度恢复满足-1/2的指数分布规律,但三维轴对称尾流最大亏损速度的恢复满足-2/3的指数分布规律。因此,按照文献[18]推荐的指数函数A*(X/D+X0/D)C对最大亏损速度沿流向的变化特征进行拟合,其中,A、X0和C为待定系数。对文献[8]中垂直特征平面内测量得到的实验数据和本文数值模拟得到的数据分别采用最小二乘法拟合得到的指数函数参数,如表2所示。
|
|
表 2 最大亏损速度拟合曲线参数 Tab.2 Fitting curve parameters of maximum velocity deficit |
表2结果表明,无论是实验测量还是数值计算的结果均证实航行体尾流最大亏损速度的恢复接近或满足-2/3的指数分布规律,而不是平面尾流的-1/2指数分布规律。由于尾流亏损速度存在上述2种不同的恢复特征,因此,对于三维回转体结构的尾流流动模拟不能直接用二维简化的模型来进行替代。进一步研究了航行体尾流亏损动量沿流向的变化特征。二维平面尾流的亏损动量定义为:
| $ M = \rho \int_{ - \infty }^\infty {{u_x}(U - {u_x}){\mathrm{d}}y}。$ | (7) |
三维空间尾流亏损动量的定义则表示为:
| $ M = \rho \int_s {{u_x}(U - {u_x}){\mathrm{d}}S}。$ | (8) |
式中:S为下游尾流区域垂直于轴向的积分面;
特别地,对于满足轴对称特征的尾流,方程(8)可等效表示为如下形式:
| $ M = 2{\text{π}} \rho \int_0^R {{u_x}(U - {u_x})r{\mathrm{d}}r}。$ | (9) |
其中,R为尾流圆形截面的半径。
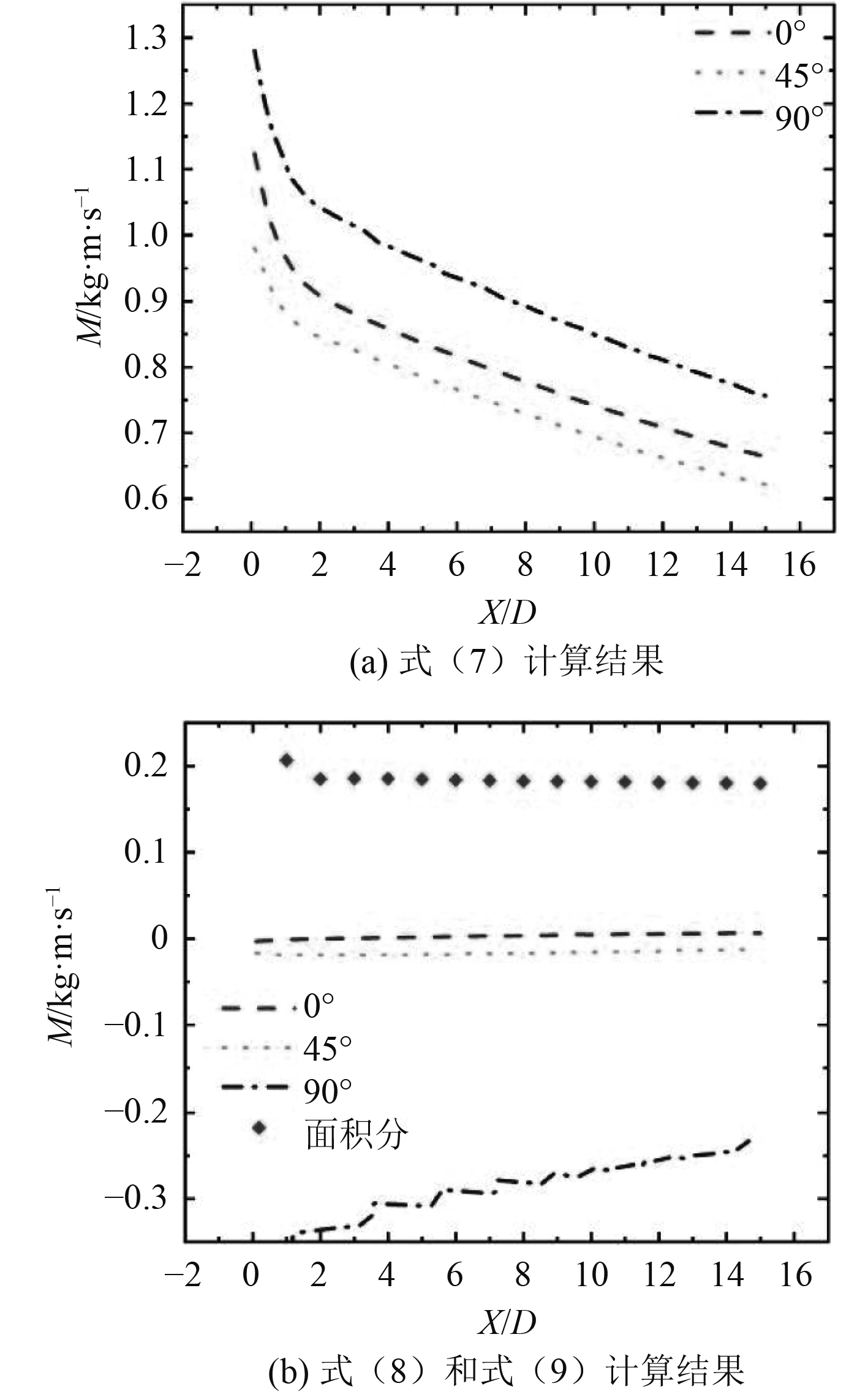
按照式(7)~式(9)的定义分别对3个周向特征截面上的尾流亏损动量进行积分计算得到的结果,如图11所示。图11(a)的结果表明,3个特征截面按照式(7)计算得到的亏损动量均不满足守恒律。因此,可进一步证实三维航行体的尾流流动模拟不能直接用二维简化的模型来进行替代。图11(b)的结果表明,0°和45°特征截面按照式(9)计算得到的亏损动量几乎满足守恒律,表明这2个特征截面上的尾流接近于轴对称尾流的特征。但图11(b)的结果也表明,90°特征截面按照式(9)计算得到的亏损动量不满足守恒律,这是由于指挥台形成的平面尾流明显破坏了轴对称尾流的演化特征。
|
图 11 水下航行体尾流亏损动量分布 Fig. 11 Distribution of momentum deficit in wake of underwater vehicle |
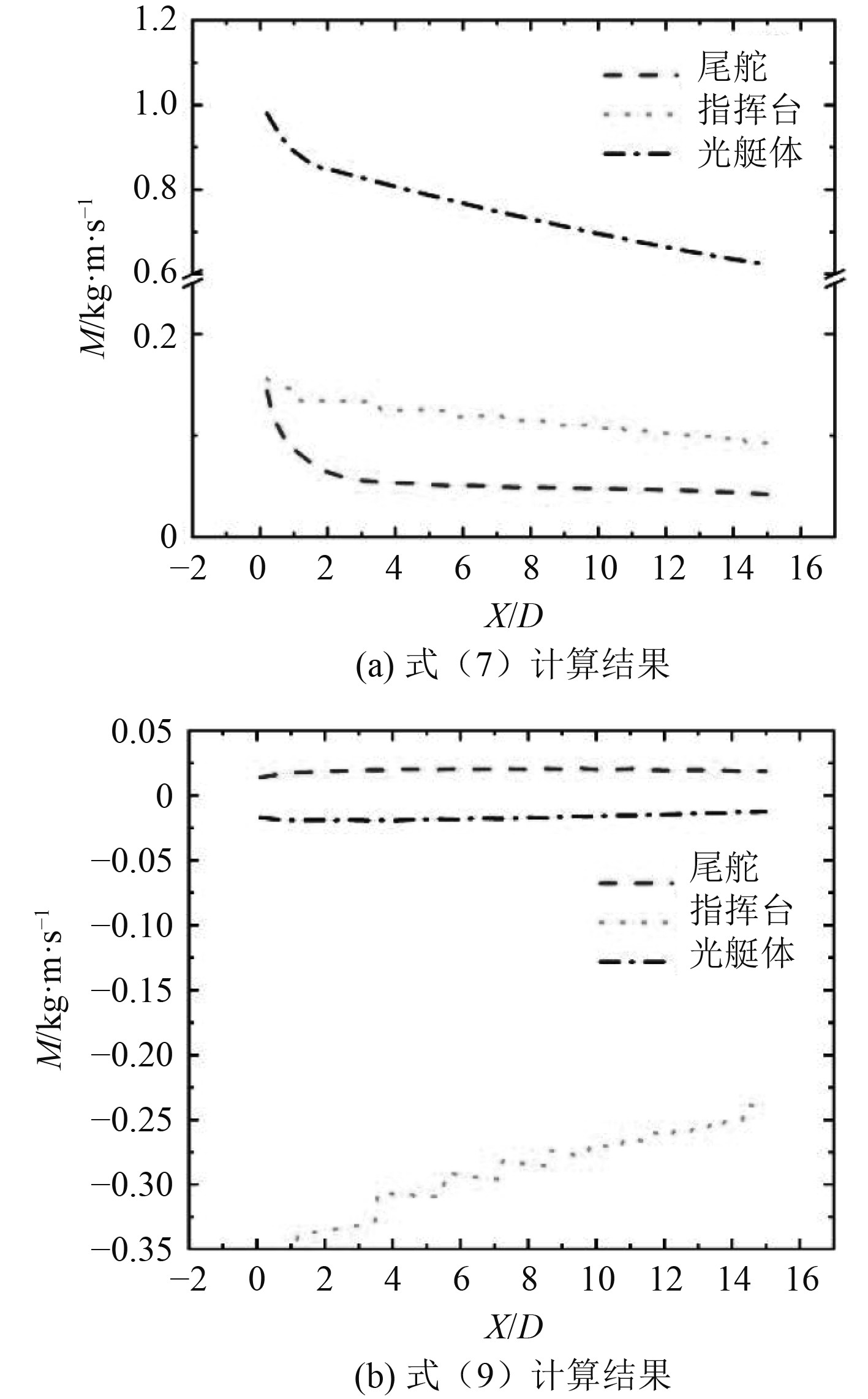
为了证实上述观点,在图11的基础上可以进一步近似得到指挥台、尾舵和光艇体尾流对应的亏损动量,结果如图12所示。其中,尾舵的亏损动量可近似认为是特征截面0°和45°上亏损动量之差,指挥台的亏损动量可近似认为是特征截面90°和0°上亏损动量之差。图12的结果表明,按照式(7)计算得到的尾舵亏损动量在X/D>3的区域内几乎保持不变,满足守恒律特征,因此,可认为尾舵尾流接近于平面尾流的特征。但尾舵尾流的亏损动量很小,因此,对整个航行体尾流演化的影响较弱。另一方面,式(7)计算得到的指挥台尾流亏损动量虽略有变化,但总体上仍然接近有满足平面射流的特征。更为重要的是,指挥台尾流亏损动量相对较大,因此,破坏了航行体尾流的轴对称结构及其演化特征。
|
图 12 水下航行体尾流亏损动量分解示意图 Fig. 12 Schematic diagram of the decomposition of the momentum deficit of the wake of underwater vehicle |
本文采用RANS方法对Suboff模型在Re =1.1
1)尾舵与艇体尾流之间的干涉略微增加了水平特征面和垂直特征面上边缘区域的亏损速度,但指挥台与艇体尾流之间的干涉的影响主要体现在垂直特征面上,破坏了艇体尾流的对称特征。另一方面,尾舵和指挥台尾流对艇体尾流的最大亏损速度则几乎不存在影响。基于上述原因,尾舵和指挥台尾流与艇体尾流的干涉延迟了航行体尾流速度分布演化的自相似状态。
2)基于二维平面尾流和三维轴对称尾流模型,分析航行体动量亏损特征的结果表明,艇体尾流速度满足Gaussian分布特征,艇体与尾舵相互作用后的尾流速度接近Gaussian分布特征,但艇体、尾舵与指挥台三者相互作用后的尾流速度则明显不满足Gaussian分布特征。
3)尾舵对整个航行体尾流的影响相对较弱,在设计中几乎可忽略不计,但需考虑指挥台对整个航行体尾流的影响。更为重要的是,艇体尾流满足的是三维轴对称尾流的动量亏损守恒律,而尾舵和指挥台则更接近于二维平面尾流的动量亏损守恒律。2种不同尾流及其对应的动量亏损守恒律,使得在设计过程中需考虑到艇体和指挥台尾流之间复杂的干涉机理。
| [1] |
柏铁朝, 卢锦国. 附体对潜艇阻力及尾部伴流场的影响[J]. 舰船科学技术, 2013, 35(3): 47-51. BAI Tiechao, LU Jinguo. Analysis of the impact of appendages on submarine resistance and wake flow field[J]. Ship science and technology, 2013, 35(3): 47-51. DOI:10.3404/j.issn.1672-7649.2013.03.010 |
| [2] |
MERZ R A, YI C H, PRZIREMBEL C E G. The subsonic near-wake of an axisymmetric semielliptical afterbody[J]. AIAA Journal, 1985, 23(10): 1512-1517. DOI:10.2514/3.9118 |
| [3] |
TSAI J F, SUNG C H, GRIFFIN M J, et al. Effects of grid resolution on axisymmetric stern flows computed with an incompressible viscous flow solver[J]. Journal of the Chinese Institute of Engineers, 1996, 19(4): 429-438. DOI:10.1080/02533839.1996.9677806 |
| [4] |
SIMPSON R L. Junction flows[J]. Annual Review of Fluid Mechanics, 2001, 33: 415-443. DOI:10.1146/annurev.fluid.33.1.415 |
| [5] |
PAN Y C, ZHANG H X, ZHOU Q D. Numerical prediction of submarine hydrodynamic coefficients using CFD Simulation[J]. Journal of Hydrodynamics, 2012, 24(6): 840-847. DOI:10.1016/S1001-6058(11)60311-9 |
| [6] |
GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA (Defense Advanced Research Projects Agency) SUBOFF models (DTRC model numbers 5470 and 5471) [R]: David Taylor Research Center Bethesda MD Ship Hydromechanics Dept, 1989.
|
| [7] |
HUANG T, LIU H. Measurements of flows over an axisymmetric body with various appendages in a wind tunnel: the DARPA SUBOFF experimental program [J]. Fiuid Dynamics, 1994.
|
| [8] |
JIMÉNEZ J M, HULTMARK M, SMITS A J. The intermediate wake of a body of revolution at high Reynolds numbers[J]. Journal of Fluid Mechanics, 2010, 659: 516-539. DOI:10.1017/S0022112010002715 |
| [9] |
ASHOK A, VAN BUREN T, SMITS A J. Asymmetries in the wake of a submarine model in pitch[J]. Journal of Fluid Mechanics, 2015, 774: 416-442. DOI:10.1017/jfm.2015.277 |
| [10] |
JIMENEZ J M, REYNOLDS R T, SMITS A J. The effects of fins on the intermediate wake of a submarine model [J]. Journal of Fluids Engineering-Transactions of the Asme, 2010, 132(3): 031102.
|
| [11] |
KUMAR P, MAHESH K. Large-eddy simulation of flow over an axisymmetric body of revolution[J]. Journal of Fluid Mechanics, 2018, 853: 537-563. DOI:10.1017/jfm.2018.585 |
| [12] |
杨琼方, 王永生, 张志宏. 全附体潜艇粘性流场的RANS模拟及场量和涡量的校验分析[J]. 计算力学学报, 2012, 29(4): 567-573. YANG Qiongfang, WANG Yongsheng, ZHANG Zhihong. RANS simulation of viscous flow over full appended submarine and field variables validation and vorticity analysis[J]. Chinese Journal of Computational Mechanics, 2012, 29(4): 567-573. |
| [13] |
邱辽原. 潜艇粘性流场的数值模拟及其阻力预报的方法研究 [D]. 武汉: 华中科技大学, 2006.
|
| [14] |
POSA A, BALARAS E. A numerical investigation about the effects of Reynolds number on the flow around an appended axisymmetric body of revolution[J]. Journal of Fluid Mechanics, 2019, 884(41): 1-38. |
| [15] |
POSA A, BALARAS E. A numerical investigation of the wake of an axisymmetric body with appendages[J]. Journal of Fluid Mechanics, 2016, 792: 470-498. DOI:10.1017/jfm.2016.47 |
| [16] |
POSA A, BALARAS E. Large-Eddy simulations of a notional submarine in towed and self-propelled configurations[J]. Computers & Fluids, 2018, 165: 116-126. |
| [17] |
QU Y, WU Q, ZHAO X, et al. Numerical investigation of flow structures around the DARPA SUBOFF model[J]. Ocean Engineering, 2021, 239: 1-13. |
| [18] |
TOWNSEND A A. The structure of turbulent shear flow[M]. THE UNIV. PR, 1956.
|
| [19] |
POPE S B. Turbulent flows [M]. Cambridge: Cambridge University Press, 2000.
|
| [20] |
LIU H-L, HUANG T T. Summary of DARPA SUBOFF experimental program data [R]. Naval surface warfare center carderock div bethesda md hydromechanics, 1998.
|
| [21] |
JIMENEZ J M. High Reynolds number flows about bodies of revolution with application to submarines and torpedoes [D]. Princeton: Princeton University, 2007.
|
| [22] |
WILCOX D C. Turbulence modeling for CFD [M]. DCW industries La Canada, CA, 1998.
|
| [23] |
TAHARA Y, WILSON R V, CARRICA P M, et al. RANS simulation of a container ship using a single-phase level-set method with overset grids and the prognosis for extension to a self-propulsion simulator[J]. Journal of Marine Science and Technology, 2006, 11(4): 209-228. DOI:10.1007/s00773-006-0231-8 |
| [24] |
SEZEN S, DOGRUL A, DELEN C, et al. Investigation of self-propulsion of DARPA Suboff by RANS method[J]. Ocean Engineering, 2018, 150: 258-271. DOI:10.1016/j.oceaneng.2017.12.051 |
| [25] |
TUMMERS M J, HANJALIĆ K, PASSCHIER D M, et al. Computations of a turbulent wake in a strong adverse pressure gradient[J]. International Journal of Heat and Fluid Flow, 2007, 28(3): 418-428. DOI:10.1016/j.ijheatfluidflow.2006.07.002 |
 2024, Vol. 46
2024, Vol. 46


